Applications of a Novel Clustering Approach Using Non-Negative Matrix Factorization to Environmental Research in Public Health
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sets
- (i)
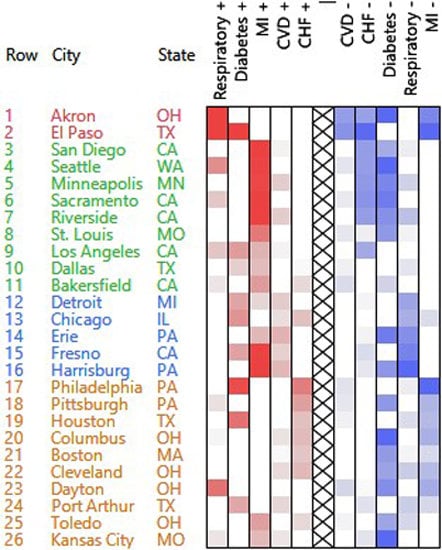
- The number of emergency hospital admissions for cardiovascular disease (CVD), myocardial infarction (MI), congestive heart failure (CHF), respiratory disease, and diabetes were collected in 26 US communities, for the years 2000–2003 [3].
- (ii)
- The Compressed Mortality File (CMF)—a county-level national mortality and population database spanning the years 1968–2010. The table contains death counts for 13 age categories.
2.2. Methods
2.2.1. Non-Negative Factorization of a General Matrix
- (i)
- Split V into the positive and negative parts : V = V+ − V− where V+ contains the positive entries, other entries being replaced by 0, and V− contains the absolute values of the negative entries, other entries being replaced by 0.
- (ii)
- When the rows are the observations and the columns are the variables, use the horizontally concatenated matrix VPN in order to give equal weight to low and high features while characterizing the clusters of observations.
- (iii)
- Apply the NMF clustering on the concatenated matrix: VPN = WHT (note that writing V = W(H+ − H−)T where H = [H+ H−] corresponds to the semi-NMF model).
- (i)
- Substract the minimum of each column: V = V0 + baseline [1].
- (ii)
- Apply the NMF clustering to V0.
2.2.2. NMF Clustering and Reordering
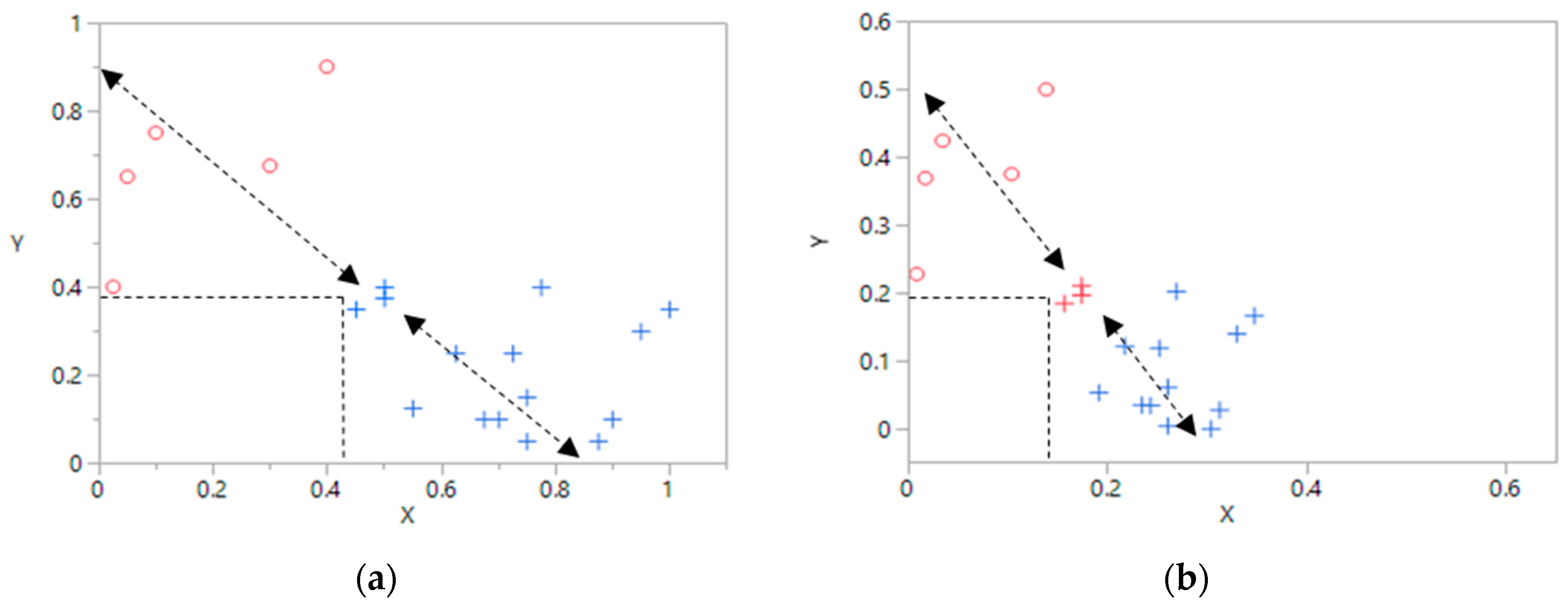
2.2.3. Stability and Specific Clustering Contribution of NMF Clusters
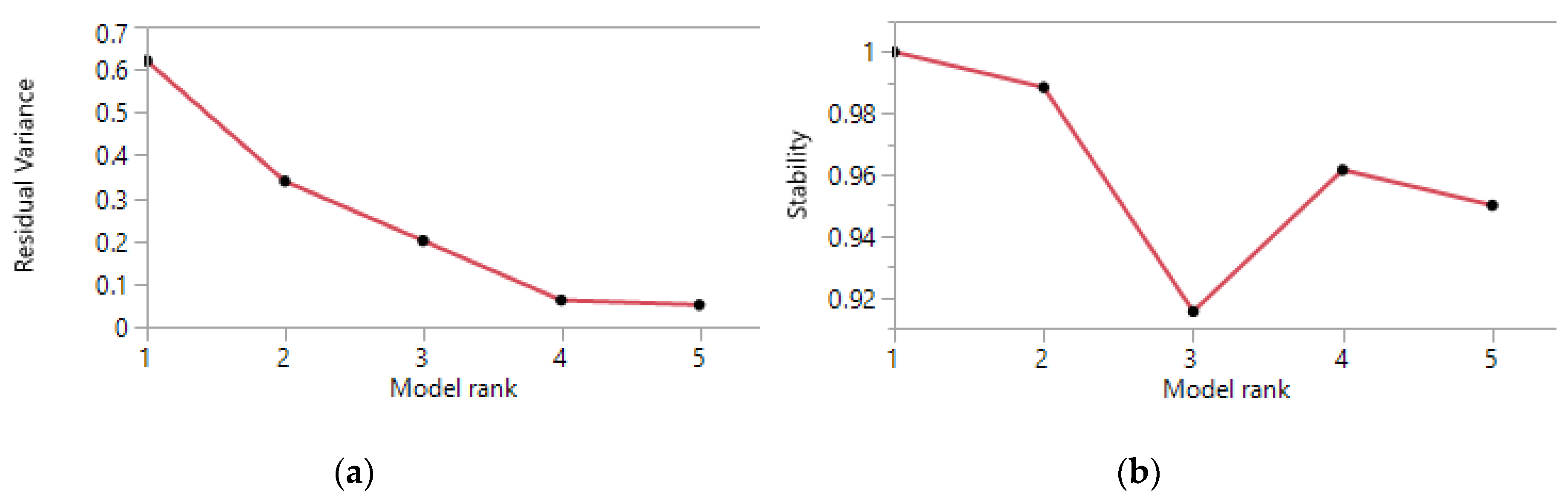
2.2.4. Rank of the NMF Factorization
2.2.5. Normalization of Contingency Tables
- (i)
- For each cell, the contingency ratio is calculated by forming the ratio of the true count over the expected count—assuming the independence of rows and columns
- (ii)
- Further normalization steps include the subtraction of the expected ratio under the assumption of independence (=1), yielding a mixed signs matrix, and a subsequent scaling of rows and columns to ensure homogeneous cell variances.
- (iii)
- The SVD is applied to the normalized matrix.
- (iv)
- A biplot based on the first two SVD components is then performed, allowing for a simultaneous clustering of the rows and columns of the table, which we will refer to as the SVD clustering. Note that PCA clustering refers to the same approach, since PCA’s eigen vectors are the column singular vectors [7].
2.3. Software
3. Results
3.1. Hospital Admissions Data
3.1.1. PosNegNMF Clustering
3.1.2. Affine NMF Clustering
3.1.3. Correspondence Analysis
3.1.4. Additional Remarks
3.2. Compressed Mortality File
4. Discussion
4.1. Performance
4.2. Alternative Approaches
4.3. Limitations
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CA | Correspondence Analysis |
| NMF | Non-Negative Matrix Factorization |
| PMF | Positive Matrix Factorization |
| SVD | Singular Value Decomposition |
| CVD | cardiovascular disease |
| MI | myocardial infarction |
| CHF | congestive heart failure |
| SCC | Specific clustering contribution |
Appendix A: Estimation of the NMF Model Components W and H
Appendix B: Calculation of Leverages
- Initialize the robust estimate by the maximum of each component.
- For each vector component q:
- For each row i of W, calculate the probability p (i, q) and the row score (Equations (C2) and (C1) respectively, Appendix C).
- Force the row score to 0 if p (i, q) < 1/k.
- Update Robust Max(q) by the weighted mean of W(i, q), where the mean is taken over all samples satisfying , and the weights are the row scores. The idea is that rows with higher row scores should weigh more on the max estimation.
- Replace all W(i, q) > Robust Max(q) by Robust Max(q).
- Repeat 2. until convergence.
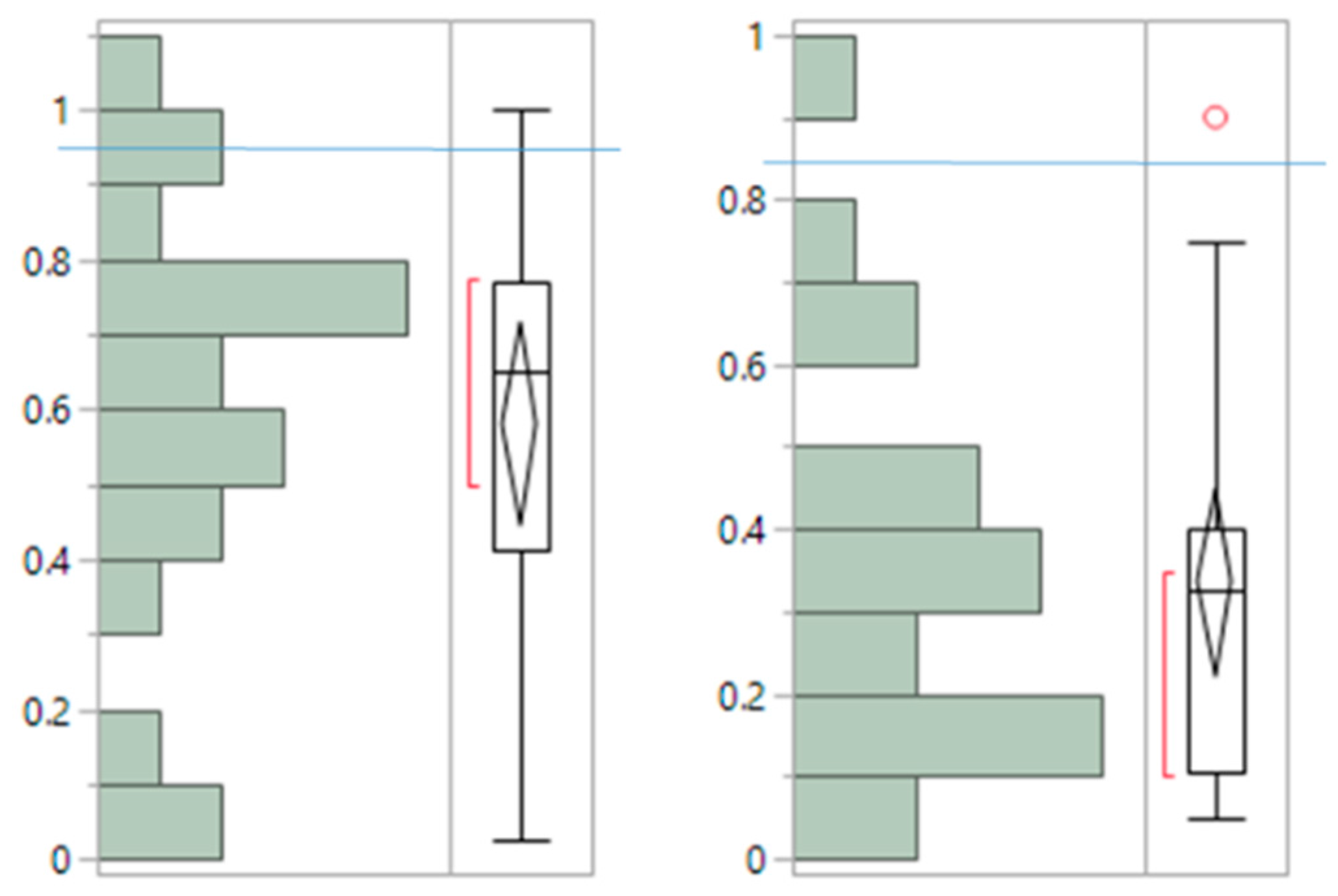
Appendix C: Stability and Specific Clustering Contribution of NMF Clusters
References
- Fogel, P.; Young, S.S.; Hawkins, D.M.; Ledirac, N. Inferential, robust non-negative matrix factorization analysis of microarray data. Bioinformatics 2007, 23, 44–49. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.H.Q.; Tao, L.; Jordan, M.I. Convex and Semi-Nonnegative Matrix Factorizations. IEEE Trans. Pattern Anal. Mach. Intelli. Arch. 2010, 32, 44–55. [Google Scholar] [CrossRef] [PubMed]
- Zanobetti, A.; Franklin, M.; Koutrakis, P.; Schwartz, J. Fine particulate air pollution and its components in association with cause-specific emergency admissions. Environ. Health 2009, 8. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.D.; Seung, H.S. Learning the Parts of Objects by Non-Negative Matrix Factorization. Nature 1999, 401, 788–791. [Google Scholar] [PubMed]
- Xu, W.; Liu, X.; Gong, Y. Document Clustering Based On Non-negative Matrix Factorization. In Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 28 July–1 August 2003.
- Kim, H.; Park, H. Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis. Bioinformatics 2007, 23, 1495–1502. [Google Scholar] [CrossRef] [PubMed]
- Fogel, P.; Hawkins, D.M.; Beecher, C.; Luta, G.; Young, S.S. A Tale of Two Matrix Factorizations. Am. Stat. 2013, 67, 207–218. [Google Scholar] [CrossRef]
- Greenacre, M.J. Tying Up the Loose Ends in Simple Correspondence Analysis. 2001. Available online: http://dx.doi.org/10.2139/ssrn.1001889 (accessed on 20 July 2007).
- SAS Institute Inc. SAS® Technical Report A-108, Cubic Clustering Criterion; SAS Institute Inc.: Cary, NC, USA, 1983; p. 56. [Google Scholar]
- Zhang, S.; Wang, W.; Ford, J.; Makedon, F. Learning from Incomplete Ratings Using Non-negative Matrix Factorization. SIAM Conf. Data Min. 2006, 6, 548–552. [Google Scholar]
- Liu, L.; Hawkins, D.M.; Ghosh, S.; Young, S.S. Robust singular value decomposition analysis of microarray data. PNAS 2003, 100, 13167–13172. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, D.M. Fitting Multiple Change-Points to Data. Comput. Stat. Data Anal. 2001, 37, 323–341. [Google Scholar] [CrossRef]
- Hawkins, D.M. Topics in Applied Multivariate Analysis; Cambridge University Press: New York, NY, USA, 1982. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. Adv. Neural Inform. Proc. Syst. 2002, 2, 849–856. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Atkins, J.E.; Boman, E.G.; Hendrickson, B. A spectral algorithm for seriation and the consecutive ones problem. SIAM J. Comput. 1998, 28, 297–310. [Google Scholar] [CrossRef]
- Liiv, I. Seriation and matrix reordering methods: An historical overview. Stat. Anal. Data Min. 2010, 3, 70–91. [Google Scholar] [CrossRef]
- Shmueli, G. To Explain or to Predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Paatero, P. Least squares formulation of robust non-negative factor analysis. Chemom. Intell. Lab. Sys. 1997, 37, 23–35. [Google Scholar] [CrossRef]
- Lin, C.J. Projected Gradient Methods for NonNegative Matrix Factorization. Tech. Rep. Inform. Support Serv. 2007, 19, 2756–2779. [Google Scholar] [CrossRef] [PubMed]
- Laurberg, H. On Affine Non-Negative Matrix Factorization. Acoust. Speech Signal Proc. 2007, 2, 653–656. [Google Scholar]
- Devarajan, K. Nonnegative Matrix Factorization: An Analytical and Interpretive Tool in Computational Biology. PLoS Comput. Biol. 2008, 4, e1000029. [Google Scholar] [CrossRef] [PubMed]
- Boutsidis, C.; Gallopoulos, E. SVD Based Initialization: A HeadStart for Nonnegative Matrix Factorization. J. Pattern Recogn. 2008, 41, 1350–1362. [Google Scholar] [CrossRef]


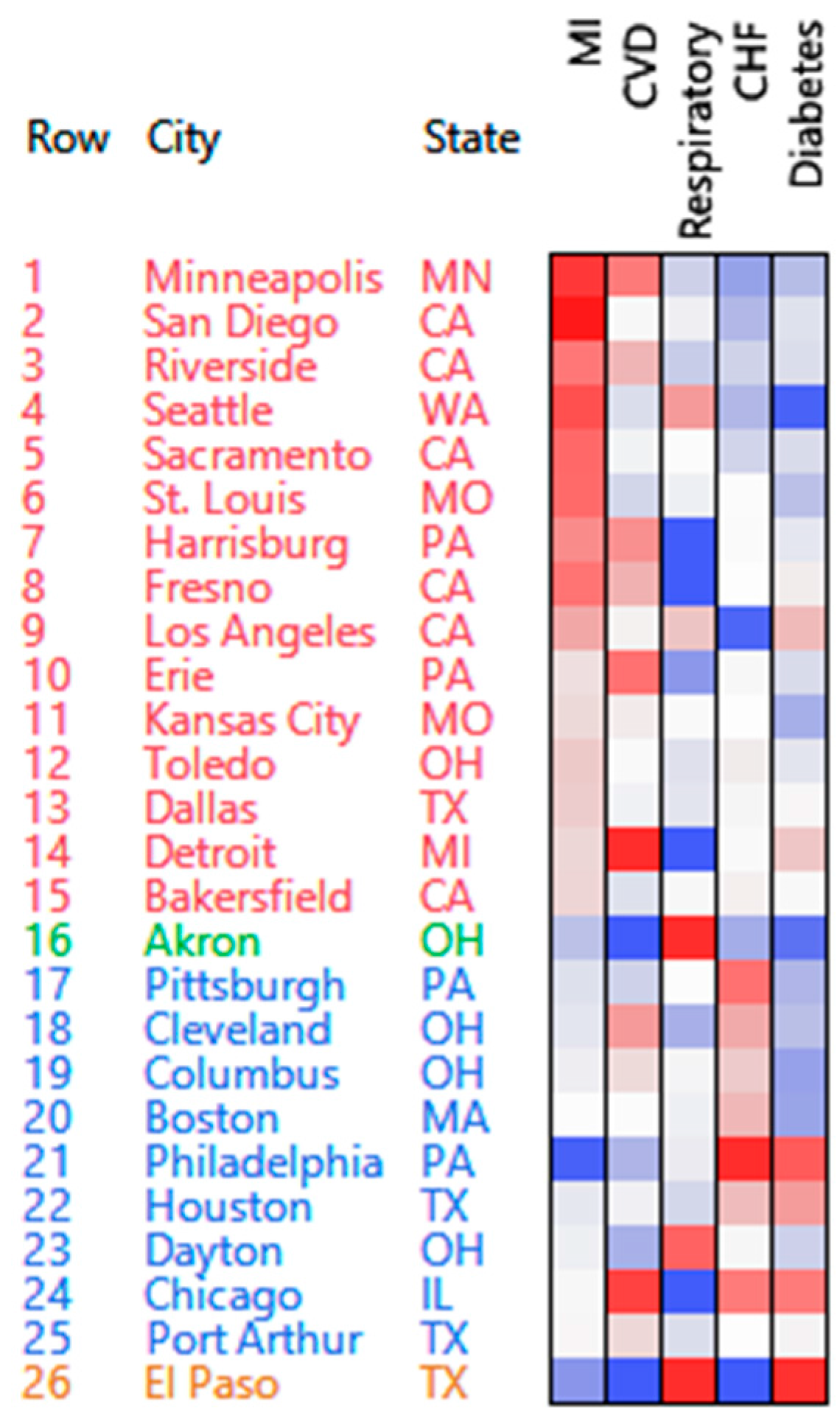
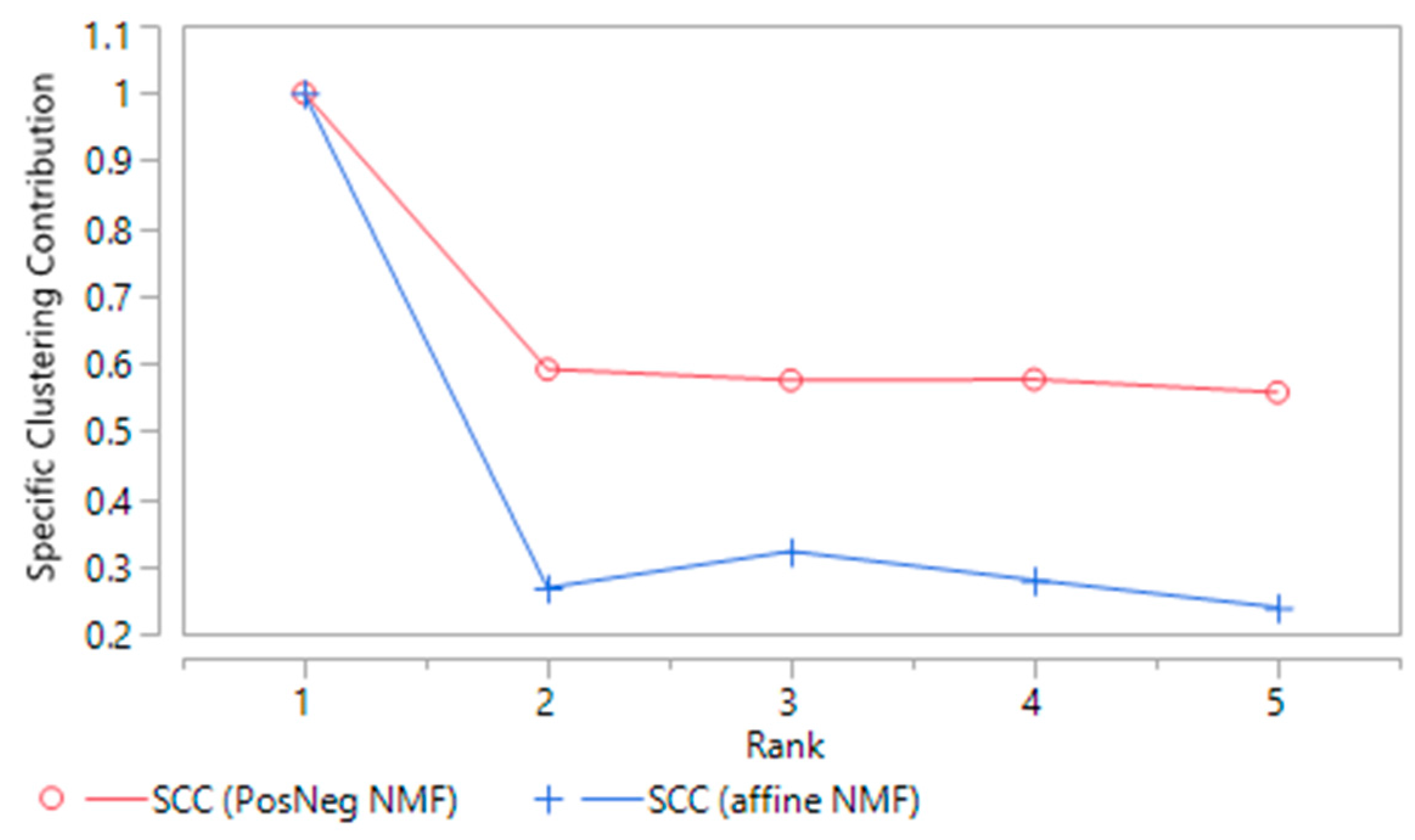
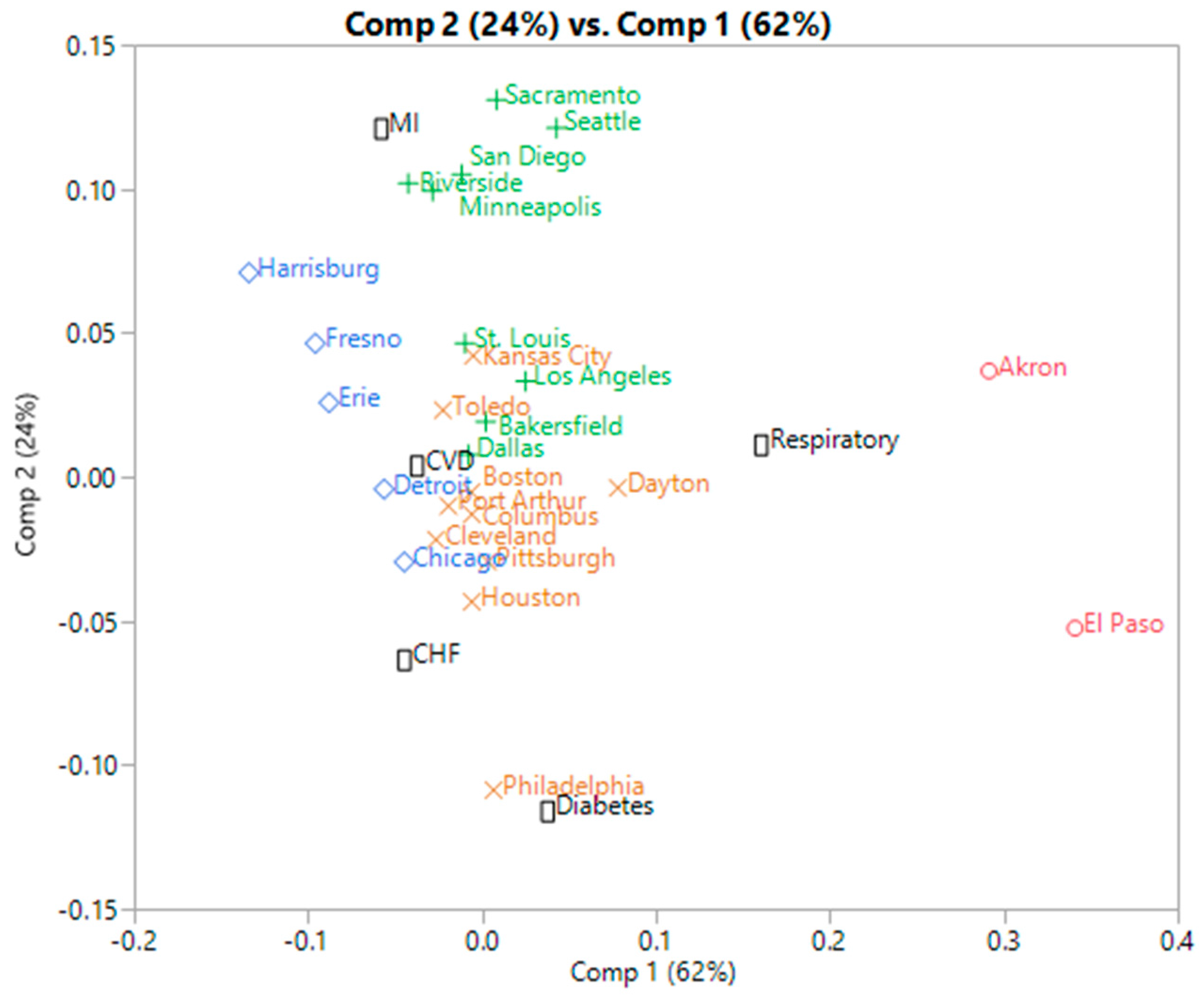

| Cluster | High Counts | Low Counts |
|---|---|---|
| 1 | Respiratory | CVD, CHF, MI |
| 2 | MI | CHF, diabetes |
| 3 | MI, CVD | Respiratory |
| 4 | CHF | Diabetes, MI |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fogel, P.; Gaston-Mathé, Y.; Hawkins, D.; Fogel, F.; Luta, G.; Young, S.S. Applications of a Novel Clustering Approach Using Non-Negative Matrix Factorization to Environmental Research in Public Health. Int. J. Environ. Res. Public Health 2016, 13, 509. https://doi.org/10.3390/ijerph13050509
Fogel P, Gaston-Mathé Y, Hawkins D, Fogel F, Luta G, Young SS. Applications of a Novel Clustering Approach Using Non-Negative Matrix Factorization to Environmental Research in Public Health. International Journal of Environmental Research and Public Health. 2016; 13(5):509. https://doi.org/10.3390/ijerph13050509
Chicago/Turabian StyleFogel, Paul, Yann Gaston-Mathé, Douglas Hawkins, Fajwel Fogel, George Luta, and S. Stanley Young. 2016. "Applications of a Novel Clustering Approach Using Non-Negative Matrix Factorization to Environmental Research in Public Health" International Journal of Environmental Research and Public Health 13, no. 5: 509. https://doi.org/10.3390/ijerph13050509
APA StyleFogel, P., Gaston-Mathé, Y., Hawkins, D., Fogel, F., Luta, G., & Young, S. S. (2016). Applications of a Novel Clustering Approach Using Non-Negative Matrix Factorization to Environmental Research in Public Health. International Journal of Environmental Research and Public Health, 13(5), 509. https://doi.org/10.3390/ijerph13050509