Cost-Sharing of Ecological Construction Based on Trapezoidal Intuitionistic Fuzzy Cooperative Games
Abstract
:1. Introduction
2. Definition and Arithmetical Operations for Trapezoidal Intuitionistic Fuzzy Numbers
2.1. Definition of Trapezoidal Intuitionistic Fuzzy Numbers
2.2. Arithmetical Operationsfor Positive Trapezoidal Intuitionistic Fuzzy Numbers
3. Quadratic Programming Model for Solving Cooperative Games with Trapezoidal Intuitionistic Fuzzy Numbers
3.1. Cooperative Games with Coalition Values Expressed by Trapezoidal Intuitionistic Fuzzy Numbers
3.2. The Solution Concept of Trapezoidal Intuitionistic Fuzzy Cooperative Games
3.3. A Quadratic Programming Model for Solving the Numerical Value Parts Based on the Least Square Method
3.4. An Improved Model Considering Efficiency and Its Optimal Solution
3.5. A Quadratic Programming Model for Solving the Membership Degrees and Nonmembership Degrees of the Optimal Solution
4. An Example Demonstrating the Cost-Sharing of Ecological Construction in Fujian Province, China
5. Discussion
- (1)
- Modeling. In this paper, we constructed a quadratic programming model to solve the cooperative game with coalition values expressed by trapezoidal intuitionistic fuzzy numbers. It is an expansion of the least square prenucleolus solution concept [31]. The quadratic programming models and methods proposed in this paper always assure that the solutions are positive if all of the coalitions’ values are positive trapezoidal intuitionistic fuzzy numbers.
- (2)
- Calculation complexity. According to the method proposed in this paper, we can easily and quickly obtain all players’ optimal trapezoidal intuitionistic fuzzy payoffs using Equations (30)–(33).
- (3)
- Efficiency. The quadratic programming model proposed in this paper takes into account efficiency, so the allocation scheme is fairly satisfactory for all players. That is to say, the cooperative surplus is distributed thoroughly among the players. In Section 4, it can easily be seen that , (i.e., 30 + 80 + 290 = 400, 46.7 + 126.7 + 476.7 = 650, 58.3 + 183.3 + 658.3 = 900, 96.7 + 246.7 + 756.7 = 1100) which implies that the cost allocation scheme satisfies the efficiency as expected. The optimal trapezoidal intuitionistic fuzzy payoff vector , which is obtained through Equations (30)–(33), is said to be efficient or a preimputation.
- (4)
- Advantages. There exists some information distortion when doing subtraction of trapezoidal intuitionistic fuzzy numbers. In this paper, we construct the optimal mathematical model based on the square of the distance in the numerical value between two trapezoidal intuitionistic fuzzy numbers, which can effectively avoid the distortion of information and enlargement of fuzziness and uncertainty brought about by subtraction of trapezoidal intuitionistic fuzzy numbers.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Estévez-Fernández, A. A game theoretical approach to sharing penalties and rewards in projects. Eur. J. Oper. Res. 2008, 216, 647–657. [Google Scholar] [CrossRef]
- Chevalier-Roignant, B.; Flath, C.M.; Huchzermeier, A.; Trigeorgis, L. Strategic investment under uncertainty: A synthesis. Eur. J. Oper. Res. 2011, 215, 639–650. [Google Scholar] [CrossRef]
- Seyedesfahani, M.M.; Biazaran, M.; Gharakhani, M. A game theoretic approach to coordinate pricing and vertical co-op advertising in manufacturer-retailer supply chains. Eur. J. Oper. Res. 2011, 211, 263–273. [Google Scholar] [CrossRef]
- Jiménez-Losada, A.; Fernández, J.R.; Ordóñez, M.; Grabisch, M. Games on fuzzy communication structures with Choquet players. Eur. J. Oper. Res. 2010, 207, 836–847. [Google Scholar] [CrossRef]
- Leng, M.; Zhu, A. Side-payment contracts in two-person nonzero-sum supply chain games: Review, discussion and applications. Eur. J. Oper. Res. 2009, 196, 600–618. [Google Scholar] [CrossRef]
- Nishizaki, I.; Sakawa, M. Equilibrium solutions in multiobjective bimatrix games with fuzzy payoffs and fuzzy goals. Fuzzy Sets Syst. 2000, 111, 99–116. [Google Scholar] [CrossRef]
- Viscolani, B. Pure-strategy Nash equilibria in an advertising game with interference. Eur. J. Oper. Res. 2012, 216, 605–612. [Google Scholar] [CrossRef]
- Collins, W.D.; Hu, C. Studying interval valued matrix games with fuzzy logic. Soft Comput. 2008, 12, 147–155. [Google Scholar] [CrossRef]
- Li, D.F. Linear programming approach to solve interval-valued matrix games. Omega 2011, 39, 655–666. [Google Scholar] [CrossRef]
- Li, D.F.; Nan, J.X.; Zhang, M.J. Interval programming models for matrix games with interval payoffs. Optim. Methods Softw. 2012, 27, 1–16. [Google Scholar] [CrossRef]
- Liu, S.T.; Kao, C. Matrix games with interval data. Comput. Ind. Eng. 2009, 56, 1697–1700. [Google Scholar] [CrossRef]
- Avşar, Z.M.; Baykal-Gürsoy, M. A note on two-person zero-sum communicating stochastic games. Oper. Res. Lett. 2006, 34, 412–420. [Google Scholar] [CrossRef]
- Lakshmana, G.N.V.; Jeevaraj, S.; Dhanasekaran, P. A linear ordering on the class of trapezoidal intuitionistic fuzzy numbers. Expert Syst. Appl. 2016, 60, 269–279. [Google Scholar]
- Nehi, H.M. A New Ranking Method for Intuitionistic Fuzzy Numbers. Int. J. Fuzzy Syst. 2010, 12, 80–86. [Google Scholar]
- Garg, H. A novel approach for analyzing the reliability of series-parallel system using credibility theory and different types of intuitionistic fuzzy numbers. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1–15. [Google Scholar] [CrossRef]
- Wan, S.P.; Wang, F.; Lin, L.L.; Dong, J.Y. Some new generalized aggregation operators for triangular intuitionistic fuzzy numbers and application to multi-attribute group decision making. Comput. Ind. Eng. 2016, 93, 286–301. [Google Scholar] [CrossRef]
- Li, D.F. A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems. Comput. Math. Appl. 2010, 60, 1557–1570. [Google Scholar] [CrossRef]
- Greer, K.; Cameron, L. The use and abuse of ecological constructs. Geoforum 2015, 65, 451–453. [Google Scholar] [CrossRef]
- Mangone, G. Constructing hybrid infrastructure: Exploring the potential ecological, social, and economic benefits of integrating municipal infrastructure into constructed environments. Cities 2016, 55, 165–179. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X.; Dong, R.; Shao, G. Landsenses ecology and ecological planning toward sustainable development. Int. J. Sustain. Dev. World Ecol. 2015, 23, 293–297. [Google Scholar] [CrossRef]
- Zheng, R.; Zhang, T.; Liu, Z.; Wang, H. An EIoT system designed for ecological and environmental management of the Xianghe Segment of China’s Grand Canal. Int. J. Sustain. Dev. World Ecol. 2015, 23, 372–380. [Google Scholar] [CrossRef]
- Liou, Y.A. Zoning eco-environmental vulnerability for environmental management and protection. Ecol. Ind. 2016, 69, 100–117. [Google Scholar]
- Yu, B.; Xu, L.; Yang, Z. Ecological compensation for inundated habitats in hydropower developments based on carbon stock balance. J. Clean. Prod. 2015, 114, 334–342. [Google Scholar] [CrossRef]
- Guan, X.; Liu, W.; Chen, M. Study on the ecological compensation standard for river basin water environment based on total pollutants control. Ecol. Ind. 2016, 69, 446–452. [Google Scholar] [CrossRef]
- Reid, J.; Bruner, A.; Chow, J.; Malky, A.; Rubio, J.C.; Vallejos, C. Ecological Compensation to Address Environmental Externalities: Lessons from South American Case Studies. J. Sustain. Forest. 2015, 34, 605–622. [Google Scholar] [CrossRef]
- Eric, M.; Anne-Sophie, D.; Grémillet, D.; Gauthier-Clerc, M.; Béchet, A. Combining correlative and mechanistic habitat suitability models to improve ecological compensation. Biol. Rev. Camb. Philos. Soc. 2014, 90, 314–329. [Google Scholar]
- Rao, H.; Lin, C.; Kong, H.; Jin, D.; Peng, B. Ecological damage compensation for coastal sea area uses. Ecol. Ind. 2014, 38, 149–158. [Google Scholar] [CrossRef]
- Villarroya, A.; Persson, J.; Puig, J. Ecological compensation: From general guidance and expertise to specific proposals for road developments. Environ. Impact Assess. Rev. 2014, 45, 54–62. [Google Scholar] [CrossRef]
- Li, D.F. Decision and Game Theory in Management with Intuitionistic Fuzzy Sets; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Wan, S.P.; Dong, J.Y. Power geometric operators of trapezoidal intuitionistic fuzzy numbers and application to multi-attribute group decision making. Appl. Soft Comput. 2015, 29, 153–168. [Google Scholar] [CrossRef]
- Ruiz, L.M.; Valenciano, F.; Zarzuelo, J.M. The least square prenucleolus and the least square nucleolus. Two values for TU games based on the excess vector. Int. J. Games Theory 1996, 25, 113–134. [Google Scholar] [CrossRef]
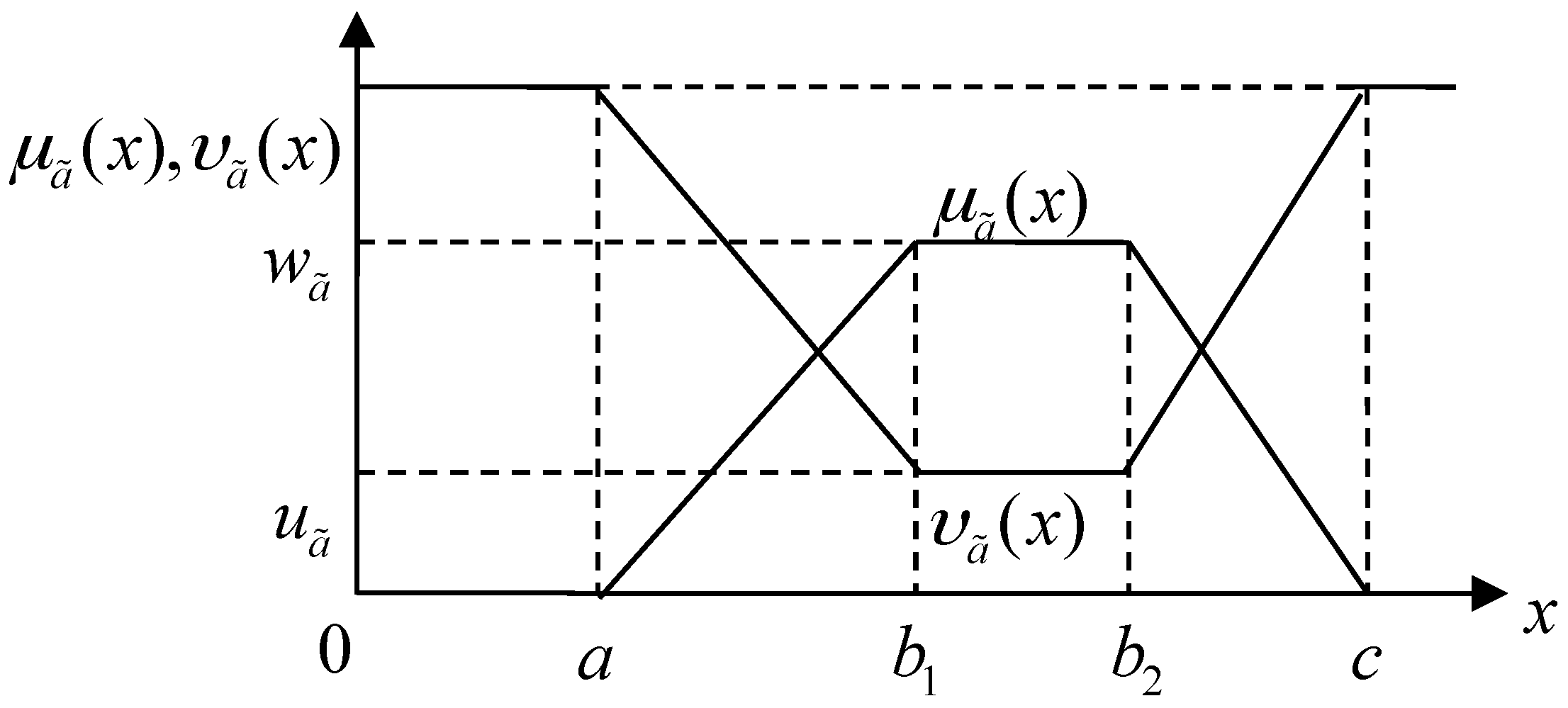
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhao, W. Cost-Sharing of Ecological Construction Based on Trapezoidal Intuitionistic Fuzzy Cooperative Games. Int. J. Environ. Res. Public Health 2016, 13, 1102. https://doi.org/10.3390/ijerph13111102
Liu J, Zhao W. Cost-Sharing of Ecological Construction Based on Trapezoidal Intuitionistic Fuzzy Cooperative Games. International Journal of Environmental Research and Public Health. 2016; 13(11):1102. https://doi.org/10.3390/ijerph13111102
Chicago/Turabian StyleLiu, Jiacai, and Wenjian Zhao. 2016. "Cost-Sharing of Ecological Construction Based on Trapezoidal Intuitionistic Fuzzy Cooperative Games" International Journal of Environmental Research and Public Health 13, no. 11: 1102. https://doi.org/10.3390/ijerph13111102
APA StyleLiu, J., & Zhao, W. (2016). Cost-Sharing of Ecological Construction Based on Trapezoidal Intuitionistic Fuzzy Cooperative Games. International Journal of Environmental Research and Public Health, 13(11), 1102. https://doi.org/10.3390/ijerph13111102




