4.1. Statistical Analysis
The statistical characteristics and Pearson correlation matrix of the twelve water quality parameters are listed in
Table 1 and
Table 2, respectively. Descriptive statistics includes minimum values, maximum values, median values, mean values, standard deviation (SD), and coefficient of variation (CV) of the water quality data in
Table 1.
Table 2 reveals the quantitative representation of these relationships for the parameters. As it can be seen in
Table 1, Susp has the biggest CV, followed by NH
3-N, while Satur O
2 has the smallest, followed by DO. This demonstrates that Susp and NH
3-N change a lot, while Satur O
2 and DO are temporally stable. Except for Susp, NH
3-N, Satur O
2, and DO, the other parameters possess medium CVs, which indicates their concentrations do not change as much as Susp and NH
3-N, but more than Satur O
2 and DO.
Table 1.
Statistical description of water quality parameters across the sample points.
Table 1.
Statistical description of water quality parameters across the sample points.
| Water Quality Parameter | Unit | Minimum | Maximum | Median | Mean | SD | CV |
|---|
| BOD5 | mg·L−1 | 0.01 | 17 | 0.8 | 1.6716 | 2.3262 | 1.3916 |
| NH3-N | mg·L−1 | 0.006 | 13 | 0.056 | 0.6021 | 1.7633 | 2.9285 |
| COD | mg·L−1 | 0.3 | 46 | 4 | 5.2942 | 4.4706 | 0.8444 |
| EC | μS/cm | 29 | 2018 | 157 | 206.5278 | 184.1479 | 0.8916 |
| DO | mg·L−1 | 4.3 | 10.6 | 8.1 | 8.1083 | 1.1248 | 0.1387 |
| TP | mg·L−1 | 0.005 | 1.4 | 0.09 | 0.1674 | 0.2348 | 1.4030 |
| NO3-N | mg·L−1 | 0.026 | 4.6 | 0.81 | 1.0202 | 0.7751 | 0.7598 |
| NO2-N | mg·L−1 | 0.00007 | 1.5 | 0.007 | 0.0674 | 0.1735 | 2.5731 |
| Satur O2 | % | 48 | 130 | 98 | 94.9672 | 11.5266 | 0.1214 |
| Susp | mg·L−1 | 0.1 | 650 | 3.4 | 9.9902 | 37.1404 | 3.7177 |
| Diss sol | mg·L−1 | 27.1 | 1296.3 | 99 | 112.0402 | 95.6936 | 0.8541 |
| T | °C | 11.2 | 33.4 | 23.5 | 23.4907 | 4.3935 | 0.1870 |
T is one of the most important water quality parameter in water quality, and limits the saturation values of gases and solids that are dissolved in it [
39]. T varies between 11.2 °C and 33.4 °C with a median value of 23.5 °C. T shows negative correlation with DO (
r = −0.466) and positive correlation with BOD
5, NH
3-N, COD, EC, TP, NO
3-N, NO
2-N, Satur O
2, Susp, and Diss sol, which are presented in
Table 2.
Table 2.
Pearson correlation matrix for the water quality parameters across the sample points.
Table 2.
Pearson correlation matrix for the water quality parameters across the sample points.
| Water Quality Parameter | BOD5 | NH3-N | COD | EC | DO | TP | NO3-N | NO2-N | Satur O2 | Susp | Diss Sol | T |
|---|
| BOD5 | 1.000 | | | | | | | | | | | |
| NH3-N | 0.646 ** | 1.000 | | | | | | | | | | |
| COD | 0.667 ** | 0.741 ** | 1.000 | | | | | | | | | |
| EC | 0.232 ** | 0.214 ** | 0.236 ** | 1.000 | | | | | | | | |
| DO | −0.340 ** | −0.182 ** | −0.350 ** | −0.315 ** | 1.000 | | | | | | | |
| TP | 0.694 ** | 0.872 ** | 0.795 ** | 0.355 ** | −0.274 ** | 1.000 | | | | | | |
| NO3-N | 0.312 ** | 0.130 ** | 0.263 ** | 0.416 ** | −0.355 ** | 0.398 ** | 1.000 | | | | | |
| NO2-N | 0.451 ** | 0.406 ** | 0.442 ** | 0.318 ** | −0.043 | 0.646 ** | 0.471 ** | 1.000 | | | | |
| Satur O2 | −0.352 ** | −0.159 ** | −0.300 ** | −0.242 ** | 0.784 ** | −0.234 ** | −0.372 ** | 0.086 | 1.000 | | | |
| Susp | 0.256 ** | 0.059 | 0.198 ** | 0.015 | −0.103 * | 0.132 ** | 0.063 | 0.040 | −0.077 | 1.000 | | |
| Diss sol | 0.277 ** | 0.278 ** | 0.343 ** | 0.705 ** | −0.060 | 0.426 ** | 0.365 ** | 0.516 ** | 0.047 | 0.059 | 1.000 | |
| T | 0.027 | 0.051 | 0.111 * | 0.156 ** | −0.466 ** | 0.080 | 0.015 | 0.167 ** | 0.177 ** | 0.052 | 0.151 ** | 1.000 |
The concentration of oxygen in surface water is a measure of self-cleaning capacity of the water body. 14 out of the 396 samples of DO concentration are below 6 mg·L−1, and the median value and mean value of the DO concentration are 8.1 mg·L−1 and 8.1083 mg·L−1, respectively. Similarly, the median value and mean value of Satur O2 are 98% and 94.9672%, respectively. DO and Satur O2 are negatively correlated with BOD5, NH3-N, COD, EC, TP, NO3-N, and Susp. DO exhibits a strong positive correlation with Satur O2 with a correlation coefficient of 0.784.
EC varies in the range of 29 μS/cm and 2018 μS/cm with a median value of 157 μS/cm. The maximum value of 2018 μS/cm occurred with Diss sol concentration as 1296.3 mg·L
−1 (the maximum value of Diss sol concentration). EC is positively correlated with Diss sol, with a correlation coefficient of 0.705, which is expressed in
Table 2. It means that an increase in Diss sol leads to an increase in EC. BOD
5, NH
3-N, COD, and TP have relatively good positive relationships with each other. BOD
5 is positively correlated with NH
3-N, COD and TP, with correlation coefficients of 0.646, 0.667 and 0.694, respectively. NH
3-N has positive relationships with COD and TP, with correlation coefficients of 0.741 and 0.872, respectively. TP and COD are correlated with a correlation coefficient of 0.795. It is noted the NO
2-N has relatively good positive relationship with TP (0.646), and slightly positive relationships with BOD
5 (0.451), NH
3-N (0.406), and COD (0.442).
4.2. PCA Results
The KMO test and Bartlett’s test were firstly implemented to examine the validity of PCA (
Table 3). The test shows that the KMO and Bartlett’s test are 0.626 and 4517.867, respectively. It means that PCA can be used to perform data reduction.
Table 3.
KMO and Bartlett’s test.
Table 3.
KMO and Bartlett’s test.
| KMO Measure of Sampling Adequacy | Bartlett’s Test of Sphericity |
|---|
| Approx. Chi-Square | df | Sig. |
|---|
| 0.626 | 4517.867 | 66 | 0.000 |
The objective of PCA is to reduce the multidimensional parameters to a set of PCs much smaller in number. According to the criteria of eigenvalue-one, four PCs were extracted, accounting for 75.894% of the total variance (
Table 4). The PCs, eigenvalues, percentage of total variance, and cumulative percentage of explained variance are shown in
Table 4.
Table 4.
Loading on components for water quality parameters.
Table 4.
Loading on components for water quality parameters.
| Water Quality Parameter | PC |
|---|
| PC1 | PC2 | PC3 | PC4 |
|---|
| BOD5 | 0.782 | | | |
| NH3-N | 0.755 | | | |
| COD | 0.819 | | | |
| EC | | | 0.629 | |
| DO | | 0.787 | | |
| TP | 0.901 | | | |
| NO3-N | 0.565 | | | |
| NO2-N | 0.663 | | | |
| Satur O2 | | 0.825 | | |
| Susp | | | | |
| Diss sol | 0.582 | | 0.544 | |
| T | | | | 0.886 |
| Eigenvalue | 4.582 | 1.784 | 1.557 | 1.184 |
| Percentage of total variance | 38.187 | 14.866 | 12.978 | 9.864 |
| Cumulative percentage of variance | 38.187 | 53.053 | 66.030 | 75.894 |
As it can be seen in
Table 4, the eigenvalues of four PCs are 4.582, 1.784, 1.557, and 1.184, respectively. The four PCs can explain 75.894% of the total variance. The first two PCs (PC1 and PC2) account for 38.187% and 14.866% of the variance, respectively, explaining more than a half of the total variance in the original dataset. PC3 and PC4 explain 12.978% and 9.864% of the total variance, respectively.The first PC (PC1) with the biggest eigenvalue 4.582 has strong positive loadings on TP, COD, BOD
5, NH
3-N, NO
2-N, Diss sol, and NO
3-N, which suggests that PC1 represents the contaminants in the study area. The coefficients of TP, COD, BOD
5, NH
3-N, and NO
2-N are higher than those of NO
2-N, Diss sol, and NO
3-N. It means that TP, COD, BOD
5, NH
3-N, and NO
2-N have bigger effect on PC1 than the other two parameters. PC2 has significant loadings by Satur O
2 and DO, representing the dissolved oxygen in the water body. PC3 has positive loadings on EC and Diss sol. EC and Diss sol are correlated as mentioned above. The existence of high concentration of Diss sol leads to the high loadings of EC. The last PC (PC4) indicates the temperature because it only has a strong loading by T. Difference in water temperature affects dissolved oxygen, the rate of photosynthesis and metabolic rates of aquatic life [
39]. PC2 and PC4 indicate the decay rate of the contaminants. PCA results represent the contaminants and the decay rate of the contaminants regardless of monitoring stations in the study area.
4.3. SOM Results
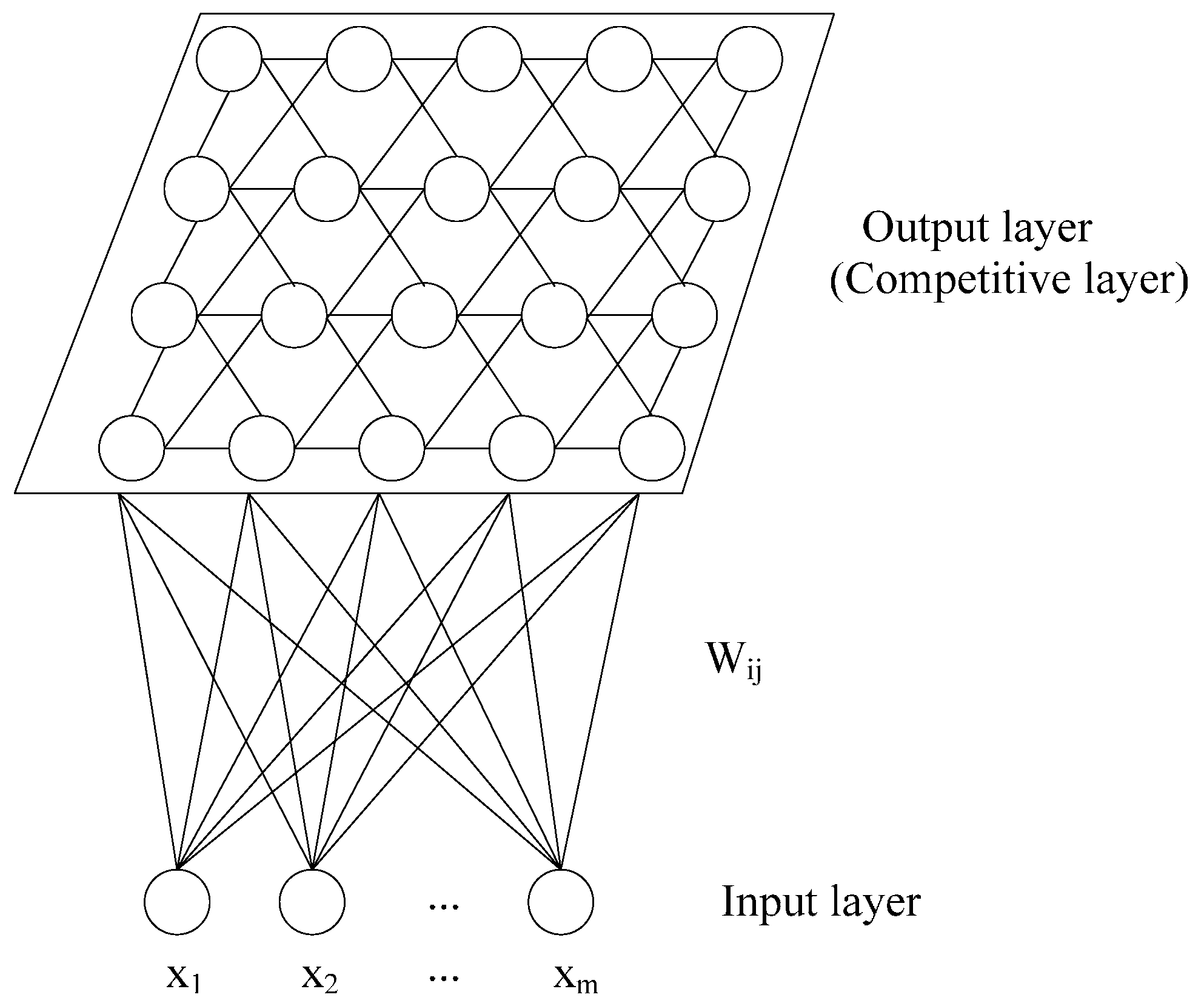
The map size is crucial for SOM technique to cluster the data set. QEs and TEs of big and small map sizes were calculated to determine the optimal number of the map units (
Table 5). It can be seen that the map size of (14 × 7) has the minimum values of QE and TE as 1.2388 and 0.0152, respectively. Therefore, SOM involved 98 output neurons displayed in 14 rows and 7 columns is chosen in this study. The total number 98 arranged in the hexagonal grid is close to 99.5 (
).
Table 5.
QEs and TEs of different map sizes.
Table 5.
QEs and TEs of different map sizes.
| Quality of Trained SOM | Map Size |
|---|
| (20 × 10) | (17 × 14) | (15 × 8) | (14 × 7) | (13 × 9) | (10 × 8) | (7 × 6) |
|---|
| QE | 7.5403 | 8.9137 | 8.8477 | 1.2388 | 8.0568 | 7.9560 | 10.0911 |
| TE | 1 | 0.5429 | 1 | 0.0152 | 0.9975 | 0.9949 | 1 |
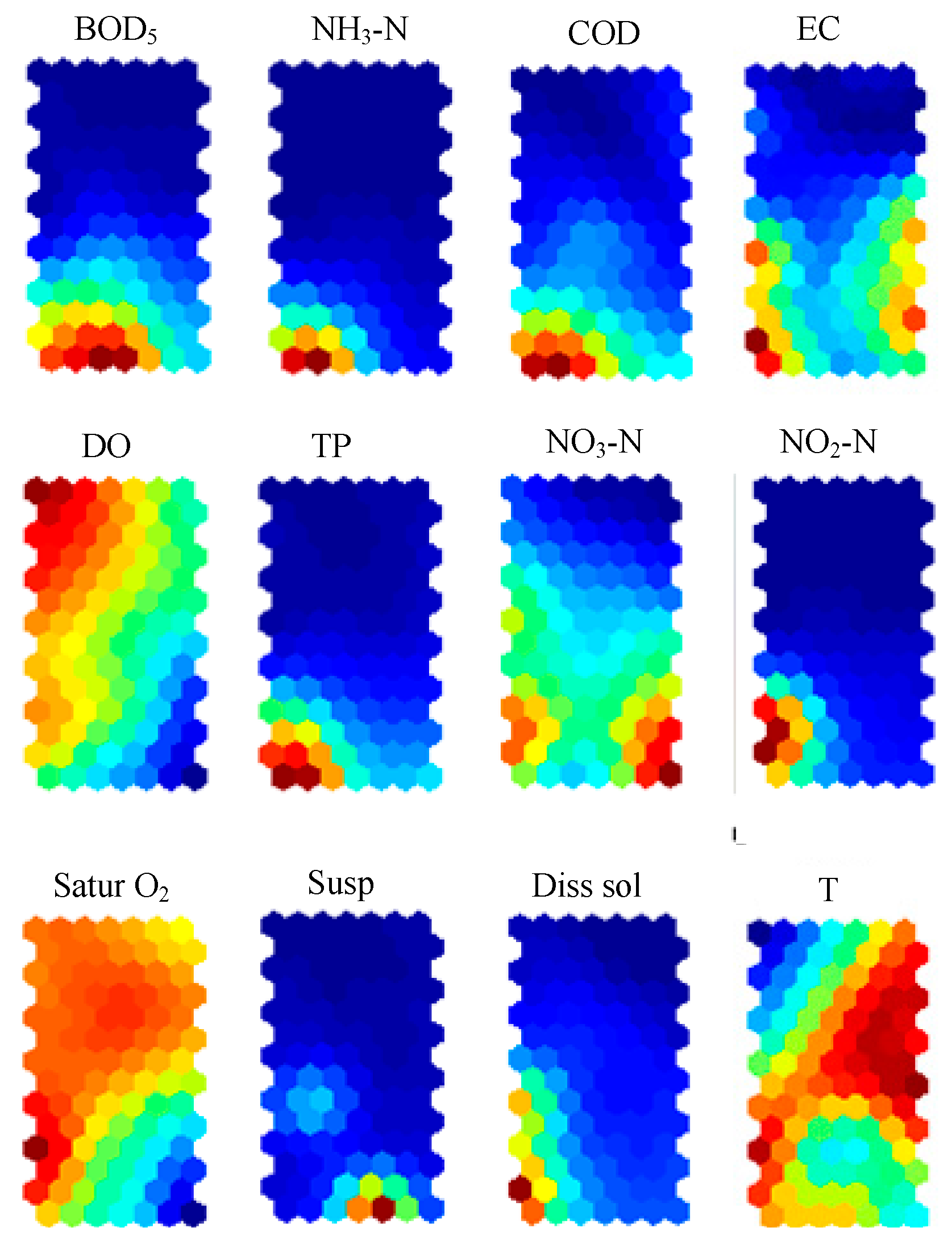
The visualization of the component planes is a good tool to figure out the interrelationship of the different water quality parameters. By comparing the component planes in
Figure 3, some parameters demonstrate positive patterns. The grouping of the parameter planes shows three well-defined groups of correlated parameters. The component planes of the same groups have positive relationships between them. The first group includes the parameters of TP, COD, BOD
5, NH
3-N, and NO
2-N. All the water quality parameters in this group have high values (red color) in the lower parts, especially in the lower left parts of the group. It is shown in
Section 4.2 above these five parameters have bigger effect on PC1 than the other two parameters (NO
3-N and Diss sol). The second group includes EC and Diss sol, which is expressed as PC2 in
Section 4.2 above. EC is a reflection of Diss sol in water. The third group comprises DO and Satur O
2. DO is correlated with Satur O
2 with a correlation coefficient of 0.784 in Pearson correlation matrix, and PC2 shows strong positive loadings on DO and with Satur O
2. The non-conventional positions of Susp, T, and NO
3-N could be explained by their ability to describe various complex pollutants and their transformations [
15].
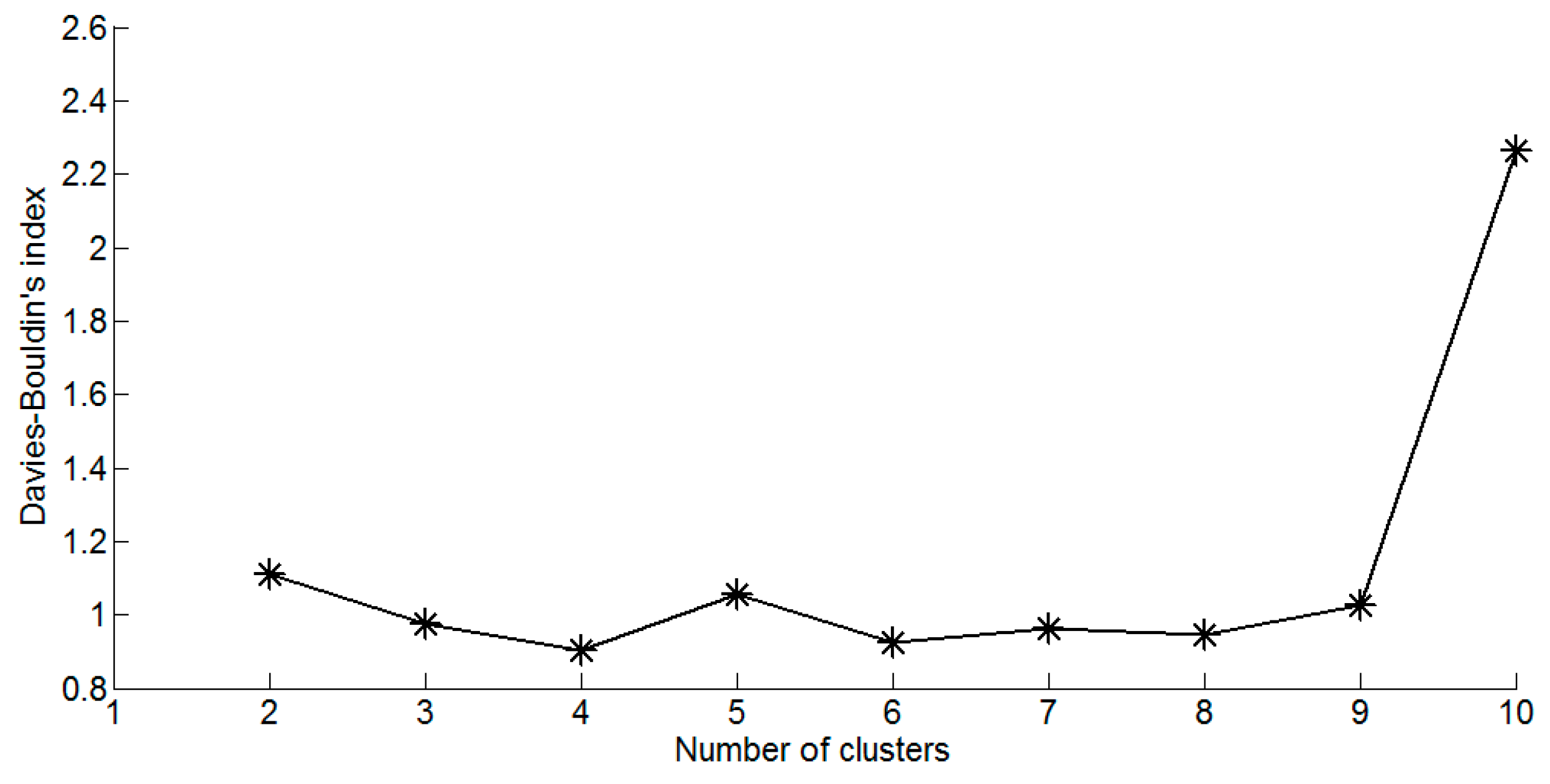
The cluster analysis of SOM is implemented by K-means clustering algorithm to find the optimal number of the clusters. Davies-Bouldin clustering index [
40] is to compute the optimal number of clusters for a dataset, which is commonly used in determining the optimal numbers of clusters [
2,
14]. As shown in
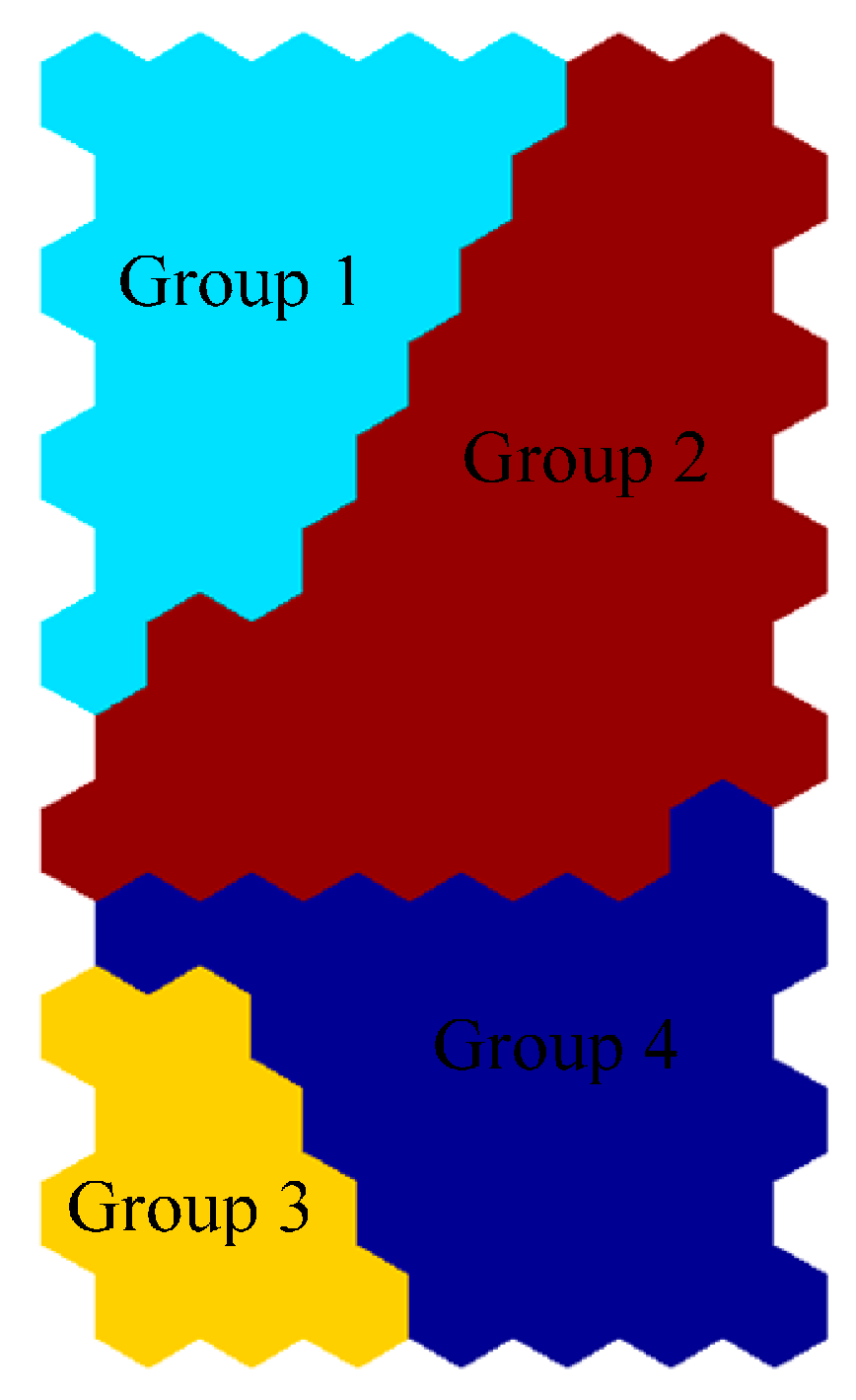
Figure 4, the Davies-Bouldin clustering index is minimized at four with the best clustering. That means the optimal number of the clusters is four, and the four-cluster structure of the map is described in
Figure 5. According to
Figure 3 and
Figure 5, the following information on water quality parameters can be concluded:
(1) High DO, low T, low BOD5, low NH3-N, low COD, low EC, low TP, low NO2-N, low Susp, and low Diss sol (Group 1).
(2) High T, high Satur O2, low BOD5, low NH3-N, low COD, low EC, low TP, low NO3-N, low NO2-N, low Susp, and low Diss sol (Group 2).
(3) High BOD5, high NH3-N, high COD, high TP, and low Susp (Group 3).
(4) High NO3-N, low NH3-N, low TP, low NO2-N, and low Diss sol (Group 4).
Figure 3.
Patterning analysis for the water quality parameters on the SOM plane.
Figure 3.
Patterning analysis for the water quality parameters on the SOM plane.
Figure 4.
Davies-Bouldin clustering index of the K-means clustering algorithm.
Figure 4.
Davies-Bouldin clustering index of the K-means clustering algorithm.
Figure 5.
Clusters of the SOM for the water quality dataset.
Figure 5.
Clusters of the SOM for the water quality dataset.
In winter, when temperature is low, high concentration of DO, low concentrations of BOD
5, NH
3-N, COD, EC, TP, NO
2-N, Susp, and Diss sol are observed in Group 1. Çinar and Merdun clustered seven groups based on 1046 surface water samples collected over six years and found that in winter when temperature is lowest and rainfall highest, high concentration of DO, and low concentrations of Na, K, Cl, NH
4-N, NO
2-N, and
o-PO
4 (ortho-phosphate), pV (organic matter) can be observed in one group, which is similar to the results in this study [
2].
The correlation matrix of the weight of the SOM is shown in
Table 6. The minimum values, maximum values, mean values, and SE values of the four groups are expressed in
Table 7. As shown in
Figure 3 and
Figure 5, Groups 2 and 4 represent the normal condition of the study area. The second group contain a total of 199 samples showing the highest frequency among the four groups, followed by the fourth group with a total of 85 samples.