A Systematic Review and Meta-Regression Analysis of Lung Cancer Risk and Inorganic Arsenic in Drinking Water
Abstract
:1. Introduction
2. Materials and Methods
2.1. Source Material
2.2. Study Populations
2.3. Exposure
2.4. Outcome Metric
2.5. Analysis
3. Results
3.1. Literature Search
3.2. Study Populations
| Author | Location | Period | Outcome | Exposure Metric | Exposure (µg/L) | Relative Risk | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ecological Studies | |||||||||||
| Ferreccio 2006 | Chile | 1985–2002 | Mortality | Highest | <10 | 1.00 (ref) | |||||
| 287 | 0.93 | ||||||||||
| 636 | 3.51 | ||||||||||
| 860 | 3.08 | ||||||||||
| Morales 2000 | Southwest Taiwan | 1973–1986 | Mortality | Pop-Wt. Mean | 33.1 | 1.00 (ref) | |||||
| 66.3 | 0.82 | ||||||||||
| 115.2 | 0.91 | ||||||||||
| 246.3 | 2.28 | ||||||||||
| 336.3 | 1.3 | ||||||||||
| 446.7 | 2.4 | ||||||||||
| 524.4 | 2.03 | ||||||||||
| 693.9 | 3.11 | ||||||||||
| Non-Ecological Studies | |||||||||||
| Case-Control Studies | |||||||||||
| Dauphine 2013 | California & Nevada, USA | 2002–2005 | Incidence | Mid-Range; Mean | ≤10 | 1.00 (ref) | |||||
| 42.5 | 0.75 | ||||||||||
| 173 | 0.84 | ||||||||||
| Ferreccio 2013 | Chile | 2007–2010 | Incidence | Pop-Wt. Mean | 10.2 | 1.00 (ref) | |||||
| 60 | 0.77 | ||||||||||
| 377.5 | 1.38 | ||||||||||
| 860 | 2.39 | ||||||||||
| Smith 2009 (Ferreccio 2000) | Chile | 1994–1996 | Incidence | Pop-Wt. Mean | 1 | 1.00 (ref) | |||||
| 12.8 | 0.7 | ||||||||||
| 154 | 3.4 | ||||||||||
| 636 | 4.7 | ||||||||||
| 600 | 5.7 | ||||||||||
| 860 | 7.1 | ||||||||||
| Cohort Study | |||||||||||
| Bogen 2014 (Chen 2010) | Northeast Taiwan | 1991–1994 | Incidence | Mean | 1 | 1.00 (ref) | |||||
| 3.26 | 0.57 | ||||||||||
| 25.9 | 0.73 | ||||||||||
| 74.3 | 0.68 | ||||||||||
| 160 | 1.08 | ||||||||||
| 711 | 1.57 | ||||||||||
3.3. Exposure Metrics
3.4. Outcome
3.5. Study Design
3.6. Dose-Response Analysis
3.6.1. Single Studies
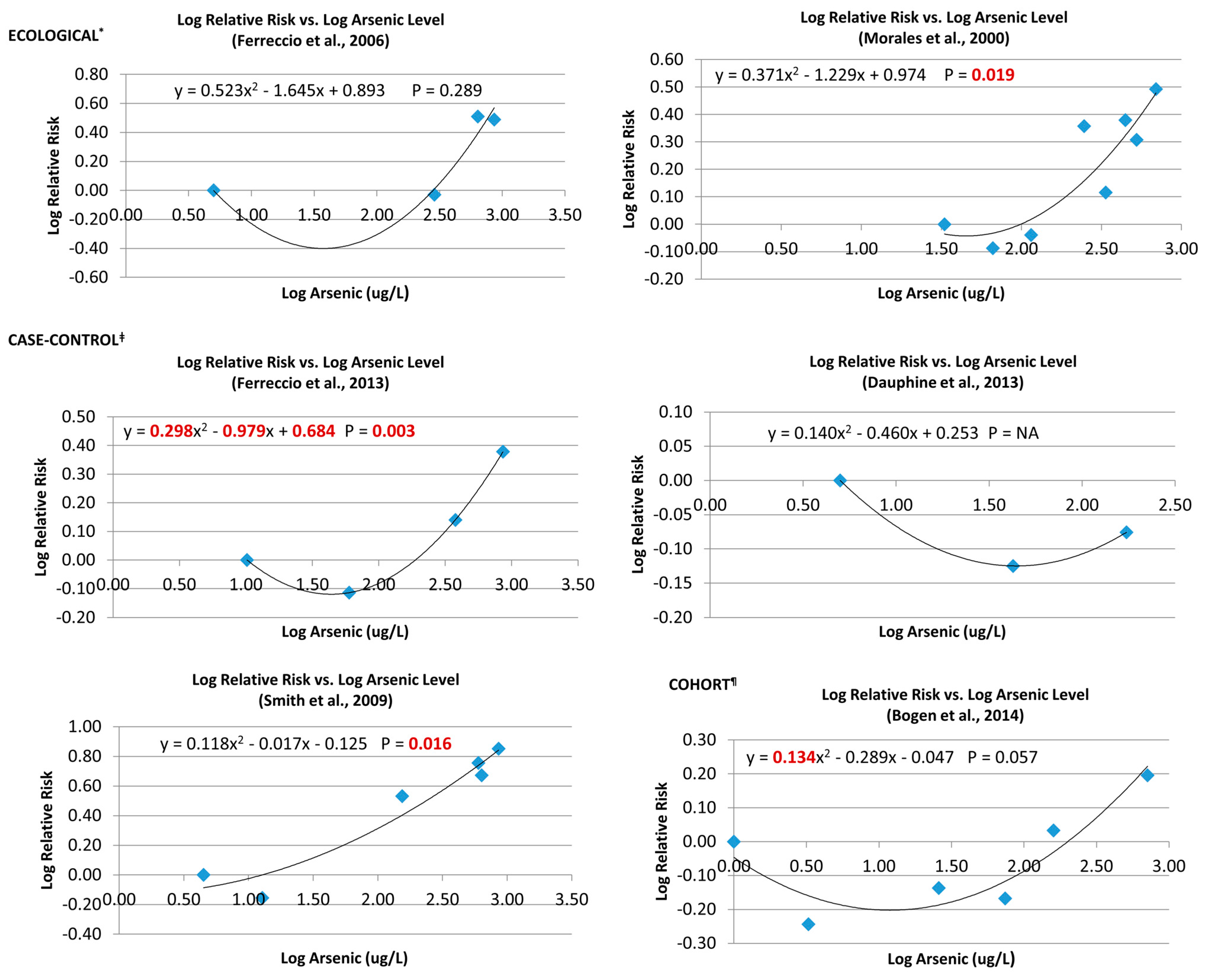
3.6.2. Pooled Analysis
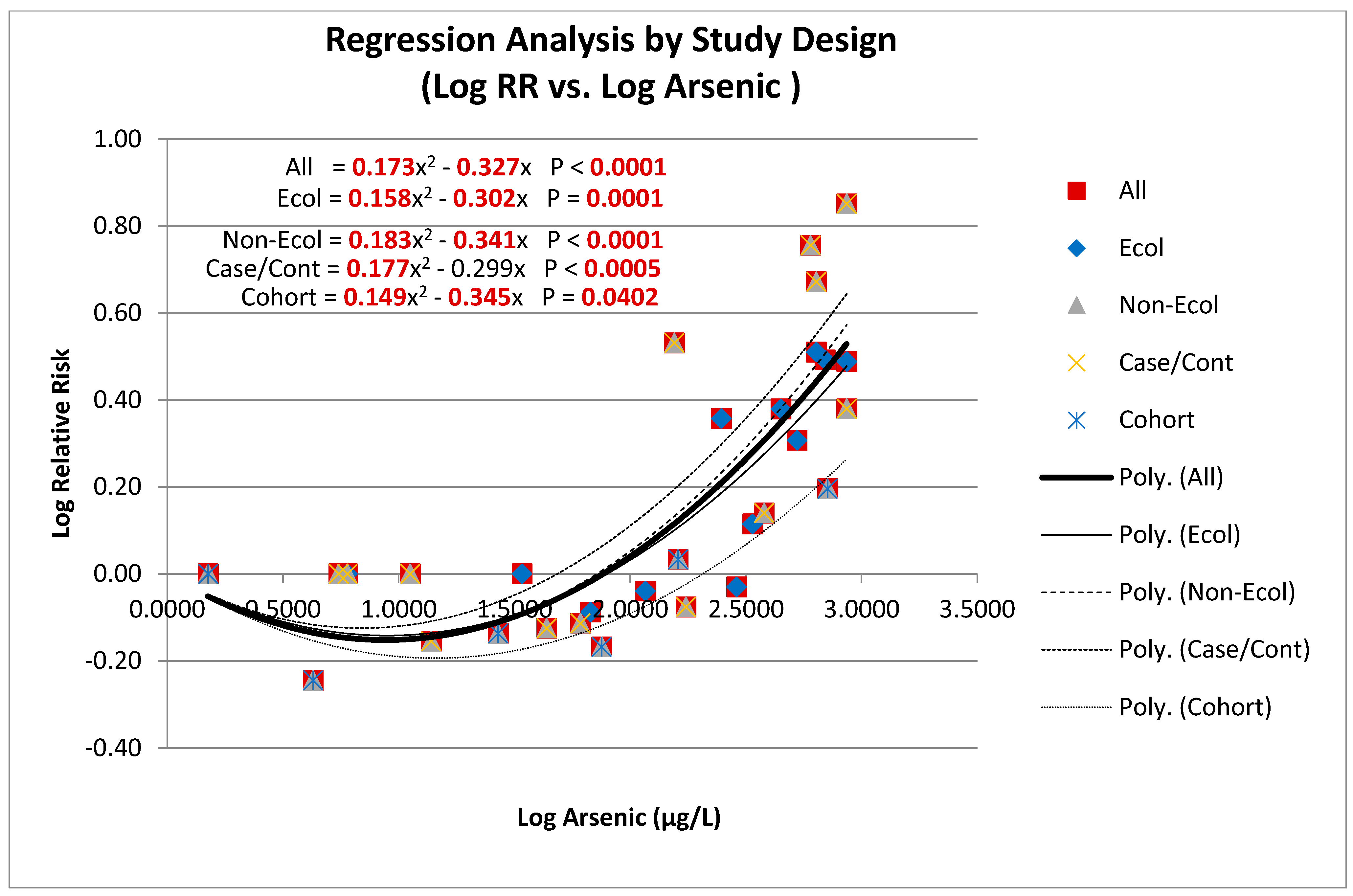
3.6.3. Meta-Regression
| (As − Ref) +1 | N o | β Quadratic | p-Quadratic * | β Linear | p-Linear * | Prob > F | Xintercept |
|---|---|---|---|---|---|---|---|
| All | 25 | 0.2139 | 0.000 | −0.4564 | 0.002 | 0.000 | 136.2 |
| Ecological | 10 | 0.2442 | 0.029 | −0.5378 | 0.065 | 0.001 | 159.4 |
| Non-Ecological | 15 | 0.1833 | 0.013 | −0.3796 | 0.034 | 0.009 | 117.7 |
| Case-Control | 10 | 0.1892 | 0.050 | −0.3766 | 0.113 | 0.022 | 97.9 |
| Cohort + | 5 | 0.1488 | 0.022 | −0.3445 | 0.023 | 0.049 | 206.9 |
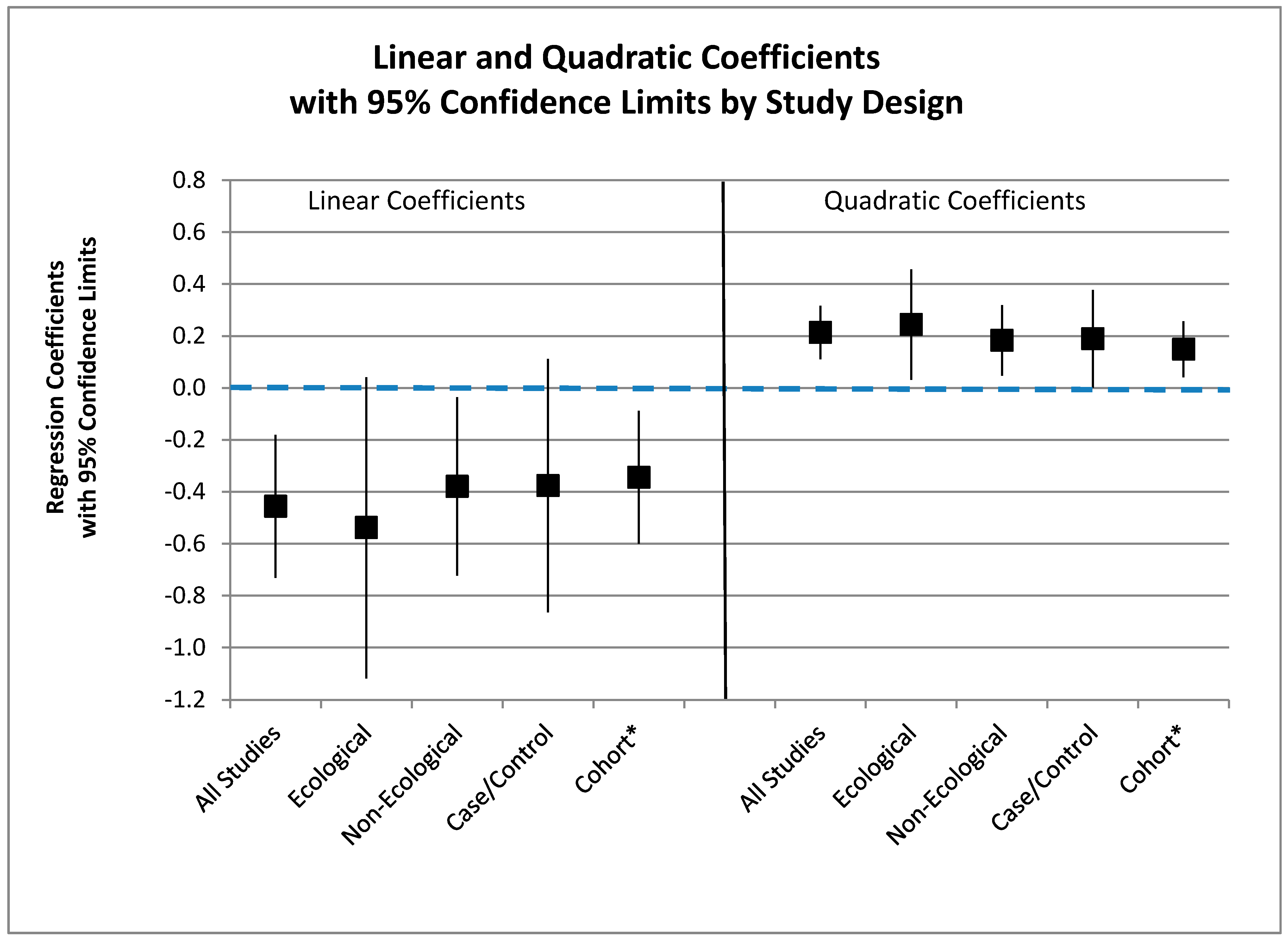
3.6.4. Zero X-Intercept
4. Discussion
4.1. Biological Plausibility
4.2. Risk Modeling
4.3. Limitations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
Description of Studies and Available Data
Ecological Studies
| City | Arsenic | SMR | RR | ||||||
| 1958–1970 | 1971–1977 | Highest | 1985–1992 | 1993–2002 | 1985–2002 | 1985–1992 | 1993–2002 | 1985–2002 | |
| Valparaiso | <10 | <10 | <10 | 136.6 | 131.8 | 133.9 | 1.00 | 1.00 | 1.00 |
| Calama | 150 | 287 | 287 | 140.7 | 112.5 | 125.0 | 1.03 | 0.85 | 0.93 |
| Tocopilla | 250 | 636 | 636 | 479.1 | 497.2 | 433.6 | 3.51 | 3.01 | 3.51 |
| Antofagasta | 860 | 110 | 860 | 420.1 | 406.1 | 412.3 | 3.08 | 3.08 | 3.08 |
| Arsenic | Mid-Range | Median Mean | Pop-Wt Mean | SMR | RR |
| 0–50 | 25 | 32 | 33.1 | 1.80 (1.11–2.75) | 1.00 |
| 50–100 | 75 | 62.5 | 66.3 | 1.47 (0.97–2.14) | 0.82 |
| 100–200 | 150 | 122.5 | 115.2 | 1.64 (0.82–2.94) | 0.91 |
| 200–300 | 250 | 245.9 | 246.3 | 4.10 (3.01–5.44) | 2.28 |
| 300–400 | 350 | 328.5 | 336.3 | 2.34 (1.21–3.84) | 1.30 |
| 400–500 | 450 | 448 | 446.7 | 4.31 (2.67–6.59) | 2.40 |
| 500–600 | 550 | 529 | 524.4 | 3.65 (2.53–5.10) | 2.03 |
| 600–818 | 767 | 665.2 | 693.9 | 5.59 (4.51–6.84) | 3.11 |
Case-control Studies
| Arsenic | Mid-Range | Median | Mean | Case-control | OR | Adj OR |
| ≤10 | 5 | 141/241 | 1.00 | 1.00 | ||
| 11–84 | 42.5 | 37/82 | 0.77 | 0.75 | ||
| ≥85 | 772.5 | 110 | 173 | 18/36 | 0.85 | 0.84 |
| Arsenic | Mid-Range | Largest City | Pop-Wt Mean | Case/Cont | OR |
| 0–59 | 30 | 10 | 10.2 | 48/138 | 1.00 |
| 60–199 | 130 | 60 | 60 | 52/193 | 0.77 |
| 200–799 | 500 | 287 | 377.5 | 69/144 | 1.38 |
| ≥800 | 900 | 860 | 860 | 137/165 | 2.39 |
| Pop-Wt | ||||||
| Arsenic | Mid-Range | (58–70) | (71–77) | Highest | Case/Cont | Adj OR |
| 0–9 | 5 | 1.0 | 1.0 | 1.0 | 11/92 | 1 |
| 10–59 | 35 | 12.8 | 12.8 | 12.8 | 7/81 | 0.7 |
| 60–199 | 130 | 97.3 | 154 | 154 | 35/87 | 3.4 |
| 200–399 | 300 | 250 | 636 | 636 | 23/44 | 4.7 |
| 400–699 | 550 | 600 | 600 | 600 | 11/12 | 5.7 |
| 700–999 | 850 | 860 | 110 | 860 | 64/103 | 7.1 |
Cohort Study
| Range | Mean | Participants | Person-Years | Cases | adj RR |
| 0–1 | 1 | 1071 | 12,558 | 32 | 1.00 |
| 1<10 | 3.26 | 1371 | 15,781 | 23 | 0.57 |
| 10–<50 | 25.9 | 2027 | 23,473 | 47 | 0.73 |
| 50–<100 | 74.3 | 880 | 9989 | 19 | 0.68 |
| 100–<300 | 160 | 873 | 10,000 | 27 | 1.08 |
| >300 | 711 | 666 | 7525 | 30 | 1.57 |
References
- World Health Organization. Exposure to Arsenic—A Major Public Health Concern. Available online: www.who.int_ipcs_features_arsenic (accessed on 17 November 2014).
- IARC. IARC monographs on the evaluation of carcinogenic risk to humans. In A Review of Human Carcinogens: Arsenic, Metals Fibers and Dusts; International Agency for Research on Cancer (IARC): Lyon, France, 2012. [Google Scholar]
- U.S. Environmental Protection Agency (USEPA). Integrated Risk Information System (IRIS) on Arsenic; National Center for Environmental Assessment, Office of Research and Development: Washington, DC, USA, 1998. [Google Scholar]
- Chen, C.J.; Chuang, Y.C.; Lin, T.M.; Wu, H.Y. Malignant neoplasms among residents of a blackfoot disease-endemic area in Taiwan: High arsenic artesian well water and cancers. Cancer Res. 1985, 45, 5895–5899. [Google Scholar] [PubMed]
- Wu, M.M.; Kuo, T.L.; Hwang, Y.H.; Chen, C.J. Dose-response relation between arsenic concentration in well water and mortality from cancers and vascular diseases. Am. J. Epidemiol. 1989, 130, 1123–1132. [Google Scholar]
- Chiou, H.Y.; Chiou, S.T.; Hsu, Y.H.; Chou, Y.L.; Tseng, C.H.; Wei, M.L.; Chen, C.J. Incidence of transitional cell carcinoma and arsenic in drinking water: A follow up study of 8102 residents in an arseniasis-endemic area in northeastern Taiwan. Am. J. Epidemiol. 2001, 153, 411–418. [Google Scholar] [CrossRef]
- Rivara, M.I.; Cebrian, M.; Corey, G.; Hernandez, M.; Romieu, I. Cancer risk in an arsenic-contaminated area of Chile. Toxicol. Ind. Health 1997, 13, 321–338. [Google Scholar] [CrossRef] [PubMed]
- Ferreccio, C.; Gonzalez, P.C.; Milosavjlevic, S.V.; Marshal, G.G.; Sancha, A.M. Lung cancer and arsenic exposure in drinking water: A case control study in northern Chile. Cad. Saude Publica 1998, 14, 193–198. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.H.; Goycolea, M.; Haque, R.; Biggs, M.L. Marked increase in bladder and lung cancer mortality in a region of northern Chile due to arsenic in drinking water. Am. J. Epidemiol. 1998, 147, 660–669. [Google Scholar] [CrossRef]
- Hopenhayn-Rich, C.; Biggs, M.L.; Fuchs, A.; Bergoglio, R.; Tello, E.E.; Nicolli, H.; Smith, A.H. Bladder cancer mortality associated with arsenic in drinking water in Argentina. Epidemiology 1996, 7, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Hopenhayn-Rich, C.; Biggs, M.L.; Smith, A.H. Lung and kidney cancer mortality associated with arsenic in drinking water in Cordoba, Argentina. Int. J. Epidemiol. 1998, 27, 561–569. [Google Scholar] [CrossRef]
- Mostafa, M.G.; McDonald, J.C.; Cherry, N.M. Lung cancer and exposure to arsenic in rural Bangladesh. Occup. Environ. Med. 2008, 65, 765–768. [Google Scholar] [CrossRef] [PubMed]
- Tsuda, T.; Babazono, A.; Yamamoto, E.; Kurumatani, N.; Mino, Y.; Ogawa, T.; Aoyama, H. Ingested arsenic and internal cancer: A historical cohort study followed for 33 years. Am. J. Epidemiol. 1995, 141, 198–209. [Google Scholar]
- Celik, I.; Gallicchio, L.; Boyd, K.; Lam, T.K.; Matanoski, G.; Tao, X.G.; Alberg, A.J. Arsenic in drinking water and lung cancer: A systematic review. Environ. Res. 2008, 108, 48–55. [Google Scholar] [CrossRef] [PubMed]
- Gibb, H.; Haver, C.; Gaylor, D.; Ramasamy, S.; Lee, J.S.; Lobdell, D.; Sams, R. Utility of recent studies to assess the national research council 2001 estimates of cancer risk from ingested arsenic. Environ. Health Perspect. 2011, 119, 284–290. [Google Scholar] [CrossRef] [PubMed]
- Cohen, S.; Arnold, L.; Beck, B.; Lewis, A.; Eldan, M. Evaluation of the carcinogenicity of inorganic arsenic. Crit. Rev. Toxicol. 2013, 43, 711–752. [Google Scholar] [CrossRef] [PubMed]
- Lamm, S.H.; Robbins, S.A.; Zhou, C.; Lu, J.; Chen, R.; Feinleib, M. Bladder/Lung cancer mortality in Blackfoot-disease (BFD)-endemic area villages with low (<150 µg/L) well water arsenic levels—An exploration of the dose-response Poisson analysis. Regul. Toxicol. Pharmacol. 2013, 65, 147–56. [Google Scholar] [PubMed]
- Schoen, A.; Beck, B.; Sharma, R.; Dube, E. Arsenic toxicity at low doses: Epidemiological and mode of action considerations. Toxicol. Appl. Pharmacol. 2004, 198, 253–267. [Google Scholar] [CrossRef] [PubMed]
- Snow, E.T.; Sykora, P.; Durham, T.R.; Kelin, C.B. Arsenic, mode of action at biologically plausible low doses: What are the implications for low dose cancer risk? Toxicol. Appl. Pharmacol. 2005, 207, 557–564. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.H.; Ercumen, A.; Yan, Y.; Steinmaus, C.M. Increased lung cancer risks are similar whether arsenic is ingested or inhaled. J. Expo. Sci. Environ. Epidemiol. 2009, 19, 343–348. [Google Scholar] [CrossRef] [PubMed]
- Bogen, K.T.; Chen, C.L.; Tsuji, J.S. Significant nonlinearity of lung cancer risk in relation to arsenic in drinking water in northeastern Taiwan. Toxicol. Sci. 2014, 138, 62. [Google Scholar]
- Microsoft Excel; Microsoft: Redmond, Washington, USA, 2010.
- Stata Statistical Software: Release 13.2; Stata Corp. Lp.: College Station, TX, USA, 2013.
- Knapp, G.; Hartung, J. Improved tests for a random-effects meta-regression with a single covariate. Stat. Med. 2003, 22, 2693–2710. [Google Scholar] [CrossRef] [PubMed]
- Harbord, R; Higgins, J. Meta-regression in Stata. Stata J. 2008, 8, 493–519. [Google Scholar]
- Putila, J.J.; Guo, N.L. Association of arsenic exposure with lung cancer incidence rates in the United States. PLoS ONE 2011, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Heck, J.; Andrew, A.; Onega, T.; Rigas, J.; Jackson, B.; Karagas, M.; Duell, E. Lung cancer in a U.S. population with low to moderate arsenic exposure. Environ. Health Perspect. 2009, 117, 1718–1723. [Google Scholar] [PubMed]
- Garcia-Esquinas, E.; Pollan, M.; Umasn, J.G.; Francesconi, K.A.; Goessler, W.; Guallar, E.; Navas-Acien, A. Arsenic exposure and cancer mortality in a U.S. based prospective cohort: The strong heart study. Cancer Epidemiol. Biomarker Prev. 2013, 22, 1944–1953. [Google Scholar] [CrossRef] [PubMed]
- Erraguntla, N.K.; Sielken, R.J.; Valdez-Flores, C.; Grant, R.L. An updated inhalation unit risk factor for arsenic and inorganic arsenic compounds based on a combined analysis of epidemiology studies. Regul. Toxicol. Pharmacol. 2012, 64, 329–341. [Google Scholar] [CrossRef] [PubMed]
- Lewis, D.R.; Southwick, J.W.; Quellet-Hellstrom, R.; Rench, J.; Calderon, R.L. Drinking water arsenic in Utah: A cohort mortality study. Environ. Health Perspect. 1999, 170, 359–365. [Google Scholar] [CrossRef]
- Guo, H. Arsenic level in drinking water and mortality of lung cancer (Taiwan). Cancer Cause. Control 2004, 15, 171–177. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.; Liaw, Y.; Hwant, B.; Cheng, Y.; Lin, M.; Kuo, Y.; Guo, H. Arsenic in drinking and lung cancer mortality in Taiwan. J. Asian Earth Sci. 2013, 77, 327–331. [Google Scholar] [CrossRef]
- Baastrup, R.; Sorensen, M.; Balstrom, T.; Frederiksen, K.; Larsen, C.; Tjonneland, A.; Raachou-Nielsen, O. Arsenic in drinking water and risk for cancer in Denmark. Environ. Health Perspect. 2006, 116, 231–237. [Google Scholar] [CrossRef] [PubMed]
- Buchet, J.P.; Lison, D. Mortality by cancer in groups of the Belgian population with a moderately increased intake of arsenic. Int. Arch. Occup. Environ. Health 1998, 71, 125–130. [Google Scholar] [CrossRef]
- Meliker, J.R.; Wahl, R. L.; Cameron, L.L.; Nriagu, J.O. Arsenic in drinking water and cerebrovascular disease, diabetes mellitus, and kidney disease in Michigan: A standardized mortality ration analysis. Environ. Health 2007, 6, 4–11. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Weissfeld, J.L.; Davis, D.L.; Talbott, E.O. Arsenic levels in ground water and cancer incidence in Idaho: An ecologic study. Int. Arch. Occup. Environ. Health 2009, 82, 843–849. [Google Scholar] [CrossRef] [PubMed]
- Steinmaus, C.M.; Ferreccio, C.; Romo, J.A.; Yuan, Y.; Cortes, S.; Marshall, G.; Smith, A.H. Drinking water arsenic in northern Chile: High cancer risks 40 years after exposure cessation. Cancer Epidemiol. Biomarker Prev. 2013, 22, 623–630. [Google Scholar] [CrossRef] [PubMed]
- Ferreccio, C.; Sancha, A.M. Arsenic exposure and its impact on health in Chile. J. Health Popul. Nutr. 2006, 24, 164–175. [Google Scholar] [PubMed]
- Ferreccio, C.; Yuan, Y.; Calle, J.; Benitez, H.; Parra, R.L.; Acevedo, J.; Steinmaus, C. Arsenic, tobacco smoke, and occupation: Association of multiple agents with lung and bladder cancer. Epidemiology 2013, 24, 898–905. [Google Scholar] [CrossRef] [PubMed]
- Morales, K.H.; Ryan, L.; Kuo, T.L.; Wu, M.; Chen, C. Risk of internal cancers from arsenic in drinking water. Environ. Health Perspect. 2000, 108, 655–661. [Google Scholar] [CrossRef] [PubMed]
- Dauphine, D.C.; Smith, A.H.; Yuan, Y.; Balmes, J.R.; Bates, M.N.; Steinmaus, C. Case control study of arsenic in drinking water and lung cancer in California and Nevada. Int. J. Environ. Res. Public Health 2013, 10, 3310–3324. [Google Scholar] [CrossRef] [PubMed]
- National Research Council. Critical Aspects of EPA’s IRIS Assessment of Inorganic Arsenic—Interim Report; National Academy Press: Washington, DC, USA, 2013. [Google Scholar]
- National Research Council. Arsenic in Drinking Water, 2nd ed.; National Academy Press: Washington, DC, USA, 1999; pp. 308–309. [Google Scholar]
- Mink, P.J.; Alexander, D.D.; Barraj, L.M.; Kelsh, M.A.; Tsuji, J.S. Low-level arsenic exposure in drinking water and bladder cancer: A review and meta-analysis. Regul. Toxicol. Pharmacol 2008, 52, 299–310. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, J.S.; Alexander, D.D.; Perez, V.; Mink, P.J. Arsenic exposure and bladder cancer: Quantitative assessment of studies in human populations to detect risks at low doses. Toxicology 2014, 317, 17–30. [Google Scholar] [CrossRef] [PubMed]
- Abernathy, C.O.; Chappell, W.R.; Meek, M.E.; Gibb, H.; Guo, H.R. Is ingested inorganic arsenic a “threshold” carcinogen? Fund. Appl. Pharmacol. 1996, 29, 168–175. [Google Scholar] [CrossRef]
- Goering, P.; Aposhian, H.V.; Mass, M.J.; Cebrian, M.; Beck, B.D.; Waalkes, M.P. The enigma of arsenic carcinogenesis: Role of metabolism. Toxicol. Sci. 1999, 49, 5–14. [Google Scholar] [CrossRef] [PubMed]
- Schmeisser, S.; Schmeisser, K.; Weimer, S.; Groth, M.; Priebe, S.; Fazius, E.; Ristow, M. Mitochondrial hormesis links low-dose arsenite exposure to lifespan extension. Aging Cell 2013, 12, 508–517. [Google Scholar] [CrossRef] [PubMed]
- U.S. Environmental Protection Agency. Guidelines for Carcinogen Risk Assessment; U.S. Environmental Protection Agency: Washington, DC, USA, 2005; pp. 3–22.
- Dourson, M.; Hertzberg, R.; Allen, B.; Haber, L.; Parker, A; Kroner, O.; Kohrman, M. Evidence-based dose-response assessment for thyroid tumorignesis from acrylamide. Regul. Toxicol. Pharmacol. 2008, 52, 264–289. [Google Scholar] [CrossRef] [PubMed]
- Ferreccio, C.; Gonzalez, C.; Milosavjlevic, V.; Marshall, G.; Sanchez, A.M.; Smith, A.H. Lung cancer and arsenic concentrations in drinking water in Chile. Epidemiology 2000, 11, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Chen, C-L.; Chiou, H-Y.; Hsu, L-I.; Hsueh, Y-M.; Wu, M-M.; Chen, C-J. Ingested arsenic, characteristics of well water consumption and risk of different histological types of lung cancer in northeastern Taiwan. Environ. Res. 2010, 110, 455–462. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamm, S.H.; Ferdosi, H.; Dissen, E.K.; Li, J.; Ahn, J. A Systematic Review and Meta-Regression Analysis of Lung Cancer Risk and Inorganic Arsenic in Drinking Water. Int. J. Environ. Res. Public Health 2015, 12, 15498-15515. https://doi.org/10.3390/ijerph121214990
Lamm SH, Ferdosi H, Dissen EK, Li J, Ahn J. A Systematic Review and Meta-Regression Analysis of Lung Cancer Risk and Inorganic Arsenic in Drinking Water. International Journal of Environmental Research and Public Health. 2015; 12(12):15498-15515. https://doi.org/10.3390/ijerph121214990
Chicago/Turabian StyleLamm, Steven H., Hamid Ferdosi, Elisabeth K. Dissen, Ji Li, and Jaeil Ahn. 2015. "A Systematic Review and Meta-Regression Analysis of Lung Cancer Risk and Inorganic Arsenic in Drinking Water" International Journal of Environmental Research and Public Health 12, no. 12: 15498-15515. https://doi.org/10.3390/ijerph121214990
APA StyleLamm, S. H., Ferdosi, H., Dissen, E. K., Li, J., & Ahn, J. (2015). A Systematic Review and Meta-Regression Analysis of Lung Cancer Risk and Inorganic Arsenic in Drinking Water. International Journal of Environmental Research and Public Health, 12(12), 15498-15515. https://doi.org/10.3390/ijerph121214990






