2.1. Dataset
The Haihe River is the biggest river system in North China and includes all rivers flowing into the Bohai Sea. The east coastline of the watershed extends from Shanhaiguan to the old Yellow River estuary, and the total area of the watershed is about 318,200 km
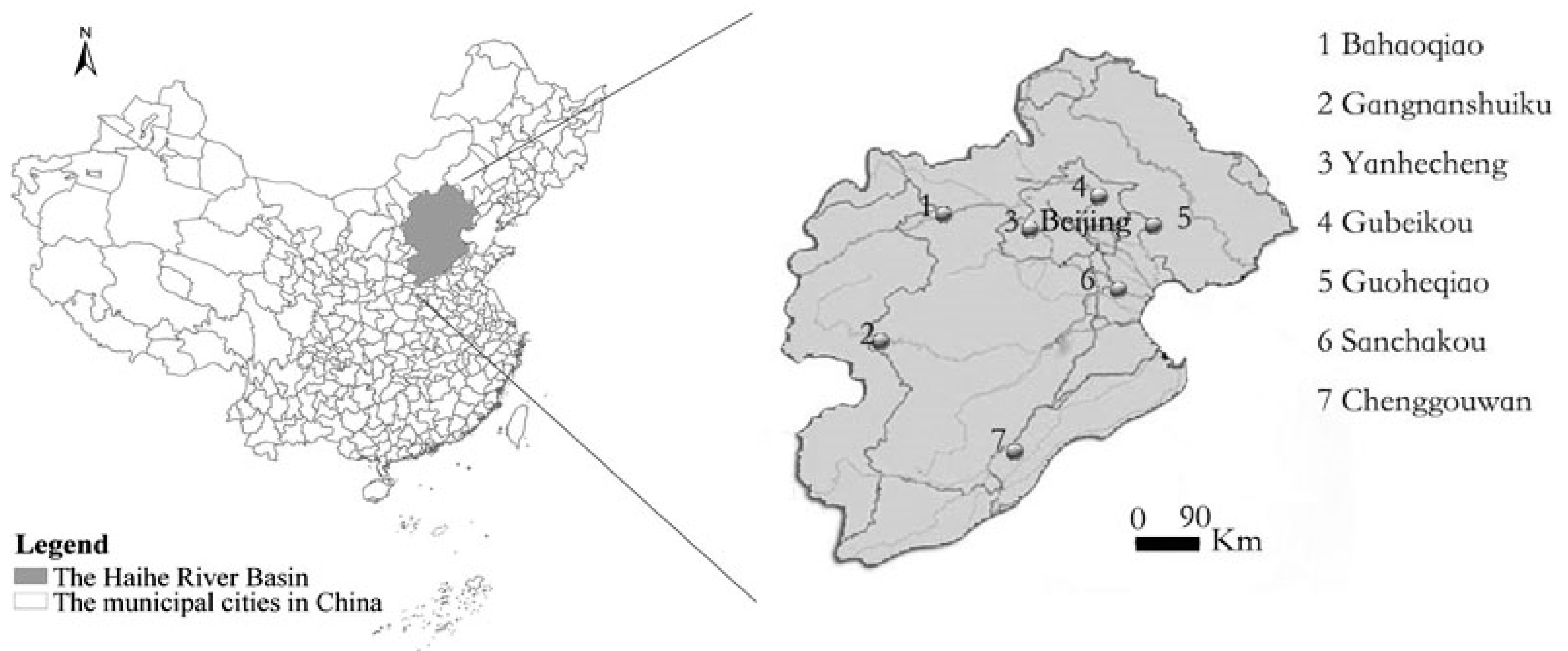
2. The main stream runs through Hebei Province, Beijing City, Tianjin City and Shandong Province. The location of the river in China and the location of the monitoring stations are illustrated in
Figure 1. The dataset from seven water quality monitoring stations on the Haihe River (Yanhecheng, Gubeikou, Gangnanshuiku, Guoheqiao, Sanchakou, Bahaoqiao and Chenggouwan), comprising four water quality indicators monitored weekly over eight years (2006–2013), was obtained from the Ministry of Environmental Protection of China. There were 2078 samples in all after eliminating unreasonable data and data worse than grade V. Samples in which one of the indicators exceeded the standard of grade V (
i.e., grade VI) were not included in the analysis because most data worse than grade V were far from the boundaries and could be considered as outliers from a statistical point of view and would affect cluster quality. The available water quality indicators included pH, dissolved oxygen (DO), chemical oxygen demand (COD) and ammonia nitrogen (NH
3-N). The surface water environmental quality standards (GB3838-2002) for DO, COD and NH
3-N are listed in
Table 1. The boundary values of DO, COD and NH
3-N defined in
Table 1 and the sample mean of pH were defined as original K cluster centroid. The descriptive statistics are summarized in
Table 2. There are five grades in GB3838-2002 omitting grade VI.
Figure 1.
Location of the Heihe River in China and location of the monitoring stations.
Figure 1.
Location of the Heihe River in China and location of the monitoring stations.
Table 1.
Boundary values of some indicators in the GB3838-2002 water quality standard.
Table 1.
Boundary values of some indicators in the GB3838-2002 water quality standard.
| Indicator | I | II | III | IV | V |
|---|
| DO (mg/L) | 7.5 | 6 | 5 | 3 | 2 |
| COD (mg/L) | 2 | 4 | 6 | 10 | 15 |
| NH3-N (mg/L) | 0.15 | 0.5 | 1 | 1.5 | 2 |
Table 2.
Descriptive statistics of water quality indicators.
Table 2.
Descriptive statistics of water quality indicators.
| Indicator | Mean | SD | SE | Minimum | Maximum |
|---|
| pH | 8.07 | 0.43 | 0.01 | 6.34 | 9.35 |
| DO (mg/L) | 9.02 | 2.83 | 0.06 | 2.02 | 25.5 |
| COD (mg/L) | 3.51 | 2.40 | 0.05 | 0.2 | 15 |
| NH3-N (mg/L) | 0.40 | 0.44 | 0.01 | 0.01 | 2 |
2.2. Dataset Treatment
In the Knowledge Discovery in Databases (KDD) process, data cleaning and preprocessing is an important step before choosing the data mining algorithms and data mining. Data cleaning and preprocessing includes basic operations, such as deciding on strategies for appropriately handling missing data fields, removing noise or outliers [
21].
For missing data, ignoring the tuple is usually done when the class label is missing. It is not effective when the percentage of missing values per attribute varies considerably [
22]. In this case there were only 18 missing tuples, so they were ignored.
In all normal distributions, the range μ ± 3σ includes nearly all cases, where μ denotes mean and σ denotes standard deviation. After z-score normalization, values higher than 3 or lower than −3 are outliers and they were deleted [
22].
Most multivariate statistical methods require variables to conform to the normal distribution, thus, the normality of the distribution of each indicator was checked by analyzing kurtosis and skewness index before multivariate statistical analysis. In all cases, the variable distribution was far from normal [
11,
23]. The original data demonstrated that kurtosis values range from 0.268 to 25.118 and skewness value range from −0.343 to 3.985, indicating that the variable distribution was far from normal with 95% confidence. Since most of kurtosis and skewness values were far from zero, the original data were transformed in the form
[
4,
23]. After log- transformation, the kurtosis and skewness values ranged from −2.380 to 0.092 and 0.025 to 14.893, respectively. In the case of CA, all log-transformed variables were also z-scale standardized (the mean and variance were set to zero and one, respectively) to minimize the effects of different units and variance of variables and to render the data dimensionless [
3,
24].
2.3. Modified Indicator Weight Self-Adjustment K-Means Algorithm (MIWAS-K-Means)
Clustering is a fundamental technique of unsupervised learning in statistics and machine learning [
25]. Clustering is generally used to find groups of similar items in a set of unlabeled data. How to select the best indicator weighting is a crucial question. Let
be a data set with M data objects and
be an indicator set with
N indicators. A sample of
can be represented as a data object
. The K-means algorithm partitions
into
clusters. Let
be a set of
clusters, coupled with a set of corresponding cluster center
In addition,
means the number of data objects to
such that
is defined as
Let
be the global center of all M data objects in the dataset, where
is defined as
Taking indicator weight into account, let
be a data set of all possible indicator weights. The weight of an indicator should reflect the importance of the indicator to cluster quality. Note that each indicator weighting leads to a different partitioning of the dataset. Intuitively, we would like to minimize the separations within clusters and maximizing the separations between clusters. Hence, the objective function is (Equation (1)):
where
denotes the membership degree of the
m-th sample belonging to the
K-th cluster.
is the sum of all separations within clusters and
is the sum of all separations between clusters.
is the difference between
and
in terms of the
n-th feature
and
is the difference between
and
in terms of the
n-th feature
.
Set
,
, where
represents the sum of separations within clusters in terms of the
n-th indicator and
represents the sum of separations between clusters in terms of the
n-th indicator. Hence, Equation (1) can be rewritten as:
The model given by Equation (2) is a linear programming problem and its feasible solution is located at the corner points of the convex polygon bounded by the
linear constraints in Equation (2) [
26]. By taking the corner points into Equation (2), the objective values will respective be
. The maxization of Equation (2) can occur at the corner-point
when
for
Accordingly, indicator weights in
are specified as (Equation (3)):
There are two philosophies behind the classification method. One is that each indicator contributes to the water quality classification. Meanwhile there is another philosophy that states that if one indicator exceeds the standard of a certain grade, the water immediately loses its functions belonging to lower grades. If for drinking water one parameter exceeds the standard, it is not suitable for drinking water any more, regardless the value for the other parameters. If for reclaimed water, it is suitable to use after disposal. From these options, we follow the first philosophy. Therefore, there is an unreasonable situation that the winner-take-all phenomenon makes other indicator weights becomes insignificant, even though they may contribute a lot to the cluster quality. A weight-adjusting procedure is combined with the original K-means algorithm. By increasing the weight of the indicator
having a higher
value, the indicator weights are adjusted [
19]. The method is as following:
Let
be the set of the
indicator weights at the
s-th iteration and each indicator weight at the
(s+1)-th iteration can be adjusted by adding an adjustment margin
at the s-th iteration as Equation (4):
Considering the contribution of the indicator to clustering quality, the adjustment margin
can be derived according to its
value at the
s-th iteration as Equation (5):
Note that the adjusted weight in (4) needs to be normalized to a value between 0 and 1. Through the normalization, each adjusted indicator weight
can be derived as (Equation (6)):
There is a shortcoming of this algorithm that
is perhaps equal to zero if all samples in a cluster have the same values or do not occur on an indicator, which causes
to not be calculated. To avoid the problem, an improved algorithm is proposed which introduces a constant
to change the adjustment margin as Equation (5), in order to avoid the difficulty in the computation [
20] (Equation (7)):
where
is the average dispersion of the entire data set for all indicators.
We note that it is an approximate method and the definition in Equation (1) is unreasonable. In this paper, we will propose an improved algorithm to avoid the shortcoming. Note that
in Equation (1) represents the separations between clusters.
is the global center of all M data objects in the dataset. We think that the definition is unreasonable and modify it as (Equation (8)):
where
is defined as (Equation (9)):
Hence, the objective function is (Equation (10)):
is the sum of all separations within clusters and
is the sum of all separations between clusters. Set
represents the sum of separations within clusters in terms of the
n-th indicator and
represents the sum of separations between clusters in terms of the
n-th indicator. Hence, Equation (10) can be rewritten as (Equation (11)):
Accordingly, indicator weights in
w are specified as (Equation (12)):
Note that if
, then
. In fact,
is not in the interval [0,1]. Therefore, a simple normalization is used as following (Equation (13)):
Each indicator weight at the
(s+1)-th iteration can be adjusted by adding an adjustment margin
at the
s-th iteration as Equation (14):
The adjustment margin
can be derived according to its
value at the
s-th iteration as Equation (15):
Therefore, each adjusted indicator weight
can be derived as (Equation (16)):
In the whole clustering process, if any parameter was not set, the improved algorithm above updates the indicator weights by the accurate adjustment margin and avoids not being calculated.
The pseudo-code of modified indicator weight self-adjustment K-means algorithm named MIWAS-K-means is illustrated in
Figure 2, the number of classes is selected as five according to GB3838-2002. The MIWAS-K-means algorithm repeats the assignment, update, and weight adjustment procedures until all elements in the object-cluster membership matrix are not changed.
Figure 2.
The pseudo-code for the MIWAS-K-means algorithm
Figure 2.
The pseudo-code for the MIWAS-K-means algorithm