Future Climate Data from RCP 4.5 and Occurrence of Malaria in Korea
Abstract
:1. Introduction
2. Malaria Occurrence in Korea
2.1. Trend of Malaria Occurrence
2.2. Data Collection
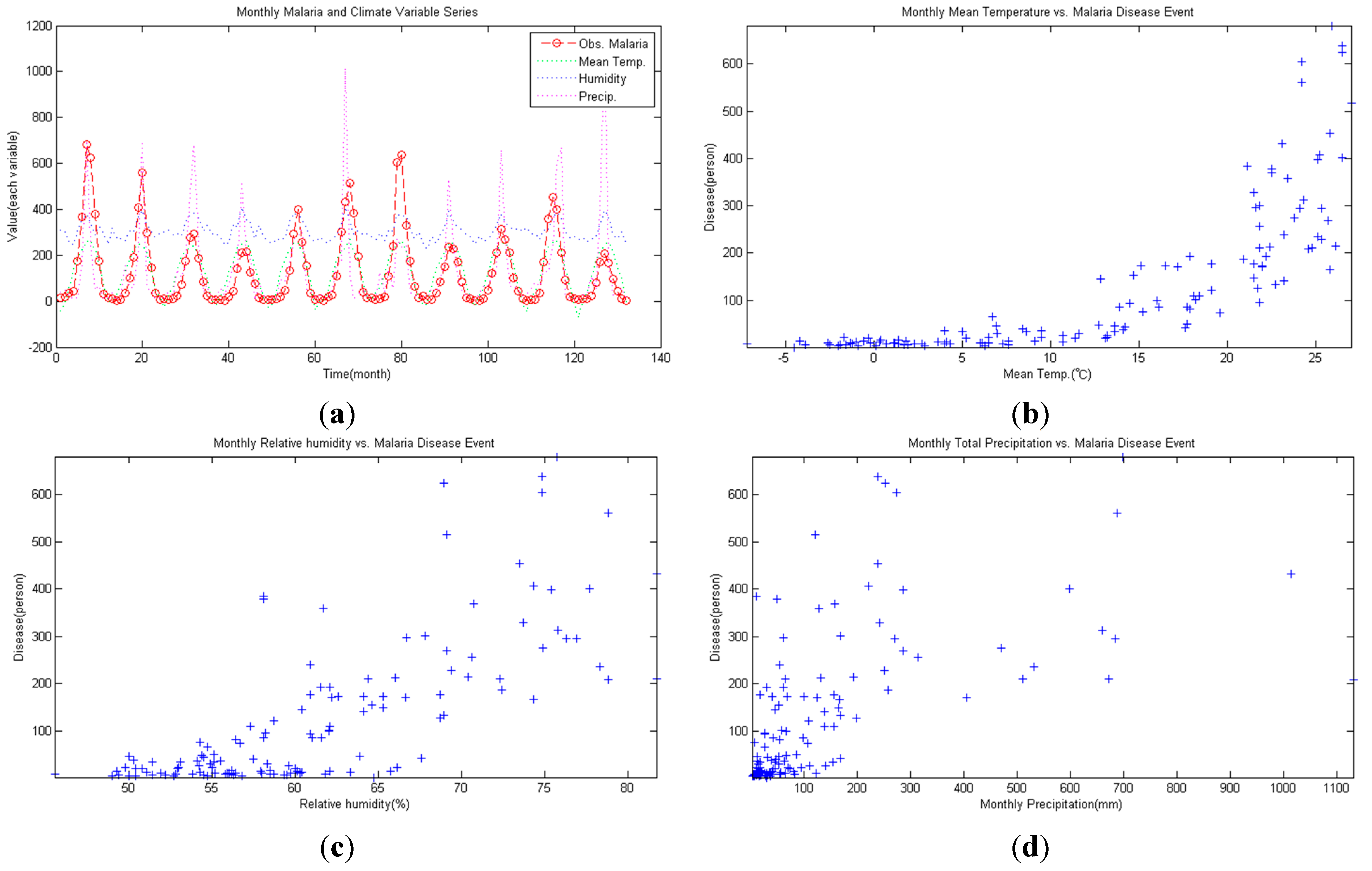
3. Methodology
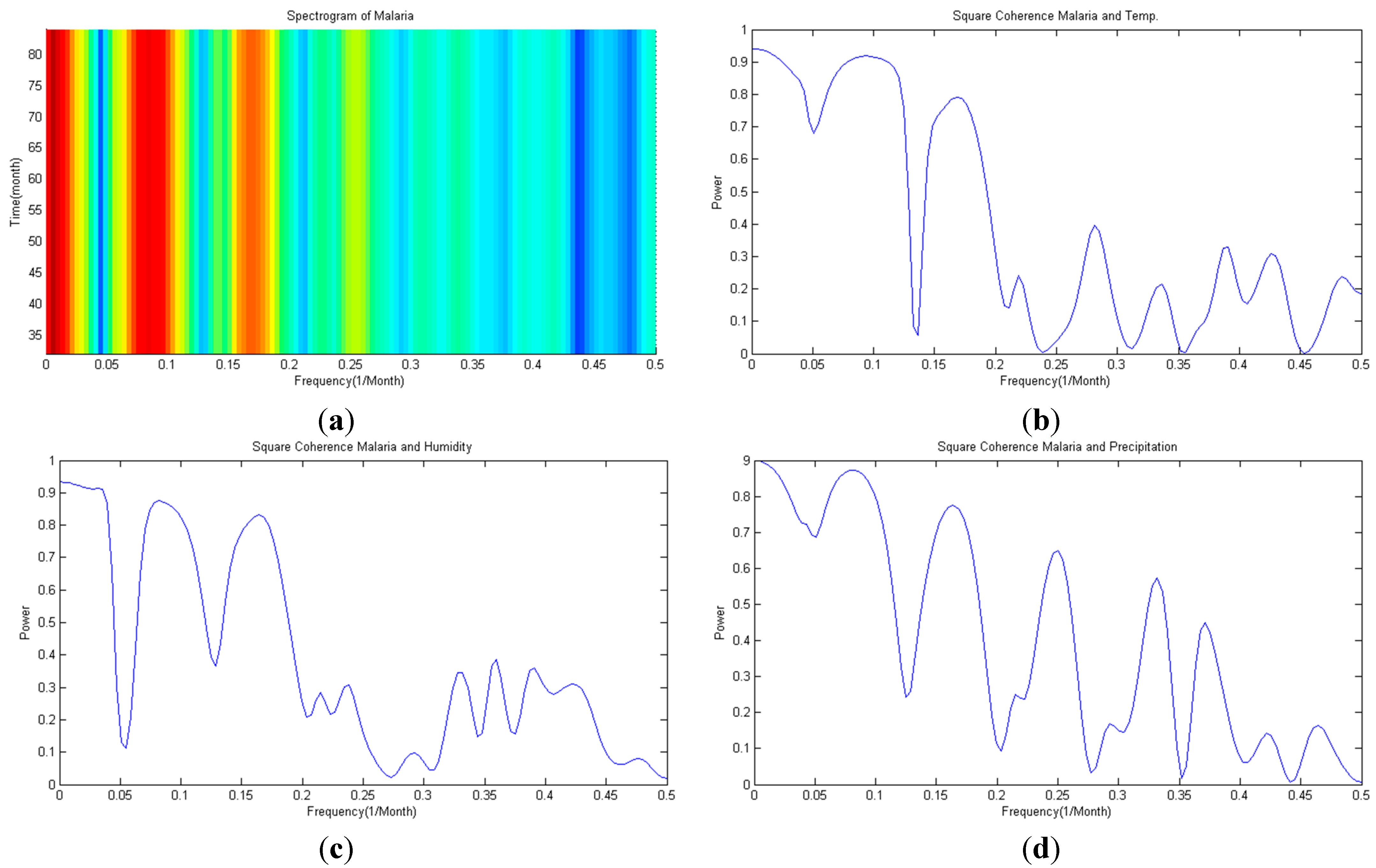
3.1. Spectral Analysis
3.2. Brock-Dechert-Scheinkman(BDS) Statistic
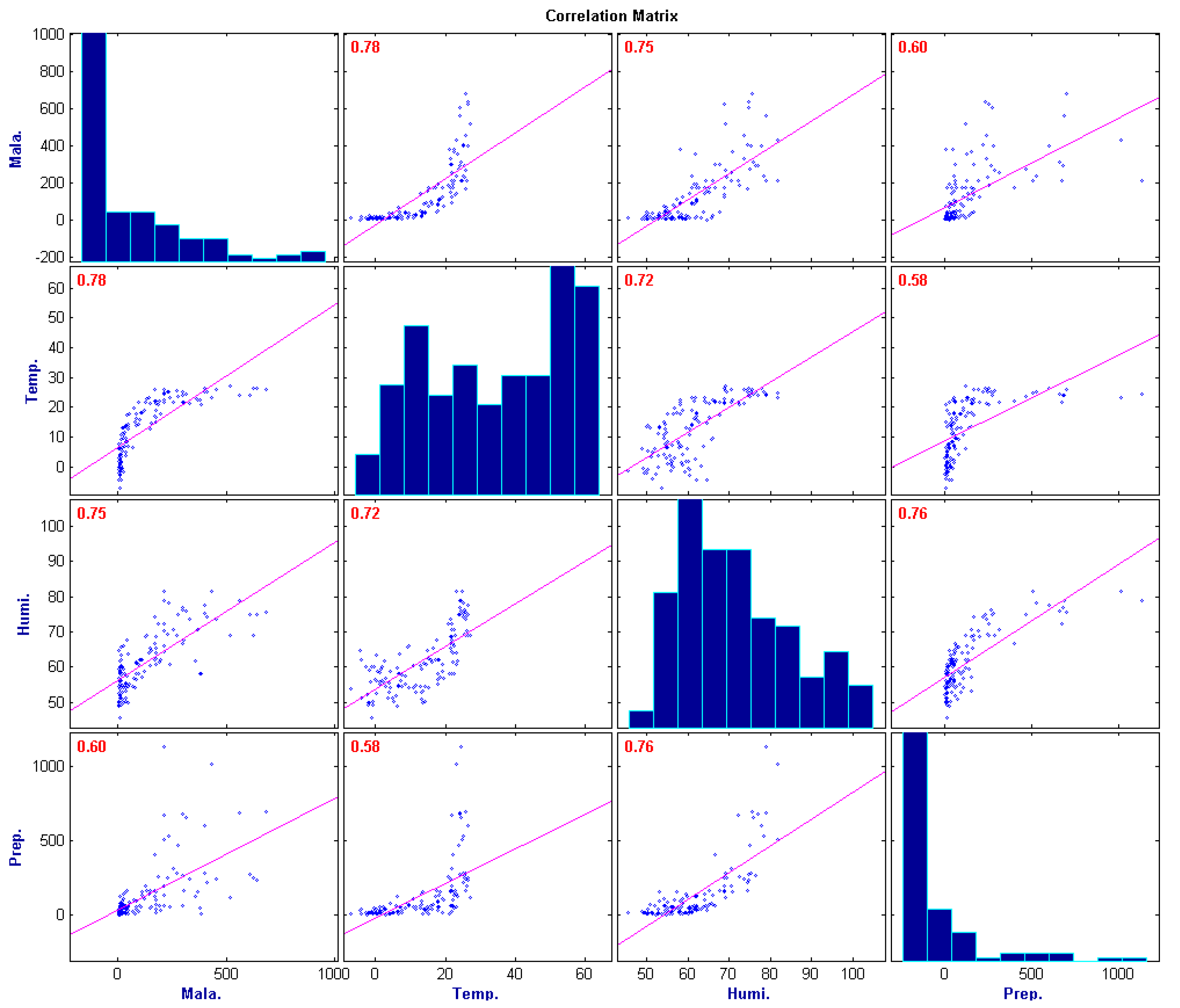
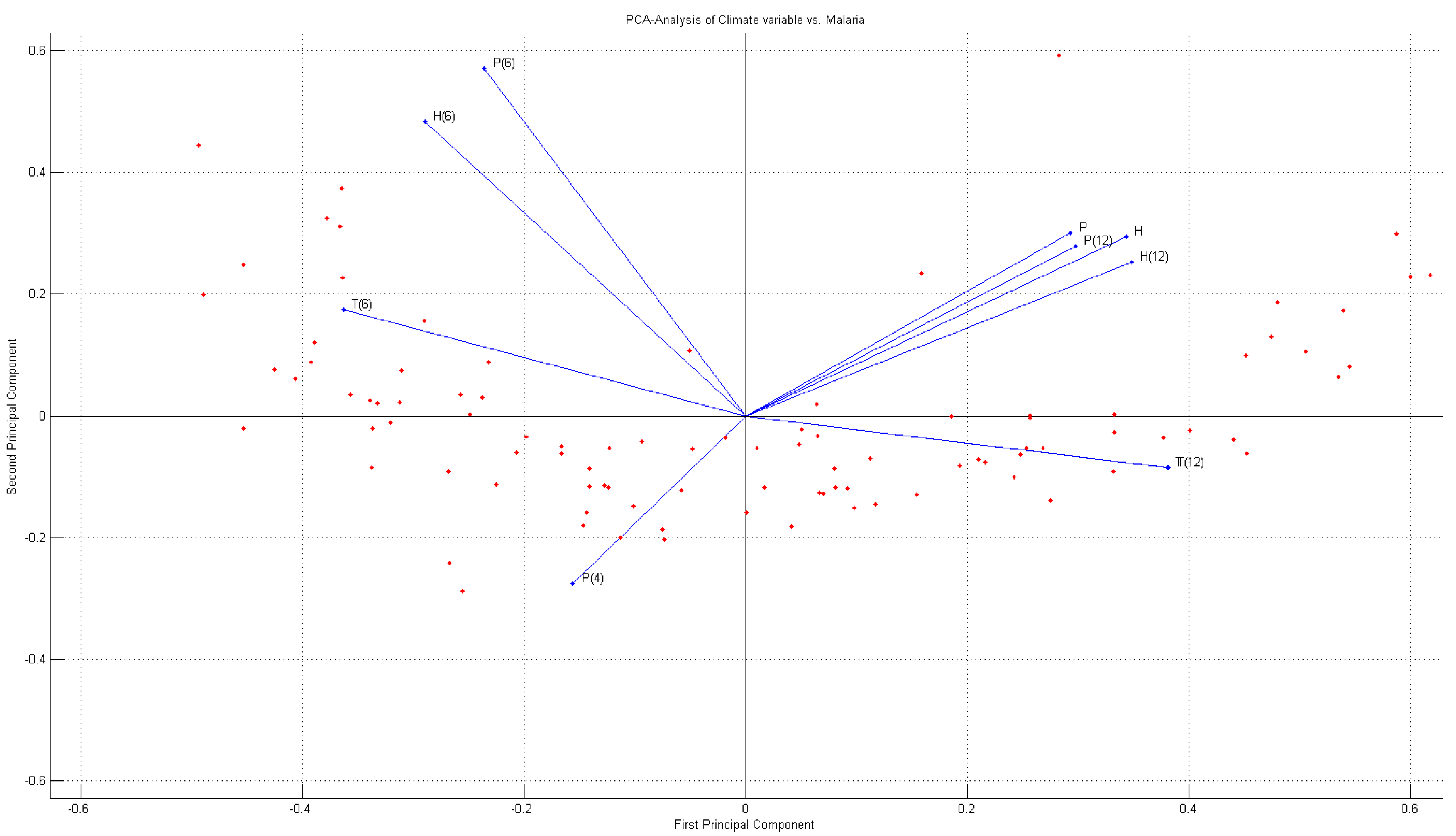
3.3. Principal Components Regression
4. Modeling of Malaria and Climate Variables
4.1. Nonlinear Regression Analysis
| Test method | Test statistic | 95% C. I. | Randomness Check | |
|---|---|---|---|---|
| Run Test | −7.3261 | [−1.96, +1.96] | X | |
| Anderson | 0.1741 | [−1.65. +1.65] | O | |
| Spearman | 0.5760 | [−1.96, +1.96] | O | |
| Turning Point | −11.9868 | [−1.96, +1.96] | X | |
| BDS(2) | 10.5150 | [−1.96, +1.96] | X | |
| BDS(3) | 9.7895 | [−1.96, +1.96] | X | |
| BDS(4) | 9.2964 | [−1.96, +1.96] | X | |
| BDS(5) | 8.9231 | [−1.96, +1.96] | X |
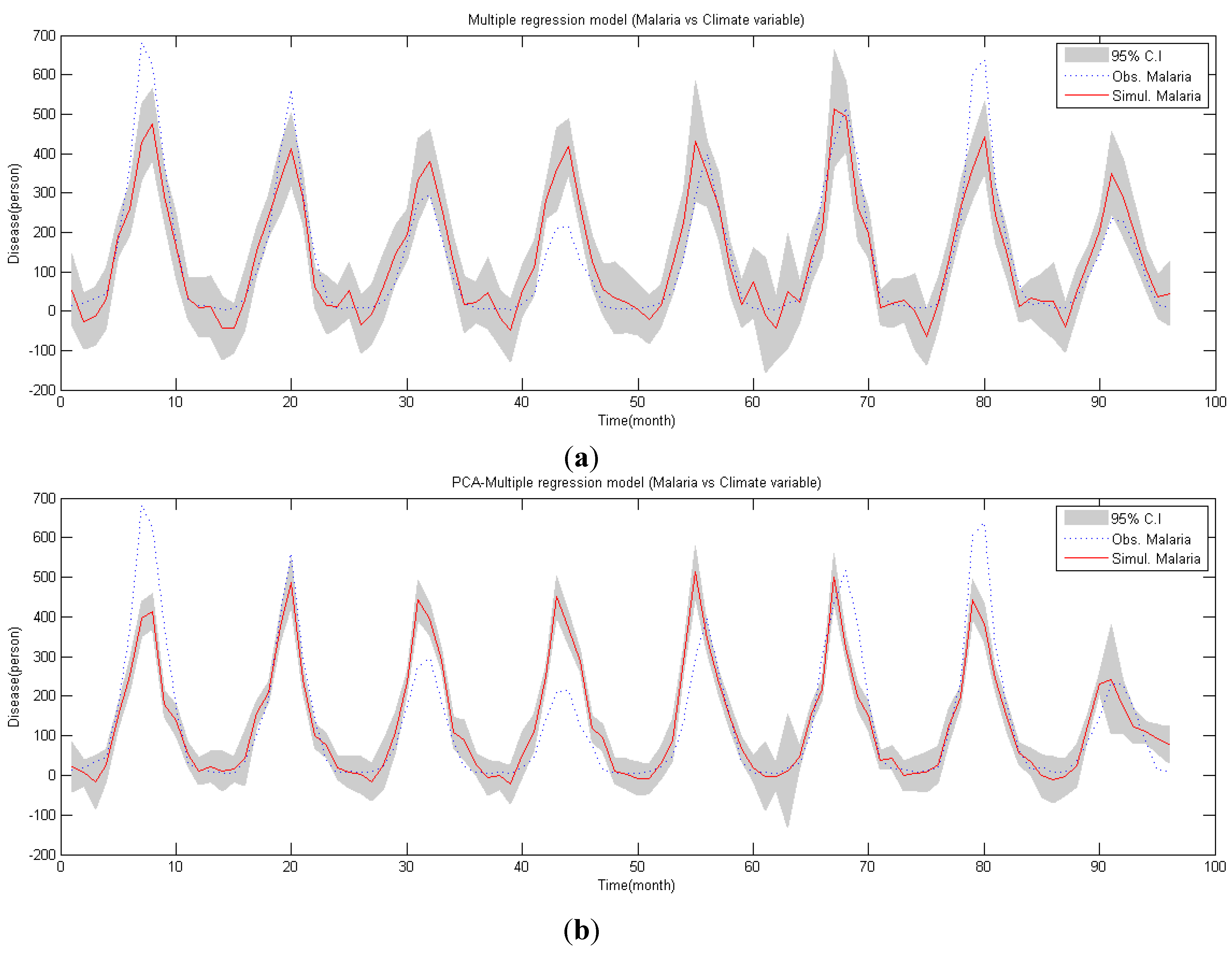
4.2. PCA-Regression Analysis
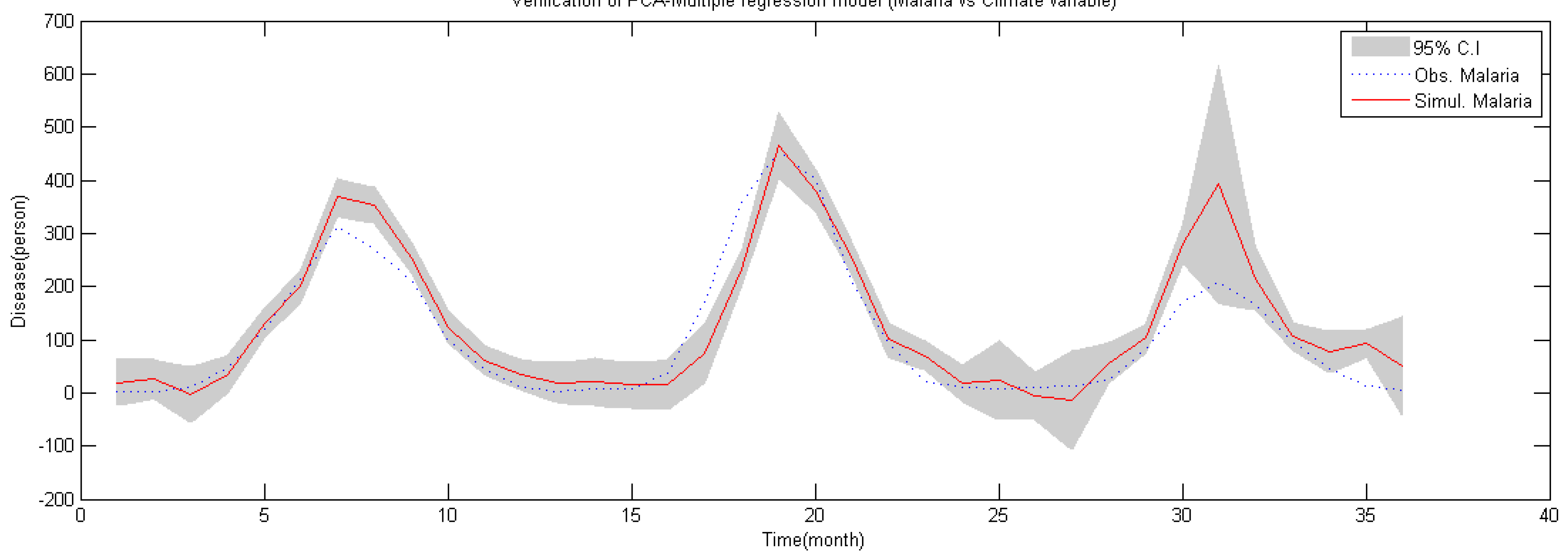
4.3. Validation of Malaria Model
5. Malaria Occurrence under Climate Change
5.1. Climate Change Scenario
| Senarios | Description | CO density (ppm) |
|---|---|---|
| RCP 2.6 | Peak in radiative forcing at ~3 W/m before 2100 year and then decline | 490 |
| RCP 4.5 | Stabilization without overshoot pathway to ~4.5 W/m at stabilization after 2100 year | 650 |
| RCP 6.0 | Stabilization without overshoot pathway to ~6 W/m at stabilization after 2100 year | 850 |
| RCP 8.5 | Rising radiative forcing pathway leading to 8.5 W/m by 2100 year | 1370 |
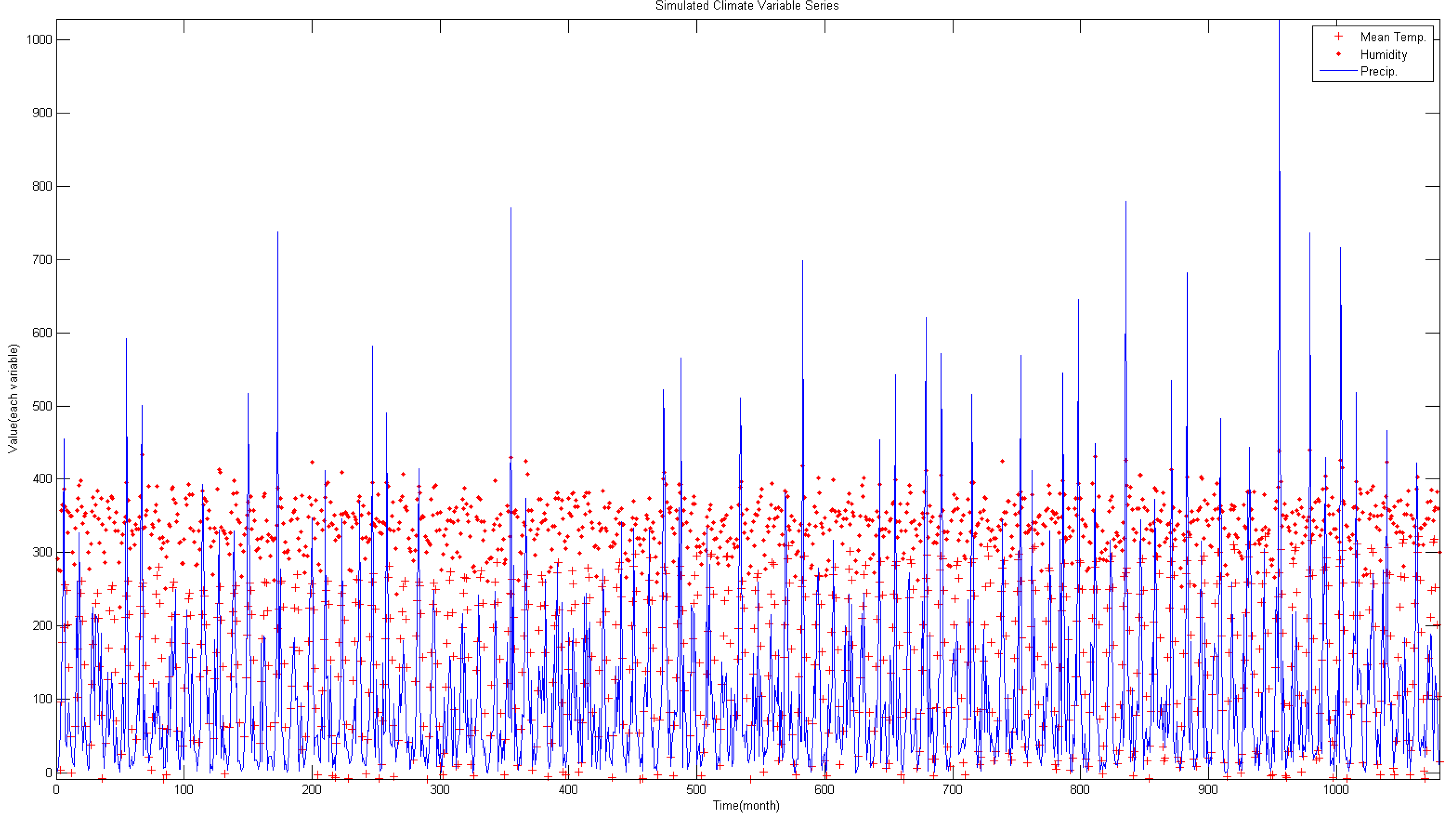
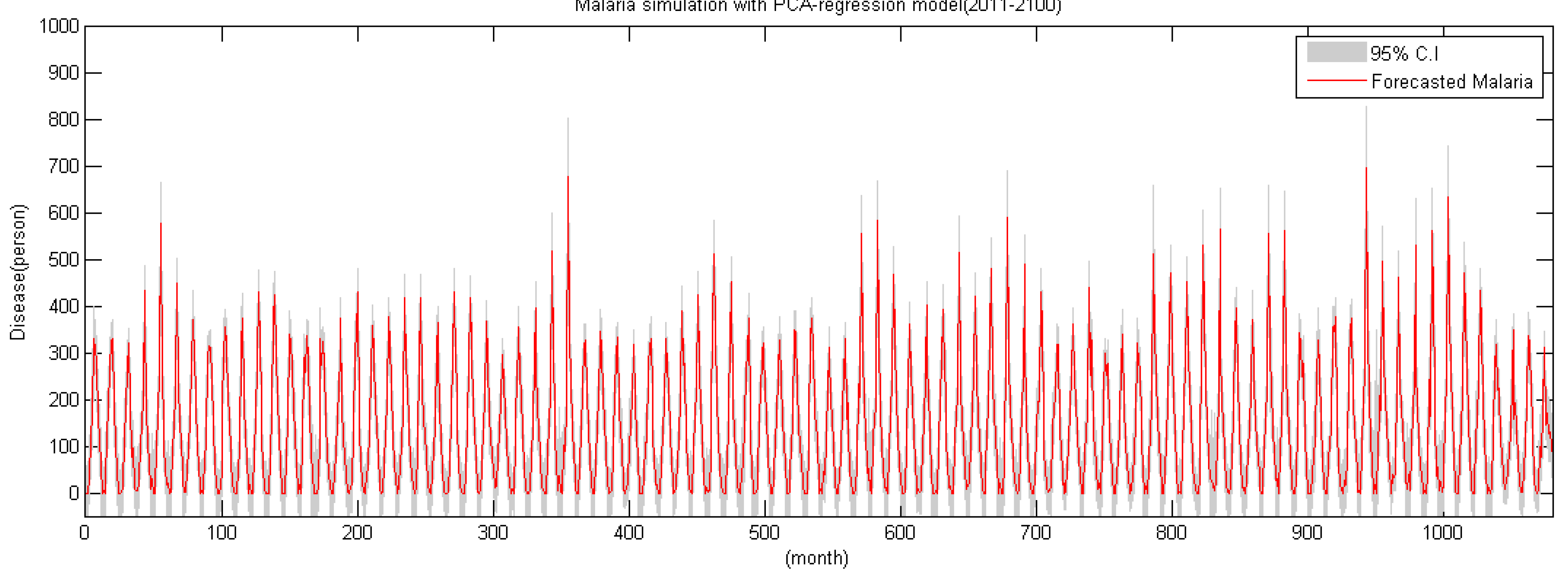
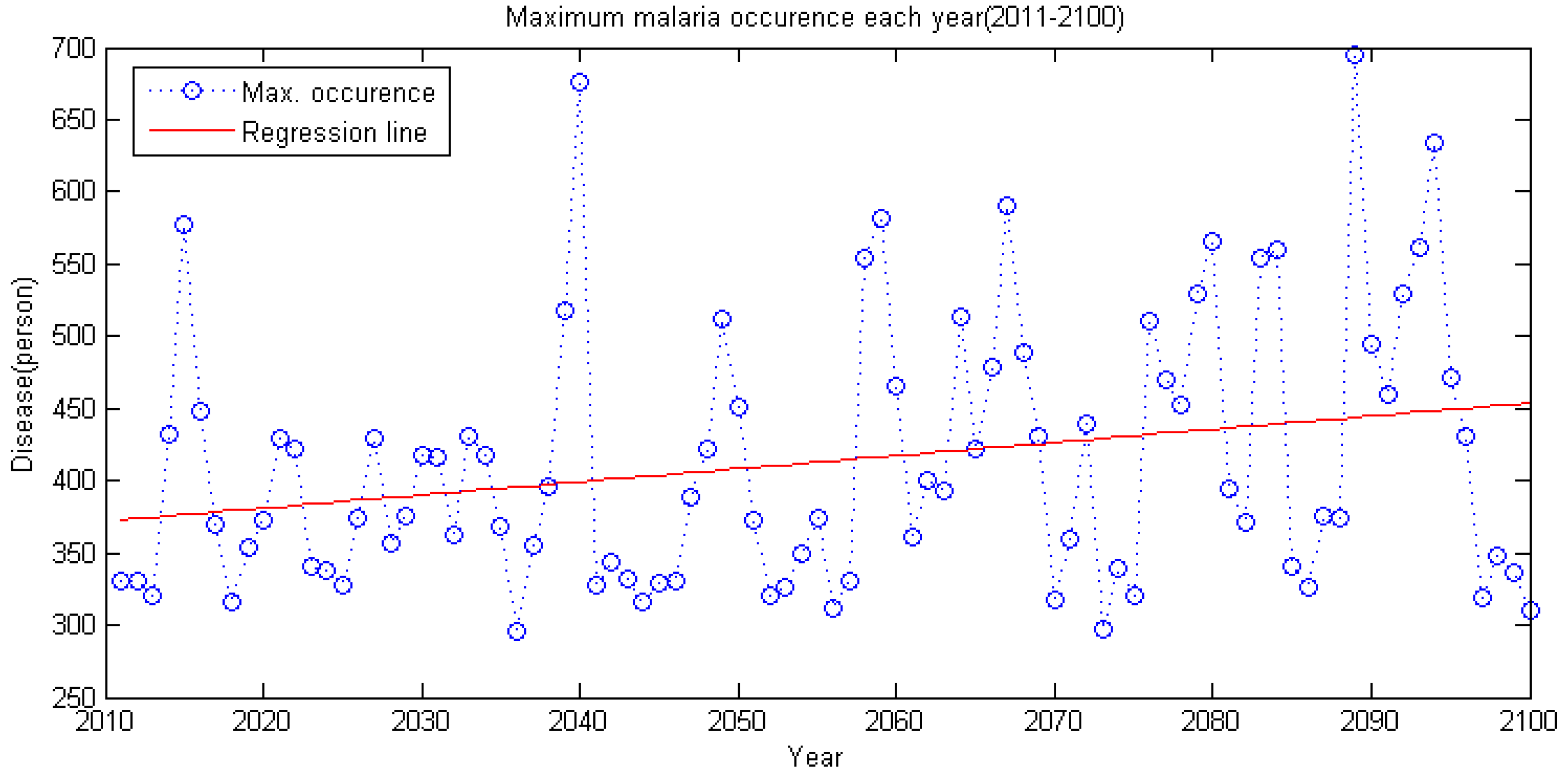
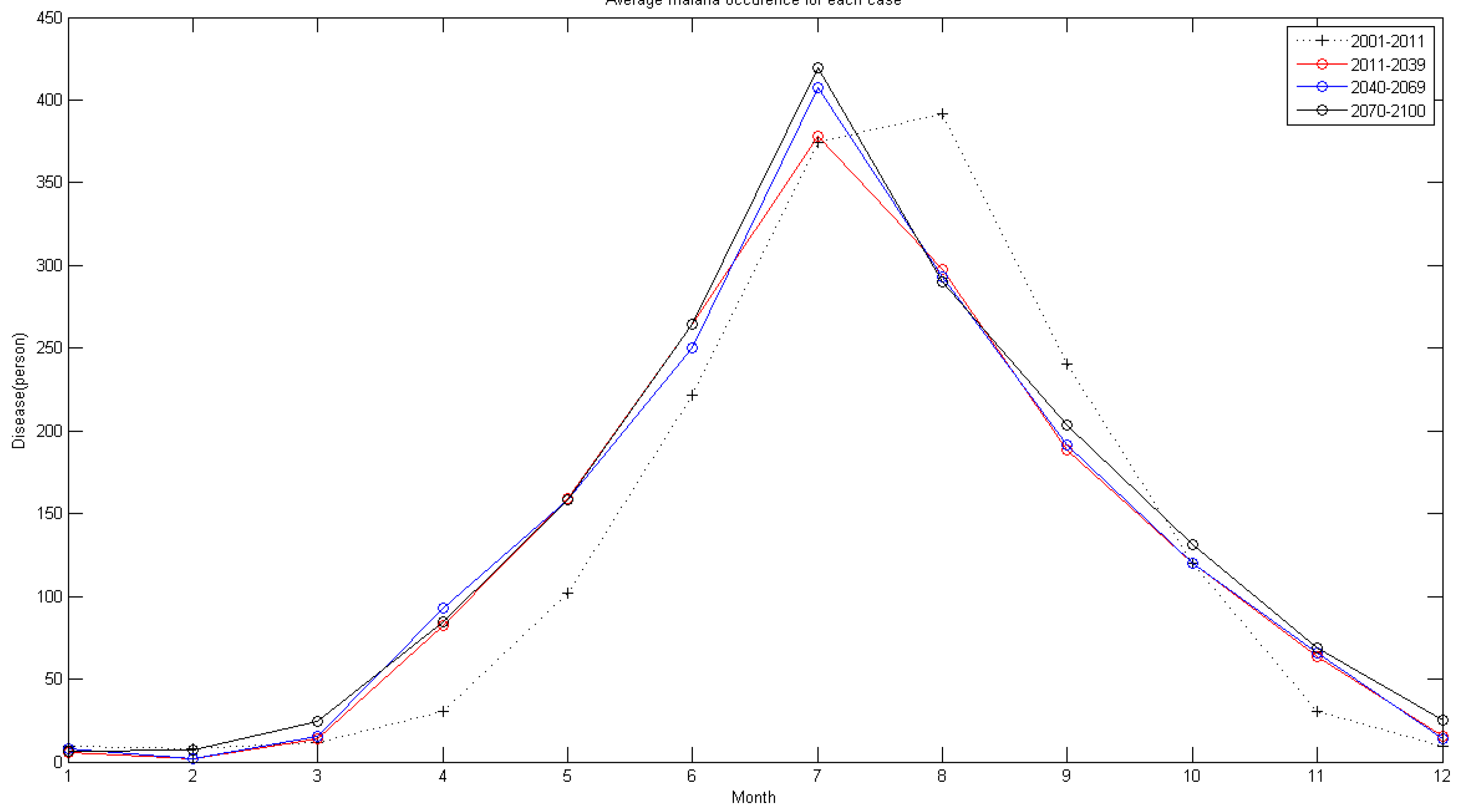
5.2. Future Malaria Simulation and Analysis

6. Conclusions
- Correlation between malaria occurrence and monthly average temperature, relative humidity and precipitation data is analyzed with time lag effect between malaria occurrence and climate variables using spectral analysis between each variable. A strong coherency between each climate variable data is clear, thus regression model is analyzed under the influence of multicollinearity. To resolve this issue, principal component regression analysis based on PCA is used to establish a regression model. Using the regression model, malaria infection occurrences from 2009–2011 are tested and coefficient of determination is 0.852, NRSE is 0.117 and RE is 0.026, which clearly accounts for malaria infection.
- By applying climate data between 2011 and 2100 using the RCP 4.5 climate change scenario and the CNCM3 climate model to the regression model, future malaria occurrence is simulated. Analysis of simulated data shows the malaria occurrence trend in general will gradually increase. Also, in the future, the occurrence period will diminish and it shows an increase of malaria occurrence before the rainy season in summer; thus, adaptation in the malaria occurrence response plan of Korea is needed.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jang, J.Y.; Cho, S.H.; Kim, S.Y.; Cho, S.N.; Kim, M.S.; Baek, K.W. Assessment of Climate Change Impact and Preparation of Adaptation Program in Korea; Ministry of Environment: Seoul, Korea, 2003. [Google Scholar]
- Patz, J.A.; Olson, S.H. Malaria risk and temperature: Influences from global climate change and local land use practices. Proc. Natl. Acad. Sci. 2006, 103, 5635–5636. [Google Scholar] [CrossRef]
- Poveda, G.; Rojas, W.; Qui.nones, M.L.; Velez, I.D.; Mantilla, R.I.; Ruiz, D.; Zuluaqa, J.S.; Rua, G.L. Coupling between annual and ENSO timescales in the malaria-climate association in Colombia. Environmental health perspectives 2001, 109, 489–493. [Google Scholar]
- Craig, M.H.; Snow, R.W.; Le Sueur, D. A climate-based distribution model of malaria transmission in sub-Saharan Africa. Parasitology today 1999, 15, 105–110. [Google Scholar] [CrossRef]
- Paaijmans, K.P.; Read, A.F.; Thomas, M.B. Understanding the link between malaria risk and climate. Proc. Natl. Acad. Sci. 2009, 106, 13844–13849. [Google Scholar] [CrossRef]
- Paaijmans, K.P.; Blanford, S.; Bell, A.S.; Blanford, J.I.; Read, A.F.; Thomas, M.B. Influence of climate on malaria transmission depends on daily temperature variation. Proc. Natl. Acad. Sci. 2010, 107, 15135–15139. [Google Scholar] [CrossRef]
- Olson, S.H.; Gangnon, R.; Elguero, E.; Durieux, L.; Gu, L.; Foley, J.A.; Patz, J.A. Links between climate, malaria, and wetlands in the Amazon Basin. Emerg. Infect. Dis. 2009, 15. [Google Scholar] [CrossRef]
- Kuhn, K.; Campbell-Lendrum, D.; Haines, A.; Cox, J.; CorvalHa, C.; Anker, M.; Malaria, R.B. Using Climate to Predict Infectious Disease Epidemics; World Health Organization: Geneva, Switzerland, 2005. [Google Scholar]
- Thomson, M.C.; Doblas-Reyes, F.J.; Mason, S.J.; Hagedorn, R.; Connor, S.J.; Phindela, T.; Palmer, T.N. Malaria early warnings based on seasonal climate forecasts from multi-model ensembles. Nature 2006, 439, 576–579. [Google Scholar] [CrossRef]
- Jhajharia, D.; Chattopadhyay, S.; Choudhary, R.; Dev, V.; Singh, V.P.; Lal, S. Influence of climate on incidences of malaria in the Thar desert, northwest India. Int. J. Climatol. 2013, 33, 312–325. [Google Scholar] [CrossRef]
- Martens, W.J.; Niessen, L.W.; Rotmans, J.; Jetten, T.H.; McMichael, A.J. Potential impact of global climate change on malaria risk. Environ. Health Perspect. 1995, 103, 458–464. [Google Scholar] [CrossRef]
- Kleinschmidt, I.; Bagayoko, M.; Clarke, G.P.Y.; Craig, M.; Le Sueur, D. A spatial statistical approach to malaria mapping. Int. J. Epidemiol. 2000, 29, 355–361. [Google Scholar] [CrossRef]
- Minakawa, N.; Sonye, G.; Mogi, M.; Githeko, A.; Yan, G. The effects of climatic factors on the distribution and abundance of malaria vectors in Kenya. J. Med. Entomol. 2002, 39, 833–841. [Google Scholar] [CrossRef]
- Small, J.; Goetz, S.J.; Hay, S.I. Climatic suitability for malaria transmission in Africa. Proc. Natl. Acad. Sci. 2003, 100, 15341–15345. [Google Scholar] [CrossRef]
- Zhou, G.; Minakawa, N.; Githeko, A.K.; Yan, G. Association between climate variability and malaria epidemics in the East African highlands. Proc. Natl. Acad. Sci. U.S.A. 2004, 101, 2375–2380. [Google Scholar] [CrossRef]
- Martens, P.; Kovats, R.S.; Nijhof, S.; De Vries, P.; Livermore, M.T.J.; Bradley, D.J.; McMichael, A.J. Climate change and future populations at risk of malaria. Global Environmental Change 1999, 9, S89–S107. [Google Scholar] [CrossRef]
- Hay, S.I.; Cox, J.; Rogers, D.J.; Randolph, S.E.; Stern, D.I.; Shanks, G.D.; Snow, R.W. Climate change and the resurgence of malaria in the East African highlands. Nature 2002, 415, 905–909. [Google Scholar] [CrossRef]
- Loevinsohn, M.E. Climatic warming and increased malaria incidence in Rwanda. Lancet 1994, 343, 714–718. [Google Scholar] [CrossRef]
- Patz, J.A.; Campbell-Lendrum, D.; Holloway, T.; Foley, J.A. Impact of regional climate change on human health. Nature 2005, 438, 310–317. [Google Scholar] [CrossRef]
- Rohr, J.R.; Dobson, A.P.; Johnson, P.T.; Kilpatrick, A.M.; Paull, S.H.; Raffel, T.R.; Thomas, M.B. Frontiers in climate change–disease research. Trends Ecol. Evol. 2011, 26, 270–277. [Google Scholar] [CrossRef]
- Ermert, V.; Fink, A.H.; Morse, A.P.; Jones, A.E.; Paeth, H.; Di Giuseppe, F.; Tompkins, A.M. Development of dynamical weather-disease models to project and forecast malaria in Africa. Malar. J. 2012a, 11. [Google Scholar] [CrossRef]
- Ermert, V.; Fink, A.H.; Morse, A.P.; Paeth, H. The impact of regional climate change on malaria risk due to greenhouse forcing and land-use changes in tropical Africa. Environ. Health Perspect. 2012b, 120, 77–84. [Google Scholar]
- Van Lieshout, M.; Kovats, R.S.; Livermore, M.T.J.; Martens, P. Climate change and malaria: Analysis of the SRES climate and socio-economic scenarios. Glob. Environ. Change 2004, 14, 87–99. [Google Scholar] [CrossRef]
- Tanser, F.C.; Sharp, B.; Le Sueur, D. Potential effect of climate change on malaria transmission in Africa. Lancet 2003, 362, 1792–1798. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Sharma, C.; Dhiman, R.C.; Mitra, A.P. Climate change and malaria in India. Curr. Science-Bangalore 2006, 90, 369–375. [Google Scholar]
- Haines, A.; Kovats, R.S.; Campbell-Lendrum, D.; Corvalan, C. Climate change and human health: impacts, vulnerability and public health. Public Health 2006, 120, 585–596. [Google Scholar] [CrossRef]
- Gage, K.L.; Burkot, T.R.; Eisen, R.J.; Hayes, E.B. Climate and vectorborne diseases. Am. J. Prev. Med. 2008, 35, 436–450. [Google Scholar] [CrossRef]
- Costello, A.; Abbas, M.; Allen, A.; Ball, S.; Bell, S.; Bellamy, R.; Patterson, C. Managing the health effects of climate change. Lancet 2009, 373, 1693–1733. [Google Scholar] [CrossRef]
- Greer, A.; Ng, V.; Fisman, D. Climate change and infectious diseases in North America: the road ahead. Can. Med. Assoc. J. 2008, 178, 715–722. [Google Scholar]
- Gething, P.W.; Smith, D.L.; Patil, A.P.; Tatem, A.J.; Snow, R.W.; Hay, S.I. Climate change and the global malaria recession. Nature 2010, 465, 342–345. [Google Scholar] [CrossRef]
- Parham, P.E.; Michael, E. Modeling the effects of weather and climate change on malaria transmission. Environ. Health Perspect. 2010, 118, 620–626. [Google Scholar] [CrossRef]
- Korea Centers for Disease Control and Prevention. Available online: http://www.cdc.go.kr/ (accessed on 10 October 2014).
- Kho, W.G. Reemergence of malaria in Korea. J. Korean Med. Assoc. 2007, 50, 959–966. [Google Scholar] [CrossRef]
- Epstein, P.R.; Diaz, H.F.; Elias, S.; Grabherr, G.; Graham, N.E.; Martens, W.J.; Susskind, J. Biological and physical signs of climate change: focus on mosquito-borne diseases. Bull. Am. Meteorol. Soc. 1998, 79, 409–417. [Google Scholar] [CrossRef]
- Chung, Y.S.; Yoon, M.B.; Kim, H.S. On climate variations and changes observed in South Korea. Clim. Change 2004, 66, 151–161. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computation, 3rd ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Strang, G. Linear Algebra and Its Applications, 9th ed.; Thomsom Leaning: London, UK, 1998. [Google Scholar]
- Dennis, W.R. Echo Signal Processing, 1st ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Brock, W.A.; Heish, D.A.; Lebaron, B. Nonlinear Dynamics, Chaos, and Instability: Statiscal Theory and Economic Evidence, 1st ed.; The MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Brock, W.A.; Dechert , W.D.; Scheinkman, J.A.; Lebaron, B. A test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Kim, H.S.; Kang, D.S.; Kim, J.H. The BDS statistic and residual test. Stoch. Environ. Res. Risk Assess. 2003, 17, 104–115. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Very Fast and Correctly Sized Estimation of the BDS Statistic. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=151669 (accessed on 10 October 2014).
- Gujarati, D. Multicollinearity: What happens if the regressors are correlated? In Basic Econometrics, 4th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Draper, N.; Smith, H. Applied Regression Analysis, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Chatterjee, S.; Hadi, A.S.; Price, B. Regression Analysis by Example, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Montgomery, D.C.; Peak, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Kutner, M.; Nachtsheim, C.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw Hill: New York, NY, USA, 2005. [Google Scholar]
- Morison, D.F. Multivariate Statistical Methods, 4th ed.; Thomsom Leaning: London, UK, 2005. [Google Scholar]
- Lin, M.; Wei, L. The small sample properties of the principal components estimator for regression coefficients. Commun. Statistic-Theory Methods 2002, 31, 271–283. [Google Scholar] [CrossRef]
- Shin, H.S.; Yun, S.M.; Jung, K.H.; Lee, S.H. Climate change, food-borne disease prediction, and future impact. Health Soc. Welf. Rev. 2011, 29, 217–237. [Google Scholar]
- Kim, S.H.; Jang, J.Y. Correlations between climate change-related infectious diseases and meteorological factors in Korea. J. Prev. Med. Public Health 2010, 43, 436–444. [Google Scholar] [CrossRef]
- Salas, J.D.; Smith, R.A.; Tabios, G.Q., III; Heo, J.H. Colorado State University: Fort Collins, CO, USA, Unpublished work. 1993.
- Armstrong, J.S.; Collopy, F. Error measures For generalizing about forecasting methods: Empirical comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; van Vuuren, D.P.; Wilbanks, T.J. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.F.; van Vuuren, D.P.P. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Change 2011, 109, 213–241. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Rose, S.K. The representative concentration pathways: An overview. Clim. Change 2011, 109, 5–31. [Google Scholar]
- Arora, V.K.; Scinocca, J.F.; Boer, G.J.; Christian, J.R.; Denman, K.L.; Flato, G.M.; Merryfield, W.J. Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Reisinger, A.; Meinshausen, M.; Manning, M. Future changes in global warming potentials under representative concentration pathways. Environ. Res. Lett. 2011, 6, 1–8. [Google Scholar] [CrossRef]
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Edmonds, J.A. RCP4. 5: A pathway for stabilization of radiative forcing by 2100. Clim. Change 2011, 109, 77–94. [Google Scholar] [CrossRef]
- Emanuel, W.R.; Janetos, A.C. Implications of Representative Concentration Pathway 4.5 Methane Emissions to Stabilize Radiative Forcing (No. PNNL-22203); Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2013. [Google Scholar]
- Good, P.; Gregory, J.M.; Lowe, J.A.; Andrews, T. Abrupt CO2 experiments as tools for predicting and understanding CMIP5 representative concentration pathway projections. Clim. Dyn. 2013, 40, 1041–1053. [Google Scholar] [CrossRef]
- Kwon, Y.; Kwon, W.; Boo, O. Future projections on the change of onset date and duration of natural seasons using SRES A1B data in South Korea. J. Korean Geogr. Soc. 2007, 42, 835–850. [Google Scholar]
- So, B. J.; Kim, M. J.; Kwon, H. H. Evaluation of the next generation scenarios for climate change of KMA. Mag. Korea Water Res. Assoc. 2012, 45, 56–70. [Google Scholar]
- Regional climate projection for East Asia and Korea using the HadGEM3-RA. Available online: http://meetingorganizer.copernicus.org/3ICESM/3ICESM-236-2.pdf (accessed on 10 October 2014).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, J.; Noh, H.; Kim, S.; Singh, V.P.; Hong, S.J.; Kim, D.; Lee, K.; Kang, N.; Kim, H.S. Future Climate Data from RCP 4.5 and Occurrence of Malaria in Korea. Int. J. Environ. Res. Public Health 2014, 11, 10587-10605. https://doi.org/10.3390/ijerph111010587
Kwak J, Noh H, Kim S, Singh VP, Hong SJ, Kim D, Lee K, Kang N, Kim HS. Future Climate Data from RCP 4.5 and Occurrence of Malaria in Korea. International Journal of Environmental Research and Public Health. 2014; 11(10):10587-10605. https://doi.org/10.3390/ijerph111010587
Chicago/Turabian StyleKwak, Jaewon, Huiseong Noh, Soojun Kim, Vijay P. Singh, Seung Jin Hong, Duckgil Kim, Keonhaeng Lee, Narae Kang, and Hung Soo Kim. 2014. "Future Climate Data from RCP 4.5 and Occurrence of Malaria in Korea" International Journal of Environmental Research and Public Health 11, no. 10: 10587-10605. https://doi.org/10.3390/ijerph111010587
APA StyleKwak, J., Noh, H., Kim, S., Singh, V. P., Hong, S. J., Kim, D., Lee, K., Kang, N., & Kim, H. S. (2014). Future Climate Data from RCP 4.5 and Occurrence of Malaria in Korea. International Journal of Environmental Research and Public Health, 11(10), 10587-10605. https://doi.org/10.3390/ijerph111010587







