May the Force (Field) Be with You: On the Importance of Conformational Searches in the Prediction of NMR Chemical Shifts
Abstract
1. Introduction
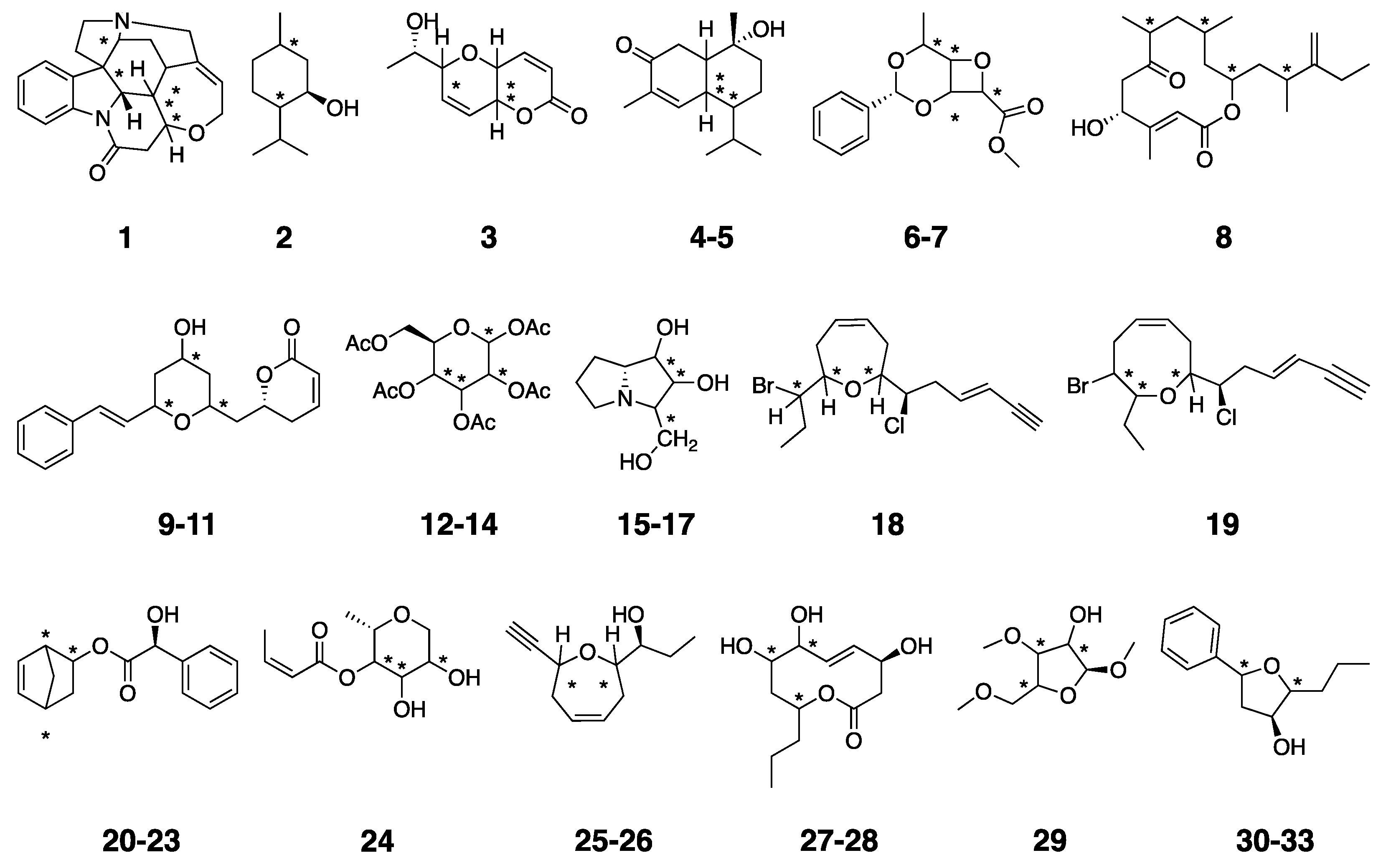
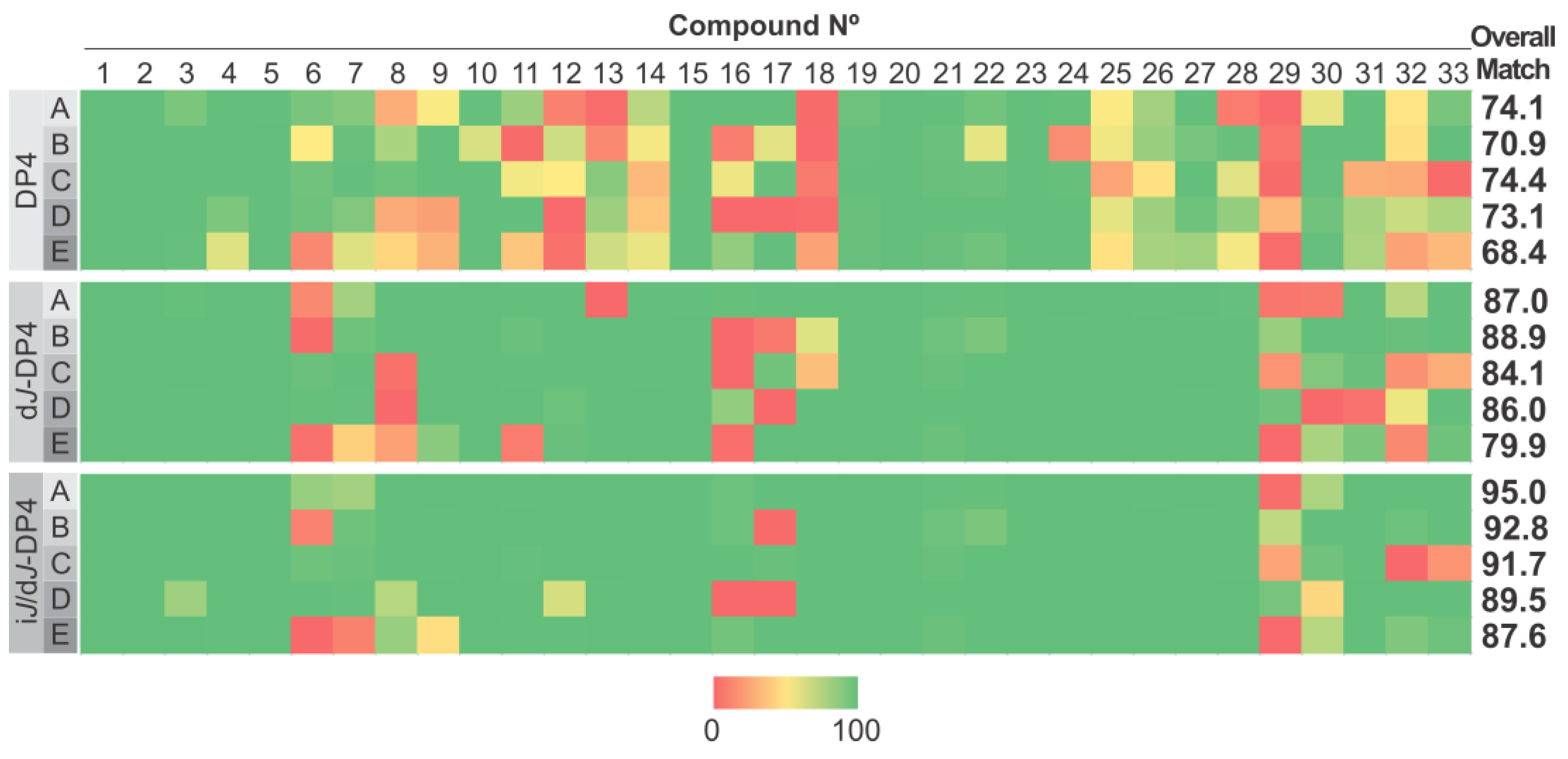
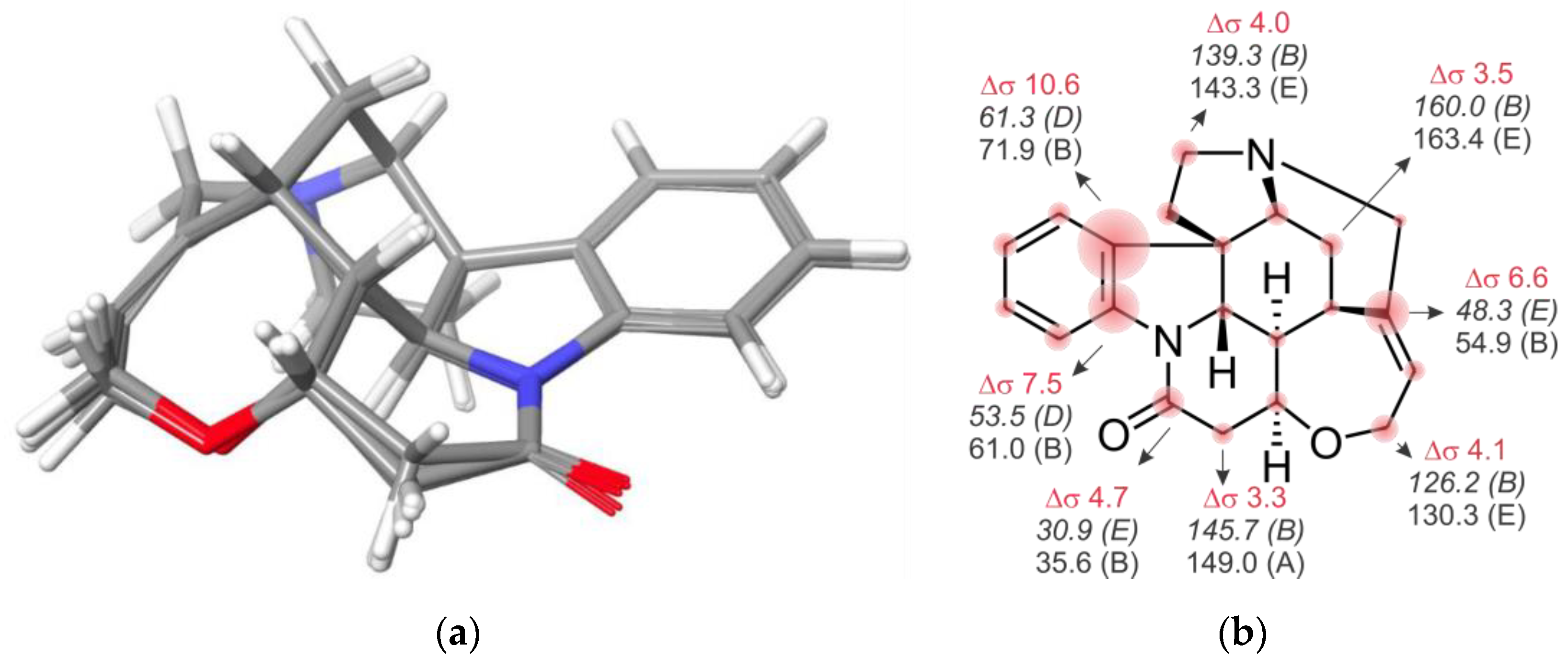
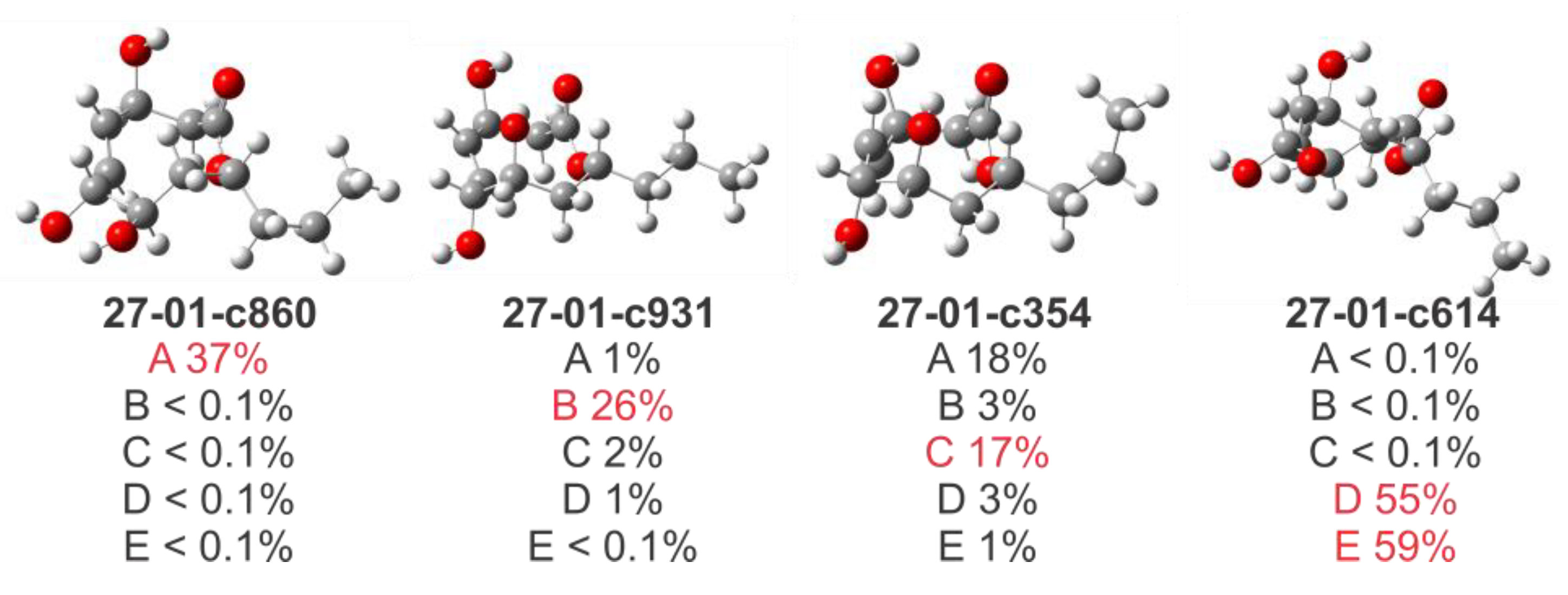
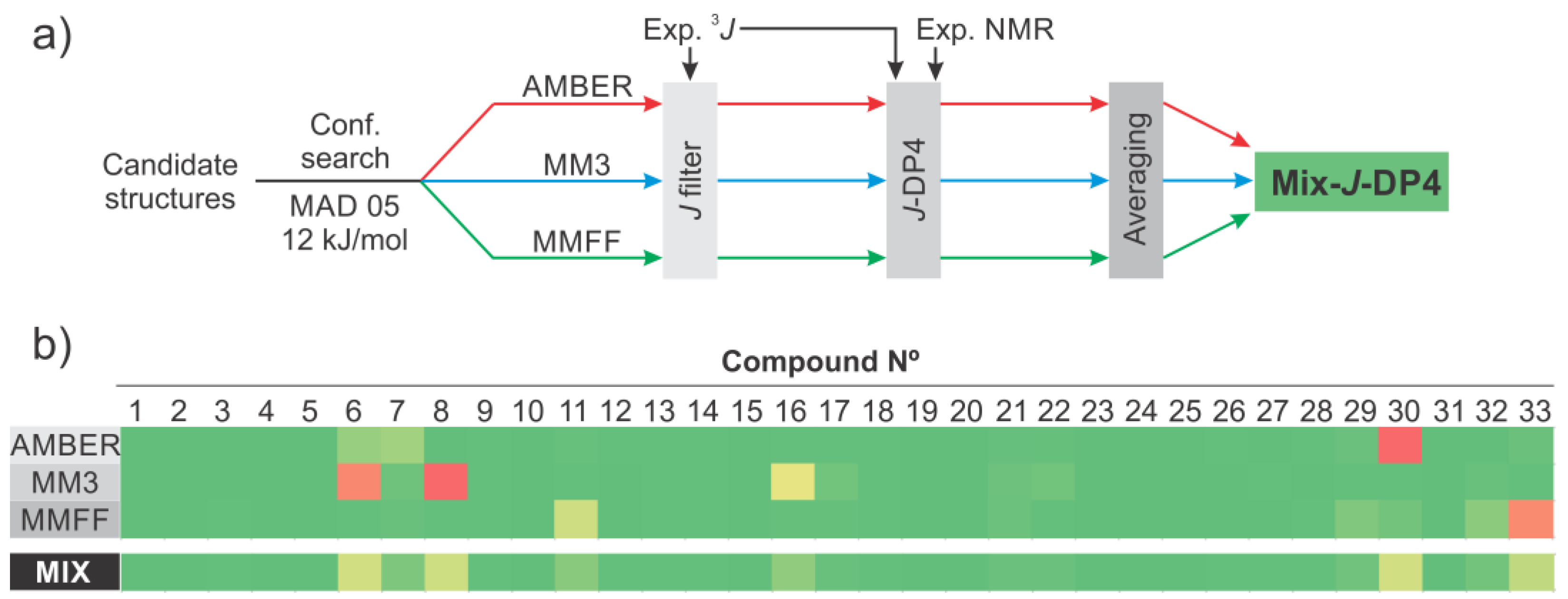
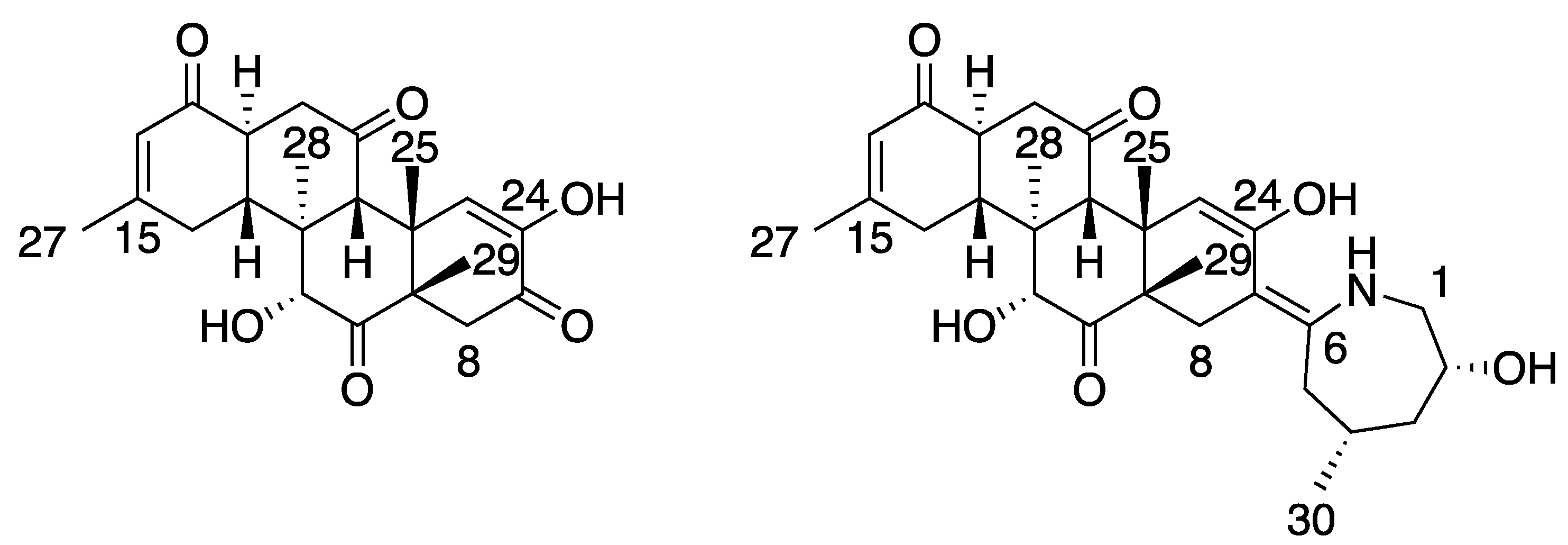
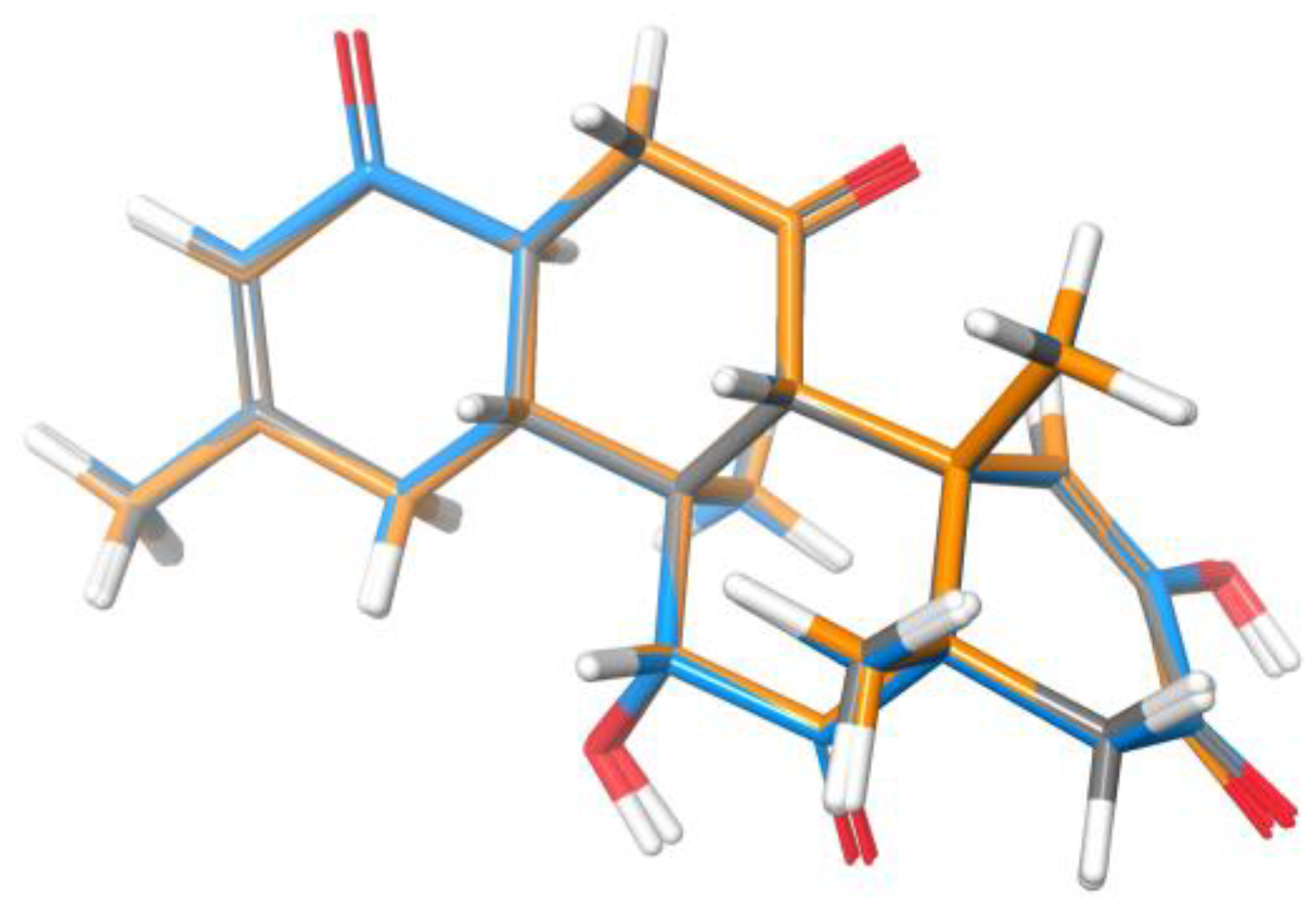
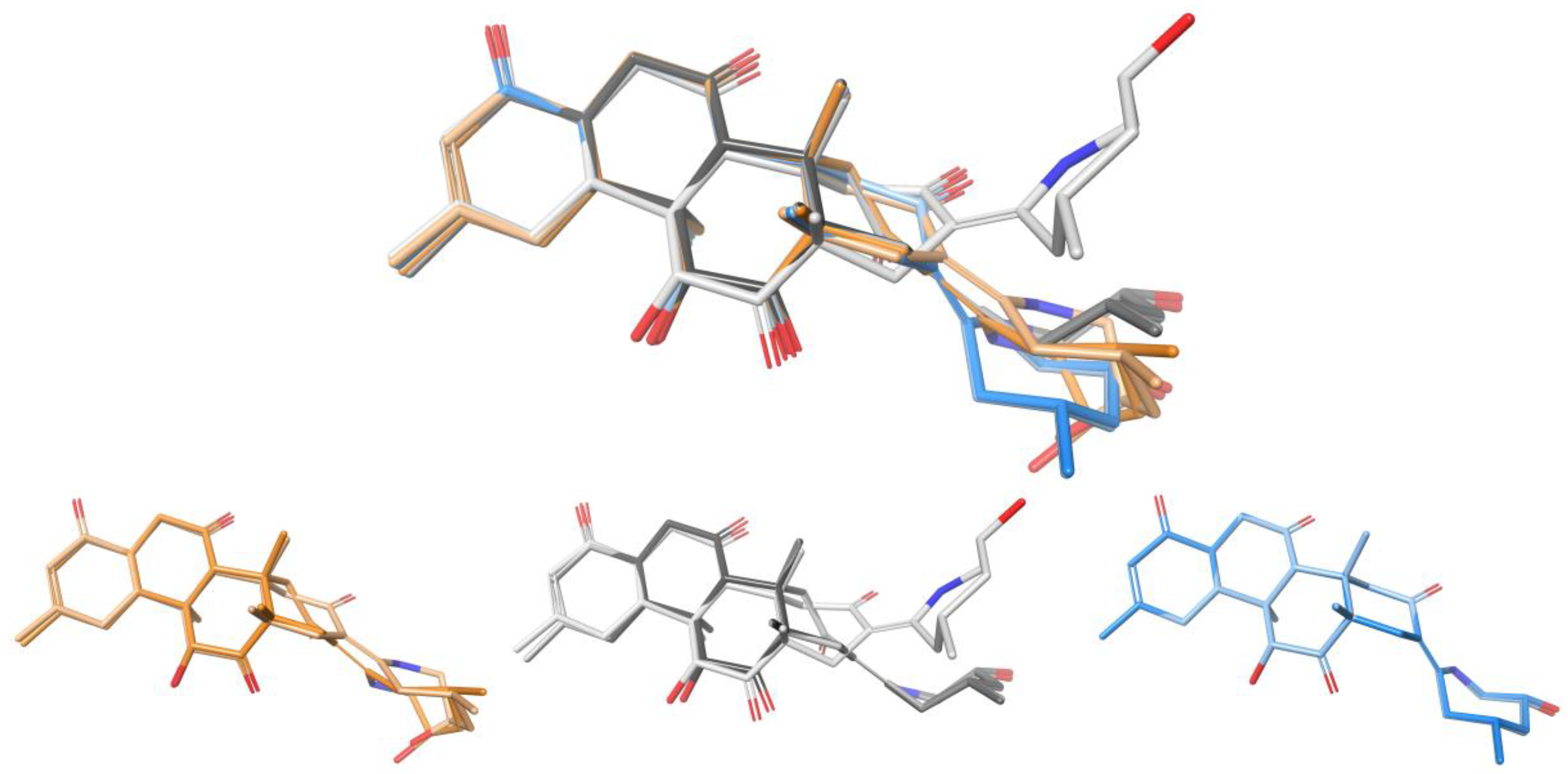
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Modern NMR Approaches to the Structure Elucidation of Natural Products; Rovnyak, D., Williams, A.J., Martin, G.E., Eds.; Royal Society of Chemistry: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Chhetri, B.K.; Lavoie, S.; Sweeney-Jones, A.M.; Kubanek, J. Recent trends in the structural revision of natural products. Nat. Prod. Rep. 2018, 35, 514–531. [Google Scholar] [CrossRef] [PubMed]
- Kutateladze, A.G.; Holt, T. Structure Validation of Complex Natural Products: Time to Change the Paradigm. What did Synthesis of Alstofolinine A Prove? J. Org. Chem. 2019, 84, 8297–8299. [Google Scholar] [CrossRef] [PubMed]
- Domínguez, H.J.; Napolitano, J.G.; Fernández-Sánchez, M.T.; Cabrera-García, D.; Novelli, A.; Norte, M.; Fernández, J.J.; Daranas, A.H. Belizentrin, a Highly Bioactive Macrocycle from the Dinoflagellate Prorocentrum belizeanum. Org. Lett. 2014, 16, 4546–4549. [Google Scholar] [CrossRef] [PubMed]
- Anderl, F.; Größl, S.; Wirtz, C.; Fürstner, A. Total Synthesis of Belizentrin Methyl Ester: Report on a Likely Conquest. Angew. Chem. Int. Ed. 2018, 57, 10712–10717. [Google Scholar] [CrossRef] [PubMed]
- Daranas, A.H.; Sarotti, A.M. Are Computational Methods Useful for Structure Elucidation of Large and Flexible Molecules? Belizentrin as a Case Study. Org. Lett. 2021, 23, 503–507. [Google Scholar] [CrossRef] [PubMed]
- Domínguez, H.J.; Cabrera-García, D.; Cuadrado, C.; Novelli, A.; Fernández-Sánchez, M.T.; Fernández, J.J.; Daranas, A.H. Prorocentroic Acid, a Neuroactive Super-Carbon-Chain Compound from the Dinoflagellate Prorocentrum hoffmannianum. Org. Lett. 2021, 23, 13–18. [Google Scholar] [CrossRef]
- Bifulco, G.; Dambruoso, P.; Gomez-Paloma, L.; Riccio, R. Determination of Relative Configuration in Organic Compounds by NMR Spectroscopy and Computational Methods. Chem. Rev. 2007, 107, 3744–3779. [Google Scholar] [CrossRef]
- Lodewyk, M.W.; Siebert, M.R.; Tantillo, D.J. Computational Prediction of 1H and 13C Chemical Shifts: A Useful Tool for Natural Product, Mechanistic, and Synthetic Organic Chemistry. Chem. Rev. 2012, 112, 1839–1862. [Google Scholar] [CrossRef]
- Marcarino, M.O.; Zanardi, M.M.; Cicetti, S.; Sarotti, A.M. NMR Calculations with Quantum Methods: Development of New Tools for Structural Elucidation and Beyond. Acc. Chem. Res. 2020, 53, 1922–1932. [Google Scholar] [CrossRef]
- Smith, S.G.; Goodman, J.M. Assigning Stereochemistry to Single Diastereoisomers by GIAO NMR Calculation: The DP4 Probability. J. Am. Chem. Soc. 2010, 132, 12946–12959. [Google Scholar] [CrossRef]
- Grimblat, N.; Zanardi, M.M.; Sarotti, A.M. Beyond DP4: An Improved Probability for the Stereochemical Assignment of Isomeric Compounds using Quantum Chemical Calculations of NMR Shifts. J. Org. Chem. 2015, 80, 12526–12534. [Google Scholar] [CrossRef]
- Grimblat, N.; Gavín, J.A.; Daranas, A.H.; Sarotti, A.M. Combining the Power of J Coupling and DP4 Analysis on Stereochemical Assignments: The J-DP4 Methods. Org. Lett. 2019, 21, 4003–4007. [Google Scholar] [CrossRef]
- Kutateladze, A.G.; Mukhina, O.A. Relativistic Force Field: Parametric Computations of Proton–Proton Coupling Constants in 1H NMR Spectra. J. Org. Chem. 2014, 79, 8397–8406. [Google Scholar] [CrossRef]
- Navarro-Vázquez, A.; Gil, R.R.; Blinov, K. Computer-Assisted 3D Structure Elucidation (CASE-3D) of Natural Products Combining Isotropic and Anisotropic NMR Parameters. J. Nat. Prod. 2018, 81, 203–210. [Google Scholar] [CrossRef]
- Gerrard, W.; Bratholm, L.A.; Packer, M.J.; Mulholland, A.J.; Glowacki, D.R.; Butts, C.P. IMPRESSION—Prediction of NMR parameters for 3-dimensional chemical structures using machine learning with near quantum chemical accuracy. Chem. Sci. 2019, 11, 508–515. [Google Scholar] [CrossRef]
- Guan, Y.; Sowndarya, S.V.S.; Gallegos, L.C.; John, P.C.S.; Paton, R.S. Real-time prediction of 1H and 13C chemical shifts with DFT accuracy using a 3D graph neural network. Chem. Sci. 2021, 12, 12012–12026. [Google Scholar] [CrossRef]
- Tsai, Y.-H.; Amichetti, M.; Zanardi, M.M.; Grimson, R.; Daranas, A.H.; Sarotti, A.M. ML-J-DP4: An Integrated Quantum Mechanics-Machine Learning Approach for Ultrafast NMR Structural Elucidation. Org. Lett. 2022, 24, 7487–7491. [Google Scholar] [CrossRef]
- Napolitano, J.G.; Norte, M.; Padrón, J.M.; Fernández, J.J.; Daranas, A.H. Belizeanolide, a Cytotoxic Macrolide from the DinoflagellateProrocentrum belizeanum. Angew. Chem. Int. Ed. 2009, 48, 796–799. [Google Scholar] [CrossRef]
- Lewis-Atwell, T.; Townsend, P.A.; Grayson, M.N. Comparisons of different force fields in conformational analysis and searching of organic molecules: A review. Tetrahedron 2021, 79, 131865. [Google Scholar] [CrossRef]
- Boudermine, S.; Parisi, V.; Lemoui, R.; Boudiar, T.; Chini, M.G.; Franceschelli, S.; Pecoraro, M.; Pascale, M.; Bifulco, G.; Braca, A.; et al. Cytotoxic Sesquiterpenoids from Ammoides atlantica Aerial Parts. J. Nat. Prod. 2022, 85, 647–656. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Riccio, R.; Lauro, G.; Bifulco, G.; Li, T.-J.; Tang, H.; Zhuang, C.-L.; Ma, H.; Sun, P.; et al. Chemistry and Selective Tumor Cell Growth Inhibitory Activity of Polyketides from the South China Sea Sponge Plakortis sp. Mar. Drugs 2017, 15, 129. [Google Scholar] [CrossRef] [PubMed]
- Jones, T.H.; Harrison, D.P.; Menegatti, C.; Mevers, E.; Knott, K.; Marek, P.; Hennen, D.A.; Kasson, M.T.; Macias, A.M.; Lovett, B.; et al. Deoxybuzonamine Isomers from the Millipede Brachycybe lecontii (Platydesmida: Andrognathidae). J. Nat. Prod. 2022, 85, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Sierra, S.; Gomez, M.V.; Jiménez, A.I.; Pop, A.; Silvestru, C.; Marín, M.L.; Boscá, F.; Sastre, G.; Gómez-Bengoa, E.; Urriolabeitia, E.P. Stereoselective, Ruthenium-Photocatalyzed Synthesis of 1,2-Diaminotruxinic Bis-amino Acids from 4-Arylidene-5(4H)-oxazolones. J. Org. Chem. 2022, 87, 3529–3545. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, M.T.; Alves, J.M.A.; Braga, A.A.C.; Wilson, D.J.D.; Barboza, C.A. Do Double-Hybrid Exchange–Correlation Functionals Provide Accurate Chemical Shifts? A Benchmark Assessment for Proton NMR. J. Chem. Theory Comput. 2021, 17, 6876–6885. [Google Scholar] [CrossRef] [PubMed]
- Han, B.Y.; Lam, N.Y.S.; MacGregor, C.I.; Goodman, J.M.; Paterson, I. A synthesis-enabled relative stereochemical assignment of the C1–C28 region of hemicalide. Chem. Commun. 2018, 54, 3247–3250. [Google Scholar] [CrossRef]
- Kouamé, T.; Bernadat, G.; Turpin, V.; Litaudon, M.; Okpekon, A.T.; Gallard, J.-F.; Leblanc, K.; Rharrabti, S.; Champy, P.; Poupon, E.; et al. Structure Reassignment of Melonine and Quantum-Chemical Calculations-Based Assessment of Biosynthetic Scenarios Leading to Its Revised and Original Structures. Org. Lett. 2021, 23, 5964–5968. [Google Scholar] [CrossRef]
- Allinger, N.L.; Yuh, Y.H.; Lii, J.H. Molecular mechanics. The MM3 force field for hydrocarbons. 1. J. Am. Chem. Soc. 1989, 111, 8551–8566. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Lu, C.; Wu, C.; Ghoreishi, D.; Chen, W.; Wang, L.; Damm, W.; Ross, G.A.; Dahlgren, M.K.; Russell, E.; Von Bargen, C.D.; et al. OPLS4: Improving Force Field Accuracy on Challenging Regimes of Chemical Space. J. Chem. Theory Comput. 2021, 17, 4291–4300. [Google Scholar] [CrossRef]
- Yu, J.S.; Park, M.; Pang, C.; Rashan, L.; Jung, W.H.; Kim, K.H. Antifungal Phenols from Woodfordia uniflora Collected in Oman. J. Nat. Prod. 2020, 83, 2261–2268. [Google Scholar] [CrossRef]
- Tan, X.; Han, X.; Teng, H.; Li, Q.; Chen, Y.; Lei, X.; Yang, G. Structural Elucidation of Garcipaucinones A and B From Garcinia paucinervis Using Quantum Chemical Calculations. J. Nat. Prod. 2021, 84, 972–978. [Google Scholar] [CrossRef]
- Li, S.-W.; Cuadrado, C.; Yao, L.-G.; Daranas, A.H.; Guo, Y.-W. Quantum Mechanical–NMR-Aided Configuration and Conformation of Two Unreported Macrocycles Isolated from the Soft Coral Lobophytum sp.: Energy Calculations versus Coupling Constants. Org. Lett. 2020, 22, 4093–4096. [Google Scholar] [CrossRef]
- Sarotti, A.M. In Silico Reassignment of (+)-Diplopyrone by NMR Calculations: Use of a DP4/J-DP4/DP4+/DIP Tandem to Revise Both Relative and Absolute Configuration. J. Org. Chem. 2020, 85, 11566–11570. [Google Scholar] [CrossRef]
- Cen-Pacheco, F.; Norte, M.; Fernández, J.J.; Daranas, A.H. Zoaramine, a Zoanthamine-like Alkaloid with a New Skeleton. Org. Lett. 2014, 16, 2880–2883. [Google Scholar] [CrossRef]
- Daranas, A.H.; Fernández, J.; Gavín, J.; Norte, M. New alkaloids from a marine zoanthid. Tetrahedron 1999, 55, 5539–5546. [Google Scholar] [CrossRef]
- Villar, R.M.; Gil-Longo, J.; Daranas, A.H.; Souto, M.L.; Fernández, J.J.; Peixinho, S.; Barral, M.A.; Santafé, G.; Rodriguez, J.; Jiménez, C. Evaluation of the effects of several zoanthamine-type alkaloids on the aggregation of human platelets. Bioorg. Med. Chem. 2003, 11, 2301–2306. [Google Scholar] [CrossRef]
- García-García, P.; Reyes, R.; Évora, C.; Delgado, A.; Fernández, J.J.; Daranas, A.H. Osteoprotective effect of the marine alkaloid norzoanthamine on an osteoporosis model in ovariectomized rat. Biomed. Pharmacother. 2022, 147, 112631. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuadrado, C.; Daranas, A.H.; Sarotti, A.M. May the Force (Field) Be with You: On the Importance of Conformational Searches in the Prediction of NMR Chemical Shifts. Mar. Drugs 2022, 20, 699. https://doi.org/10.3390/md20110699
Cuadrado C, Daranas AH, Sarotti AM. May the Force (Field) Be with You: On the Importance of Conformational Searches in the Prediction of NMR Chemical Shifts. Marine Drugs. 2022; 20(11):699. https://doi.org/10.3390/md20110699
Chicago/Turabian StyleCuadrado, Cristina, Antonio Hernández Daranas, and Ariel M. Sarotti. 2022. "May the Force (Field) Be with You: On the Importance of Conformational Searches in the Prediction of NMR Chemical Shifts" Marine Drugs 20, no. 11: 699. https://doi.org/10.3390/md20110699
APA StyleCuadrado, C., Daranas, A. H., & Sarotti, A. M. (2022). May the Force (Field) Be with You: On the Importance of Conformational Searches in the Prediction of NMR Chemical Shifts. Marine Drugs, 20(11), 699. https://doi.org/10.3390/md20110699





