Chemical Reactivity Properties, pKa Values, AGEs Inhibitor Abilities and Bioactivity Scores of the Mirabamides A–H Peptides of Marine Origin Studied by Means of Conceptual DFT
Abstract
1. Introduction
2. Theoretical Background
3. Settings and Computational Methods
4. Results and Discussion
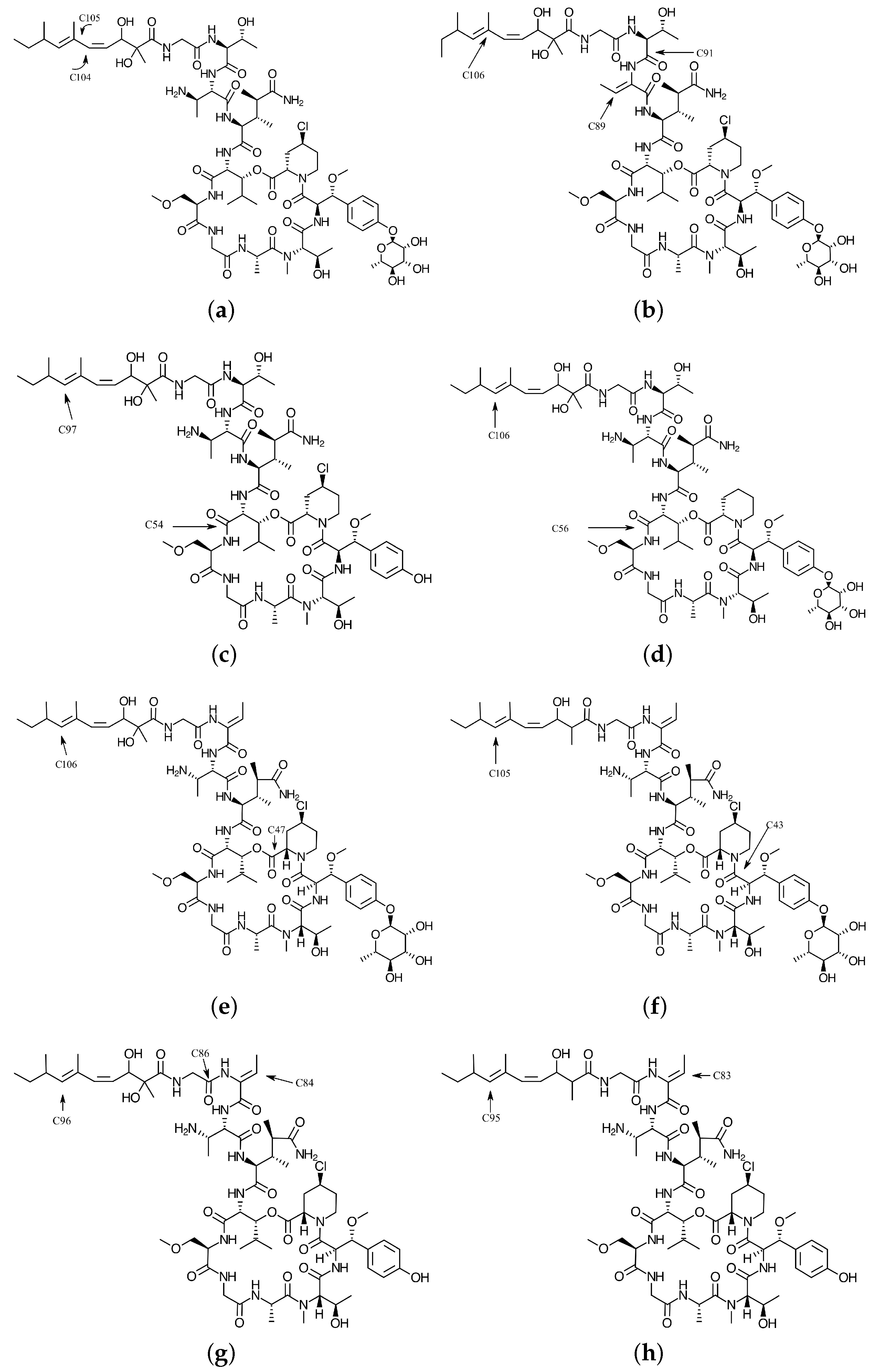
4.1. Local Reactivity Descriptors Calculation
4.2. Calculation of the p of the Peptides
4.3. Quantification of the AGEs Inhibitor Ability
4.4. Bioactivity Scores
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- La Barre, S.; Kornprobst, J.M. Outstanding Marine Molecules; Wiley-Blackwell: Weinheim, Germany, 2014. [Google Scholar]
- Kim, S.K. Marine Proteins and Peptides-Biological Activities and Applications; Wiley-Blackwell: Chichester, UK, 2013. [Google Scholar]
- Rekka, E.; Kourounakis, P. Chemistry and Molecular Aspects of Drug Design and Action; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Náray-Szabó, G.; Warshel, A. Computational Approaches to Biochemical Reactivity; Kluwer Academic Publishers: New York, NY, USA, 2002. [Google Scholar]
- Parr, R.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual Density Functional Theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef] [PubMed]
- Ayers, P.; Parr, R. The Variational Principles for Describing Chemical Reactions: The Fukui Function and Chemical Hardness Revisited. J. Am. Chem. Soc. 2000, 122, 2010–2018. [Google Scholar] [CrossRef]
- Poater, A.; Saliner, A.G.; Carbó-Dorca, R.; Poater, J.; Solà, M.; Cavallo, L.; Worth, A.P. Modeling the Structure-Property Relationships of Nanoneedles: A Journey Toward Nanomedicine. J. Comput. Chem. 2009, 30, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Poater, A.; Saliner, A.G.; Solá, M.; Cavallo, L.; Worth, A.P. Computational Methods to Predict the Reactivity of Nanoparticles Through Structure-Property Relationships. Expert Opin. Drug Deliv. 2010, 7, 295–305. [Google Scholar] [CrossRef] [PubMed]
- Plaza, A.; Gustchina, E.; Baker, H.L.; Kelly, M.; Bewley, C.A. Mirabamides A–D, Depsipeptides from the Sponge Siliquariaspongia mirabilis That Inhibit HIV-1 Fusion. J. Nat. Prod. 2007, 70, 1753–1760. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Van Wagoner, R.M.; Harper, M.K.; Baker, H.L.; Hooper, J.N.A.; Bewley, C.A.; Ireland, C.M. Mirabamides E–H, HIV-Inhibitory Depsipeptides from the Sponge Stelletta clavosa. J. Nat. Prod. 2011, 74, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Frau, J.; Hernández-Haro, N.; Glossman-Mitnik, D. Computational Prediction of the pKas of Small Peptides through Conceptual DFT Descriptors. Chem. Phys. Lett. 2017, 671, 138–141. [Google Scholar] [CrossRef]
- Frau, J.; Glossman-Mitnik, D. Chemical Reactivity Theory Study of Advanced Glycation Endproduct Inhibitors. Molecules 2017, 22, 226. [Google Scholar] [CrossRef] [PubMed]
- Gupta, G.K.; Kumar, V. Chemical Drug Design; Walter de Gruyter GmbH: Berlin, Germany, 2016. [Google Scholar]
- Gore, M.; Jagtap, U.B. Computational Drug Discovery and Design; Springer: New York, NY, USA, 2018. [Google Scholar]
- Frau, J.; Glossman-Mitnik, D. Molecular Reactivity and Absorption Properties of Melanoidin Blue-G1 through Conceptual DFT. Molecules 2018, 23, 559. [Google Scholar] [CrossRef] [PubMed]
- Frau, J.; Glossman-Mitnik, D. Conceptual DFT Study of the Local Chemical Reactivity of the Dilysyldipyrrolones A and B Intermediate Melanoidins. Theor. Chem. Acc. 2018, 137, 1210. [Google Scholar] [CrossRef]
- Frau, J.; Glossman-Mitnik, D. Conceptual DFT Study of the Local Chemical Reactivity of the Colored BISARG Melanoidin and Its Protonated Derivative. Front. Chem. 2018, 6, 136. [Google Scholar] [CrossRef] [PubMed]
- Frau, J.; Glossman-Mitnik, D. Molecular Reactivity of some Maillard Reaction Products Studied through Conceptual DFT. Contemp. Chem. 2018, 1, 1–14. [Google Scholar]
- Frau, J.; Glossman-Mitnik, D. Computational Study of the Chemical Reactivity of the Blue-M1 Intermediate Melanoidin. Comput. Theor. Chem. 2018, 1134, 22–29. [Google Scholar] [CrossRef]
- Frau, J.; Glossman-Mitnik, D. Chemical Reactivity Theory Applied to the Calculation of the Local Reactivity Descriptors of a Colored Maillard Reaction Product. Chem. Sci. Int. J. 2018, 22, 1–14. [Google Scholar] [CrossRef]
- Frau, J.; Glossman-Mitnik, D. Blue M2: An Intermediate Melanoidin Studied via Conceptual DFT. J. Mol. Model. 2018, 24, 138. [Google Scholar] [CrossRef] [PubMed]
- Lewars, E. Computational Chemistry-Introduction to the Theory and Applications of Molecular and Quantum Mechanics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Young, D. Computational Chemistry—A Practical Guide for Applying Techniques to Real-World Problems; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry, 2nd ed.; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Cramer, C. Essentials of Computational Chemistry—Theories and Models, 2nd ed.; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Iikura, H.; Tsuneda, T.; Yanai, T.; Hirao, K. A Long-Range Correction Scheme for Generalized-Gradient-Approximation Exchange Functionals. J. Chem. Phys. 2001, 115, 3540–3544. [Google Scholar] [CrossRef]
- Chai, J.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G. Efficient Hybrid Density Functional Calculations in Solids: Assessment of the Heyd-ìScuseria-ìErnzerhof Screened Coulomb Hybrid Functional. J. Chem. Phys. 2004, 121, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Stein, T.; Kronik, L.; Baer, R. Reliable Prediction of Charge Transfer Excitations in Molecular Complexes Using Time-Dependent Density Functional Theory. J. Am. Chem. Soc. 2009, 131, 2818–2820. [Google Scholar] [CrossRef] [PubMed]
- Stein, T.; Kronik, L.; Baer, R. Prediction of Charge-Transfer Excitations in Coumarin-Based Dyes Using a Range-Separated Functional Tuned From First Principles. J. Chem. Phys. 2009, 131, 244119. [Google Scholar] [CrossRef] [PubMed]
- Stein, T.; Eisenberg, H.; Kronik, L.; Baer, R. Fundamental Gaps in Finite Systems from Eigenvalues of a Generalized Kohn-Sham Method. Phys. Rev. Lett. 2010, 105, 266802-4. [Google Scholar] [CrossRef] [PubMed]
- Karolewski, A.; Stein, T.; Baer, R.; Kümmel, S. Communication: Tailoring the Optical Gap in Light-Harvesting Molecules. J. Chem. Phys. 2011, 134, 151101-5. [Google Scholar] [CrossRef] [PubMed]
- Kuritz, N.; Stein, T.; Baer, R.; Kronik, L. Charge-Transfer-Like π → π* Excitations in Time-Dependent Density Functional Theory: A Conundrum and Its Solution. J. Chem. Theory Comput. 2011, 7, 2408–2415. [Google Scholar] [CrossRef] [PubMed]
- Ansbacher, T.; Srivastava, H.K.; Stein, T.; Baer, R.; Merkx, M.; Shurki, A. Calculation of Transition Dipole Moment in Fluorescent Proteins-Towards Efficient Energy Transfer. Phys. Chem. Chem. Phys. 2012, 14, 4109–4117. [Google Scholar] [CrossRef] [PubMed]
- Kronik, L.; Stein, T.; Refaely-Abramson, S.; Baer, R. Excitation Gaps of Finite-Sized Systems from Optimally Tuned Range-Separated Hybrid Functionals. J. Chem. Theory Comput. 2012, 8, 1515–1531. [Google Scholar] [CrossRef] [PubMed]
- Stein, T.; Autschbach, J.; Govind, N.; Kronik, L.; Baer, R. Curvature and Frontier Orbital Energies in Density Functional Theory. J. Phys. Chem. Lett. 2012, 3, 3740–3744. [Google Scholar] [CrossRef] [PubMed]
- Halgren, T.A. Merck Molecular Force Field. I. Basis, Form, Scope, Parameterization, and Performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck Molecular Force Field. II. MMFF94 van der Waals and Electrostatic Parameters for Intermolecular Interactions. J. Comput. Chem. 1996, 17, 520–552. [Google Scholar] [CrossRef]
- Halgren, T.A. MMFF VI. MMFF94s Option for Energy Minimization Studies. J. Comput. Chem. 1999, 20, 720–729. [Google Scholar] [CrossRef]
- Halgren, T.A.; Nachbar, R.B. Merck Molecular Force Field. IV. Conformational Energies and Geometries for MMFF94. J. Comput. Chem. 1996, 17, 587–615. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck Molecular Force field. V. Extension of MMFF94 Using Experimental Data, Additional Computational Data, and Empirical Rules. J. Comput. Chem. 1996, 17, 616–641. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-fitting Basis Sets for H to R. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.; Cramer, C.; Truhlar, D. Universal Solvation Model Based on Solute Electron Density and a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Peverati, R.; Truhlar, D.G. Screened-Exchange Density Functionals with Broad Accuracy for Chemistry and Solid-State Physics. Phys. Chem. Chem. Phys. 2012, 14, 16187–16191. [Google Scholar] [CrossRef] [PubMed]
- Pelay-Gimeno, M.; Tulla-Puche, J.; Albericio, F. “Head-to-Side-Chain” Cyclodepsipeptides of Marine Origin. Mar. Drugs 2013, 11, 1693–1717. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.; Szentpaly, L.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Gázquez, J.; Cedillo, A.; Vela, A. Electrodonating and Electroaccepting Powers. J. Phys. Chem. A 2007, 111, 1966–1970. [Google Scholar] [CrossRef] [PubMed]
- Chattaraj, P.; Chakraborty, A.; Giri, S. Net Electrophilicity. J. Phys. Chem. A 2009, 113, 10068–10074. [Google Scholar] [CrossRef] [PubMed]
- Toro-Labbé, A. (Ed.) Theoretical Aspects of Chemical Reactivity; Elsevier Science: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Morell, C.; Grand, A.; Toro-Labbé, A. New Dual Descriptor for Chemical Reactivity. J. Phys. Chem. A 2005, 109, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Morell, C.; Grand, A.; Toro-Labbé, A. Theoretical Support for Using the Δf(r) Descriptor. Chem. Phys. Lett. 2006, 425, 342–346. [Google Scholar] [CrossRef]
- Martínez-Araya, J.I. Revisiting Caffeate’s Capabilities as a Complexation Agent to Silver Cation in Mining Processes by means of the Dual Descriptor—A Conceptual DFT Approach. J. Mol. Model. 2012, 18, 4299–4307. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Araya, J.I. Explaining Reaction Mechanisms Using the Dual Descriptor: A Complementary Tool to the Molecular Electrostatic Potential. J. Mol. Model. 2012, 19, 2715–2722. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Araya, J.I. Why is the Dual Descriptor a More Accurate Local Reactivity Descriptor than Fukui Functions? J. Math. Chem. 2015, 53, 451–465. [Google Scholar] [CrossRef]
- Domingo, L.R.; Pérez, P.; Sáez, J. Understanding the Local Reactivity in Polar Organic Reactions through Electrophilic and Nucleophilic Parr Functions. RSC Adv. 2013, 3, 1486–1494. [Google Scholar] [CrossRef]
- Chamorro, E.; Pérez, P.; Domingo, L.R. On the Nature of Parr Functions to Predict the Most Reactive Sites along Organic Polar Reactions. Chem. Phys. Lett. 2013, 582, 141–143. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, N. Advanced Glycation Endproducts—Role in Pathology of Diabetic Complications. Diabetes Res. Clin. Pract. 2005, 67, 3–21. [Google Scholar] [CrossRef] [PubMed]
- Rahbar, S.; Figarola, J.L. Novel Inhibitors of Advanced Glycation Endproducts. Arch. Biochem. Biophys. 2003, 419, 63–79. [Google Scholar] [CrossRef] [PubMed]
- Peyroux, J.; Sternberg, M. Advanced Glycation Endproducts (AGEs): Pharmacological Inhibition in Diabetes. Pathol. Biol. 2006, 54, 405–419. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Perez, P. The Nucleophilicity N Index in Organic Chemistry. Org. Biomol. Chem. 2011, 9, 7168–7175. [Google Scholar] [CrossRef] [PubMed]
- Leeson, P. Drug Discovery: Chemical Beauty Contest. Nature 2012, 481, 455–456. [Google Scholar] [CrossRef] [PubMed]
- Martin, Y.C. A Bioavailability Score. J. Med. Chem. 2005, 48, 3164–3170. [Google Scholar] [CrossRef] [PubMed]

| Molecule | Eo | E+ | E− | HOMO | LUMO | SOMO | SL | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Mirabamide A | −5856.10 | −5855.88 | −5856.15 | −6.36 | −1.17 | −1.19 | 0.00 | 0.01 | 0.01 | 0.02 |
| Mirabamide B | −5799.59 | −5799.37 | −5799.63 | −6.10 | −1.09 | −1.07 | 0.02 | 0.01 | 0.03 | 0.02 |
| Mirabamide C | −5321.42 | −5321.19 | −5321.45 | −6.26 | −0.99 | −0.99 | 0.02 | 0.00 | 0.02 | 0.00 |
| Mirabamide D | −5396.70 | −5396.47 | −5396.74 | −6.19 | −1.03 | −1.03 | 0.02 | 0.00 | 0.02 | 0.00 |
| Mirabamide E | −5779.75 | −5779.52 | −5779.79 | −6.07 | −1.21 | −1.18 | 0.02 | 0.01 | 0.02 | 0.03 |
| Mirabamide F | −5704.64 | −5704.42 | −5704.68 | −6.13 | −1.06 | −1.07 | 0.02 | 0.00 | 0.02 | 0.01 |
| Mirabamide G | −5245.09 | −5244.86 | −5245.12 | −6.16 | −0.96 | −0.94 | 0.02 | 0.01 | 0.02 | 0.02 |
| Mirabamide H | −5169.97 | −5169.74 | −5170.02 | −6.13 | −1.23 | −1.22 | 0.02 | 0.01 | 0.02 | 0.02 |
| Molecule | Electronegativity () | Chemical Hardness () | Electrophilicity () |
|---|---|---|---|
| Mirabamide A | 3.6281 | 4.9155 | 1.3389 |
| Mirabamide B | 3.5956 | 5.0132 | 1.2894 |
| Mirabamide C | 3.6227 | 5.2665 | 1.2460 |
| Mirabamide D | 3.6066 | 5.1555 | 1.2615 |
| Mirabamide E | 3.6397 | 4.8640 | 1.3617 |
| Mirabamide F | 3.5969 | 5.0654 | 1.2771 |
| Mirabamide G | 3.5582 | 5.1968 | 1.2181 |
| Mirabamide H | 3.6822 | 4.8970 | 1.3844 |
| Electrodonating Power() | Electroaccepting Power() | Net Electrophilicity () | |
| Mirabamide A | 4.7992 | 1.1711 | 5.9702 |
| Mirabamide B | 4.6900 | 1.0944 | 5.7843 |
| Mirabamide C | 4.6324 | 1.0097 | 5.6421 |
| Mirabamide D | 4.6486 | 1.0420 | 5.6905 |
| Mirabamide E | 4.8473 | 1.2077 | 6.0550 |
| Mirabamide F | 4.6692 | 1.0723 | 5.7415 |
| Mirabamide G | 4.5401 | 0.9819 | 5.5220 |
| Mirabamide H | 4.9160 | 1.2338 | 6.1498 |
| Atom | (M) | (N) | (M) | (M) | (H) | (H) |
|---|---|---|---|---|---|---|
| 26 O | −1.79 | −0.50 | 0.0269 | 0.0370 | 0.0424 | 0.0408 |
| 101 C | 2.04 | 2.88 | −0.0058 | −0.0344 | 0.0340 | 0.0121 |
| 104 C | 10.28 | 9.54 | 0.1742 | −0.0281 | 0.1833 | 0.0581 |
| 105 C | −9.00 | −7.61 | 0.0390 | 0.1956 | 0.0881 | 0.1629 |
| 108 C | −1.47 | −0.27 | 0.0087 | 0.0208 | 0.0230 | 0.0287 |
| Atom | (M) | (N) | (M) | (M) | (H) | (H) |
|---|---|---|---|---|---|---|
| 18 O | 2.98 | 5.26 | 0.0367 | 0.0000 | 0.0373 | 0.0000 |
| 21 O | 12.11 | 13.61 | 0.1365 | 0.0000 | 0.1426 | 0.0000 |
| 26 O | −3.06 | −3.51 | 0.0000 | 0.0363 | 0.0000 | 0.0365 |
| 31 N | 1.70 | 2.03 | 0.0074 | 0.0000 | 0.0190 | 0.0000 |
| 36 N | 1.17 | −0.64 | −0.0481 | 0.0000 | 0.0269 | 0.0000 |
| 82 C | 5.22 | 2.97 | 0.0540 | 0.0000 | 0.0521 | 0.0000 |
| 85 C | 12.40 | 5.97 | 0.1118 | 0.0000 | 0.1064 | 0.0000 |
| 89 C | 25.07 | 22.13 | 0.3306 | 0.0000 | 0.2286 | 0.0000 |
| 91 C | 25.31 | 18.18 | 0.3485 | 0.0000 | 0.2251 | 0.0000 |
| 92 C | 2.01 | −0.99 | −0.0317 | 0.0000 | 0.0308 | 0.0000 |
| 94 C | 2.47 | 0.83 | 0.0308 | 0.0000 | 0.0247 | 0.0000 |
| 100 C | −1.16 | 1.01 | 0.0000 | −0.0143 | 0.0000 | 0.0222 |
| 102 C | −16.25 | −15.76 | 0.0000 | 0.2328 | 0.0000 | 0.1676 |
| 103 C | −8.25 | −1.92 | 0.0000 | 0.0195 | 0.0000 | 0.0823 |
| 104 C | −23.40 | −17.03 | 0.0000 | 0.2363 | 0.0000 | 0.1973 |
| 105 C | −1.27 | 2.50 | 0.0000 | −0.0113 | 0.0000 | 0.0335 |
| 106 C | −32.17 | −26.77 | 0.0000 | 0.4139 | 0.0000 | 0.3301 |
| 107 C | −2.47 | −0.42 | 0.0000 | 0.0230 | 0.0000 | 0.0315 |
| 109 C | −1.71 | 1.68 | 0.0002 | 0.0282 | 0.0001 | 0.0542 |
| Atom | (M) | (N) | (M) | (M) | (H) | (H) |
|---|---|---|---|---|---|---|
| 4 O | 2.28 | 3.61 | 0.0347 | 0.0000 | 0.0379 | 0.0000 |
| 7 O | 17.48 | 16.50 | 0.1732 | 0.0000 | 0.1830 | 0.0000 |
| 15 O | 2.40 | 3.70 | 0.0222 | 0.0000 | 0.0246 | 0.0000 |
| 22 O | −1.70 | −2.56 | 0.0000 | 0.0203 | 0.0000 | 0.0237 |
| 27 N | 5.60 | 3.77 | 0.0116 | 0.0000 | 0.0593 | 0.0000 |
| 31 N | 1.56 | 1.51 | 0.0097 | 0.0000 | 0.0167 | 0.0000 |
| 41 C | 2.57 | 0.43 | 0.0231 | 0.0000 | 0.0337 | 0.0000 |
| 43 C | 5.37 | 6.75 | 0.1091 | 0.0000 | 0.0757 | 0.0000 |
| 45 C | 3.98 | 0.12 | 0.0036 | 0.0000 | 0.0404 | 0.0000 |
| 52 C | 1.68 | 1.44 | 0.0105 | 0.0000 | 0.0170 | 0.0000 |
| 54 C | 36.46 | 24.72 | 0.4387 | 0.0000 | 0.2865 | 0.0000 |
| 61 C | 2.57 | 0.33 | 0.0312 | 0.0000 | 0.0526 | 0.0000 |
| 74 C | 5.99 | 3.60 | 0.0814 | 0.0000 | 0.0513 | 0.0000 |
| 93 C | −17.66 | −17.46 | 0.0000 | 0.2636 | 0.0000 | 0.1817 |
| 94 C | −6.66 | −0.48 | 0.0000 | −0.0190 | 0.0000 | 0.0562 |
| 95 C | −25.33 | −18.94 | 0.0000 | 0.2674 | 0.0000 | 0.2175 |
| 96 C | −1.60 | 2.92 | 0.0000 | −0.0046 | 0.0000 | 0.0439 |
| 97 C | −33.20 | −28.08 | 0.0000 | 0.4218 | 0.0000 | 0.3425 |
| 99 C | −1.20 | 2.14 | 0.0000 | 0.0233 | 0.0000 | 0.0517 |
| 100 C | −2.87 | −0.54 | 0.0000 | 0.0368 | 0.0000 | 0.0439 |
| Atom | (M) | (N) | (M) | (M) | (H) | (H) |
|---|---|---|---|---|---|---|
| 1 O | 1.29 | 2.19 | −0.0009 | 0.0000 | 0.0266 | 0.0000 |
| 3 O | 4.05 | 6.90 | 0.0575 | 0.0000 | 0.0663 | 0.0000 |
| 7 O | 15.21 | 15.15 | 0.1317 | 0.0000 | 0.1416 | 0.0000 |
| 25 O | −1.21 | −1.80 | 0.0000 | 0.0148 | 0.0000 | 0.0155 |
| 30 N | 6.69 | 3.82 | 0.0218 | 0.0000 | 0.0764 | 0.0000 |
| 44 C | 1.13 | 1.33 | 0.0162 | 0.0000 | 0.0107 | 0.0000 |
| 45 C | 2.71 | 1.64 | 0.0275 | 0.0000 | 0.0347 | 0.0000 |
| 47 C | 10.51 | 9.80 | 0.2036 | 0.0000 | 0.1360 | 0.0000 |
| 48 C | 4.13 | −0.50 | −0.0126 | 0.0000 | 0.0461 | 0.0000 |
| 56 C | 35.91 | 20.68 | 0.4392 | 0.0000 | 0.2739 | 0.0000 |
| 85 C | 2.57 | 0.20 | 0.0217 | 0.0000 | 0.0135 | 0.0000 |
| 100 C | −1.47 | 1.55 | 0.0000 | −0.0048 | 0.0000 | 0.0352 |
| 102 C | −15.85 | −16.36 | 0.0001 | 0.2247 | 0.0001 | 0.1596 |
| 103 C | −7.09 | −0.93 | 0.0000 | 0.0042 | 0.0000 | 0.0701 |
| 104 C | −24.77 | −18.19 | 0.0000 | 0.2629 | 0.0000 | 0.2108 |
| 105 C | −1.18 | 2.47 | 0.0000 | −0.0157 | 0.0000 | 0.0283 |
| 106 C | −32.26 | −26.83 | 0.0000 | 0.4080 | 0.0000 | 0.3312 |
| 107 C | −2.34 | −0.36 | 0.0000 | 0.0212 | 0.0000 | 0.0293 |
| 108 C | −1.67 | 1.81 | 0.0000 | 0.0273 | 0.0000 | 0.0560 |
| 109 C | −1.15 | 0.15 | 0.0000 | 0.0155 | 0.0000 | 0.0199 |
| Atom | (M) | (N) | (M) | (M) | (H) | (H) |
|---|---|---|---|---|---|---|
| 1 Cl | 1.21 | 2.34 | 0.0098 | 0.0000 | 0.0117 | 0.0000 |
| 2 O | 7.00 | 6.14 | 0.0226 | 0.0000 | 0.0800 | 0.0000 |
| 4 O | 18.05 | 17.88 | 0.1574 | 0.0000 | 0.1865 | 0.0000 |
| 8 O | 1.12 | 2.68 | 0.0197 | 0.0001 | 0.0192 | 0.0000 |
| 24 O | −1.93 | −2.03 | 0.0000 | 0.0260 | 0.0000 | 0.0225 |
| 25 O | −2.92 | −3.48 | 0.0000 | 0.0331 | 0.0000 | 0.0335 |
| 39 C | 3.55 | −0.74 | −0.0346 | 0.0000 | 0.0471 | 0.0000 |
| 40 C | 2.74 | 0.03 | 0.0175 | 0.0000 | 0.0342 | 0.0000 |
| 41 C | 1.34 | 0.20 | 0.0143 | 0.0000 | 0.0125 | 0.0000 |
| 47 C | 47.05 | 32.44 | 0.6208 | 0.0000 | 0.3907 | 0.0000 |
| 56 C | 2.34 | 0.88 | 0.0288 | −0.0003 | 0.0336 | 0.0000 |
| 57 C | 1.30 | 1.47 | 0.0195 | 0.0000 | 0.0130 | 0.0000 |
| 98 C | −1.50 | −0.65 | 0.0001 | 0.0156 | 0.0000 | 0.0161 |
| 100 C | −1.70 | 1.32 | 0.0000 | 0.0042 | 0.0000 | 0.0387 |
| 102 C | −15.73 | −14.81 | 0.0001 | 0.2123 | 0.0001 | 0.1588 |
| 103 C | −9.70 | −4.25 | 0.0001 | 0.0503 | 0.0001 | 0.0967 |
| 104 C | −21.41 | −14.92 | 0.0000 | 0.2162 | 0.0001 | 0.1804 |
| 105 C | −1.38 | 2.25 | 0.0000 | −0.0111 | 0.0000 | 0.0353 |
| 106 C | −28.96 | −24.20 | 0.0002 | 0.3703 | 0.0001 | 0.2972 |
| 107 C | −2.56 | −0.46 | 0.0000 | 0.0274 | 0.0000 | 0.0325 |
| 108 C | −1.06 | 1.75 | 0.0001 | 0.0174 | 0.0004 | 0.0424 |
| Atom | (M) | (N) | (M) | (M) | (H) | (H) |
|---|---|---|---|---|---|---|
| 2 O | 1.83 | 2.09 | −0.0002 | 0.0000 | 0.0182 | 0.0000 |
| 3 O | 12.58 | 13.06 | 0.1557 | 0.0000 | 0.1606 | 0.0000 |
| 4 O | 7.22 | 7.19 | 0.0594 | 0.0000 | 0.0649 | 0.0000 |
| 24 O | −4.19 | −4.69 | 0.0000 | 0.0494 | 0.0000 | 0.0502 |
| 25 N | 4.63 | 2.78 | 0.0150 | 0.0000 | 0.0407 | 0.0000 |
| 26 N | 1.05 | 1.03 | 0.0043 | 0.0000 | 0.0260 | 0.0000 |
| 38 C | 1.43 | −0.47 | −0.0101 | 0.0000 | 0.0252 | 0.0000 |
| 43 C | 25.56 | 20.56 | 0.3308 | 0.0000 | 0.2266 | 0.0000 |
| 45 C | 4.14 | 0.43 | 0.0265 | 0.0000 | 0.0453 | 0.0000 |
| 46 C | 17.37 | 9.70 | 0.1869 | 0.0000 | 0.1239 | 0.0000 |
| 55 C | 1.50 | 0.91 | 0.0186 | 0.0000 | 0.0156 | 0.0000 |
| 58 C | 1.46 | 1.25 | 0.0169 | 0.0000 | 0.0132 | 0.0000 |
| 66 C | 2.41 | 3.02 | 0.0221 | 0.0000 | 0.0276 | 0.0000 |
| 67 C | 1.50 | 2.17 | 0.0185 | 0.0000 | 0.0203 | 0.0000 |
| 74 C | 2.00 | 2.19 | 0.0362 | 0.0000 | 0.0267 | 0.0000 |
| 75 C | 2.25 | 2.51 | 0.0392 | 0.0000 | 0.0300 | 0.0000 |
| 99 C | −1.18 | 1.08 | 0.0000 | −0.0094 | 0.0000 | 0.0226 |
| 101 C | −17.34 | −16.63 | 0.0000 | 0.2448 | 0.0000 | 0.1801 |
| 102 C | −8.93 | −2.85 | 0.0000 | 0.0242 | 0.0000 | 0.0824 |
| 103 C | −22.46 | −16.32 | 0.0000 | 0.2238 | 0.0000 | 0.1902 |
| 104 C | −1.43 | 2.42 | 0.0001 | −0.0137 | 0.0001 | 0.0331 |
| 105 C | −31.09 | −26.23 | 0.0000 | 0.4019 | 0.0000 | 0.3214 |
| 106 C | −2.76 | −0.58 | 0.0002 | 0.0278 | 0.0005 | 0.0337 |
| 107 C | −1.06 | 1.90 | 0.0000 | 0.0196 | 0.0000 | 0.0449 |
| Atom | (M) | (N) | (M) | (M) | (H) | (H) |
|---|---|---|---|---|---|---|
| 17 O | 5.31 | 7.35 | 0.0502 | 0.0001 | 0.0592 | 0.0001 |
| 18 O | 10.57 | 10.62 | 0.1287 | 0.0002 | 0.1339 | 0.0001 |
| 20 O | −1.74 | −2.48 | 0.0055 | 0.0263 | 0.0049 | 0.0234 |
| 21 O | −1.45 | 0.00 | 0.0000 | 0.0186 | 0.0000 | 0.0208 |
| 28 N | 3.69 | 3.00 | 0.0170 | 0.0000 | 0.0420 | 0.0000 |
| 64 C | 1.19 | −0.41 | 0.0170 | 0.0000 | 0.0111 | 0.0000 |
| 81 C | 11.78 | 0.00 | 0.1661 | −0.0001 | 0.1104 | 0.0000 |
| 83 C | 11.17 | 22.77 | 0.0670 | 0.0002 | 0.0882 | 0.0003 |
| 84 C | 21.83 | −1.85 | 0.2825 | 0.0009 | 0.2041 | 0.0007 |
| 86 C | 20.87 | −0.58 | 0.2631 | −0.0001 | 0.1909 | 0.0000 |
| 88 C | −1.01 | 0.99 | 0.0004 | 0.0121 | 0.0005 | 0.0107 |
| 92 C | −19.65 | −3.97 | 0.0000 | 0.2798 | 0.0000 | 0.2050 |
| 93 C | −10.38 | 2.63 | 0.0000 | 0.0335 | 0.0000 | 0.0868 |
| 94 C | −1.31 | −15.06 | 0.0000 | −0.0100 | 0.0000 | 0.0347 |
| 95 C | −20.37 | −26.51 | 0.0000 | 0.1902 | 0.0000 | 0.1721 |
| 96 C | −30.34 | 0.30 | 0.0000 | 0.3993 | 0.0000 | 0.3179 |
| 98 C | −2.48 | 1.80 | 0.0000 | 0.0335 | 0.0000 | 0.0410 |
| Atom | (M) | (N) | (M) | (M) | (H) | (H) |
|---|---|---|---|---|---|---|
| 17 O | 6.06 | 7.35 | 0.0672 | 0.0003 | 0.0700 | 0.0004 |
| 18 O | 8.62 | 10.62 | 0.1056 | 0.0001 | 0.1078 | 0.0001 |
| 20 O | −1.56 | −2.48 | 0.0001 | 0.0193 | 0.0001 | 0.0230 |
| 28 N | 3.30 | 3.00 | 0.0140 | 0.0009 | 0.0328 | 0.0007 |
| 33 N | −1.35 | −1.12 | 0.0062 | 0.0279 | 0.0130 | 0.0238 |
| 80 C | 11.08 | 7.23 | 0.1338 | −0.0002 | 0.0996 | 0.0000 |
| 82 C | 13.09 | 7.21 | 0.0740 | 0.0001 | 0.1039 | 0.0000 |
| 83 C | 29.19 | 22.77 | 0.3995 | −0.0001 | 0.2770 | 0.0000 |
| 85 C | 16.66 | 13.06 | 0.2195 | 0.0002 | 0.1554 | 0.0001 |
| 90 C | −0.18 | 0.00 | 0.0004 | 0.0026 | 0.0004 | 0.0031 |
| 91 C | −19.87 | −18.12 | 0.0005 | 0.2872 | 0.0002 | 0.2052 |
| 92 C | −10.07 | −3.97 | −0.0003 | 0.0233 | 0.0001 | 0.0838 |
| 93 C | −1.35 | 2.63 | 0.0000 | −0.0076 | 0.0000 | 0.0392 |
| 94 C | −21.32 | −15.06 | 0.0005 | 0.2032 | 0.0002 | 0.1794 |
| 95 C | −31.07 | −26.51 | −0.0002 | 0.4064 | 0.0004 | 0.3225 |
| 97 C | −2.47 | −0.49 | 0.0000 | 0.0332 | 0.0000 | 0.0400 |
| 98 C | −1.00 | 1.80 | 0.0000 | 0.0192 | 0.0000 | 0.0422 |
| Molecule | p |
|---|---|
| Mirabamide A | 12.245 |
| Mirabamide B | 12.164 |
| Mirabamide C | 11.954 |
| Mirabamide D | 12.046 |
| Mirabamide E | 12.287 |
| Mirabamide F | 12.121 |
| Mirabamide G | 12.012 |
| Mirabamide H | 12.260 |
| Molecule | miLog P | TPSA | nAtoms | nON | nOHNH | Nviol | Nrotb | Volume | MW |
|---|---|---|---|---|---|---|---|---|---|
| Mirabamide A | −4.35 | 576.45 | 111 | 38 | 20 | 3 | 29 | 1447.27 | 1597.22 |
| Mirabamide B | −2.61 | 550.43 | 110 | 37 | 18 | 3 | 28 | 1429.74 | 1580.19 |
| Mirabamide C | −3.64 | 517.53 | 101 | 34 | 18 | 3 | 27 | 1323.41 | 1451.08 |
| Mirabamide D | −4.41 | 576.45 | 110 | 38 | 20 | 3 | 29 | 1433.71 | 1562.78 |
| Mirabamide E | −3.13 | 556.23 | 110 | 37 | 19 | 3 | 28 | 1433.02 | 1579.21 |
| Mirabamide F | −2.19 | 536.00 | 109 | 36 | 18 | 3 | 28 | 1425.32 | 1563.21 |
| Mirabamide G | −2.36 | 497.30 | 100 | 33 | 17 | 3 | 26 | 1309.15 | 1433.07 |
| Mirabamide H | −1.41 | 477.07 | 99 | 32 | 16 | 3 | 26 | 1301.46 | 1417.07 |
| Molecule | GPCR Ligand | Ion Channel Modulator | Kinase Inhibitor | Nuclear Receptor Ligand | Protease Inhibitor | Enzyme Inhibitor |
|---|---|---|---|---|---|---|
| Mirabamide A | −3.99 | −4.04 | −4.05 | −4.05 | −3.95 | −3.99 |
| Mirabamide B | −3.99 | −4.04 | −4.06 | −4.05 | −3.95 | −3.99 |
| Mirabamide C | −3.94 | −4.00 | −4.01 | −4.00 | −3.89 | −4.05 |
| Mirabamide D | −3.98 | −4.03 | −4.05 | −4.04 | −3.94 | −3.98 |
| Mirabamide E | −3.99 | −4.04 | −4.06 | −4.05 | −3.95 | −3.99 |
| Mirabamide F | −3.98 | −4.04 | −4.06 | −4.05 | −3.95 | −3.98 |
| Mirabamide G | −3.94 | −4.00 | −4.02 | −4.01 | −3.89 | −3.94 |
| Mirabamide H | −3.93 | −4.00 | −4.02 | −4.01 | −3.89 | −3.94 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frau, J.; Flores-Holguín, N.; Glossman-Mitnik, D. Chemical Reactivity Properties, pKa Values, AGEs Inhibitor Abilities and Bioactivity Scores of the Mirabamides A–H Peptides of Marine Origin Studied by Means of Conceptual DFT. Mar. Drugs 2018, 16, 302. https://doi.org/10.3390/md16090302
Frau J, Flores-Holguín N, Glossman-Mitnik D. Chemical Reactivity Properties, pKa Values, AGEs Inhibitor Abilities and Bioactivity Scores of the Mirabamides A–H Peptides of Marine Origin Studied by Means of Conceptual DFT. Marine Drugs. 2018; 16(9):302. https://doi.org/10.3390/md16090302
Chicago/Turabian StyleFrau, Juan, Norma Flores-Holguín, and Daniel Glossman-Mitnik. 2018. "Chemical Reactivity Properties, pKa Values, AGEs Inhibitor Abilities and Bioactivity Scores of the Mirabamides A–H Peptides of Marine Origin Studied by Means of Conceptual DFT" Marine Drugs 16, no. 9: 302. https://doi.org/10.3390/md16090302
APA StyleFrau, J., Flores-Holguín, N., & Glossman-Mitnik, D. (2018). Chemical Reactivity Properties, pKa Values, AGEs Inhibitor Abilities and Bioactivity Scores of the Mirabamides A–H Peptides of Marine Origin Studied by Means of Conceptual DFT. Marine Drugs, 16(9), 302. https://doi.org/10.3390/md16090302







