Is There a Need for a More Precise Description of Biomolecule Interactions to Understand Cell Function?
Abstract
1. Introduction: Why Is There a Need for Elaborate Parameters to Describe the Properties of Cellular Components?
- (i)
- Define and identify informative cell properties (i.e., features or attributes). The choice of considering a particular property is somewhat arbitrary and depends on the function that is being explored. As an example, the set of gene transcription rates may be thought to account for a cell differentiation state [3]. More transient properties are cell polarization, i.e., asymmetrical organization, or motility state: whether a cell is immobile on a surface or migrating throughout a living organism. The activity of a particular signaling pathway is another example. A cell state may be defined as the time-dependent set of values of a suitable group of properties.
- (ii)
- Define and identify the pieces of information, or signals, provided to cells by the extracellular medium. A signal may consist of the application of a force on a region of the cell membrane or binding of a ligand to a cell surface receptor. As will be discussed below, multiple binding interactions are continually formed and broken, and a choice may be necessary to define significant signals, which depends on the function that is being explored. Additionally, the effect of a signal may be strongly dependent on its localization and temporal evolution. These features must, therefore, be included in the parameters used to describe signals.
- (iii)
- Discover rules allowing to predict the temporal evolution of cell states as a function of received signals. It must be emphasized that the way rules are expressed may involve somewhat hidden assumptions. Thus, it may be implicitly assumed that the description of a cell state does not need to include its history, i.e., that cell evolution may be described as a Markov process, an assumption that is not always warranted [4,5].
2. The Initial Choice of Parameters Used to Describe Cell Properties Strongly Influences the Performance of Quantitative Methods Currently Used to Study Cell Function
2.1. An Exhaustive Ab Initio Description of Cell Function Seems out of Reach in the near Future, and It Is not as “Parameter-Independent” as Might Be Thought: Lessons from Molecular Dynamics
2.2. The “Omic” Approach: Representative Examples of Strategies Used to Analyze Huge Datasets
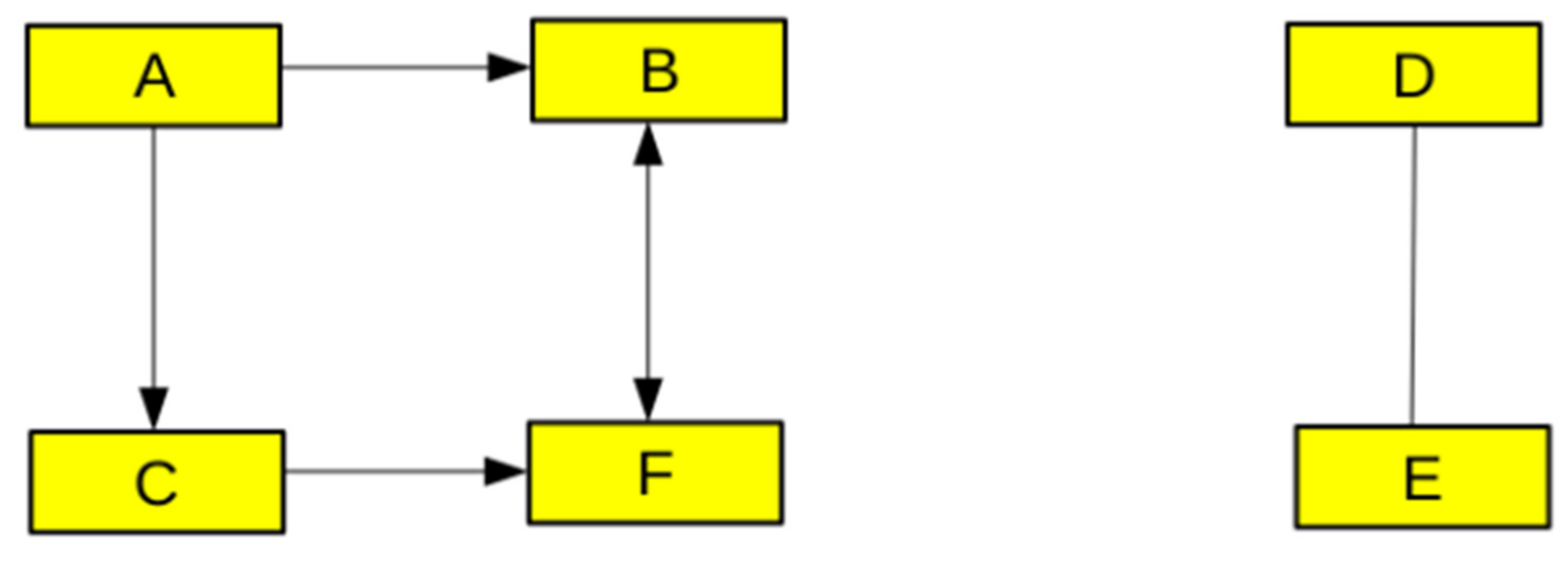
2.2.1. Graph Theory, Networks, and Logic-Based Models
2.2.2. Viewing Cells as Mobile Points Moving on a Multidimensional Landscape
2.3. Data Processing with Multivariate Statistics and Machine Learning
3. Is There a Need for a More Precise Description of Biomolecule Interactions?
3.1. Current State of Interactome Databases
- (i)
- The term “interaction” may refer to different phenomena. Physical binding and unbinding of a molecular pair in solution can be quantified with high accuracy with standard techniques, as will be detailed below. High throughput maps of binary interactions involving about 17,500 human proteins (about 90% of the protein-coding genome) were built with the standard yeast two-hybrid method, yielding about 53,000 interactions [60]. The validity of results was fed into public databases such as IntAct (https://www.ebi.ac.uk/intact/ accessed on 7 December 2021) after careful validation [60]. However, as was well acknowledged by the authors, the occurrence of physiologically relevant molecular interactions requires that molecular partners might encounter each other within cells. Additionally, molecular interactions may display significant differences in vitro and within cells [64]. Affinity purification-mass spectrometry (AP-MS) is currently used to obviate this difficulty [65,66]. This relies on the use of cells expressing tagged “baits” that may be purified after cell lysis before identification of binding partners with quantitative mass spectrometry. As a recent example, a network of 118,162 interactions among 14,586 proteins was obtained after affinity-purification of 10,128 proteins expressed by human epithelial kidney cells, yielding the Bioplex 3.0 network [21]. Interestingly, comparison with data obtained on another cell line (from human colorectal carcinoma) revealed, as expected, significant differences between interatomic networks found with two different cell types. Additionally, when AP-MS was studied to monitor, for a period of time of 600 s, primary T lymphocytes subjected to antigen-receptor mediated stimulation, the expected evolution of signalosome interactions was clearly evidenced [65]. In conclusion, while a reliable and nearly exhaustive network of the physical interaction of human proteins under standard conditions may be available, an exhaustive description of interactions involving relevant epigenetic states of the proteome and cellular environments is currently out of reach [21,60], despite the impressive amount of information gathered by combining data mining and experiments, as exemplified by the STRING database [22]. As clearly stated [60]: “It remains infeasible to assemble a reference interactome map by systematically identifying endogenous protein–protein interactions (PPIs) in thousands of physiological and pathological cellular contexts”.
- (ii)
- As already mentioned in the aforementioned examples, the quantitative properties of biomolecule interactions may display huge variations. As an example, the dissociation constant of biomolecular bonds may vary between picomolar values (as exemplified by hormone-receptor interaction) and millimolar values [67], which may be considered to represent ultra-weak interactions, of which the biological importance is, however, recognized [68]. The lifetime of a ligand-receptor bond may vary between less than a second (as was sometimes reported on cadherins [69] or antigen-antibody pairs [70]) and hours.
3.2. Parameters Currently Available to Describe Biomolecule Interactions
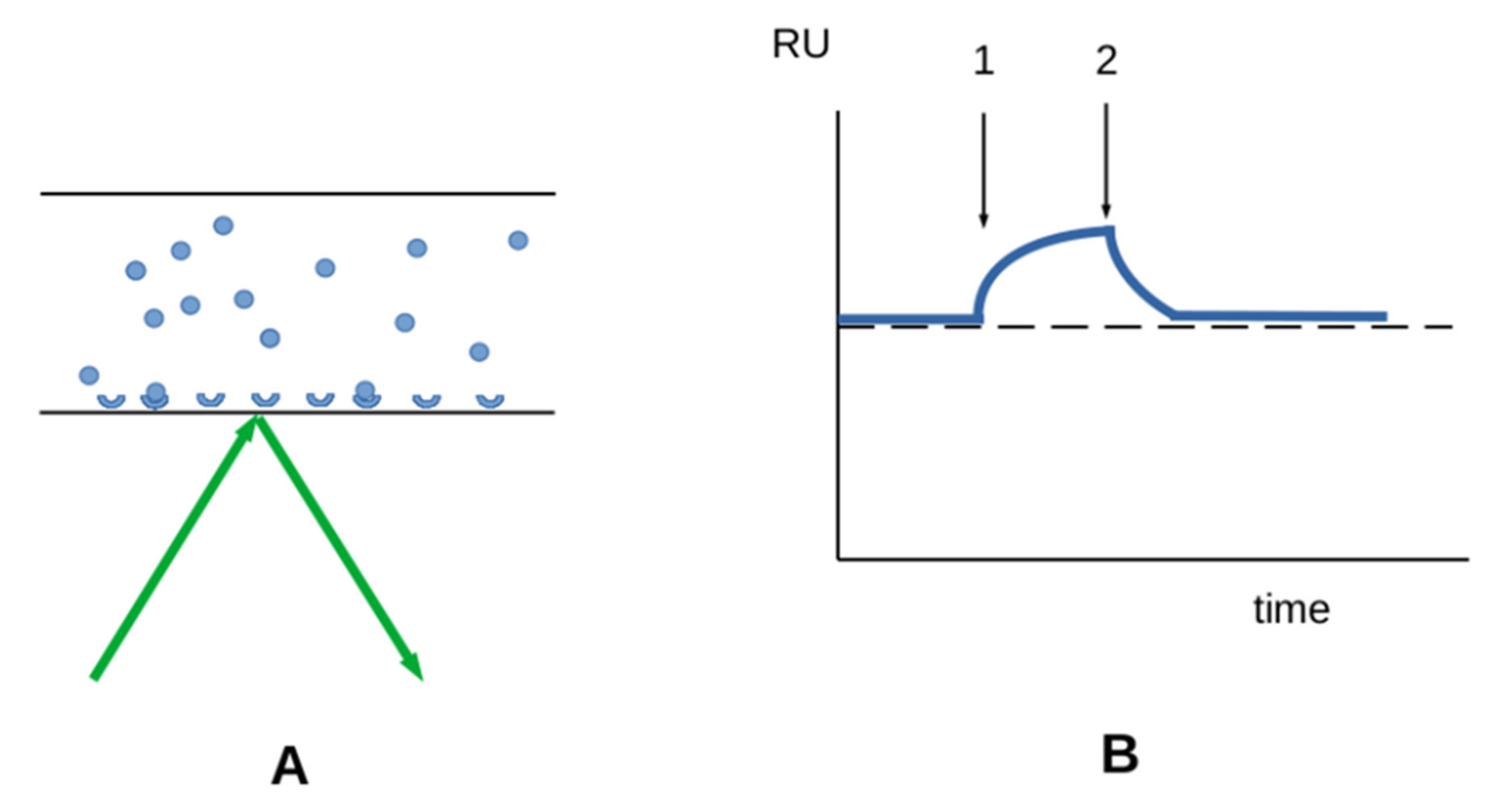
3.2.1. Interaction between Soluble Molecules and Surface-Bound Receptors
3.2.2. Interaction between Surface-Bound Ligands and Receptors
3.2.3. Additional Parameters May Be Obtained with Computer Simulation
3.3. Physical and Biological Significance of Parameters Allowing to Account for Biomolecule Interactions
3.3.1. The Equilibrium Constant
- It is difficult to use Equation (1) to assess the biological significance of a reported interaction. Indeed, it would reasonable to conclude that an interaction AB is significant if either Ka[A] or Ka[B] is not too close to zero. But this would require to know the value of [A] close to a molecule [B] or [B] close to [A], which is not always the case. As a striking example, it was recently shown that spatio-temporal cAMP signaling is under precise control of nanoscale domains [88]. Additionally, local molecular crowding may alter effective concentrations [89]. More generally, the in vivo affinity of a reaction may differ significantly from the affinity measured in a standard buffer. Thus, the qualitative demonstration of a physical interaction between two molecules within a cell as evidenced with AP-MS [21] may be more informative than quantitative in vitro affinity measurement.
- Many biomolecule interactions involve surface-bound molecules. Indeed, as was recently emphasized [90], nearly 30% of human genes encode membrane proteins. Unfortunately, as already explained [75], the affinity between surface-bound molecules is difficult to derive from 3D affinity, and even to define: the outcome of an encounter between two bound molecules is dependent on a number of parameters independent of binding sites such as molecular length and flexibility [91], lateral mobility, and distance between surfaces [92].
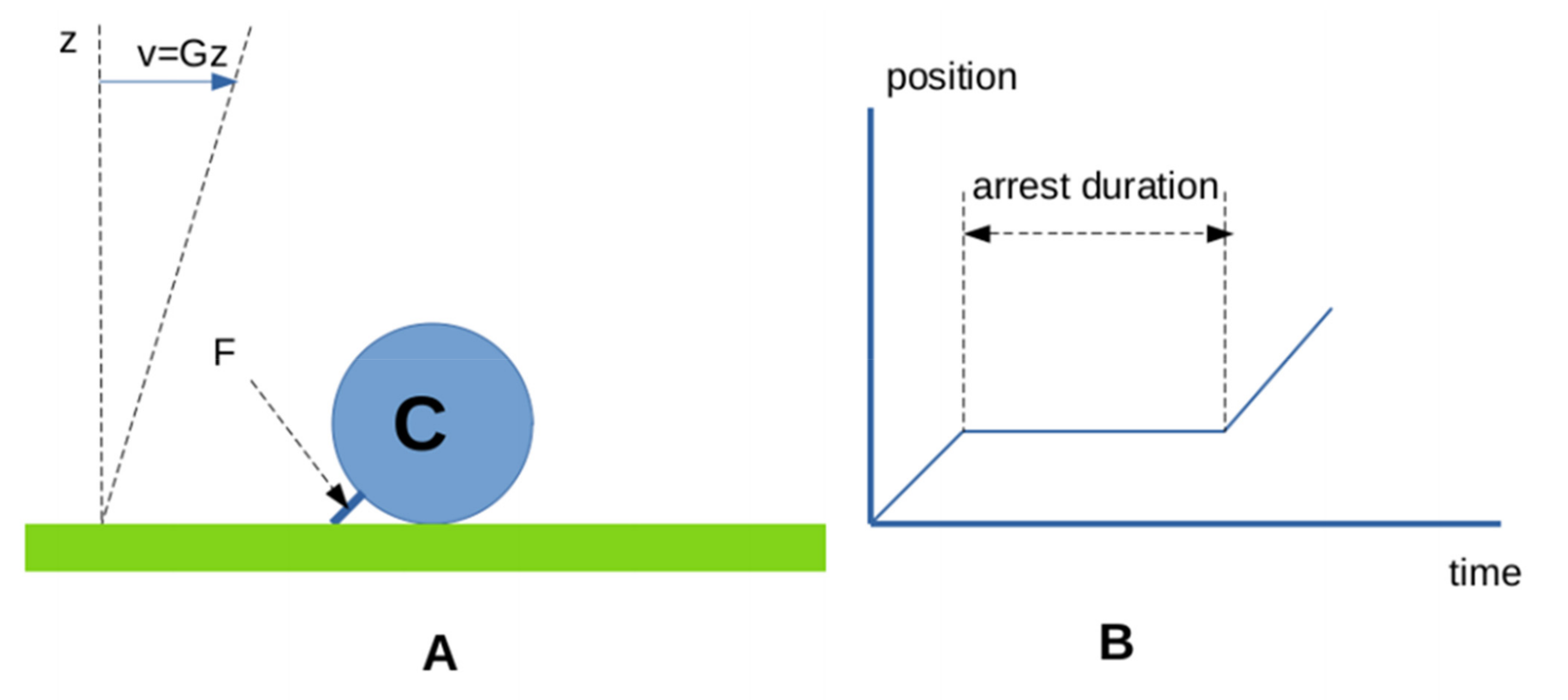
3.3.2. Kinetic Rates Provide an Informative Means of Accounting for Biomolecule Interactions
- First, biomolecular attachments often appear as multistep reactions, the description of which may require numerous parameters to account for several energy barriers in reaction paths. The number of required parameters was somewhat reduced when it was found that the kinetics of bond formation between different antigen and antibody might be modeled as a progression along a rugged energy landscape, accounted for by a single effective diffusion constant, and matched the intuitively appealing interpretation that bond formation required a minimal contact time that was estimated as a few milliseconds [94,95,96]. Thus, in contrast with the predictions of Equation (2), a fairly long contact may not always be replaced with many transient ones to allow bond formation.
- Second, the on-rate is difficult to define under 2D conditions, since it depends on many properties independent of the molecular binding interface [75,92]. Additionally, the bond lifetime is certainly as dependent on the disruptive forces exerted by surfaces, as it depends on the intrinsic bond stability [97].
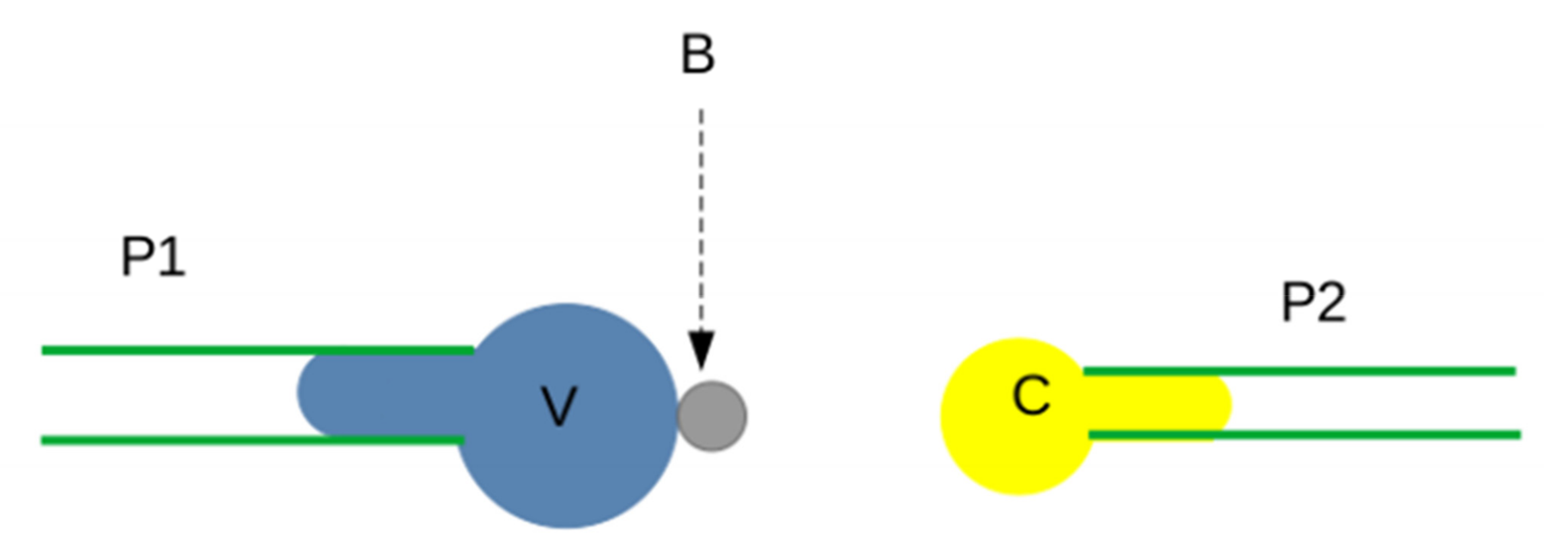
3.3.3. Accounting for the Effect of Forces on Bonds
- 1.
- Integrin mediated cell adhesion. Integrins are important mediators of cell adhesion. A well-known peptide ligand of integrins (the RGD tripeptide) was bound to surfaces with DNA constructs of varying strengths. Cell adhesion required that the linkers be able to resist a force of at least 40 pN for 2 s [118].
- 2.
- Signaling. Similarly, the use of calibrated DNA tethers showed that notch signaling required that the strength of the ligand attachment to a surface be higher than 12 pN [118]. When T lymphocytes were made to contact ligands deposited on a probe connected to a BFP allowing real-time determination of interaction force, the triggering of a calcium rise indicative of cell activation was correlated to the application of a force of about 10 pN on the TCR [119]. Additionally, a force of 10 pN applied on TCRs with an optical trap was reported to strongly increase signaling [119]. Furthermore, some reports supported the hypothesis that TCR signaling required that the TCR-ligand bond behave as a catch bond [119,120]. More work is, however, needed to assess the generality of this requirement [96]. More recently, it was suggested that talin, a cytoskeleton associated molecules that acted as a force sensor, could filter mechanical noise as a consequence of specific mechanical properties [102].
- 3.
- Ligand discrimination. The capacity of membrane receptors to discriminate between a high number of potential ligands is an essential requirement for cell function. It is, therefore, important to emphasize that forces may play an important role in ligand discrimination. The capacity of B lymphocytes to select and extract antigens bound to surfaces was shown to rely on forces [121,122]. Forces were also reported to modulate the preference of αvβ3 integrin for fibronectin or vitronectin [123].
3.3.4. Receptor Length and Conformational Dynamics
- 1.
- In addition to the molecular properties of binding sites, the efficiency of the bond formation between surface-attached molecules is strongly dependent on the length and flexibility of binding molecules so that binding sites might contact each other with a suitable orientation [91]. As a well-known example, the remarkable capacity of P-selectin molecules to tether rapidly flowing leukocytes in blood vessels is partly due to the unusually high length of the ligand-receptor couple (nearly 0.1 µm). Length and flexibility also play an important role in modulating multivalent attachments that are key to the avidity of interactions. Avidity might be loosely defined as some kind of “functional affinity” [116].
- 2.
- Receptor-mediated signaling is also highly dependent on the capacity of binding molecules to form multivalent attachments, since clustering of membrane molecules is often a key event of signal generation [61]. Indeed, an early step of the triggering of a signaling cascade is often the phosphorylation of a dedicated site on a molecule by a kinase brought close to this site. The molecular reach of molecules such as kinases or phosphatases is obviously dependent on the size and conformational flexibility of involved molecules [124]. Another important role of receptor length in the signaling process is the reorganization of intercellular contact zones as a consequence of the exclusion of bulky molecules from tight contact zones generated by short ligand-receptor couples. The importance of this mechanism was well demonstrated since the exclusion of the bulky CD45 phosphatase was found sufficient to trigger a signaling cascade in T lymphocytes [125,126,127].
- 3.
- The formation of multimolecular assemblies plays an important role in signal generation (as related to signalosome formation) as well as cell structural organization. Conformation flexibility may play a key role in this process [128] if bond formation results in the transient appearance of docking sites that may recruit additional molecules. Two points may be mentioned in this respect. (i) For the sake of simplicity, model systems used to study molecular associations most often rely on binary interactions with the underlying assumption that they are additive, which is not always warranted [129]. (ii) Recent progress in molecular dynamics may strongly improve our understanding of reaction paths and transient molecular states, which may increase our interest in ternary and multimolecular interactions.
4. Discussion and Conclusions: What Is the Take-Home Message?
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Alberts, B.; Johnson, A.; Lewis, J.; Morgan, D.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 6th ed.; Garland: New York, NY, USA, 2015. [Google Scholar]
- Netz, R.; Eaton, W.A. Estimating computational limites on theoretical descriptions of biological cells. Proc. Natl. Acad. Sci. USA 2021, 118, e2022753118. [Google Scholar] [CrossRef] [PubMed]
- Schiebinger, G.; Shu, J.; Tabaka, M.; Cleary, B.; Subramanian, V.; Solomon, A.; Gould, J.; Liu, S.; Lin, S.; Berube, P.; et al. Optimal-transport analysis of single-cell gene expression identifies developmental trajectories in reprogramming. Cell 2019, 176, 928–943. [Google Scholar] [CrossRef] [PubMed]
- Sander, M.; Dobicki, H.; Ott, A. Large amplitude oscillatory shear rheology of living fibroblasts: Path-dependent steady states. Biophys. J. 2017, 113, 1561–1573. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Prentice-Mott, H.V.; Meroz, Y.; Carlson, A.; Levine, M.A.; Davidson, M.W.; Irimia, D.; Charras, G.T.; Mahadevan, L.; Shah, J.V. Directional memory arises from long-lived cytoskeletal asymmetries in polarized chemotactic cells. Proc. Natl. Acad. Sci. USA 2016, 113, 1272–1627. [Google Scholar] [CrossRef] [PubMed]
- Bongrand, P. Biomolecular Recognition: The Current Challenge. In Dynamic Force Spectroscopy and Biomolecular Recognition; Bizzari, A.R., Cannistraro, R., Eds.; CRC Press: Boca Raton, FL, USA, 2012; pp. 1–50. Available online: http://www.hal.inserm.fr/inserm-01070064 (accessed on 7 December 2021).
- Battimelli, G.; Ciccotti, G.; Greco, P. Computer Meets Theoretical Physics; Springer: Cham, Switzerland, 2021; pp. 1–148. [Google Scholar]
- Abraham, M.J.; van der Spoel, D.; Lindahl, E.; Hess, B.; GROMACS Development Team. GROMACS User Manual Version 5.07. 2015. Available online: www.gromacs.org (accessed on 11 December 2019).
- Mykuliak, V.V.; Sikora, M.; Booth, J.V.; Cieplak, M.; Shalashilin, D.V.; Yytönen, V.P. Mechanical unfolding of proteins—A comparative nonequilibrum molecular dynamics study. Biophys. J. 2020, 119, 939–949. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Gao, J. Enhanced receptor binding of SARS-CoV-2 through networks of hydrogen-bonding and hydrophobic interactions. Proc. Natl. Acad. Sci. USA 2020, 117, 13967–13974. [Google Scholar] [CrossRef]
- Chen, C.; Boorla, V.S.; Banerjee, D.; Chowdhury, R.; Cavener, V.S.; Nissly, R.H.; Gontu, A.; Boye, N.R.; Vandegrift, K.; Nair, M.S.; et al. Computational prediction of the effect of amino acid changes on the binding affinity between Sars-CoV-2 spike RBD and human ACE2. Proc. Natl. Acad. Sci. USA 2021, 118, e2106480118. [Google Scholar] [CrossRef]
- Croll, T.I.; Williams, C.J.; Chen, V.B.; Richardson, D.C.; Richardson, J.S. Improving Sars-CoV-2 structures: Peer review by early coordinate release. Biophys. J. 2021, 120, 1085–1096. [Google Scholar] [CrossRef]
- Kamenik, A.S.; Singh, I.; Lak, P.; Balius, T.E.; Liedl, K.R.; Shoichet, B.K. Energy penalties enhance flexible receptor docking in a model cavity. Proc. Natl. Acad. Sci. USA 2021, 118, e2106195118. [Google Scholar] [CrossRef]
- Wang, Z.; Jumper, J.M.; Freed, K.F.; Sosnick, T.R. On the interpretation of force-induced unfolding studies of membrane proteins using fast simulations. Biophys. J. 2019, 117, 1429–1441. [Google Scholar] [CrossRef]
- Dickson, A. Mapping the ligand binding landscape. Biophys. J. 2018, 115, 1707–1719. [Google Scholar] [CrossRef]
- Ozsvar, J.; Wang, R.; Tarakanova, A.; Buehler, M.J.; Weiss, A.S. Fuzzy binding model of molecular interactions between tropoelastin and integrin alphaVbeta3. Biophys. J. 2021, 120, 3138–3151. [Google Scholar] [CrossRef]
- Fleetwood, O.; Kasimova, M.A.; Westerlund, A.M.; Delemotte, L. Molecular insights from conformational ensembles via machine learning. Biophys. J. 2020, 118, 765–780. [Google Scholar] [CrossRef]
- Kusebauch, U.; Campbell, D.S.; Deutsch, E.W.; Chu, C.S.; Spicer, D.A.; Brusniak, M.-Y.; Slagel, J.; Sun, Z.; Stevens, J.; Grimes, B.; et al. Human SRMAtlas: A Resource of Targeted Assays to Quantify the Complete Human Proteome. Cell 2016, 166, 766–778. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, R.; Wang, R.; Weng, Y.; Wang, R.; Zou, P.; Chen, P.R. Spatiotemporally resolved subcellular proteomics. Proc. Natl. Acad. Sci. USA 2021, 118, e2025299118. [Google Scholar] [CrossRef]
- Saoi, M.; Britz-McKibbin, P. New advances in tissue metabolomics: A review. Metabolites 2021, 11, 672. [Google Scholar] [CrossRef]
- Huttlin, E.L.; Bruckner, R.J.; Navarrete-Perea, J.; Cannon, J.R.; Baltier, K.; Gebreab, F.; Gygi, M.P.; Thornock, A.; Zarraga, G.; Tam, S.; et al. Dual proteome-scale networks reveal cell-specific remodeling of the human interactome. Cell 2021, 184, 3022–3040. [Google Scholar] [CrossRef]
- Szklarczyk, D.; Gable, A.L.; Nastou, K.C.; Lyon, D.; Kirsch, R.; Pyysalo, S.; Doncheva, N.T.; Legeay, M.; Fang, T.; Bork, P.; et al. The STRING database in 2021: Customizable protein-protein networks, and functional characterization of user-uploaded gene/measureent sets. Nucleic Acids Res. 2021, 49, D605–D612. [Google Scholar] [CrossRef]
- Newman, M.E.J. Networks; Oxford University Press: Oxford, UK, 2010; pp. 1–12. [Google Scholar]
- Calvano, S.E.; Xiao, W.; Richards, D.R.; Felciano, R.M.; Baker, H.; Cho, R.; Chen, R.O.; Brownstein, B.H.; Cobb, J.P.; Tschoeke, S.K.; et al. Inflammation and host response to injury large scale collaborative research. A network-based analysis of systemic inflammation in humans. Nature 2005, 432, 1032–1037. [Google Scholar] [CrossRef]
- Zaidel-Bar, R.; Itzkovitz, S.; Maayan, A.; Iyengar, R.; Geiger, B. Functional atlas of the integrin adhesome. Nat. Cell Biol. 2007, 9, 858–867. [Google Scholar] [CrossRef]
- Barabasi, A.-L.; Oltvai, Z.N. Network Biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101–113. [Google Scholar] [CrossRef]
- Alon, U. Network motifs: Theory and experimental approaches. Nat. Rev. Genet. 2007, 8, 450–461. [Google Scholar] [CrossRef]
- Morris, M.K.; Saez-Rodriguez, J.; Sorger, P.K.; Lauffenburger, D.A. Logic-based models for the analysis of cell signaling networks. Biochemistry 2010, 49, 3216–3224. [Google Scholar] [CrossRef]
- Martinez-Sanchez, M.E.; Mendoza, L.; Villareal, C.; Alvarez-Buylla, E.R. A minimal regulatory network of extrinsic and intrinsic factors recovers observed patterns of CD4+ T cell differentiation and plasticity. PLoS Comput. Biol. 2015, 11, e1004324. [Google Scholar] [CrossRef]
- Schwab, J.D.; Ikonomi, N.; Werle, S.D.; Weidner, F.M.; Geiger, H.; Kestler, H.A. Reconstructing boolean network ensembles from single-cell data for unraveling dynamics in the aging of human hematopoietic stem cells. Comp. Struct. Biotechnol. J. 2021, 19, 5321–5332. [Google Scholar] [CrossRef]
- Avila-Ponce de Leon, U.; Vazquez-Jimenez, A.; Madadamas-Guzman, M.; Pelayo, R.; Resendis-Antonio, O. Transcriptional and microenvironmental landscape of macrophage transition in cancer: A boolean analysis. Front. Immunol. 2021, 12, 642842. [Google Scholar] [CrossRef]
- Adridge, B.B.; Saez-Rodriguez, J.; Muhlich, J.L.; Sorger, P.K.; Lauffenburger, D.A. Fuzzy logic analysis of kinase pathway crosstalk in TNF/EGF/Insulin-induced signaling. PLoS Comput. Biol. 2009, 5, e1000340. [Google Scholar]
- Wittmann, D.M.; Krumsiek, J.; Saez-Rodriguez, J.; Lauffenburger, D.A.; Klamt, S.; Theis, F.J. Transforming Boolean models to continuous models: Methodology and application to T-cell receptor signaling. BMC Syst. Biol. 2009, 3, 98. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, K.; Xu, L.; Wang, E. Quantifying the Waddington landscape and biological paths for development and differentiation. Proc. Natl Acad. Sci. USA 2011, 108, 8257–8262. [Google Scholar] [CrossRef]
- Morris, R.; Sancho-Martinez, I.; Sharpee, T.O.; Belmonge, J.C.I. Mathematical approaches to modeling development and reprogramming. Proc. Natl. Acad. Sci. USA 2014, 111, 5076–5082. [Google Scholar] [CrossRef]
- Lang, J.; Nie, Q.; Li, C. Landscape and kinetic path quantify critical transitions in epithelial-mesenchyme transition. Biophys. J. 2021, 120, 4484–4500. [Google Scholar] [CrossRef] [PubMed]
- Tan, H.; Yang, K.; Li, Y.; Shaw, T.I.; Wang, Y.; Blanco, D.B.; Wang, X.; Cho, J.-H.; Wang, H.; Rankin, S.; et al. Integrative proteomics and phosphoproteomics profiling reveals dynamic signaling networks and bioenergetics pathways underlying T cell activation. Immunity 2017, 46, 488–503. [Google Scholar] [CrossRef] [PubMed]
- Bolouri, H.; Speake, C.; Skibinski, D.; Long, S.A.; Hocking, A.M.; Campbell, D.J.; Hamerman, J.A.; Malhotra, U.; Buckner, J.H. Benaroya Research Institute Covid-19 Research Team. The Covid-19 immune landscape is dynamically and reversibly correlated with disease severity. J. Clin. Investig. 2021, 131, e143648. [Google Scholar] [CrossRef] [PubMed]
- Zmurchok, C.; Holmes, W.R. Simple Rho GTPase dynamics generate a complex regulatory landscape associated with cell shape. Biophys. J. 2020, 118, 1438–1454. [Google Scholar] [CrossRef]
- Rand, D.A.; Raju, A.; Saez, M.; Corson, F.; Siggia, E.D. Geometry of gene regulatory dynamics. Proc. Natl. Acad. Sci. USA 2017, 118, e2109729118. [Google Scholar] [CrossRef]
- Venkatachalapathy, H.; Azarin, S.; Sarkar, C.A. Trajectory-based energy landscapes of gene regulatory networks. Biophys. J. 2021, 120, 687–698. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2017; pp. 1–8, Corrected at 12th printing. [Google Scholar]
- Lee, S.-I.; Batzoglou, S. Application of independent component analysis to microarrays. Genome Biol. 2003, 4, R76. Available online: http://genomebiology.com/2003/4/11/R76 (accessed on 28 December 2009). [CrossRef]
- Lutter, D.; Ugocscai, P.; Grandl, M.; Orso, E.; Theis, F.; Lang, E.W.; Schmitz, G. Analyzing M-CSF dependent monocyte/macrophage differentiation: Expression modes and meta-modes derived from an independent component analysis. BMC Bioinform. 2008, 9, 100. [Google Scholar] [CrossRef]
- Rajaei, P.; Jahanian, K.H.; Beheshti, A.; Band, S.S.; Dehzangi, A.; Alinejad-Rokny, H. VIRMOTIF: A user-friendly tool for viral sequence analysis. Genes 2021, 12, 186. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Sejnowski, T.J. The unreasonable effectiveness of deep learning in artificial intelligence. Proc. Natl. Acad. Sci. USA 2020, 117, 30033–30038. [Google Scholar] [CrossRef]
- Baraniuk, R.; Donoho, D.; Gavish, M. The science of deep learning. Proc. Natl. Acad. Sci. USA 2020, 117, 30029–30032. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional networks. Proc. Adv. Neural Inf. Process. Syst. 2012, 25, 1090–1098. [Google Scholar] [CrossRef]
- Goecks, J.; Jalili, V.; Heiser, L.M.; Gray, J.W. How machine learning will transform biomedicine. Cell 2020, 181, 92–101. [Google Scholar] [CrossRef]
- Callaway, E. It will change everything:AI makes gigantic leap in solving protein structures. Nature 2020, 588, 203–204. [Google Scholar] [CrossRef]
- Maslova, A.; Ramirez, R.N.; Ma, K.; Schmutz, H.; Wang, C.; Fox, C.; Ng, B.; Benoist, C.; Mostafavi, S.; Project, I.G. Immunological genome project. Deep learning of immune cell differentiation. Proc. Natl. Acad. Sci. USA 2020, 117, 25655–25666. [Google Scholar] [CrossRef]
- Nagata, Y.; Zhao, R.; Awada, H.; Kerr, C.M.; Mirzaev, I.; Kongkiatkamon, S.; Nazha, A.; Makishima, H.; Radivoyevitch, T.; Scott, J.G.; et al. Machine learning demonstrates that somatic mutations imprint invariant morphologic features in myelodysplastic syndromes. Blood 2020, 136, 2249–2262. [Google Scholar] [CrossRef]
- Papyan, V.; Han, X.Y.; Donoho, D.L. Prevalence of neural collapse during the terminal phase of deep learning training. Proc. Natl. Acad. Sci. USA 2020, 117, 24652–24663. [Google Scholar] [CrossRef]
- Amey, J.L.; Keeley, J.; Choudhury, T.; Kuprov, I. Neural network interpretation using descrambler groups. Proc. Natl. Acad. USA 2021, 118, e2016917118. [Google Scholar] [CrossRef]
- Haibe-Kains, B.; Adam, G.A.; Hosny, A.; Khodakarami, F.; Shraddha, T.; Kusko, R.; Sansone, S.-A.; Tong, W.; Wolfinger, R.D.; Mason, C.E.; et al. Transparency and reproducibility in artificial intelligence. Nature 2020, 586, E14–E16. [Google Scholar] [CrossRef]
- Eshete, B. Making machine learning trustworthy. Science 2021, 373, 743–744. [Google Scholar] [CrossRef]
- Stavroglou, S.K.; Pantelous, A.A.; Stanley, E.H.; Zuev, K.M. Unveiling causal interactions in complex systems. Proc. Natl. Acad. Sci. USA 2020, 117, 7599–7605. [Google Scholar] [CrossRef]
- Huttlin, E.L.; Bruckner, R.J.; Paulo, J.A.; Cannon, J.R.; Ting, L.; Baltier, K.; Colby, G.; Gebreab, F.; Gygi, M.P.; Parzen, H.; et al. Architecture of the human interactome defines protein communities and disease networks. Nature 2017, 545, 505–509. [Google Scholar] [CrossRef]
- Luck, K.; Kim, D.-K.; Lambourne, L.; Spirohn, K.; Begg, B.E.; Bian, W.; Brignall, R.; Cafarelli, T.; Campos-Laborie, F.J.; Charloteaux, B.; et al. A reference map of the human binary protein interactome. Nature 2020, 580, 402–408. [Google Scholar] [CrossRef]
- Puech, P.-H.; Bongrand, P. Mechanotransduction as a major driver of cell behaviour: Mechanisms, and relevance to cell organization and future research. Open Biol. 2021, 11, 210256. [Google Scholar] [CrossRef]
- Ghosh, I.; Singh, R.K.; Mishra, M.; Kapoor, S.; Jana, S.S. Switching between blebbing and lamellipodia depends on the degree of non-muscle myosin II activity. J. Cell Sci. 2021, 134, jcs248732. [Google Scholar]
- Dadwall, N.; Mix, C.; Reinhold, A.; Witte, A.; Freund, C.; Schraven, B.; Kliche, S. The multiple roles of the cytosolic adapter proteins ADAP, SKAP1 and SKAP2 for TCR/CD3-mediated signaling events. Front. Immunol. 2021, 12, 703534. [Google Scholar] [CrossRef]
- Ostrowska, N.; Feig, M.; Trylska, J. Crowding affects structural dynamics and contributes to membrane association of the NS3/4A complex. Biophys. J. 2021, 120, 3795–3806. [Google Scholar] [CrossRef]
- Voisinne, G.; Kersse, K.; Chaoui, K.; Lu, L.; Chaix, J.; Zhang, L.; Goncalves Menoita, M.; Girard, L.; Ounoughene, Y.; Wang, H.; et al. Quantitative interactomics in primary T cells unveils TCR signal diversification extent and dynamics. Nat. Immunol. 2019, 20, 1530–1541. [Google Scholar] [CrossRef]
- Hein, M.Y.; Hubner, N.C.; Poser, I.; Cox, J.; Nagaraj, N.; Toyoda, Y.; Gak, I.A.; Weisswange, I.; Mansfeld, J.; Bucholz, F.; et al. A human interactome in three quantitative dimensions organized by stoichiometries and abundances. Cell 2015, 163, 712–723. [Google Scholar] [CrossRef]
- Kale, S.; Strickland, M.; Peterkofsly, A.; Liu, J.; Tjandra, N. Model of a kinetically driven crosstalk between paralogous protein encounter complexes. Biophys. J. 2019, 117, 1655–1665. [Google Scholar] [CrossRef] [PubMed]
- Parker, B.W.; Goncz, E.J.; Krist, D.T.; Statsyuk, A.V.; Nesvizhskii, A.I.; Weiss, E.L. Mapping low-affinity/high-specificity peptide-protein interactions using ligand-footprinting mass spectrometry. Proc. Natl. Acad. Sci. USA 2019, 116, 21001–21011. [Google Scholar] [CrossRef] [PubMed]
- Shashikanth, N.; Kisting, M.A.; Leckband, D.E. Kinetic measurements reveal enhanced protein-protein interactions at intercellular junctions. Sci. Rep. 2016, 6, 23623. [Google Scholar] [CrossRef] [PubMed]
- Bongrand, P. Ligand-receptor interactions. Rep. Prog. Phys. 1999, 62, 921–968. Available online: https://www.hal.inserm.fr/hal-00320498 (accessed on 7 December 2021). [CrossRef]
- Lawrence, M.; Springer, T.A. Leukocytes Roll on a Selectin at Physiologic Flow Rates: Distinction from and Prerequisite for Adhesion through lntegrins. Cell 1991, 65, 859–873. [Google Scholar] [CrossRef]
- Marshall, B.T.; Long, M.; Piper, J.W.; Yago, T.; McEver, R.P.; Zhu, C. Direct observation of catch bonds involving cell-adhesion molecules. Nature 2003, 423, 190–193. [Google Scholar] [CrossRef]
- Rispens, T.; Velthuis, H.T.; Hemker, P.; Speijer, H.; Hermens, W.; Aarden, L. Label-free assessment of high-affinity antibody-antigen binding constants. Comparison of bioassay, SPR, and PEIA-ellipsometry. J. Immunol. Methods 2011, 365, 50–57. [Google Scholar] [CrossRef]
- Heinrich, L.; Tissot, N.; Hartmann, D.J.; Cohen, R. Comparison of the results obtained by ELISA and surface plasmon resonance for the determination of antibody affinity. J. Immunol. Methods 2010, 352, 13–22. [Google Scholar] [CrossRef]
- Pierres, A.; Benoliel, A.M.; Zhu, C.; Bongrand, P. Diffusion of microspheres in shear flow near a wall: Use to measure binding rates between attached molecules. Biophys. J. 2001, 81, 25–42. [Google Scholar] [CrossRef]
- Robert, P.; Benoliel, A.M.; Pierres, A.; Bongrand, P. What is the biological relevance of the specific bond properties revealed by single-molecule studies? J. Mol. Recognit. 2007, 20, 432–447. [Google Scholar] [CrossRef]
- Pyrpassopoulos, S.; Shuman, H.; Ostap, E.M. Adhesion force and attachment lifetime of the KIF16B-PX domain interaction with lipid membranes. Mol. Biol. Cell 2017, 28, 3315–3322. [Google Scholar] [CrossRef]
- Paananen, A.; Weich, S.; Szilvay, G.R.; Leitner, M.; Tappura, K.; Ebner, A. Quantifying biomolecular hydrophobicity: Single molecule force spectroscopy of class II hydrophobins. J. Biol. Chem. 2021, 296, 100728. [Google Scholar] [CrossRef]
- Farzi, B.; Young, D.; Scrimgeour, J.; Cetinkaya, C. Mechanical properties of P-selectin PSGL-1 bonds. Colloids Surf. B Biointerfaces 2019, 173, 529–538. [Google Scholar] [CrossRef]
- Puech, P.-H.; Nevoltris, D.; Robert, P.; Limozin, L.; Boyer, C.; Bongrand, P. Force measurements of TCR/pMHC recognition at T cell surface. PLoS ONE 2011, 6, e22344. [Google Scholar] [CrossRef]
- Merkel, R.; Nassoy, P.; Leung, A.; Ritchie, K.; Evans, E. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature 1999, 397, 50–53. [Google Scholar] [CrossRef]
- Pierres, A.; Benoliel, A.M.; Bongrand, P. Studying molecular interactions at the single bond level with a laminar flow chamber. Cell. Mol. Bioeng. 2008, 1, 247–262. [Google Scholar] [CrossRef][Green Version]
- Johnson, K.C.; Thomas, W.E. How do we know when single-molecule force spectroscopy really tests single bonds? Biophys. J. 2018, 114, 2032–2039. [Google Scholar] [CrossRef]
- Makarov, D.E. Life in silico: Are we close yet? Proc. Natl. Acad. Sci. USA 2021, 118, e2100278118. [Google Scholar] [CrossRef]
- Murray, D.; Petrey, D.; Honig, B. Integrating 3D structural information into systems biology. J. Biol. Chem. 2021, 296, 100562. [Google Scholar] [CrossRef]
- Koudriavtsev, A.B.; Jameson, R.F.; Linert, W. The Law of Mass Action; Springer: Berlin/Heidelberg, Germany, 2001; 328p. [Google Scholar]
- Williams, A.F. Out of equilibrium. Nature 1991, 353, 473–474. [Google Scholar] [CrossRef]
- Bock, A.; Annibale, P.; Konrad, C.; Hannawacker, A.; Anton, S.E.; Maiellaro, I.; Zabel, U.; Sivaramakrishnan, S.; Falcke, M.; Lose, M.J. Optical mapping of cAMP signaling at the nanometer scale. Cell 2020, 182, 1519–1530. [Google Scholar] [CrossRef]
- Stroberg, W.; Schnell, S. Concentration sensing in crowded environments. Biophys. J. 2021, 120, 1718–1731. [Google Scholar] [CrossRef]
- Cao, S.; Peterson, S.M.; Müller, S.; Reichelt, M.; McRoberts Amador, C.; Martinez-Martin, N. A membrane protein display platform for receptor interactome discovery. Proc. Natl. Acad. Sci. USA 2021, 118, e2025451118. [Google Scholar] [CrossRef]
- Pierres, A.; Benoliel, A.M.; Bongrand, P. Studying receptor-mediated cell adhesion at the single molecule level. Cell Adhes. Commun. 1998, 5, 375–395. Available online: http://www.hal.inserm.fr/inserm-00358477 (accessed on 7 December 2021). [CrossRef][Green Version]
- Barua, D.; Nagel, M.; Winklbauer, R. Cell-cell contact landscapes in Xenopus gastrula tissues. Proc. Natl. Acad. Sci. USA 2021, 118, e2107953118. [Google Scholar] [CrossRef]
- Malissen, B.; Bongrand, P. Early T cell activation: Integrating biochemical, structural, and biophysical cues. Annu. Rev. Immunol. 2015, 33, 539–561. [Google Scholar] [CrossRef]
- Robert, P.; Limozin, L.; Pierres, A.; Bongrand, P. Biomolecule association rates do not provide a complete description of bond formation. Biophys. J. 2009, 96, 4642–4650. [Google Scholar] [CrossRef]
- Limozin, L.; Bongrand, P.; Robert, L. A rough energy landscape to describe surface -linked antibody and antigen bond formation. Sci. Rep. 2016, 6, 35193. [Google Scholar] [CrossRef] [PubMed]
- Limozin, L.; Bridge, M.; Bongrand, P.; Dushek, O.; van der Merwe, P.A.; Robert, P. TCR-pMHC kinetics under force in a cell-free system show no intrinsic catch bond, but a minimal encounter duration before binding. Proc. Natl. Acad. Sci. USA 2019, 116, 16943–16948. [Google Scholar] [CrossRef] [PubMed]
- Pullen, R.H., III; Abel, S.M. Catch bonds at T cell interfaces: Impact of surface reorganization and membrane fluctuations. Biophys. J. 2017, 113, 120–131. [Google Scholar] [CrossRef] [PubMed]
- Gruber, S.; Löft, A.; Sedlak, S.M.; Benoit, M.; Gaub, H.E.; Lipfert, J. Designed anchoring geometries determine lifetimes of biotin-streptavidin bonds under constant load and enable ulstra-stable coupling. Nanoscale 2020, 12, 21131–21137. [Google Scholar] [CrossRef]
- Luca, V.C.; Kim, B.C.; Ge, C.; Kaluda, S.; Wu, D.; Roein-Peikar, M.; Haltiwanger, R.S.; Zhu, C.; Ha, T.; Garcia, K.C. Notch-Jagged complex structure implicates a catch bond in tuning ligand sensitivity. Science 2017, 355, 1320–1324. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, Y.; Blanchard, A.T.; Chang, Y.; Brockmann, J.M.; Ma, V.P.-Y.; Lam, W.A.; Salaita, K. Platelet integrins exhibit anisotropic mechanosensing and harness piconewton forces to mediate platelet aggregation. Proc. Natl. Acad. Sci. USA 2018, 115, 325–330. [Google Scholar] [CrossRef]
- Fölser, M.; Motsch, V.; Platzer, R.; Huppa, J.B.; Schütz, G.J. A multimodal platform for simultaneous T-cell imaging, defined activation, and mechanobiological characterization. Cells 2021, 10, 235. [Google Scholar] [CrossRef]
- Tapia-Rojo, R.; Alonso-Caballero, A.; Fernandez, J.M. Talin folding as the tuning fork of cellular mechanotransduction. Proc. Natl. Acad. Sci. USA 2020, 117, 21346–21353. [Google Scholar] [CrossRef]
- Milles, L.F.; Schulten, K.; Gaub, H.E.; Bernardi, R.C. Molecular mechanism of extreme mechanostability in a pathogen adhesin. Science 2018, 259, 1527–1533. [Google Scholar] [CrossRef]
- Bell, G.I. Models for the specific adhesion of cells to cells. Science 1978, 200, 618–627. [Google Scholar] [CrossRef]
- Chen, S.; Springer, T.A. Selectin receptor-ligand bonds: Formation limited by shear rate and dissociation governed by the Bell model. Proc. Natl. Acad. Sci. USA 2001, 98, 950–955. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Hinczewski, M.; Thirumalai, D. Phenomenological and microscopic theories for catch bonds. J. Struct. Biol. 2017, 197, 50–56. [Google Scholar] [CrossRef]
- Pierres, A.; Benoliel, A.M.; Bongrand, P. Measuring the lifetime of bonds made between surface-linked molecules. J. Biol. Chem. 1995, 270, 26586–26592. [Google Scholar] [CrossRef]
- Thomas, W.E.; Trintchina, E.; Forero, M.; Vogel, V.; Sokurenko, E.V. Bacterial adhesion to target cells enhanced by shear force. Cell 2002, 109, 913–923. [Google Scholar] [CrossRef]
- Jahed, Z.; Haydari, Z.; Rathish, A.; Mofrad, M.R.K. Kindlin is mechanosensitive: Force-induced conformational switch mediates cross-talk among integrins. Biophys. J. 2019, 116, 1011–1024. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.; Mallis, R.J.; Lang, M.J.; Reinherz, E.L. The αβTCR mechanosensor exploits dynamic ectodomain allostery to optimize its ligand recognition site. Proc. Natl. Acad. Sci. USA 2020, 117, 21336–21345. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Moran, J.; Weddle, C.; Hinczewski, M. Unraveling the mechanism of cadherin-catenin-actin catch bond. PLoS Comput. Biol. 2018, 14, e1006399. [Google Scholar] [CrossRef] [PubMed]
- Dahlke, K.; Zhao, J.; Sing, C.E.; Banigan, E.J. Force-dependent facilitated dissociation can generate protein-DNA catch bonds. Biophys. J. 2019, 117, 1085–1100. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.T.; Takeuchi, K.; Sun, Z.-Y.J.; Touma, M.; Castro, C.E.; Fahmy, A.; Lang, M.J.; Wagner, G.; Reinherz, E.L. The ab T cell receptor is an anisotropic mechanosensor. J. Biol. Chem. 2009, 284, 31028–31037. [Google Scholar] [CrossRef]
- Vitte, J.; Benoliel, A.M.; Eymeric, P.; Bongrand, P.; Pierres, A. Beta 1 integrin-mediated adhesion may be initiated by multiple incomplete bonds, thus accounting for the functional importance of receptor clustering. Biophys. J. 2004, 86, 4059–4074. [Google Scholar] [CrossRef]
- Pierres, A.; Touchard, D.; Benoliel, A.M.; Bongrand, P. Dissecting streptavidin-biotin interaction with a laminar flow chamber. Biophys. J. 2002, 82, 3214–3223. [Google Scholar] [CrossRef]
- Lo Schiavo, V.; Robert, P.; Limozin, L.; Bongrand, P. Quantitative modeling assesses the contribution of bond strenthening, rebinding and force sharing to the avidity of biomolecule interactions. PLoS ONE 2012, 7, e44070. [Google Scholar] [CrossRef]
- Gonzalez, C.; Chames, P.; Kerfelec, B.; Baty, D.; Robert, P.; Limozin, L. Nanobody-CD16 catch bond reveals NK cell mechanosensitivity. Biophys. J. 2019, 116, 1516–1526. [Google Scholar] [CrossRef]
- Wang, X.; Ha, T. Defining single molecular forces required to activate integrin and notch signaling. Science 2013, 340, 991–994. [Google Scholar] [CrossRef]
- Liu, B.; Chen, W.; Evavold, B.D.; Zhu, C. Accumulation of dynamic catch bonds between TCR and agonist peptide-MHC triggers T cell signaling. Cell 2014, 157, 357–368. [Google Scholar] [CrossRef]
- Sibener, L.V.; Fernandes, R.A.; Kolawole, E.M.; Carbone, C.B.; Liu, F.; McAffee, D.; Birnbaum, M.E.; Yang, X.; Su, L.F.; Yu, W.; et al. Isolation of a structural mechanism for uncoupling T cell receptor signaling from peptide-MHC binding. Cell 2018, 174, 672–687. [Google Scholar] [CrossRef]
- Natkanski, E.; Lee, W.-Y.; Mistry, B.; Casal, A.; Molloy, J.E.; Tolar, P. B cells use mechanical energy to discriminate antigen affinities. Science 2013, 340, 1587–1590. [Google Scholar] [CrossRef]
- Kumari, A.; Pineau, J.; Saez, P.J.; Maruin, M.; Lankar, D.; San Roman, M.; Hennig, K.; Boura, V.F.; Voituriez, R.; Karlsson, M.C.I.; et al. Actomysosin-driven force patterning controls endocytosis at the immune synapse. Nat. Com. 2019, 10, 2870. [Google Scholar] [CrossRef]
- Bachmann, M.; Schäfer, M.; Mykuliak, V.V.; Ripamonti, M.; Heiser, L.; Weissenbruch, K.; Krübel, S.; Franz, C.M.; Hytönen, V.P.; Wehrle-Haller, B.; et al. Induction of ligand promiscuity of aVb3 integrin by mechanical force. J. Cell Sci. 2020, 133, jcs242404. [Google Scholar] [CrossRef]
- Clemens, L.; Kutuzov, M.; Bayer, K.V.; Goyette, J.; Allard, J.; Duschek, O. Determination of the molecular reach of the protein tyrosine phosphatase SHP-1. Biophys. J. 2021, 120, 2054–2066. [Google Scholar] [CrossRef]
- Davis, S.J.; van der Merwe, P.A. The kinetic-segregation model: TCR triggering and beyond. Nat. Immunol. 2006, 7, 803–809. [Google Scholar] [CrossRef]
- Chang, V.T.; Fernandes, F.A.; Ganzinger, K.A.; Lee, S.F.; Siebold, C.; McColl, J.; Jönsson, P.; Palayret, M.; Harlos, K.; Coles, C.H.; et al. Initiation of T cell signaling by CD45 segregation at ‘close contacts’. Nat. Immunol. 2016, 17, 574–582. [Google Scholar] [CrossRef]
- Razvag, Y.; Neve-Oz, Y.; Sajman, J.; Yakovian, O.; Reches, M.; Sherman, E. T-cell activation through isolated tight contacts. Cell Rep. 2019, 29, 3506–3521. [Google Scholar] [CrossRef]
- Van Hateren, A.; Anderson, M.; Bailey, A.; Werner, J.M.; Skipp, P.; Elliott, T. Direct evidence for conformational dynamics in major histocompatibility complex class I molecules. J. Biol. Chem. 2017, 292, 20255–20269. [Google Scholar] [CrossRef]
- Boulton, S.; Van, K.; VanSchouwen, B.; Augustine, J.; Akimoto, M.; Melacini, G. Allosteric mechanisms of nonadditive substituent contributions to protein-ligand binding. Biophys. J. 2020, 119, 1135–1146. [Google Scholar] [CrossRef]
- Orchard, S.; Kerrien, S.; Abbani, S.; Aranda, B.; Bhate, J.; Bidwell, S.; Bridge, A.; Briganti, L.; Brinkman, F.S.L.; Cesareni, G.; et al. Protein interaction data curation: The international molecular exchange (IMEx) consortium. Nat. Methods 2012, 9, 345–350. [Google Scholar] [CrossRef]
- Snider, J.; Kotlyar, M.; Saraon, P.; Yao, Z.; Jurisica, I.; Stagljar, I. Fundamentals of protein interaction network mapping. Mol. Syst. Biol. 2015, 11, 848. [Google Scholar] [CrossRef]
- Srivasta, P.; Bej, S.; Yordanova, K.; Wolkenhauer, O. Self-attention based models for the extraction of molecular interactions from biological texts. Biomolecules 2021, 11, 1591. [Google Scholar] [CrossRef]
- Maddox, J. Is molecular biology yet a science? Nature 1992, 355, 201. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Hempel, T.; del Razo, M.J.; Lee, C.T.; Taylor, B.C.; Amaro, R.E.; Noé, F. Independent markov decomposition: Toward modeling kinetics of biomolecular complexes. Proc. Natl. Acad. Sci. USA 2021, 118, e2105230118. [Google Scholar] [CrossRef]

| Database | Website | CD162 Ligand | Affinity or Kinetic Constants | Catch Bond | Rolling Function | Nb of PUBLICATIONS Quoted |
|---|---|---|---|---|---|---|
| Biogrid | https://thebiogrid.org/ accessed on 7 December 2021 | + | - | - | - | 1 |
| Dip | https://dip.doe-mbi.ucla.edu/dip/ accessed on 7 December 2021 | + | - | - | - | 0 |
| HPRD | http://hprd.org/ accessed on 7 December 2021 | + | - | - | - | 3 |
| IntAct | https://www.ebi.ac.uk/intact/ accessed on 7 December 2021 | + | - | - | - | 4 |
| Mint | https://mint.bio.uniroma2.it/ accessed on 7 December 2021 | - | - | - | - | - |
| String | https://string-db.org/ accessed on 7 December 2021 | + | - | - | + | 0 |
| Uniprot | https://www.uniprot.org/uniprot accessed on 7 December 2021 | + | +/- | - | + | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bongrand, P. Is There a Need for a More Precise Description of Biomolecule Interactions to Understand Cell Function? Curr. Issues Mol. Biol. 2022, 44, 505-525. https://doi.org/10.3390/cimb44020035
Bongrand P. Is There a Need for a More Precise Description of Biomolecule Interactions to Understand Cell Function? Current Issues in Molecular Biology. 2022; 44(2):505-525. https://doi.org/10.3390/cimb44020035
Chicago/Turabian StyleBongrand, Pierre. 2022. "Is There a Need for a More Precise Description of Biomolecule Interactions to Understand Cell Function?" Current Issues in Molecular Biology 44, no. 2: 505-525. https://doi.org/10.3390/cimb44020035
APA StyleBongrand, P. (2022). Is There a Need for a More Precise Description of Biomolecule Interactions to Understand Cell Function? Current Issues in Molecular Biology, 44(2), 505-525. https://doi.org/10.3390/cimb44020035






