Process Analytical Technology Obtained Metastable Zone Width, Nucleation Rate and Solubility of Paracetamol in Isopropanol—Theoretical Analysis
Abstract
1. Introduction
2. Results and Discussion
2.1. PAT-Obtained Solubility
2.2. PAT-Obtained Metastable Zone Width
2.3. Nyvlt’s Approach to the Nucleation Kinetics
2.4. Kubota’s Approach
2.5. Sangwal’s Approach
2.6. Our Kinetic Model: Homogeneous 3D Nucleation Model
3. Materials and Methods
3.1. Solubility Experiment Assisted by Process Analytical Technology Tool, In Situ FTIR
3.2. Metastable Zone Width Prediction Using PAT
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Sarma, B.; Evans, J.M.B.; Myerson, A.S. Pharmaceutical Crystallization. Cryst. Growth Des. 2011, 11, 887–895. [Google Scholar] [CrossRef]
- Wood, B.; Girard, K.P.; Polster, C.S.; Croker, D.M. Progress to Date in the Design and Operation of Continuous Crystallization Processes for Pharmaceutical Applications. Org. Process Res. Dev. 2019, 23, 122–144. [Google Scholar] [CrossRef]
- Weng, J.; Huang, Y.; Hao, D.; Ji, Y. Recent Advances of Pharmaceutical Crystallization Theories. Chin. J. Chem. Eng. 2020, 28, 935–948. [Google Scholar] [CrossRef]
- Kumar, K.V.; Ramisetty, K.A.; Devi, K.R.; Krishna, G.R.; Heffernan, C.; Stewart, A.A.; Guo, J.; Gadipelli, S.; Brett, D.J.L.; Favvas, E.P.; et al. Pure Curcumin Spherulites from Impure Solutions via Nonclassical Crystallization. ACS Omega 2021, 6, 23884–23900. [Google Scholar] [CrossRef] [PubMed]
- Mullin, J.W. (Ed.) Crystallization, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2001; ISBN 9780750648332. [Google Scholar]
- Pu, S.; Hadinoto, K. Habit Modification in Pharmaceutical Crystallization: A Review. Chem. Eng. Res. Des. 2024, 201, 45–66. [Google Scholar] [CrossRef]
- Giulietti, M.; Seckler, M.M.; Derenzo, S.; Ré, M.I.; Cekinski, E. Industrial Crystallization and Precipitation from Solutions: State of the Technique. Braz. J. Chem. Eng. 2001, 18, 423–440. [Google Scholar] [CrossRef]
- Mersmann, A. (Ed.) Crystallization Technology Handbook, 1st ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Cruz-Cabeza, A.J.; Feeder, N.; Davey, R.J. Open Questions in Organic Crystal Polymorphism. Commun. Chem. 2020, 3, 142. [Google Scholar] [CrossRef]
- Dunitz, J.D.; Bernstein, J. Disappearing Polymorphs. Acc. Chem. Res. 1995, 28, 193–200. [Google Scholar] [CrossRef]
- Cruz-Cabeza, A.J.; Reutzel-Edens, S.M.; Bernstein, J. Facts and Fictions about Polymorphism. Chem. Soc. Rev. 2015, 44, 8619–8635. [Google Scholar] [CrossRef]
- Vashistha, M.; Cliffe, C.; Murphy, E.; Palanisamy, P.; Stewart, A.; Gadipelli, S.; Howard, C.A.; Brett, D.J.L.; Kumar, K.V. Dotted Crystallisation: Nucleation Accelerated, Regulated, and Guided by Carbon Dots. CrystEngComm 2023, 25, 4729–4744. [Google Scholar] [CrossRef]
- Sangwal, K. Additives and Crystallization Processes: From Fundamentals to Applications, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Khaddour, I.; Rocha, F. Metastable Zone Width for Secondary Nucleation and Secondary Nucleation inside the Metastable Zone. Cryst. Res. Technol. 2011, 46, 373–382. [Google Scholar] [CrossRef]
- Kakkar, S.; Devi, K.R.; Svärd, M.; Rasmuson, Å. Crystal Nucleation of Salicylamide and a Comparison with Salicylic Acid. CrystEngComm 2020, 22, 3329–3339. [Google Scholar] [CrossRef]
- Kakkar, S.; Devi, K.R.; Rasmuson, Å.C. Molecular Clustering of Fenoxycarb and Salicylic Acid in Organic Solvents and Relation to Crystal Nucleation. Cryst. Growth Des. 2022, 22, 2824–2836. [Google Scholar] [CrossRef]
- Zeglinski, J.; Kuhs, M.; Khamar, D.; Hegarty, A.C.; Devi, R.K.; Rasmuson, Å.C. Crystal Nucleation of Tolbutamide in Solution: Relationship to Solvent, Solute Conformation, and Solution Structure. Chem.—A Eur. J. 2018, 24, 4916–4926. [Google Scholar] [CrossRef]
- McTague, H.; Rasmuson, Å.C. Nucleation of the Theophylline:Salicylic Acid 1:1 Cocrystal. Cryst. Growth Des. 2021, 21, 2711–2719. [Google Scholar] [CrossRef]
- Zeglinski, J.; Kuhs, M.; Devi, K.R.; Khamar, D.; Hegarty, A.C.; Thompson, D.; Rasmuson, Å.C. Probing Crystal Nucleation of Fenoxycarb from Solution through the Effect of Solvent. Cryst. Growth Des. 2019, 19, 2037–2049. [Google Scholar] [CrossRef]
- Nordström, F.L.; Svärd, M.; Rasmuson, Å.C. Primary Nucleation of Salicylamide: The Influence of Process Conditions and Solvent on the Metastable Zone Width. CrystEngComm 2013, 15, 7285–7297. [Google Scholar] [CrossRef]
- Nordström, F.L.; Svärd, M.; Malmberg, B.; Rasmuson, Å.C. Influence of Solution Thermal and Structural History on the Nucleation of M-Hydroxybenzoic Acid Polymorphs. Cryst. Growth Des. 2012, 12, 4340–4348. [Google Scholar] [CrossRef][Green Version]
- Kuhs, M.; Zeglinski, J.; Rasmuson, Å.C. Influence of History of Solution in Crystal Nucleation of Fenoxycarb: Kinetics and Mechanisms. Cryst. Growth Des. 2014, 14, 905–915. [Google Scholar] [CrossRef]
- Jolliffe, H.G.; Gerogiorgis, D.I. Process Modelling, Design and Technoeconomic Evaluation for Continuous Paracetamol Crystallisation. Comput. Chem. Eng. 2018, 118, 224–235. [Google Scholar] [CrossRef]
- Yeh, K.L.; Lee, H.L.; Lee, T. Crystallization of Form II Paracetamol with the Assistance of Carboxylic Acids toward Batch and Continuous Processes. Pharmaceutics 2022, 14, 1099. [Google Scholar] [CrossRef] [PubMed]
- Urwin, S.J.; Yerdelen, S.; Houson, I.; Ter Horst, J.H. Impact of Impurities on Crystallization and Product Quality: A Case Study with Paracetamol. Crystals 2021, 11, 1344. [Google Scholar] [CrossRef]
- Jiang, M.; Ni, X.W. Reactive Crystallization of Paracetamol in a Continuous Oscillatory Baffled Reactor. Org. Process Res. Dev. 2019, 23, 882–890. [Google Scholar] [CrossRef]
- Kaur Bhangu, S.; Ashokkumar, M.; Lee, J. Ultrasound Assisted Crystallization of Paracetamol: Crystal Size Distribution and Polymorph Control. Cryst. Growth Des. 2016, 16, 1934–1941. [Google Scholar] [CrossRef]
- McDonagh, A.F.; Tajber, L. The Control of Paracetamol Particle Size and Surface Morphology through Crystallisation in a Spray Dryer. Adv. Powder Technol. 2020, 31, 287–299. [Google Scholar] [CrossRef]
- Chewle, S.; Emmerling, F.; Weber, M. Effect of Choice of Solvent on Crystallization Pathway of Paracetamol: An Experimental and Theoretical Case Study. Crystals 2020, 10, 1107. [Google Scholar] [CrossRef]
- Nguyen, T.T.H.; Khan, A.; Bruce, L.M.; Forbes, C.; O’Leary, R.L.; Price, C.J. The Effect of Ultrasound on the Crystallisation of Paracetamol in the Presence of Structurally Similar Impurities. Crystals 2017, 7, 294. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.; Gao, T.; Nagy, Z.K. Integrated Upstream and Downstream Application of Wet Milling with Continuous Mixed Suspension Mixed Product Removal Crystallization. Cryst. Growth Des. 2015, 15, 5879–5885. [Google Scholar] [CrossRef]
- Nývlt, J. Kinetics of Nucleation in Solutions. J. Cryst. Growth 1968, 3–4, 377–383. [Google Scholar] [CrossRef]
- Sangwal, K. A Novel Self-Consistent Nývlt-like Equation for Metastable Zone Width Determined by the Polythermal Method. Cryst. Res. Technol. 2009, 44, 231–247. [Google Scholar] [CrossRef]
- Kubota, N. A New Interpretation of Metastable Zone Widths Measured for Unseeded Solutions. J. Cryst. Growth 2008, 310, 629–634. [Google Scholar] [CrossRef]
- Granberg, R.A.; Rasmuson, Å.C. Solubility of Paracetamol in Pure Solvents. J. Chem. Eng. Data 1999, 44, 1391–1395. [Google Scholar] [CrossRef]
- Simon, L.L.; Pataki, H.; Marosi, G.; Meemken, F.; Hungerbühler, K.; Baiker, A.; Tummala, S.; Glennon, B.; Kuentz, M.; Steele, G.; et al. Assessment of Recent Process Analytical Technology (PAT) Trends: A Multiauthor Review. Org. Process Res. Dev. 2015, 19, 3–62. [Google Scholar] [CrossRef]
- Nývlt, J.; Rychlý, R.; Gottfried, J.; Wurzelová, J. Metastable Zone-Width of Some Aqueous Solutions. J. Cryst. Growth 1970, 6, 151–162. [Google Scholar] [CrossRef]
- Kubota, N. A Unified Interpretation of Metastable Zone Widths and Induction Times Measured for Seeded Solutions. J. Cryst. Growth 2010, 312, 548–554. [Google Scholar] [CrossRef]
- Mitchell, N.A.; Frawley, P.J.; Ó’Ciardhá, C.T. Nucleation Kinetics of Paracetamolethanol Solutions from Induction Time Experiments Using Lasentec FBRM®. J. Cryst. Growth 2011, 321, 91–99. [Google Scholar] [CrossRef]
- Brown, C.J.; Ni, X.W. Determination of Metastable Zone Width, Mean Particle Size and Detectable Number Density Using Video Imaging in an Oscillatory Baffled Crystallizer. CrystEngComm 2012, 14, 2944–2949. [Google Scholar] [CrossRef]
- Hazi Mastan, T.; Lenka, M.; Sarkar, D. Nucleation Kinetics from Metastable Zone Widths for Sonocrystallization of L-Phenylalanine. Ultrason. Sonochem. 2017, 36, 497–506. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J.; Zhang, K.; Wu, S.; Liu, S.; Li, K.; Yu, B.; Gong, J. Nucleation Behavior of Eszopiclone-Butyl Acetate Solutions from Metastable Zone Widths. Chem. Eng. Sci. 2016, 155, 248–257. [Google Scholar] [CrossRef]
- Maharana, A.; Sarkar, D. Effects of Ultrasound and Its Amplitude on the Metastable Zone Width, Induction Time, and Nucleation Kinetics of Pyrazinamide in Acetone. Ind. Eng. Chem. Res. 2022, 61, 11262–11275. [Google Scholar] [CrossRef]
- Sangwal, K. Nucleation and Crystal Growth: Metastability of Solutions and Melts; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- McTague, H.; Rasmuson, Å.C. Nucleation in the Theophylline/Glutaric Acid Cocrystal System. Cryst. Growth Des. 2021, 21, 3967–3980. [Google Scholar] [CrossRef]
- Granberg, R.A.; Ducreux, C.; Gracin, S.; Rasmuson, Å.C. Primary Nucleation of Paracetamol in Acetone-Water Mixtures. Chem. Eng. Sci. 2001, 56, 2305–2313. [Google Scholar] [CrossRef]
- Dalvi, S.V.; Yadav, M.D. Effect of Ultrasound and Stabilizers on Nucleation Kinetics of Curcumin during Liquid Antisolvent Precipitation. Ultrason. Sonochem. 2015, 24, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Vashishtha, M.; Kakkar, S.; Ranjbar, M.; Kumar, K.V. Crystallisation: Solving Crystal Nucleation Problem in the Chemical Engineering Classroom Based on the Research Grade Experiments Deployed in Virtual Mode. Educ. Chem. Eng. 2024, 49, 12–25. [Google Scholar] [CrossRef]
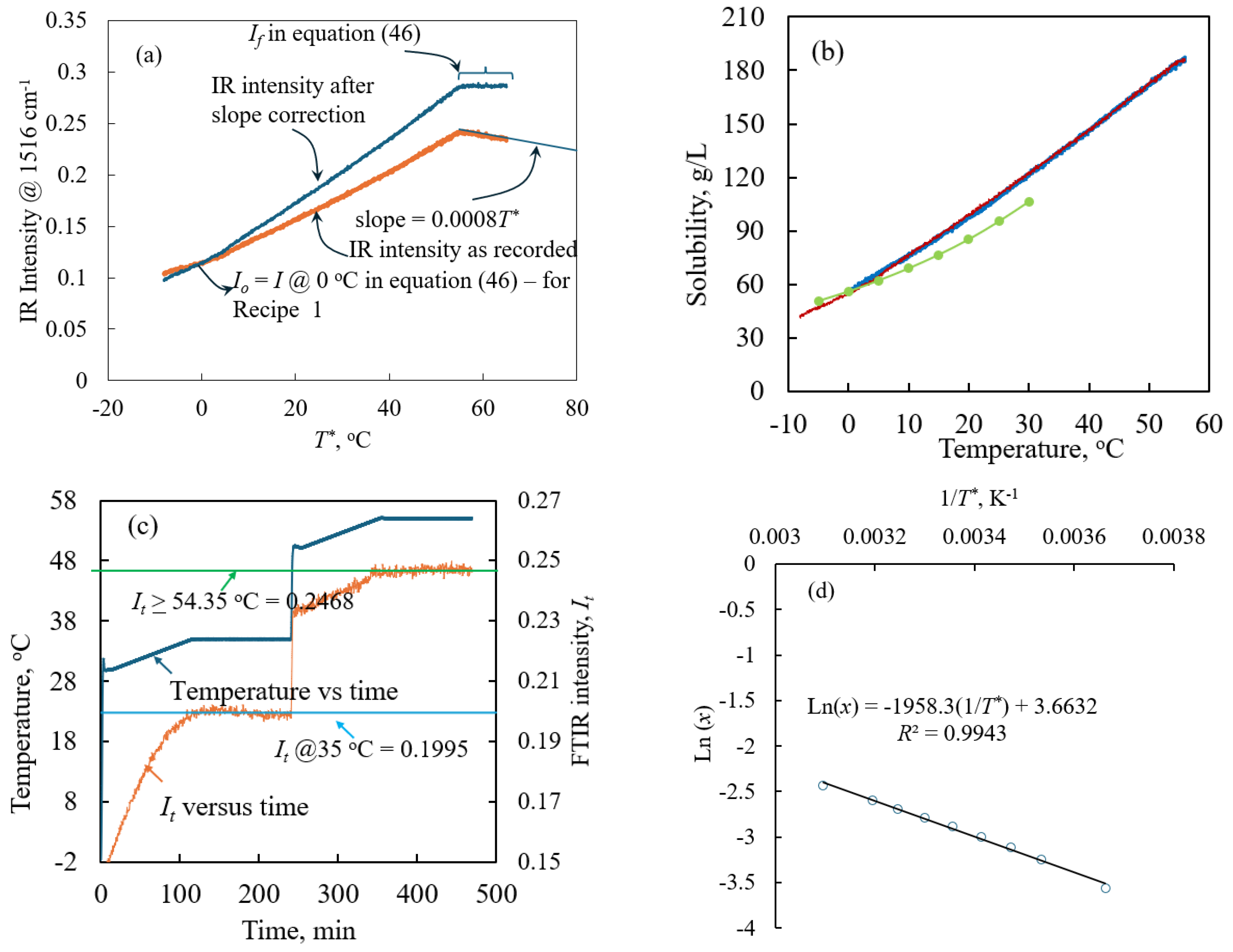

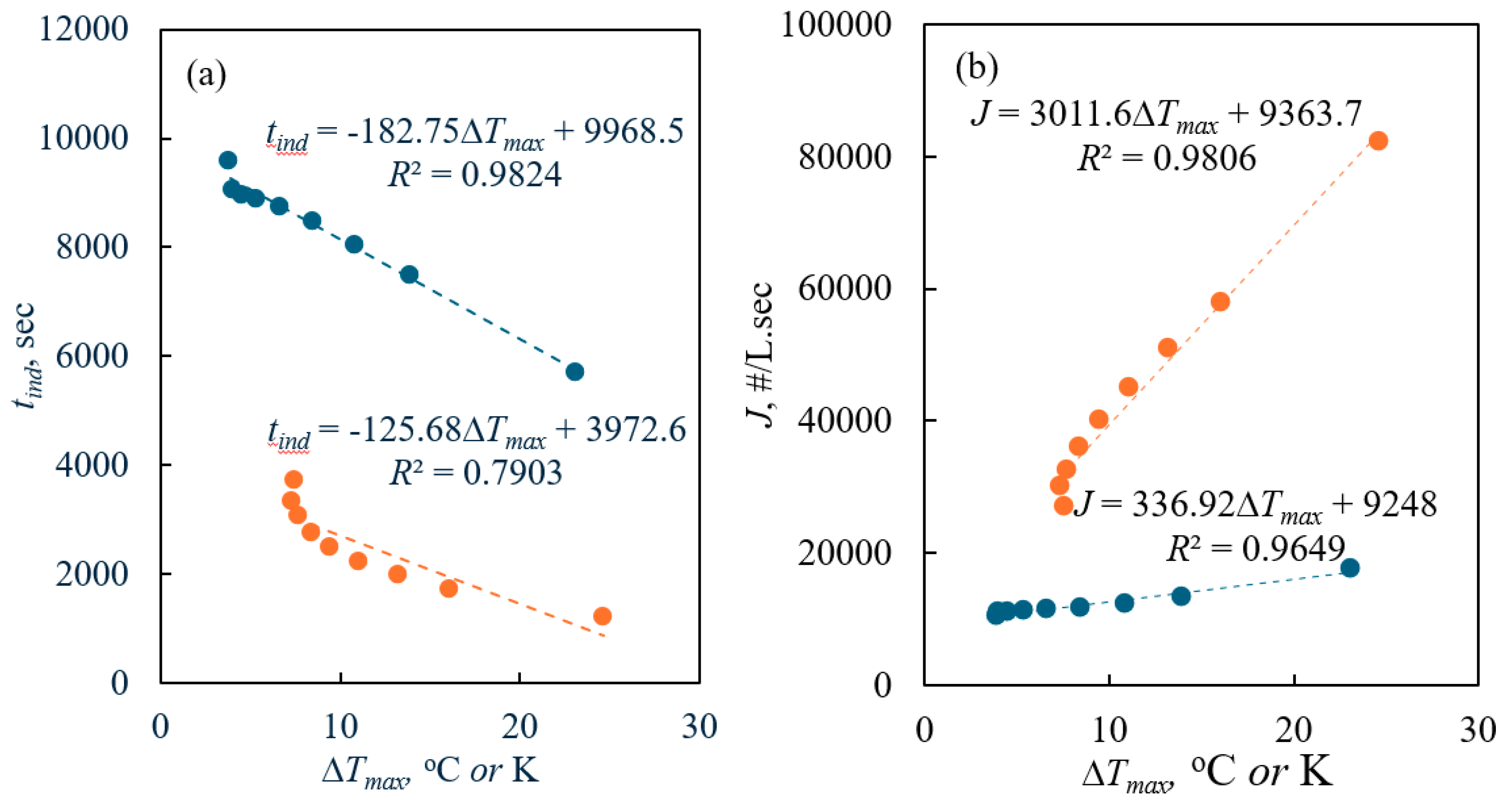
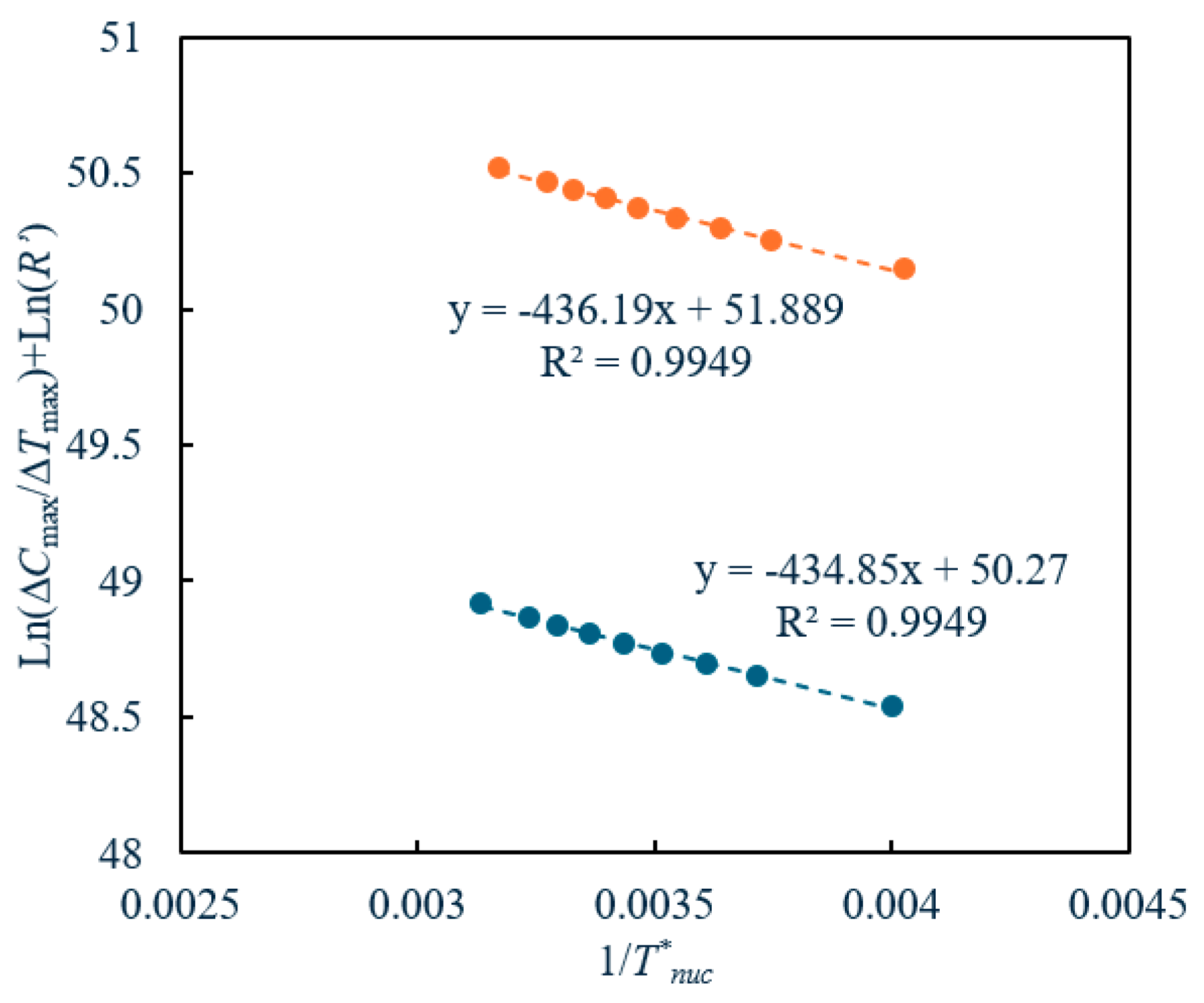
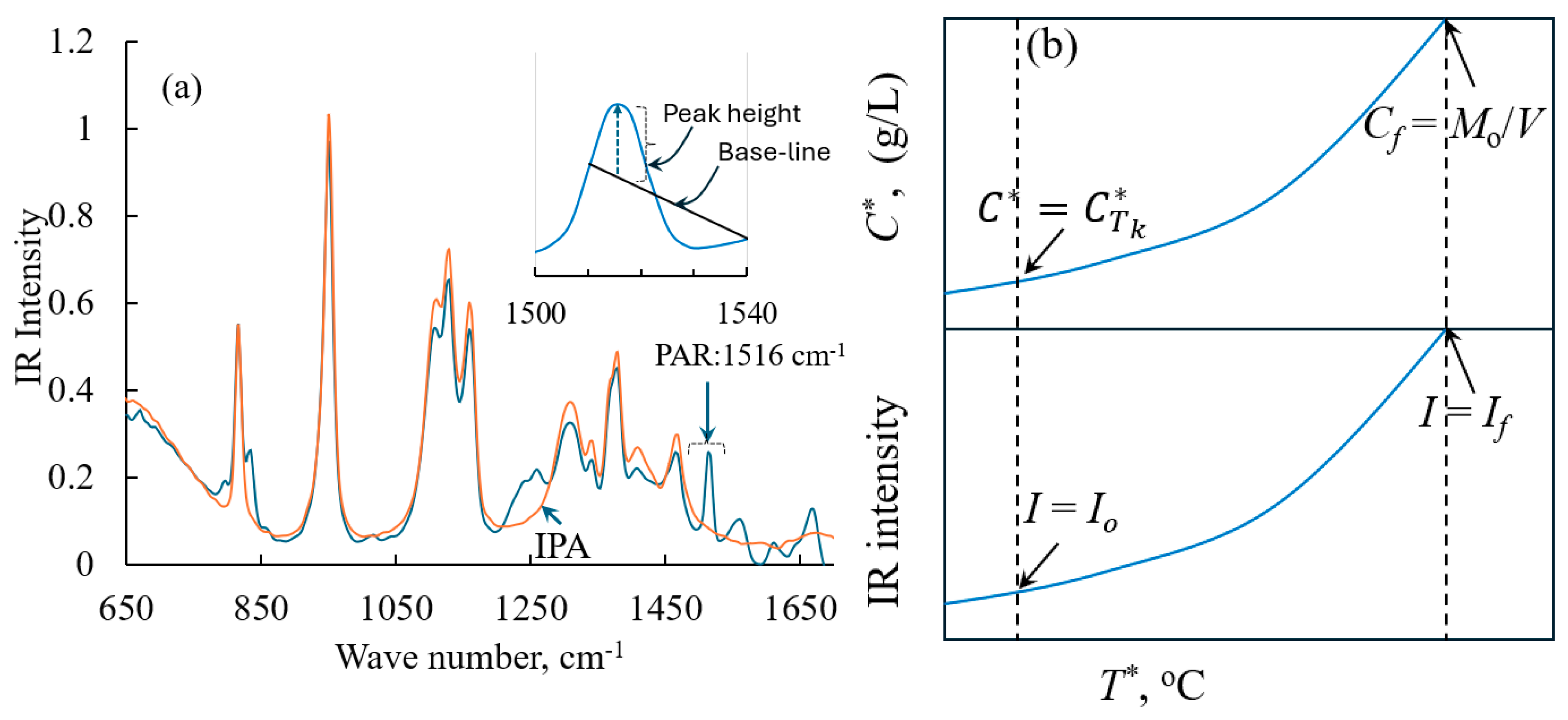
| Initial Conditions | Cooling Rate: 0.01 K/min | Cooling Rate: 0.05 K/min | Nucleation Parameters (Nyvlt) | Nucleation Parameters (Kubota) | Nucleation Parameters (Sangwal) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C* | ΔCmax | ΔCmax | n | kn | kn1/n | J | n | kn | km | n | |||||
| (°C) | (g/L) | (°C) | (g/L) | (g/L) | (°C) | (g/L) | (g/L) | - | (g1−n/L1−n.s) | (g1−n/L1−n.s)1/n | (#/m3.min) | - | (#/L.Kn.s) | (#/L.s) | - |
| 0 | 56.32 | −23.09 | 14.33 | 41.99 | −24.67 | 11.74 | 44.58 | 24.39 | 1.06 × 10−44 | 1.57 × 10−2 | 4.25 × 1022 | 23.39 | 2.25 × 10−28 | 2.42 × 1022 | 24.39 |
| 10 | 76.82 | −3.94 | 48.64 | 28.18 | −6.08 | 44.53 | 32.28 | 11.22 | 1.11 × 10−20 | 1.67 × 10−2 | 2.28 × 1023 | 10.22 | 2.69 × 10−8 | 1.31 × 1023 | 11.22 |
| 15 | 87.59 | 4.17 | 64.69 | 22.90 | 1.77 | 59.85 | 27.74 | 8.06 | 2.97 × 10−15 | 1.58 × 10−2 | 3.08 × 1023 | 7.06 | 6.09 × 10−4 | 6.25 × 1022 | 8.06 |
| 20 | 98.71 | 11.55 | 80.11 | 18.60 | 8.93 | 74.56 | 24.15 | 5.97 | 8.39 × 10−12 | 1.40 × 10−2 | 3.66 × 1023 | 4.97 | 2.89 × 10−1 | 2.41 × 1022 | 5.97 |
| 25 | 110.19 | 18.33 | 94.97 | 15.22 | 15.52 | 88.72 | 21.46 | 4.57 | 1.41 × 10−9 | 1.15 × 10−2 | 4.07 × 1023 | 3.57 | 1.32 × 101 | 9.45 × 1021 | 4.57 |
| 30 | 122.01 | 24.63 | 109.32 | 12.69 | 21.62 | 102.39 | 19.61 | 3.62 | 3.79 × 10−8 | 8.95 × 10−3 | 4.37 × 1023 | 2.62 | 1.37 × 102 | 4.23 × 1021 | 3.62 |
| 35 | 134.18 | 30.50 | 123.20 | 10.98 | 27.32 | 115.62 | 18.56 | 3.01 | 2.91 × 10−7 | 6.76 × 10−3 | 4.6 × 1023 | 2.01 | 5.40 × 102 | 2.29 × 1021 | 3.01 |
| 40 | 146.71 | 36.01 | 136.67 | 10.03 | 32.66 | 128.44 | 18.27 | 2.65 | 9.21 × 10−7 | 5.23 × 10−3 | 4.79 × 1023 | 1.65 | 1.13 × 103 | 1.53 × 1021 | 2.65 |
| Kinetics, thermodynamics and parameters relevant to nucleation for MSZW obtained at a cooling rate of 0.01 K/min | |||||||||
| T, °C | kv, #/m3.s | S = C/C* | ΔG, kJ | J, #/m3.s | γ, mJ/m2 | rc, m | # of u.c. in rc | Nm/V,#/m3 | tind, s |
| 0 | 6.79 × 1021 | 4.80 | 3.62 | 3.87 × 1022 | 14.81 | 6.28 × 10−10 | 1 | 5.88 × 1027 | 29,605 |
| 10 | 1.72 | 3.42 × 1022 | 8.02 | 9.45 × 10−10 | 2 | 3.39 × 1027 | 19,302 | ||
| 15 | 1.46 | 3.26 × 1022 | 6.38 | 1.10 × 10−9 | 2 | 2.66 × 1027 | 15,871 | ||
| 20 | 1.32 | 3.13 × 1022 | 5.18 | 1.26 × 10−9 | 2 | 2.14 × 1027 | 13,280 | ||
| 25 | 1.24 | 3.02 × 1022 | 4.29 | 1.43 × 10−9 | 3 | 1.77 × 1027 | 11,378 | ||
| 30 | 1.19 | 2.93 × 1022 | 3.62 | 1.61 × 10−9 | 3 | 1.52 × 1027 | 10,054 | ||
| 35 | 1.16 | 2.85 × 1022 | 3.15 | 1.76 × 10−9 | 3 | 1.35 × 1027 | 9220 | ||
| 40 | 1.14 | 2.77 × 1022 | 2.85 | 1.88 × 10−9 | 3 | 1.26 × 1027 | 8808 | ||
| 50 | 1.13 | 2.65 × 1022 | 2.67 | 1.97 × 10−9 | 3 | 1.24 × 1027 | 9044 | ||
| Kinetics, thermodynamics and parameters relevant to nucleation for MSZW obtained at a cooling rate of 0.05 K/min | |||||||||
| T, °C | kv, #/m3.s | S | J, #/m3.s | γ, mJ/m2 | rc, m | # of u.c. in rc | Nm/V,#/m3 | tind, s | |
| 0 | 3.43 × 1022 | 4.80 | 3.63 | 1.99 × 1023 | 16.03 | 5.97 × 10−10 | 1 | 5.88 × 1027 | 29,605 |
| 10 | 1.72 | 1.76 × 1023 | 8.88 | 8.84 × 10−10 | 2 | 3.39 × 1027 | 19,302 | ||
| 15 | 1.46 | 1.68 × 1023 | 7.28 | 1.01 × 10−9 | 2 | 2.66 × 1027 | 15,871 | ||
| 20 | 1.32 | 1.61 × 1023 | 6.16 | 1.13 × 10−9 | 2 | 2.14 × 1027 | 13,280 | ||
| 25 | 1.24 | 1.55 × 1023 | 5.35 | 1.24 × 10−9 | 2 | 1.77 × 1027 | 11,378 | ||
| 30 | 1.19 | 1.51 × 1023 | 4.77 | 1.34 × 10−9 | 2 | 1.52 × 1027 | 10,054 | ||
| 35 | 1.16 | 1.47 × 1023 | 4.37 | 1.42 × 10−9 | 3 | 1.35 × 1027 | 9220 | ||
| 40 | 1.14 | 1.43 × 1023 | 4.13 | 1.47 × 10−9 | 3 | 1.26 × 1027 | 8808 | ||
| 50 | 1.13 | 1.37 × 1023 | 3.99 | 1.51 × 10−9 | 3 | 1.24 × 1027 | 9044 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ranjbar, M.; Vashishtha, M.; Walker, G.; Kumar, K.V. Process Analytical Technology Obtained Metastable Zone Width, Nucleation Rate and Solubility of Paracetamol in Isopropanol—Theoretical Analysis. Pharmaceuticals 2025, 18, 314. https://doi.org/10.3390/ph18030314
Ranjbar M, Vashishtha M, Walker G, Kumar KV. Process Analytical Technology Obtained Metastable Zone Width, Nucleation Rate and Solubility of Paracetamol in Isopropanol—Theoretical Analysis. Pharmaceuticals. 2025; 18(3):314. https://doi.org/10.3390/ph18030314
Chicago/Turabian StyleRanjbar, Mahmoud, Mayank Vashishtha, Gavin Walker, and K. Vasanth Kumar. 2025. "Process Analytical Technology Obtained Metastable Zone Width, Nucleation Rate and Solubility of Paracetamol in Isopropanol—Theoretical Analysis" Pharmaceuticals 18, no. 3: 314. https://doi.org/10.3390/ph18030314
APA StyleRanjbar, M., Vashishtha, M., Walker, G., & Kumar, K. V. (2025). Process Analytical Technology Obtained Metastable Zone Width, Nucleation Rate and Solubility of Paracetamol in Isopropanol—Theoretical Analysis. Pharmaceuticals, 18(3), 314. https://doi.org/10.3390/ph18030314






