The Role of Outcome Response Rate in Planning Biosimilar Studies Using Different Evaluation Metrics
Abstract
1. Introduction
2. Results
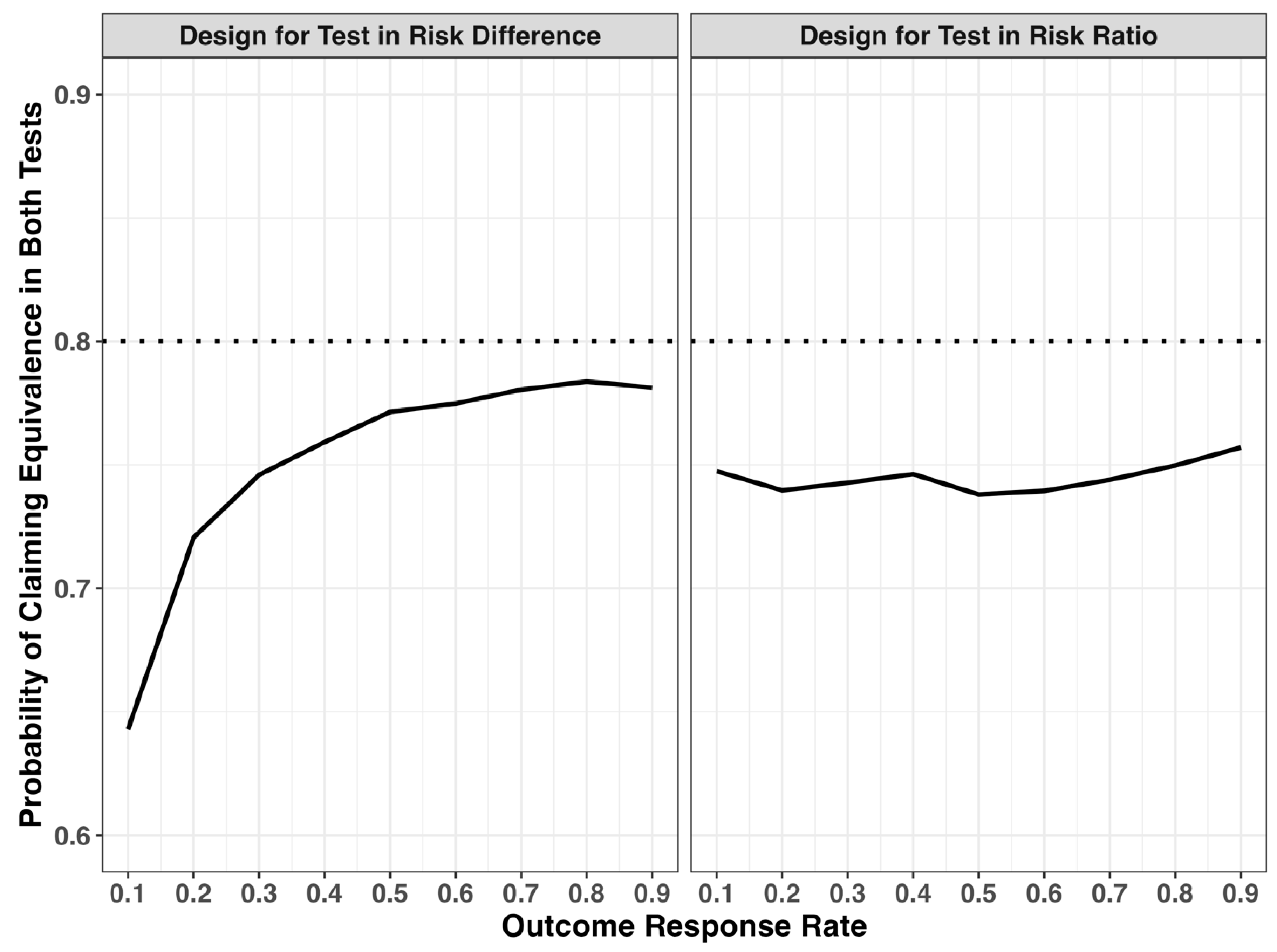
2.1. Discordance of Equivalence Test in Risk Difference and Risk Ratio Scales
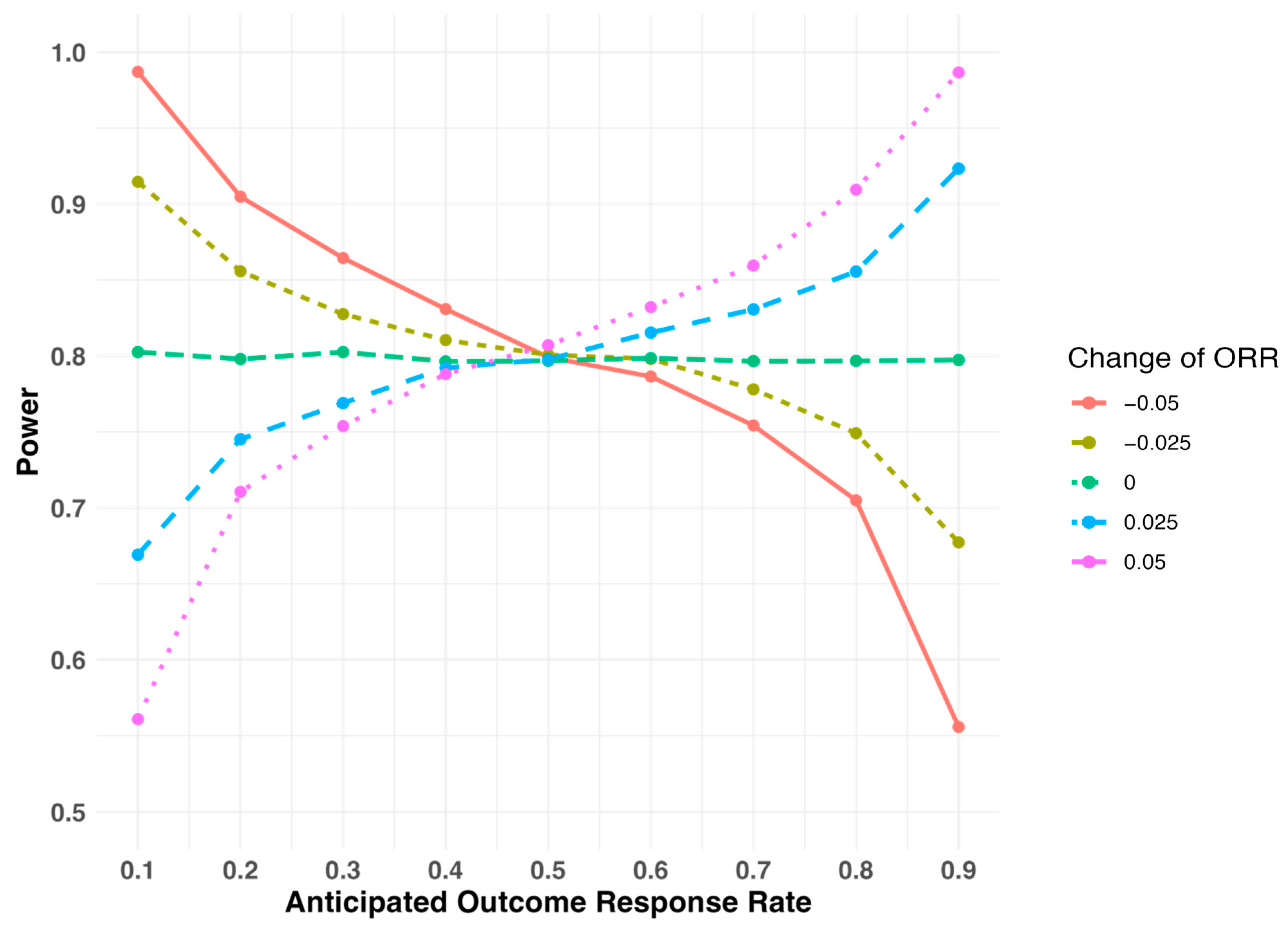
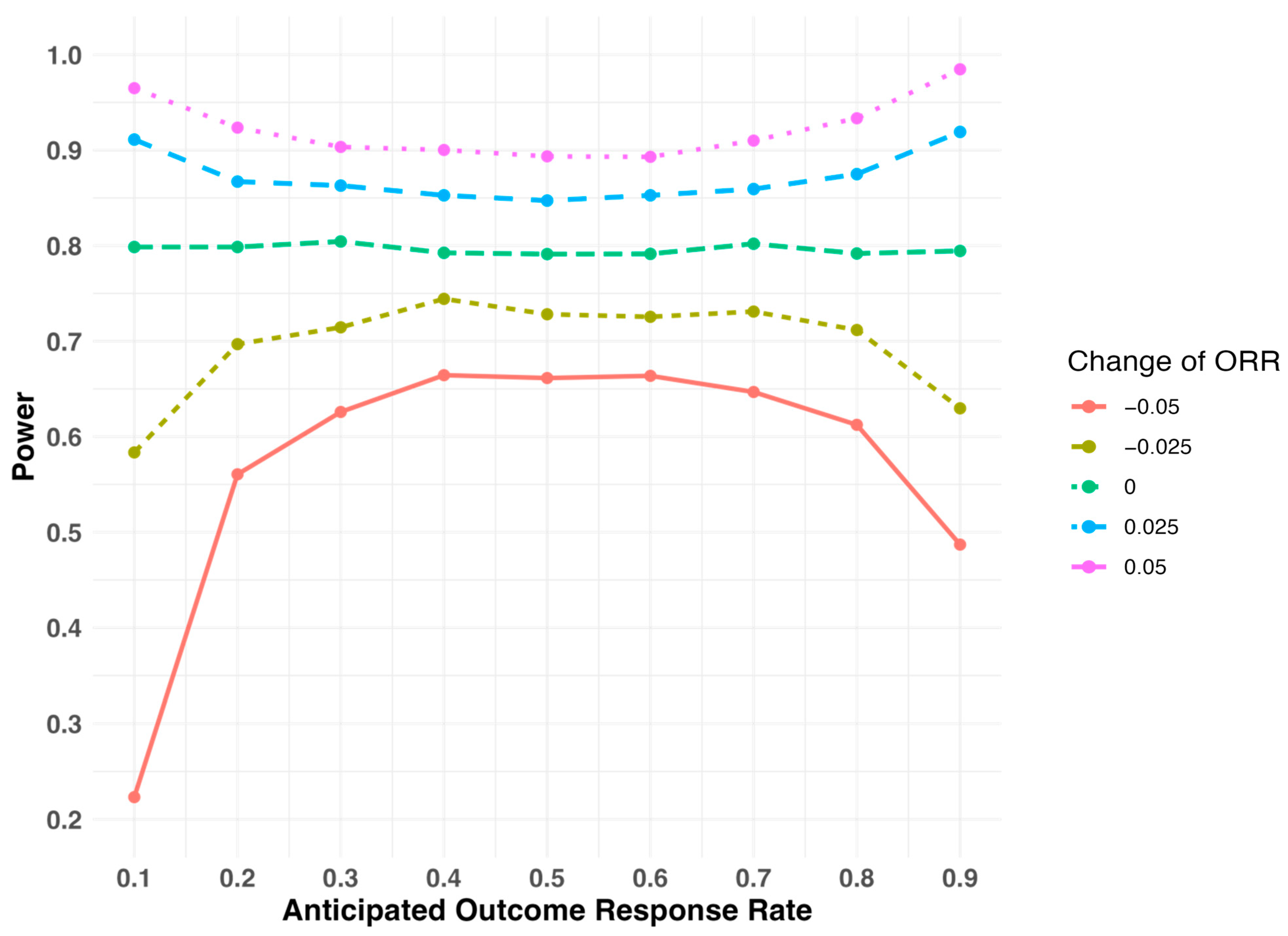
2.2. Sensitivity of Study Power When the Outcome Response Rate Deviates from the Assumed Level During Study Design
3. Discussions
4. Methods
4.1. Equivalence Test of Outcome Response Rate
4.2. Equivalence Margin Conversion Between Risk Difference and Risk Ratio Scale
4.3. Simulation Study Setup
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- U.S. Food and Drug Administration. Scientific Considerations in Demonstrating Biosimilarity to a Reference Product. 2015. Available online: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/scientific-considerations-demonstrating-biosimilarity-reference-product (accessed on 20 December 2024).
- Uno, H.; Schrag, D.; Kim, D.H.; Tang, D.; Tian, L.; Rugo, H.S.; Wei, L.-J. Assessing Clinical Equivalence in Oncology Biosimilar Trials with Time-to-Event Outcomes. JNCI Cancer Spectr. 2019, 3, pkz058. [Google Scholar] [CrossRef] [PubMed]
- European Medicines Agency. Biosimilars in the EU: Information Guide for Healthcare Professionals. 2017. Available online: https://www.ema.europa.eu/en/documents/leaflet/biosimilars-eu-information-guide-healthcare-professionals_en.pdf (accessed on 20 December 2024).
- U.S. Food and Drug Administration. Non-Inferiority Clinical Trials to Establish Effectiveness: Guidance for Industry. 2016. Available online: https://www.fda.gov/media/78504/download (accessed on 20 December 2024).
- U.S. Food and Drug Administration. Statistical Principles for Clinical Trials. 1998. Available online: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/e9-statistical-principles-clinical-trials (accessed on 20 December 2024).
- Walker, E.; Nowacki, A.S. Understanding Equivalence and Noninferiority Testing. J. Gen. Intern. Med. 2011, 26, 192–196. [Google Scholar] [CrossRef]
- Li, Z.; Quartagno, M.; Böhringer, S.; van Geloven, N. Choosing and Changing the Analysis Scale in Non-Inferiority Trials with a Binary Outcome. Clin. Trials 2022, 19, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Wellek, S. Statistical Methods for the Analysis of Two-Arm Non-Inferiority Trials with Binary Outcomes. Biom. J. J. Math. Methods Biosci. 2005, 47, 48–61. [Google Scholar] [CrossRef] [PubMed]
- Isakov, L.; Jin, B.; Jacobs, I.A. Statistical Primer on Biosimilar Clinical Development. Am. J. Ther. 2016, 23, e1903–e1910. [Google Scholar] [CrossRef] [PubMed]
- Hilton, J.F. Noninferiority Trial Designs for Odds Ratios and Risk Differences. Stat. Med. 2010, 29, 982–993. [Google Scholar] [CrossRef]
- Macaya, F.; Ryan, N.; Salinas, P.; Pocock, S.J. Challenges in the Design and Interpretation of Noninferiority Trials: Insights from Recent Stent Trials. J. Am. Coll. Cardiol. 2017, 70, 894–903. [Google Scholar] [CrossRef] [PubMed]
- Dettori, J.R.; Norvell, D.C.; Chapman, J.R. Is the Sample Size Big Enough? 4 Things You Need to Know! Glob. Spine J. 2022, 12, 1027–1028. [Google Scholar] [CrossRef]
- Barbier, L.; Declerck, P.; Simoens, S.; Neven, P.; Vulto, A.G.; Huys, I. The Arrival of Biosimilar Monoclonal Antibodies in Oncology: Clinical Studies for Trastuzumab Biosimilars. Br. J. Cancer 2019, 121, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Pivot, X.; Bondarenko, I.; Nowecki, Z.; Dvorkin, M.; Trishkina, E.; Ahn, J.-H.; Vinnyk, Y.; Im, S.-A.; Sarosiek, T.; Chatterjee, S.; et al. Phase III, Randomized, Double-Blind Study Comparing the Efficacy, Safety, and Immunogenicity of SB3 (Trastuzumab Biosimilar) and Reference Trastuzumab in Patients Treated with Neoadjuvant Therapy for Human Epidermal Growth Factor Receptor 2–Positive Early Breast Cancer. J. Clin. Oncol. 2018, 36, 968–974. [Google Scholar] [PubMed]
- Von Minckwitz, G.; Ponomarova, O.; Morales, S.; Zhang, N.; Hanes, V. Efficacy and Safety of Biosimilar ABP 980 Compared with Trastuzumab in HER2 Positive Early Breast Cancer. Ann. Oncol. 2017, 28, v44. [Google Scholar] [CrossRef]
- von Minckwitz, G.; Colleoni, M.; Kolberg, H.-C.; Morales, S.; Santi, P.; Tomasevic, Z.; Zhang, N.; Hanes, V. Efficacy and Safety of ABP 980 Compared with Reference Trastuzumab in Women with HER2-Positive Early Breast Cancer (LILAC Study): A Randomised, Double-Blind, Phase 3 Trial. Lancet Oncol. 2018, 19, 987–998. [Google Scholar] [CrossRef]
- Rugo, H.S.; Barve, A.; Waller, C.F.; Hernandez-Bronchud, M.; Herson, J.; Yuan, J.; Manikhas, A.; Bondarenko, I.; Mukhametshina, G.; Nemsadze, G.; et al. Heritage: A Phase III Safety and Efficacy Trial of the Proposed Trastuzumab Biosimilar Myl-1401O versus Herceptin. J. Clin. Oncol. 2016. Available online: https://ascopubs.org/doi/10.1200/JCO.2016.34.18_suppl.LBA503 (accessed on 30 December 2024). [CrossRef]
- Rugo, H.S.; Barve, A.; Waller, C.F.; Hernandez-Bronchud, M.; Herson, J.; Yuan, J.; Sharma, R.; Baczkowski, M.; Kothekar, M.; Loganathan, S.; et al. Effect of a Proposed Trastuzumab Biosimilar Compared with Trastuzumab on Overall Response Rate in Patients with ERBB2 (HER2)–Positive Metastatic Breast Cancer: A Randomized Clinical Trial. JAMA 2017, 317, 37–47. [Google Scholar] [CrossRef] [PubMed]
- Pivot, X.; Bondarenko, I.; Nowecki, Z.; Dvorkin, M.; Trishkina, E.; Ahn, J.-H.; Im, S.-A.; Sarosiek, T.; Chatterjee, S.; Wojtukiewicz, M.; et al. A Phase III Study Comparing SB3 (a Proposed Trastuzumab Biosimilar) and Trastuzumab Reference Product in HER2-Positive Early Breast Cancer Treated with Neoadjuvant-Adjuvant Treatment: Final Safety, Immunogenicity and Survival Results. Eur. J. Cancer 2018, 93, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Stebbing, J.; Baranau, Y.; Baryash, V.; Manikhas, A.; Moiseyenko, V.; Dzagnidze, G.; Zhavrid, E.; Boliukh, D.; Stroyakovskii, D.; Pikiel, J.; et al. CT-P6 Compared with Reference Trastuzumab for HER2-Positive Breast Cancer: A Randomised, Double-Blind, Active-Controlled, Phase 3 Equivalence Trial. Lancet Oncol. 2017, 18, 917–928. [Google Scholar] [CrossRef] [PubMed]
- Stebbing, J.; Mainwaring, P.N.; Curigliano, G.; Pegram, M.; Latymer, M.; Bair, A.H.; Rugo, H.S. Understanding the Role of Comparative Clinical Studies in the Development of Oncology Biosimilars. J. Clin. Oncol. 2020, 38, 1070–1080. [Google Scholar] [CrossRef] [PubMed]
- Moore, T.J.; Mouslim, M.C.; Blunt, J.L.; Alexander, G.C.; Shermock, K.M. Assessment of Availability, Clinical Testing, and US Food and Drug Administration Review of Biosimilar Biologic Products. JAMA Intern. Med. 2021, 181, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Chow, S.-C.; Liu, J. Design and Analysis of Bioavailability and Bioequivalence Studies, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2008; ISBN 978-1-58488-668-6. [Google Scholar]
| Response Rate | Sample Size Per Arm | RR Margin 1,2 | Percent Time with Positive Test Result | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RD Test | RR Test | Both Test | RD Test Only | RR Test Only | Discordance 3 | ||||
| 0.1 | 757 | 0.50 | 1.50 | 79.7% | 73.7% | 64.3% | 15.5% | 9.4% | 24.9% |
| 0.2 | 1345 | 0.75 | 1.25 | 79.8% | 78.1% | 72.1% | 7.8% | 6.1% | 13.8% |
| 0.3 | 1766 | 0.83 | 1.17 | 79.4% | 79.1% | 74.6% | 4.8% | 4.5% | 9.3% |
| 0.4 | 2018 | 0.88 | 1.13 | 79.7% | 79.1% | 75.9% | 3.8% | 3.2% | 7.0% |
| 0.5 | 2102 | 0.90 | 1.10 | 80.1% | 79.8% | 77.1% | 3.0% | 2.6% | 5.6% |
| 0.6 | 2018 | 0.92 | 1.08 | 80.0% | 79.8% | 77.5% | 2.6% | 2.3% | 4.8% |
| 0.7 | 1766 | 0.93 | 1.07 | 79.9% | 79.8% | 78.0% | 1.9% | 1.8% | 3.6% |
| 0.8 | 1345 | 0.94 | 1.06 | 80.2% | 80.2% | 78.4% | 1.8% | 1.8% | 3.6% |
| 0.9 | 757 | 0.94 | 1.06 | 80.0% | 79.7% | 78.1% | 1.8% | 1.6% | 3.4% |
| Overall Response Rate | Sample Size Per Arm | RD Margin 1,2 | Percent Time with Positive Test Result | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RD Test | RR Test | Both Test | RD Test Only | RR Test Only | Discordance 3 | ||||
| 0.1 | 5712 | −0.02 | 0.02 | 79.5% | 80.5% | 74.7% | 4.7% | 5.8% | 10.5% |
| 0.2 | 2530 | −0.03 | 0.04 | 78.3% | 79.7% | 74.0% | 4.4% | 5.8% | 10.1% |
| 0.3 | 1483 | −0.05 | 0.06 | 79.1% | 79.8% | 74.3% | 4.9% | 5.5% | 10.4% |
| 0.4 | 954 | −0.07 | 0.08 | 79.1% | 80.3% | 74.6% | 4.5% | 5.7% | 10.2% |
| 0.5 | 628 | −0.08 | 0.10 | 78.8% | 79.6% | 73.8% | 5.0% | 5.8% | 10.9% |
| 0.6 | 418 | −0.10 | 0.12 | 79.0% | 79.4% | 73.9% | 5.1% | 5.5% | 10.6% |
| 0.7 | 274 | −0.12 | 0.14 | 79.0% | 79.9% | 74.4% | 4.6% | 5.5% | 10.1% |
| 0.8 | 160 | −0.13 | 0.16 | 80.2% | 80.0% | 75.0% | 5.2% | 5.0% | 10.2% |
| 0.9 | 72 | −0.15 | 0.18 | 80.7% | 80.7% | 75.7% | 5.0% | 5.0% | 10.0% |
| Assumed Response Rate | Study Design I | Study Design II | ||
|---|---|---|---|---|
| Actual Response Rate Is 0.05 Smaller Than Expected | Actual Response Rate Is 0.05 Larger Than Expected | Actual Response Rate Is 0.05 Smaller Than Expected | Actual Response Rate Is 0.05 Larger Than Expected | |
| 0.1 | 98.8% | 55.4% | 22.3% | 96.5% |
| 0.2 | 90.2% | 69.9% | 56.1% | 92.4% |
| 0.3 | 85.8% | 75.5% | 62.6% | 90.3% |
| 0.4 | 83.8% | 77.9% | 66.4% | 90.0% |
| 0.5 | 81.0% | 80.4% | 66.1% | 89.4% |
| 0.6 | 78.7% | 83.2% | 66.4% | 89.3% |
| 0.7 | 75.1% | 86.1% | 64.7% | 91.0% |
| 0.8 | 70.5% | 90.8% | 61.2% | 93.3% |
| 0.9 | 55.6% | 98.6% | 48.7% | 98.5% |
| Study Design I | Study Design II | |
|---|---|---|
| Metric of evaluation | Risk Difference | Risk Ratio |
| Reference response rate | 10% to 90% | 10% to 90% |
| Expected difference between treatments | RD = 0 | RR = 1 |
| Equivalence margin | [−0.05, 0.05] | , 1.2] |
| Type I error | 0.05 | 0.05 |
| Study power | 0.8 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cen, L.; Arani, R.; Tang, D. The Role of Outcome Response Rate in Planning Biosimilar Studies Using Different Evaluation Metrics. Pharmaceuticals 2025, 18, 243. https://doi.org/10.3390/ph18020243
Cen L, Arani R, Tang D. The Role of Outcome Response Rate in Planning Biosimilar Studies Using Different Evaluation Metrics. Pharmaceuticals. 2025; 18(2):243. https://doi.org/10.3390/ph18020243
Chicago/Turabian StyleCen, Liyi, Ramin Arani, and Dejun Tang. 2025. "The Role of Outcome Response Rate in Planning Biosimilar Studies Using Different Evaluation Metrics" Pharmaceuticals 18, no. 2: 243. https://doi.org/10.3390/ph18020243
APA StyleCen, L., Arani, R., & Tang, D. (2025). The Role of Outcome Response Rate in Planning Biosimilar Studies Using Different Evaluation Metrics. Pharmaceuticals, 18(2), 243. https://doi.org/10.3390/ph18020243






