Solubility, Solution Thermodynamics, and Preferential Solvation of Amygdalin in Ethanol + Water Solvent Mixtures
Abstract
1. Introduction
2. Results and Discussion
2.1. Solubility of Amygdalin in [Ethanol (1) + Water (2)] Cosolvent Mixtures
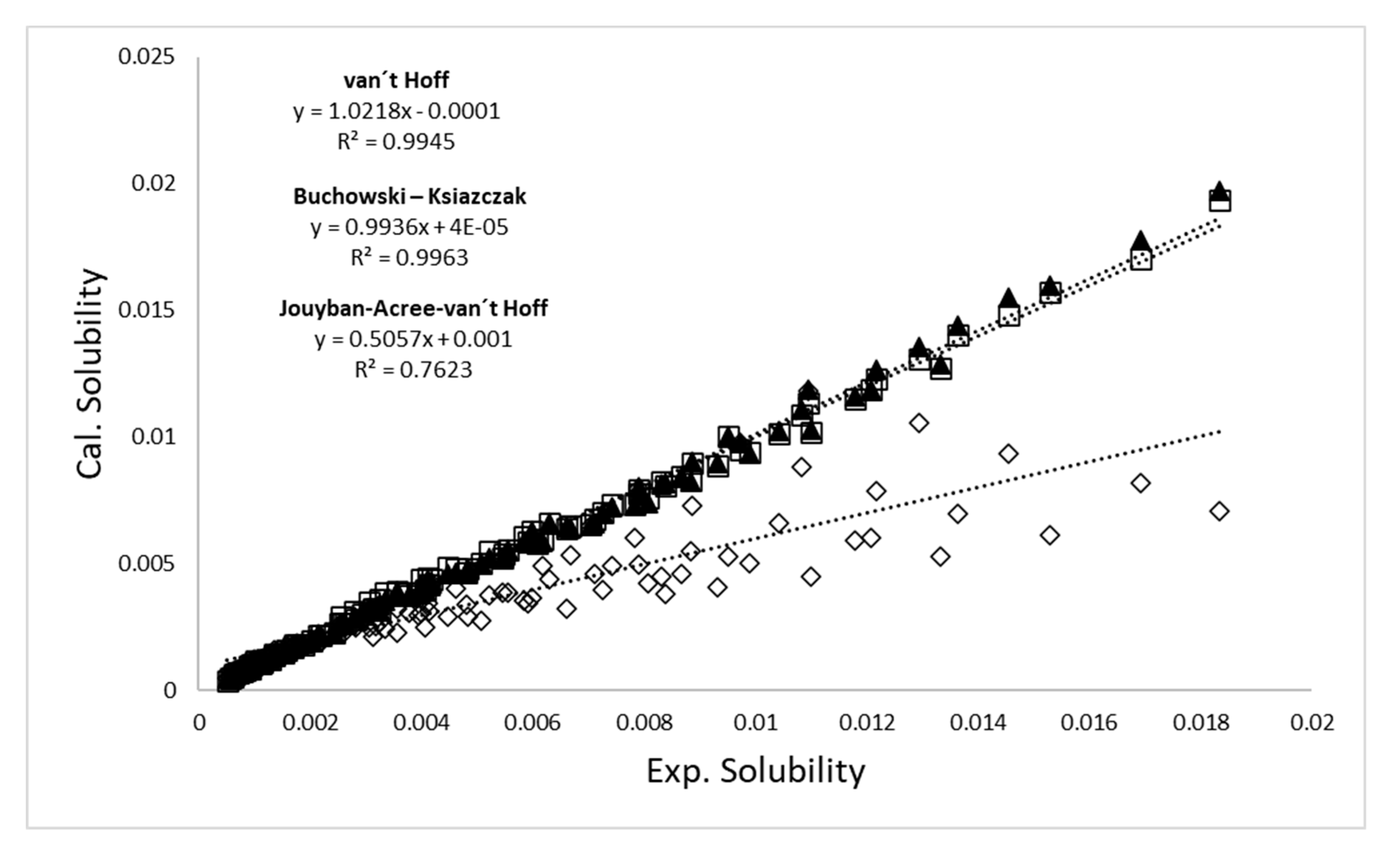
2.2. Computational Validation
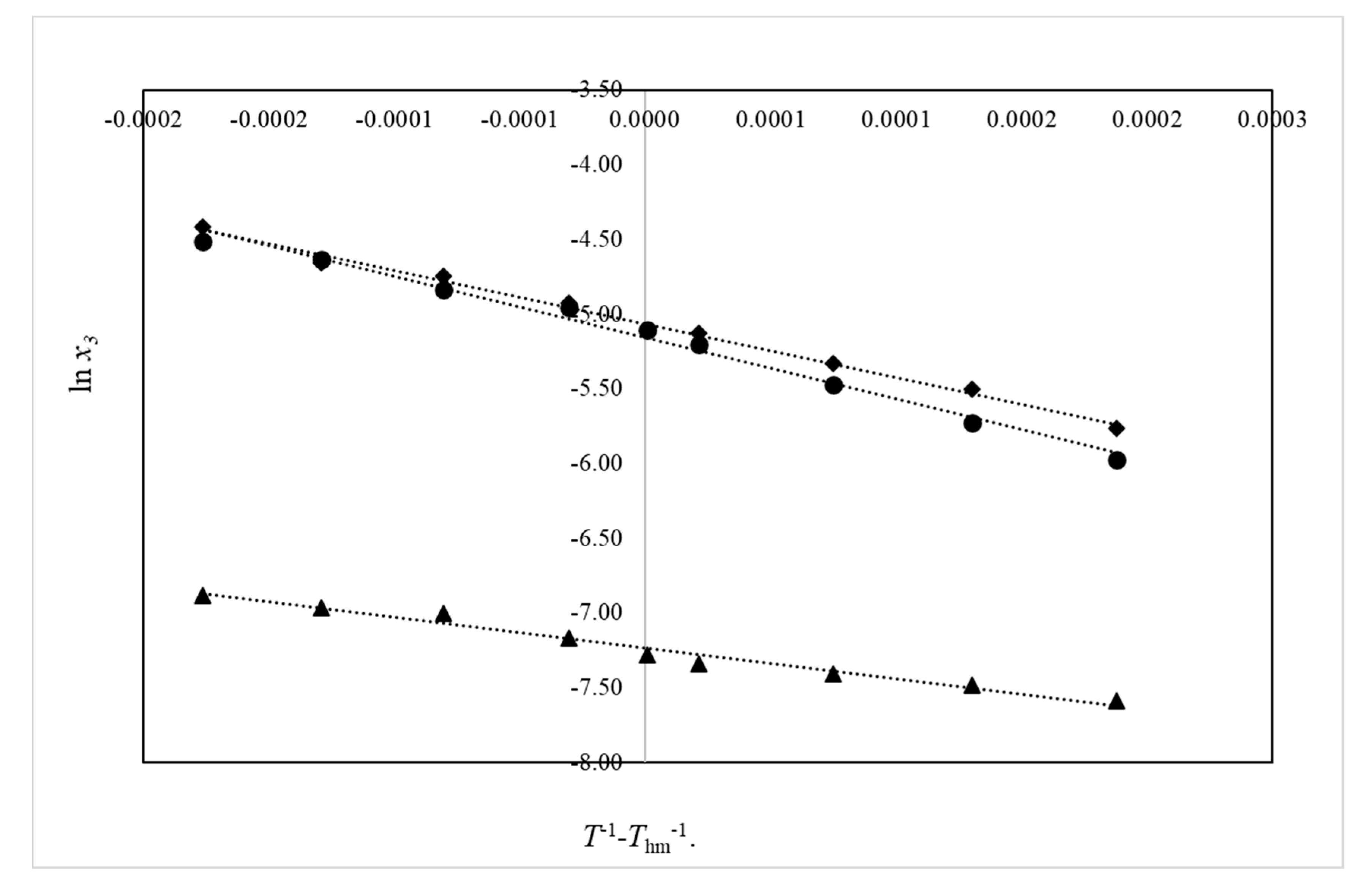
2.3. Thermodynamic Functions of Dissolution
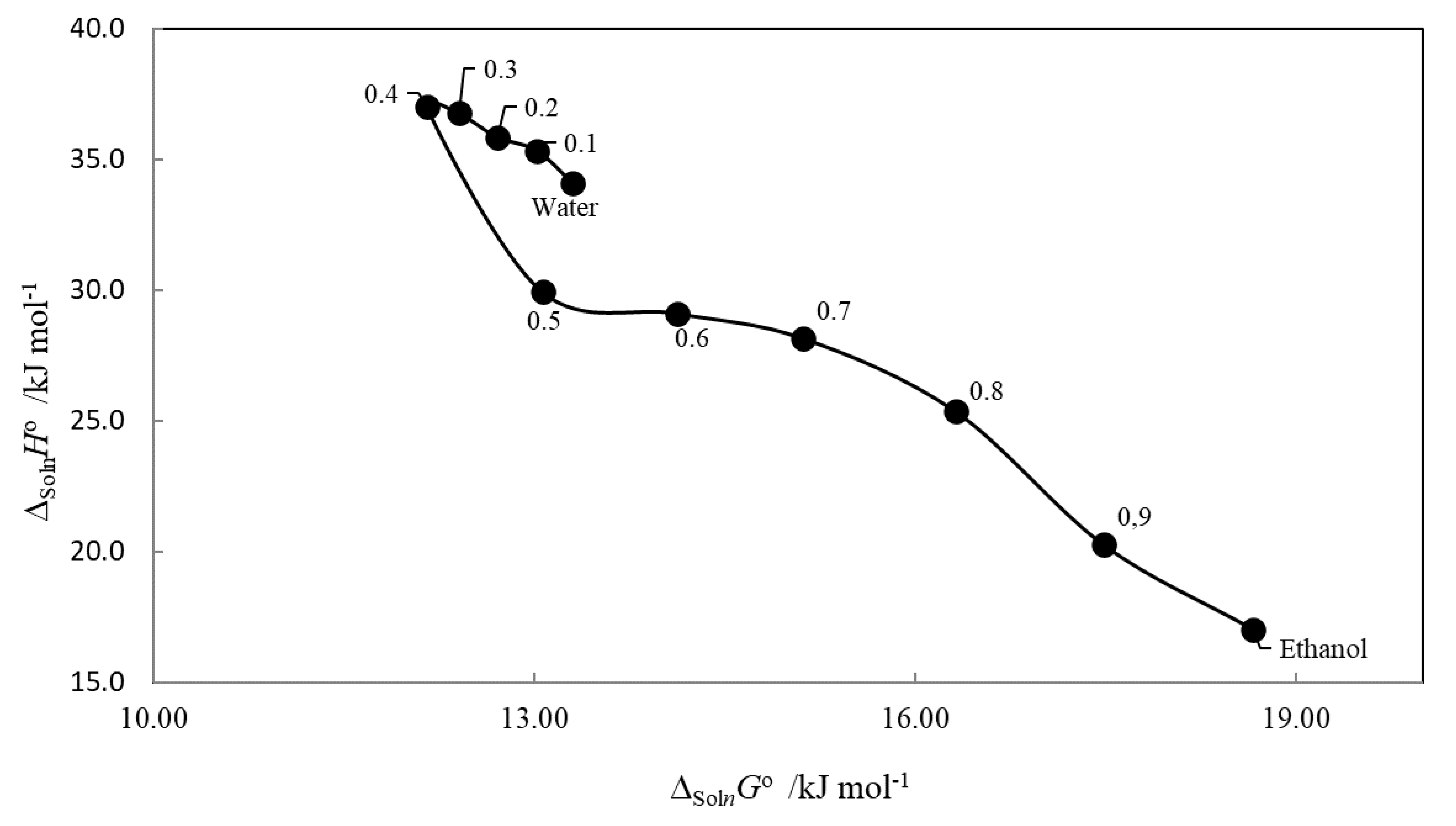
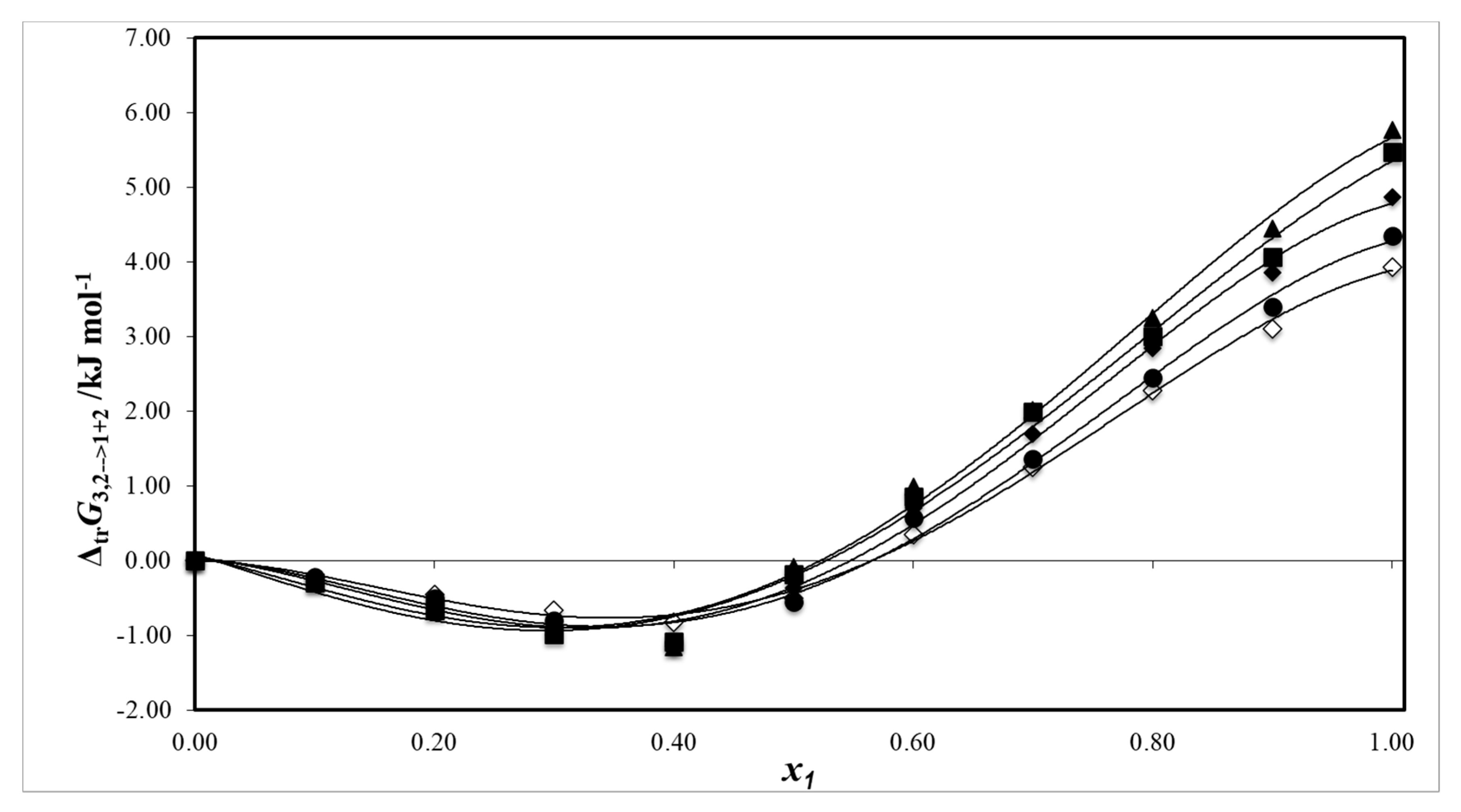
2.4. Enthalpy–Entropy Compensation
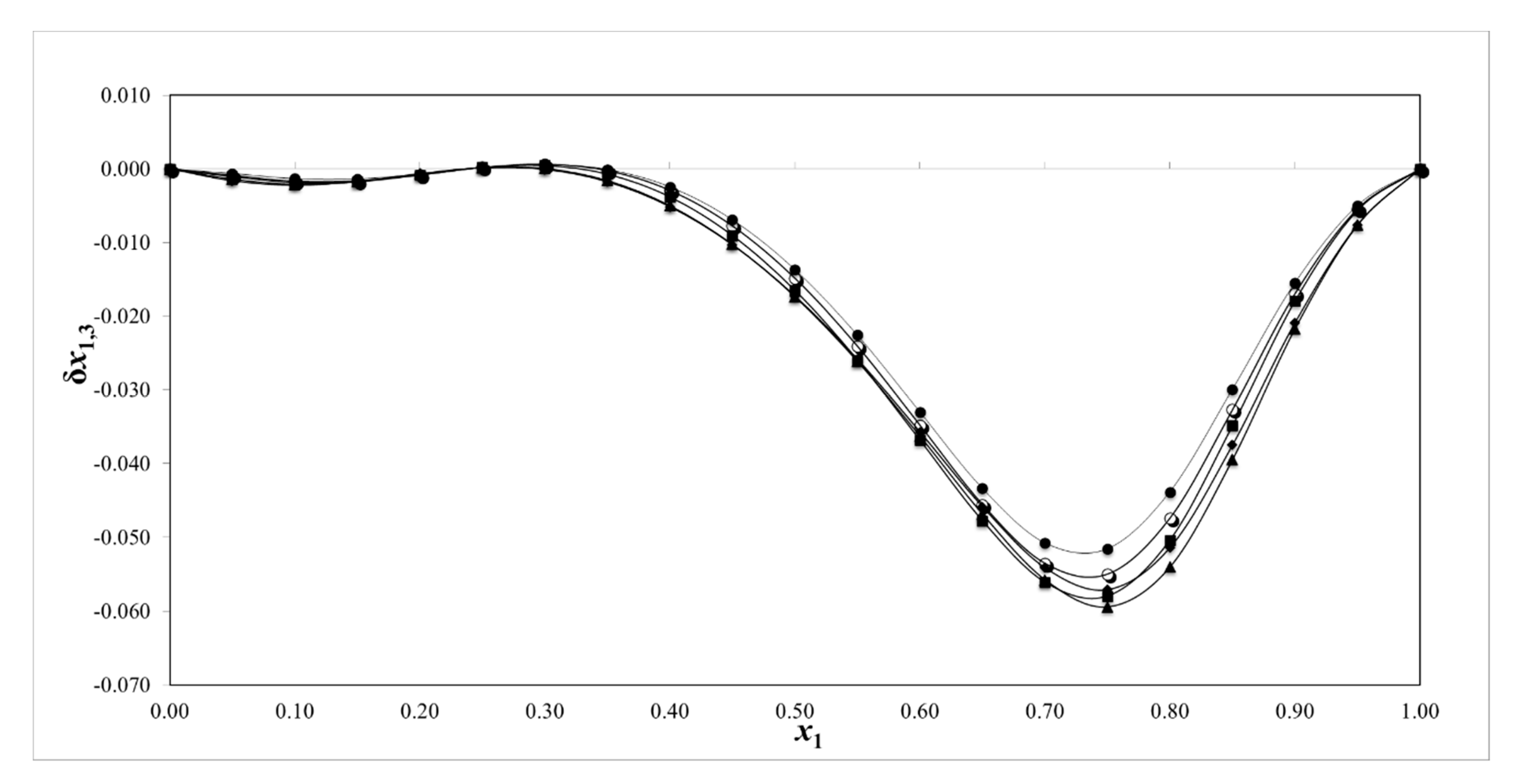
2.5. Preferential Solvation
3. Experimental procedures
3.1. Reagents
3.2. Solubility Determination
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jaswal, V.; Palanivelu, J.; Ramalingam, C. Effects of the Gut microbiota on Amygdalin and its use as an anti-cancer therapy: Substantial review on the key components involved in altering dose efficacy and toxicity. Biochem. Biophys. Rep. 2018, 14, 125–132. [Google Scholar] [CrossRef]
- Guo, J.; Wu, W.; Sheng, M.; Yang, S.; Tan, J. Amygdalin inhibits renal fibrosis in chronic kidney disease. Mol. Med. Rep. 2013, 7, 1453–1457. [Google Scholar] [CrossRef]
- Carter, J.H.; McLafferty, M.A.; Goldman, P. Role of the gastrointestinal microflora in Amygdalin (laetrile)-induced cyanide toxicity. Biochem. Pharmacol. 1980, 29, 301–304. [Google Scholar] [CrossRef]
- Li, Y.; Li, Q.; Liu, R.; Shen, X. Chinese Medicine Amygdalin and β-Glucosidase Combined with Antibody Enzymatic Prodrug System as A Feasible Antitumor Therapy. Chin. J. Integr. Med. 2015, 24, 237–240. [Google Scholar] [CrossRef]
- Moon, J.Y.; Kim, S.W.; Yun, G.M.; Lee, H.S.; Kim, Y.D.; Jeong, G.J.; Ullah, I.; Rho, G.J.; Jeon, B.G. Inhibition of cell growth and down-regulation of telomerase activity by Amygdalin in human cancer cell lines. Anim. Cells Syst. 2015, 19, 295–304. [Google Scholar] [CrossRef][Green Version]
- Song, Z.; Xu, X. Advanced research on anti-tumor effects of Amygdalin. J. Cancer Res. Ther. 2014, 10, 3. [Google Scholar]
- Zhang, X.; Hu, J.; Zhuo, Y.; Cui, L.; Li, C.; Cui, N.; Zhang, S. Amygdalin improves microcirculatory disturbance and attenuates pancreatic fibrosis by regulating the expression of endothelin-1 and calcitonin gene-related peptide in rats. J. Chin. Med. Assoc. 2018, 81, 437–443. [Google Scholar] [CrossRef]
- Hwang, H.J.; Lee, H.J.; Kim, C.J.; Shim, I.; Hahm, D.H. Inhibitory effect of Amygdalin on lipopolysaccharide-inducible TNF-alpha and IL-1beta mRNA expression and carrageenan-induced rat arthritis. J. Microbiol. Biotechnol. 2008, 18, 1641–1647. [Google Scholar]
- Zhu, Y.P.; Su, Z.W.; Li, C.H. Analgesic effect and no physical dependence of Amygdalin. China J. Chin. Mater. Med. 1994, 19, 105–107. [Google Scholar]
- Jiagang, D.; Li, C.; Wang, H.; Hao, E.; Du, Z.; Bao, C.; Lv, J.; Wang, Y. Amygdalin mediates relieved atherosclerosis in apolipoprotein E deficient mice through the induction of regulatory T cells. Biochem. Biophys. Res. Commun. 2011, 411, 523–529. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Yang, Z. Amygdalin attenuates atherosclerosis progress through inhibiting of toll-like receptors expression and activity. J. Anim. Vet. Adv. 2012, 11, 1613–1621. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, K.; Wang, G.; Guan, X.; Pang, Z.; Guo, Y.; Yuan, Y.; Ran, N.; Liu, Y.; Wang, F. Protective effect of Amygdalin on epithelial—mesenchymal transformation in experimental chronic obstructive pulmonary disease mice. Phytother. Res. 2019, 33, 808–817. [Google Scholar] [CrossRef] [PubMed]
- He, X.Y.; Wu, L.J.; Wang, W.X.; Xie, P.J.; Chen, Y.H.; Wang, F. Amygdalin-A pharmacological and toxicological review. J. Ethnopharmacol. 2020, 112717. [Google Scholar] [CrossRef]
- Nabavizadeh, F.; Alizadeh, A.M.; Sadroleslami, Z.; Adeli, S. Gastroprotective effects of Amygdalin on experimental gastric ulcer: Role of NO and TNF-α. J. Med. Plant Res. 2011, 5, 3122–3127. [Google Scholar]
- Lee, H.M.; Moon, A. Amygdalin regulates apoptosis and adhesion in Hs578T triple-negative breast cancer cells. Biomol. Ther. 2016, 24, 62. [Google Scholar] [CrossRef] [PubMed]
- Haisman, D.R.; Knight, D.J. The enzymic hydrolysis of Amygdalin. Biochem. J. 1967, 103, 528–534. [Google Scholar] [CrossRef]
- Bolarinwa, I.F.; Orfila, C.; Morgan, M.R. Amygdalin content of seeds, kernels and food products commercially-available in the UK. Food Chem. 2014, 52, 133–139. [Google Scholar] [CrossRef]
- Krieble, V.K. The amygdalins and their inter-reactions with emulsin. J. Am. Chem. Soc. 1912, 34, 716–735. [Google Scholar] [CrossRef][Green Version]
- Boháčová, I.; Procházková, S.; Halko, R. Separation and determination of Amygdalin and unnatural neoAmygdalin in natural food supplements by HPLC-DAD. Food Addit. Contam. Part A 2019, 36, 1445–1452. [Google Scholar] [CrossRef]
- Thapa, R.K.; Choi, H.G.; Kim, J.O.; Yong, C.S. Analysis and optimization of drug solubility to improve pharmacokinetics. J. Pharm. Investig. 2017, 47, 95–110. [Google Scholar] [CrossRef]
- Pacheco, D.P.; Martínez, F. Thermodynamic analysis of the solubility of naproxen in ethanol + water cosolvent mixtures. Phys. Chem. Liq. 2007, 45, 581–595. [Google Scholar] [CrossRef]
- Di, L.; Fish, P.V.; Mano, T. Bridging solubility between drug discovery and development. Drug Discov. Today 2012, 17, 486–495. [Google Scholar] [CrossRef]
- Sun, H.; Li, M.; Jia, J.; Tang, F.; Duan, E. Measurement and correlation of the solubility of 2, 6-diaminohexanoic acid hydrochloride in aqueous methanol and aqueous ethanol mixtures. J. Chem. Eng. Data. 2012, 57, 1463–1467. [Google Scholar] [CrossRef]
- Delgado, D.R.; Martínez, F. Solubility and solution thermodynamics of sulfamerazine and sulfamethazine in some ethanol+ water mixtures. Fluid Phase Equilibria 2013, 360, 88–96. [Google Scholar] [CrossRef]
- Pobudkowska, A.; Domańska, U.; Jurkowska, B.A.; Dymczuk, K. Solubility of pharmaceuticals in water and alcohols. Fluid Phase Equilibria 2015, 392, 56–64. [Google Scholar] [CrossRef]
- Allen, L.; Ansel, H.C. Ansel’s Pharmaceutical Dosage Forms and Drug Delivery Systems; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2013. [Google Scholar]
- Wijesekera, R.O.B. The Medicinal Plant Industry; Routledge: Abingdon-on-Thames, UK, 2017. [Google Scholar]
- Marcus, Y. Preferential solvation in mixed solvents. In Fluctuation Theory of Solutions: Applications in Chemistry, Chemical Engineering, and Biophysics; CRC Press: Boca Raton, FL, USA, 2013; pp. 65–92. [Google Scholar]
- Marcus, Y. Preferential solvation of drugs in binary solvent mixtures. Pharm. Anal. Acta 2017, 8, 537. [Google Scholar] [CrossRef]
- Yalkowsky, S.H. Solubility and Solubilization in Aqueous Media; American Chemical Society: New York, USA, 1999. [Google Scholar]
- Williams, R.O., III; Watts, A.B.; Miller, D.A. Formulating Poorly Water Soluble Drugs; American Association of Pharmaceutical Scientists: Austin, TX, USA, 2016. [Google Scholar]
- Delgado, D.R.; Rodríguez, G.A.; Martínez, F. Thermodynamic study of the solubility of sulfapyridine in some ethanol + water mixtures. J. Mol. Liq. 2013, 177, 156–161. [Google Scholar] [CrossRef]
- Muñoz, M.d.; Delgado, D.R.; Peña, M.Á.; Jouyban, A.; Martínez, F. Solubility and preferential solvation of sulfadiazine, sulfamerazine and sulfamethazine in propylene glycol + water mixtures at 298.15 K. J. Mol. Liq. 2015, 204, 132–136. [Google Scholar] [CrossRef]
- Barton, A. CRC Handbook of Solubility Parameters and Other Cohesion Parameters, 2nd ed.; CRC Press: New York, NY, USA, 1991. [Google Scholar]
- Delgado, D.R.; Mogollon-Waltero, E.M.; Ortiz, C.P.; Peña, M.; Almanza, O.A.; Martínez, F.; Jouyban, A. Enthalpy-entropy compensation analysis of the triclocarban dissolution process in some {1,4-dioxane (1) + water (2)} mixtures. J. Mol. Liq. 2018, 271, 522–529. [Google Scholar] [CrossRef]
- Hildebtand, J.H.; Prausnitz, J.M.; Scott, R.L. Regular and Related Solutions: The Solubility of Gases, Liquids, and Solids; Van Nostrand Reinhold Company: New Tork, NY, USA, 1970. [Google Scholar]
- Grant, D.J.W.; Mehdizadeh, M.; Chow, A.H.L.; Fairbrother, J.E. Non-linear van’t Hoff solubility-temperature plots and their pharmaceutical interpretation. Int. J. Pharm. 1984, 18, 25–38. [Google Scholar] [CrossRef]
- Jouyban, A.; Acree, W.E. Mathematical derivation of the Jouyban-Acree model to represent solute solubility data in mixed solvents at various temperatures. J. Mol. Liq. 2018, 256, 541–547. [Google Scholar] [CrossRef]
- Ruidiaz, M.; Delgado, D.R.; Martínez, F. Correlating the solubility of indomethacin in 1,4-dioxane + water mixtures by means of the Jouyban-Acree model. Rev. Colomb. Cienc. Químico Farm. 2010, 39, 211–226. [Google Scholar]
- Acree, W.; Jouyban, A.; Acree, W.E. In silico prediction of drug solubility in water-ethanol mixtures using Jouyban-Acree model. J. Pharm Pharm. Sci. 2006, 9, 262–269. [Google Scholar]
- Nieto, A.M.R.; Cerquera, N.E.; Delgado, D.R. Measurement and correlation of solubility of ethylparaben in pure and binary solvents and thermodynamic properties of solution. Rev. Colomb. Cienc. Químico Farm. 2019, 48, 332–347. [Google Scholar] [CrossRef]
- Ksia̧ẑczak, A.; Kosinski, J.J. Vapour pressure of binary, three-phase (S-L-V) systems and solubility. Fluid Phase Equilibria 1988, 44, 211–236. [Google Scholar] [CrossRef]
- Ksiazczak, A.; Moorthi, K.; Nagata, I. Solid-solid transition and solubility of even n-alkanes. Fluid Phase Equilibria 1994, 95, 15–29. [Google Scholar] [CrossRef]
- Krajangsod, S.; Chotikamas, S.; Tawai, A.; Sriariyanun, M. Measurement and thermodynamic modelling of erythritol solubility in aqueous solvents. Orient. J. Chem. 2018, 34, 265–275. [Google Scholar] [CrossRef]
- Blanco-Márquez, J.H.; Quigua-Medina, Y.A.; García-Murillo, J.D.; Castro-Camacho, J.K.; Ortiz, C.P.; Cerquera, N.E.; Delgado, D.R. Thermodynamic analysis and applications of the Abraham solvation parameter model in the study of the solubility of some sulfonamides. Rev. Colomb. Cienc. Químico-Farm. 2020, 49, 234–255. [Google Scholar]
- Khoubnasabjafari, M.; Delgado, D.R.; Martinez, F.; Jouyban, A.; Acree, W.E. Predicting the solubility, thermodynamic properties and preferential solvation of sulphamethazine in {acetonitrile + water} mixtures using a minimum number of experimental data points. Phys. Chem. Liq. 2020. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-entropy compensation. 1. Some fundamental statistical problems associated with the analysis of van’t Hoff and arrhenius data. J. Phys. Chem. 1976, 80, 2335–2341. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistical effect. J. Phys. Chem. 1976, 80, 2341–2351. [Google Scholar] [CrossRef]
- Delgado, D.R.; Jouyban, A.; Martínez, F. Solubility and preferential solvation of meloxicam in methanol+ water mixtures at 298.15 K. J. Mol. Liq. 2014, 197, 368–373. [Google Scholar] [CrossRef]
- Blanco-Márquez, J.H.; Ortiz, C.P.; Cerquera, N.E.; Martínez, F.; Jouyban, A.; Delgado, D.R. Thermodynamic analysis of the solubility and preferential solvation of sulfamerazine in (acetonitrile + water) cosolvent mixtures at different temperatures. J. Mol. Liq. 2019, 293, 111507. [Google Scholar] [CrossRef]
- Valvani, S.C.; Yalkowsky, S.H.; Amidon, G.L. Solubility of nonelectrolytes in polar solvents. VI. Refinements in molecular surface area computations. J. Phys. Chem. 1976, 80, 829–835. [Google Scholar] [CrossRef]
- Machatha, S.G.; Bustamante, P.; Yalkowsky, S.H. Deviation from linearity of drug solubility in ethanol/water mixtures. Int. J. Pharm. 2004, 283, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Volkova, T.V.; Levshin, I.B.; Perlovich, G.L. New antifungal compound: Solubility thermodynamics and partitioning processes in biologically relevant solvents. J. Mol. Liq. 2020, 310, 113148. [Google Scholar] [CrossRef]
- Perlovich, G.L.; Strakhova, N.N.; Kazachenko, V.P.; Volkova, T.V.; Tkachev, V.V.; Schaper, K.J.; Raevsky, O.A. Sulfonamides as a subject to study molecular interactions in crystals and solutions: Sublimation, solubility, solvation, distribution and crystal structure. Int. J. Pharm. 2008, 349, 300–313. [Google Scholar] [CrossRef]
- Bustamante, P.; Escalera, B. Enthalpy and Entropy Contributions to the Solubility of Sulphamethoxypyridazine in Solvent Mixtures Showing Two Solubility Maxima. J. Pharm. Pharmacol. 1995, 47, 550–555. [Google Scholar] [CrossRef]
- Bustamante, E.P.; Ochoa, R.; Reillo, A.; Escalera, J.-B. Chameleonic Effect of Sulfanilamide and Sulfamethazine in Solvent Mixtures. Solubility Curves with Two Maxima. Chem. Pharm. Bull. 1994, 42, 1129–1133. [Google Scholar] [CrossRef]
- Ben-Naim, A. Theory of preferential solvation of nonelectrolytes. Cell Biophys. 1988, 12, 255–269. [Google Scholar] [CrossRef]
- Ben-Naim, A. Theoretical aspects of self-assembly of proteins: A Kirkwood-Buff-theory approach. J. Chem. Phys. 2013, 138, 06B609_1. [Google Scholar] [CrossRef] [PubMed]
- Ben-Naim, A.; Navarro, A.M.; Leal, J.M. A Kirkwood-Buff analysis of local properties of solutions. Phys. Chem. Chem. Phys. 2008, 10, 2451–2460. [Google Scholar] [CrossRef] [PubMed]
- Marcus, Y. Solvent Mixtures: Properties and Selective Solvation; CRC Press: New York, NY, USA, 2002. [Google Scholar]
- Marcus, Y. On the preferential solvation of drugs and PAHs in binary solvent mixtures. J. Mol. Liq. 2008, 140, 61–67. [Google Scholar] [CrossRef]
- Delgado, D.R.; Vargas, E.F.; Martínez, F. Preferential solvation of xylitol in ethanol + water co-solvent mixtures according to the IKBI and QLQC methods. Rev. Colomb. Quim. 2013, 42, 125–133. [Google Scholar]
- Marcus, Y. Preferential solvation in mixed solvents. 16. Mixtures of N,N-dimethylformamide or propylene carbonate with organic solvents. J. Chem. Thermodyn. 2020, 140, 105903. [Google Scholar] [CrossRef]
- Delgado, D.R.; Peña, M.A.; Martínez, F. Preferential solvation of acetaminophen in ethanol + water solvent mixtures according to the inverse Kirkwood-Buff integrals method. Rev. Colomb Cienc. Químico Farm. 2013, 42, 298–314. [Google Scholar]
- Marcus, Y. Preferential solvation in mixed solvents. 15. Mixtures of acetonitrile with organic solvents. J. Chem. Thermodyn. 2019, 135, 55–59. [Google Scholar] [CrossRef]
- Castro, J.J.S.; Ortiz, C.P.; Rodríguez-Rubiano, J.D.; Rodríguez-Rodríguez, G.A.; Delgado, D.R. Preferential solvation of tricin in {ethanol (1) + water (2)} mixtures at several temperatures. Rev. Colomb. Cienc. Químico Farm. 2018, 47, 135–148. [Google Scholar] [CrossRef]
- Marcus, Y. Preferential solvation. Part 3.—Binary solvent mixtures. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases. 1989, 85, 381–388. [Google Scholar] [CrossRef]
- Marcus, Y. The Properties of Solvents; John Wiley & Sons Ltd.: New York, NY, USA, 1999. [Google Scholar]
- Jiménez, J.; Manrique, J.; Martínez, F. Effect of temperature on some volumetric properties for ethanol + water mixtures. Rev. Colomb. Cienc. Químico Farm. 2004, 33, 145–155. [Google Scholar]
- Aldana, G.A.d.A.; Rubio, D.I.C.; Rodríguez, G.A.R.; Lozano, A.C.; Mehrdad, A.; Delgado, D.R.; Carmona, N.A.P. Solution thermodynamics and preferential solvation of 3-chloro-N-phenyl-phthalimide in acetone + methanol mixtures. Rev. Colomb. Cienc. Químico Farm. 2016, 45, 256. [Google Scholar] [CrossRef][Green Version]
- Taft, R.W.; Kamlet, M.J. The Solvatochromic Comparison Method. 2. The α-Scale of Solvent Hydrogen-Bond Donor (HBD) Acidities. J. Am. Chem. Soc. 1976, 98, 2886–2894. [Google Scholar] [CrossRef]
- Noubigh, A. Stearic acid solubility in mixed solvents of (water + ethanol) and (ethanol + ethyl acetate): Experimental data and comparison among different thermodynamic models. J. Mol. Liq. 2019, 296, 112101. [Google Scholar] [CrossRef]
- Noubigh, A.; Aydi, A.; Abderrabba, M. Experimental measurement and correlation of solubility data and thermodynamic properties of protocatechuic acid in four organic solvents. J. Chem. Eng. Data 2017, 60, 514–518. [Google Scholar] [CrossRef]
- Noubigh, A.; Akremi, A. Solution thermodynamics of trans-Cinnamic acid in (methanol + water) and (ethanol + water) mixtures at different temperatures. J. Mol. Liq. 2019, 274, 752–758. [Google Scholar] [CrossRef]
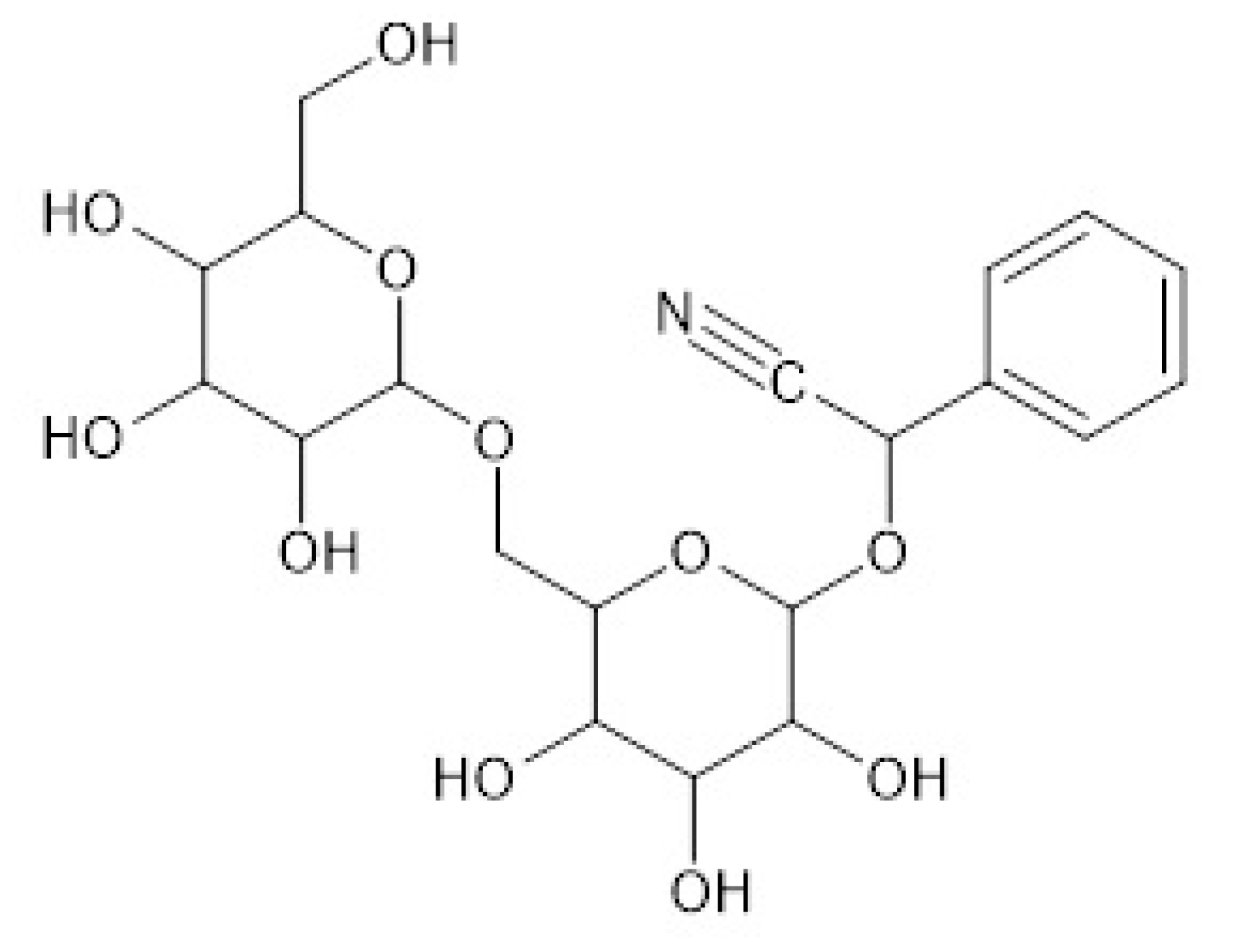


| x1c,d | Temperature/K e | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 310.15 | 313.15 | 318.15 | 323.15 | 328.15 | |
| 0.00 | 2.54 | 3.25 | 4.19 | 5.49 | 6.07 | 7.04 | 7.91 | 9.73 | 11.0 |
| 0.10 | 2.80 | 3.55 | 4.61 | 6.16 | 6.69 | 7.83 | 8.86 | 10.8 | 12.9 |
| 0.20 | 3.07 | 3.99 | 5.21 | 7.12 | 7.42 | 8.84 | 10.4 | 12.2 | 14.6 |
| 0.30 | 3.34 | 4.48 | 5.84 | 8.08 | 8.32 | 9.90 | 11.8 | 13.6 | 16.9 |
| 0.40 | 3.56 | 5.06 | 6.60 | 8.39 | 9.32 | 11.0 | 13.3 | 15.3 | 18.3 |
| 0.50 | 3.12 | 4.06 | 4.84 | 5.90 | 5.99 | 7.26 | 8.67 | 9.52 | 12.1 |
| 0.60 | 2.20 | 2.58 | 3.17 | 3.94 | 4.14 | 4.81 | 5.55 | 6.30 | 7.89 |
| 0.70 | 1.53 | 1.88 | 2.14 | 2.52 | 2.83 | 3.25 | 3.77 | 4.12 | 5.45 |
| 0.80 | 1.00 | 1.21 | 1.36 | 1.70 | 1.76 | 2.02 | 2.44 | 2.62 | 2.93 |
| 0.90 | 0.71 | 0.83 | 0.91 | 1.12 | 1.15 | 1.27 | 1.35 | 1.57 | 1.70 |
| 1.00 | 0.51 | 0.56 | 0.61 | 0.65 | 0.69 | 0.77 | 0.91 | 0.94 | 1.03 |
| Group or Atom | Quantity | ∆V (cm3 mol−1) | ∆U (kJ mol−1) |
|---|---|---|---|
| –CH2 | 2 | 16.1 | 4.94 |
| –CH< | 11 | 13.5 | 4.31 |
| –OH | 7 | 10 | 29.8 |
| –O– | 4 | 3.8 | 3.35 |
| –C≡N | 1 | 24 | 25.5 |
| Phenyl | 1 | 71.4 | 31.9 |
| Ring closure | 1 | 16 | 1.05 |
| Total | 377.3 | 337.74 | |
| δ3 = (337,740/377.3)1/2 = 29.9 MPa1/2 | |||
| x1a | ΔsolnGo/ kJ mol−1 | ΔsolnHo/ kJ mol−1 | ΔsolnSo/ J mol−1 K−1 | TΔsolnSo/ kJ mol−1 | ζH b | ζTS b |
|---|---|---|---|---|---|---|
| 0.00 | 13.31 | 34.10 | 67.03 | 20.79 | 0.621 | 0.379 |
| 0.10 | 13.02 | 35.34 | 71.93 | 22.31 | 0.613 | 0.387 |
| 0.20 | 12.71 | 35.86 | 74.62 | 23.15 | 0.608 | 0.392 |
| 0.30 | 12.41 | 36.77 | 78.52 | 24.36 | 0.601 | 0.399 |
| 0.40 | 12.15 | 37.04 | 80.21 | 24.88 | 0.598 | 0.402 |
| 0.50 | 13.07 | 29.92 | 54.31 | 16.85 | 0.640 | 0.360 |
| 0.60 | 14.13 | 29.10 | 48.26 | 14.97 | 0.660 | 0.340 |
| 0.70 | 15.12 | 28.14 | 41.95 | 13.01 | 0.684 | 0.316 |
| 0.80 | 16.32 | 25.36 | 29.14 | 9.04 | 0.737 | 0.263 |
| 0.90 | 17.48 | 20.26 | 8.96 | 2.78 | 0.879 | 0.121 |
| 1.00 | 18.66 | 17.03 | −5.25 | −1.63 | 0.913 | 0.087 |
| Coefficient | 293.15 K | 298.15 K | 303.15 K | 308.15 K | 313.15 K |
|---|---|---|---|---|---|
| a | −0.0022 | 0.0356 | 0.0446 | 0.0879 | 0.0706 |
| b | −0.3574 | −1.2782 | 1.8586 | −5.1881 | −3.8227 |
| c | −20.48 | −19.625 | −18.477 | −1.9751 | −8.7567 |
| d | 53.775 | 55.874 | 57.349 | 32.26 | 43.505 |
| e | −29.053 | −30.735 | 32.277 | −19.838 | −25.332 |
| R2 | 0.998 | 0.994 | 0.995 | 0.993 | 0.994 |
| x1 a | δx1,3 | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.050 | −0.001 | −0.001 | −0.001 | −0.002 | −0.001 |
| 0.100 | −0.001 | −0.002 | −0.002 | −0.002 | −0.002 |
| 0.150 | −0.001 | −0.002 | −0.002 | −0.002 | −0.002 |
| 0.200 | −0.001 | −0.001 | −0.001 | −0.001 | −0.001 |
| 0.250 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.300 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 |
| 0.350 | 0.000 | 0.000 | −0.001 | −0.002 | −0.002 |
| 0.400 | −0.002 | −0.003 | −0.004 | −0.005 | −0.005 |
| 0.450 | −0.007 | −0.008 | −0.009 | −0.010 | −0.010 |
| 0.500 | −0.014 | −0.015 | −0.017 | −0.017 | −0.017 |
| 0.550 | −0.023 | −0.024 | −0.026 | −0.026 | −0.026 |
| 0.600 | −0.033 | −0.035 | −0.037 | −0.036 | −0.036 |
| 0.650 | −0.043 | −0.046 | −0.048 | −0.046 | −0.047 |
| 0.700 | −0.051 | −0.054 | −0.056 | −0.054 | −0.056 |
| 0.750 | −0.052 | −0.055 | −0.058 | −0.057 | −0.059 |
| 0.800 | −0.044 | −0.047 | −0.050 | −0.051 | −0.054 |
| 0.850 | −0.030 | −0.033 | −0.035 | −0.037 | −0.039 |
| 0.900 | −0.016 | −0.017 | −0.018 | −0.021 | −0.022 |
| 0.950 | −0.005 | −0.005 | −0.006 | −0.008 | −0.008 |
| 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aydi, A.; Ayadi, C.; Ghachem, K.; Al-Khazaal, A.Z.; Delgado, D.R.; Alnaief, M.; Kolsi, L. Solubility, Solution Thermodynamics, and Preferential Solvation of Amygdalin in Ethanol + Water Solvent Mixtures. Pharmaceuticals 2020, 13, 395. https://doi.org/10.3390/ph13110395
Aydi A, Ayadi C, Ghachem K, Al-Khazaal AZ, Delgado DR, Alnaief M, Kolsi L. Solubility, Solution Thermodynamics, and Preferential Solvation of Amygdalin in Ethanol + Water Solvent Mixtures. Pharmaceuticals. 2020; 13(11):395. https://doi.org/10.3390/ph13110395
Chicago/Turabian StyleAydi, Abdelkarim, Cherifa Ayadi, Kaouther Ghachem, Abdulaal Z. Al-Khazaal, Daniel R. Delgado, Mohammad Alnaief, and Lioua Kolsi. 2020. "Solubility, Solution Thermodynamics, and Preferential Solvation of Amygdalin in Ethanol + Water Solvent Mixtures" Pharmaceuticals 13, no. 11: 395. https://doi.org/10.3390/ph13110395
APA StyleAydi, A., Ayadi, C., Ghachem, K., Al-Khazaal, A. Z., Delgado, D. R., Alnaief, M., & Kolsi, L. (2020). Solubility, Solution Thermodynamics, and Preferential Solvation of Amygdalin in Ethanol + Water Solvent Mixtures. Pharmaceuticals, 13(11), 395. https://doi.org/10.3390/ph13110395








