Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors
Abstract
:1. Introduction
2. Theory
2.1. Definitions
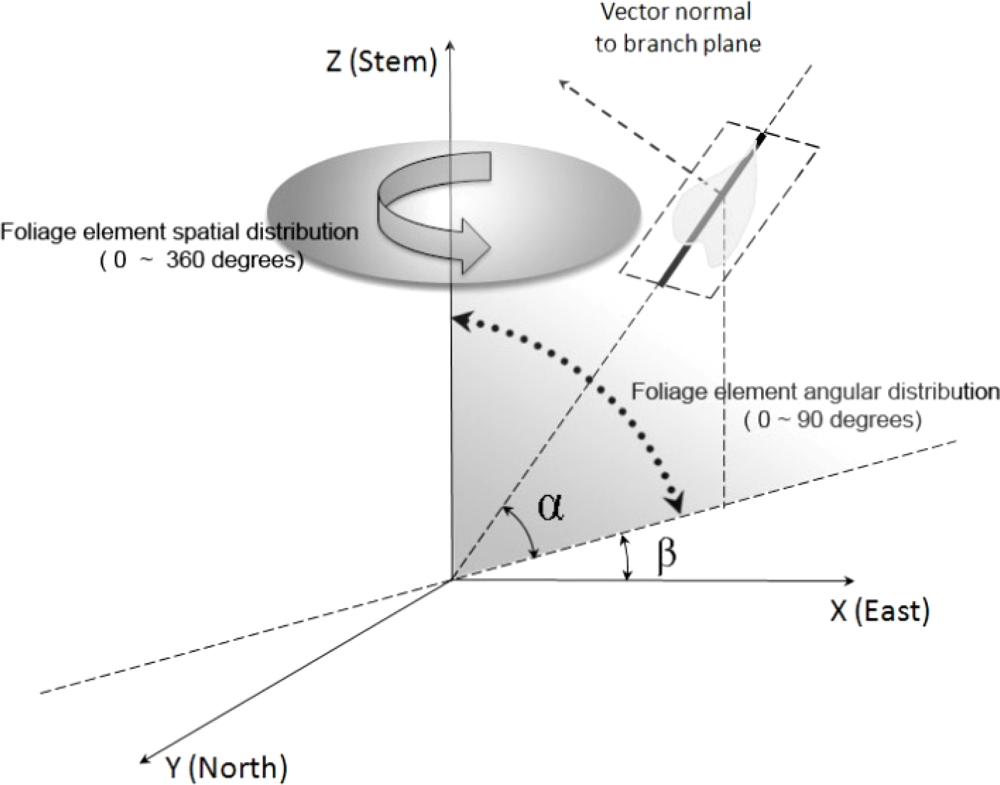
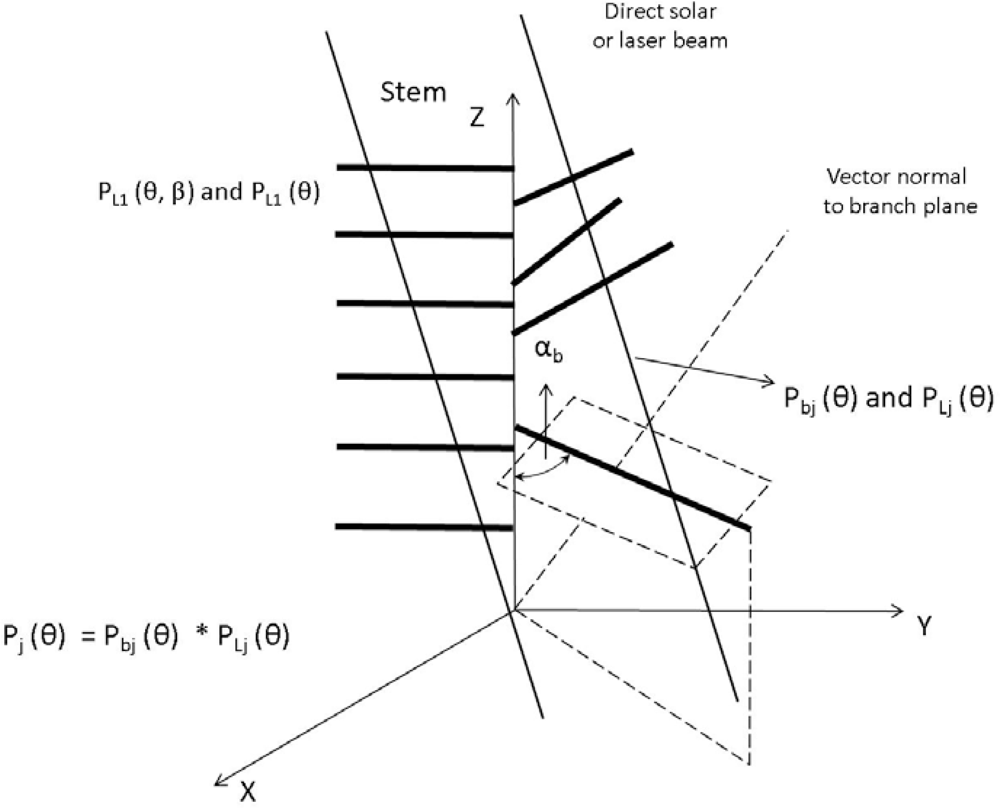
2.2. Canopy Distribution and Leaf Inclination
2.3. Gap Fraction
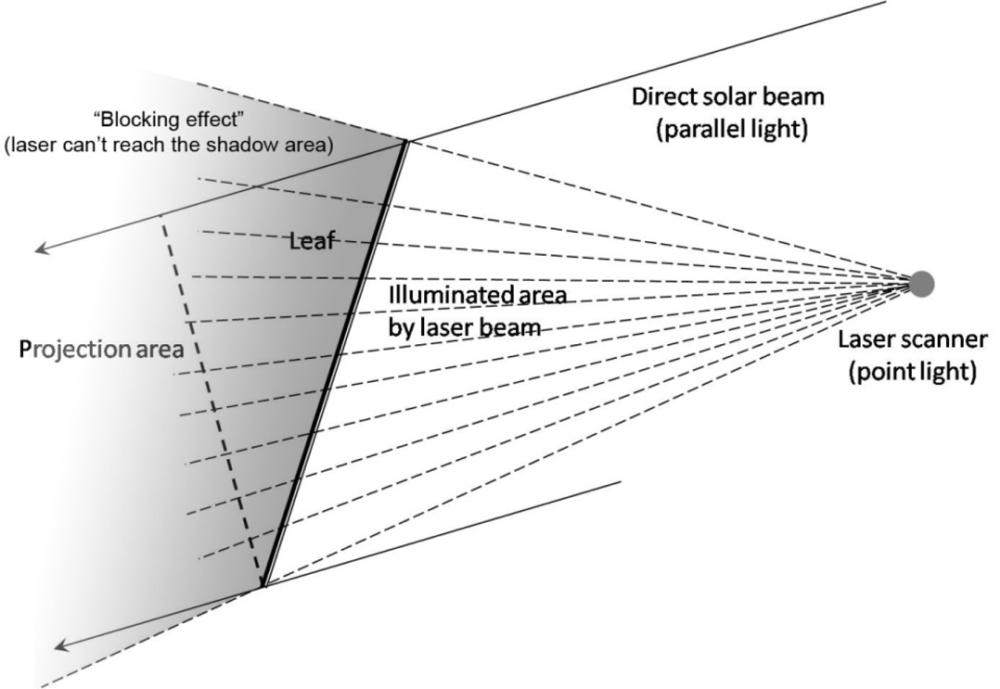
2.3.1. Clumping and Gap Size
3. Measurement Methods and Sensors
3.1. Direct Methods
3.2. Indirect Methods
3.2.1. Passive Sensors
Terrestrial
Airborne
Satellite
3.2.2. Active Sensors
Terrestrial
Airborne
Satellite
3.3. Scaling Issues
4. Conclusions
Acknowledgments
References
- Duchemin, B.; Hadriab, R.; Errakib, S.; Bouleta, G.; Maisongrandea, P.; Chehbounia, A.; Escadafala, R.; Ezzaharb, J.; Hoedjesa, J.C.B.; Kharroud, M.H.; Khabbab, S.; Mougenota, B.; Oliosoe, A.; Rodriguezf, J.C.; Simonneauxa, V. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manage 2006, 79, 1–27. [Google Scholar]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ 2007, 106, 285–304. [Google Scholar]
- Jongschaap, R.E.E. Run-time calibration of simulation models by integrating remote sensing estimates of leaf area index and canopy nitrogen. Eur. J. Agron 2006, 24, 316–324. [Google Scholar]
- Chen, J.M.; Chen, X.Y.; Ju, W.M.; Geng, X.Y. Distributed hydrological model for mapping evapotranspiration using remote sensing inputs. J. Hydrol 2005, 305, 15–39. [Google Scholar]
- Dietz, J.; Hölscher, D.; Leuschnerb, C.; Hendrayanto. Rainfall partitioning in relation to forest structure in differently managed montane forest stands in Central Sulawesi, Indonesia. For. Ecol. Manage 2006, 237, 170–178. [Google Scholar]
- Leuning, R.; Cleugh, H.A.; Zegelin, S.J.; Hughes, D. Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry savanna in Australia: measurements and comparison with MODIS remote sensing estimates. Agric. For. Meteorol 2005, 129, 151–173. [Google Scholar]
- Soegaard, H. Fluxes of carbon dioxide, water vapour and sensible heat in a boreal agricultural area of Sweden - scaled from canopy to landscape level. Agric. For. Meteorol 1999, 98, 463–478. [Google Scholar]
- Chen, B.Z.; Chen, J.M.; Ju, W.M. Remote sensing-based ecosystem-atmosphere simulation scheme (EASS) - Model formulation and test with multiple-year data. Ecol. Modell 2007, 209, 277–300. [Google Scholar]
- Waring, R.H.; Pitman, G.B. Modifying lodgepole pine stand of change susceptibility to mountain pine-beetle attack. Ecology 1985, 66, 889–897. [Google Scholar]
- Green, E.P.; Murnby, P.J.; Edwards, A.J.; Clark, C.D.; Ellis, A.C. Estimating leaf area index of mangroves from satellite data. Aquat. Bot 1997, 58, 11–19. [Google Scholar]
- Liu, J.; Chen, J.M.; Cihlar, J.; Park, W.M. A process-based boreal ecosystem productivity simulator using remote sensing inputs. Remote Sens. Environ 1997, 62, 158–175. [Google Scholar]
- Wulder, M.A.; Franklin, S.E. Remote sensing of forest environments: concepts and case studies; Kluwer Academic Publishers: Boston, USA, 2003. [Google Scholar]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and Landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ 1999, 70, 52–68. [Google Scholar]
- Berterretche, M.; Hudak, A.T.; Cohen, W.B.; Maiersperger, T.K.; Gower, S.T.; Dungan, J. Comparison of regression and geostatistical methods for mapping Leaf Area Index (LAI) with Landsat ETM+ data over a boreal forest. Remote Sens. Environ 2005, 96, 49–61. [Google Scholar]
- Soudani, K.; François, C.; Maire, G.L.; Dantec, V.L.; Dufrêne, E. Comparative analysis of IKONOS, SPOT, and ETM+ data for leaf area index estimation in temperate coniferous and deciduous forest stands. Remote Sens. Environ 2006, 102, 161–175. [Google Scholar]
- Tian, Q.; Luo, Z.; Chen, J.M.; Chen, M.; Hui, F. Retrieving leaf area index for coniferous forest in Xingguo County, China with Landsat ETM+ images. J. Environ. Manage 2007, 85, 624–627. [Google Scholar]
- Zheng, G.; Tian, Q.J.; Chen, J.M.; Ju, W.M.; Xia, X.Q. Combining remote sensing imagery and forest age inventory for biomass mapping. J. Remote Sens 2006, 10, 932–940. [Google Scholar]
- Lee, K.S.; Cohen, W.B.; Kennedy, R.E.; Maiersperger, T.K.; Gower, S.T. Hyperspectral versus multispectral data for estimating leaf area index in four different biomes. Remote Sens. Environ 2004, 91, 508–520. [Google Scholar]
- Colombo, R.; Meroni, M.; Marchesi, A.; Busetto, L.; Rossini, M.; Giardino, C.; Panigada, C. Estimation of leaf and canopy water content in poplar plantations by means of hyperspectral indices and inverse modeling. Remote Sens. Environ 2008, 112, 1820–1834. [Google Scholar]
- Feng, W.; Zhu, Y.; Yao, X.; Tian, Y.C.; Cao, W.X. Monitoring leaf nitrogen status with hyperspectral reflectance in wheat. Eur. J. Agron 2008, 28, 394–404. [Google Scholar]
- Houldcroft, C.J.; Campbell, C.L.; Davenport, I.J.; Gurney, R.J.; Holden, N. Measurement of canopy geometry characteristics using LiDAR laser altimetry: A feasibility study. IEEE Trans. Geosci. Remote Sens 2005, 43, 2270–2282. [Google Scholar]
- Evans, D.L.; Roberts, S.D.; Parker, R.C. LiDAR - A new tool for forest measurements? Forestry Chronicle 2006, 82, 211–218. [Google Scholar]
- Henning, J.G.; Radtke, P.J. Ground-based laser imaging for assessing three-dimensional forest canopy structure. Photogram. Eng. Remote Sens 2006, 72, 1349–1358. [Google Scholar]
- Coops, N.C.; Hilker, T.; Wulder, M. A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. Estimating canopy structure of Douglas-fir forest stands from discrete-return LiDAR. Trees-Structure and Function 2007, 21, 295–310. [Google Scholar]
- Omasa, K.; Hosoi, F.; Konishi, A. 3D lidar imaging for detecting and understanding plant responses and canopy structure. J. Exper. Bot 2007, 58, 881–898. [Google Scholar]
- Goodwin, N.R.; Coops, N.C.; Culvenor, D.S. Assessment of forest structure with airborne LiDAR and the effects of platform altitude. Remote Sens. Environ 2006, 103, 140–152. [Google Scholar]
- Hanssen, K.H.; Solberg, S. Assessment of defoliation during a pine sawfly outbreak: Calibration of airborne laser scanning data with hemispherical photography. For. Ecol. Manage 2007, 250, 9–16. [Google Scholar]
- Solberg, S.; Næsset, E.; Hanssen, K.H.; Christiansen, E. Mapping defoliation during a severe insect attack on Scots pine using airborne laser scanning. Remote Sens. Environ 2006, 102, 364–376. [Google Scholar]
- Clawges, R.; Clawges, R.; Vierling, L.A.; Calhoon, M.; Toomey, M.P. Use of a ground-based scanning lidar for estimation of biophysical properties of western larch (Larix occidentalis). Int. J. Remote Sens 2007, 28, 4331–4344. [Google Scholar]
- Henning, J.G.; Radtke, P.J. Detailed stem measurements of standing trees from ground-based scanning lidar. Forest Science 2006, 52, 67–80. [Google Scholar]
- Hosoi, F.; Omasa, K. Factors contributing to accuracy in the estimation of the woody canopy leaf area density profile using 3D portable lidar imaging. J. Exper. Bot 2007, 58, 3463–3473. [Google Scholar]
- Koetz, B.; Morsdorf, F.; Sun, G.; Ranson, K.J.; Itten, K.; Allgower, B. Inversion of a lidar waveform model for forest biophysical parameter estimation. IEEE Geosci. Remote Sens. Lett 2006, 3, 49–53. [Google Scholar]
- Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manage 2005, 213, 54–70. [Google Scholar]
- Hosoi, F.; Omasa, K. Voxel-based 3-D modeling of individual trees for estimating leaf area density using high-resolution portable scanning lidar. IEEE Trans. Geosci. Remote Sens 2006, 44, 3610–3618. [Google Scholar]
- Takeda, T.; Oguma, H.; Sano, T.; Yone, Y.; Fujinuma, Y. Estimating the plant area density of a Japanese larch (Larix kaempferi Sarg.) plantation using a ground-based laser scanner. Agric. For. Meteorol 2008, 148, 428–438. [Google Scholar]
- Van der Zande, D.; Hoet, W.; Jonckheere, I.; van Aardt, J.; Coppin, P. Influence of measurement set-up of ground-based LiDAR for derivation of tree structure. Agric. For. Meteorol 2006, 141, 147–160. [Google Scholar]
- Naesset, E. Assessing sensor effects and effects of leaf-off and leaf-on canopy conditions on biophysical stand properties derived from small-footprint airborne laser data. Remote Sens. Environ 2005, 98, 356–370. [Google Scholar]
- Straatsma, M.; Middelkoop, H. Extracting structural characteristics of herbaceous floodplain vegetation under leaf-off conditions using airborne laser scanner data. Int. J. Remote Sens 2007, 28, 2447–2467. [Google Scholar]
- Mishra, K.B.; Gopal, R. Detection of nickel-induced stress using laser-induced fluorescence signatures from leaves of wheat seedlings. Int. J. Remote Sens 2008, 29, 157–173. [Google Scholar]
- Thomas, V.; Treitz, P.; Mccaughey, J.H.; Noland, T.; Rich, L. Canopy chlorophyll concentration estimation using hyperspectral and lidar data for a boreal mixedwood forest in northern Ontario, Canada. Int. J. Remote Sens 2008, 29, 1029–1052. [Google Scholar]
- Smolander, S.; Stenberg, P. Simple parameterizations of the radiation budget of uniform broadleaved and coniferous canopies. Remote Sens. Environ 2005, 94, 355–363. [Google Scholar]
- Ganguly, S.; Ganguly, S.; Schull, M.A.; Samanta, A.; Shabanov, N.V.; Milesi, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Generating vegetation leaf area index Earth system data record from multiple sensors. Part 2: Implementation, analysis and validation. Remote Sens. Environ 2008, 112, 4318–4332. [Google Scholar]
- Ganguly, S.; Ganguly, S.; Schull, M.A.; Samanta, A.; Shabanov, N.V.; Milesi, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Generating vegetation leaf area index earth system data record from multiple sensors. Part 1: Theory. Remote Sens. Environ 2008, 112, 4333–4343. [Google Scholar]
- Schull, M.A.; Ganguly, S.; Samanta, A.; Huang, D.; Shabanov, N.V.; Jenkins, J.P.; Chiu, J.C.; Marshak, A.; Blair, J.B.; Myneni, R.B.; Knyazikhin, Y. Physical interpretation of the correlation between multi-angle spectral data and canopy height. Geophys. Res. Lett 2007, 34, L18405:1–L18045:5. [Google Scholar]
- Groeneveld, D.P. Vertical point quadrat sampling and an extinction factor to calculate leaf area index. J. Arid Environ 1997, 36, 475–485. [Google Scholar]
- Wilson, J.W. Stand structure and light penetration: 1. Analysis by point quadrats. J. Appl. Ecol 1965, 2, 383–390. [Google Scholar]
- Campbell, G.S. Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination distribution. Agric. For. Meteorol 1986, 36, 317–321. [Google Scholar]
- Norman, J.M.; Campbell, G.S. Plant Physiological Ecology. Field Methods and Instrumentation. Pearcy, R.W., Ehleringer, J.R., Mooney, H.A., Rundel, P.W, Eds.; Chapman and Hall: New York, USA, 1989; pp. 301–325. [Google Scholar]
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-drivern model of bidirectional reflectance. J. Geophys. Res. Atmos 1995, 100, 21077–21089. [Google Scholar]
- Leblanc, S.G.; Bicheron, P.; Chen, J.M.; Leroy, M.; Cihlar, J. Investigation of directional reflectance in boreal forests with an improved four-scale model and airborne POLDER data. IEEE Trans. Geosci. Remote Sens 1999, 37, 1396–1414. [Google Scholar]
- Watson, D. Comparative physiological studies in the growth of field crops. 1.Variation in net assimilation rate and leaf area between species and varieties, and within and between years. Ann. Bot 1947, 11, 41–76. [Google Scholar]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J. L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; Lotsch, A.; Friedl, M.; Morisette, J.T.; Votava, P.; Nemani, R.R.; Running, S.W. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ 2002, 83, 214–231. [Google Scholar]
- Knyazikhin, Y.; Martonchik, J.V.; Diner, D.J.; Myneni, R.B.; Verstraete, M.; Pinty, B.; Gobron, N. Estimation of vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from atmosphere-corrected MISR data. J. Geophys. Res. Atmos 1998, 103, 32239–32256. [Google Scholar]
- Running, S.W.; Peterson, D.L.; Spanner, M.A.; Teuber, K.B. Remote-sensing coniferous forest leaf area. Ecology 1986, 67, 273–276. [Google Scholar]
- Ross, J. 1.3 Phytometric methods. In The radiation regime and architecture of plant stands; Kluwer academic publishers: Holand, 1981; pp. 42–44. [Google Scholar]
- Smith, W.K.; Schoettle, A.W.; Cui, M. Importance of the method of leaf area measurement to the interretation of gas-exchange of complex shoots. Tree Physiol 1991, 8, 121–127. [Google Scholar]
- Black, T.A.; Chen, J.M.; Lee, X.H.; Sagar, R.M. Characteristics of shortwave and longwave irradiances under douglas-fir forest stand. Can. J. For. Res 1991, 21, 1020–1028. [Google Scholar]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ 1992, 15, 421–429. [Google Scholar]
- Lang, A.R.G. Application of some of Cauchy's theorems to estimation of surface areas of leaves, needles and branches of plants, and light transmittance. Agric. For. Meteorol 1991, 55, 191–212. [Google Scholar]
- Yang, X.S.; Miller, D.R.; Montgomery, M.E. Vertical distributions of canopy foliage and biologically-active radiation in a defoliated/refoliated hardwood forest. Agric. For. Meteorol 1993, 67, 129–146. [Google Scholar]
- Campbell, G.S. Derivation of an angle density-fucntion for canopies with ellipsoidal leaf angle distributions. Agric. For. Meteorol 1990, 49, 173–176. [Google Scholar]
- Pearcy, R.W. Plant physiological ecology : field methods and instrumentation. Chapman and Hall: New York, 1989. [Google Scholar]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol 1971, 8, 25–38. [Google Scholar]
- Miller, J.B. A formula for average foliage density. Aust. J. Bot 1967, 15, 141–144. [Google Scholar]
- Chen, J.M. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agric. For. Meteorol 1996, 80, 135–163. [Google Scholar]
- Nilson, T.; Kuusk, A. Improved algorithm for estimating canopy indices from gap fraction data in forest canopies. Agric. For. Meteorol 2004, 124, 157–169. [Google Scholar]
- Zhang, Y.; Chen, J.M.; Miller, J.R. Determining digital hemispherical photograph exposure for leaf area index estimation. Agric. For. Meteorol 2005, 133, 166–181. [Google Scholar]
- Miller, E.E.; Norman, J.M. Sunfleck theory for plant canopies: 1. lengths of sunlit segments along a transect. Agron. J 1971, 63, 735–738. [Google Scholar]
- Miller, E.E.; Norman, J.M. Sunfleck theory for plant canopies: 2. penumbra effect - intensity distributions along sunfleck segments. Agron. J 1971, 63, 739–743. [Google Scholar]
- Nilson, T. Theoretical analysis of frequency of gaps in plant stands. Agric. Meteorol 1971, 8, 25–38. [Google Scholar]
- Chen, J.M.; Black, T.A. Foliage area and architecture of plant canopies from sunfleck size distributions. Agric. For. Meteorol 1992, 60, 249–266. [Google Scholar]
- Chen, J.M.; Cihlar, J. Plant canpy gap-size analysis theory for improving optical measurement of leaf-area index. Appl. Opt 1995, 34, 6211–6222. [Google Scholar]
- Chen, J.M.; Cihlar, J. Quantifying the effect of canopy architecture on optical measurement of leaf area index using 2 gap size analysis mehtods. IEEE Trans. Geosci. Remote Sens 1995, 33, 777–787. [Google Scholar]
- Chen, J.M.; Rich, P.M.; Gower, S.T.; Norman, J.M.; Plummer, S. Leaf area index of boreal forests: Theory, techniques, and measurements. J. Geophys. Res. Atmos 1997, 102, 29429–29443. [Google Scholar]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination - Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol 2004, 121, 19–35. [Google Scholar]
- Levy, E.B.; Madden, E.A. The point method of pasture analysis. New Zealand J. Agric 1933, 46, 267–279. [Google Scholar]
- Tinney, F.W.; Aamodt, O.S.; Ahlgren, H.L. Preliminary report on a study of methods used in botanical analysis of pasture swards. J. Amer. Soc. Agron 1937, 835–840. [Google Scholar]
- Warren, J.W. Analysis of the spatial distribution of foliage by two-dimensional point quadrats. New Phytol 1959, 58, 92–99. [Google Scholar]
- Chen, J.M.; Black, T.A. Measuring leaf area index of plant canopies with branch architecture. Agric. For. Meteorol 1991, 57, 1–12. [Google Scholar]
- Zhang, Y.Q.; Chen, J.M.; Miller, J.R.; Noland, T.L. Leaf chlorophyll content retrieval from airborne hyperspectral remote sensing imagery. Remote Sens. Environ 2008, 112, 3234–3247. [Google Scholar]
- Jacquemoud, S.; Baret, F. Prospect - a model of leaf optical-properties spectra. Remote Sens. Environ 1990, 34, 75–91. [Google Scholar]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens 1997, 35, 1316–1337. [Google Scholar]
- Gonzalez-Sanpedro, M.C.; Toan, T.L.; Moreno, J.; Kergoat, L.; Rubio, E. Seasonal variations of leaf area index of agricultural fields retrieved from Landsat data. Remote Sens. Environ 2008, 112, 810–824. [Google Scholar]
- Kotz, B.; Schaepman, M.; Morsdorf, F.; Bowyer, P.; Itten, K.; Allgöwer, B. Radiative transfer modeling within a heterogeneous canopy for estimation of forest fire fuel properties. Remote Sens. Environ 2004, 92, 332–344. [Google Scholar]
- Wardley, N.W.; Curran, P.J. The estimation of green leaf area index from remotely sensed airborne multispectral scanner data. Int. J. Remote Sens 1984, 5, 671–679. [Google Scholar]
- Walthall, C.L.; Pachepsky, Y.; Dulaney, W.P.; Timlin, D.J.; Daughtry, C.S.T. Exploitation of spatial information in high resolution digital imagery to map leaf area index. Prec. Agric 2007, 8, 311–321. [Google Scholar]
- Curran, P.J.; Williamson, H.D. Estimating the green leaf area index of grassland with airborne multispectral scanner data. Oikos 1987, 49, 141–148. [Google Scholar]
- Jordan, C.F. Derivation of leaf-area index from quality of light on forest floor. Ecology 1969, 50, 663–666. [Google Scholar]
- Deering, D.W. Rangeland reflectance characteristics measured by aircraft and spacecraft sensors. College Station, Texas A&M Univ.: Deering, USA, 1978. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ 2002, 83, 195–213. [Google Scholar]
- Brown, L.; Chen, J.M.; Leblanc, S.G.; Cihlar, J. A shortwave infrared modification to the simple ratio for LAI retrieval in boreal forests: An image and model analysis. Remote Sens. Environ 2000, 71, 16–25. [Google Scholar]
- Stenberg, P.; Rautiainen, M.; Manninen, T.; Voipio, P.; Smolander, H. Reduced simple ratio better than NDVI for estimating LAI in Finnish pine and spruce stands. Silva Fennica 2004, 38, 3–14. [Google Scholar]
- Jiang, Z.Y.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ 2008, 112, 3833–3845. [Google Scholar]
- Cohen, W.B.; Maiersperger, T.K.; Stith, T.G.; Tumer, D.P. An improved strategy for regression of biophysical variables and Landsat ETM+ data. Remote Sens. Environ 2003, 84, 561–571. [Google Scholar]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using landsat TM images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.R.; de Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ 2005, 99, 271–287. [Google Scholar]
- Gupta, R.K.; Vijayan, D.; Prasad, T.S. The relationship of hyper-spectral vegetation indices with leaf area index (LAI) over the growth cycle of wheat and chickpea at 3 nm spectral resolution. Adv. Space Res 2006, 38, 2212–2217. [Google Scholar]
- Schlerf, M.; Atzberger, C. Inversion of a forest reflectance model to estimate structural canopy variables from hyperspectral remote sensing data. Remote Sens. Environ 2006, 100, 281–294. [Google Scholar]
- Pu, R.L.; Kelly, M.; Anderson, G.L.; Gong, P. Using CASI hyperspectral imagery to detect mortality and vegetation stress associated with a new hardwood forest disease. Photogram. Eng. Remote Sens 2008, 74, 65–75. [Google Scholar]
- Cheng, Y.B.; Zarco-Tejada, P.J.; Riaño, D.; Rueda, C.A.; Ustin, S.L. Estimating vegetation water content with hyperspectral data for different canopy scenarios: Relationships between AVIRIS and MODIS indexes. Remote Sens. Environ 2006, 105, 354–366. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ 2004, 90, 337–352. [Google Scholar]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote estimation of crop chlorophyll content using spectral indices derived from hyperspectral data. IEEE Trans. Geosci. Remote Sens 2008, 46, 423–437. [Google Scholar]
- Hu, B.X.; Qian, S.E.; Haboudane, D.; Miller, J.R.; Hollinger, A.B.; Tremblay, N.; Pattey, E. Retrieval of crop chlorophyll content and leaf area index from decompressed hyperspectral data: the effects of data compression. Remote Sens. Environ 2004, 92, 139–152. [Google Scholar]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ 2001, 76, 156–172. [Google Scholar]
- Tian, Q.; Chen, J.M.; Zheng, G.; Xia, X.Q.; Chen, J.Y. Quantitative retrieving forest ecological parameters based on remote a sensing in Liping County of China. Proceeding of International Society for Optical Engineering, Stockholm, Sweden, 2006; SPIE: Bellingham, WA, USA, 2006; 6359, pp. 1–10. [Google Scholar]
- Gu, Y.X.; Bélair, S.; Mahfouf, J.F.; Deblonde, G. Optimal interpolation analysis of leaf area index using MODIS data. Remote Sens. Environ 2006, 104, 283–296. [Google Scholar]
- Brakke, T.W.; Kanemasu, E.T.; Steiner, J.L.; Ulaby, F.T.; Wilson, E. Microwave Radar response to canopy moisture, leaf area index and dry weight of wheat, corn, and sorghum. Remote Sens. Environ 1981, 11, 207–220. [Google Scholar]
- Van der Zande, D.; Hoet, W.; Jonckheere, I.; van Aardt, J.; Coppin, P. Influence of measurement set-up of ground-based LiDAR for derivation of tree structure. Agric. For. Meteorol 2006, 141, 147–160. [Google Scholar]
- Danson, F.M.; Hetherington, D.; Morsdorf, F.; Koetz, B.; Allgöwer, B. Forest canopy gap fraction from terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett 2007, 4, 157–160. [Google Scholar]
- Morsdorf, F.; Kötz, B.; Meier, E.; Itten, K.I.; Allgöwer, B. Estimation of LAI and fractional cover from small footprint airborne laser scanning data based on gap fraction. Remote Sens. Environ 2006, 104, 50–61. [Google Scholar]
- Durden, S.L.; Morrissey, L.A.; Livingston, G.P. Microwave backscatter and attenuation dependence on leaf area index for flooded rice fields. IEEE Geosci. Remote Sens. Lett 1995, 33, 807–810. [Google Scholar]
- Prevot, L.; Champion, I.; Guyot, G. Estimating surface soil-moisture and leaf area index of a wheat canopy using a dual-frequency (C and X-bands) scaaterometer. Remote Sens. Environ 1993, 46, 331–339. [Google Scholar]
- Chand, T.R.K.; Badarinath, K.V.S. Analysis of ENVISAT ASAR data for forest parameter retrieval and forest type classification - a case study over deciduous forests of central India. Int. J. Remote Sens 2007, 28, 4985–4999. [Google Scholar]
- Liu, L.Y.; Wang, J.; Bao, Y.; Huang, W.; Ma, Z.; Zhao, C. Predicting winter wheat condition, grain yield and protein content using multi-temporal EnviSat-ASAR and Landsat TM satellite images. Int. J. Remote Sens 2006, 27, 737–753. [Google Scholar]
- Singh, D. Scatterometer performance with polarization discrimination ratio approach to retrieve crop soybean parameter at X-band. Int. J. Remote Sens 2006, 27, 4101–4115. [Google Scholar]
- Xu, H.; Steven, M.D.; Jaggard, K.W. Monitoring leaf area of sugar beet using ERS-1 SAR data. Int. J. Remote Sens 1996, 17, 3401–3410. [Google Scholar]
- Manninen, T.; Stenberg, P.; Rautiainen, M.; Voipio, P.; Smolander, H. Leaf area index estimation of boreal forest using ENVISAT ASAR. IEEE Trans. Geosci. Remote Sens 2005, 43, 2627–2635. [Google Scholar]
- Chen, J.M. Spatial scaling of a remotely sensed surface parameter by contexture. Remote Sens. Environ 1999, 69, 30–42. [Google Scholar]
- Jin, Z.; Tiana, Q.; Chenb, J.M.; Chenb, M. Spatial scaling between leaf area index maps of different resolutions. J. Environ. Manage 2007, 85, 628–637. [Google Scholar]
- Tian, Y.H.; Wang, Y.J.; Zhang, Y.; Knyazikhin, Y.; Bogaert, J.; Myneni, R.B. Radiative transfer based scaling of LAI retrievals from reflectance data of different resolutions. Remote Sens. Environ 2003, 84, 143–159. [Google Scholar]

| Type | Definition | Application | Reference |
|---|---|---|---|
| Total Leaf Area Index (ToLAI) | Total one-sided area of photosynthetic tissue per unit ground surface area. | Applicable to broad leaves. | [51,52] |
| Projected Leaf Area Index (PLAI) | The area of horizontal shadow that is cast beneath a horizontal leaf from a light at infinite distance directly above it. | Maximum area of leaves from the overhead orbital view – varies depending on the zenith angle of sensor. | [52–55] |
| Silhouette Leaf Area Index (SLAI) | The area of leaves inclined to the horizontal surface. | Investigates the radiation interception for different shapes of leaves. | [56] |
| Effective Leaf Area Index (ELAI) | One half of the total area of light intercepted by leaves per unit horizontal ground surface area – assume the foliage spatial distribution is random. | Precisely describes the radiation interception and radiation regime within and under canopy. | [57] |
| True Leaf Area Index (TLAI) | One half the total green leaf area per unit horizontal ground surface area. | Quantitatively characterizes radiation regime within and under canopy, and simulates leaf-controlled ecological process. | [58,59] |
© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors 2009, 9, 2719-2745. https://doi.org/10.3390/s90402719
Zheng G, Moskal LM. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors. 2009; 9(4):2719-2745. https://doi.org/10.3390/s90402719
Chicago/Turabian StyleZheng, Guang, and L. Monika Moskal. 2009. "Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors" Sensors 9, no. 4: 2719-2745. https://doi.org/10.3390/s90402719
APA StyleZheng, G., & Moskal, L. M. (2009). Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors, 9(4), 2719-2745. https://doi.org/10.3390/s90402719




