Automatic Registration of Terrestrial Laser Scanning Point Clouds using Panoramic Reflectance Images
Abstract
:1. Introduction
2. Pair-wise Registration
2.1. Registration Process
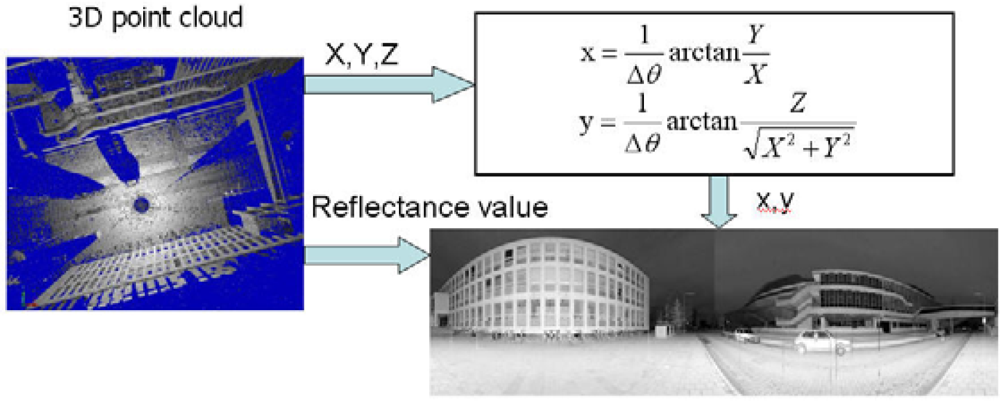
2.2. Generation of Reflectance Images
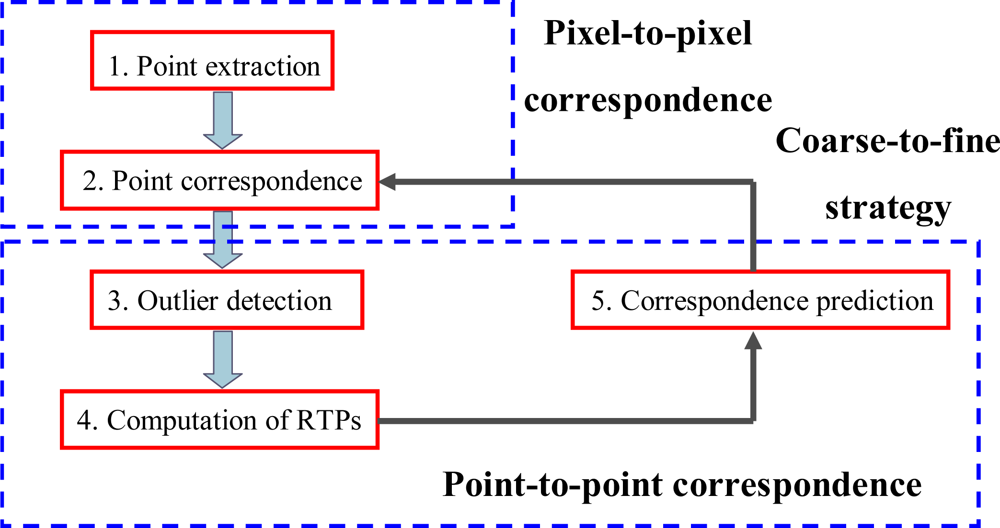
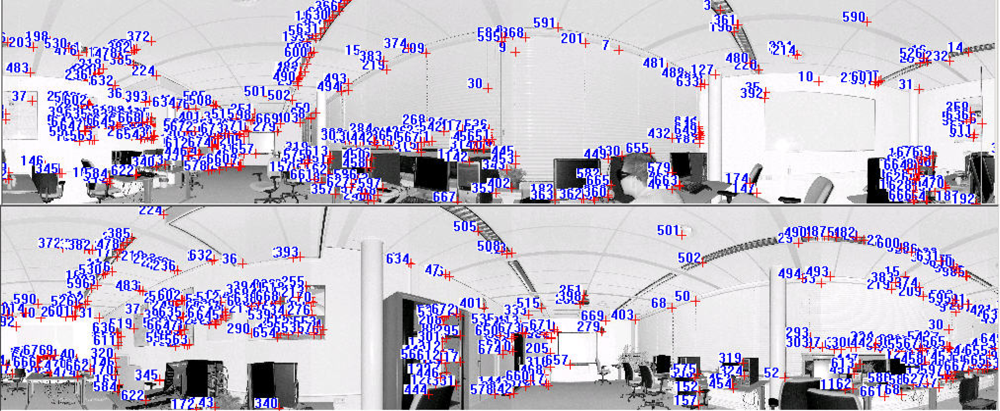
2.3. Pixel-to-Pixel Correspondence
- Scale-space extrema detection: employing a difference-of-Gaussian function to identify potential points of interest that are invariant to scale and orientation,
- Key-point localisation: fitting an analytical model (mostly in the form of a parabola) at each candidate location to determine the location and scale,
- Orientation assignment: assigning one or more orientations to each key-point location based on local image gradient directions, and
- Key-point descriptor: measuring the local image gradients at the selected scale in the region around each key-point.
2.4. Point-to-Point Correspondence
2.4.1 Outlier Detection
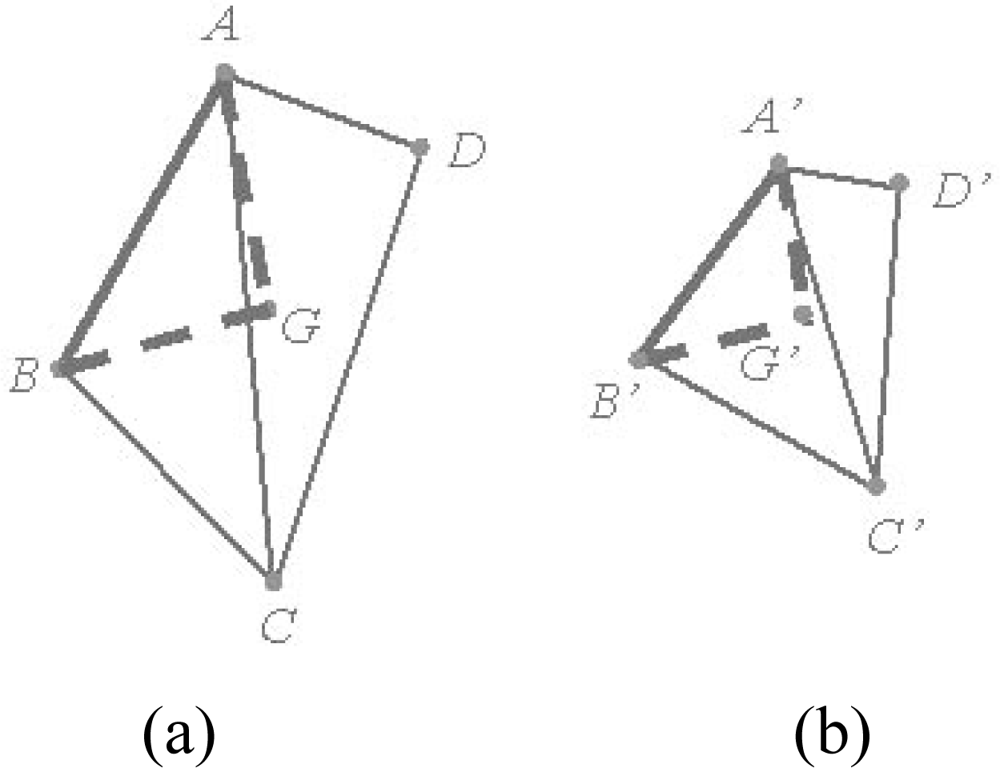
2.4.2. Computation of Transformation Parameters
2.4.3. Correspondence Prediction
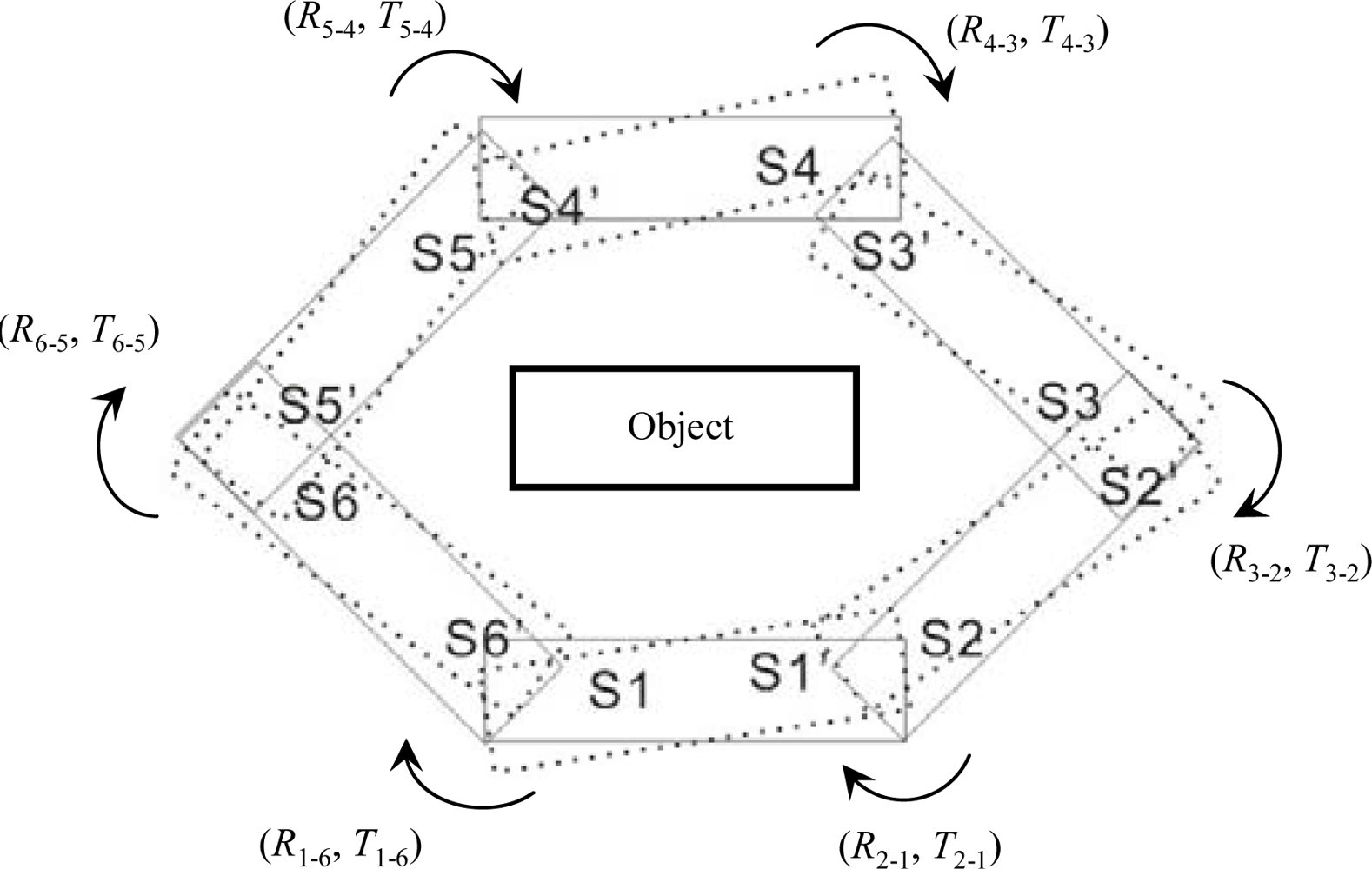
3. Global Registration
4. Results and Discussion
4.1. Pair-Wise Registration Results
4.2. Global Registration Results
5. Summary and Outlook
Acknowledgments
References and Notes
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell 1992, 14(2), 239–256. [Google Scholar]
- Godin, G.; Boulanger, P. Range image registration through viewpoint invariant computation of curvature. International Archives of Photogrammetry and Remote Sensing, Zurich, Switzerland, 1995; 30, pp. 170–175.
- Sharp, G.C.; Lee, S.W.; Wehe, D.K. ICP registration using invariant features. IEEE Trans. Pattern Anal. Mach. Intell 2002, 24(1), 90–102. [Google Scholar]
- Sequeira, V.; Ng, K.; Wolfart, E.; Goncalves, J.G.M.; Hogg, D. Automated reconstruction of 3D models from real environments. ISPRS J. Photogramm. Remote Sens 1999, 54(1), 1–22. [Google Scholar]
- Bae, K-H.; Lichti, D.D. Automated registration of unorganised point clouds from terrestrial laser scanners. International Archives of Photogrammetry and Remote Sensing, Istanbul, Turkey, 12–23 July, 2004; 35, pp. 222–227.
- Rabbani, T.; Dijkman, S.; van den Heuvel, F.; Vosselman, G. An integrated approach for modelling and global registration of point clouds. ISPRS J. Photogramm. Remote Sens 2007, 61(6), 355–370. [Google Scholar]
- Dold, C.; Brenner, C. Registration of terrestrial laser scanning data using planar patches and image data. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Dresden, Germany, 25–27 September, 2006; 36, pp. 78–83.
- Wendt, A. On the automation of the registration of point clouds using the metropolis algorithm. International Archives of Photogrammetry and Remote Sensing Istanbul, Turkey, 12–23 July, 2004; 35, pp. 106–111.
- Seo, J.K.; Sharp, G.C.; Lee, S.W. Range data registration using photometric features. Proceeding of International Conference on Computer Vision and Pattern Recognition 05, San Diego, CA, USA, 20–25 June, 2005; 2, pp. 1140–1145.
- Al-Manasir, K.; Fraser, C.S. Registration of terrestrial laser scanner data using imagery. Photogramm. Record 2006, 21(115), 255–268. [Google Scholar]
- Barnea, S.; Filin, S. Registration of terrestrial laser scans via image based features. International Archives of Photogrammetry and Remote Sensing Espoo, Finland, 12–14 September, 2007; 36, pp. 32–37.
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with application to image analysis and automated cartography. Comm. ACM 1981, 24(6), 381–395. [Google Scholar]
- Barnea, S.; Filin, S. Keypoint based autonomous registration of terrestrial laser point-clouds. ISPRS J. Photogramm. Remote Sens 2008, 63, 19–35. [Google Scholar]
- Kang, Z.; Zlatanova, S. Automatic registration of terrestrial scan data based on matching corresponding points from reflectivity images. Proceeding of 2007 Urban Remote Sensing Joint Event, Paris, France, 11–13 April, 2007; pp. 1–7.
- Kang, Z.; Zlatanova, S.; Gorte, B. Automatic registration of terrestrial scanning data based on registered imagery. Proceeding of 2007 FIG Working Wee, Hong Kong SAR, China, 13–17 May, 2007.
- Moravec, H.P. Towards Automatic Visual Obstacle Avoidance. Proceeding of 5th International Joint Conference on Artificial Intelligence, Cambridge, MA, August, 1977; p. 584.
- Chen, Y.; Medioni, G.G. Object modeling by registration of multiple range images. IVC 1992, 10(3), 145–155. [Google Scholar]
- Masuda, T.; Yokoya, N. A robust method for registration and segmentation of multiple range images. CVIU 1995, 61(3), 295–307. [Google Scholar]
- Pulli, K. Multiview registration for large data sets. Proceeding of Int’l Conf. 3D Digital Imaging and Modeling, Ottawa, Ont., Canada, 04–08 October, 1999; pp. 160–168.
- Bergevin, R.; Soucy, M.; Gagnon, H.; Laurendeau, D. Towards a general multi-view registration technique. IEEE Trans. Pattern Anal. Mach. Intell 1996, 18(5), 540–547. [Google Scholar]
- Benjemaa, R.; Schmitt, F. Fast global registration of 3D sampled surfaces using a multi- z-buffer technique. IVC 1999, 17(2), 113–123. [Google Scholar]
- Sharp, G.C.; Lee, S.W.; Wehe, D.K. Multiview registration of 3D scenes by minimizing error between coordinate frames. IEEE Trans. Pattern Anal. Mach. Intell 2004, 26(8), 1037–1049. [Google Scholar]
- Hu, S.; Zha, H.; Zhang, A. Registration of multiple laser scans based on 3D contour features. Proceeding 10th Int. Conf. on Information Visualisation, London, UK, July 5–7, 2006; pp. 725–730.
- Stoddart, A.J.; Hilton, A. Registration of multiple point sets. Proceeding of 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August, 1996; 2, pp. 40–44.
- Neugebauer, P.J. Reconstruction of real-world objects via simultaneous registration and robust combination of multiple range images. Int. J. Shap. Modell 1997, 3(1–2), 71–90. [Google Scholar]
- Eggert, D.W.; Fitzgibbon, A.W.; Fisher, R.B. Simultaneous registration of multiple range views for use in reverse engineering of CAD models. CVIU 1998, 69(3), 253–272. [Google Scholar]
- Williams, J.; Bennamoun, M. A multiple view 3D registration algorithm with statistical error modeling. IEICE Trans. Inf. Sys 2000, 83(8), 1662–1670. [Google Scholar]
- Kang, Z.; Zlatanova, S. A new point matching algorithm for panoramic reflectance images. Proc of the 5th International Symposium on Multispectral Image Processing and Pattern Recognition (MIPPR07), Wuhan, China, 15–17 November, 2007; p. 67882F-1-10.
- Forkuo, E.; King, B. Automatic fusion of photogrammetric imagery and laser scanner point clouds. International Archives of Photogrammetry and Remote Sensing, Istanbul, Turkey, 12–23 July, 2004; 35, pp. 921–926.
- Aguilera, D.G.; Gonzalvez, P.R.; Lahoz, J.G. Automatic co-registration of terrestrial laser scanner and digital camera for the generation of hybrids models. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Espoo, Finland, 12–14 September, 2007; 36, pp. 162–168.
- Li, M. High-precision relative orientation using feature-based matching techniques. ISPRS J. Photogramm. Remote Sens 1990, 44, 311–324. [Google Scholar]
- Mikolajczyk, K.; Schmid, C. Scale and affine invariant interest point detectors. IJCV 2004, 60(1), 63–86. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. IJCV 2004, 60(2), 91–110. [Google Scholar]
- Bleyer, M.; Gelautz, M. A layered stereo matching algorithm using image segmentation and global visibility constraints. ISPRS J. Photogramm. Remote Sens 2005, 59, 128–150. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Comm. of the ACM 1975, 18(9), 509–517. [Google Scholar]
- Boehler, W.; Vicent, M. Bogas; Marbs, A. Investigating laser scanner accuracy. Proceeding of CIPA XIXth International Symposium, Antalya, Turkey, 30 September–4 October, 2003; pp. 696–702.
- Lichti, D.D. Error modelling, calibration and analysis of an AM-CW terrestrial laser scanner system. ISPRS J. Photogramm. Remote Sens 2007, 61, 307–324. [Google Scholar]
- Mikhail, E.M.; Bethel, J.S.; McGlone, J.C. Introduction to Modern Photogrammetry; John Wiley: New York, 2001. [Google Scholar]
- Simon, D. Fast and Accurate Shape-Based Registration; Technical report CMU-RI-TR-96-45,; Robotics Institute, Carnegie Mellon University, 1996. [Google Scholar]
- Kretschmer, U.; Abmayr, T.; Thies, M.; Frohlich, C. Traffic construction analysis by use of terrestrial laser scanning. Proceeding of the ISPRS working group VIII/2: “Laser Scanners for Forrest and Landscape Assessment”, Freiburg, Germany, 3–6 October, 2004; 36, pp. 232–236.
- Haala, N.; Reulke, R.; Thies, M.; Aschoff, T. Combination of terrestrial laser scanning with high resolution panoramic images for investigations in forest applications and tree species recognition. International Archives of Photogrammetry and Remote Sensing, Dresden, Germany, 19–22 February, 2004.
- Amiri Parian, J.; Gruen, A. Integrated laser scanner and intensity image calibration and accuracy assessment. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Enschede, The Netherlands, 12–14 September, 2005; 36, pp. 18–23.
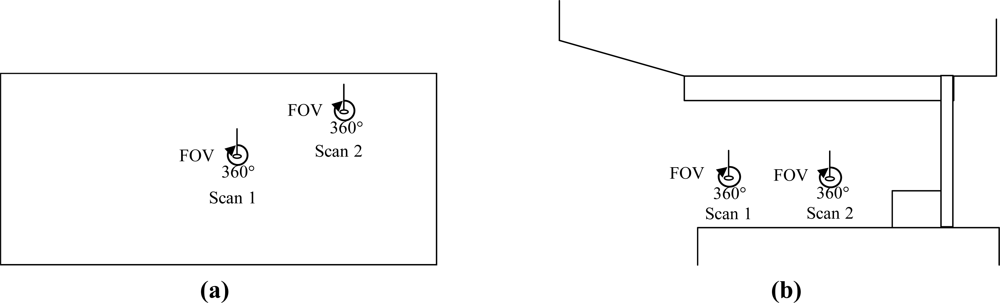
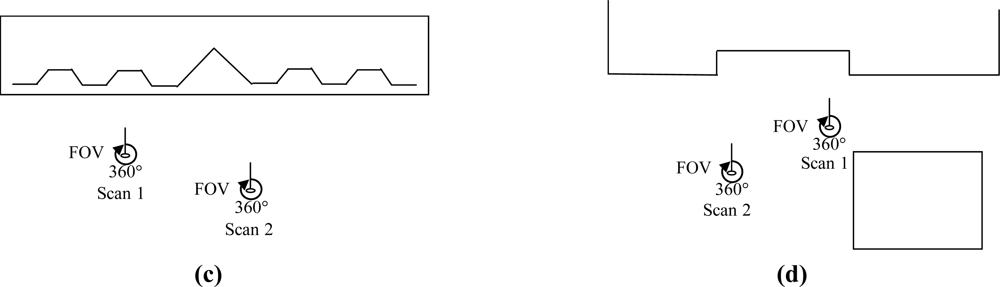









| Point cloud | Scan/Image Angular resolution | Angular accuracy | Range accuracy |
|---|---|---|---|
| Datasets 1 and 2 | 0.036° | ±0.009° | ±3 mm |
| Datasets 3 and 4 | 0.045° | ±0.009° | ±3 mm |
| Proposed method | n1 n2 | iter | rms (m) | max (m) | min (m) | avg (m) | Time (min) |
|---|---|---|---|---|---|---|---|
| Dataset 1 | 11987424 | 2 | 0.0037 | 0.0053 | 0.0009 | 0.0035 | 5.0 |
| 11974976 | |||||||
| Dataset 2 | 16726500 | 2 | 0.0044 | 0.0145 | 0.0018 | 0.0066 | 6.0 |
| 16713375 | |||||||
| Dataset 3 | 10006564 | 3 | 0.0038 | 0.0185 | 0.0025 | 0.0078 | 5.5 |
| 10046768 | |||||||
| Dataset 4 | 13266288 | 4 | 0.0039 | 0.0083 | 0.0010 | 0.0041 | 6.3 |
| 13259400 |
| Proposed method | iter | rms (m) | time (min) | Proposed method | iter | Rms (m) | time (min) |
|---|---|---|---|---|---|---|---|
| Scan 2-1 | 3 | 0.0058 | 5.4 | Scan 12-11 | 3 | 0.0073 | 5.3 |
| Scan 3-2 | 3 | 0.0067 | 5.5 | Scan 13-12 | 5 | 0.0098 | 6.6 |
| Scan 4-3 | 4 | 0.0079 | 5.9 | Scan 14-13 | 5 | 0.0085 | 6.7 |
| Scan 5-4 | 5 | 0.0074 | 6.7 | Scan 15-14 | 3 | 0.0023 | 5.3 |
| Scan 6-5 | 4 | 0.0036 | 6.1 | Scan 16-15 | 4 | 0.0075 | 6.1 |
| Scan 7-6 | 4 | 0.0082 | 6.0 | Scan 17-16 | 4 | 0.0056 | 6.1 |
| Scan 8-7 | 5 | 0.0098 | 6.6 | Scan 18-17 | 5 | 0.0069 | 6.8 |
| Scan 9-8 | 5 | 0.0095 | 6.7 | Scan 19-18 | 4 | 0.0039 | 6.0 |
| Scan 10-9 | 4 | 0.0037 | 6.2 | Scan 20-19 | 3 | 0.0015 | 5.4 |
| Scan 11-10 | 4 | 0.0051 | 6.0 | Scan 1–20 | 5 | 0.0079 | 6.7 |
| Model | iter | RMS (m) | Time (min) |
|---|---|---|---|
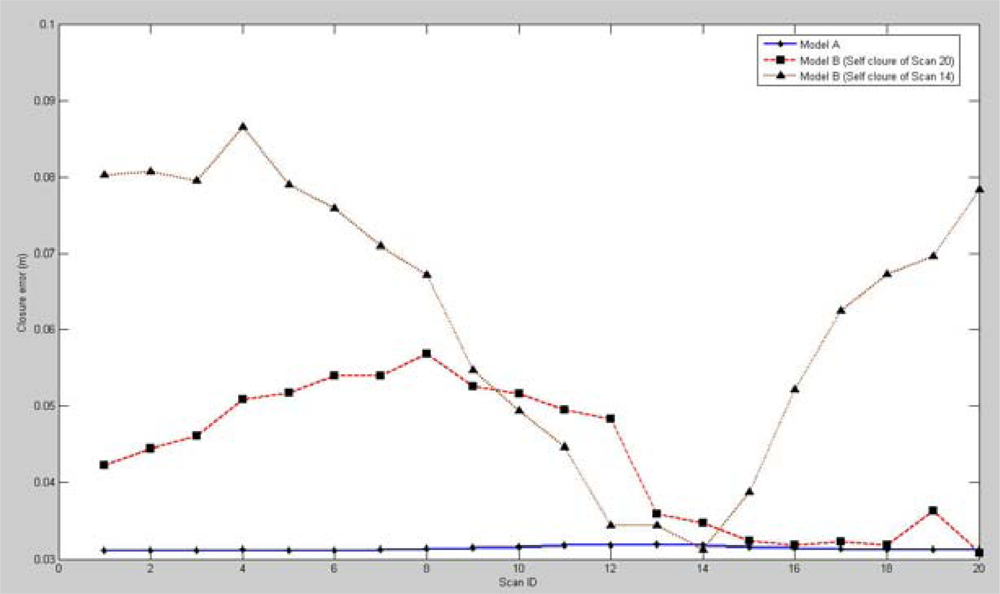
| A | 6 | 0.0340 | 1.98 |
| B (Scan 20) | 4 | 0.0351 | 0.62 |
| B (Scan 14) | 4 | 0.0352 | 0.62 |
| C | 4 | 0.0381 | 0.63 |
© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kang, Z.; Li, J.; Zhang, L.; Zhao, Q.; Zlatanova, S. Automatic Registration of Terrestrial Laser Scanning Point Clouds using Panoramic Reflectance Images. Sensors 2009, 9, 2621-2646. https://doi.org/10.3390/s90402621
Kang Z, Li J, Zhang L, Zhao Q, Zlatanova S. Automatic Registration of Terrestrial Laser Scanning Point Clouds using Panoramic Reflectance Images. Sensors. 2009; 9(4):2621-2646. https://doi.org/10.3390/s90402621
Chicago/Turabian StyleKang, Zhizhong, Jonathan Li, Liqiang Zhang, Qile Zhao, and Sisi Zlatanova. 2009. "Automatic Registration of Terrestrial Laser Scanning Point Clouds using Panoramic Reflectance Images" Sensors 9, no. 4: 2621-2646. https://doi.org/10.3390/s90402621
APA StyleKang, Z., Li, J., Zhang, L., Zhao, Q., & Zlatanova, S. (2009). Automatic Registration of Terrestrial Laser Scanning Point Clouds using Panoramic Reflectance Images. Sensors, 9(4), 2621-2646. https://doi.org/10.3390/s90402621







