Vibration and Fluorescence Spectra of Porphyrin- CoredBis(methylol)-propionic Acid Dendrimers
Abstract
:1. Introduction
2. Results and Discussion
2.1. General Appearance of Porphyrin Optical Absorption Spectra
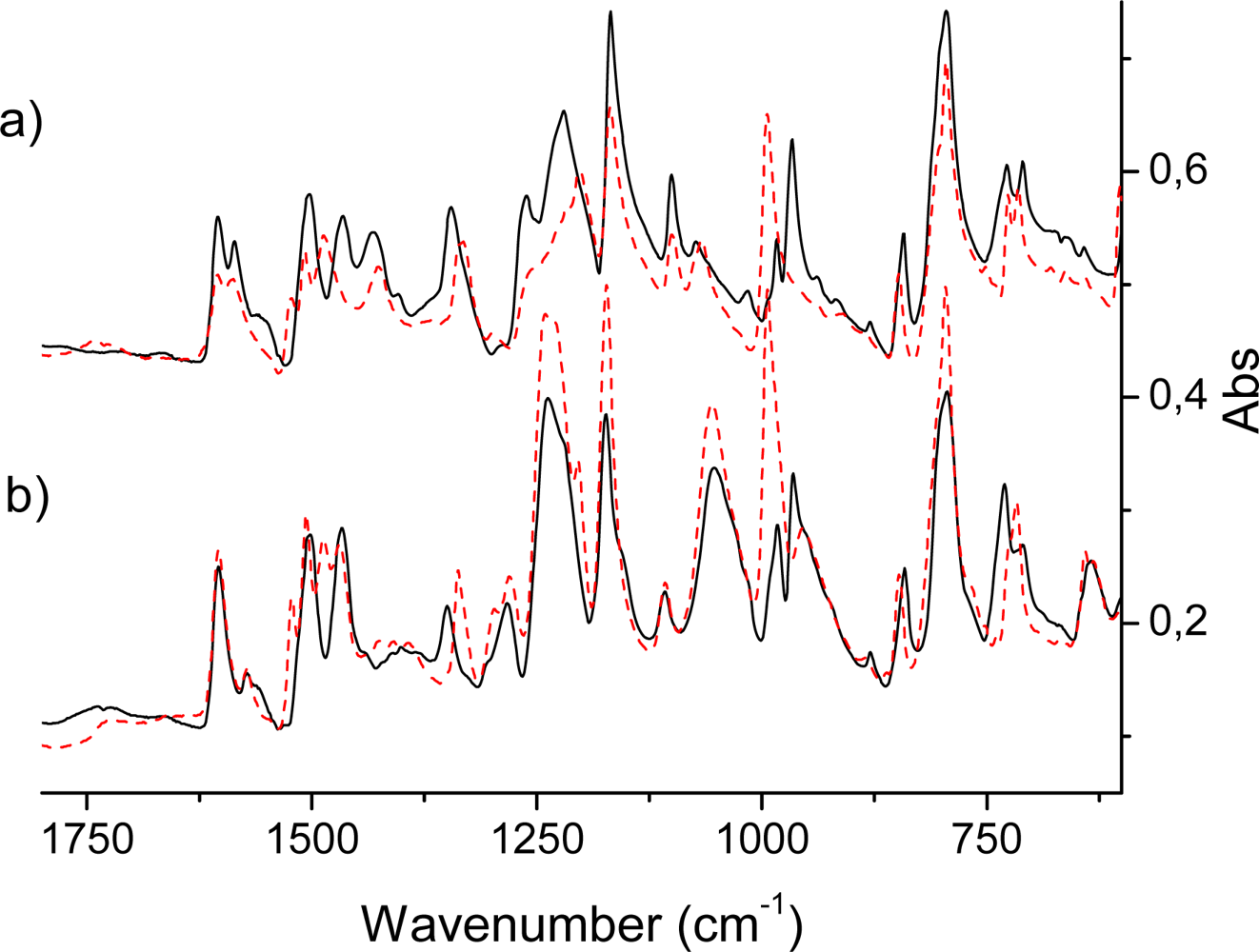
2.2. IR Spectra of TPPH2, TPPZn and Porphyrin Dendrimers
IR active intense out-of-plane porphyrin ring vibrations
IR active in-plane porphyrin ring vibrations
2.3. Raman Active Modes
In-plane vibrations active in Raman spectra
2.4. Interpretation of Optical Absorption Spectra
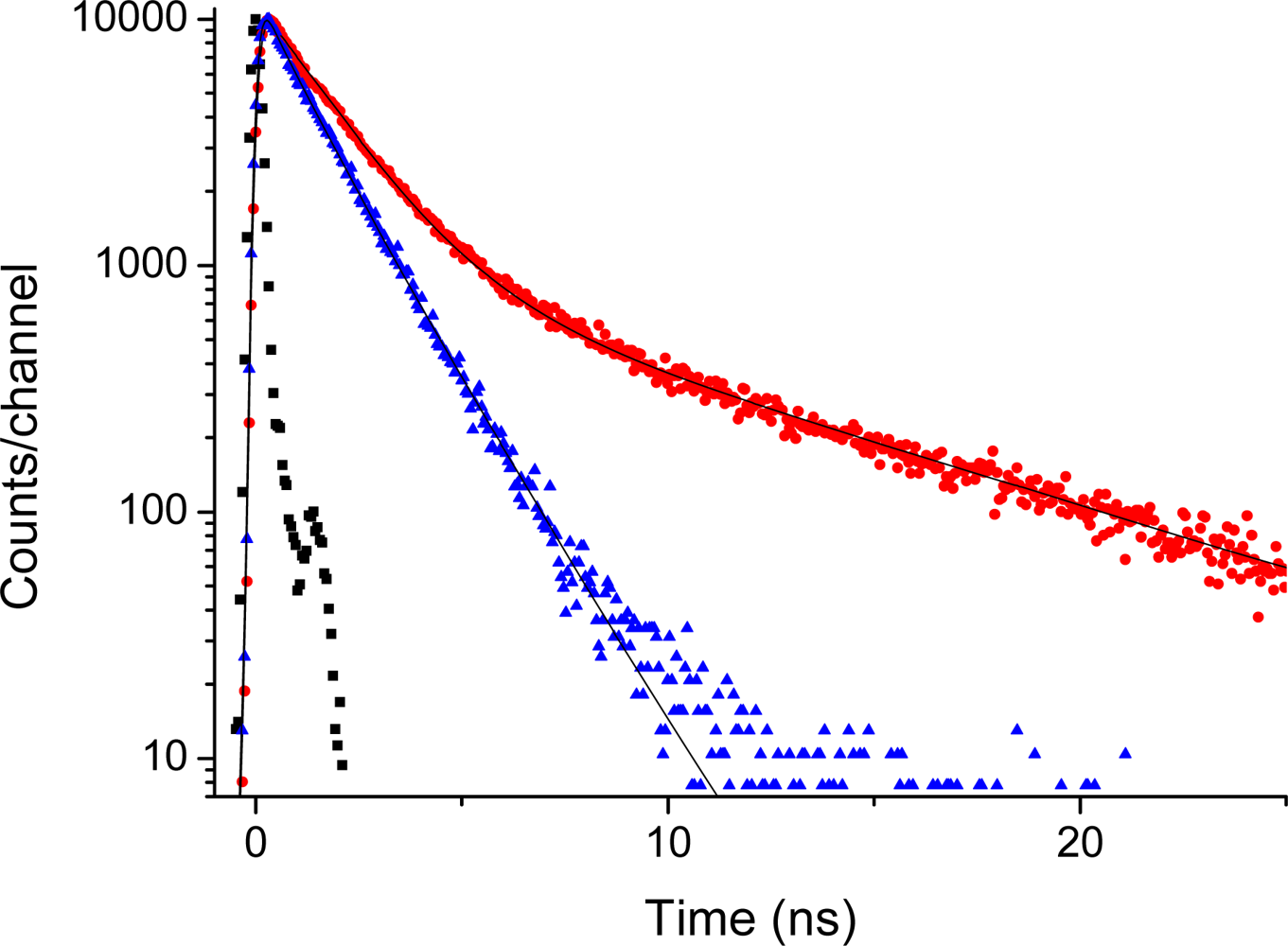
2.5. Fluorescence of Porphyrin bis-MPA Dendrimers
3. Methodology
3.1. Sample Preparation
3.2. Spectroscopy
3.3. Theory
4. Conclusions
Acknowledgments
References and Notes
- Hoff, A.J.; Deisenhofer, J. Structure and spectroscopy of reaction centers of purple bacteria. Phys. Rep 1997, 287, 1–21. [Google Scholar]
- Rogers, J.; Nguyen, K.; Hufnagle, D.C.; McLean, D.G.; Su, W.; Gossett, K.M.; Burke, A.R.; Vinogradov, S.A.; Pachter, R.; Fleitz, P.A. Observation and interpretation of annulated porphyrins: studies on the photophysical properties of meso-tetraphenylmetalloporphyrins. J. Phys. Chem. A 2003, 107, 11331–11339. [Google Scholar]
- Krasnovskii, A.A.; Bashtanov, M.E.; Drozdova, N.N.; Yuzhakova, O.A.; Luk’yanets, E.A. Laser induced singlet-oxygen-sensitised delayed fluorescence of dyes in aqueous solutions. Quantum Electron 2002, 32, 83–86. [Google Scholar]
- Henderson, B.W.; Dougherty, T.J. How does photodynamic therapy work? Photochem. Photobiol 1992, 55, 145–157. [Google Scholar]
- Felber, B.; Diederich, F. Synthesis of dendritic metalloporphyrins with distal H-bond donors as model systems for hemoglobin. Helv. Chim. Acta 2005, 88, 120–153. [Google Scholar]
- Oakes, R.E.; Bell, S.E.J. DFT studies of the resonance raman spectra of ground and excited triplet state free base meso-tetraphenylporphyrin (H2TPP). J. Phys. Chem. A 2003, 107, 10953–10959. [Google Scholar]
- Jarzecki, A.A.; Kozlowski, P.M.; Pulay, P.; Ye, B.-H.; Li, X.-Y. Scaled quantum mechanical and experimental vibrational spectra of magnesium and zinc porphyrins. Spectrochim. Acta 1997, 53, 1195–1209. [Google Scholar]
- Nakatsuji, H.; Hasegawa, J.; Hada, M. Excited and ionized states of free base porphin studied by the symmetry adapted cluster-configuration interaction (SAC-CI) method. J. Chem. Phys 1996, 104, 2321–2329. [Google Scholar]
- Ohkawa, K.; Hada, M.; Nakatsuji, H. Excited states of four hemes in a c-type cytochrome subunit of the photosynthetic reaction center of Rhodopseudomonas viridis: SAC-CI calculations. J. Porphyr. Phthalocya 2001, 5, 256–266. [Google Scholar]
- Sundholm, D. Interpretation of the electronic absorption spectrum of free-base porphin using time-dependent density-functional theory. Phys. Chem. Chem. Phys 2000, 2, 2275–2281. [Google Scholar]
- Nguyen, K.A.; Day, P.N.; Pachter, R. Triplet excited states of free-base porphin and its β-octahalogenated derivatives. J. Phys. Chem. A 2000, 104, 4748–4754. [Google Scholar]
- Nguyen, K.A.; Pachter, R. Jahn–Teller triplet excited state structures and spectra of zinc complexes of porphyrin and phthalocyanine: A density functional theory study. J. Chem. Phys 2003, 118, 5802–5810. [Google Scholar]
- Edwards, L.; Dolphin, D.H.; Gouterman, M.; Adler, A.D. Porphyrins XVII. Vapor absorption spectra and redox reactions: tetraphenylporphins and porphin. J. Mol. Spectroscopy 1971, 38, 16–32. [Google Scholar]
- Kharlamov, B.M.; Bykovskaya, L.A.; Personov, R.I. Hole-burning spectra. A new method for obtaining fine structure in absorption spectra of organic molecules. Chem. Phys. Lett 1977, 50, 407–411. [Google Scholar]
- Bykovskaya, L.A.; Gradushko, A.T.; Personov, R.I.; Romanovskii Yu, V.; Solovjov, K.N.; Staruchin, A.S.; Shulga, A.M. Method for determining of the polarization of vibronic transitions of polyatomic molecules in isotropic media upon selective laser excitation. Izv. Akad. Nauk SSSR 1980, 44, 822–826. (in Russian).. [Google Scholar]
- Minaev, B.; Ågren, H. Theoretical DFT study of phosphorescence from porphyrins. Chem. Phys 2005, 315, 215–239. [Google Scholar]
- Minaev, B.; Wang, Y.-H.; Wang, C.-K.; Luo, Y.; Ågren, H. Density functional theory study of vibronic structure of the first absorption Qx band in free-base porphin. Spectrochim. Acta. Part A 2006, 65, 308–323. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Zakrzewski, V.G.; Montgomery, J.A., Jr.; Stratmann, R.E.; Burant, J.C.; Dapprich, S.; Millam, J.M.; Daniels, A.D.; Kudin, K.N.; Strain, M.C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Cli®ord, S.; Ochterski, J.; Petersson, G.A.; Ayala, P.Y.; Cui, Q.; MoroKUMa, K.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Cioslowski, J.; Ortiz, J.V.; Stefanov, B.B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong, M.W.; Andres, J.L.; Gonzalez, C.; Head-Gordon, M.; Replogle, E.S.; Pople, J.A. Gaussian 98; 1998; Gaussian Inc: Pittsburgh PA, 1998; ( www.gaussian.com).
- Radziszewski, J.G.; Waluk, J.; Nepras, M.; Michl, J. Fourier transform fluorescence and phosphorescence of porphine in rare gas matrixes. J. Phys. Chem 1991, 95, 1963–1969. [Google Scholar]
- Li, X.Y.; Zgierski, M.Z. Porphine force field: in-plane normal modes of free-base porphine; comparison with metalloporphines and structural implications. J. Phys. Chem 1991, 95, 4268–4287. [Google Scholar]
- Kawa, M.; Fréchet, J.M.J. Self-assembled lanthanide-cored dendrimer complexes: enhancement of the luminescence properties of lanthanide ions through site-isolation and antenna effects. Chem. Mater 1998, 10, 286–296. [Google Scholar]
- Dichtel, W.R.; Hecht, S.; Fréchet, J.M.J. Functionally layered dendrimers: a new building block and its application to the synthesis of multichromophoric light-harvesting systems. Org. Lett 2005, 7, 4451–4454. [Google Scholar]
- Lindgren, M.; Minaev, B.; Glimsdal, E.; Vestberg, R.; Westlund, R.; Malmström, E. Electronic states and phosphorescence of dendron functionalized platinum(II) acetylides. J. Luminesc 2007, 124, 302–310. [Google Scholar]
- Pitois, C.; Hult, A.; Lindgren, M. Lanthanide-cored fluorinated dendrimer complexes: synthesis and luminescence characterization. J. Luminesc 2005, 111, 265–283. [Google Scholar]
- Westlund, R.; Malmstrom, E.; Lopes, C.; Ohgren, J.; Rodgers, T.; Saito, Y.; Kawata, S.; Glimsdal, E.; Lindgren, M. Efficient nonlinear absorbing platinum(II) acetylide chromophores in solid PMMA matrices. Adv. Funct. Mater 2008, 18, 1939–1948. [Google Scholar]
- Vestberg, R.; Westlund, R.; Eriksson, A.; Lopes, C.; Carlsson, M.; Eliasson, B.; Glimsdal, E.; Lindgren, M.; Malmstrøm, E. Dendron decorated platinum(II) acetylides for optical power limiting. Macromolecules 2006, 39, 2238–2246. [Google Scholar]
- Westlund, R.; Glimsdal, E.; Lindgren, M.; Vestberg, R.; Hawker, C.; Lopes, C.; Malmström, E. Click chemistry for photonic applications: triazole-functionalized platinum(II) acetylides for optical power limiting. J. Mater. Chem 2008, 18, 166–175. [Google Scholar]
- Gunnlaugsson, T.; Leonard, J.P. Responsive lanthanide luminescent cyclen complexes: from switching/sensing to supramolecular architectures. Chem. Commun 2005, 25, 3114–3131. [Google Scholar]
- Vestberg, R.; Nystrom, A.; Lindgren, M.; Malmstrom, E.; Hult, A. Porphyrin-cored 2,2-bis(methylol)propionic acid dendrimers. Chem. Mater 2004, 16, 794–2804. [Google Scholar]
- Gillies, E.R.; Fréchet, J.M.J. Designing Macromolecules for Therapeutic Applications: Polyester Dendrimer — Poly(ethylene oxide) “Bow-Tie” Hybrids with Tunable Molecular Weight and Architecture. J. Am. Chem. Soc 2002, 124, 14137–14146. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- Alben, J.O.; Choi, S.S.; Adler, A.D.; Caughey, WS. Infrared spectroscopy of porphyrins. Ann. N. Y. Acad. Sci 1973, 206, 278–295. [Google Scholar]
- Kincaid, J.R.; Nakamoto, K. Vibrational spectra of transition metal complexes of tetraphenylporphine. J. Inorg. Nucl. Chem 1975, 37, 85–89. [Google Scholar]
- Kozuka, M.; Nakamoto, K. Vibrational studies of (tetraphenylporphyrinato)cobalt(II) and its adducts with carbon monoxide, nitric oxide, and oxygen in gas matrixes. J. Am. Chem. Soc 1981, 103, 2162–2168. [Google Scholar]
- Li, X.Y.; Czernuszewicz, R.S.; Kincaid, J.R.; Su, Y.O; Spiro, T.G. Consistent porphyrin force field. 1. Normal-mode analysis for nickel porphine and nickel tetraphenylporphine from resonance Raman and infrared spectra and isotope shifts. J. Phys. Chem 1990, 94, 31–47. [Google Scholar]
- Guo, H.; Jiang, J.; Shi, Y.; Wang, Y.; Liu, J.; Dong, S. UV-vis spectrophotometric titrations and vibrational spectroscopic characterization of meso-(p-hydroxy-phenyl)porphyrins. J. Phys. Chem. B 2004, 108, 10185–10191. [Google Scholar]
- Andersson, L.A.; Loehr, T.M.; Thompson, R.G.; Strauss, S.H. Influence of symmetry on the vibrational spectra of Zn(TPP), Zn(TPC), and Zn(TPiBC). Inorg. Chem 1990, 29, 2142–2147. [Google Scholar]
- Kozlowski, P.M.; Jarzecki, A.A.; Pulay, P.; Li, X.Y.; Zgierski, M.Z. Vibrational assignment and definite harmonic force field for porphine. 2. Comparison with nonresonance Raman data. J. Phys. Chem 1996, 100, 13985–13992. [Google Scholar]
- Tazi, M.; Lagant, P.; Vergoten, G. Use of the Resonance Raman Intensities To Check the Density Functional Theory Derived Force Field of the Free Base Porphine. J. Phys. Chem. A 2000, 104, 618–625. [Google Scholar]
- Oakes, R.E.; Spence, S.J.; Bell, S.E.J. Resonance Raman and DFT studies of tetra-tert-butyl porphine: assignment of strongly enhanced distortion modes in a ruffled porphyrin. J. Phys. Chem. A 2003, 107, 2964–2973. [Google Scholar]
- Gouterman, M. Spectra of porphyrins. J. Mol. Spectroscopy 1961, 6, 138–163. [Google Scholar]
- Almlöf, J. Ab Initio calculation on porphin. Int. J. Quant. Chem 1974, 8, 915–924. [Google Scholar]
- Nakatsuji, H.; Takashima, H.; Hada, M. Spin-orbit effect on the magnetic shielding constant using the ab initio UHF method. Chem. Phys. Lett 1995, 233, 95–101. [Google Scholar]
- Serrano-Andrés, L.; Merchán, M.; Rubio, M.; Roos, B.O. Interpretation of the electronic absorption spectrum of free base porphin by using multiconfigurational second-order perturbation theory. Chem. Phys. Lett 1998, 295, 195–203. [Google Scholar]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett 1996, 256, 454–464. [Google Scholar]
- Minaev, M. Theoretical study of the external heavy atom effect on phosphorescence of free-base porphin molecule. Spectrochim. Acta. Part A 2004, 60, 3213–3224. [Google Scholar]
- Loboda, O.; Tunnell, I.; Minaev, B.; Ågren, H. Theoretical study of triplet state properties of free-base porphin. Chem. Phys 2005, 312, 299–309. [Google Scholar]
- Liao, M.S.; Scheiner, S. Electronic structure and bonding in metal porphyrins, metal=Fe, Co, Ni, Cu, Zn. J. Chem. Phys 2002, 117, 205–219. [Google Scholar]
- Kruk, M.; Karotki, A.; Drobizhev, M.; Kuzmitsky, V.; Gael, V.; Rebane, A. Two-photon absorption of tetraphenylporphin free base. J. Luminesc 2003, 105, 45–55. [Google Scholar]
- Gouterman, M. Optical spectra and electronic structure of porphyrins and related rings. In The Porphyrins, 2nd Ed; Dolphin, D., Ed.; Academic Press: New York, 1978; Volume 3. [Google Scholar]
- Albrecht, A. Vibronic-spin-orbit perturbations and the assignment of the lowest triplet state of benzene. J. Chem. Phys 1963, 38, 354–365. [Google Scholar]
- Köppel, H.; Domcke, W.; Cederbaum, L.S. Multi-mode molecular dynamics beyond the Born-Oppenheimer approximation. Adv. Chem. Phys 1984, 57, 59–246. [Google Scholar]
- Stanton, J.F.; Sattelmeyer, K.W.; Gauss, J.; Allan, M.; Skalicky, T.; Bally, T. On the photoelectron spectrum of p-benzoquinone. J. Chem. Phys 2001, 115, 1–4. [Google Scholar]
- Gladkov, L.L.; Gradyushko, A.T.; Shulga, A.M.; Solovyov, K.N-; Starukhin, A.S. Experimental and theoretical investigation of infrared spectra of porphin, its deuterated derivatives and their metal complexes. J. Mol. Struct 1978, 47, 463–493. [Google Scholar]
- Kozlowski, P.M.; Jarzecki, A.A.; Pulay, P. Vibrational assignment and definite harmonic force field for porphine. 1. Scaled quantum mechanical results and comparison with empirical force field. J. Phys. Chem 1996, 100, 7007–7013. [Google Scholar]
- Gladkov, L.L.; Solovyov, K.N. The normal coordinate analysis of porphin and its derivatives based on the solution of the inverse spectral problem for porphin and Cu porphin - I. A valence force field for in-plane vibrations of the porphin molecule. Spectrochim. Acta Part A 1985, 41, 1437–1442. [Google Scholar]
- Kitagawa, T.; Ozaki, Y. Infrared and Raman spectra of metalloporphyrins. Struct. Bond 1987, 64, 71–114. [Google Scholar]
- Kim, D.; Terner, J.; Spiro, T.G. Excited triplet state resonance Raman spectra of magnesium, zinc, and palladium tetraphenylporphine. J. Am. Chem. Soc 1986, 108, 2097–2099. [Google Scholar]
- Matos, M.; Hofkens, J.; Verheijen, W.; De Schryver, F.C.; Hecht, S.; Pollak, K.W.; Fréchet, J.M.J.; Forier, B.; Dehaen, W. Effects of generation number and solvent on photophysical and hydrodynamic properties of dendrimers with porphyrin and metalloporphyrin as core. Macromolecules 2000, 33, 2967–2973. [Google Scholar]
- Minaev, B.F.; Minaev, A.B. Calculation of the phosphorescence of porphyrins by the density functional method. Opt. Spectrosc 2005, 98, 214–219. [Google Scholar]
- Weinkauf, J.R.; Cooper, S.W.; Schweiger, A.; Wamser, C.C. Substituent and solvent effects on the hyperporphyrin spectra of diprotonated tetraphenylporphyrins. J. Phys. Chem. A 2003, 107, 3486–3496. [Google Scholar]
- Retsek, J.L.; Medforth, C.J.; Nurco, D.J.; Gentemann, S.; Chirvony, V.S.; Smith, K.M.; Holten, D. Conformational and electronic effects of phenyl-ring fluorination on the photophysical properties of nonplanar dodecaarylporphyrins. J. Phys. Chem. B 2001, 105, 6396–6411. [Google Scholar]
- Wasbotten, I.H.; Conradie, J.; Ghosh, A. Electronic absorption and resonance Raman signatures of hyperporphyrins and nonplanar porphyrins. J. Phys. Chem. B 2003, 107, 3613–3623. [Google Scholar]
- Bour, P.; Záruba, K.; Urbanová, M.; Setnicka, V.; Matejka, P.; Fiedler, Z.; Král, V.; Volka, K. Vibrational circular dichroism of tetraphenylporphyrin in peptide complexes? A computational study. Chirality 2000, 12, 191–198. [Google Scholar]
- Tobita, S.; Kaizu, Y.; Kobayashi, H.; Tanaka, I. Study of higher excited singlet states of zinc(II)-tetraphenylporphin. J. Chem. Phys 1984, 81, 2962–2969. [Google Scholar]






| H2P | TPPH2 | ZnP | TPPZn | ||||||
|---|---|---|---|---|---|---|---|---|---|
| D2h | 6-31G** | Exp.a | 6-31G** | Exp.a | D4h | 6-31G** | Exp.a | 6-31G** | Exp.a |
| 13B2u | 1.46 | 1.56 | 1.39 | 1.50 | 13Eu | 1.74 | 1.82 | 1.70 | 1.61 |
| 13B3u | 1.81 | 1.87 | 1.69 | 1.70 | 13Eu | 1.74 | 1.82 | 1.70 | 1.61 |
| 11B3u | 2.27(10−4) | 1.98(0.01) | 2.15(0.03) | 1.87(0.08) | 11Eu | 2.45(10−3) | 2.18(0.04) | 2.31(0.03) | 2.09(0.04) |
| 11B2u | 2.44(10−3) | 2.42(0.06) | 2.15(0.03) | 1.87(0.08) | 11Eu | 2.45(10−3) | 2.18(0.04) | 2.31(0.03) | 2.09(0.04) |
| 11B2g | 3.76(0.00) | - | 3.74(0.00) | - | 11Eg | 3.33(0.00) | - | 3.29(0.01) | - |
| 11B3g | 3.86(0.00) | - | 3.85(0.00) | - | 11Eg | 3.33(0.00) | - | 3.29(0.01) | - |
| 21B3u | 3.33(0.41) | 3.33(0.56) | 3.16(0.85) | 3.08(0.70) | 21Eu | 3.49(0.90) | 3.22(0.70) | 3.24(0.67) | 3.05(0.70) |
| 21B2u | 3.41(0.60) | 3.33(0.56) | 3.21(0.85) | 3.08(0.70) | 21Eu | 3.49(0.90) | 3.22(0.70) | 3.26(0.81) | 3.05(0.70) |
| 11B1g | 3.39(0.00) | - | 3.38(0.00) | - | 11A2g | 3.41(0.00) | - | 3.43(0.00) | - |
| 11B1g | 3.50(0.00) | - | 3.51(0.00) | - | 11B2g | 3.64(0.00) | - | 3.55(0.00) | - |
| 31B2u | 3.56(0.45) | 3.50(0.05) | 3.82(0.10) | 3.80(0.06) | 31Eu | 3.80(0.04) | 3.82(0.05) | 3.45(0.08) | 3.57 |
| 31B3u | 3.61(0.86) | 3.50(0.05) | 3.82(0.10) | 3.80(0.06) | 31Eu | 3.80(0.04) | 3.82(0.05) | 3.47(0.09) | 3.57 |
| 11B1u | 3.85(10−3) | 3.65(<0.1) | 3.82(0.01) | - | 11A2u | 3.65(0.01) | - | 3.60(0.02) | - |
| 41B3u | 3.89(0.57) | - | 4.12(0.24) | 4.96(0.1) | 41Eu | 4.26(0.09) | - | 4.02(0.06) | - |
| 41B2u | 3.92(0.48) | - | 5.37(0.09) | 5.97(0.1) | 41Eu | 4.26(0.09) | - | 4.05(0.07) | - |
| 21B1u | 5.89(0.003) | - | 5.82(0.01) | 5.97(0.1) | 21A2u | 5.01(0.08) | - | 4.92(0.09) | - |
| In-plane | Out-of-plane | ||
|---|---|---|---|
| ZnP | H2P | ZnP | H2P |
| eu | b2u | eg | b2g |
| eu | b3u | eg | b3g |
| a1g | ag | a1u | au |
| b1g | ag | b1u | au |
| a2g | b1g | a2u | b1u |
| b2g | b1g | b2u | b1u |
| 6-31G** (this work) | Scaled 6-31G* Ref [38] | Exp. Refs [54, 67] | ||||
|---|---|---|---|---|---|---|
| i | Sym | νi | Int. | νi | Int. | νi |
| 41 | b1u | 795.8 | 60.54 | 776.1 | 53.2 | 773 |
| 43 | b1u | 808.1 | 120.13 | 786.0 | 140.1 | 785 |
| 48 | b1u | 872.0 | 143.75 | 853.3 | 145.4 | 852 |
| 53 | b2u | 973.3 | 82.79 | 945.2 | 89.30 | 951 |
| 55 | b3u | 994.3 | 54.61 | 968.0 | 56.4 | 971 |
| 57 | b2u | 1011.7 | 10.41 | 981.5 | 5.7 | 977 |
| 59 | b3u | 1023.4 | 0.08 | 996.3 | 0.4 | 994 |
| 61 | b3u | 1079.4 | 43.58 | 1048.6 | 43.0 | 1043 |
| 62 | b2u | 1083.8 | 35.90 | 1053.0 | 35.7 | 1054 |
| 66 | b3u | 1172.9 | 20.62 | 1137.8 | 20.5 | 1134 |
| 67 | b2u | 1188.6 | 0.02 | 1155.8 | 0 | 1165 |
| 70 | b3u | 1231.7 | 2.82 | 1206.4 | 3.4 | 1177 |
| 72 | b2u | 1269.2 | 57.07 | 1225.4 | 57.8 | 1228 |
| 73 | b2u | 1282.9 | 0.78 | 1251.7 | 0.3 | 1255 |
| 74 | b3u | 1321.9 | 1.64 | 1286.3 | 1.8 | 1287 |
| 78 | b2u | 1393.7 | 4.41 | 1354.8 | 4.5 | 1357 |
| 81 | b3u | 1444.7 | 28.9 | 1407.6 | 26.0 | 1396 |
| 82 | b3u | 1448.7 | 4.00 | 1400.0 | 6.4 | 1412 |
| 83 | b2u | 1451.8 | 10.81 | 1409.3 | 10.3 | 1406 |
| 89 | b3u | 1570.4 | 7.03 | 1522.3 | 5.0 | 1522 |
| 90 | b2u | 1591.8 | 24.76 | 1546.8 | 22.6 | 1540 |
| 93 | b2u | 1644.8 | 17.23 | 1594.6 | 16.4 | - |
| 6-31G* Ref [7] | 6-31G** This work | Exp. Ref [7] | ||||
|---|---|---|---|---|---|---|
| i | D4h | νi | Int. | νi | Int. | νi |
| 37,36 | eu | 742 | 25.0 | 755 | 24.0 | 739 |
| 43,42 | eu | 799 | 3.3 | 808 | 5.0 | 799 |
| 54,55 | eu | 990 | 94.8 | 1016 | 95.0 | 993 |
| 59,60 | eu | 1020 | 0.9 | 1044 | 0.1 | 1019 |
| 62,63 | eu | 1055 | 56.8 | 1086 | 56.2 | 1052 |
| 67,68 | eu | 1153 | 1.0 | 1186 | 8.1 | 1151 |
| 71,72 | eu | 1252 | 0.1 | 1280 | 0.2 | - |
| 73,74 | eu | 1304 | 10.7 | 1342 | 15.3 | 1299 |
| 80,81 | eu | 1397 | 10.9 | 1427 | 6.3 | 1384 |
| 84,83 | eu | 1436 | 2.2 | 1482 | 3.0 | 1438 |
| 87,88 | eu | 1529 | 8.7 | 1572 | 9.2 | 1517 |
| 90,89 | eu | 1551 | 9.7 | 1603 | 7.5 | 1558 |
| 11 | a2u | 209 | 34.6 | 148 | 29.3 | - |
| 15 | a2u | 344 | 13.0 | 343 | 7.0 | - |
| 34 | a2u | 712 | 12.8 | 714 | 8.8 | 699 |
| 38 | a2u | 766 | 63.2 | 779 | 69 | 765 |
| 49 | a2u | 49 | 145 | 879 | 122 | 849 |
| 6-31G** This work | 6-31G* Ref [38] | Exp. Ref [19] | Exp. Ref [38, 54] | ||||
|---|---|---|---|---|---|---|---|
| i | D2h | νi | R | νi | R | νi | νi |
| 4 | b1g | 98.9 | 17.2 | 86.9 | 16.9 | - | 109 |
| 7 | ag | 156.6 | 27.9 | 152.9 | 27.4 | - | 155 |
| 13 | ag | 310.4 | 74.8 | 303.8 | 77.0 | - | 309 |
| 18 | b1g | 395.9 | 0.10 | 388.4 | 0.2 | - | 389 |
| 19 | b2g | 420.1 | 1.29 | 410.2 | 1.0 | - | 418 |
| 30 | b2g | 712.9 | 9.89 | 700.3 | 9.9 | - | - |
| 31 | b3g | 714.6 | 11.3 | 700.3 | 11.5 | - | - |
| 32 | ag | 734.0 | 19.0 | 720.6 | 25.5 | 723 | 723 |
| 33 | ag | 738.5 | 12.5 | 727.8 | 9.4 | - | 736 |
| 54 | ag | 976.8 | 88.3 | 950.8 | 66.5 | 953 | 952 |
| 56 | b1g | 999.0 | 5.06 | 966.5 | 4.4 | 972 | 976 |
| 58 | ag | 1013.1 | 43.6 | 984.7 | 51.4 | 987 | 988 |
| 60 | b1g | 1028.5 | 8.59 | 1002.1 | 7.1 | 1005 | 1005 |
| 63 | ag | 1086.9 | 0.71 | 1055.8 | 0.6 | 1063 | 1063 |
| 64 | ag | 1093.7 | 6.13 | 1061.9 | 6.2 | - | 1064 |
| 65 | b1g | 1169.6 | 0.14 | 1133.2 | 0.1 | - | 1138 |
| 68 | ag | 1210.1 | 37.6 | 1179.3 | 36.2 | 1177 | 1177 |
| 69 | b1g | 1222.8 | 1.62 | 1186.3 | 1.6 | - | 1182 |
| 71 | b1g | 1261.9 | 2.46 | 1219.5 | 1.9 | 1221 | 1226 |
| 75 | b1g | 1357.3 | 55.7 | 1320.5 | 52.3 | 1316 | 1313 |
| 76 | ag | 1392.1 | 42.2 | 1358.1 | 45.5 | 1360 | 1353 |
| 77 | b1g | 1393.3 | 13.44 | 1354.7 | 17.4 | 1352 | 1374 |
| 79 | b1g | 1422.4 | 28.0 | 1381.1 | 31.3 | 1388 | 1388 |
| 80 | ag | 1442.2 | 224 | 1402.0 | 224 | - | 1384 |
| 84 | ag | 1477.7 | 110 | 1430.4 | 105 | - | 1425 |
| 86 | b1g | 1538.6 | 13.6 | 1491.2 | 15.3 | 1497 | 1493 |
| 87 | ag | 1551.1 | 297 | 1504.2 | 279 | 1502 | 1492 |
| 91 | ag | 1604.3 | 292 | 1558.7 | 280 | 1575 | 1544 |
| 92 | b1g | 1640.7 | 0.26 | 1590.3 | 0.40 | 1578 | 1600 |
| 94 | ag | 1654.8 | 203 | 1605.9 | 213 | 1614 | 1609 |
| 6-31G** This work | 6-31G* Ref [7] | Exp. Ref [7] | ||||
|---|---|---|---|---|---|---|
| i | D4h | νi | R | νi | R | νi |
| 7 | b1g | 177.6 | 23.2 | 177.2 | 23.7 | - |
| 9,10 | eg | 208.5 | 7.50 | 204.2 | 7.50 | 208.5 |
| 11 | b2g | 224.4 | 19.4 | 221.9 | 19.0 | - |
| 18 | a1g | 372.3 | 91.4 | 363.0 | 91.4 | 363 |
| 33,32 | eg | 715.4 | 10.8 | 707.6 | 11.5 | - |
| 34 | b2g | 738.6 | 6.25 | 726.5 | 24.5 | 728 |
| 56 | a1g | 1021.7 | 110.5 | 1001.4 | 102.4 | 995 |
| 65 | a1g | 1093.8 | 1.51 | 1063.4 | 38.3 | 1066 |
| 69 | ag | 1208.5 | 48.5 | 1182.4 | 39.1 | - |
| 70 | b2g | 1216.8 | 1.00 | 1181.6 | 0.4 | - |
| 75 | a2g | 1362.4 | 0.00 | 1329.5 | 0.00 | 1322 |
| 76 | a2g | 1388.7 | 0.00 | 1350.6 | 0.00 | 1353 |
| 77 | b2g | 1392.8 | 87.1 | 1357.2 | 86.2 | 1347 |
| 78 | a1g | 1399.9 | 39.3 | 1371.8 | 68.1 | 1357 |
| 79 | b1g | 1419.8 | 215 | 1387.3 | 202 | 1385 |
| 84 | a1g | 1485.1 | 111 | 1437.3 | 124 | 1432 |
| 86 | b1g | 1551.1 | 400 | 1503.6 | 378 | 1494 |
| 91 | a1g | 1603.2 | 289 | 1557.6 | 261 | 1544 |
| 93 | b1g | 1663.7 | 209 | 1612.6 | 229 | 1607 |
© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Minaev, B.; Lindgren, M. Vibration and Fluorescence Spectra of Porphyrin- CoredBis(methylol)-propionic Acid Dendrimers. Sensors 2009, 9, 1937-1966. https://doi.org/10.3390/s90301937
Minaev B, Lindgren M. Vibration and Fluorescence Spectra of Porphyrin- CoredBis(methylol)-propionic Acid Dendrimers. Sensors. 2009; 9(3):1937-1966. https://doi.org/10.3390/s90301937
Chicago/Turabian StyleMinaev, Boris, and Mikael Lindgren. 2009. "Vibration and Fluorescence Spectra of Porphyrin- CoredBis(methylol)-propionic Acid Dendrimers" Sensors 9, no. 3: 1937-1966. https://doi.org/10.3390/s90301937
APA StyleMinaev, B., & Lindgren, M. (2009). Vibration and Fluorescence Spectra of Porphyrin- CoredBis(methylol)-propionic Acid Dendrimers. Sensors, 9(3), 1937-1966. https://doi.org/10.3390/s90301937





