1. Introduction
In the last three decades, the idea of extracting the 3D information of a scene from its 2D images has been widely investigated. Several contact and non-contact measurement techniques have been employed in many science and engineering applications to compute the 3-D surface of an object. Basically, the aim is to extract the useful depth information from an image in an efficient and automatic way. Then, the obtained information can be used to guide various processes such as robotic manipulation, automatic inspection, reverse engineering, 3D depth map for navigation and virtual reality applications [
1]. Among all the diverse methodologies, one of the most widely used is the fringe projection. Fringe processing methods are widely used in non-destructive testing, optical metrology and 3D reconstruction systems. Some of the desired characteristics in these methods are high accuracy, noise-immunity and fast processing speed.
Scarcely used fringe processing methods are the well-known Fourier Transform Profilometry (FTP) method [
2] and Phase-shifting Interferometry [
3]. It is also well-established that one of the main challenges for these methods is the wrapped phase information problem. The first algorithm for this purpose was proposed by Takeda and Mutoh in 1982 [
2]. Later Berryman [
4] and Pedraza [
5-
7] proposed a modified Fourier Transform Profilometry by carrying out global and local analyses in the phase unwrapping. Then, unwrapping algorithms (temporal and spatial) were introduced and modified [
8-
10]. Another solution is to extract the information by the use of a wavelet transform.
Due to the fact that the wavelet transform offers multiresolution in time and space frequency, it is a tool that offers advantages over the Fourier transform [
11,
12]. The computation in the method can be carried out by analyzing the projected fringe patterns using a wavelet transform. Mainly, this analysis consists of demodulating the deformed fringe patterns and extracting the phase information encoded into it and hence the height profile of the object can be calculated, quite similar to Fourier transform.
Different wavelet algorithms are used in the demodulation process to extract the phase of the deformed fringe patterns. They can be classified into two categories: phase estimation and frequency estimation techniques.
The phase estimation algorithm employs complex mother wavelets to estimate the phase of a fringe pattern. The extracted phase suffers from 2π discontinuities and a phase unwrapping algorithm is required to remove these 2π jumps. Zhong
et al. [
11] have applied Gabor wavelets to extract the phase distribution where a phase unwrapping algorithm is required.
The frequency estimation technique estimates the instantaneous frequencies in a fringe pattern, which are then integrated to estimate the phase. The phase extracted using this technique is continuous; consequently, phase unwrapping algorithms are not required. Complex or real mother wavelets can be used to estimate the instantaneous frequencies in the fringe pattern. Dursun
et al. [
13] and Afifi
et al. [
14] have used Morlet and Paul wavelets, respectively, to obtain the phase distribution of projected fringes without using any unwrapping algorithms. Also, Gdeisat
et al. [
15] have proposed a 1D continuous wavelet transform approach to retrieve phase information in temporally and spatially fringe patterns, moreover, several algorithms were used for ridge extraction in the phase of the fringe patters.
Most of the previous research is focused on using the Fourier and wavelet transforms separately to obtain the 3D information from an object; pre-filtering the images, extracting the phase information of fringe patterns, using phase unwrapping algorithms, and so on.
In the present research, a simple profilometrical approach to obtain the 3D information from an object is presented. Here, the spatial frequency of the projected fringe pattern is obtained. The mathematical description to obtain the spatial frequency is a contribution in this research. Then, a modified Fourier transform method of an extended 1D wavelet based profilometry is applied. Later, a robust phase unwrapping algorithm is developed and used to obtain the desired 3D information. The main contribution of this work is the methodology. In addition, this novel approach is compared with other similar research and the results are presented. In order to validate the methodology, some virtual objects were created for use in computer simulations and experiments.
2. Theoretical Background
As described in the previous section, there are several fringe projection techniques which are used to extract the three-dimensional information from the objects. In this section, a Modified Fourier Transform is explained and the Wavelet Profilometry is introduced.
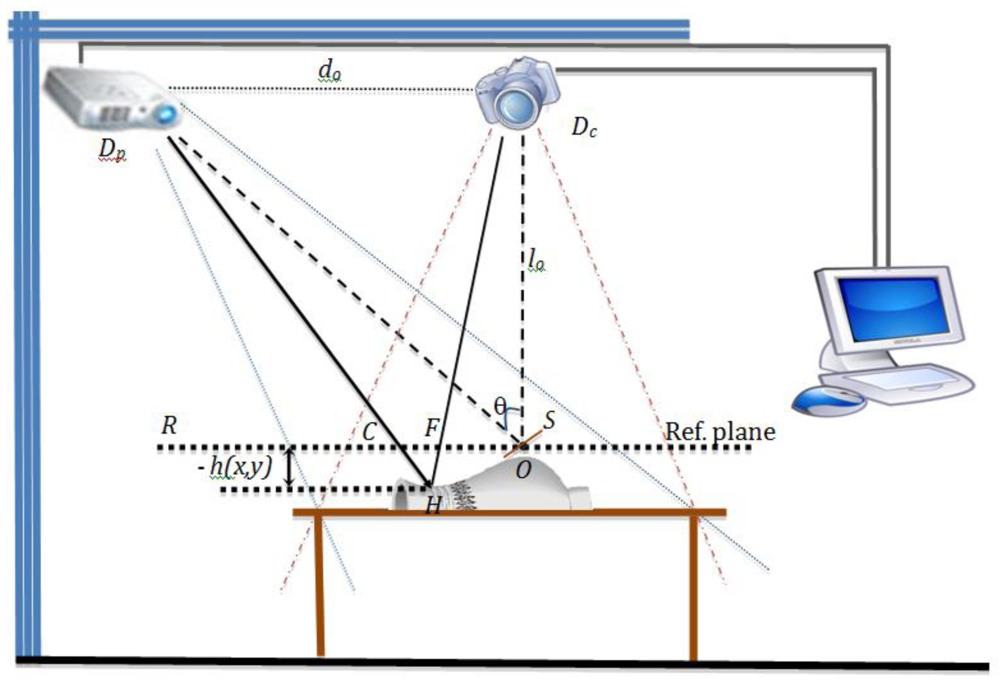
3. Experimental Setup
The experimental setup shown in
Figure 1 is used to apply the methodology proposed in
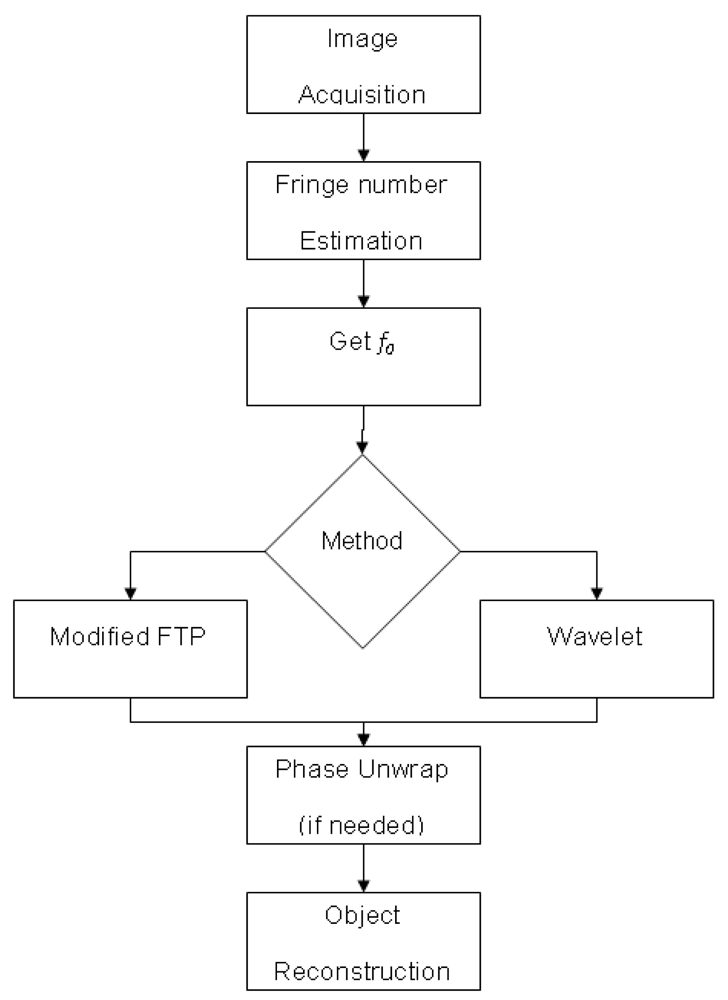
Figure 3. The first step is to acquire the image. Due to the nature of the image, sometimes a filtering to eliminate the noise is necessary. In this research, only a 9 × 9 Gaussian filter is used in the Fourier transform. In the wavelet transform application, no filter is applied. Next, the number of fringes is estimated due to the fact that has a direct relationship with the fundamental frequency
fo. Then, the
fo is obtained by applying an algorithm. At this point, it is necessary to decide whether the Fourier or wavelet method would be applied. Both methods, Fourier and wavelet analysis use the algorithms described in the previous section.
When using the Fourier method, a robust unwrapping algorithm is needed, followed by an unwrapping algorithm with local and global analysis. The main algorithm for the local discontinuity analysis [
5] is described as follows: (a) first, the wrapped phase map is divided into regions giving different weights (w
1,w
2, .., w
n) to each region, (b) the modulation unit is defined that helps to detect the fringe quality and divides the fringes into regions, (c) regions are grouped from the biggest to the smallest modulation value, (d) next, the unwrapping process is started from the biggest to the smallest region, (e) later, an evaluation of the phase changes is carried out to avoid variations smaller than
fo.
If the wavelet transform method is used then a simple unwrapping algorithm is enough to obtain the three-dimensional shape from the object. The final step is to obtain the object reconstruction and in some cases to determine the error (in case of virtual created objects).
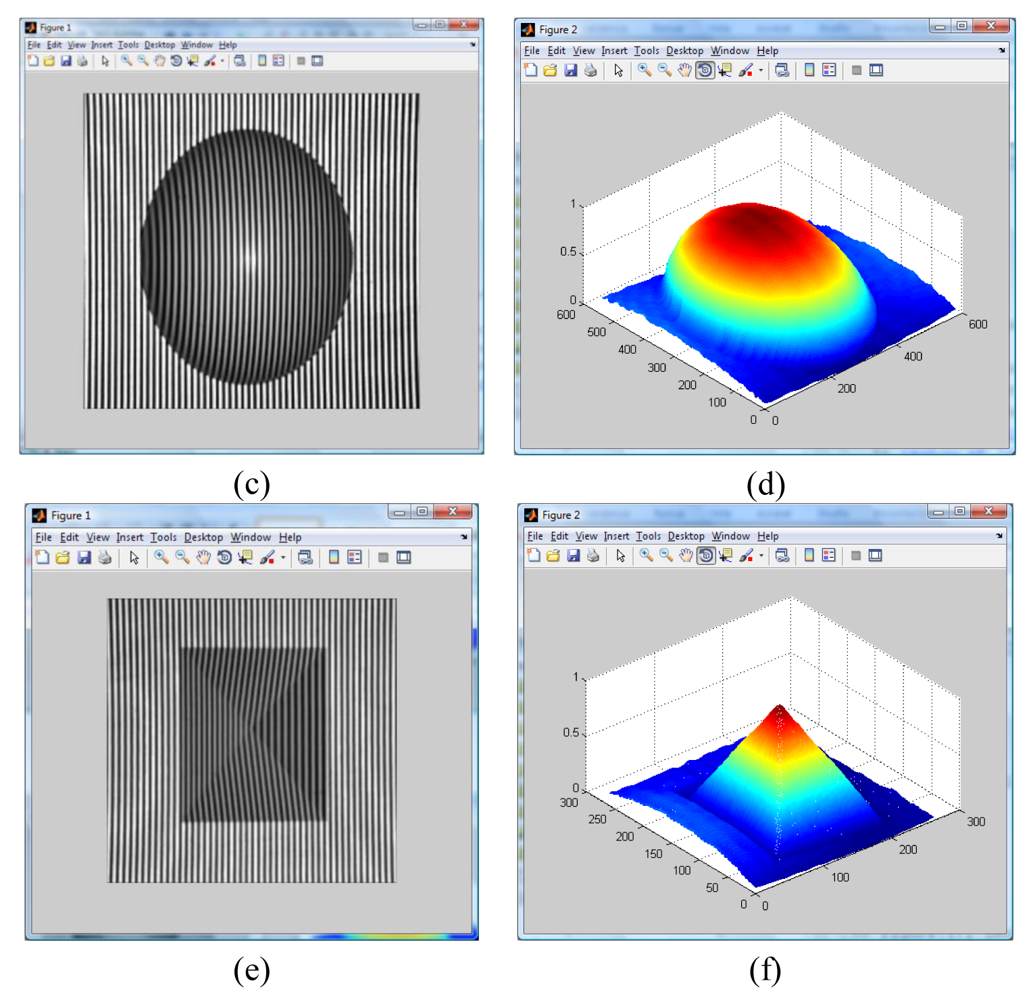
In the experimental setup, a high-resolution digital CCD camera can be used. The reference plane can be any flat surface like a plain wall, or a whiteboard. In the reference plane it is important to consider a non reflective-surface to minimize the unwanted reflection effects that may cause some problems for the image acquisition process. The object of interest can be any three-dimensional object and for this work, three objects are considered (
Figure 10); the first one is a mask, the second is an oval the third one is symmetrical pyramid.
It is also important to develop software able to produce several different fringe patterns. To create several patterns, it is necessary to modify the spatial frequency (number of fringes per unit area), and resolution (number of levels to create the sinusoidal pattern) of the fringe pattern. It may also be necessary to include into the software development a routine capable of performing phase shifting as well as to include the horizontal or vertical orientation projection of the fringe pattern.
Computer Simulation
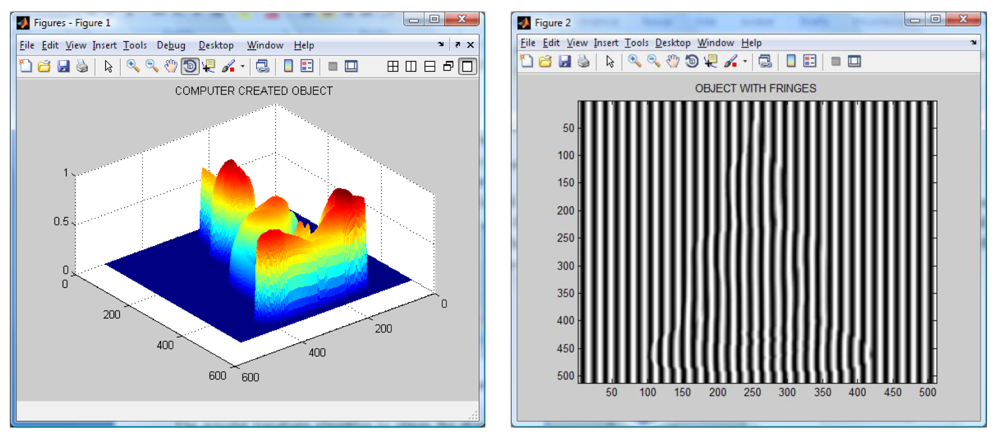
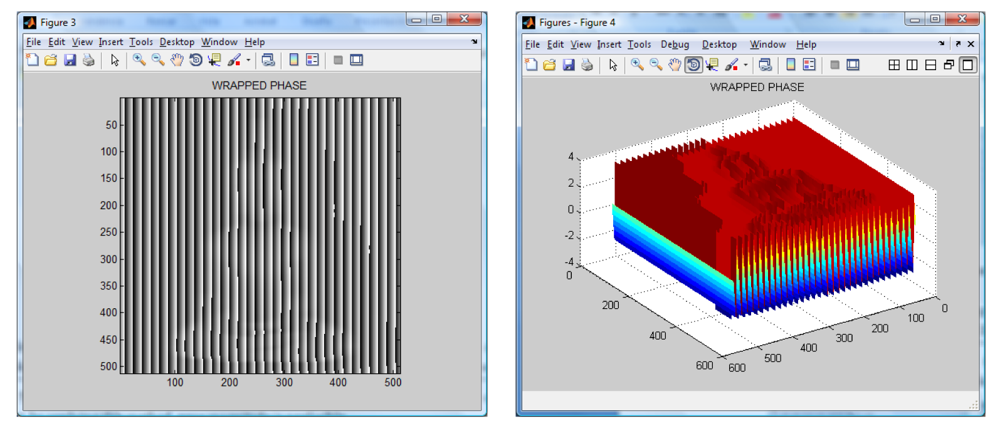
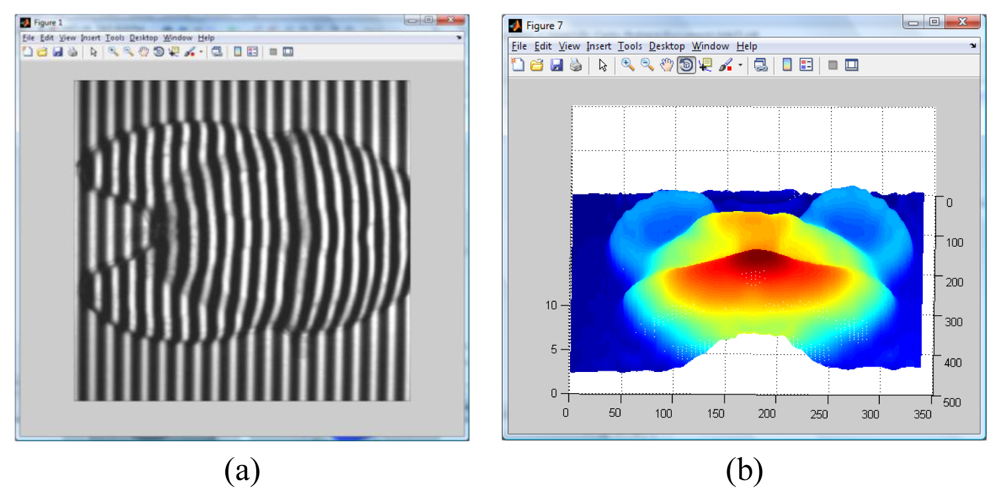
An object with a Buddha shape generated by computer is used to test the algorithms. The generated Buddha in shown in
Figure 4. Then, a sinusoidal fringe pattern of known spatial frequency is created and later is added to the shape of the created object. The resulting image is shown in
Figure 4. It is worth noting the distortions of the fringe pattern due to the object shape.
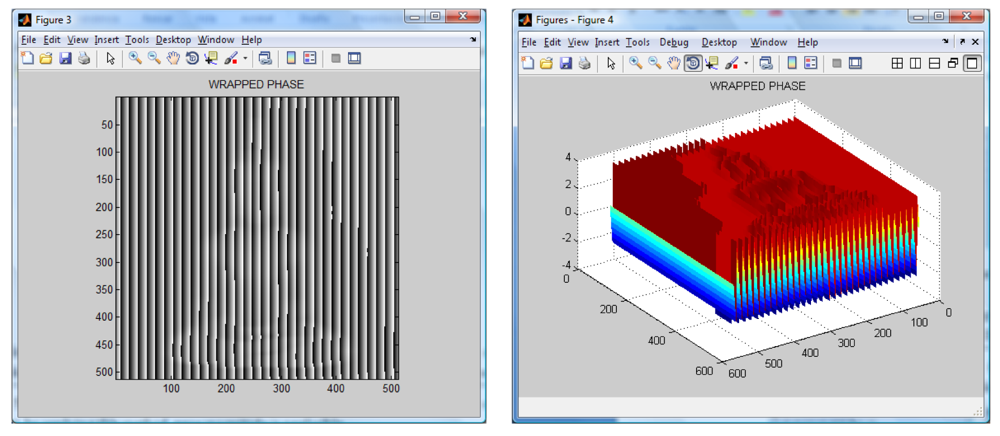
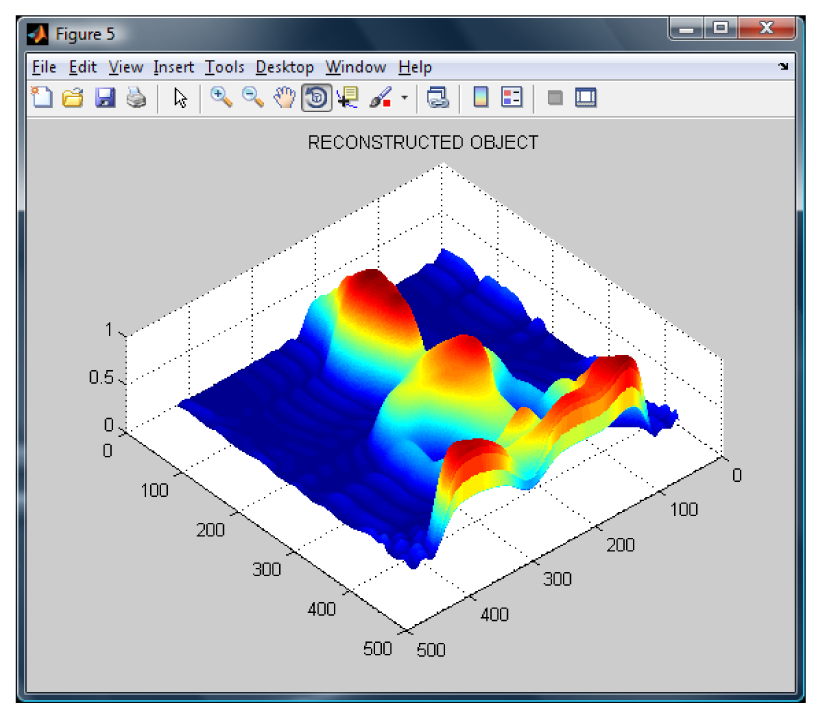
The wavelet transform algorithm is considered o obtain the shape of the Buddha. The resulting wrapped phase and its mesh are shown in
Figure 5. The reconstructed Buddha using the modified Fourier Transform Profilometry can be seen in
Figure 6. Notice that, by applying this method, the shape of the Buddha looks almost equal, however it has an error magnitude of about 3.5%.
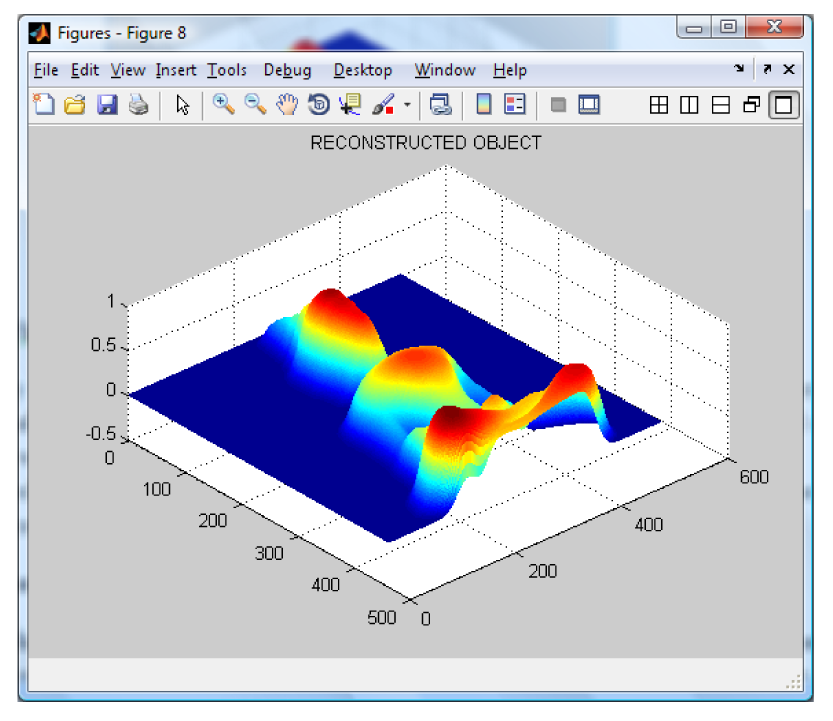
By applying the Wavelet Profilometry, the mesh shown on
Figure 7 is obtained; the whole volume presents an error of about 1.5%. At this point, it can be seen that even the amount of error seem to be almost equal for both methods, but the Fourier one is bigger and the final shape is more defined in the case of the wavelet method. The computer simulation allowed us to test and validate both methods.
As a preliminary conclusion, it is clear that the wavelet transform gives a better performance than the Fourier transform for the selected object shape. Therefore, the wavelet transform is selected and used. The error of the wavelet method is about 1 to 2% and using the Fourier one it is about 3 to 5%.
To validate the methodology, the following experiments were conducted. Several objects with different shapes were created by computer, where the height is known in every point in the object. Then, the Fourier and wavelet based analysis are applied as well as the methodology proposed by Gdeisat
et al. [
15]. The height of the virtual object was compared with each one of the analysis and the results are presented in
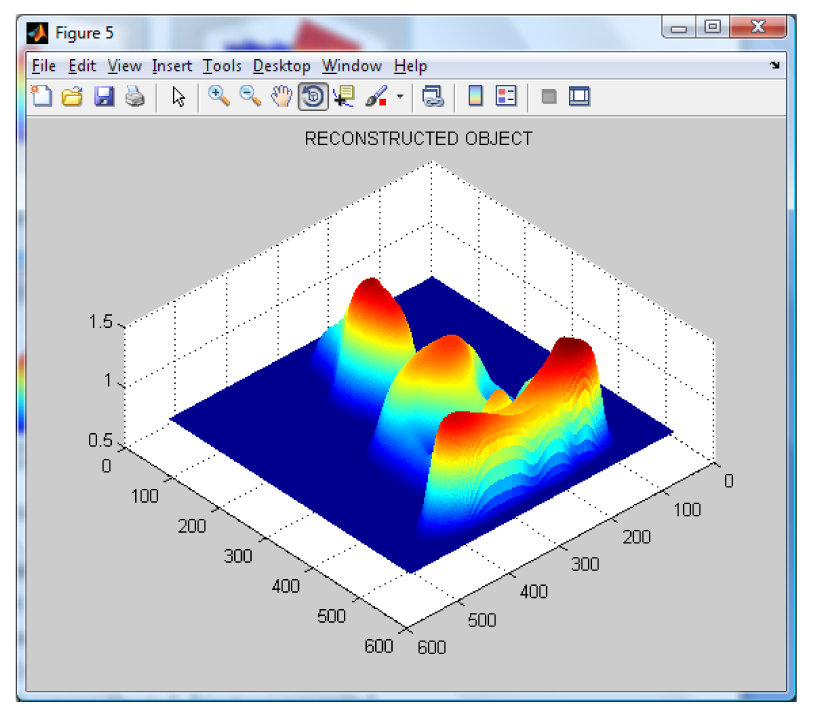
Table 1. Finally, the wavelet method has been applied to several real objects, and the respective results of the reconstruction process can be seen in
Figure 10.
4. Conclusions and Future Work
In this paper, a three-dimensional reconstruction methodology was presented. The method is based on the modified Fourier Transform Profilometry or Wavelet Transform Profilometry. In the first part of the proposed method the high frequencies that mostly affect the performance on the phase unwrapping in the Fourier method are obtained analytically. An object generated by the computer was virtually created and a known spatial sinusoidal fringe pattern was projected on it. Both Fourier and wavelet analysis were conducted, showing a good performance. In the comparison, the wavelet method was the one that showed a minimal error. Later, a real object was selected and the wavelet analysis was carried out and an accurate reconstruction of the object was achieved. This methodology could be widely used to digitize diverse objects for reverse engineering, virtual reality, 3D navigation, and so on.
Notice that the method can reconstruct only the part of the object that can be seen by the camera, if a full 3D reconstruction (360 degrees) is needed, a rotating table is can be used and the methodology will be applied n times, where n is the rotation angle of the table. As a future work, several tests could be carried out using objects with different shapes. Another option is to change the wavelet type and characterize the system.
One big challenge is to obtain the 3D reconstruction in real time. As a part of the solution, an optical filter could be implemented to obtain the FFT directly, or else, the algorithm can be implemented into a FPGA to carry out a parallel processing and minimize the processing time.