Real-Time Accumulative Computation Motion Detectors
Abstract
:1. Introduction
2. Accumulative Computation (AC) in Motion Detection
2.1. Classical Motion Detection Approaches
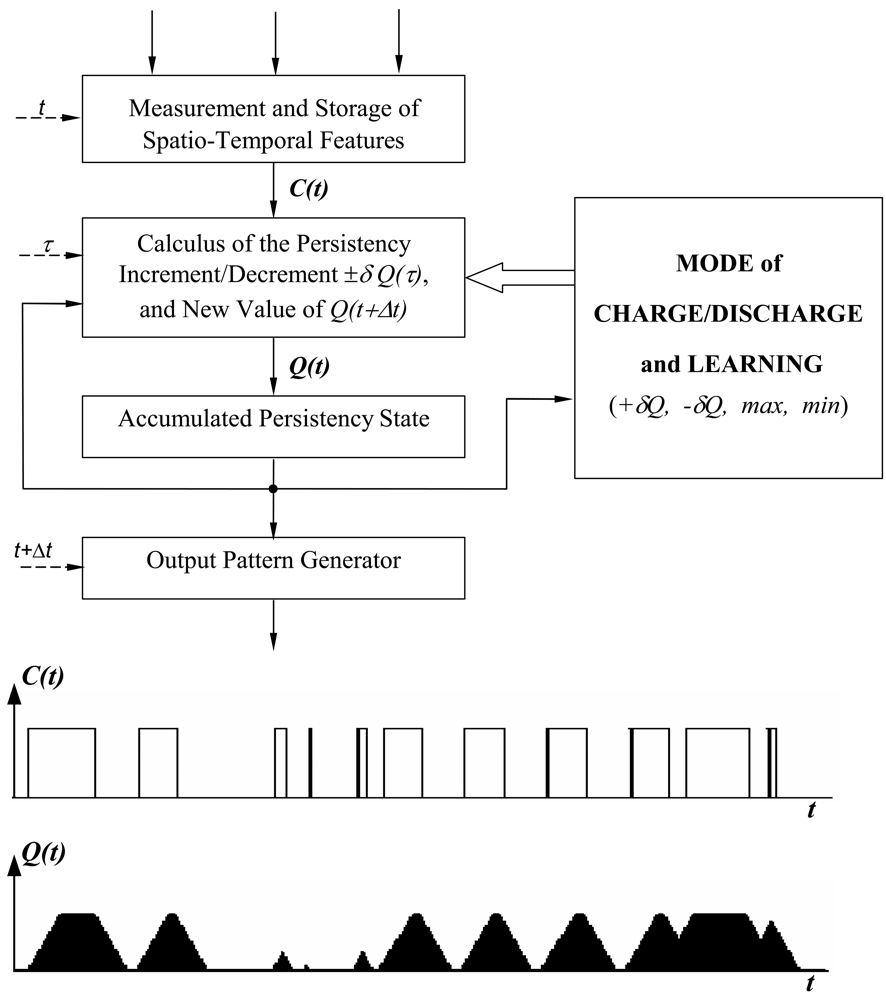
2.2. Description of Accumulative Computation
- The presence of specific spatio-temporal features with values over a certain threshold.
- The persistency in the presence of these features.
- The increment or decrement values (±δQ) in the accumulated state of activity of each feature and the corresponding current value, Q(t).
- The control and learning mechanisms.
3. Simplified Model for AC in Motion Detection
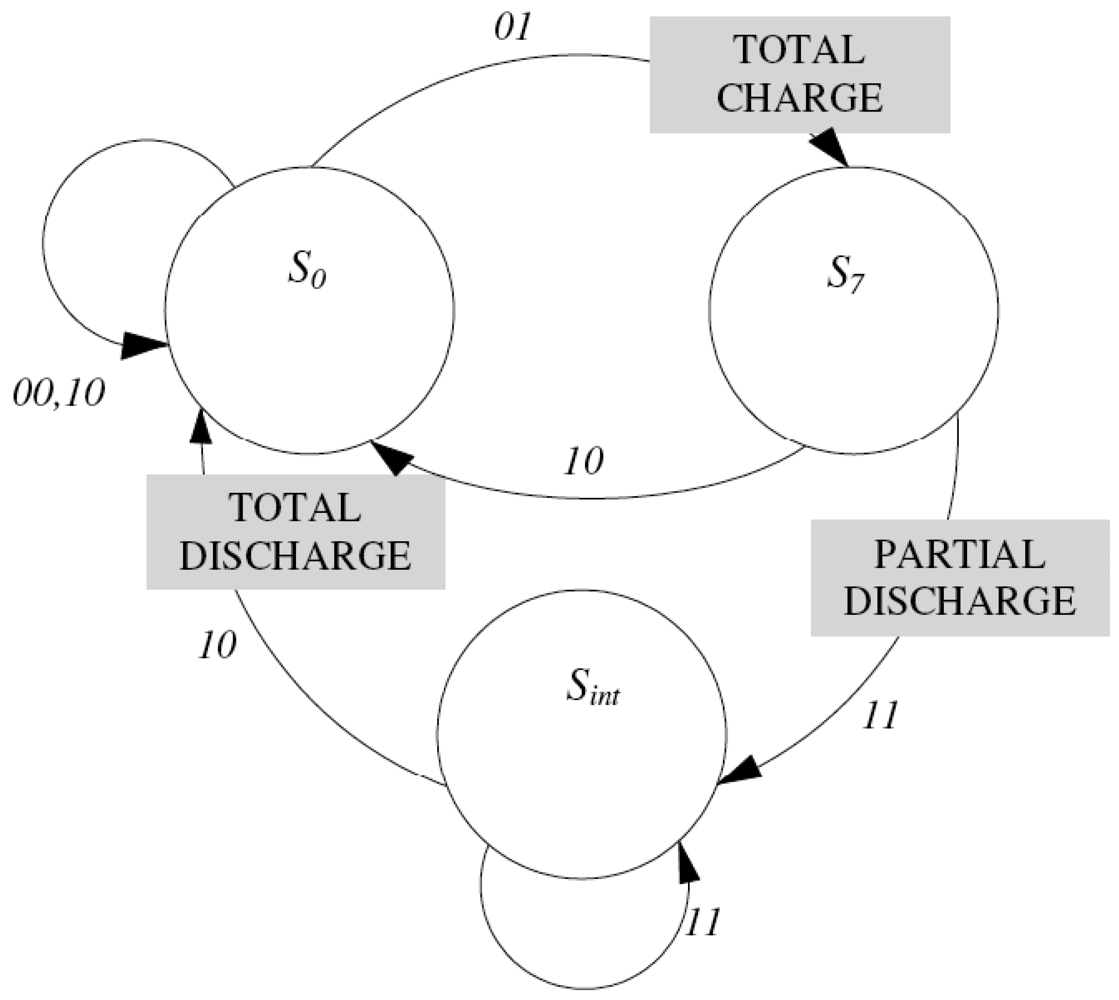
3.1. Initial Model
- Ik(i, j; t − Δt) = {0, 1}, Ik(i, j; t) = 0In this case the calculation element (i, j) is not able to detect any contrast with respect to the input of a moving object in that band (Ik(i, j; t) = 0). It may have detected it (or not) in the previous interval (Ik(i, j; t − Δt) = 1, Ik(i, j; t) = 0). In any case, the element passes to state S0, the state of complete discharge, independently of which was the initial state.
- Ik(i, j; t − Δt) = 0, Ik(i, j; t) = 1The calculation element has detected in t a contrast in its band (Ik(i, j; t) = 1), and it did not in the previous interval (Ik(i, j; t − Δt) = 0). It passes to state S7, the state of total charge, independently of which was the previous state.
- Ik(i, j; t − Δt) = 1, Ik(i, j; t) = 1The calculation element has detected the presence of an object in its band (Ik(i, j; t) = 1), and it had also detected it in the previous interval (Ik(i, j; t − Δt) = 1). In this case, it diminishes its charge value in a certain value, δQ. This discharge - partial discharge - can proceed from an initial state of saturation S7, or from some intermediate state (S6, …, S1). This partial discharge due to the persistence of the object in that position and in that band, is described by means of a transition from S7 to an intermediate state, Sint, without arriving to the discharge, S0. The descent in the element's state is equivalent to the descent in the pixel's charge, as you may appreciate on Figure 2.
3.2. Hysteresis Bands
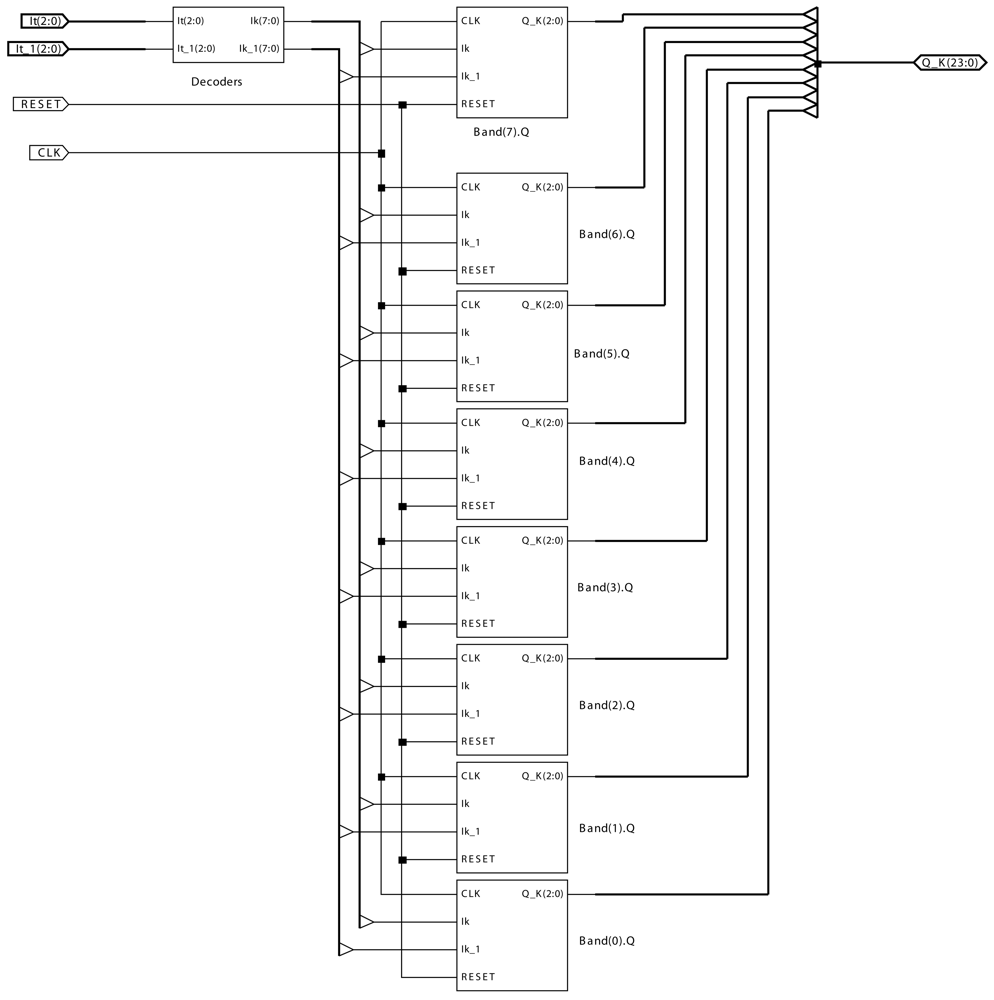
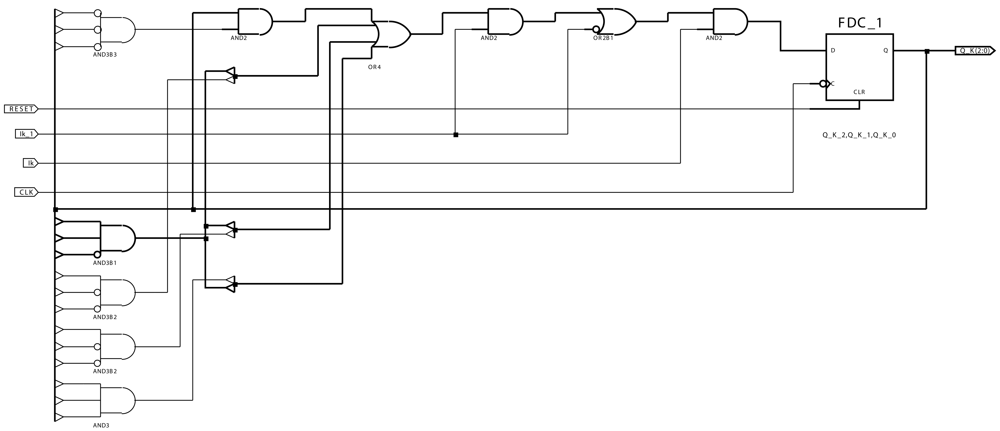
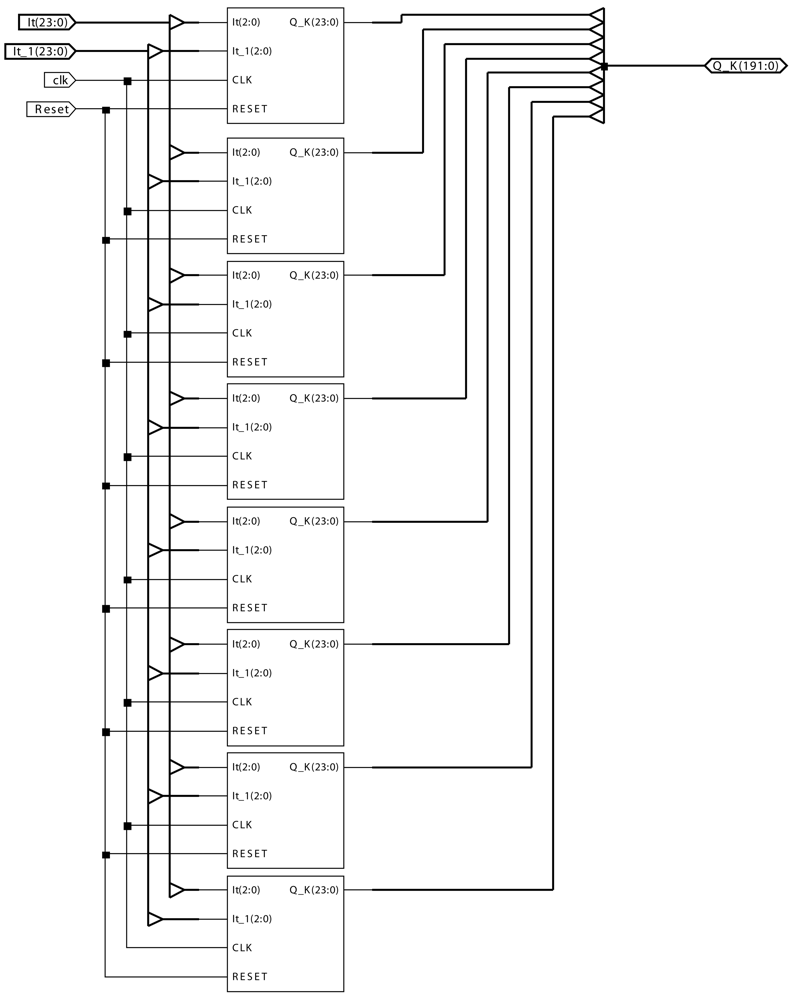
4. Real-time Hardware Implementation of Motion-Detection AC Modules
- It is the input value at each pixel at time instant t.
- It_1 is the input value at each pixel at time instant t − Δt.
- CLK is the clock signal to control the automata associated to the AC module.
- RESET is the signal to reset the AC module.
5. Data and Results
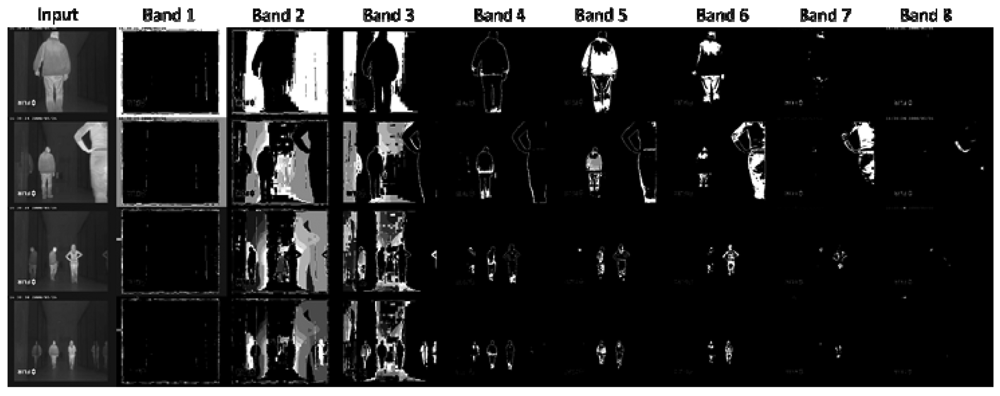
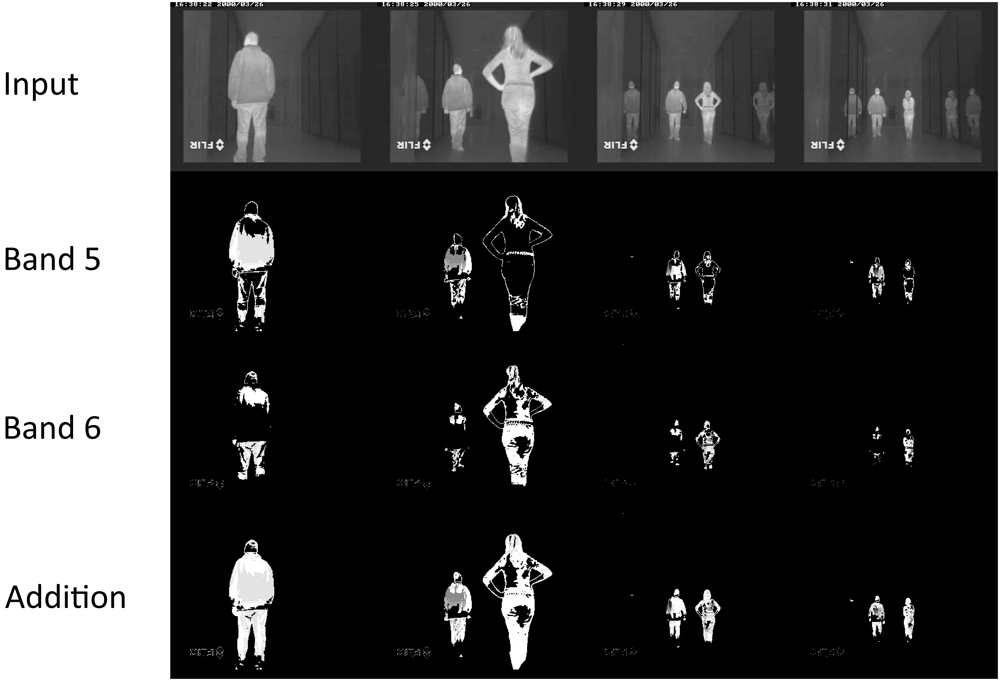
5.1. Infrared-Based People Segmentation
5.2. Color-Based People Tracking
Simple tracking algorithm
Enhanced tracking algorithm
6. Conclusions
Acknowledgments
References and Notes
- Howe, N.R. Flow lookup and biological motion perception. Proceedings of the IEEE International Conference on Image Processing, Genoa, Italy, September 2005; Vol. 3. pp. 1168–1171.
- Diaz, J.; Ros, E.; Pelayo, F.; Ortigosa, E.M.; Mota, S. FPGA-based real-time optical-flow system. IEEE Trans. Circ. Syst. Vid. 2006, 16, 274–279. [Google Scholar]
- Correia, M.V.; Campilho, A.C. Real-time implementation of an optical flow algorithm. Proceedings of the 16th International Conference on Pattern Recognition, Québec City, QC, Canada, August 2002; Vol. 4. pp. 247–250.
- Claveau, D.; Wang, C. Space-variant motion detection for active visual target tracking. Rob. Auton. Syst. 2009, 57, 11–22. [Google Scholar]
- Cheng, C.C.; Lin, G.L. Motion estimation using the single-row superposition-type planar compound-like eye. Sensors 2007, 7, 1047–1068. [Google Scholar]
- Aubépart, F.; Franceschini, N. Bio-inspired optic flow sensors based on FPGA: application to micro-air-vehicles. Microprocess. Microsyst. 2007, 31, 408–419. [Google Scholar]
- Deng, Z.; Carlson, T.J.; Duncan, J.P.; Richmond, M.C. Six-degree-of-freedom sensor fish design and instrumentation. Sensors 2007, 7, 3399–3415. [Google Scholar]
- Reichel, L.; Liechti, D.; Presser, K.; Liu, S.C. Range estimation on a robot using neuromorphic motion sensors. Rob. Auton. Syst. 2005, 51, 167–174. [Google Scholar]
- Fernández-Caballero, A.; Mira, J.; Delgado, A.E.; Fernández, M.A. Lateral interaction in accumulative computation: a model for motion detection. Neurocomputing 2003, 50, 341–364. [Google Scholar]
- Fernández-Caballero, A.; Mira, J.; Fernández, M.A.; Delgado, A.E. On motion detection through a multi-layer neural network architecture. Neural Netw. 2003, 16, 205–222. [Google Scholar]
- Mira, J.; Delgado, A.E.; Fernández-Caballero, A.; Fernández, M.A. Knowledge modelling for the motion detection task: the lateral inhibition method. Exp. Syst. Appl. 2004, 7, 169–185. [Google Scholar]
- Fernández-Caballero, A.; López, M.T.; Mira, J.; Delgado, A.E.; López-Valles, J.M.; Fernández, M.A. Modelling the stereovision-correspondence-analysis task by lateral inhibition in accumulative computation problem-solving method. Exp. Syst. Appl. 2007, 33, 955–967. [Google Scholar]
- Fernández-Caballero, A.; Mira, J.; Fernández, M.A.; López, M.T. Segmentation from motion of non-rigid objects by neuronal lateral interaction. Pattern Recognit. Lett. 2001, 22, 1517–1524. [Google Scholar]
- Fernández-Caballero, A.; Fernández, M.A.; Mira, J.; Delgado, A.E. Spatio-temporal shape building from image sequences using lateral interaction in accumulative computation. Pattern Recognit. 2003, 36, 1131–1142. [Google Scholar]
- Martínez-Cantos, J.; Carmona, E.; Fernández-Caballero, A.; López, M.T. Parametric improvement of lateral interaction in accumulative computation in motion-based segmentation. Neurocomputing 2008, 71, 776–786. [Google Scholar]
- López, M.T.; Fernández-Caballero, A.; Fernández, M.A.; Mira, J.; Delgado, A.E. Visual surveillance by dynamic visual attention method. Pattern Recognit. 2006, 39, 2194–2211. [Google Scholar]
- López, M.T.; Fernández-Caballero, A.; Fernández, M.A.; Mira, J.; Delgado, A.E. Motion features to enhance scene segmentation in active visual attention. Pattern Recognit. Lett. 2006, 27, 469–478. [Google Scholar]
- López, M.T.; Fernández-Caballero, A.; Fernández, M.A.; Mira, J.; Delgado, A.E. Dynamic visual attention model in image sequences. Image Vision Comput. 2007, 25, 597–613. [Google Scholar]
- Ñeco, R.P.; Forcada, M.L. Asynchronous translations with recurrent neural nets. Proceedings of the International Conference on Neural Networks, Stockholm, Sweden, June 1997; Vol. 4. pp. 2535–2540.
- McCulloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar]
- Kleene, S.C. Representation of events in nerve nets and finite automata. In Automata Studies; Princeton University Press: Princeton, NJ, USA, 1956. [Google Scholar]
- Minsky, M.L. Computation: Finite and Infinite Machines; Prentice-Hall: Englewood, NJ, USA, 1967. [Google Scholar]
- Carrasco, R.C.; Oncina, J.; Forcada, M.L. Efficient encoding of finite automata in discrete-time recurrent neural networks. Proceedings of the Ninth International Conference on Artificial Neural Networks, Edinburgh, Scotland, September 1999; Vol. 2. pp. 673–677.
- Carrasco, R.C.; Forcada, M.L. Finite state computation in analog neural networks: steps towards biologically plausible models. Lect. Notes Comput. Sci. 2001, 2036, 482–486. [Google Scholar]
- Prat, F.; Casacuberta, F.; Castro, M.J. Machine translation with grammar association: combining neural networks and finite state models. Proceedings of the Second Workshop on Natural Language Processing and Neural Networks, Tokyo, Japan, November 2001; pp. 53–60.
- Sun, G.Z.; Giles, C.L.; Chen, H.H. The neural network pushdown automaton: architecture, dynamics and training. Lect. Notes Comput. Sci. 1998, 1387, 296–345. [Google Scholar]
- Cleeremans, A.; Servan-Schreiber, D.; McClelland, J.L. Finite state automata and simple recurrent networks. Neural Comput 1989, 1, 372–381. [Google Scholar]
- Giles, C.L.; Miller, C.B.; Chen, D.; Chen, H.H.; Sun, G.Z.; Lee, Y.C. Learning and extracted finite state automata with second-order recurrent neural networks. Neural Comput. 1992, 4, 393–405. [Google Scholar]
- Manolios, P.; Fanelli, R. First order recurrent neural networks and deterministic finite state automata. Neural Comput. 1994, 6, 1154–1172. [Google Scholar]
- Gori, M.; Maggini, M.; Martinelli, E.; Soda, G. Inductive inference from noisy examples using the hybrid finite state filter. IEEE Trans. Neural Netw. 1998, 9, 571–575. [Google Scholar]
- Geman, S.; Bienenstock, E.; Dourstat, R. Neural networks and the bias/variance dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar]
- Shavlik, J. Combining symbolic and neural learning. Mach. Learn. 1994, 14, 321–331. [Google Scholar]
- Omlin, C.W.; Giles, C.L. Constructing deterministic finite state automata in recurrent neural networks. J. ACM 1996, 43, 937–972. [Google Scholar]
- Duda, O.R.; Hart, P.E. Pattern Classification and Scene Analysis; Wiley-Interscience: New York, NY, USA, 1973. [Google Scholar]
- Fennema, C.L.; Thompson, W.B. Velocity determination in scenes containing several multiple moving objects. Comput. Graphics Image Proc. 1979, 9, 301–315. [Google Scholar]
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar]
- Marr, D.; Ullman, S. Directional selectivity and its use in early visual processing. Pr. Roy Soc. London B 1981, 211, 151–180. [Google Scholar]
- Adelson, E.H.; Movshon, J.A. Phenomenal coherence of moving visual patterns. Nature 1982, 300, 523–525. [Google Scholar]
- Hildreth, E.C. The Measurement of Visual Motion; The MIT Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Wallach, H. On perceived identity: 1. The direction of motion of straight lines. In On Perception; Wallach, W., Ed.; Quadrangle: New York, NY, USA, 1976. [Google Scholar]
- Emerson, R.C.; Coleman, L. Does image movement have a special nature for neurons in the cat's striate cortex? Invest. Ophthalmol. Vis. Sci. 1981, 20, 766–783. [Google Scholar]
- Lawton, T.B. Outputs of paired Gabor filters summed across the background frame of reference predict the direction of movement. IEEE Trans. Biomed. Eng. 1989, 36, 130–139. [Google Scholar]
- Hassenstein, B.; Reichardt, W.E. Functional structure of a mechanism of perception of optical movement. Proceedings of the 1st International Congress of Cybernetics, Namur, Belgium, June 1956; pp. 797–801.
- Barlow, H.B.; Levick, R.W. The mechanism of directional selectivity in the rabbit's retina. J. Physiol. 1965, 173, 477–504. [Google Scholar]
- Adelson, E.H.; Bergen, J.R. Spatiotemporal energy models for the perception of motion. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1985, 2, 284–299. [Google Scholar]
- Heeger, D.J. Model for the extraction of image flow. J. Opt. Soc. Am. A Opt. Image. Sci. Vis. 1987, 4, 1455–1471. [Google Scholar]
- Watson, A.B.; Ahumada, A.J. Model of visual-motion sensing. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1985, 2, 322–341. [Google Scholar]
- Koch, C.; Marroquin, J.; Yuille, A. Analog neuronal networks in early vision. Proc. Natl. Acad. Sci. USA 1986, 83, 4263–4267. [Google Scholar]
- Yuille, A.L.; Grzywacz, N. A computational theory for the perception of coherent visual motion. Nature 1988, 333, 71–74. [Google Scholar]
- Fernández, M.A.; Mira, J. Permanence memory–a system for real time motion analysis in image sequences. Proceedings of the IAPR Workshop on Machine Vision Applications, Tokyo, Japan, December 1992; pp. 249–252.
- Bensaali, F.; Amira, A. Accelerating colour space conversion on reconfigurable hardware. Image Vision Comput. 2005, 23, 935–942. [Google Scholar]
- Isaacs, J.C.; Watkins, R.K.; Foo, S.Y. Cellular automata PRNG: Maximal performance and minimal space FPGA implementations. Eng. Appl. Artif. Intell. 2003, 16, 491–499. [Google Scholar]
- Amer, I.; Badawy, W.; Jullien, G. A proposed hardware reference model for spatial transformation and quantization in H.264. J. Vis. Commun. Image R. 2006, 17, 533–552. [Google Scholar]
- Moon, H.; Sedaghat, R. FPGA-based adaptive digital predistortion for radio-over-fiber links. Microprocess. Microsyst. 2006, 30, 145–154. [Google Scholar]
- Bojanic, S.; Caffarena, G.; Petrovic, S.; Nieto-Taladriz, O. FPGA for pseudorandom generator cryptanalysis. Microprocess. Microsyst. 2006, 30, 63–71. [Google Scholar]
- Damaj, I.W. Parallel algorithms development for programmable logic device. Adv. Eng. Soft. 2006, 37, 561–582. [Google Scholar]
- Perri, S.; Lanuzza, M.; Corsonello, P.; Cocorullo, G. A high-performance fully reconfigurable FPGA-based 2-D convolution processor. Microprocess. Microsyst. 2005, 29, 381–391. [Google Scholar]
- Abutaleb, M.M.; Hamdy, A.; Saad, E.M. FPGA-based real-time video-object segmentation with optimization schemes. Int. J. Circ. Syst. Sign. Proc. 2008, 2, 78–86. [Google Scholar]




| Minimum period | 1.287 ns |
| Maximum frequency | 777.001 MHz |
| Minimum input required time before clock | 2.738 ns |
| Maximum output delay after clock | 3.271 ns |
| Slice Logic Utilization: | |
| Number of Slice Registers | 24 out of 20480 (0%) |
| Number of Slice LUTs | 40 out of 20480 (0%) |
| Number used as Logic | 40 out of 20480 (0%) |
| Slice Logic Distribution: | |
| Number of LUT Flip Flop pairs used | 40 |
| Number with an unused Flip Flop | 16 out of 40 (40%) |
| Number with an unused LUT | 0 out of 40 (0%) |
| Number of fully used LUT-FF pairs | 24 out of 40 (60%) |
| Number of unique control sets | 1 |
| IO Utilization: | |
| Number of IOs | 32 |
| Number of bonded IOBs | 32 out of 360 |
| Minimum period | 2.736 ns |
| Maximum frequency | 365.497 MHz |
| Minimum input required time before clock | 2.834 ns |
| Maximum output delay after clock | 3.271 ns |
| Maximum combinational path delay | 4.348 ns |
| Slice Logic Utilization: | |
| Number of Slice Registers | 248 out of 20480 (1%) |
| Number of Slice LUTs | 467 out of 20480 (2%) |
| Number used as Logic | 467 out of 20480 (2%) |
| Slice Logic Distribution: | |
| Number of LUT Flip Flop pairs used | 492 |
| Number with an unused Flip Flop | 244 out of 492 (49%) |
| Number with an unused LUT | 25 out of 492 (5%) |
| Number of fully used LUT-FF pairs | 223 out of 492 (45%) |
| Number of unique control sets | 2 |
| IO Utilization: | |
| Number of IOs | 260 |
| Number of bonded IOBs | 260 out of 360 (72%) |
| Number of BUFG/BUFGCTRLs | 1 out of 32 (3%) |
| Number of Cases: | 1109 |
| Number of Correct Cases: | 1066 |
| Accuracy: | 96.1% |
| Sensitivity: | 95.8% |
| Specificity: | 96.4% |
| Positive Cases Missed: | 24 |
| Negative Cases Missed: | 19 |
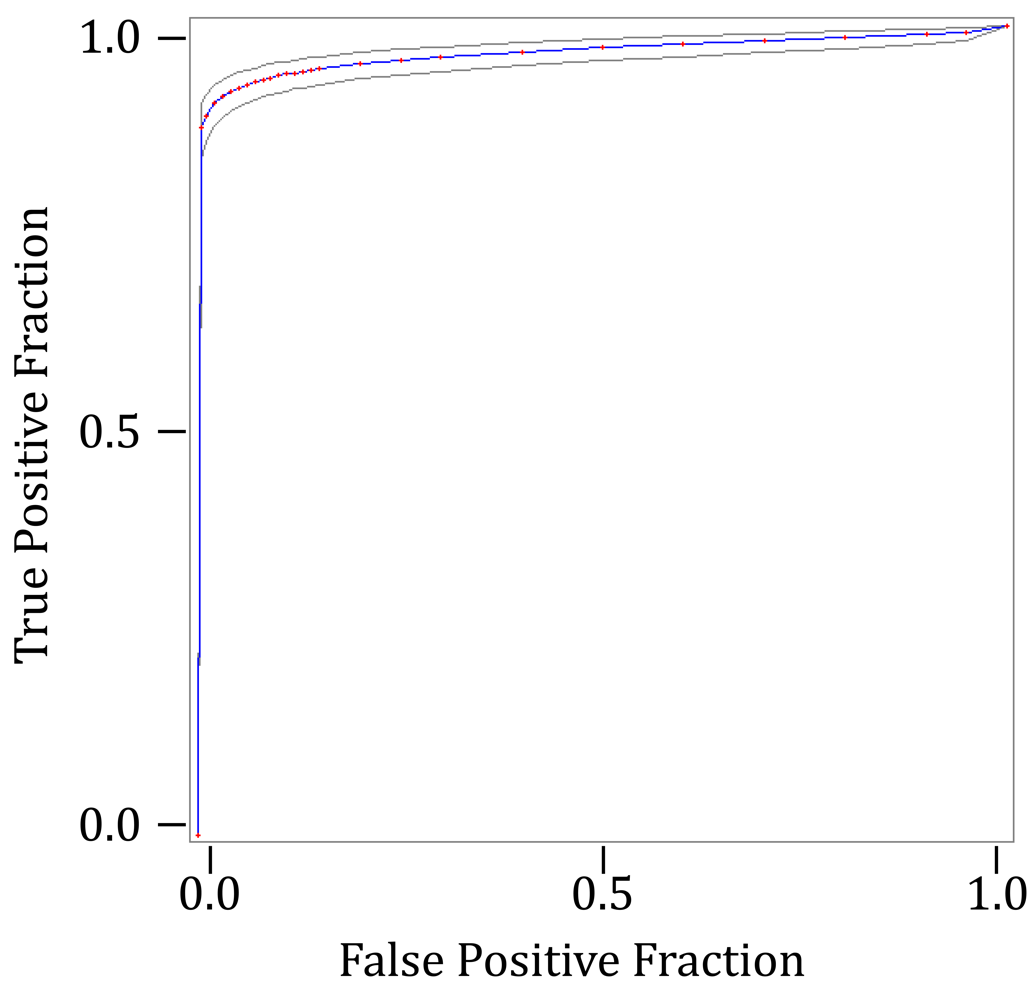
| Fitted ROC Area: | 0.968 |
| Empiric ROC Area: | 0.964 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fernández-Caballero, A.; López, M.T.; Castillo, J.C.; Maldonado-Bascón, S. Real-Time Accumulative Computation Motion Detectors. Sensors 2009, 9, 10044-10065. https://doi.org/10.3390/s91210044
Fernández-Caballero A, López MT, Castillo JC, Maldonado-Bascón S. Real-Time Accumulative Computation Motion Detectors. Sensors. 2009; 9(12):10044-10065. https://doi.org/10.3390/s91210044
Chicago/Turabian StyleFernández-Caballero, Antonio, María Teresa López, José Carlos Castillo, and Saturnino Maldonado-Bascón. 2009. "Real-Time Accumulative Computation Motion Detectors" Sensors 9, no. 12: 10044-10065. https://doi.org/10.3390/s91210044
APA StyleFernández-Caballero, A., López, M. T., Castillo, J. C., & Maldonado-Bascón, S. (2009). Real-Time Accumulative Computation Motion Detectors. Sensors, 9(12), 10044-10065. https://doi.org/10.3390/s91210044





