Optical Remote Sensing of Glacier Characteristics: A Review with Focus on the Himalaya
Abstract
:1. Introduction
2. Optical remote sensors for glacier monitoring
3. Remote sensing methods for glacier monitoring
3.1. Glacier ice delineation
3.2 Extracting glacier parameters from DEMs
3.3. Volume-area scaling techniques for mass balance estimations
3.4. The remote sensing geodetic method
3.5 AAR-ELA methods for mass balance estimations
4. Case study: Application of remote sensing methods to the Himalaya
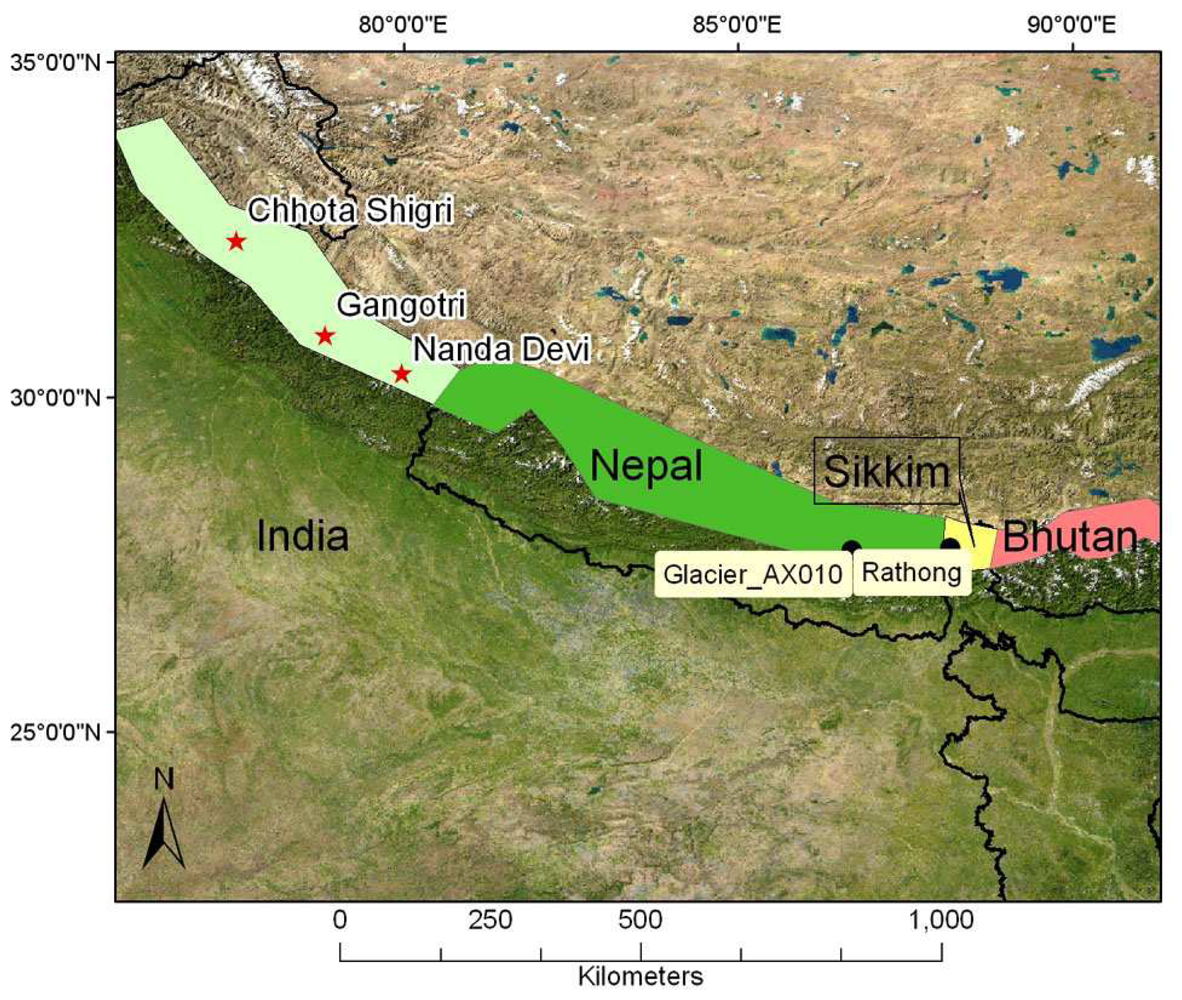
4.1 Himalayan glacier fluctuations
4.2 Himalayan glaciologic data
4.3 Previous remote sensing mass balance estimations in the Himalaya
4.4 Progress on mapping of Himalayan glaciers using remote sensing
5. Conclusions
Acknowledgments
References and Notes
- Arendt, A.A.; Echelmeyer, K.A.; Harrison, W.D.; Lingle, C.S.; Valentine, V.B. Rapid wastage of Alaska glaciers and their contribution to rising sea level. Science 2002, 297(5580), 382–386. [Google Scholar]
- Rignot, E.; Rivera, A.; Casassa, G. Contribution of the Patagonia Icefields of South America to sea level rise. Science 2003, 302(5644), 434–437. [Google Scholar]
- Racoviteanu, A.; Arnaud, Y.; Williams, M. Decadal changes in glacier parameters in Cordillera Blanca, Peru derived from remote sensing. J Glaciol 2008, in press. [Google Scholar]
- Kaser, G.; Ames, A.; Zapata, M. Glacier fluctuations and climate in the Cordillera Blanca, Perú. Ann Glaciol 1990, 14, 136–140. [Google Scholar]
- Hasternath, S.; Ames, A. Recession of Yanamarey glacier in Cordillera Blanca, Perú during the 20th century. J Glaciol 1995, 41(137), 191–196. [Google Scholar]
- Georges, C. The 20th century glacier fluctuations in the Cordillera Blanca (Perú). Arctic Antarct Alpine Res 2004, 36(2), 100–107. [Google Scholar]
- Paul, F.; Kääb, A.; Maisch, M.; Kellenberger, T.; Haeberli, W. The new remote-sensing-derived Swiss glacier inventory: I. Methods. Ann Glaciol 2002, 34, 355–361. [Google Scholar]
- Paul, F.; Kääb, A.; Maisch, M.; Kellenberger, T.; Haeberli, W. Rapid disintegration of Alpine glaciers observed with satellite data. Geoph Res Lett 2004a, 31(21), L21402. [Google Scholar] [CrossRef]
- Kääb, A.; Paul, F.; Maisch, M.; Hoelzle, M.; Haeberli, W. The new remote-sensing-derived Swiss glacier inventory: II. First results. Ann Glaciol 2002a, 34, 362–366. [Google Scholar]
- Kääb, A. Combination of SRTM3 and repeat ASTER data for deriving alpine glacier flow velocities in the Bhutan Himalaya. Rem Sens Environ 2005, 94(4), 463–474. [Google Scholar]
- Fujita, K.; Kadota, T.; Rana, B.; Kayastha, R.B.; Ageta, Y. Shrinkage of Glacier AX010 in Shorong region, Nepal Himalayas in the 1990s. Bull Glacier Res 2001, 18, 51–54. [Google Scholar]
- Fujita, K.; Nakawo, M.; Fujii, Y.; Paudyal, P. Changes in glaciers in Hidden Valley, Mukut Himal, Nepal Himalayas, from 1974 to 1994. J Glaciol 1997, 43(145), 583–588. [Google Scholar]
- Yamada, T.; Shiraiwa, H.; Kadota, T.; Watanabe, O.; Rana, B.; Ageta, Y.; Fushimi, H. Fluctuations of the glaciers from the 1970s to 1989 in the Khumbu, Shorong and Langtang regions, Nepal Himalayas. Bull Glacier Res 1992, 10, 11–19. [Google Scholar]
- Kulkarni, A.V.; Rathore, B.P.; Mahajan, S.; Mathur, P. Alarming retreat of Parbati glacier, Beas basin, Himachal Pradesh. Curr Sci 2005, 88(11), 1844–1850. [Google Scholar]
- Bahuguna, I.M.; Kulkarni, A.V.; Nayak, S. DEM from IRS-1C PAN stereo coverages over Himalayan glaciated region - accuracy and its utility. Int J Rem Sens 2004, 25(19), 4029–4041. [Google Scholar]
- Kulkarni, A.V.; Bahuguna, I.M. Glacial retreat in the Baspa basin, Himalaya, monitored with satellite stereo data. J Glaciol 2002, 48(160), 171–172. [Google Scholar]
- Bolch, T. Climate change and glacier retreat in northern Tien Shan (Kazakhstan/Kyrgyzstan) using remote sensing data. Global Planet Change 2007, 56(1-2), 1–12. [Google Scholar]
- Surazakov, A.B.; Aizen, V.B. Estimating volume change of mountain glaciers using SRTM and map-based topographic data. IEEE Trans Geosci Rem Sens 2006, 44(10), 2991–2995. [Google Scholar]
- Khromova, T.E.; Osipova, G.B.; Tsvetkov, D.G.; Dyurgerov, M.B.; Barry, R.G. Changes in glacier extent in the eastern Pamir, Central Asia, determined from historical data and ASTER imagery. Rem Sens Environ 2006, 102(1-2), 24–32. [Google Scholar]
- Dyurgerov, M. Glacier Mass Balance and Regime: Data of Measurements and Analysis; INSTAAR Occasional Paper No. 55; Institute of Arctic and Alpine Research, University of Colorado. Distributed by National Snow and Ice Data Center: Boulder, CO, 2002; updated 2005. [Google Scholar]
- Dyurgerov, M.B.; Meier, M.F. Twentieth century climate change: Evidence from small glaciers. PNAS 2000, 97(4), 1406–1411. [Google Scholar]
- Benn, D.I.; Evans, D.J.A. Glaciers and glaciations; John Wiley & Sons, Inc: New York, 1998. [Google Scholar]
- Mayo, L.R.; Meier, M.; Tangborn, W. A system to combine stratigraphic and annual mass balance systems: a contribution to the International Hydrological decade. J Glaciol 1962, 11(61), 3–14. [Google Scholar]
- Kaser, G.; Fountain, A.G.; Jansson, P. A manual for monitoring the mass balance of mountain glaciers. IHP-VI- Technical documents in hydrology 2002, 59 pp. [Google Scholar]
- Østrem, G.; Brugman, M. Glacier-mass balance measurements : a manual for field and office work; National Hydrology Research Institute; NHRI Science Report; Saskatoon, Sask, 1991; p. 224 pp. [Google Scholar]
- Paterson, W.S.B. The Physics of Glaciers, 3rd ed.; Pergamon: Oxford, 1994. [Google Scholar]
- IPCC. Climate Change 2007: The Physical Science Basis. In Summary for Policymakers; Paris, 2007; p. 21. [Google Scholar]
- Kulkarni, A.V. Mass Balance of Himalayan Glaciers Using AAR and ELA Methods. J Glaciol 1992a, 38(128), 101–104. [Google Scholar]
- Tangborn, W.; Rana, B. Mass balance and runoff of the partially debris-covered Langtang Glacier, Nepal. In Debris-covered glaciers; Fountain, A., Ed.; IAHS: Wallingsford, 2000; Volume 264, pp. 53–61. [Google Scholar]
- Wagnon, P.; Kumar, R.; Arnaud, Y.; Linda, A.; Sharma, P.; Vincent, C.; Pottakal, J.; Berthier, E.; Ramanathan, A.; Hassnain, S.I.; Chevalier, P. Four years of mass balance on Chhota Shigri Glacier, Himachal Pradesh, India, a new benchmark glacier in the western Himalaya. J Glaciol 2007, 53(183), 603–611. [Google Scholar]
- Ageta, Y.; Higuchi, K. Estimation of mass balance components of a summer-accumulation type glacier in the Nepal Himalaya. Geogr Ann Phys Geogr 1984, 66(3), 249–255. [Google Scholar]
- Mool, P.K.; Bajracharya, S.R.; Joshi, S.P.; Sakya, K.; Baidya, A. Inventory of glaciers, glacial lakes and glacial lake outburst floods monitoring and early warning systems in the Hindu-Kush Himalayan region, Nepal; International Center for Integrated Mountain Development: Kathmandu, Nepal, 2002; p. 227 pp. [Google Scholar]
- Mool, P.K.; Wangda, D.; Bajracharya, S.R.; Kunzang, K.; Gurung, D.R.; Joshi, S.P. Inventory of Glaciers, Glacial Lakes and Glacial Lake Outburst Floods Monitoring and Early Warning Systems in the Hindu-Kush Himalayan region, Bhutan; International Center for Integrated Mountain Development: Kathmandu, Nepal., 2002; p. 364 pp. [Google Scholar]
- Bahuguna, I.M.; Kulkarni, A.V.; Arrawatia, M.L.; Shresta, D.G. Glacier Atlas of Tista Basin (Sikkim Himalaya); SAC/RESA/MWRGGLI/SN/16; Ahmedabad, India, 2001. [Google Scholar]
- Kulkarni, A.V. Glacier inventory in the Himalaya. Natural resources management - a new perspective; NNRMS: Bangalore, 1992b; pp. 474–478. [Google Scholar]
- Kulkarni, A.V.; Buch, A.M. Glacier Atlas of Indian Himalaya; SAC/RSA/RSAG-MWRD/SN/05/91; 1991; p. 52 pp. [Google Scholar]
- Bamber, J.L.; Kwok, R. Remote-sensing techniques. In Mass balance of the cryosphere: Observations and modelling of contemporary and future changes; Payne, R., Ed.; Cambridge University press: Cambridge, 2004. [Google Scholar]
- Rees, W.G. Remote sensing of snow and ice; Taylor & Francis, 2003. [Google Scholar]
- Taschner, S.; Ranzi, R. Landsat-TM and ASTER data for monitoring a debris covered glacier in the Italian Alps within the GLIMS project. Proc IGARSS 2002, 4, 1044–1046. [Google Scholar]
- EORS. ALOS user handbook. 2007. Electronic source. Available online at: http://www.eorc.jaxa.jp/ALOS/doc/alos_userhb_en.pdf Accessed on: 03-12-08.
- Narama, C.; Kääb, A.; Kajiura, T.; Abdrakhmatov, K. Spatial variability of recent glacier area and volume changes in Central Asia using Corona, Landsat, ASTER and ALOS optical satellite data. Geophys Res Abstr 2007, 9(08178). SRef-ID: 1607-7962/gra/EGU2007-A-08178. [Google Scholar]
- Aizen, V.B.; Aizen, E.M.; Kuzmichonok, V.A. Glaciers and hydrological changes in the Tien Shan: simulation and prediction. Environ Res Lett 2007, 2(045019). [Google Scholar] [CrossRef]
- Bishop, M.P.; Kargel, J.S.; Kieffer, H.H.; MacKinnon, D.J.; Raup, B.H.; Shroder, J.F. Remote-sensing science and technology for studying glacier processes in high Asia. Ann Glaciol 2000, 31, 164–170. [Google Scholar]
- Kargel, J.S.; Abrams, M.J.; Bishop, M.P.; Bush, A.; Hamilton, G.; Jiskoot, H.; Kaab, A.; Kieffer, H.H.; Lee, E.M.; Paul, F.; Rau, F.; Raup, B.; Shroder, J.F.; Soltesz, D.; Stainforth, D.; Stearns, L.; Wessels, R. Multispectral imaging contributions to global land ice measurements from space. Rem Sens Environ 2005, 99(1-2), 187–219. [Google Scholar]
- Raup, B.H.; Kieffer, H.H.; Hare, T.M.; Kargel, J.S. Generation of data acquisition requests for the ASTER satellite instrument for monitoring a globally-distributed target: glaciers. IEEE Trans Geosci Rem Sens 2000, 38, 1105–1112. [Google Scholar]
- Luckman, A.; Quincey, D.; Bevan, S. The potential of satellite radar interferometry and feature tracking for monitoring flow rates of Himalayan glaciers. Rem Sens Environ 2007, 111(2 - 3), 172–181. [Google Scholar]
- Quincey, D.J.; Richardson, S.D.; Luckman, A.; Lucas, R.M.; Reynolds, J.M.; Hambrey, M.J.; Glasser, N.F. Early recognition of glacial lake hazards in the Himalaya using remote sensing datasets. Global Planet Change 2007, 56(1 - 2), 137–152. [Google Scholar]
- Shi, J.C.; Dozier, J. Mapping seasonal snow with SIR-C/X-SAR in mountainous areas. Rem Sens Environ 1997, 59(2), 294–307. [Google Scholar]
- Albright, T.P.; Painter, T.H.; Roberts, D.A.; Shi, J.C.; Dozier, J.; Fielding, E. Classification of surface types using SIR-C/X-SAR, Mount Everest Area, Tibet. J Geophys Res B Solid Earth Planets 1998, 25823–25837. [Google Scholar]
- Paterson, W.S.B. The Physics of Glaciers, third ed.; Pergamon: Oxford, 1994. [Google Scholar]
- Vaughan, D.G.; Bamber, J.L.; Giovinetto, M.; Russell, J.; Cooper, A.P.R. Reassessment of Net Surface Mass Balance in Antarctica. J Clim 1999, 12(4), 933–946. [Google Scholar]
- Bamber, J.L.; Rivera, A. A review of remote sensing methods for glacier mass balance determination. Global Planet Change 2007, 59(1-4), 138–148. [Google Scholar]
- Barry, R.G. The status of research on glaciers and global glacier recession: a review. Progr Phys Geogr 2006, 30(3), 285–306. [Google Scholar]
- Bahr, D.B. Width and length scaling of glaciers. J Glaciol 1997, 43(145), 557–562. [Google Scholar]
- Bahr, D.B.; Meier, M.F.; Peckham, S.D. The physical basis of glacier volume-area scaling. J Geophys Res B Solid Earth Planets 1997, 102(B9), 20355–20362. [Google Scholar]
- Klein, A.G.; Isacks, B.L. Glaciers: tracking change in the central Andes Mountains. GIS World 1996, 9, 48–52. [Google Scholar]
- Duncan, C.C.; Klein, A.J.; Masek, J.G.; Isacks, B.L. Comparison of late Pleistocene and modern glacier extents in central Nepal based on digital elevation data and satellite imagery. Quaternary Res 1998, 49, 241–254. [Google Scholar]
- Hoelzle, M.; Haeberli, W.; Dischl, M.; Peschke, W. Secular glacier mass balances derived from cumulative glacier length changes. Global Planet Change 2003, 36(4), 295–306. [Google Scholar]
- Paul, F. The new Swiss glacier inventory 2000: Application of remote sensing and GIS. PhD thesis, Department of Geography, University of Zürich, Zürich, 2003; p. 198 pp. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Rem Sens Environ 1991, 37, 35–46. [Google Scholar]
- Dozier, J. Remote sensing of snow in the visible and near-infrared wavelengths. In Theory and Applications of Optical Remote Sensing; Asrar, G., Ed.; John Wiley and Sons: New York, 1989; pp. 527–547. [Google Scholar]
- Dozier, J. Snow reflectance from Landsat-4 Thematic Mapper. IEEE Trans Geosci Rem Sens 1984, GE-22, 323–328. [Google Scholar]
- Hall, D.K.; G. Riggs, A.; Salomonson, V.V. Development of methods for mapping global snow cover using moderate resolution imaging spectroradiometer data. Rem Sens Environ 1995, 54, 127–140. [Google Scholar]
- Sidjak, R. Glacier mapping of the Illecillewaet icefield, British Columbia, Canada, using Landsat TM and digital elevation data. Int J Rem Sens 1999, 20(2), 273–284. [Google Scholar]
- Bayr, J.J.; Hall, D.K.; Kovalick, W.M. Observations on glaciers in the eastern Austrian Alps using satellite data. Int J Rem Sens 1994, 15(9), 1733–1742. [Google Scholar]
- Dozier, J. Spectral Signature of Alpine Snow Cover from the Landsat Thematic Mapper. Rem Sens Environ 1989, 28, 9–22. [Google Scholar]
- Wessels, R.; Kargel, J.S.; Kieffer, H.H. ASTER measurement of supraglacial lakes in the Mount Everest region of the Himalaya. Ann Glaciol 2002, 34, 399–408. [Google Scholar]
- Zhang, H.; Suhong, L.; Qizhong, L.; Jiacheng, S. Sub-pixel lake mapping in Tibetan Plateau. IEEE Trans Geosci Rem Sens 2004, 0-7803-8742-2/04. 3073–3076. [Google Scholar]
- Paul, F.; Huggel, C.; Kääb, A. Combining satellite multispectral image data and a digital elevation model for mapping debris-covered glaciers. Rem Sens Environ 2004b, 89(4), 510–518. [Google Scholar]
- Nakawo, M.; Rana, B. Estimate of ablation rate of glacier ice under a supraglacial debris layer. Geogr Ann Phys Geogr 1999, 81A(4), 695–701. [Google Scholar]
- Mattson, L.E.; Gardner, J.S.; Young, G.J. Ablation on debris covered glaciers: an example from the Rakhiot Glacier, Panjab, Himalaya. In Snow and Glacier Hydrology, Proceedings of the International Symposium, Kathmandu, Nepal, 16-21 November 1992; Young, G.J., Ed.; IAHS Publication, 1993; p. 218. [Google Scholar]
- Takeuchi, Y.; Naruse, R.; Satow, K.; Ishikawa, N. Comparison of heat balance characteristics at five glaciers in the Southern Hemisphere. Global Planet Change 1999, 22(1-4), 201–208. [Google Scholar]
- Nakawo, M.; Morohoshi, T.; Uehara, S. Satellite data utilization for estimating ablation of debris covered glaciers. In Snow and Glacier Hydrology, Proceedings of the International Symposium, Kathmandu, Nepal, 16-21 November 1992; Young, G.J., Ed.; IAHS/AISH Publication, 1993; 218, pp. 75–83. [Google Scholar]
- Manley, W.F. Geospatial inventory and analysis of glaciers: A case study for the eastern Alaska Range. In Satellite Image Atlas of Glaciers of the World; Williams, R.S., Ferrigno, J. G., Jr, Eds.; USGS Professional Paper 1386-K; 2007; in press. [Google Scholar]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission--a new class of digital elevation models acquired by spaceborne radar. ISPRS J Photogram Rem Sens 2003, 57(4), 241–262. [Google Scholar]
- Berthier, E.; Arnaud, Y.; Baratoux, D.; Vincent, C.; Remy, F. Recent rapid thinning of the ”Mer de Glace“ glacier derived from satellite optical images. Geoph Res Lett 2004, 31(17). [Google Scholar]
- Berthier, E.; Vadon, H.; Baratoux, D.; Arnaud, Y.; Vincent, C.; Feigl, K.L.; Remy, F.; Legresy, B. Surface motion of mountain glaciers derived from satellite optical imagery. Rem Sens Environ 2005, 95(1), 14–28. [Google Scholar]
- Berthier, E.; Arnaud, Y.; Kumar, R.; Ahmad, S.; Wagnon, P.; Chevallier, P. Remote sensing estimates of glacier mass balances in the Himachal Pradesh (Western Himalaya, India). Rem Sens Environ 2007, 108(3), 327–338. [Google Scholar]
- Bolch, T.; Buchroithner, M.F.; Pieczonka, T.; Kunert, A. Planimetric and Volumetric Glacier Changes in the Khumbu Himalaya since 1962 Using Corona, Landsat TM and ASTER Data. J Glaciol in press. 2008. [Google Scholar]
- Lang, H.R.; Welch, R. Algorithm Theoretical Basis Document for ASTER Digital Elevation Models, Version 3.0; Jet Propulsion Laboratory: Pasadena, CA, 1999; p. 69. [Google Scholar]
- Kääb, A.; Huggel, C.; Paul, F.; Wessels, R.; Raup, B.; Kieffer, H.; Kargel, J. Glacier Monitoring from ASTER Imagery: Accuracy and Applications. Proceedings of EARSeL LIS-SIG Workshop, Berne, March 11-13, 2002; 2003. [Google Scholar]
- Eckert, S.; Kellenberger, T.; Itten, K. Accuracy assessment of automatically derived digital elevation models from ASTER data in mountainous terrain. Int J Rem Sens 2005, 26(9), 1942–1957. [Google Scholar]
- Kamp, U.; Bolch, T.; Olsenholler, J. Geomorphometry of Cerro Sillajhuay, Chile/Bolivia: comparison of DEMs derived from ASTER remote sensing data and contour maps. Geocarto International 2005, 20(1), 23–24. [Google Scholar]
- Fujita, K.; Suzuki, R.; Nuimura, T.; Sakai, A. Performance of ASTER and SRTM DEMs, and their potential for assessing glacial lakes in the Lunana region, Bhutan Himalaya. J Glaciol 2008, 54(185), 220–228. [Google Scholar]
- Fujisada, H.; Bailey, G.B.; Kelly, G.G.; Hara, S.; Abrams, M.J. ASTER DEM performance. IEEE Trans Geosci Rem Sens 2005, 43(12), 2702–2717. [Google Scholar]
- Welch, R.; Jordan, T.; Lang, H.; Murakami, H. ASTER as a source for topographic data in the late 1990's. IEEE Trans Geosci Rem Sens 1998, 36(4), 1282–1289. [Google Scholar]
- Hirano, A.; Welch, R.; Lang, H. Mapping from ASTER stereo image data: DEM validation and accuracy assessment. ISPRS J Photogram Rem Sen 2003, 57(5-6), 356–370. [Google Scholar]
- Bahr, D.B.; Dyurgerov, M. Characteristic mass-balance scaling with valley glacier size. J Glaciol 1999, 45(149), 17–21. [Google Scholar]
- Pfeffer, W.T.; Sassolas, C.; Bahr, D.B.; Meier, M.F. Response time of glaciers as a function of size and mass balance: 2. Numerical experiments. J Geophys Res B Solid Earth Planets 1998, 103(B5), 9783–9789. [Google Scholar]
- Oerlemans, J.; Dyurgerov, M.; Van de Wal, R.S.W. Reconstructing the glacier contribution to sea-level rise back to 1850. The Cryosphere Discuss. 2007, 1, pp. 77–97. www.the-cryosphere-discuss.net/1/77/2007/.
- Hoelzle, M.; Chinn, T.; Stumm, D.; Paul, F.; Zemp, M.; Haeberli, W. The application of glacier inventory data for estimating past climate change effects on mountain glaciers: A comparison between the European Alps and the Southern Alps of New Zealand. Global Planet Change 2007, 56(1-2), 69–82. [Google Scholar]
- Racoviteanu, A.E.; Manley, W.F.; Arnaud, Y.; Williams, M. Evaluating digital elevation models for glaciologic applications: An example from Nevado Coropuna, Peruvian Andes. Global Planet Change 2007, 59(1-4), 110–125. [Google Scholar]
- Rivera, A.; Casassa, G. Volume changes on Pio XI glacier, Patagonia: 1975-1995. Global Planet Change 1999, 22(1-4), 233–244. [Google Scholar]
- Kääb, A. Glacier Volume Changes using ASTER Optical Stereo. A Test Study in Eastern Svalbard. IEEE Trans Geosci Rem Sens 2007, 10.1109/IGARSS.2007.4423724. 3994–3996. [Google Scholar]
- Dedieu, J.-P.; Rabatel, A.; Vincent, C.; Valla, F.; Thibert, E.; Arnaud, Y. Glacier mass balance determination by remote sensing in the French Alps: progress and limitation for time series monitoring. Proceedings of Geoscience and Remote Sensing Symposium, IGARSS '032003; vol.4.
- Surazakov, A.B.; Aizen, V.B.; Aizen, E.M.; Nikitin, S.A. Glacier changes in the Siberian Altai mountains, Ob river basin (1952 - 2006) estimated with high resolution imagery. Environ Res Lett 2007. 10.1088/1748-9326/2/4/045017. [Google Scholar]
- Rabatel, A.; Dedieu, J.P.; Vincent, C. Using remote-sensing data to determine equilibrium-line altitude and mass-balance time series: validation on three French glaciers, 1994-2002. J Glaciol 2005, 51(175), 539–546. [Google Scholar]
- Rabatel, A.; Dedieu, J.-P.; Thibert, E.; Letreguilly, A.; Vincent, C. Twenty-five years of equilibrium-line altitude and mass balance reconstruction on the Glacier Blanc, French Alps (1981-2005), using remote-sensing method and meteorological data. J Glaciol 2008, (in press). [Google Scholar]
- Hagg, W.; Braun, L.; Uvarov, V.N.; Makarevich, K.G. A Comparison of three Methods of Mass Balance Determination in the Tuyuksu Glacier Region, Tien Shan. J Glaciol 2004, 50(171), 505–510. [Google Scholar]
- Berthier, E.; Arnaud, Y.; Vincent, C.; Remy, F. Biases of SRTM in high-mountain areas: Implications for the monitoring of glacier volume changes. Geoph Res Lett 2006, 33(8), L08502. [Google Scholar] [CrossRef]
- Dyurgerov, M. Substitution of long-term mass balance data by measurements of one summer. Zeitschrift für Gletscherkunde und Glazialgeologie 1996, 32, 177–184. [Google Scholar]
- Dyurgerov, M.; Chaohai, L.; Zichou, X. (Eds.) Oledenenie Tian Shanya (Tien Shan glaciers); VINITI: Moscow, Russia, In russian; 1995.
- Meier, M.F.; Post, A.S. Recent variations in mass net budgets of glaciers in western North America. Proceedings of Symposium of Obergurgl; 1962 IASH-AISH Publication, 1962; 58, pp. 63–67. [Google Scholar]
- Kaser, G.; Osmaston, H.A. Tropical glaciers; Cambridge University Press: Oxford, 2002. [Google Scholar]
- Kulkarni, A.V.; Rathore, B.P.; Alex, S. Monitoring of glacial mass balance in the Baspa basin using accumulation area ratio method. Curr Sci 2004, 86(1), 185–190. [Google Scholar]
- Khalsa, S.J.S.; Dyurgerov, M.B.; Khromova, T.; Raup, B.H.; Barry, R.G. Space-based mapping of glacier changes using ASTER and GIS tools. IEEE Trans Geosci Rem Sens 2004, 42(10), 2177–2183. [Google Scholar]
- Kayastha, R.B.; Takeuchi, Y.; Nakawo, M.; Ageta, Y. Practical prediction of ice melting beneath various thickness of debris cover on Khumbu Glacier, Nepal, using a positive degree-day factor. In Debris-Covered Glaciers; Raymond, C.F., Nakawo, M., Fountain, A., Eds.; IAHS: Wallingford, UK, 2000; Volume 264, pp. 71–81. [Google Scholar]
- Takeuchi, Y.; Kayastha, R.B.; Nakawo, M. Characteristics of ablation and heat balance in debris-free and debris-covered areas on Khumbu Glacier, Nepal Himalayas, in the pre-monsoon season. In Debris-covered glaciers; Fountain, A., Ed.; IAHS: Wallingsford, 2000; Volume 264, pp. 53–61. [Google Scholar]
- Nakawo, M.; Fujita, K.; Ageta, U.; Shankar, K.; Pokhrel, P.A.; Tandong, Y. Basic studies for assessing the impacts of the global warming on the Himalayan cryosphere. Bull Glacier Res 1997, 15, 53–58. [Google Scholar]
- Kaser, G.; Cogley, J.G.; Dyurgerov, M.B.; Meier, M.F.; Ohmura, A. Mass balance of glaciers and ice caps: Consensus estimates for 1961-2004. Geoph Res Lett 2006, 33(19). [Google Scholar]
- Ashish, A.; Joshi, V.; Sharma, A.; Anthwal, S. Retreat of Himalayan glaciers - indicator of climate change. Nat Sci 2006, 4(4), 53–60. [Google Scholar]
- Shen, Y. An overview of glaciers, retreating glaciers and their impact in the Tibetan Plateau; Cold and Arid Regions Environmental and Engineering Research Institute (CAREERI), Chinese Academy of Sciences (CAS): Lanzhou, China, 2004; p. 42. [Google Scholar]
- Mayewski, P.A.; Jeschke, P.A. Himalayan and Trans-Himalayan Glacier Fluctuations since Ad 1812. Arctic Antarct Alpine Res 1979, 11(3), 267–287. [Google Scholar]
- Dobhal, D.P.; Gergan, J.T.; Thayyen, R.J. Recession and morphogeometrical changes of Dokriani glacier (1962-1995) Garhwal Himalaya, India. Curr Sci 2004, 86(5), 692–696. [Google Scholar]
- Ageta, Y.; Iwata, S. Report of Japan-Bhutan joint research 1998 on the assessment of glacier lake outburst flood (GLOF) in Bhutan; IHAS, Nagoya University, 1999. [Google Scholar]
- Kadota, T.; Katsumoto, S.; Tatsuto, A.; Shuji, I.; Satoru, Y. Shrinkage of the Khumbu Glacier, east Nepal from 1978 to 1995. In Debris-covered glaciers; Fountain, A., Ed.; IAHS publication: Wallingsford, 2000; Volume 264, pp. 235–243. [Google Scholar]
- Shrestha, A.B.; Wake, C.P.; Mayewski, P.A.; Dibb, J.E. Maximum Temperature Trends in the Himalaya and Its Vicinity: An Analysis Based on Temperature Records from Nepal for the Period 1971–94. J Am Meteorol Soc 1999, 12, 2775–2786. [Google Scholar]
- Conway, H.; Rasmussen, L.A M. Summer temperature profiles within supraglacial debris on Khumbu Glacier, Nepal. In Debris-covered glaciers; Fountain, A., Ed.; IAHS: Wallingsford, 2000; Volume 264, pp. 53–61. [Google Scholar]
- Bahuguna, I.M.; Kulkarni, A.V. Application of Digital Elevation Model and ortho images derived from IRS-1C stereo data in monitoring variations in glacial dimensions. J Indian Soc Remote Sens 2005, 33(1), 107–112. [Google Scholar]
- Bahuguna, I.M.; Kulkarni, A.V.; Nayak, S.; Rathore, B.P.; Negi, H.S.; Mathur, P. Himalayan glacier retreat using IRS 1C PAN stereo data. Int J Rem Sens 2007, 28(2), 437–432. [Google Scholar]
- Carabajal, C.C.; Harding, D.J. SRTM C-band and ICESat laser altimetry elevation comparisons as a function of tree cover and relief. Photogramm Eng Rem Sens 2006, 72(3), 287–298. [Google Scholar]
- Dobhal, D.P.; Kumar, S. Inventory of glacier basins in Himachal Himalaya. J Geol Soc India 1996, 48(6), 671–681. [Google Scholar]
- Kulkarni, A.V. Glacier retreat in the Himalaya using Indian remote sensing data. In Agric Hydrol Appl Rem Sen; Saito, G., Ed.; Proc. of SPIE; 2006; Vol. 6411. [Google Scholar] [CrossRef]
- Kulkarni, A.V.; Bahuguna, I.M.; Rathore, B.P.; Singh, S.K.; Randhawa, S.S.; Sood, R.K.; Dhar, S. Glacial retreat in Himalaya using Indian Remote Sensing satellite data. Curr Sci 2007, 92(1), 69–74. [Google Scholar]
- Krishna, A.P. Snow cover and glacier assessments in parts of the Sikkim Himalaya by remote sensing and GIS. Proceedings of NSSW'99 National Snow Science Workshop, Snow and Avalanche Study Establishment (SASE), Manali, India; DRDO, Govt. of India, 1999; pp. 33–40. [Google Scholar]
- Krishna, A.P. Satellite remote sensing applications for snow cover characterization in the morphogenetic regions of upper Tista River basin, Sikkim Himalaya. Int J Rem Sens 1996, 17(4), 651–656. [Google Scholar]
- Puri, V.M.K.; Shukla, S.P. Tongue fluctuation studies of Gangotri glacier, Uttarkashi district, Uttar Pradesh. Geol Surv India 1996, 21(2), 289–291. [Google Scholar]
- Ahmad, S.; Hasnain, S.I.; Arha, C.D.; Ramamurthy, V.S.; Mathur, K.N.; Bassi, U.K. Analysis of satellite imageries for characterization of glacio-morphological features of the Gangotri Glacier, Ganga headwater, Garhwal Himalaya. Proceedings of Workshop on Gangotri Glacier Special Publication Series - Geological Survey of India; 2004; 80, pp. 61–67. [Google Scholar]
- Kayastha, R.B.; Ohata, T.; Ageta, Y. Application of a mass-balance model to a Himalayan glacier. J Glaciol 1999, 45(151), 559–567. [Google Scholar]
- Ueno, K.; Kayastha, R.B.; Chitrakar, M.R.; Bajracharya, O.R.; Pokhrel, A.P.; Fujinami, H.; Kadota, T.; Iida, H.; Manandhar, D.P.; Hattori, M.; Yasunari, T.; Nakawo, M. Meteorological observations during 1994-2000 at the Automatic Weather Station (GEN-AWS) in Khumbu region, Nepal Himalayas. Bull Glacier Res 2001, 18, 23–30. [Google Scholar]
- Ueno, K.; Iida, H.; Yabuki, H.; Seko, K.; Lhakupa, G.S.; Kayastha, R.B.; Pokhrel, A.P.; Shrestha, M.L.; Yasunari, T.; Nakawo, M. Establishment of the GEN Automatic Weather Station (AWS) in Khumbu region, Nepal Himalayas. Bull Glacier Res 1996, 14, 13–32. [Google Scholar]
- Krishna, A.P. Snow and glacier cover assessment in the high mountains of Sikkim Himalaya. Hydrolog Process 2005, 19(12), 2375–2383. [Google Scholar]
- Bishop, M.P.; Bonk, R.; Kamp, U.J.F.; Shroder, J. Terrain analysis and data modeling for alpine glacier mapping. Polar Geogr 2001, 25(3), 182–201. [Google Scholar]
- Bolch, T.; Buchroithner, M.F.; Kunert, A.; Kamp, U. Automated delineation of debris-covered glaciers based on ASTER data. In Geoinformation in Europe (Proc. of 27th EARSel Symposium, 04 - 07 June 2007); Bozen, Italy, 2007; pp. 403–410. [Google Scholar]
- Nakawo, M.; Yabuki, H.; Sakai, A. Characteristics of Khumbu Glacier, Nepal Himalaya: recent change in the debris-covered area. Ann Glaciol 1999, 28, 118–122. [Google Scholar]
- Suzuki, R.; Fujita, K.; Ageta, Y. Spatial distribution of thermal properties on debris-covered glaciers in the Himalayas derived from ASTER data. Bull Glacier Res. 2007, 24, 13–22. [Google Scholar]




© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Racoviteanu, A.E.; Williams, M.W.; Barry, R.G. Optical Remote Sensing of Glacier Characteristics: A Review with Focus on the Himalaya. Sensors 2008, 8, 3355-3383. https://doi.org/10.3390/s8053355
Racoviteanu AE, Williams MW, Barry RG. Optical Remote Sensing of Glacier Characteristics: A Review with Focus on the Himalaya. Sensors. 2008; 8(5):3355-3383. https://doi.org/10.3390/s8053355
Chicago/Turabian StyleRacoviteanu, Adina E., Mark W. Williams, and Roger G. Barry. 2008. "Optical Remote Sensing of Glacier Characteristics: A Review with Focus on the Himalaya" Sensors 8, no. 5: 3355-3383. https://doi.org/10.3390/s8053355
APA StyleRacoviteanu, A. E., Williams, M. W., & Barry, R. G. (2008). Optical Remote Sensing of Glacier Characteristics: A Review with Focus on the Himalaya. Sensors, 8(5), 3355-3383. https://doi.org/10.3390/s8053355



