1. Introduction
Diabetes is a common disease related to endocrine metabolism. At present there is no method which can cure diabetes totally. The main therapy is to prevent or alleviate the occurrence of complications through frequent monitoring and adjustment of the glucose level. Physicians suggest that the glucose level should be tested at least four times per day. A non-invasive method could realize this requirement easily, because it is painless and does not infect the patient with other diseases. If it works, it would be the most effective way to make the diabetic's life easier.
At present, the research on non-invasive glucose measurement focuses mainly on the technique of spectrum detection, such as near infrared detection [
1-
4], mid-IR detection [
5], Raman Spectrum detection [
6], optoacoustic detection [
7], polarimetry [
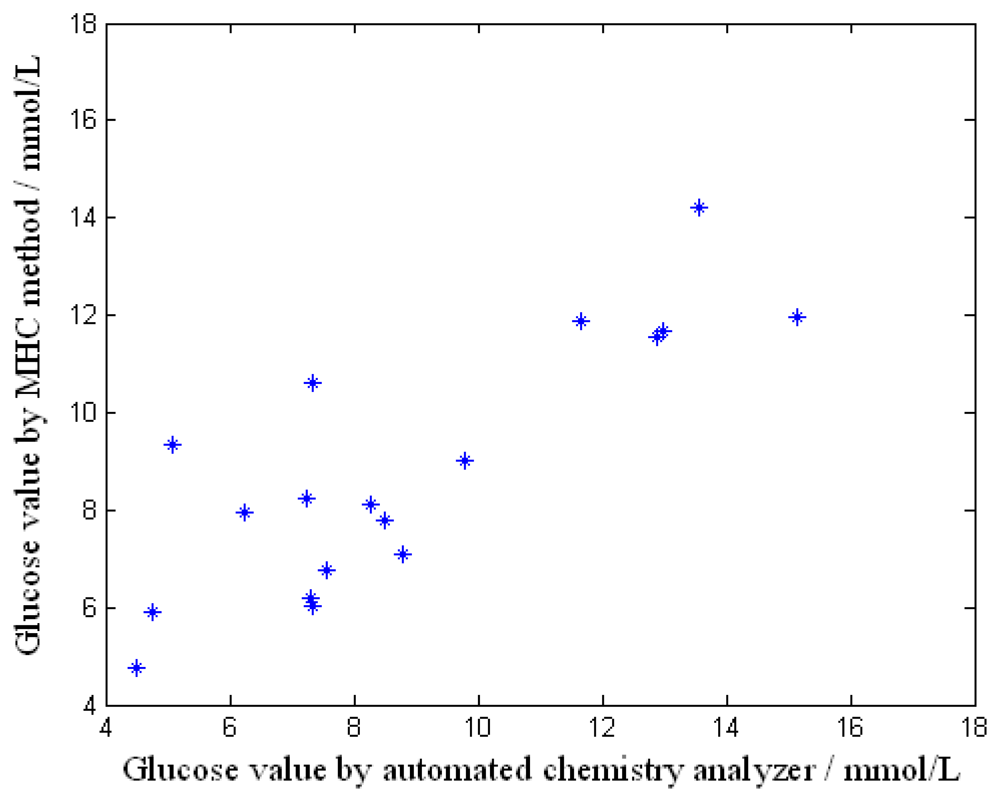
8], and so on. Though these methods have been studied for years, they have remarkably achieved no great improvements in sensitivity and accuracy. In this paper, a non-invasive glucose measurement system based on the MHC method is developed and the clinical tests show that this method has good effect and high optimization potential.
2. Detection Principle
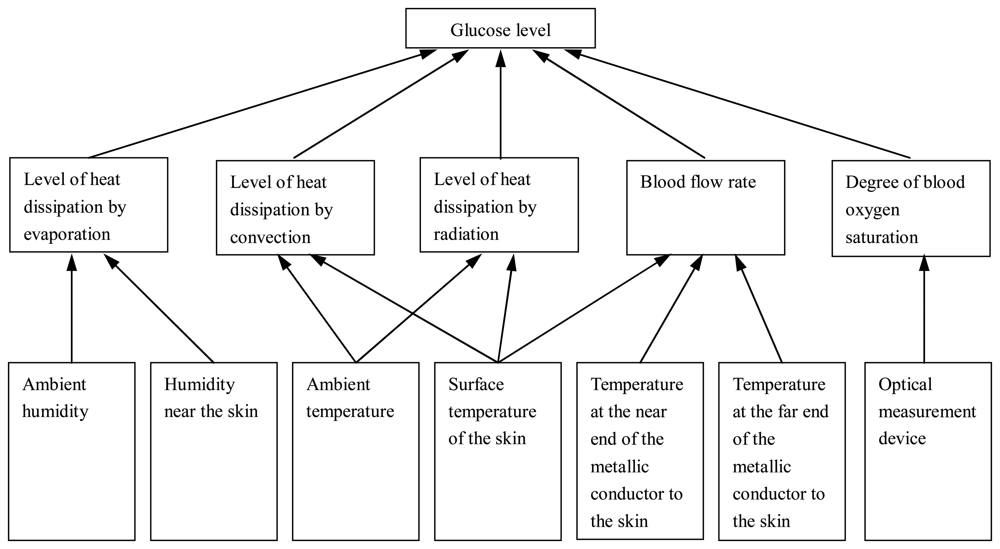
The homoeostatic circadian rhythm of the human body depends on the correlation between metabolic heat, local oxygen supply level and glucose level. Glucose and oxygen are supplied to the cells in the body through the blood circulation system. The oxidation of glucose is related to the generation of energy which can be emitted into the environment in the form of heat, so the quantity of dissipated heat is correlated to the quantity of dissipative glucose and oxygen [
9]. The MHC method is based on this. Since the quantity of supplied oxygen is the function of the degree of blood oxygen saturation and the blood flow rate in the capillary vessel, the quantity of dissipated heat will be
where
H is the quantity of dissipated heat,
G is the glucose level,
BF is the blood flow rate and
O is the degree of blood oxygen saturation. The glucose level can be obtained as long as
H,
BF and
O are measured.
The main forms of the heat emitted in the environment are radiation, convection and evaporation. The heat dissipated through radiation is related to the skin's surface temperature and ambient temperature. According to the Stefan-Boltzmann law, the heat transferred by radiation can be obtained through measurement of the skin's surface temperature by the infrared sensor and measurement of the ambient temperature by the thermal resistor, which is
where
R is the quantity of heat dissipated by radiation,
δ is the coefficient of radiation,
S is the area of radiation,
TS is the absolute temperature of the surface and
TA is the absolute temperature of ambience.
The heat dissipated by convection is also conditionally related to the surface temperature and ambient temperature. According to Newton's formula of cooling, the transferred heat is
where
C is the quantity of heat transferred by convection and
hc is the coefficient of heat transferred by convection.
The heat dissipated by evaporation is related to the quantity of evaporation from the skin's surface. The skin is supposed to be dry and there is no sweat to make the skin wet. Then the skin is in the state of insensible perspiration which Vanger thinks is not controlled by the regulating system of heat, and can be expressed as
where
E is the heat dissipated by evaporation,
r is the latent heat of vaporization,
m is the permeability coefficient of the skin,
psk is saturated pressure component of the water vapour in the air on the skin's surface and
pa is partial pressure of ambient water vapour.
When the skin surface contacts a heat conductor with lower temperature, heat transmission will occur between them. Then the surface temperature changes, and so does the temperature of the heat conductor's two ends. The quantity of variation relies on the quantity of heat transferred from the surface to the heat conductor, which relies on the blood flow rate in the capillary vessel. So the blood flow rate can be calculated through measurement of the temperature change of the conductor's ends. This method of measurement will be described in the next section.
The degree of blood oxygen saturation can be measured by the optical method, for which the formula is
where
Chbo2 and
Chb are concentrations of oxyhaemoglobin and haemoglobin respectively,
k1hb and
k2hb are extinction coefficients of haemoglobin to two kinds of light with different wavelengths,
k1hbo2 and
k2hbo2 are extinction coefficients of oxyhaemoglobin to two kinds of light with different wavelengths and Δ
A1 and Δ
A2 are the intensities of two kinds of light with different wavelengths absorbed by arterial blood.
3. Principle and Simulation of Blood Flow Rate Measurement by Use of Thermal Diffusion
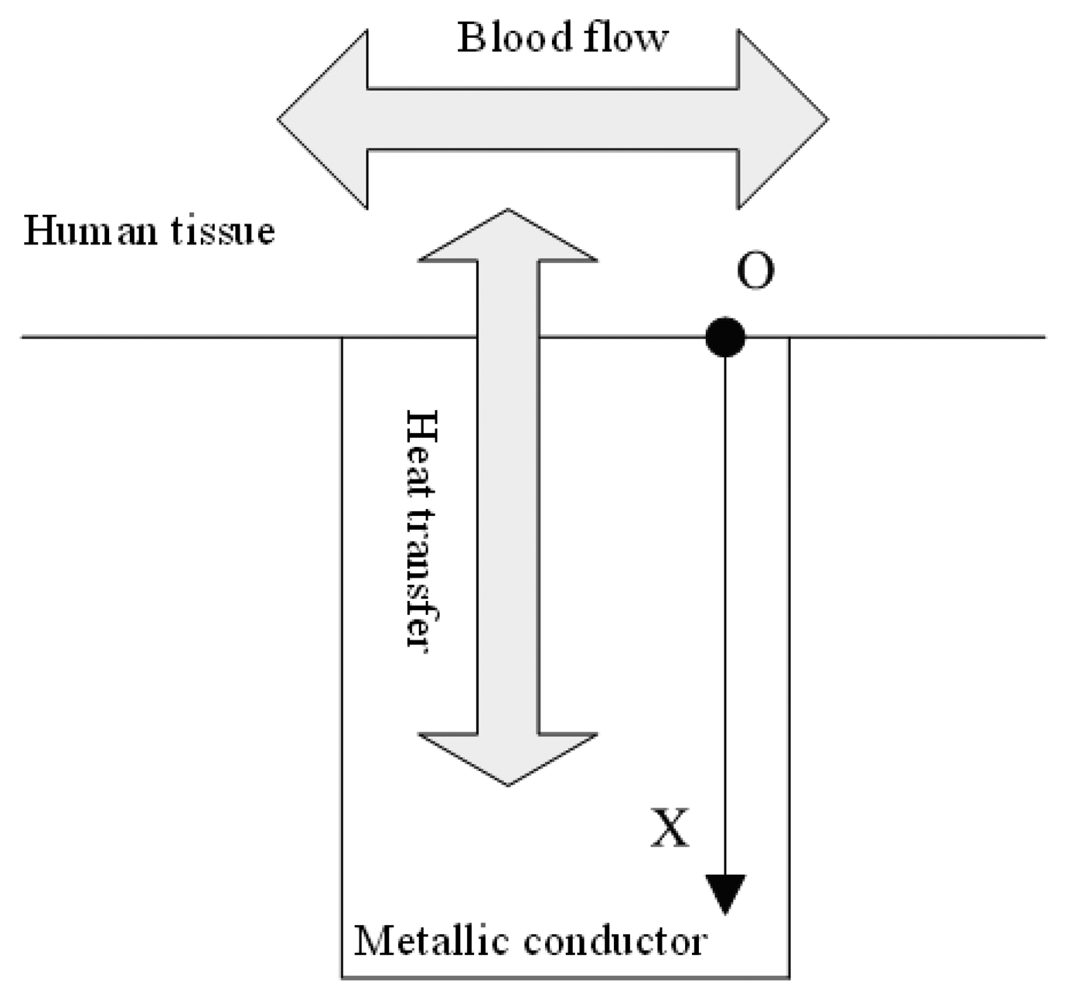
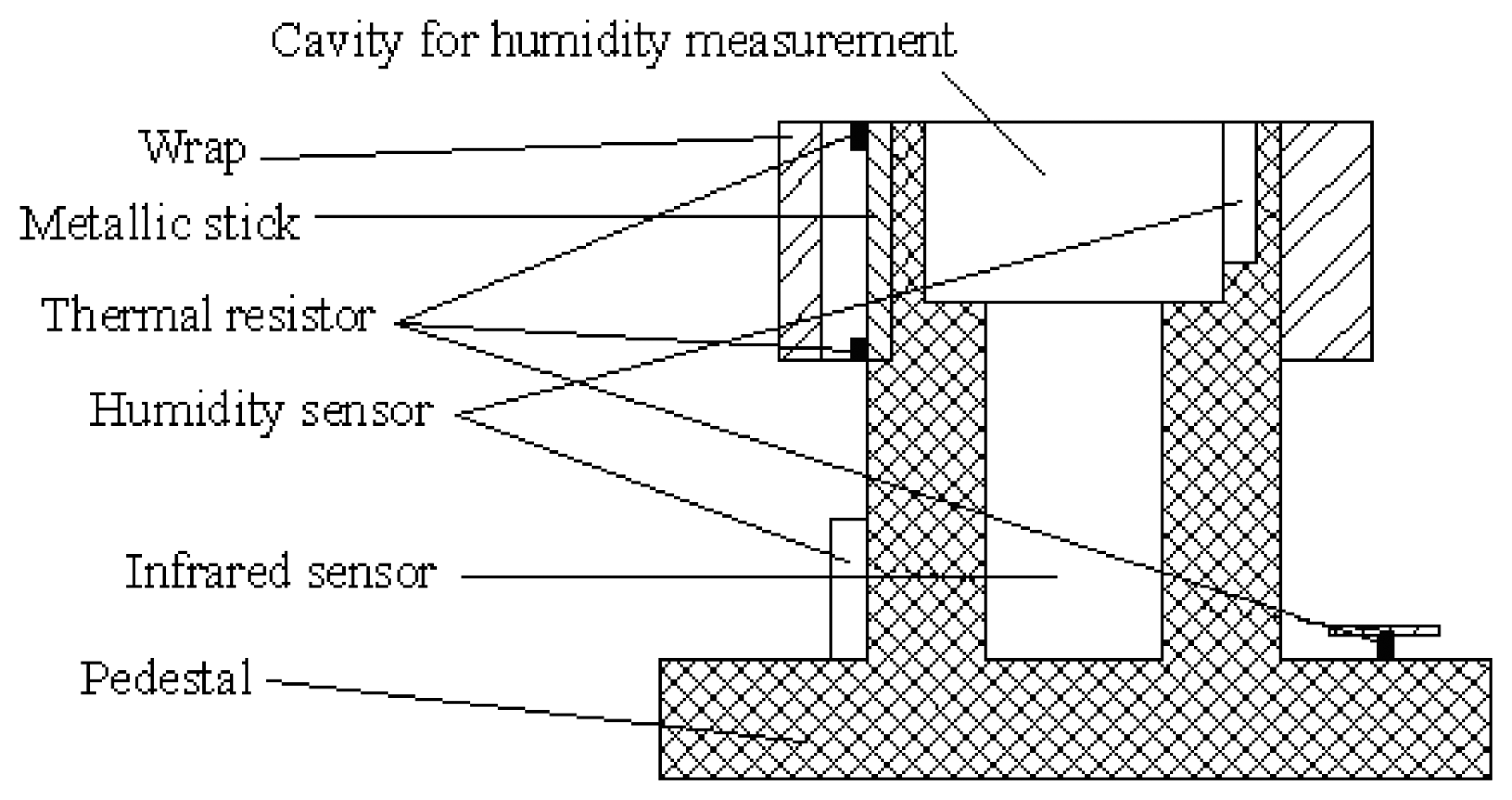
When the skin contacts a metallic conductor of lower temperature, heat transmission will occur between them, and the temperature of the skin will change, as shown in
Fig. 1.
After the variation of the dermal temperature, heat transmission will occur between the blood and skin for the temperature difference. The quantity of heat transferred from blood to skin is
where
T2 is the skin temperature,
T1 is the blood initial temperature,
c1 is the heat capacity of the blood,
ρ1 is the density of the blood and
v1 is the flow rate of the blood.
In the time of d
t, the quantity of heat transmitted from the contact point of the finger to the conductor is
where
T3(0) is the temperature of the conductor at the contact point and
u2 is the heat transfer coefficient between the skin and the conductor.
In the conductor, the quantity of heat transmitted is
where d
w3+ is the quantity of heat transmitted from any point in the conductor to the positive x axis, d
w3- is the quantity of heat transmitted from any point in the conductor to the negative x axis,
T′
3+ is the right-hand derivative of the temperature,
T′
3- is the left-hand derivative of the temperature,
u1 is the coefficient of heat conduction of the conductor and
s is the cross-sectional area of the conductor.
The quantity of heat change in the skin of the finger is the difference between the quantity of heat transmitted from blood to the skin and the quantity of heat transmitted from the skin to the conductor
where
m2 is the equivalent mass of the finger skin and
c2 is the equivalent heat capacity of the finger skin.
The equation of temperature change at the contact point between the conductor and the skin is
where
ρ3 is the density of the conductor and
c3 is the heat capacity of the conductor.
The equation of temperature change at any point in the conductor is
The equation of temperature change at the other end of the conductor is
where
L is the length of the conductor.
The temperature variation curve at any point of the conductor with different blood flow rate can be obtained from (6) - (13) by programming. The temperature change at any point of the conductor can reflect the changes of blood flow rate theoretically, so there are two methods to express the blood flow rate, which are the temperature change at the near end of the conductor to the skin and the temperature difference between the near end and the far end.
To compare the temperature curve at different skin temperatures and ambient temperatures, the temperature at any point of the conductor is normalized. The formula is
where
T(
t) is the normalized temperature,
Tx(
t) is the temperature at any point of the conductor,
Ts is the initial of the skin and
Tc is the initial temperature of the conductor.
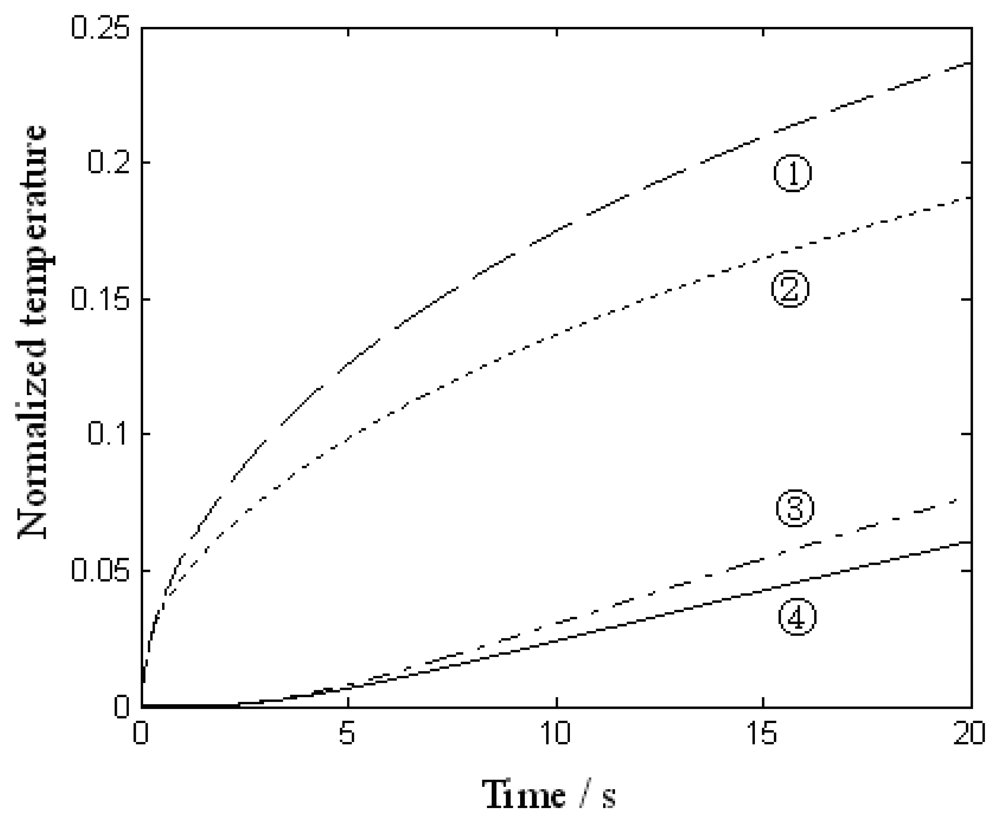
With the initial temperature of blood at 33 degrees Celsius, skin at 33 degrees Celsius and metallic conductor at 23 degrees Celsius, the normalized temperature curves at the contact point between the conductor and the skin, and the curves at the other end of the conductor at blood flow rate
νb1 and
νb2,
νb1<
νb2, are shown in
Fig. 2. Lines 1 and 3 are the curve at the contact point and the curve at the other end at
νb2. Lines 2 and 4 are the curve at the contact point and the curve at the other end at
νb1. It can be concluded from the figure that when the blood flow rate is larger, the rate of normalized temperature rise is larger.
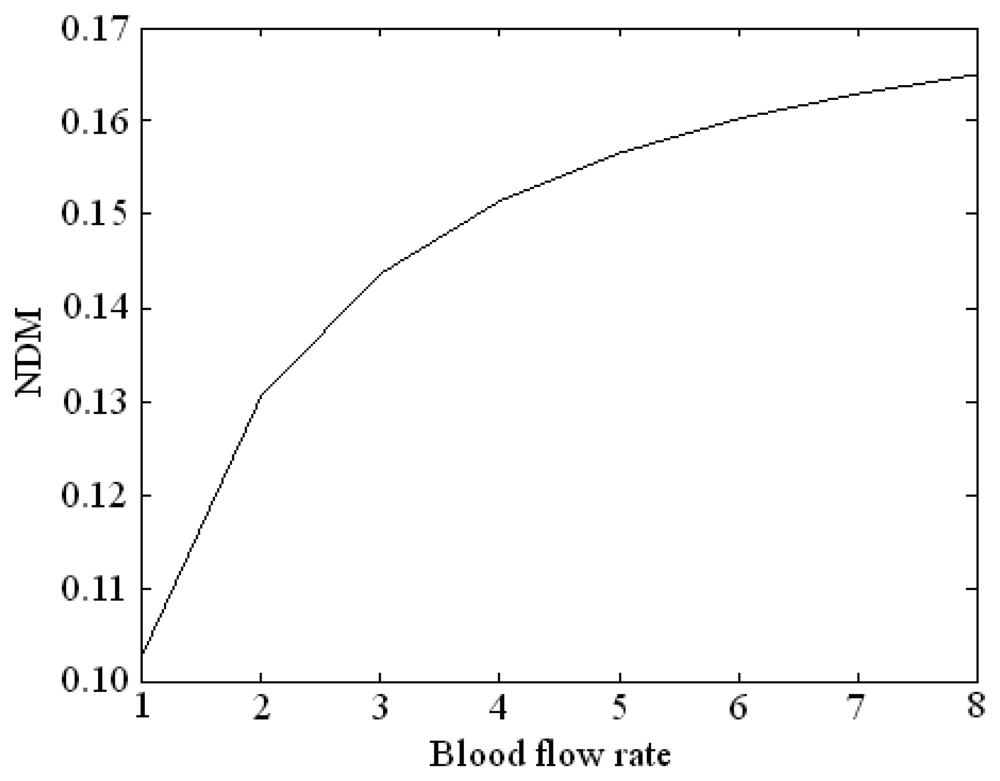
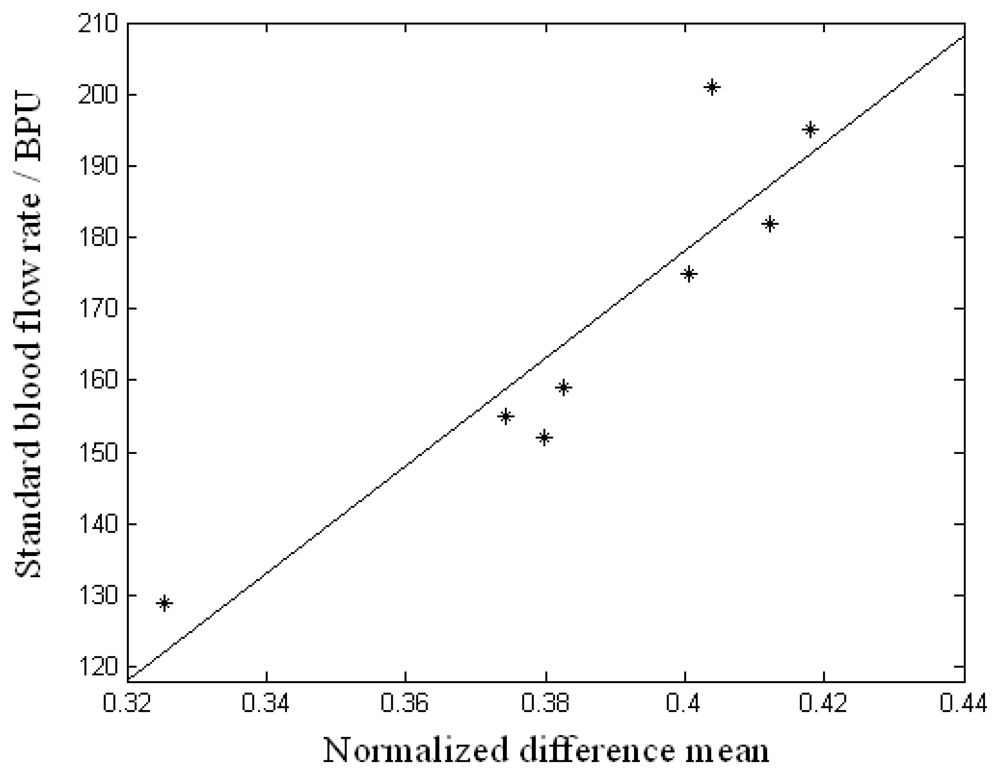
The normalized temperature curve can be reflected quantitatively by median value, slope or mean. Since the median value and the slope use only several points of the curve, local error has greater influence on the result. Thus the so-called normalized difference mean (NDM) is chosen to express the magnitude of the blood flow rate. The NDM is defined as the difference of the area integral of the two normalized temperature curves at the two ends of the conductor divided respectively by the integral length of the x axis at a blood flow rate. The NDMs for different blood flow rates, are shown in
Fig. 3. It can be seen that when the blood flow rate is larger, the NDM is larger.