Alpine Grassland Phenology as Seen in AVHRR, VEGETATION, and MODIS NDVI Time Series - a Comparison with In Situ Measurements
Abstract
:1. Introduction
1.1. Scientific Context
1.2. Study Overview
2. Data and Methods
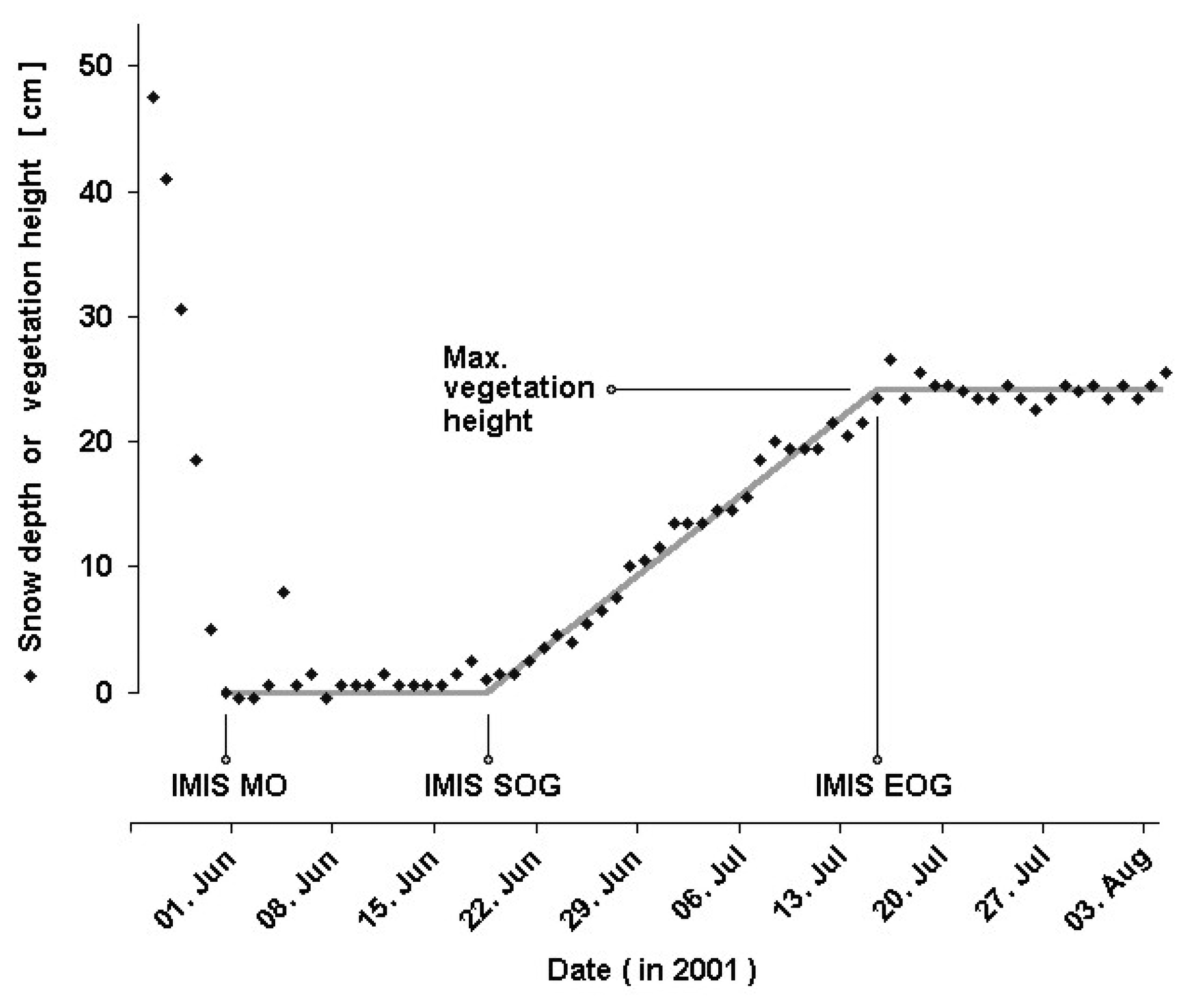
2.1. Ground Data Set
2.2. Remote Sensing Data Sets
2.2.1. NOAA AVHRR
2.2.2. SPOT VEGETATION
2.2.3. TERRA MODIS
2.3. Application of Smoothing Algorithms
2.3.1. Fourier Adjustment
2.3.2. Savitzky-Golay Filter
2.4. Comparison of Remote Sensing and Ground Data
3. Results
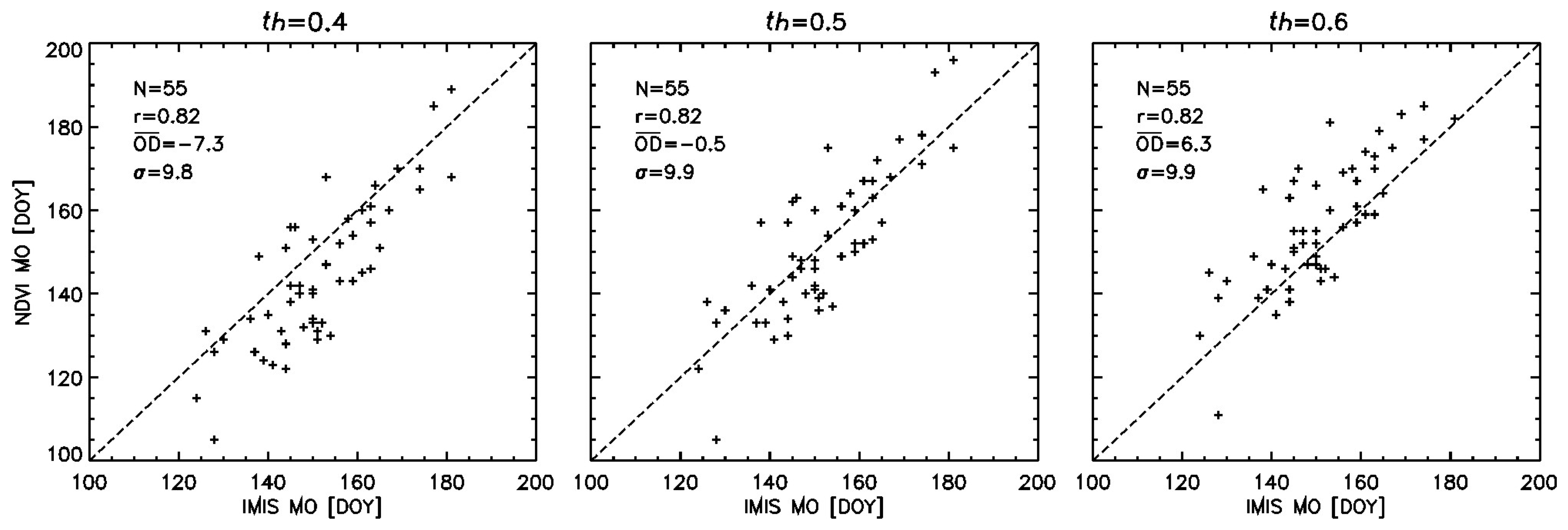
3.1. Comparison of AVHRR NDVI Time Series and IMIS phenological dates
3.2. Comparison to VGT and MODIS products
4. Discussion
4.1. Determination of Thresholds
- Melt-out: th≈0.6
- Start of growth: th≈0.75
- End of growth: th≈0.98
4.2. Smoothing Algorithm Performance
4.3. AVHRR vs. Newer Generation Sensors
4.4. Explanation of OD Standard Deviation
5. Conclusion and Outlook
Acknowledgments
References
- Studer, S.; Stöckli, R.; Appenzeller, C.; Vidale, P. A comparative study of satellite and ground-based phenology. International Journal of Biometeorology 2007, 51, 405–414. [Google Scholar]
- Menzel, A. Trends in phenological phases in Europe between 1951 and 1996. International Journal of Biometeorology 2000, 44, 76–81. [Google Scholar]
- Roetzer, T.; Wittenzeller, M.; Haeckel, H.; Nekovar, J. Phenology in central Europe - differences and trends of spring phenophases in urban and rural areas. International Journal of Biometeorology 2000, 44, 60–66. [Google Scholar]
- Defila, C.; Clot, B. Phytophenological trends in Switzerland. International Journal of Biometeorology 2001, 45, 203–207. [Google Scholar]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. Journal of Geophysical Research 2001, 106, 20069–20084. [Google Scholar]
- Fisher, J.I.; Mustard, J. F. Cross-scalar satellite phenology from ground, Landsat, and MODIS data. Remote Sensing of Environment 2007, 109, 261–273. [Google Scholar]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Global Biogeochemical Cycles 1997, 11, 217–234. [Google Scholar]
- Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. Journal of Vegetation Science 1994, 5, 703–714. [Google Scholar]
- Chen, X.; Xu, C.; Tan, Z. An analysis of relationships among plant community phenology and seasonal metrics of Normalized Difference Vegetation Index in the northern part of the monsoon region of China. International Journal of Biometeorology 2001, 45, 170–177. [Google Scholar]
- Braun, P.; Hense, A. Combining ground-based and satellite data for calibrating vegetation indices. Proceedings SPOT 4/5 Vegetation unser's Conference, Antwerp; 2004; pp. 137–141. [Google Scholar]
- Fisher, J.I.; Mustard, J.F.; Vadeboncoeur, M.A. Green leaf phenology at landsat resolution: Scaling from the field to the satellite. Remote Sensing of Environment 2006, 100, 265–279. [Google Scholar]
- Fensholt, R.; Sandholt, I.; Stisen, S. Evaluating MODIS, MERIS, and VEGETATION vegetation indices using in situ measurements in a semiarid environment. IEEE Transactions on Geoscience and Remote Sensing 2006, 44, 1774–1786. [Google Scholar]
- Stöckli, R.; Vidale, P.L. European plant phenology and climate as seen in a 20 year AVHRR land-surface parameter dataset. International Journal of Remote Sensing 2004, 25, 3303–3330. [Google Scholar]
- Justice, C.O.; Townshend, J.R.G.; Holben, B.N.; Tucker, C.J. Analysis of the phenology of global vegetation using meteorological satellite data. International Journal of Remote Sensing 1985, 6, 1271–1318. [Google Scholar]
- Tucker, C.J.; Sellers, P.J. Satellite remote sensing of primary production. International Journal of Remote Sensing 1986, 7, 1395–1416. [Google Scholar]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. International Journal of Remote Sensing 1986, 7, 1417–1434. [Google Scholar]
- Gutman, G.G. Vegetation indices from AVHRR: An update and future prospects. Remote Sensing of Environment 1991, 35, 121–136. [Google Scholar]
- Viovy, N.; Arino, O.; Belward, A. The Best Index Slope Extraction (BISE): a method for reducing noise in NDVI time-series. International Journal of Remote Sensing 1992, 13, 1585–1590. [Google Scholar]
- Sellers, P.; Los, S.O.; Tucker, C.J.; Justice, C.O.; Dazlich, D.A.; Collatz, G.J.; Randall, D.A. A revised land surface parametrization (SiB2) for atmospheric GCMs. Part II. The generation of global fields of terrestrial biophysical parameters from satellite data. Journal of Climate 1996, 9, 706–737. [Google Scholar]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sensing of Environment 2004, 91, 332–344. [Google Scholar]
- Jönsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Transactions on Geoscience and Remote Sensing 2002, 40, 1824–1832. [Google Scholar]
- Beniston, M.; Diaz, H.F.; Bradley, R.S. Climatic change at high elevation sites: An overview. Climatic Change 1997, 36, 233–251. [Google Scholar]
- Wanner, H.; Holzhauser, H.; Pfister, C.; Zumbühl, H. Interannual to century scale climate variability in the European Alps. Erdkunde 2000, 24, 62–69. [Google Scholar]
- Wanner, H.; Rickli, R.; Salvisberg, E.; Schmutz, C.; Schuepp, M. Global climate change and variability and its influence on Alpine climate - concepts and observations. Theoretical and Applied Climatology 1997, 58, 221–243. [Google Scholar]
- Grabherr, G.; Gottfried, M.; Pauli, H. Climate effects on mountain plants. Nature 1994, 369, 448–448. [Google Scholar]
- Walther, G.R.; Beissner, S.; Pauli, H. Trends in the upward shift of alpine plants. Journal of Vegetation Science 2005, 16, 541–548. [Google Scholar]
- James, M.; Kalluri, S. The pathfinder AVHRR land data set: An improved coarse resolution data set for terrestrial monitoring. International Journal of Remote Sensing 1994, 15, 3347–3363. [Google Scholar]
- Studer, S.; Appenzeller, C.; Defila, C. Inter-annual variability and decadal trends in Alpine spring phenology: A multivariate analysis approach. Climatic Change 2005, 73, 395–414. [Google Scholar]
- Rhyner, J.; Bründl, M.; Etter, H. J.; Steiniger, M.; Stöckli, U.; Stucki, T.; Zimmerli, M.; Amman, W. Avalanche warning Switzerland - consequences of the avalanche winter 1999. Proceedings of the 13th Int. Snow Science Workshop, Penticton, B.C., Canada; 2002. [Google Scholar]
- Jonas, T.; Rixen, C.; Sturm, M.; Stöckli, V. How alpine plant growth is linked to snow cover and climate variability. Journal of Geophysical Research - BioGeoSciences. in press.
- Goodrum, G.; Kidwell, K. B.; Winston, W. NOAA KLM user's guide; Technical report; National Environmental Satellite, Data, and Information Services (NESDIS), 2000. [Google Scholar]
- Key, J. The cloud and surface parameter retrieval (CASPR) system for polar AVHRR - user's guide; Technical report; Cooperative Institute for Meteorological Satellite Studies, University of Wisconsin: 1225 West Dayton St., Madison, WI; p. 53562. 2002. [Google Scholar]
- Di Vittorio, A.V.; Emery, W. J. An automated, dynamic threshold cloud-masking algorithm for daytime AVHRR images over land. IEEE Transactions on Geoscience and Remote Sensing 2002, 40, 1682–1694. [Google Scholar]
- Hauser, A.; Oesch, D.; Foppa, N.; Wunderle, S. NOAA AVHRR derived Aerosol Optical Depth over land. Journal of Geophysical Research 2005, 110, 8204, −+. [Google Scholar]
- VEGETATION Programme. SPOT Vegetation User Guide. 1998. http://www.spot-vegetation.com/.
- Barnes, W.L.; Pagano, T.S.; Salomonson, V.V. Prelaunch characteristics of the Moderate resolution Imaging Spectroradiometer (MODIS) on EOS-AM1. IEEE Transactions on Geoscience and Remote Sensing 1998, 36, 1088–1100. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Analytical Chemistry 1964, 36, 1627–1639. [Google Scholar]
- Jönsson, P.; Eklundh, L. TIMESAT–a program for analyzing time-series of satellite sensor data. Computers and Geosciences 2004, 30, 833–845. [Google Scholar]
- Tucker, C.J.; Vanpraet, C.L.; Sharman, M.J.; Van Ittersum, G. Satellite remote sensing of total herbaceous biomass production in the Senegalese Sahel: 1980-1984. Remote Sensing of Environment 1985, 17, 233–249. [Google Scholar]
- Kennedy, P. Monitoring the vegetation of Tunisian grazing lands using the normalized difference vegetation index. Ambio 1989, 18, 119–123. [Google Scholar]
- Kawamura, K.; Akiyama, T.; Watanabe, O.; Hasegawa, H.; Zhang, F.; Yokota, H.; Wang, S. Estimation of aboveground biomass in Xilingol Steppe, Inner Mongolia using NOAA/NDVI. Grassland Science 2003, 49, 1–9. [Google Scholar]
- Wilson, T.; Meyers, T. Determining vegetation indices from solar and photosynthetically active radiation fluxes. Agricultural and Forest Meteorology 2007, 144, 160–179. [Google Scholar]
- Vescovo, L.; Gianelle, D. Mapping the green herbage ratio of grasslands using both aerial and satellite-derived spectral reflectance. Agriculture, Ecosystems & Environment 2006, 115, 141–149. [Google Scholar]
- Vescovo, L.; Gianelle, D. Using the MIR bands in vegetation indices for the estimation of grassland biophysical parameters from satellite remote sensing in the Alps region of Trentino (Italy). Advances in Space Research 2007, in press. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J. MODIS NDVI optimization to fit the AVHRR data series–spectral considerations. Remote Sensing of Environment 1998, 66, 343–350. [Google Scholar]
- Teillet, P.M.; Staenz, K.; William, D.J. Effects of spectral, spatial, and radiometric characteristics on remote sensing vegetation indices of forested regions. Remote Sensing of Environment 1997, 61, 139–149. [Google Scholar]
- Cihlar, J.; Ly, H.; Li, Z.; Chen, J.; Pokrant, H.; Huang, F. Multitemporal, multichannel AVHRR data sets for land biosphere studies - artifacts and corrections. Remote Sensing of Environment 1997, 60, 35–57. [Google Scholar]
- Los, S.; North, P.; Grey, W.; Barnsley, M. A method to convert AVHRR Normalized Difference Vegetation Index time series to a standard viewing and illumination geometry. Remote Sensing of Environment 2005, 99, 400–411. [Google Scholar]
- Lee, T.Y.; Kaufman, Y. J. Non-Lambertian effects on remote sensing of surface reflectance and vegetation index. IEEE Transactions on Geoscience and Remote Sensing 1986, 24, 699–708. [Google Scholar]
- Kawamura, K.; Akiyama, T.; Yokota, H.-o.; Tsutsumi, M.; Yasuda, T.; Watanabe, O.; Wang, S. Comparing modis vegetation indices with AVHRR NDVI for monitoring the forage quantity and quality in Inner Mongolia grassland, China. Grassland Science 2005, 51, 33–40. [Google Scholar]
- Justice, C.; Eck, T.; Tanré, D.; Holben, B. The effect of water vapor on the normalized difference vegetation index derived for the Sahelian region from NOAA AVHRR data. International Journal of Remote Sensing 1991, 12, 1165–1187. [Google Scholar]
- Kästner, M.; Kriebel, K.T. Alpine cloud climatology using long-term NOAA AVHRR satellite data. Theoretical and Applied Climatology 2001, 68, 175–195. [Google Scholar]
- Winkler, P.; Lugauer, M.; Reitbuch, O. Alpine pumping. promet 2006, 32, 34–42. [Google Scholar]
- Liston, G.E.; Sturm, M. A snow-transport model for complex terrain. Journal of Glaciology 1998, 44, 498–516. [Google Scholar]
- Keller, F.; Goyette, S.; Beniston, M. Sensitivity analysis of snow cover to climate change scenarios and their impact on plant habitats in alpine terrain. Climatic Change 2005, 72, 299–319. [Google Scholar]
- Liston, G.E. Interrelationships among snow distribution, snowmelt, and snow cover depletion: Implications for atmospheric, hydrologic, and ecologic modeling. Journal of Applied Meteorology 1999, 38, 1474–1487. [Google Scholar]


| AVHRR/3 [32] | VGT [36] | MODIS [37] | |
|---|---|---|---|
| red [nm] | 580-680 | 610-680 | 620-670 |
| NIR [nm] | 725-1000 | 780-890 | 841-876 |
| [a] AVHRR (1 km) | [b] VEGETATION (1 km) | [c] MODIS (500 m) | [d] MODIS (1 km) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fourier | |||||||||||||||
| N=55 | th | r | th | r | th | r | th | r | |||||||
| MO | 0.5 | 0.61 | −7.1±13.3 | MO | 0.5 | 0.78 | −3.6±11.0 | MO | 0.4 | 0.82 | −7.3±9.8 | MO | 0.4 | 0.8 | −6.8±11.4 |
| 0.6 | 0.61 | 0.3±13.4 | 0.6 | 0.78* | 3.5±10.9 | 0.5 | 0.82* | −0.5±9.9* | 0.5 | 0.8* | 0.2±11.7 | ||||
| 0.7 | 0.60 | 7.9±13.4 | 0.7 | 0.79 | 10.7±10.8 | 0.6 | 0.82 | 6.3±9.9 | 0.6 | 0.81 | 7.1±11.3 | ||||
| SOG | 0.7 | 0.63 | −6.2±13.4 | SOG | 0.7 | 0.77 | −3.4±11.4 | SOG | 0.6 | 0.79 | −7.8±10.8 | SOG | 0.6 | 0.75 | −7.0±12.6 |
| 0.75 | 0.64 | −2.2±13.3 | 0.75 | 0.77 | 0.5±11.3 | 0.7 | 0.79 | −0.6±10.7 | 0.7 | 0.75 | 0.4±12.4 | ||||
| 0.8 | 0.64 | 2.2±13.2 | 0.8 | 0.77 | 4.7±11.3 | 0.75 | 0.79 | 3.3±10.8 | 0.75 | 0.75 | 4.3±12.3 | ||||
| EOG | 0.95 | 0.67 | −6.4±12.8 | EOG | 0.95 | 0.72 | −3.4±12.9 | EOG | 0.9 | 0.77 | −8.7±11.7 | EOG | 0.9 | 0.75 | −8.0±12.4 |
| 0.98 | 0.68 | 0.7±12.4•• | 0.98 | 0.69 | 3.2±13.2 | 0.95 | 0.76 | −1.5±12.4•• | 0.95 | 0.74 | −1.0±12.4 | ||||
| 1.0 | 0.66 | 12.7±12.6 | 1.0 | 0.67 | 14.4±13.5 | 0.98 | 0.74 | 4.7±12.9 | 0.98 | 0.74 | 5.4±12.4 | ||||
| Savitzky-Golay | |||||||||||||||
| N=55 | th | r | th | r | th | r | th | r | |||||||
| MO | 0.5 | 0.55 | −5.3±14.4 | MO | 0.5 | 0.76 | −7.9±11.2 | MO | 0.4 | 0.79 | −4.8±11.9 | MO | 0.4 | 0.81 | −4.7±11.6 |
| 0.6 | 0.53 | 1.5±15.0 | 0.6 | 0.76* | −2.4±11.2* | 0.5 | 0.81** | 0.3±11.3* | 0.5 | 0.81** | 0.6±11.4 | ||||
| 0.7 | 0.52 | 7.8±15.5 | 0.7 | 0.76 | 3.6±11.3 | 0.6 | 0.80 | 4.6±11.5 | 0.6 | 0.8 | 5.6±11.8 | ||||
| SOG | 0.7 | 0.59 | −6.4±14.7 | SOG | 0.75 | 0.76 | −7.1±11.4 | SOG | 0.7 | 0.79 | −3.8±11.4 | SOG | 0.7 | 0.75 | −3.4±13.0 |
| 0.75 | 0.57 | −1.6±14.7 | 0.8 | 0.76* | −3.5±11.5 | 0.75 | 0.79* | −0.5±12.4 | 0.75 | 0.73 | −0.1±13.6 | ||||
| 0.8 | 0.47 | 3.0±17.3 | 0.9 | 0.72 | 6.9±12.4 | 0.8 | 0.78 | 3.4±13.2 | 0.8 | 0.74 | 3.1±13.8 | ||||
| EOG | 0.9 | 0.50 | −13.0±18.5 | EOG | 0.95 | 0.71 | −11.4±13.1 | EOG | 0.95 | 0.63 | −4.8±17.4 | EOG | 0.95 | 0.74 | −9.1±13.6 |
| 0.95 | 0.51 | −3.7±20.1 | 0.98 | 0.64 | −2.5±15.2* | 0.98 | 0.63 | 0.7±17.7 | 0.98 | 0.72* | −1.7±14.5* | ||||
| 0.98 | 0.60 | 5.2±18.2 | 1.0 | 0.49 | 8.5±19.5 | 1.0 | 0.57 | 11.8±19.8 | 1.0 | 0.63 | 8.9±18.0 | ||||
© 2008 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Fontana, F.; Rixen, C.; Jonas, T.; Aberegg, G.; Wunderle, S. Alpine Grassland Phenology as Seen in AVHRR, VEGETATION, and MODIS NDVI Time Series - a Comparison with In Situ Measurements. Sensors 2008, 8, 2833-2853. https://doi.org/10.3390/s8042833
Fontana F, Rixen C, Jonas T, Aberegg G, Wunderle S. Alpine Grassland Phenology as Seen in AVHRR, VEGETATION, and MODIS NDVI Time Series - a Comparison with In Situ Measurements. Sensors. 2008; 8(4):2833-2853. https://doi.org/10.3390/s8042833
Chicago/Turabian StyleFontana, Fabio, Christian Rixen, Tobias Jonas, Gabriel Aberegg, and Stefan Wunderle. 2008. "Alpine Grassland Phenology as Seen in AVHRR, VEGETATION, and MODIS NDVI Time Series - a Comparison with In Situ Measurements" Sensors 8, no. 4: 2833-2853. https://doi.org/10.3390/s8042833
APA StyleFontana, F., Rixen, C., Jonas, T., Aberegg, G., & Wunderle, S. (2008). Alpine Grassland Phenology as Seen in AVHRR, VEGETATION, and MODIS NDVI Time Series - a Comparison with In Situ Measurements. Sensors, 8(4), 2833-2853. https://doi.org/10.3390/s8042833




