3.1. C and X bands
For C and X bands, only the WM emissivity model has been used.
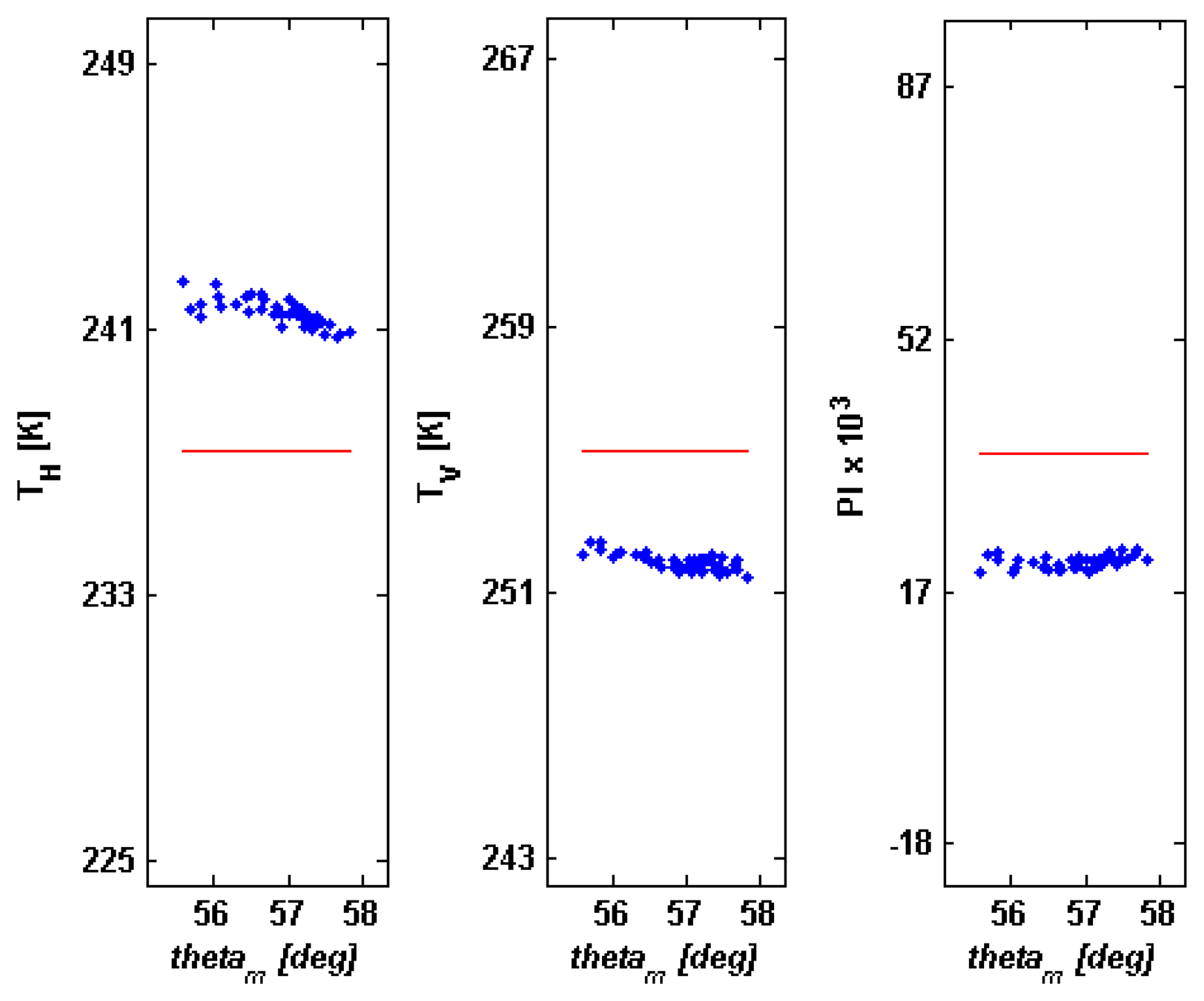
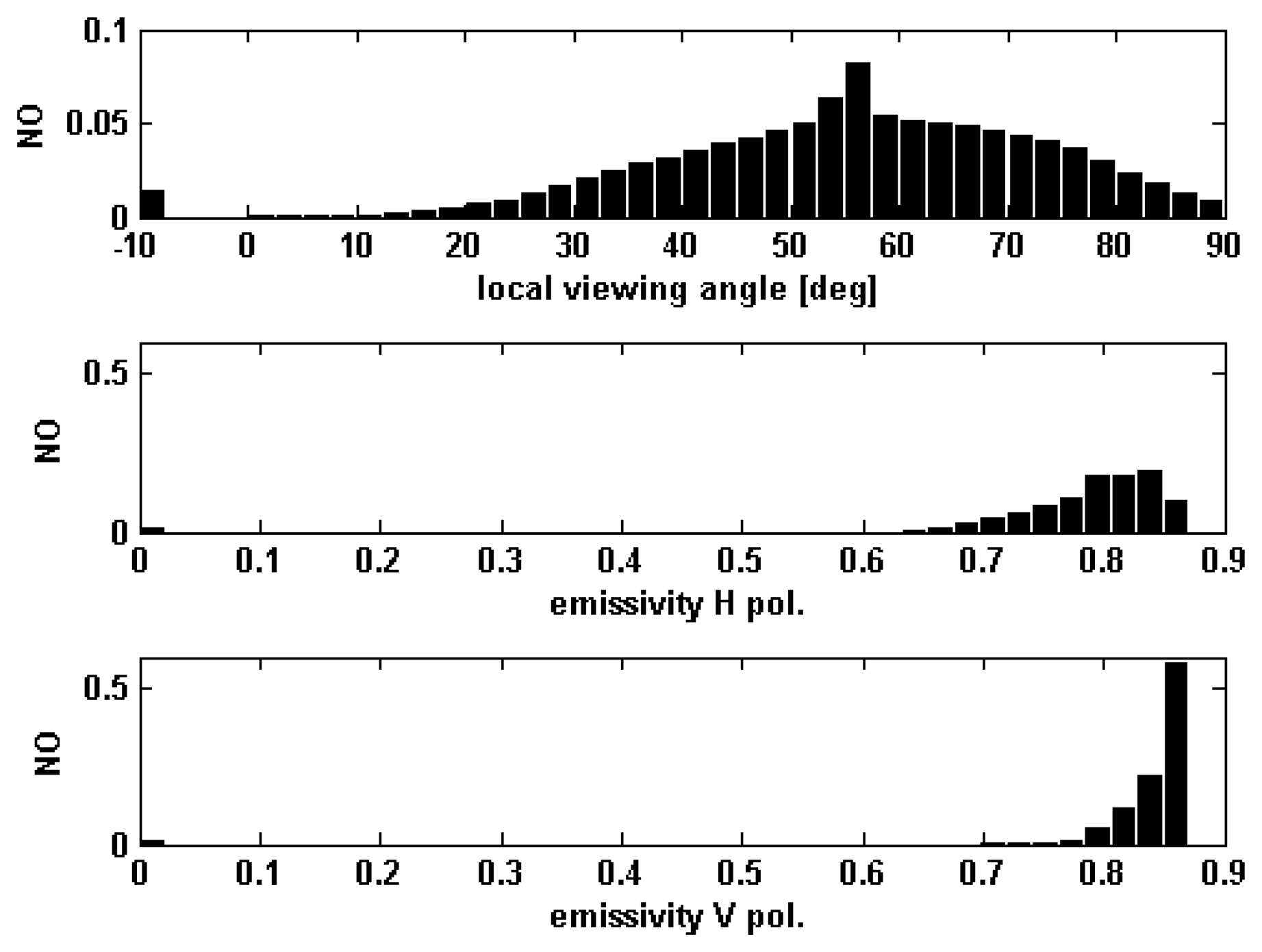
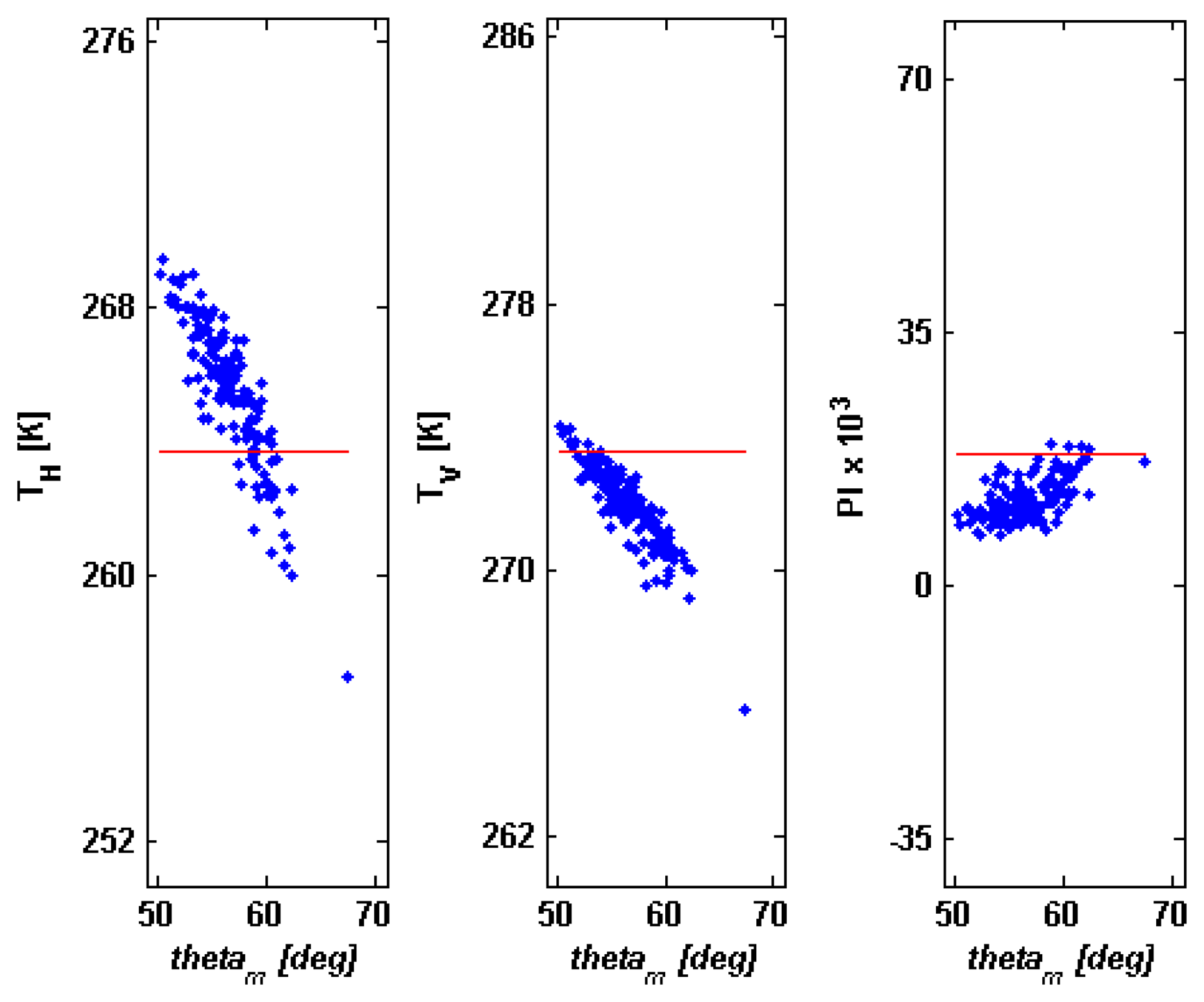
Figure 4 shows, for the 6 GHz band and for
s=0.89 cm, the values of the various
TA 's that we have obtained through our simulation procedure, versus the average observation angle
θm of a radiometric IFOV, that is the mean value of
θli 's inside the antenna footprint. Left panel concerns
H polarization (
TH), central panel
V polarization (
TV). The polarization index (
PI), equal to
is also displayed in the right panel of
Figure 4 (scaled by factor of 10
3 for the sake of representation clarity). The values obtained for a flat terrain are also shown (red solid lines:
THflat,
TVflat,
PIflat).
Table 1 quantifies the result reporting, for the 6 GHz band, the statistics of the differences between the
TA 's, i.e., of Δ
TH=
TH−
THflat, Δ
TV=
TV−
TVflat and of Δ
PI=
PI−
PIflat.
Figure 4 suggests that
TV and
PI are always underestimated, whilst the opposite occurs for
TH. The maximum decrease of
TV is equal to 3.79 K and the maximum rise of
TH is 5.10 K (
Table 1). To explain these results, we have to consider that three factors contribute to the variation of
TA with respect to that measured over a flat terrain [see
Equation (5)]: i) the dependence of
TBi on the local angle
θli; ii) the dependence of Ω
i on the weighting quantity (cos
θli/cos
βi); iii) the rotation of the polarization plane. We can analyze these factors separately.
The modification of the local observation angle tends to lower the emissivity, especially at
H polarization, which, as previously underlined, is more sensitive to this parameter. By neglecting both depolarization and weighting, the mean values of Δ
TH and Δ
TV at C band would be in the order of −6 K and −4 K, respectively, instead of 4.16 K and −3.31 K (
Table 1). This is due to the presence within the antenna footprint of facets with large
θli whose impact is fairly strong, because of the decrease of the emissivity with the rise of the observation angle (
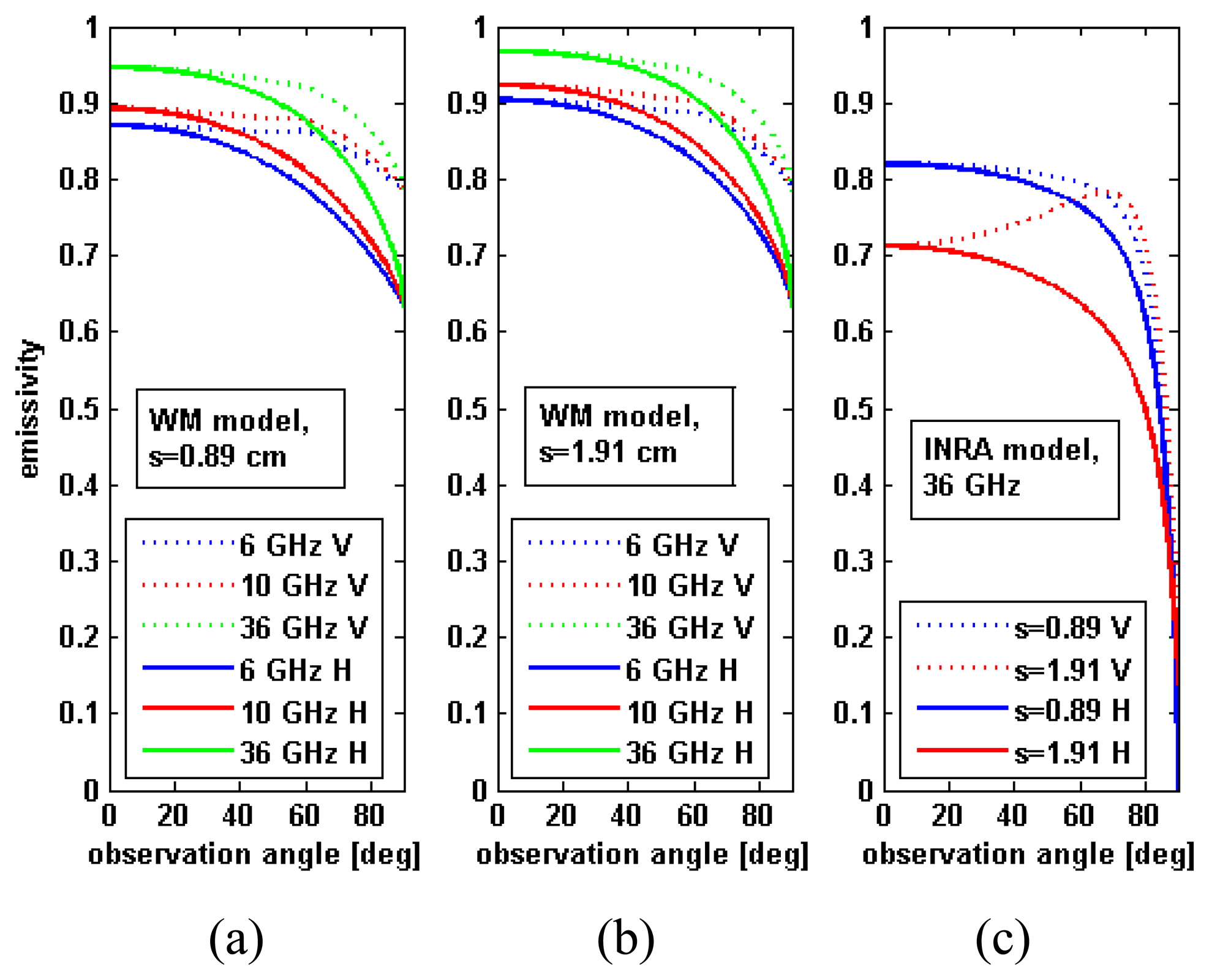
Figure 1, left panel). Furthermore, some facets are not visible by the radiometer, as previously pointed out.
Regarding the impact of the beam weighting, due to the presence of the term (cos
θli/cos
βi) in
Equation (5), for a flat terrain we would have cos
θli=cos(55°) and cos
βi=1 for all the elements of the DEM, so that
Equation (5) would reduce to a simple average of
TBi 's over the number of facets within the IFOV. For a mountainous scene, the weighting gives rise to an increase of
TA with respect to a simple average. This is due to the fact that the facets with the highest emissivity are those whose
θli is small (
Figure 1, left panel), i.e., the surfaces that are almost orthogonal to the radiometer direction of observation (
Figure 2, lower panel). Since for these facets (cos
θli /cos
βi) is high, they appear to the radiometer under a large solid angle Ω
i [see
Equation (5)]. In other words, the facets that weight most in
Equation (5) are those characterized by high
TBi, thus implying an overall increase of
TA. This increase is more evident for
TH, being smaller than
TV. Finally, the rotation of the polarization plane produces a coupling between the vertically and horizontally polarized emissivities [see
Equation (3)] that implies a rise of
TH and a lowering of
TV.
We can now explain the results of
Figure 4 and
Table 1. The decrease of the emission of a radiometric pixel due to the change in the local angle is contrasted by the beam weighting (especially for
H polarization), whilst the rotation of the polarization plane may enlarge (
V polarization) or attenuate (
H polarization) the lowering of
TA. Consequently,
TV and
PI are always underestimated and
TH is overpredicted.
The differences (bias as well as standard deviation) quantified in
Table 1 may affect the retrieval of bio-geophysical parameters, such as soil moisture, based on inversion algorithms tuned for flat terrains. To give an evaluation of the impact of these errors on estimates of soil moisture content (SMC), we have carried out a simple inversion of the forward model in which all the characteristics of the terrain specified at the beginning of Section 2 (standard deviation of height, dry soil density, fractions of sand and clay, etc.) are supposed known except SMC. Moreover, an angle of 55° (i.e., the radiometer nominal observation angle) is assumed. From the C band emissivities at
H polarization (
eH) computed with our simulation procedure (i.e., the
TH 's divided by 296 K), we have determined the corresponding specular emissivities
e0H through
equation (1a). Then, we have inverted the Fresnel equation to calculate the dielectric constant of the
k-th radiometric pixel
ε as done in [
7]:
Finally, we have fitted the model of Dobson et al. [
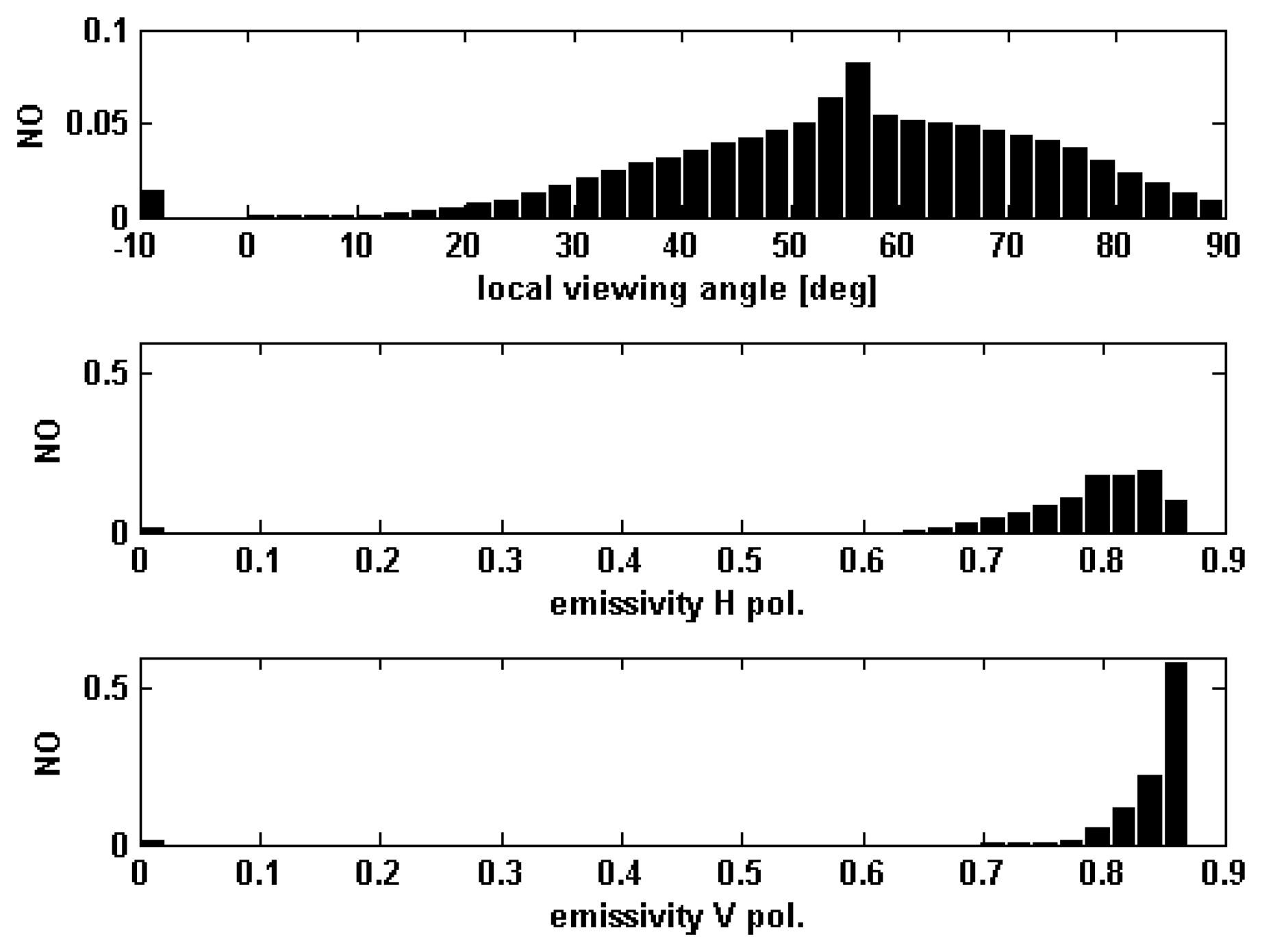
1] to retrieve SMC. The histogram of the estimated SMC's is shown in
Figure 5. The SMC values have to be compared with 0.3, which, as mentioned at the beginning of Section 2, is the nominal SMC for which the simulation has been accomplished. It can be inferred that neglecting the modification of the observation angle (i.e., considering a constant angle of 55°) leads to an underestimation of SMC, due to the overestimation of
eH. The mean value of the retrieved SMC is 0.24.
The results for X band,
s=0.89 cm, are quantified in
Table 2. The dynamic range and the standard deviation are slightly larger with respect to C band because of the higher spatial resolution of the X band radiometric pixel that reduces the smoothing effect due to antenna beamwidth integration.
By observing left and central panels of
Figure 1, it can be noted that the sensitivity of the emissivity to the observation angle is fairly similar, so that the results achieved for
s=0.89 cm do not substantially change for
s=1.91 cm and the explanation yielded above on the effects of the three factors on
TA still applies. The mean values of Δ
TH, Δ
TV and Δ
PI obtained for the latter case are reported in
Table 3. The magnitude of the biases is slightly smaller with respect to the case of a less rough terrain.
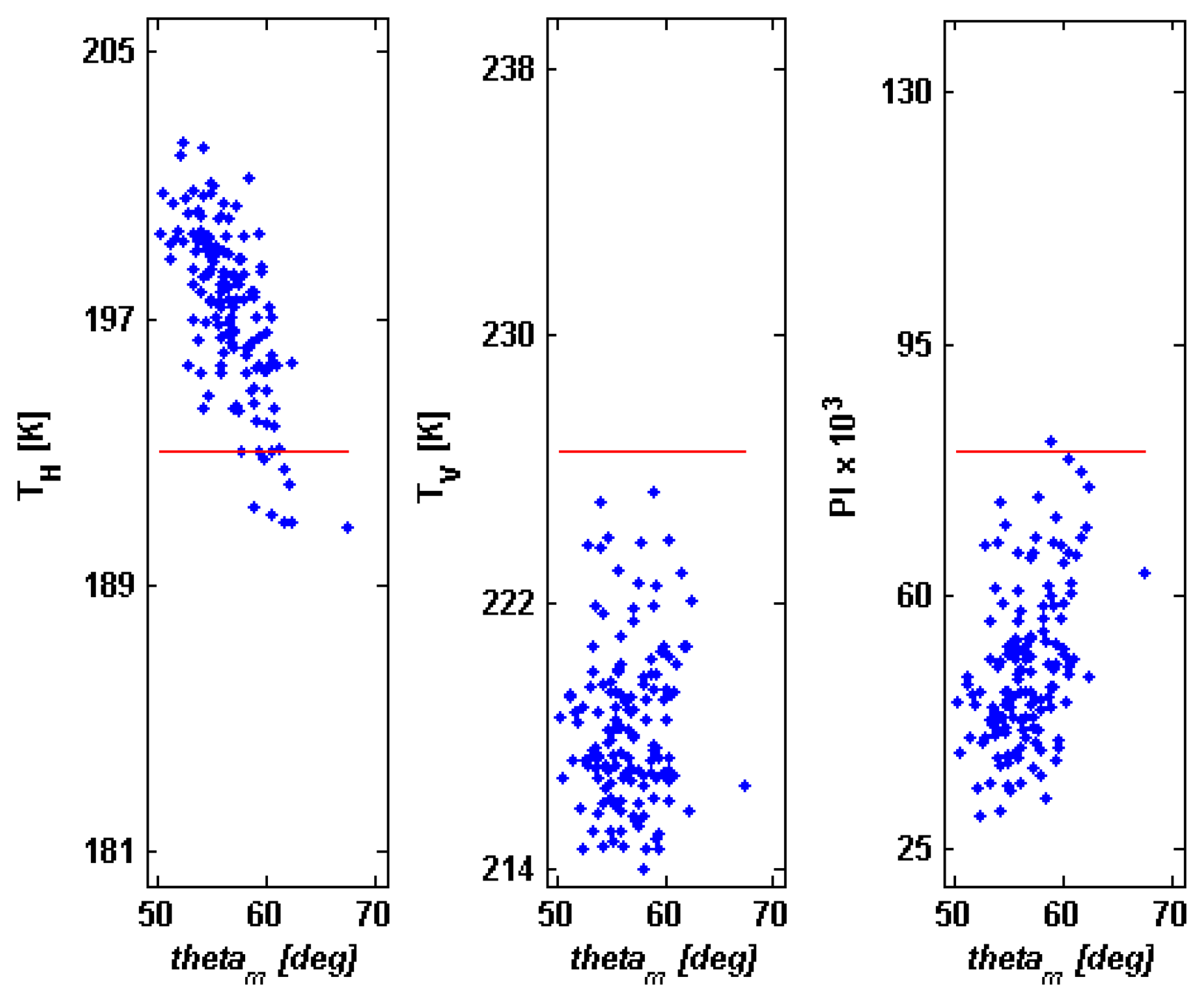
3.2. Ka band
Figure 6 is the analogous to
Figure 4, but for the 36.5 GHz band (WM model,
s=0.89 cm). First of all, it is understood that, in this case, actual measurements at Ka band are affected by the atmosphere. Limiting ourselves to the emission term, the analysis of Ka band allows us to better single out the topography effect and its dependence on local observation angle, since the smoothing effect of the low-resolution radiometric pixel noted for C and X bands is reduced. The general overestimation of
TH and underprediction of
TV and
PI are confirmed. The clearest differences with respect to C band are represented by the increase of the correlation between
TA and
θm, by the widening of the range of
θm and by the increase of both the dynamics and the standard deviation of
TA. Furthermore, some situations in which
TH is underpredicted and few cases (small
θm, in the order of 50°) in which
TV is slightly greater than
TVflat occur.
Table 4 quantifies the result shown in
Figure 6. The maximum decrease of
TV is equal to −7.70 K and the maximum rise of
TH is 5.83 K. It is worth mentioning that, neglecting depolarization and weighting, the mean values of Δ
TH and Δ
TV at Ka band would be in the order of −7 K and −5 K and that the decrease of
TH would reach −16.5 K. Again, beam weighting and rotation of the polarization plane cause an effect that contrasts this lowering of
TH. However, for largest
θm's the effect of the local angle prevails and
TH <
THflat.
It must be considered that the results that we have obtained so far depend on the sensitivity of the emissivity to the observation angle as predicted by the WM model. It is interesting to verify whether the use of another model, characterized by a different trend emissivity-observation angle, leads to different results. We have applied our procedure, for the 36 GHz band, by adopting the INRA model too, whose behavior, especially for
s=0.89 cm,
V polarization, is fairly different with respect to the WM one (
Figure 1). The result is presented in
Figure 7 and quantified in
Table 5.
The general overprediction of
TH and the underestimation of
TV and
PI are confirmed and enlarged using the INRA model. This enlargement can be explained by considering that, on one hand, the high sensitivity to the observation angle presented by the INRA model (
Figure 1, right panel) causes a larger lowering of
TA (for high
θli's, greater than the Brewster angle, at
V polarization) if the effect of the modification of the observation angle is singled out (i.e., neglecting depolarization and beam weighting). On the other hand, the considerable difference between the emissivities at
V and
H polarizations occurring for
s =0.89 cm (
Figure 1, right panel), amplifies the effect of the rotation of the polarization plane. The coupling of the polarizations yields therefore a strong increase of
TH and a large lowering of
TV. Moreover, for
V polarization the facets producing the highest emission are observed under the Brewster angle and their weighting quantity (cos
θli /cos
βi) is fairly low, thus limiting the effect of the beam weighting. The overall result is that
TH is largely overestimated (the maximum increase with respect to
THflat is 9.28 K) and both
TV and
PI are considerably underpredicted (the decreases reach 12.51 K and 50.23×10
-3, respectively). With respect to
Figure 6, it can be noted a lower correlation between
TV and
θm due to the Brewster angle effect, which implies that the emissivity at
V polarization does not monotonically decrease with the observation angle (
Figure 1, right panel).
The mean values of Δ
TH, Δ
TV and Δ
PI for the case of Ka band,
s=1.91 cm are reported in
Table 6 (both models). The magnitude of the biases is smaller with respect to the case of
s=0.89 cm. This is particularly evident for the INRA model. As for
H polarization, the smaller difference with respect to the emissivity at
V polarization, due to the increase of roughness, limits the increase of
TH caused by the rotation of the polarization plane. At
V polarization, the increase of roughness implies the disappearance of the Brewster effect, so that the facets with the highest emissivity present a small
θli (
Figure 1, right panel) and a large weighting quantity (cos
θli /cos
βi). In other words, the beam weighting effect is not limited, as conversely occurs for
s=0.89 cm (INRA model).
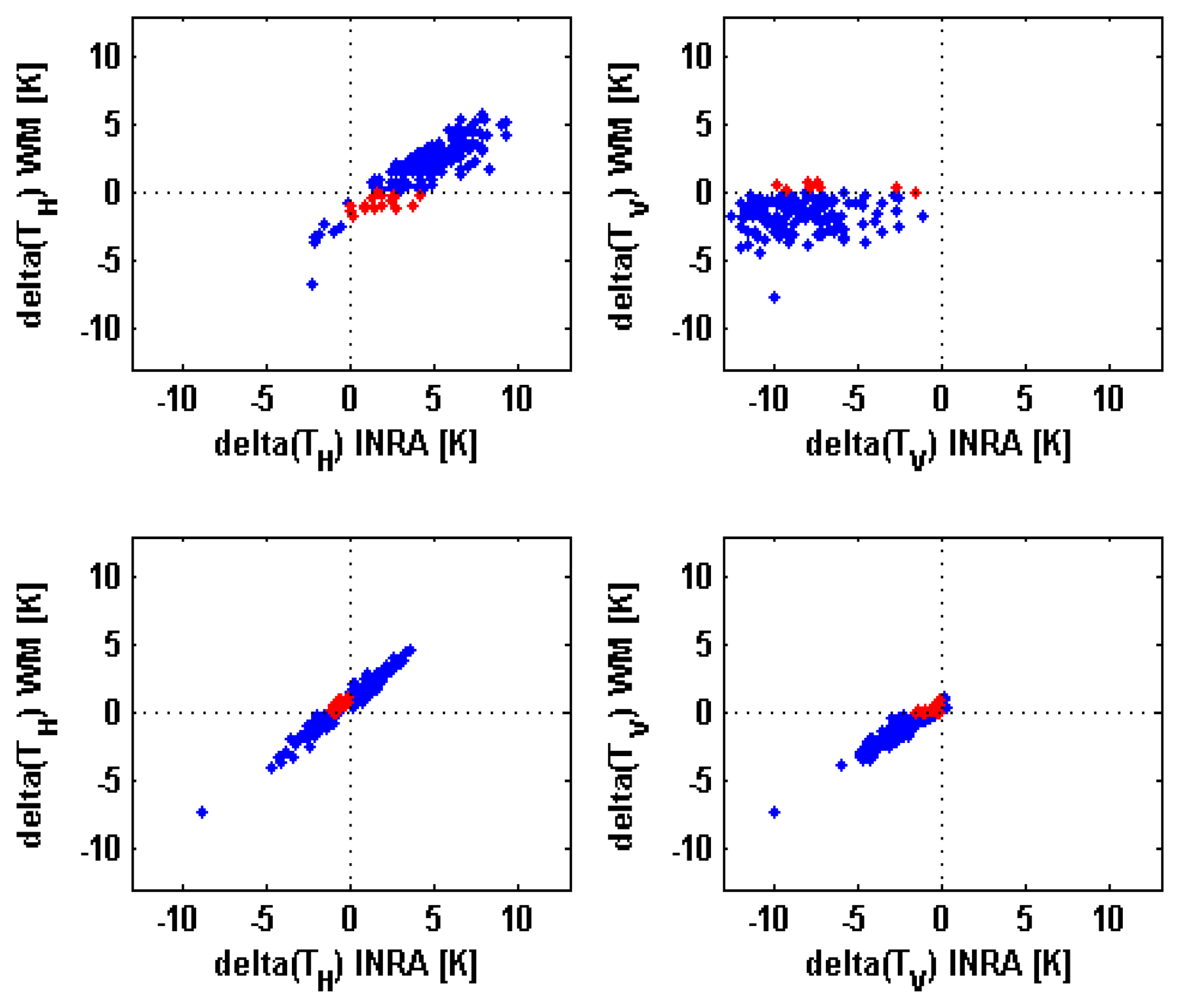
Figure 8 compares for Ka band, the values of Δ
TH achieved by using the INRA model with those obtained with the WM model. The purpose is to show that situations which may be critical for our results, in which the relief causes an overestimation of
TH using one model and an underprediction adopting the other, occur for only few cases (red points in
Figure 8). It is worth noting that although for
s=0.89 cm the correlation between Δ
TV's is small, the percentage of red points is 5% only. The maximum value of this percentage is 12% (
s=0.89 cm,
H polarization). We can therefore conclude this discussion on Ka band affirming that, despite the different sensitivities to the observation angle predicted by WM and INRA models, the results that we have achieved can be considered fairly general. What changes is only the magnitude of under- or overestimation, which is model dependent, as expected.