Water Productivity Mapping (WPM) Using Landsat ETM+ Data for the Irrigated Croplands of the Syrdarya River Basin in Central Asia
Abstract
:1. Introduction
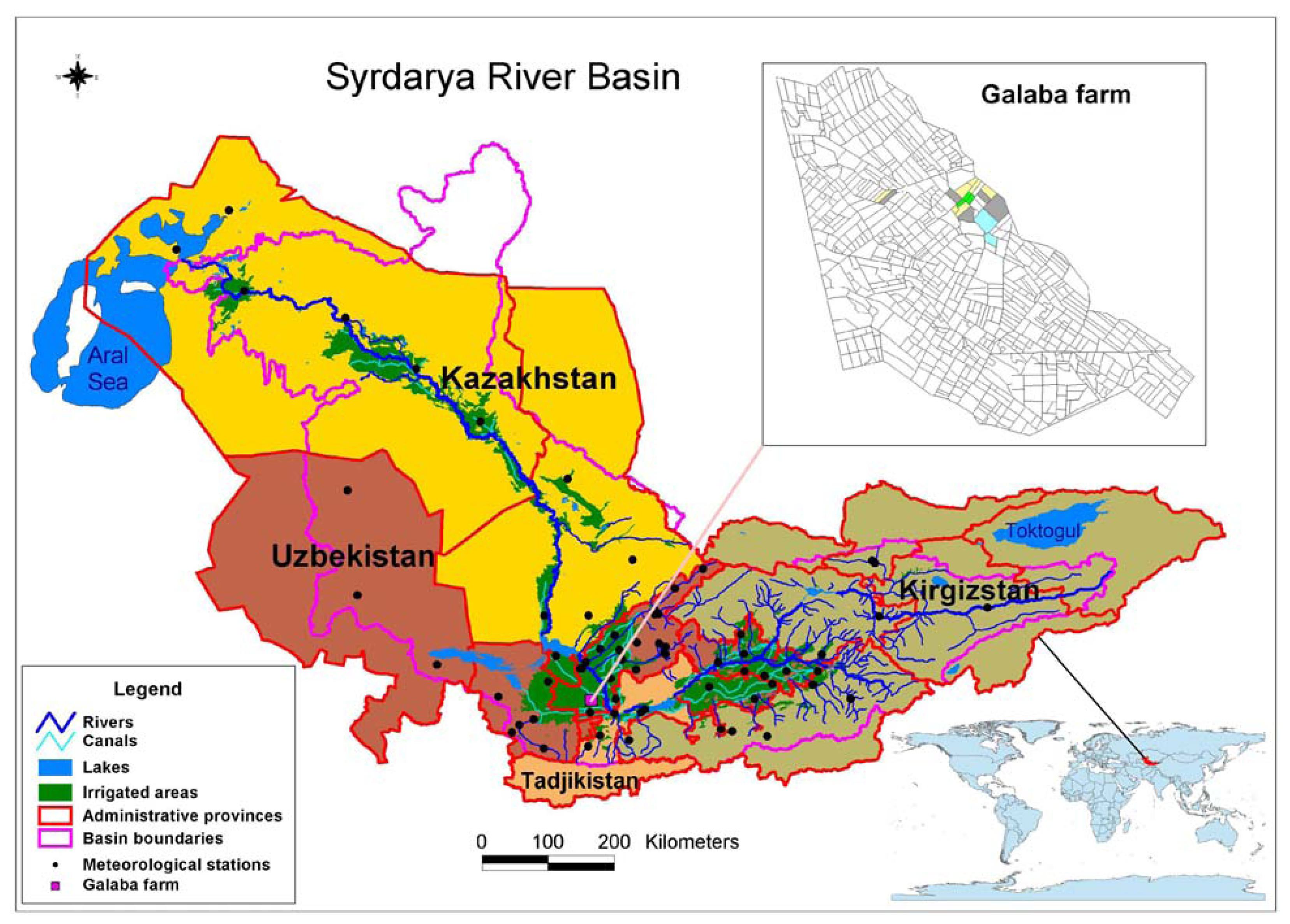
2. Study area
3. Processing of satellite images
3.1 Digital number to radiance
3.2 Radiance to reflectance
3.3 At-sensor temperature from thermal bands
- K2 – calibration constant, (for Landsat-7: K2 = 1282.71)
- K1 – calibration constant, (for Landsat-7: K1 = 666.09)
- Lλ – spectral radiance in W m-2 sr-1 μm-1
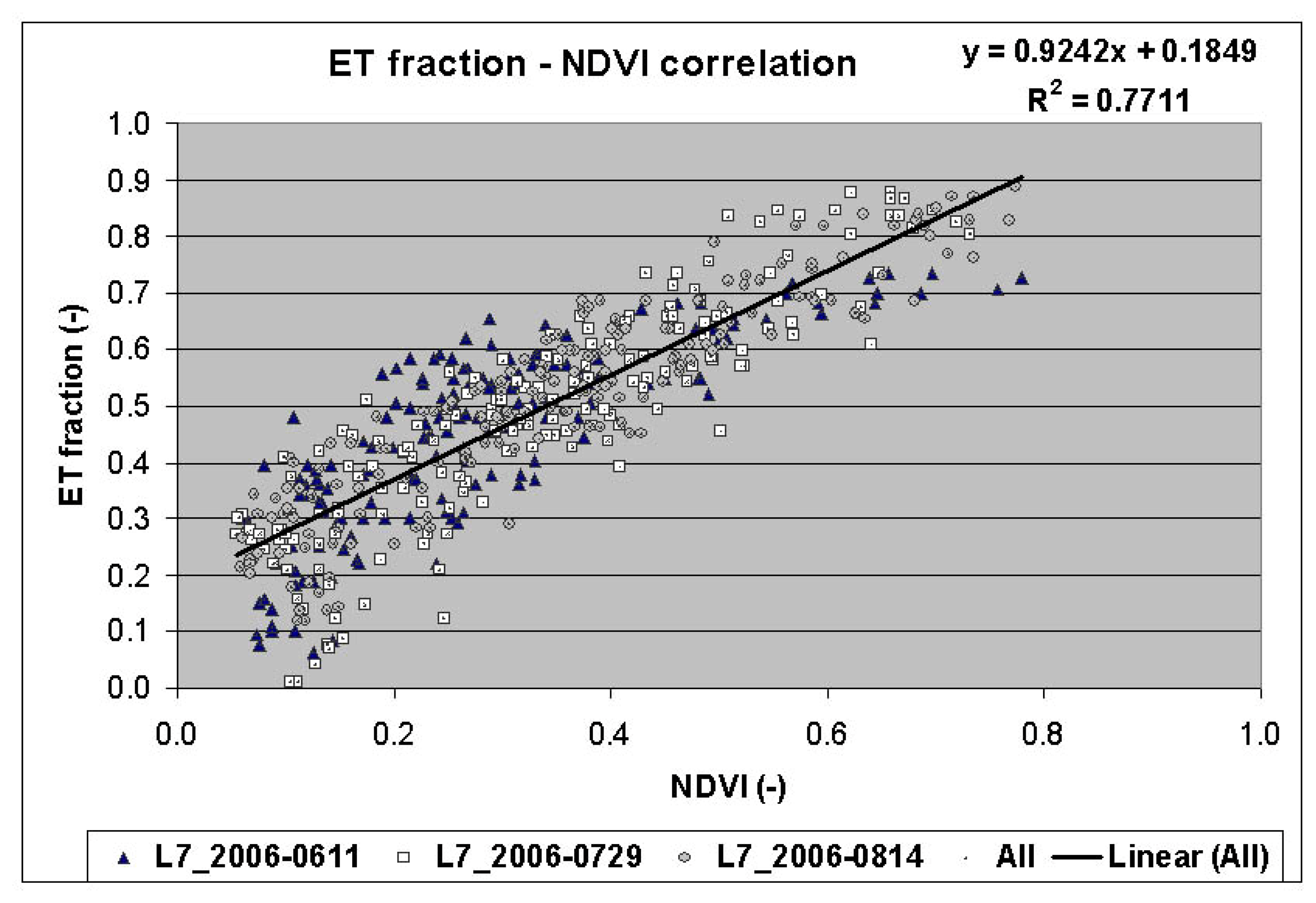
3.4 Normalized difference vegetation index (NDVI)
4. Field-plot data characteristics
5. Methods
- Crop productivity mapping (CPM);
- Water use (actual evapotranspiration) mapping (WUM); and
- Water productivity mapping (WPM).
5.1 Crop productivity maps (CPMs)
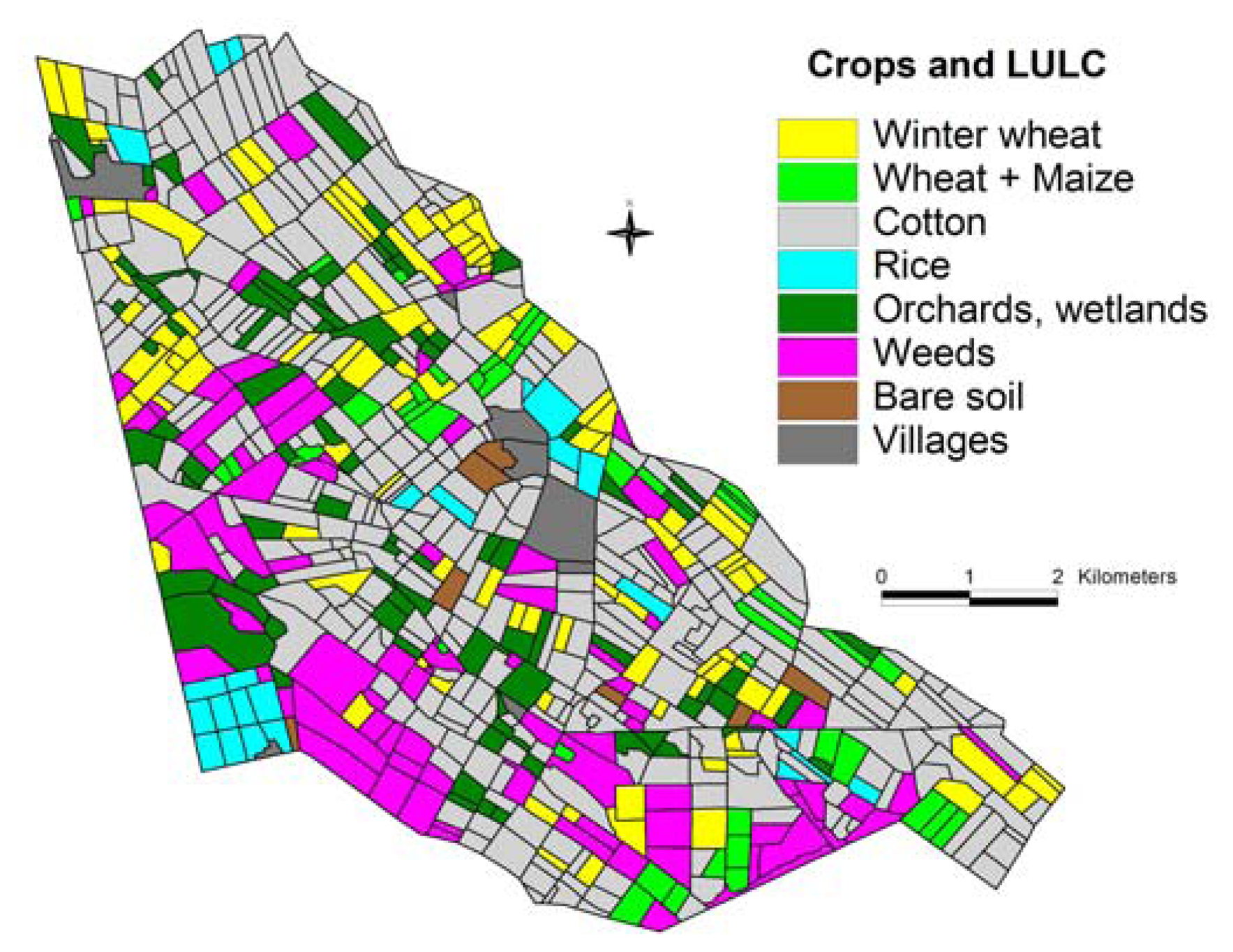
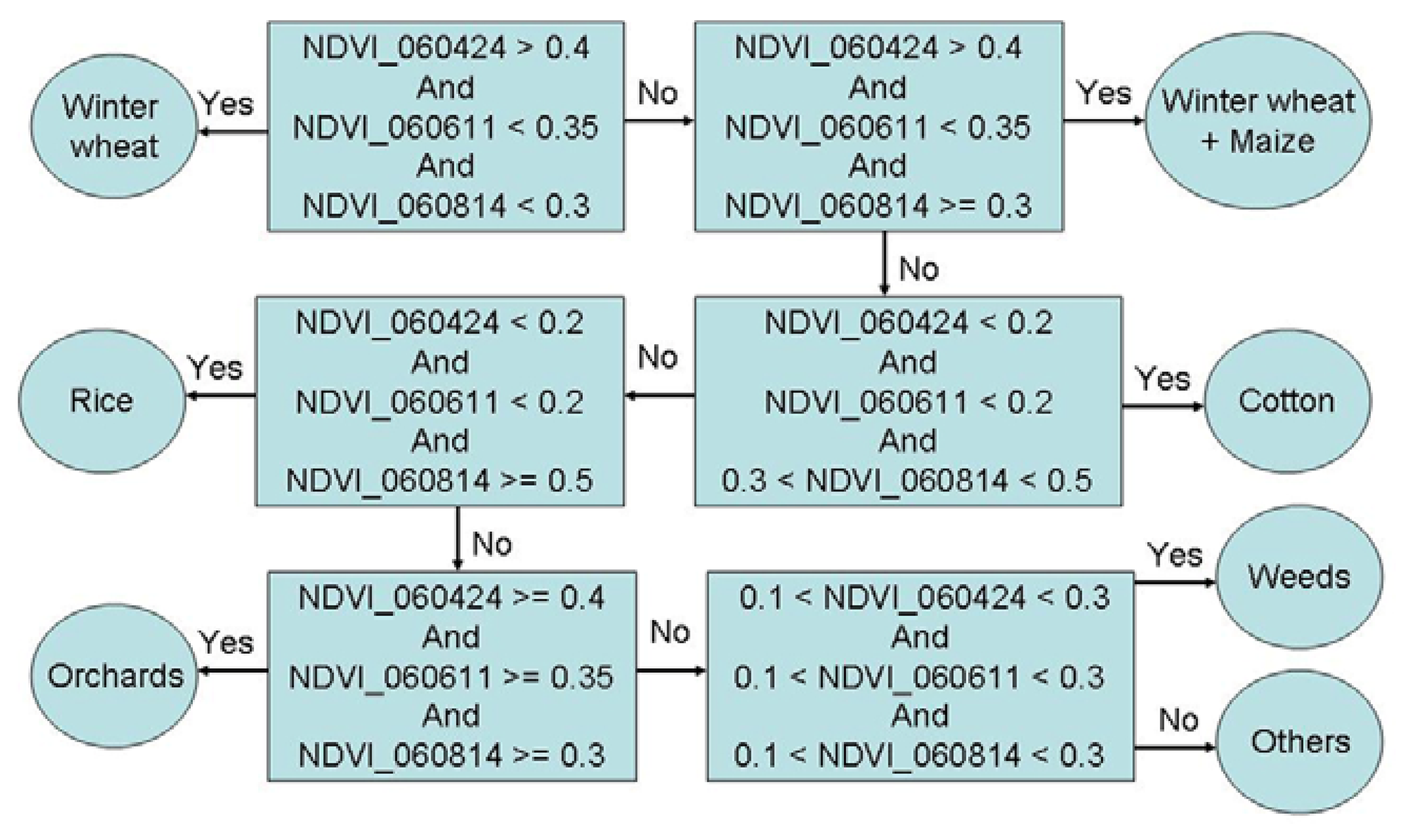
5.1.1 Crop type mapping using remote sensing
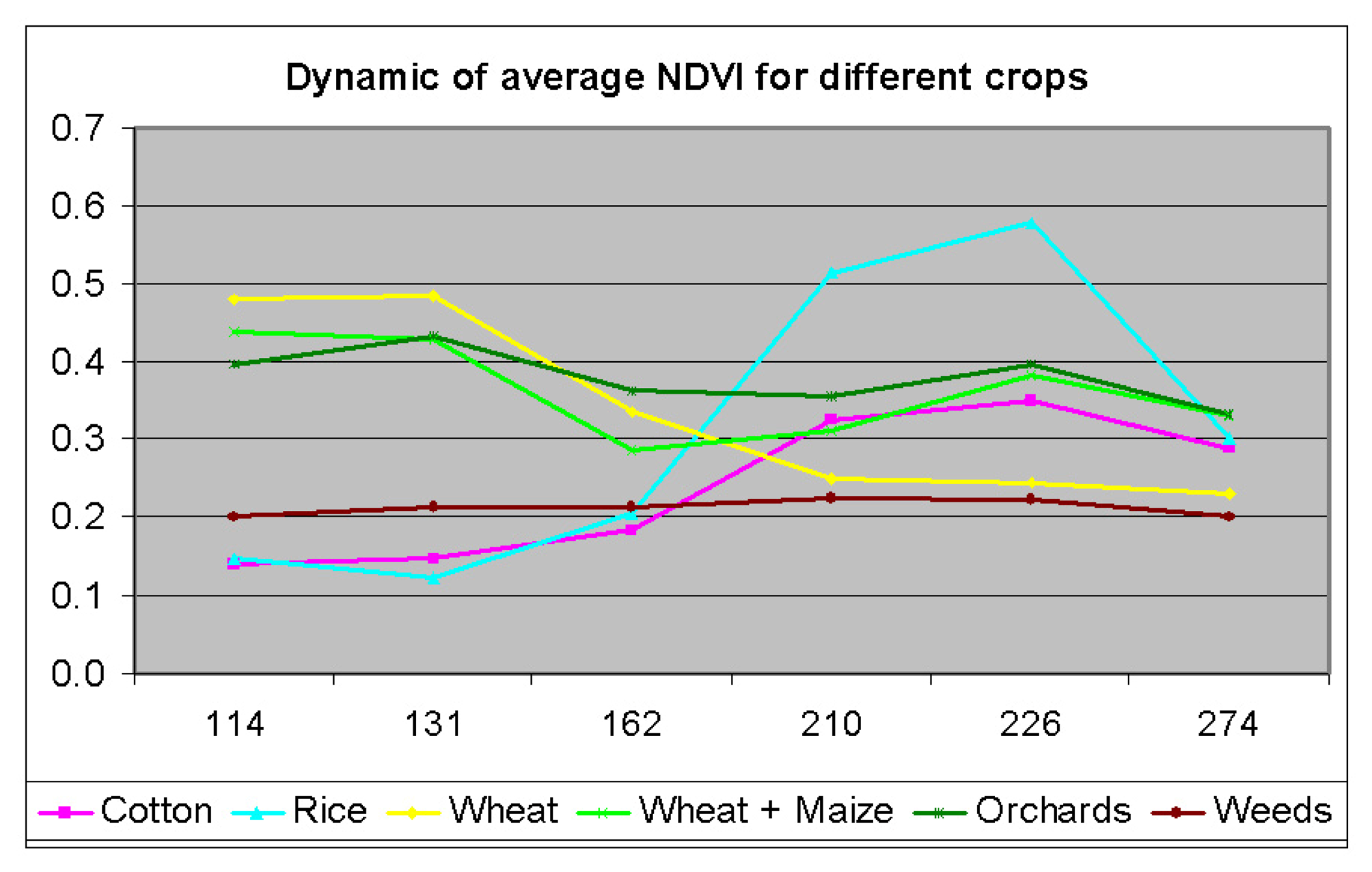
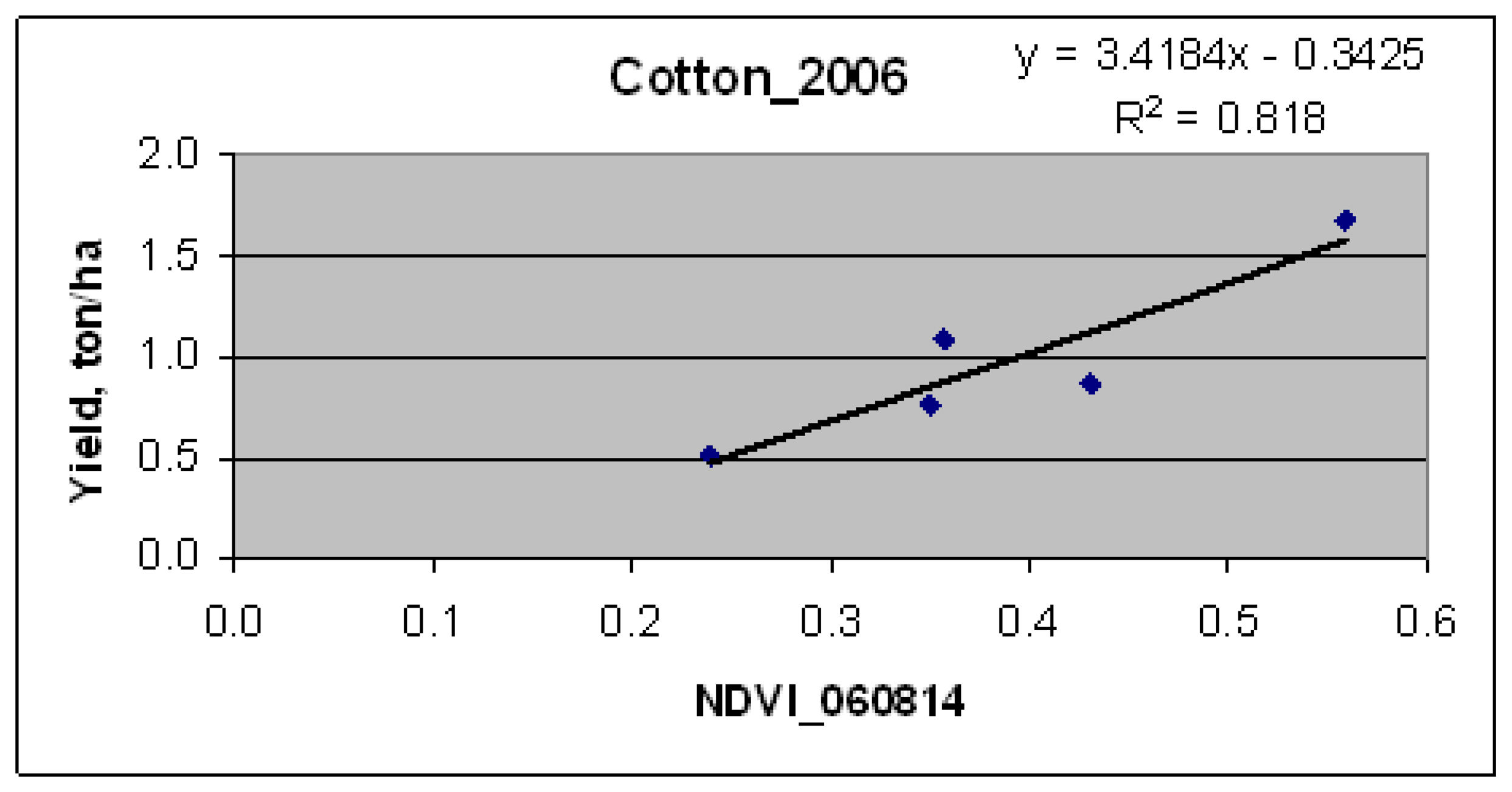
5.1.2 Crop yield modeling by relating remote sensing indices with field-measured yield
5.1.3 Crop productivity maps (CPMs) by applying best yield models to specific crops
- (a)
- measuring crop variables through field campaign (Table 3);
- (b)
- acquiring the images that correspond to field campaign dates (Table 1);
- (c)
- delineating the crop types (section 5.1.1);
- (d)
- developing modes that relate vegetation index with actual crop yield (section 5.1.2); and
- (e)
- extrapolating the best models to larger areas using remotely sensed data (section 5.1.3).
5.2 Water use (actual evapotranspiration) map
- determining the ET fraction from Landsat ETM+ thermal data;
- calculating the reference ET by applying Penman-Monteith equations; and
- computing the actual ET by multiplying ET fraction with reference ET.
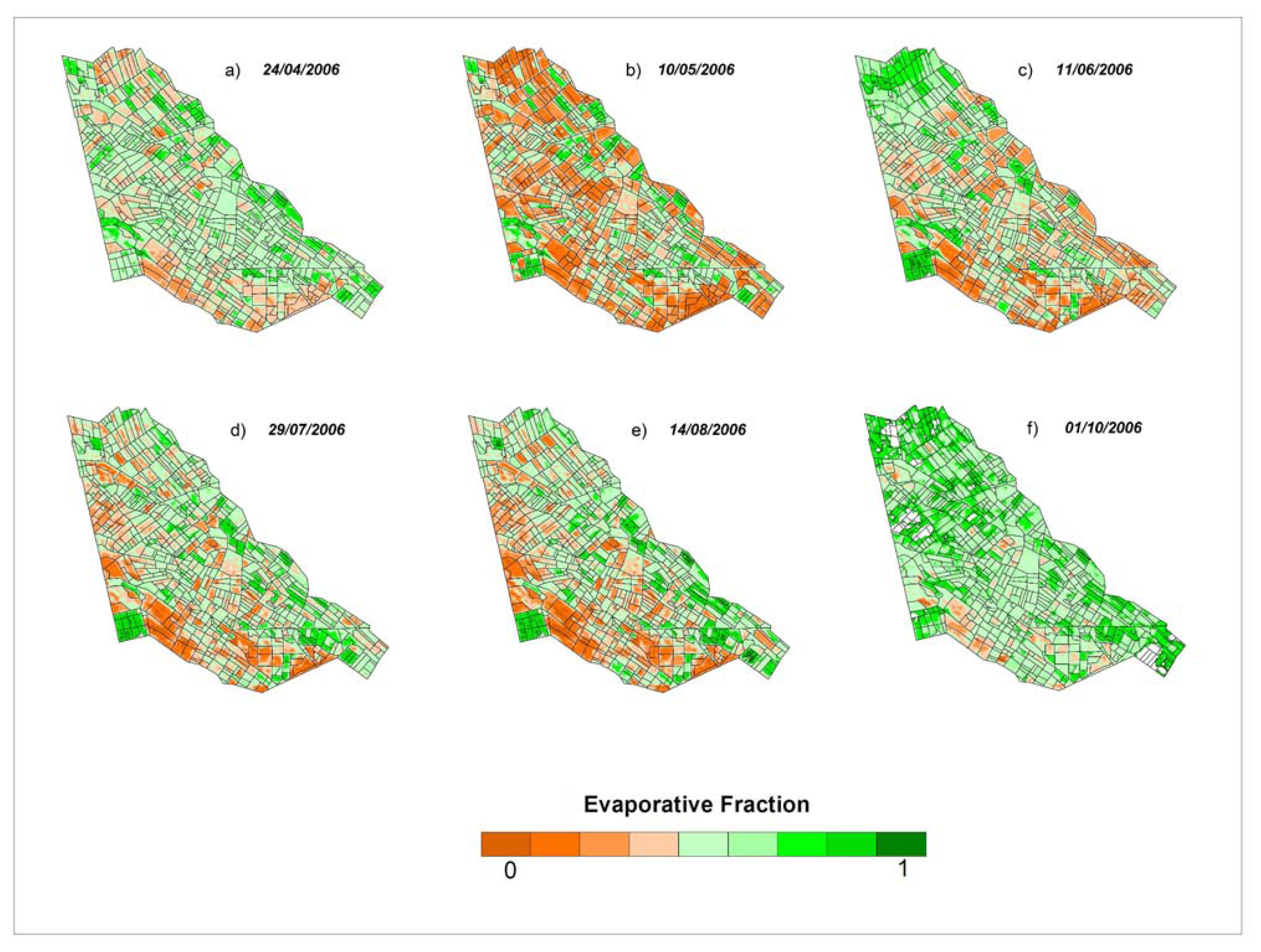
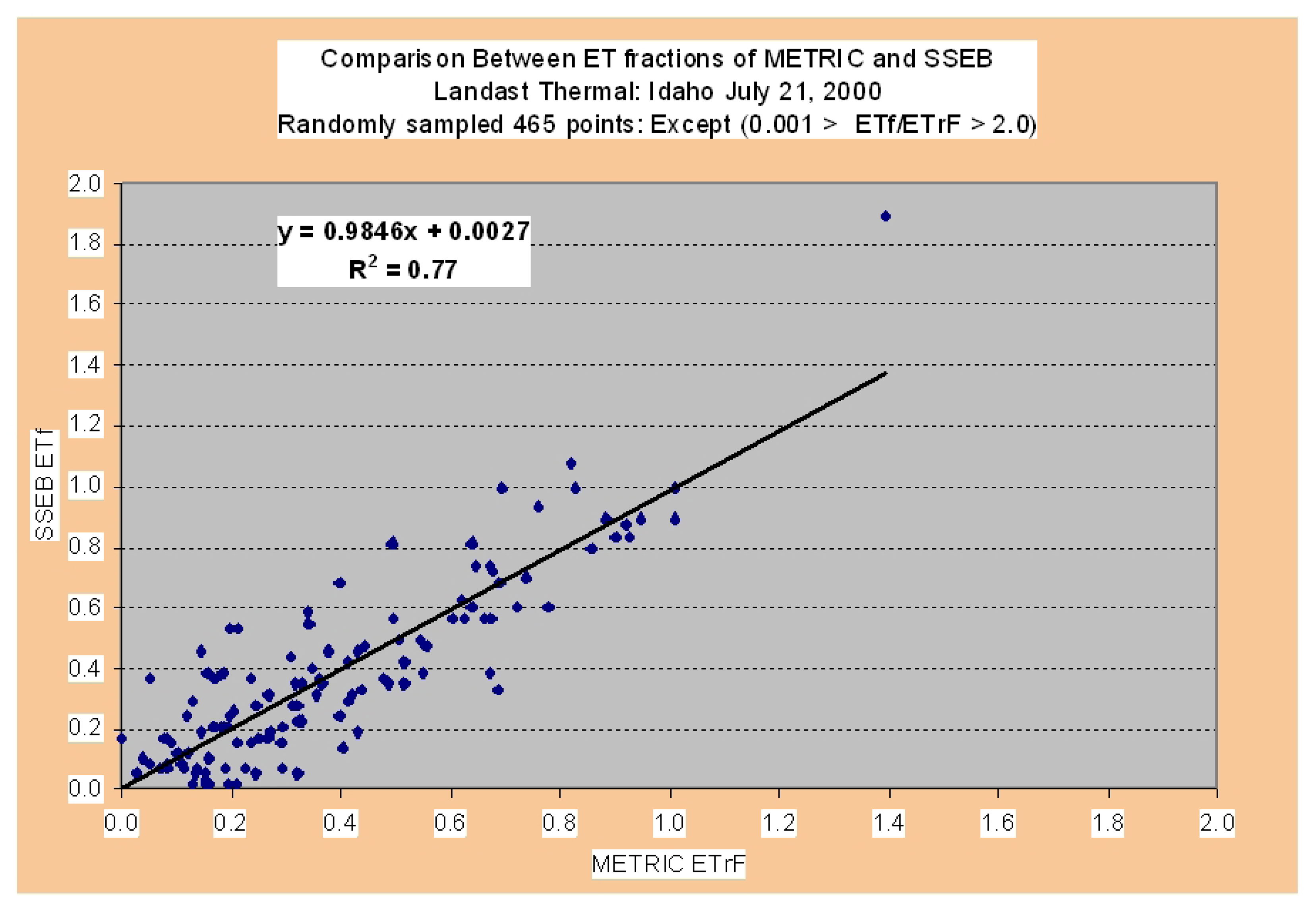
5.2.1 Modeling of ET fraction (crop coefficients) by SSEB model
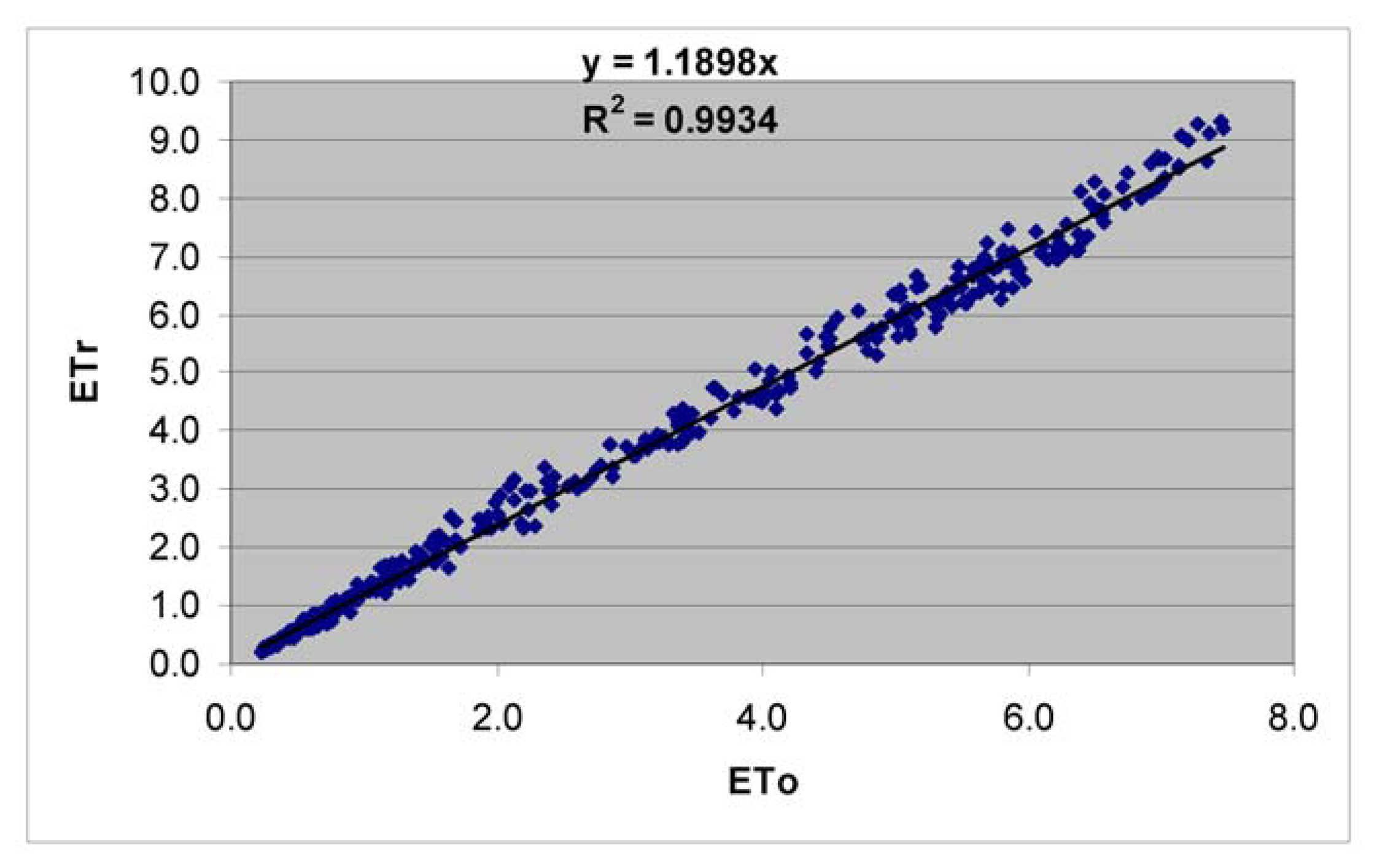
5.2.2 Calculation of the reference ET
- FAO method: Allen et al [52] recommended to use the clipped grass (hypothetical crop) having the plant height of 0.12 m, a surface resistance of 70 s m-1 and an albedo of 0.23 for reference ET (ETo) calculation.
- ASCE Method: The ASCE-PM method uses as a reference the alfalfa crop of 0.5 m plant height, albedo of 0.23, but different surface resistance of 50 s m-1 at daytime and 200 s m-1 at nighttime, for reference ET (ETr) calculation. The method compares well against lysimeter measurements of alfalfa ET at Kimberly, Idaho [50] and at Bushland, Texas [53].
- Rn - the net radiation at the crop surface [MJ m-2 day-1],
- G - the soil heat flux density [MJ m-2 day-1],
- T - the mean daily air temperature at 2 m height [°C],
- u2 - the wind speed at 2 m height [m s-1],
- es - the saturation vapour pressure [kPa],
- ea - the actual vapour pressure [kPa],
- (es - ea) - the saturation vapour pressure deficit [kPa],
- Δ_ _ - the slope vapour pressure curve [kPa °C-1],
- γ_ - the psychrometric constant [kPa C-1].
5.2.3 Calculation of actual seasonal ET (water use) for selected crops
5.3 Water productivity mapping (WPM)
6. Results and discussions
6.1 Crop productivity calculations
6.1.1 Crop type classification
6.1.2 Crop yield modeling
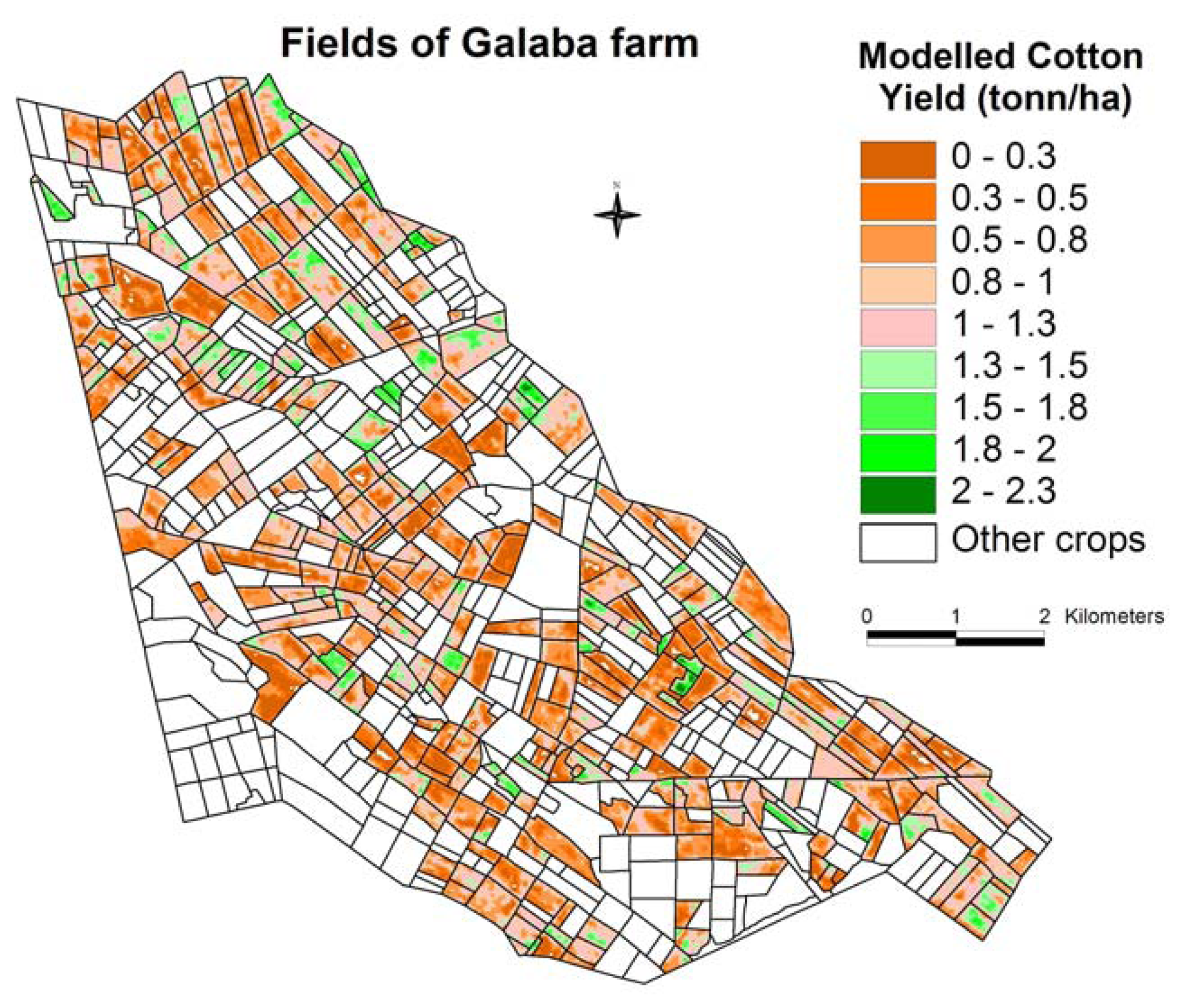
6.1.3 Crop productivity calculations by extrapolating to larger areas
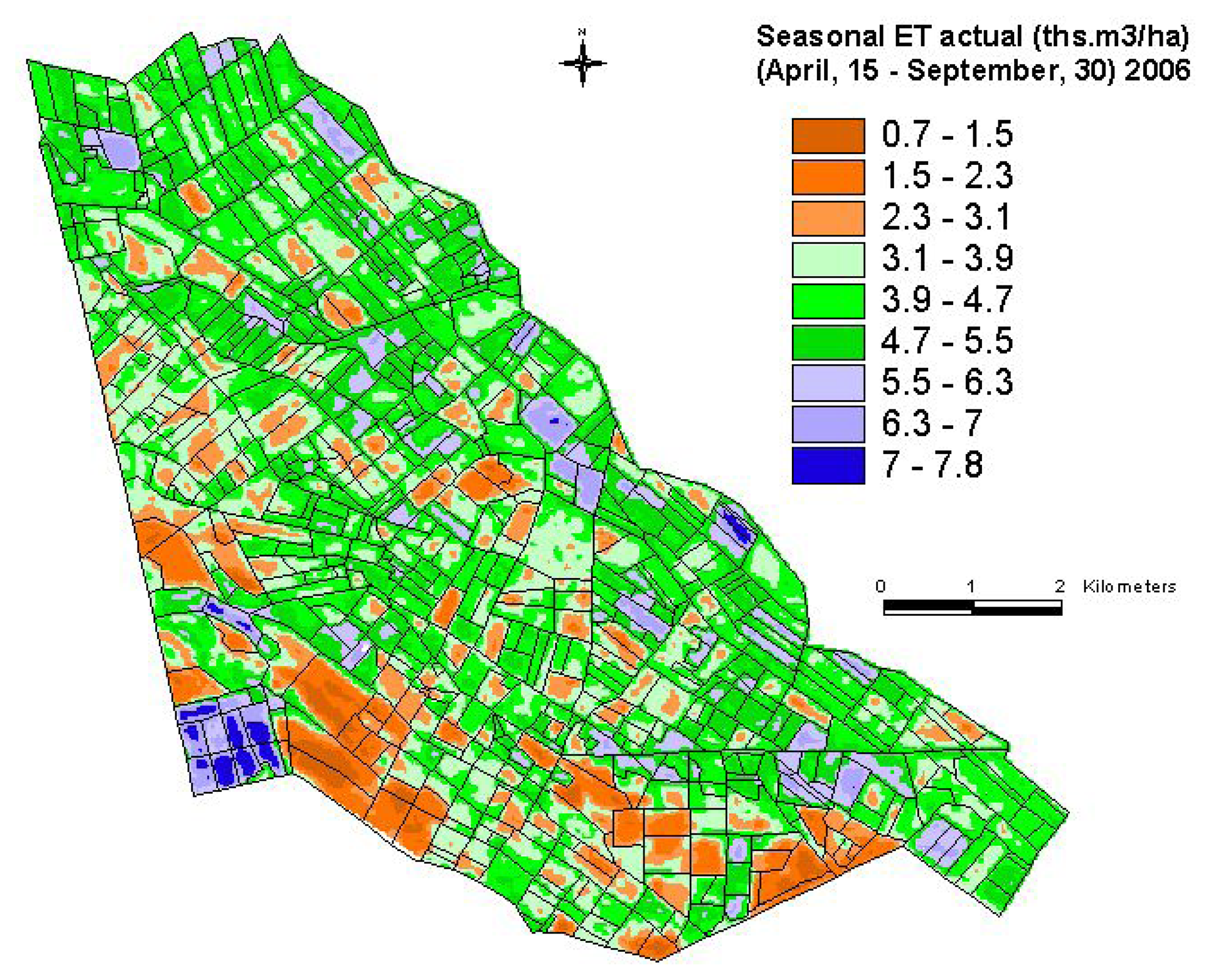
6.2 Water use (seasonal ETactual)
6.2.1 Modeling of ET fraction (crop coefficient)
6.2.2 Reference ET calculation
6.2.3 Water use (ETactual) calculation
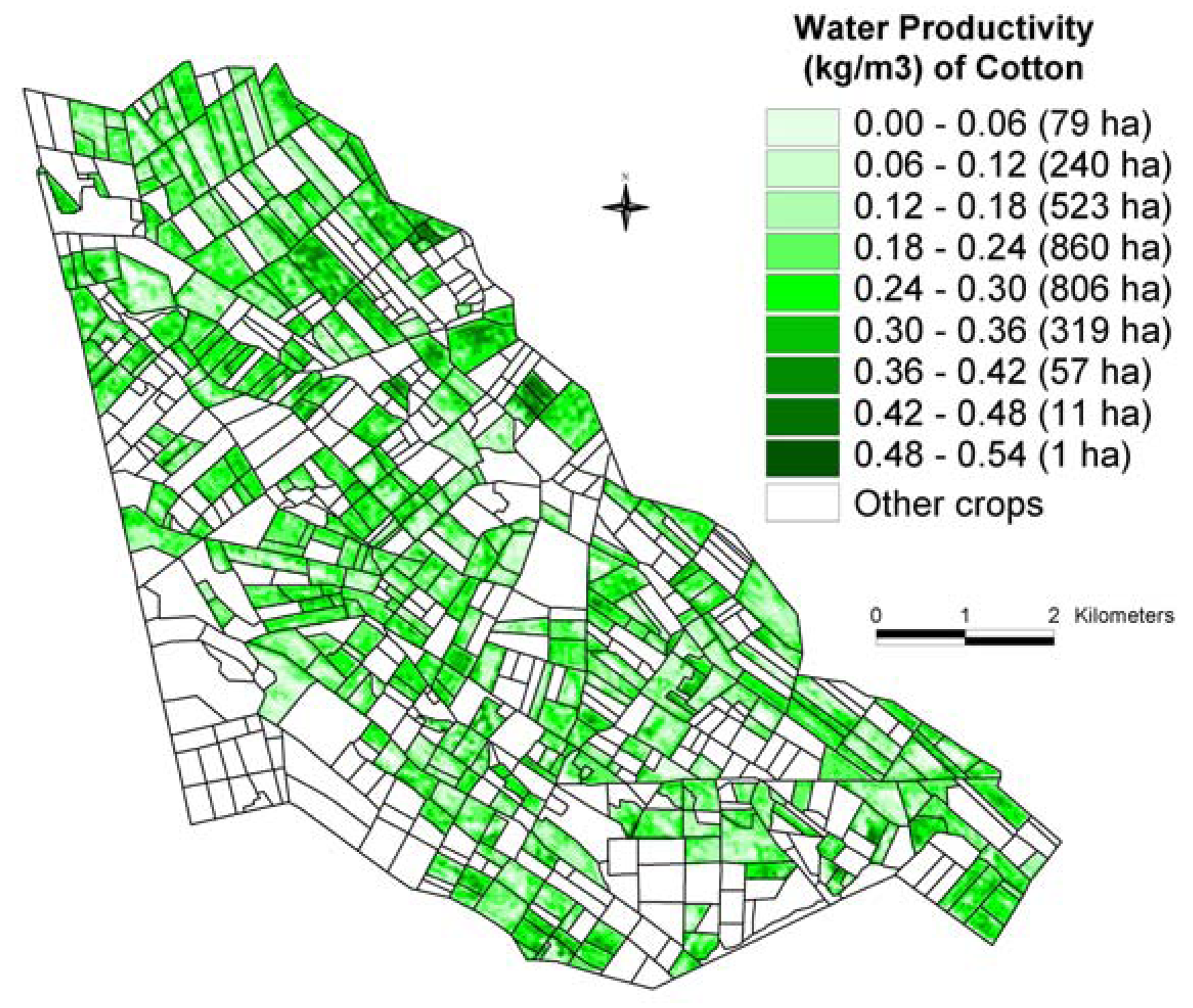
6.3 Water productivity mapping (WPM)
6.4 Discussions and validations
7. Conclusions
Acknowledgments
References
- Molden, D. Accounting for water use and productivity; SWIM paper 1; International Water Management Institute: Colombo, Sri Lanka, 1997. [Google Scholar]
- Passioura, J. Increasing crop productivity when water is scarce – from breeding to field management. Agr. Water Manage. 2006, 80, 176–196. [Google Scholar]
- Thenkabail, P.S.; Biradar, C.M.; Noojipady, P.; Dheeravath, V.; Li, Y.J.; Velpuri, M.; Gumma, M.; Reddy, G.P.O.; Turral, H.; Cai, X.L.; Vithanage, J.; Schull, M.; Dutta, R. Global Irrigated Area Map (GIAM) for the End of the Last Millennium Derived from Remote Sensing. Int. J. Remote Sens. 2008. accepted. [Google Scholar]
- Zward, S.J.; Bastiaanssen, W.G.M. Review of measured crop water productivity values for irrigated wheat, rice, cotton and maize. Agr. Water Manage. 2004, 69, 115–133. [Google Scholar]
- Wesseling, J.G.; Feddes, R.A. Assessing crop water productivity from field to regional scale. Agr. Water Manage. 2006, 86, 30–39. [Google Scholar]
- Molden, D.J.; Sakthivadivel, R.; Perry, C.J.; De Fraiture, C.; Kloezen, W.H. Indicators for comparing performance of irrigated agricultural systems.; Research report 20; International Water Management Institute: Colombo, Sri Lanka, 1998; pp. 1–26. [Google Scholar]
- Ahmad, M.D.; Masih, I.; Turral, H. Diagnostic analysis of spatial and temporal variations in crop water productivity: A field scale analysis of the rice-wheat cropping system of Punjab, Pakistan. J. App. Irrig. Sci. 2004, 39(1), 43–63. [Google Scholar]
- Bouman, B.A.M.; Peng, S.; Castaneda, A.R.; Visperas, R.M. Yield and water use of irrigated tropical aerobic rice systems. Agr. Water Manage. 2005, 74, 87–105. [Google Scholar]
- Droogers, P.; Kite, G.R. Water productivity from irrigated basin modeling. Irr. Drain. Sys. 1999, 13, 275–290. [Google Scholar]
- Oweis, T.; Hachum, A.; Pala, M. Faba bean productivity under rainfed and supplemental irrigation in northern Syria. Agr. Water Manage. 2005, 73, 57–72. [Google Scholar]
- Bastiaanssen, W.G.M.; Bos, M.G. Irrigation performance indicators based on remotely sensed data: A review of literature. Irrig. Drain. Sys. 1999, 13(4), 297–311. [Google Scholar]
- Bastiaanssen, W.G.M.; Ahmad, M.D.; Tahir, Z. Upscaling water productivity in irrigated agriculture using remote-sensing and GIS technologies. In Water productivity in agriculture: Limits and opportunities for improvement; Kijne, J.W., Barker, R., Molden, D., Eds.; CABI: Wallingford, UK, 2003; pp. 289–300. [Google Scholar]
- Chemin, Y.; Platonov, A.; Abdullaev, I.; Ul-Hassan, M. Supplementing farm-level water productivity assessment by remote sensing in transition economies. Water Int. 2005, 4, 513–521. [Google Scholar]
- Conrad, C.; Dech, S.W.; Hafeez, M.; Lamers, J.; Maritus, C.; Strunz, G. Mapping and assessing water use in a Central Asian irrigation system by utilizing MODIS remote sensing products. Irrig. Drain. Sys. 2007, 21, 197–218. [Google Scholar]
- El Magd, A.I.; Tanton, T.W. Remote sensing and GIS for estimation of irrigation crop water demand. Int. J. Remote Sens. 2005, 26, 2359–2370. [Google Scholar]
- Immerzeel, W.W.; Gaur, A.; Zwart, S.J. Integrating remote sensing and a process-based hydrological model to evaluate water use and productivity in a south Indian catchment. Agr. Water Manage. 2008, 95, 11–24. [Google Scholar]
- Allen, R.G.; Robison, C.W. Evapotranspiration and consumptive irrigation water requirements for Idaho. IDWR, Research Technical Completion Report. University of Idaho, 2007. Available at http://www.ecy.wa.gov/programs/wr/wig/images/pdf/et_cir_wa_102008.pdf.
- Bastiaanssen, W.G.M.; Samia, A. A new crop yield forecasting model based on satellite measurements applied across the Indus Basin, Pakistan. Agr. Ecosyst. Environ. 2003, 949, 321–340. [Google Scholar]
- Hafeez, M.M.; Bouman, B.A.M.; Van De Giesen, N.; Vlek, P. Scale effects on water use and water productivity in a rice-based irrigation system (UPRIIS) in the Philippines. Agr. Water Manage. 2007, 92, 81–89. [Google Scholar]
- Liu, J.; Jimmy, R.; Williams; Zehnder, A.J.B.; Yang, H. GEPIC-modelling wheat yield and crop water productivity with high resolution on a global scale. Agr. Sys. 2007, 94(2), 478–493. [Google Scholar]
- Liu, J.; Wiberg, D.; Zehnder, A.J.B.; Yang, H. Modelling the role of irrigation in winter wheat yield and crop water productivity in China. Irr. Sci. 2007, 26(1), 21–3. [Google Scholar]
- Liu, J. A GIS-based tool for modelling large scale crop-water relations. Environ. Model. Software. 2008, 24, 411–422. [Google Scholar]
- Tucker, C.J.; Grant, D.M.; Dyktra, J.D. NASA's Global Orthorectified Landsat dataset. Photogramm. Eng. Remote Sens. 2005, 70, 313–322. [Google Scholar]
- Markham, B.L.; Barker, J.L. Spectral characterization of the LANDSAT Thematic Mapper sensors. Int. J. Remote Sens. 1985, 6, 697–716. [Google Scholar]
- Markham, B.L.; Barker, J.L. Radiometric properties of U.S. processed Landsat MSS data. Remote Sens. Environ. 1987, 22, 39–71. [Google Scholar]
- Neckel, H.; Labs, D. The solar radiation between 3300 and 12500 A. Solar Physics 1984, 90, 205–258. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear effects in remote sensing. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar]
- Decagon Devices. AccuPAR ceptometer LP-80 operator's manual; 2004. [Google Scholar]
- Spectrum Technologies. WatchDog weather station operational manual; 2005. [Google Scholar]
- ESRI. ArcView User Guide; 2001. [Google Scholar]
- Boissard, P.; Guerif, M.; Pointel, J.G.; Guinot, J.P. Application of SPOT data to wheat yield estimation. Adv. Space Res. 1989, 8, 143–154. [Google Scholar]
- Shao, Y.; Fan, X.; Liu, H.; Xiao, J.; Ross, S.; Brisco, B.; Brown, R.; Staples, G. Rice monitoring and production estimation using multitemporal RADARSAT. Remote Sens. Environ. 2001, 76, 310–325. [Google Scholar]
- Thenkabail, P.S. Biophysical and yield information for precision farming from near-real time and historical Landsat TM images. Int. J. Remote Sens. 2003, 24, 2879–2904. [Google Scholar]
- Enclona, E.A.; Thenkabail, P.S.; Celis, D.; Diekmann, J. Within-field wheat yield prediction from IKONOS data: a new matrix approach. Int. J. Remote Sens. 2003, 24, 1–12. [Google Scholar]
- Lelong, C.C.D.; Pinet, P.C.; Poilve, H. Hyperspectral imaging and stress mapping in agriculture: A case study on wheat in Beauce (France). Remote Sens. Environ. 1998, 66, 179–191. [Google Scholar]
- Seelan, S.K.; Laguette, S.; Casady, G.M.; Seielstad, A. Remote Sensing applications for precision agriculture: A learning community approach. Remote Sens. Environ. 2003, 88, 157–169. [Google Scholar]
- Thenkabail, P.S.; Smith, R.B.; De-Pauw, E. Hyperspectral vegetation indices for determining agricultural crop characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar]
- Thenkabail, P.S.; Smith, R.B.; De-Pauw, E. Evaluation of Narrowband and Broadband Vegetation Indices for Determining Optimal Hyperspectral Wavebands for Agricultural Crop Characterization. Photogramm. Eng. Remote Sens. 2002, 68, 607–621. [Google Scholar]
- Thenkabail, P.S.; Enclona, E.A.; Ashton, M.S. Van Der Meer. Accuracy Assessments of Hyperspectral Waveband Performance for Vegetation Analysis Applications. Remote Sens. Environ. 2004, 91, 354–376. [Google Scholar]
- Doraiswamy, P.C.; Hatfield, J.L.; Jackson, T.J.; Akhmedov, B.; Prueger, J.; Stern, A. Crop condition and yield simulations using Landsat and MODIS. Remote Sens. Environ. 2004, 92, 548–559. [Google Scholar]
- Goward, S.N.; Huemmrich, K.F. Vegetation canopy PAR absorptance and the normalized difference vegetation index: an assessment using the SAIL model. Remote Sens. Environ. 1992, 39, 119–140. [Google Scholar]
- Pinter, P.J.; Hatfield, J.L.; Schepers, J.S.; Barnes, E.M.; Moran, M.S.; Daughtry, C.S.T.; Upchurch, D.R. Remote Sensing for crop management. Photogramm. Eng. Remote Sens. 2003, 69, 647–664. [Google Scholar]
- Thenkabail, P.S.; Ward, A.D.; Lyon, J.G.; Merry, C.J. Thematic Mapper vegetation indices for determining soybean and corn crop growth parameters. Photogramm. Eng. Remote Sens. 1994, 60, 437–442. [Google Scholar]
- Hay, R.K.M. Harvest index: a review of its use in plant breeding and crop physiology. Ann. Appl. Biol. 1995, 126, 197–210. [Google Scholar]
- Soltani, A.; Torabi, B.; Zarei, H. Modeling crop yield using a modified harvest index-based approach: application in chickpea. Field Crops Res. 2005, 91, 273–285. [Google Scholar]
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A coupled Remote Sensing and Simplified Surface Energy Balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holstag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): Formulation. J. Hydrology 1998, 213, 198–212. [Google Scholar]
- Allen, R.; Tasumi, M.; Morse, A.; Trezza, R. Satellite-based energy balance for mapping evapo-transpiration with internalized calibration (METRIC)-Model. J. Irrig. Drain. Sys. 2007, 19, 251–268. [Google Scholar]
- Kassam, A.; Smith, M. FAO methodologies on crop water use and crop water productivity.; Expert meeting on crop water productivity, Paper No CWP-M07; Rome, Italy, 2001. [Google Scholar]
- Wright, J.L.; Allen, R.G.; Howell, T.A. Conversion between evapotranspiration - references and methods. Proc. 4th Decennial National Irrigation Symposium, Phoenix, AZ, ASAE, St. Joseph, MI; 2000; pp. 251–259. [Google Scholar]
- Wright, J.L.; Jensen, M.E. Development and evaluation of evapotranspiration models for irrigation scheduling. Trans. ASAE 1978, 21, 87–96. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements; Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Todd, R.W.; Evett, S.R.; Howell, T.A. The Bowen ratio-energy balance method for estimating latent heat flux of irrigated alfalfa evaluated in a semi-arid, advective environment. Agric. Forest Meteorol. 2000, 103, 335–348. [Google Scholar]
- ASCE – EWRI. The ASCE standardized reference evapotranspiration equation. ASCE-EWRI Standardization of Reference Evapotranspiration Task Comm. Report. January 2005. http://www.kimberly.uidaho.edu/water/asceewri/ascestzdetmain2005.pdf.
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. The FAO-56 dual crop coefficient method for predicting evaporation from soil and application extensions. J. Irrig. Drain. Eng. 2005, 131(1), 2–13. [Google Scholar]
- Basiaanssen, W.G.M.; Pelgrm, H.; Wang, J.; Ma, Y.; Moreno, J.; Boerink, G.J.; Van Der Wal, T. The surface energy balance algorithm for land (SEBAL): Validation. J. Hydrology 1998, 213, 213–229. [Google Scholar]
- Bastiaanssen, W.G.M. SEBAL-basedsensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrology 2000, 229, 87–100. [Google Scholar]
- Tasumi, M. Progress in operational estimation of regional evapotranspiration using satellite imagery. PhD thesis, Dept. Biological and Agricultural Engineering, Univ. Idaho, 2003. [Google Scholar]
- Allen, R.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.; Bastiaansses, W.; Kramber, W.; Lorite, I.; Robinson, C. Satellite-based energy balance for mapping evapo-transpiration with internalized calibration (METRIC)-Applications. ASCE 2007, 133, 1–395. [Google Scholar]
- Allen, R.; Morse, A.; Tasumi, M.; Trezza, R.; Bastiaanssen, W.; Wright, J.; Kramber, W. Evapotranspiration from a satellite-based surface energy balance for the Snake Plain Aquifer in Idaho. Proc. USCID Conference, USCID, Denver; 2002. [Google Scholar]
- Leica Geosystems. ERDAS Imagine User Guide; 2003. [Google Scholar]
- Cai, X.; Thenkabail, P.S.; Platonov, A.; Biradar, C.; Gumma, M.; Dheeravath, V.; Cohen, Y.; Goldshlager, N.; Ben-Dor, E.; Alchanatis, V.; Vithanage, J.V.; Manthrithilake, H.; Kendjabaev, Sh.; Isaev, S. Water Productivity Mapping and the factors affecting water productivity using remote sensing data of various resolutions. Photogrammetric Engineering and Remote Sensing. in review.
- Biradar, C.M.; Thenkabail, P.S.; Platonov, A.; Xiangming, X.; Geerken, R.; Vithanage, J.; Turral, H.; Noojipady, P. Water Productivity Mapping Methods using Remote Sensing. J. Appl. Remote Sens. 2008, 2, 023544. [Google Scholar]
- Allen, R.G.; Jensen, M.E.; Wright, J.L.; Burman, R.D. Operational estimates of reference evapotranspiration. Agron. J. 2004, 81, 650–662. [Google Scholar]
- Nagler, P.L.; Scott, R.L.; Westenburg, C.; Cleverly, J.R.; Glenn, E.P.; Huete, A.R. Evapotranspiration on western U.S. rivers estimated using the Enhanced Vegetation Index from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sens. Environ. 2005, 97, 337–351. [Google Scholar]
- Allen, R.G.; Jensen, M.E.; Wright, J.L.; Burman, R.D. Operational estimates of reference evapotranspiration. Agron. J. 2004, 81, 650–662. [Google Scholar]
- Nagler, P.L.; Scott, R.L.; Westenburg, C.; Clevery, J.R.; Glenn, E.P.; Huete, A.R. Evapotranspiration on western U.S. rivers estimated using the Enhanced Vegetation Index from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sens. Environ. 2005, 97, 337–351. [Google Scholar]
- Kamilov, B.; Ibragimov, N.; Esanbekov, Y.; Evett, S.; Heng, L. Irrigation scheduling study of drip irrigated cotton by use of soil moisture neutron probe. Proceedings of the UNCGRI/IAEA National Workshop in Optimization of Water and Fertilizer use for Major Crops of Cotton Rotation, Tashkent, Uzbekistan, December 24–25, 2002.


| Acquisition Date | Julian Day | Sun Elevation | Sun Azimuth | Earth-Sun distance |
|---|---|---|---|---|
| (deg.) | (deg.) | (Astronomic unit) | ||
| 2006_0424 | 114 | 56.388 | 138.573 | 1.005779 |
| 2006_0510 | 131 | 60.608 | 134.262 | 1.010059 |
| 2006_0611 | 162 | 64.404 | 125.537 | 1.015454 |
| 2006_0729 | 210 | 60.030 | 128.871 | 1.015165 |
| 2006_0814 | 226 | 56.740 | 134.465 | 1.012679 |
| 2006_1001 | 274 | 42.732 | 152.052 | 1.000576 |
| Gain | Band1 | Band2 | Band3 | Band4 | Band5 | Band6 | Band7 | |
|---|---|---|---|---|---|---|---|---|
| Low | LMin | -6.2 | -6.4 | -5.0 | -5.1 | -1.0 | 0.0 | -0.35 |
| Low | LMax | 293.7 | 300.9 | 234.4 | 241.1 | 47.57 | 17.04 | 16.54 |
| High | LMin | -6.2 | -6.4 | -5.0 | -5.1 | -1.0 | 3.2 | -0.35 |
| High | LMax | 191.6 | 196.5 | 152.9 | 157.4 | 31.06 | 12.65 | 10.80 |
| ESUNλ | 1969 | 1840 | 1551 | 1044 | 225.7 | 82.07 | ||
| Crop | Number of samples | Day of Year | Mean values from the samples | |||
| Wet biomass | Dry biomass | Leaf Area Index | Crop Yield | |||
| (kg/m2) | (kg/m2) | (m2/m2) | (ton/ha) | |||
| Wheat | 28 | 127 | 1.69 | 0.4 | 2.16 | 1.850 |
| 145 | 1.33 | 0.65 | 2.17 | |||
| 158 | 0.65 | 0.43 | 1.32 | |||
| Cotton | 162 | 127 | 0.02 | 0.00 | 0.07 | 1.230 |
| 145 | 0.04 | 0.01 | 0.28 | |||
| 158 | 0.12 | 0.02 | 0.49 | |||
| 173 | 0.25 | 0.05 | 0.60 | |||
| 188 | 0.88 | 0.23 | 1.78 | |||
| 200 | 1.25 | 0.26 | 2.38 | |||
| 214 | 1.22 | 0.35 | 2.04 | |||
| 229 | 1.52 | 0.62 | 2.53 | |||
| 247 | 3.05 | 1.41 | 1.71 | |||
| 256 | 3.09 | 1.36 | 1.87 | |||
| 271 | 1.90 | 1.06 | 1.40 | |||
| Rice | 43 | 173 | 0.29 | 0.04 | 0.65 | 4.315 |
| 188 | 0.75 | 0.24 | 1.59 | |||
| 200 | 1.02 | 0.24 | 1.24 | |||
| 214 | 1.54 | 0.80 | 2.12 | |||
| 229 | 1.91 | 0.72 | 5.56 | |||
| 247 | 3.49 | 1.58 | 5.60 | |||
| 256 | 4.41 | 2.18 | 3.24 | |||
| 271 | 1.17 | 0.65 | 1.24 | |||
| Maize | 40 | 173 | 0.02 | 0.00 | 0.19 | 3.305 |
| 188 | 0.04 | 0.01 | 0.25 | |||
| 200 | 0.07 | 0.01 | 0.47 | |||
| 214 | 0.37 | 0.07 | 0.87 | |||
| 229 | 1.05 | 0.48 | 0.99 | |||
| 247 | 3.63 | 1.90 | 1.48 | |||
| 256 | 3.25 | 1.74 | 1.52 | |||
| 271 | 3.09 | 1.98 | 1.05 | |||
| Calculation time step | Short Reference (ETo) | Tall Reference (ETr) | ||
|---|---|---|---|---|
| (clipped grass) | (alfalfa) | |||
| Cn | Cd | Cn | Cd | |
| Daily | 900 | 0.34 | 1600 | 0.38 |
| Hourly during daytime | 37 | 0.24 | 66 | 0.25 |
| Hourly during nighttime | 37 | 0.96 | 66 | 1.7 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cotton | 15 | 31 | 30 | 31 | 31 | 30 | ||||||
| ETo | 0.6 | 0.944 | 1.753 | 3.398 | 5.081 | 6.716 | 7.066 | 6.269 | 4.466 | 2.587 | 1.103 | 0.656 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Platonov, A.; Thenkabail, P.S.; Biradar, C.M.; Cai, X.; Gumma, M.; Dheeravath, V.; Cohen, Y.; Alchanatis, V.; Goldshlager, N.; Ben-Dor, E.; et al. Water Productivity Mapping (WPM) Using Landsat ETM+ Data for the Irrigated Croplands of the Syrdarya River Basin in Central Asia. Sensors 2008, 8, 8156-8180. https://doi.org/10.3390/s8128156
Platonov A, Thenkabail PS, Biradar CM, Cai X, Gumma M, Dheeravath V, Cohen Y, Alchanatis V, Goldshlager N, Ben-Dor E, et al. Water Productivity Mapping (WPM) Using Landsat ETM+ Data for the Irrigated Croplands of the Syrdarya River Basin in Central Asia. Sensors. 2008; 8(12):8156-8180. https://doi.org/10.3390/s8128156
Chicago/Turabian StylePlatonov, Alexander, Prasad S. Thenkabail, Chandrashekhar M. Biradar, Xueliang Cai, Muralikrishna Gumma, Venkateswarlu Dheeravath, Yafit Cohen, Victor Alchanatis, Naftali Goldshlager, Eyal Ben-Dor, and et al. 2008. "Water Productivity Mapping (WPM) Using Landsat ETM+ Data for the Irrigated Croplands of the Syrdarya River Basin in Central Asia" Sensors 8, no. 12: 8156-8180. https://doi.org/10.3390/s8128156
APA StylePlatonov, A., Thenkabail, P. S., Biradar, C. M., Cai, X., Gumma, M., Dheeravath, V., Cohen, Y., Alchanatis, V., Goldshlager, N., Ben-Dor, E., Vithanage, J., Manthrithilake, H., Kendjabaev, S., & Isaev, S. (2008). Water Productivity Mapping (WPM) Using Landsat ETM+ Data for the Irrigated Croplands of the Syrdarya River Basin in Central Asia. Sensors, 8(12), 8156-8180. https://doi.org/10.3390/s8128156





