Abstract
The proper assessment of evapotranspiration and soil moisture content are fundamental in food security research, land management, pollution detection, nutrient flows, (wild-) fire detection, (desert) locust, carbon balance as well as hydrological modelling; etc. This paper takes an extensive, though not exhaustive sample of international scientific literature to discuss different approaches to estimate land surface and ecosystem related evapotranspiration and soil moisture content. This review presents:
- (i)
- a summary of the generally accepted cohesion theory of plant water uptake and transport including a shortlist of meteorological and plant factors influencing plant transpiration;
- (ii)
- a summary on evapotranspiration assessment at different scales of observation (sap-flow, porometer, lysimeter, field and catchment water balance, Bowen ratio, scintillometer, eddy correlation, Penman-Monteith and related approaches);
- (iii)
- a summary on data assimilation schemes conceived to estimate evapotranspiration using optical and thermal remote sensing; and
- (iv)
- for soil moisture content, a summary on soil moisture retrieval techniques at different spatial and temporal scales is presented.
Concluding remarks on the best available approaches to assess evapotranspiration and soil moisture content with and emphasis on remote sensing data assimilation, are provided.
1. Introduction
1.1. The significance of evapotranspiration and soil moisture content
The monitoring and modelling of land surface and vegetation processes is an essential tool for the assessment of water and carbon dynamics of terrestrial ecosystems. The proper estimation of evapotranspiration (ET) and soil moisture content (SMC) is a fundamental issue as well in food security research, land management systems, pollution detection, nutrient flows, (wild-)fire detection, (desert) locust and carbon balance modelling. Knowledge on ET is fundamental when dealing with water resources management issues such as the provision of drinking and irrigation water, industrial water use or water reserve management. These issues go from questions of agricultural and life sustainability to even direct human life support measures for large parts of the globe. They will even shift closer to direct life support in the years to come [1]. Soil moisture content is a soil status condition, directly connected with the process of ET since SMC is usually related to moisture contained in the upper 1-2 m of a soil profile, moisture which can potentially evaporate. Evidently, SMC is one of the prime environmental variables related to land surface climatology, hydrology and ecology [2]. Variations in SMC entail a strong impact on land surface energy dynamics, regional runoff dynamics and vegetation productivity (actual crop yield) [3]. More specifically, datasets of ET and SMC are indispensable for accurate estimates of carbon fluxes used in carbon balance models such as C-Fix [4] [5] [6] or CASA (Carnegie-Ames-Stanford Approach, [7]). This is especially true in water limited areas, of which there are many distributed over the globe. Moreover in Europe, a direct link is observed between soil water status, gross primary productivity of vegetation and soil respiration [8]. As such, soil moisture and ET affect terrestrial carbon uptake and release from and towards the atmosphere. Hence, knowledge on ET and SMC dynamics has a strong impact on the interpretation of global change effects [9] and hence, the implementation and impact of the Kyoto protocol on the global society. Early detection of dry soil conditions or potential drought is important for crop yield forecasting and hence, crop harvest optimization [10]. Yield forecasting, is an important early warning tool for farmers, and is important for the preparation and logistics of humanitarian food aid missions in famine struck areas. It also serves as an information base for commodity brokers. SMC can also be applied as a predictor for flood conditions, when soils become completely saturated. Under saturated conditions, soil cannot retain any surplus run-on or precipitation, hence a sharp rise in flooding risk. SMC is an important parameter in watershed modelling [11] as well and provides information related to hydro-electric or irrigation capacity. In areas with active deforestation or vegetation cover change, SMC estimates help to predict run-off, evaporation rates, and soil erosion [12]. Last but not least, SMC and ET are important status indicators in fire risk danger systems.
Despite the importance of SMC, its accurate assessment is difficult. The standard procedure for soil water determination against which all other SMC methods are calibrated is the gravimetric method. This standard procedure is essentially a point measurement. Hence, local scale variations in soil properties, terrain, and vegetation cover make the selection of representative field sites difficult if not impossible. Moreover, field methods are complex, labour intensive and therefore expensive. In contrast with the previous, remote sensing (RS) techniques are promising because of their spatially aggregated measurements as well as their relatively low cost [13].
1.2. Descriptions of evapotranspiration and soil moisture content
ET is the process whereby water - originating from a wide range of sources - is transferred from the soil compartment and/or vegetation layer to the atmosphere. ET includes evaporation from surface water bodies, land surfaces, soil, sublimation of snow and ice, plant transpiration as well as intercepted canopy water. ET represents both a mass and an energy flux. An allocation of ET into plant transpiration, soil evaporation and intercepted water evaporation fluxes, is generally accepted [14] [15]. Evaporation is the physically based process of transferring water - stored in the soil or on the surface of canopies, stems, branches, soils and paved areas - to the atmosphere. Transpiration is the evaporation of water in the vascular system of plants through leaf stomata. Opening and closure of stomata is controlled by their guard cells. Hence, transpiration is a bio-physical process since it involves a living organism and its tissues. The transpiration-pull explained by cohesion theory, determines the dynamics of water transport from soils over plant systems towards the atmosphere. Cohesion theory was first formulated in the 19th century by Dixon and Joly [16] and quantified by van den Honert [17].
Apart from ET, potential, reference and actual evapotranspiration are important as well, as ET related quantities. Thornthwaite [18] was the first to introduce the concept of potential evapotranspiration (ETpot). He defined ETpot as the maximal water quantity transferred to the atmosphere, from a vegetation cover in a state of full physiological activity and unlimited water and nutrient availability. As published by Choisnel et al. [19], ETpot corresponds with water consumed by a grass lawn cover during its active phase and without restriction of water and nutritional elements uptake. This quantity is also referred to as potential or reference evapotranspiration (ETref or ET0). A crop factor (Kc) is used to estimate ETpot for other vegetation than lawns. A widely used approach to estimate ET is the FAO-24 [20] and by extension the FAO-56 procedure, based on ET0 and Kc [21].
Since most ET assessments are only indirectly based on plant physiological knowledge, it has to be born in mind that plant water transport involves active (energy consuming) plant physiological processes. Hence, a brief description is given of the mechanism of water transport in plants before an overview of some ET assessment methods is given. The backbone to present this brief account is that in general, modelling beyond plant and field scales can shift plant physiological mechanisms in the background. This can be understood in the sense that basic plant processes may be of less importance at larger spatial scales. It is however the physiological basis of the ET process that creates a better framework to understand the application of remote sensing (RS) for ET estimation and its limiting factors. It can also explain why some approaches to estimate ET were developed and even why other possibilities were or should be chosen.
Summarizing, the main focus of this paper is the provision of an overview of the international scientific literature describing different methods to determine land surface ET and SMC with an emphasis on ET. A wide range of literature sources has been consulted (reports, international journals, PhD's) in an attempt to provide optimal accessibility of the problem area for the reader. An important focus is the identification of methods, optimally suited for specific applications as well. Whether it be ET, estimated as a singular parameter or as a parameter assimilated in integrated agro-ecological applications. The sub-objectives of this review have been identified as follows:
- (i)
- A summary of the theory of plant water uptake and transport and the presentation of a shortlist of environmental factors influencing plant transpiration;
- (ii)
- A summary of ET assessment methods at different spatial scales, with a discussion on pro's and con's in different applications;
- (iii)
- A summary of SMC assessment methods at different spatial scales, with a discussion on pro's and con's in different applications;
- (iv)
- An account on the linkage of ET and SMC assessment approaches with existing remote sensing techniques.
Evidently, this review paper does not attempt to exhaustively cover the broad application field of ET and SMC. It should rather be perceived as an attempt to present the reader the broadly used as well as accepted measuring and modelling concepts to assess ET and SMC without going into ultimate detail. From this perspective, this paper can be seen as a guide to the application fields of ET and SMC research and development from plant, patch, regional to continental scales.
2. Notions on crop water consumption
2.1. The water pathway in plants from the physiological point-of-view: Cohesion Theory
When considering terrestrial plant ecosystems, transpiration is a water flux from the vegetation layer towards the atmosphere, originating from soil water uptake by the plant root system. The transpiration-pull theory offers a cognitive framework explaining the water pathway from soils over plant systems towards the atmosphere. Because of the critical role of the physical concept of cohesion, this theory is also known as Cohesion Theory and was formulated in the 19th century by Dixon and Joly [16]. Quantification was attempted by van den Honert [17]. A review article about the current controversies of this theory was written by Tyree [22].
The three basic elements of Cohesion Theory are:
- (i)
- driving force;
- (ii)
- hydration (adhesion) and;
- (iii)
- cohesion of water.
The driving force is a gradient of decreasing (more negative) soil water potential, over the soil - plant – atmosphere continuum. Water moves in this continuum from the soil, through the epidermis, cortex, and endodermis, into the vascular tissue of roots, up through the xylem of vascular plant systems, into its leaves, and finally, by transpiration through the stomatal pores, into the atmosphere. Fig. 1 depicts a schematic view of the water movement pathway from soil to xylem.
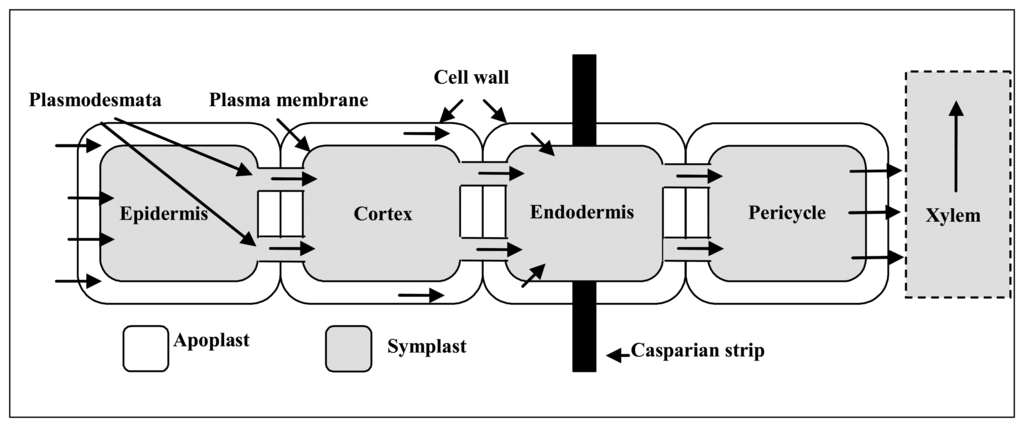
Figure 1.
Water pathway of vascular plants: From soil through the root tissue up to the xylem.
Soil water enters the root system through root hairs, protrusions into the soil matrix of the root system epidermal cells. Apparently, water travels both in the living cytoplasm and the nonliving vascular system of the root cells, respectively denoted as the symplast and apoplast. Water crosses the plasma membrane and then passes from cell to cell through plasmodesmata. The water in the apoplast does not cross plasma membranes. The endodermis however is impervious to water because of the casparian strips. Therefore, before passing by the plasmodesmata into the cells of the stele, apoplastic water must enter the symplasm of the endodermal cells. Once inside the stele, water can freely move between cells as well as through them. In young roots, water enters directly into the xylem vessels and/or trachea (nonliving water conducting elements of the apoplast). Xylem tissue is the most important water pathway in woody species and is composed of four cell types, i.e., trachea, vessel elements, fibres, and the xylem parenchyma. After the active transport of water from the soil to the roots, water reaches plant leaves under nominal conditions.
Adhesion and especially cohesion forces are the primary drivers for water transport in vascular plants. Hydratation forces between water molecules and plant cell walls are based on the Van der Waals bondage. In the specific environment of xylem tissues the pathway taken by water, implies cohesive forces so strong that, when water is pulled from its holding points in the cell walls at the top of a plant or tall tree, the pull extends all the way down through the stem or trunk and roots into the soil. When the pull force is larger than tensile strength (the ability to resist stretching without breaking) the phenomenon of cavitation occurs, usually when severe water stress impacts on a vascular plant. A continuous water column can break when the water potential drops below a critical level. This results in an embolism in the transporting elements of a vascular plant water transport structure. It is believed that a reversal of embolism can take place, even after cavitation has occurred, because of the containment of atmospheric and water vapour. Water vapour can convert into its liquid state and hence refill the conducting tissue or vessels. Cavitated vessels can also be re-filled with atmosphere or by-passed. As water stress builds up during drought episodes, cavitation first occurs in leaves. These can then wilt or even die, although the water transport system in the trunk remains relatively intact.
2.2. Quantification of evapotranspiration
Basically, the process of evaporation is the diffusion of water molecules into the atmosphere. In that respect the general formulation of Fick's First Law (introduced in the mid 1800's) is an equation based on a concentration gradient per unit area [m2]:
In Eq. (1):
- K is a turbulence factor [m2 s-1];
- E is the amount of water evaporated [m s-1];
- dC dz-1 the concentration gradient [10-3 kg m-3 m-1].
In evaporation theory, Dalton first proposed the mass transfer formula in 1802:
In Eq. (2):
- f(va) is a function of wind speed [m s-1 millibar-1];
- va is wind speed [m s-1];
- es is the vapour pressure in the saturated region of a water surface [millibar];
- ea is the vapour pressure in the atmospheric space above the saturated region [millibar].
Many functions of wind speed are a combination of wind velocity and some coefficient(s). If this boundary condition is satisfied, evaporation only depends on wind speed and the difference in moisture content of the water saturated atmospheric space above the water surface and the atmospheric space above the saturated region. Clearly, measurements of wind speed, surface and atmospheric temperature as well as the relative humidity above the water surface are required to enable the use of Eq. (2).
To enable the determination of leaf transpiration, mass transfer models of evaporation can be modified to reflect the atmospheric conditions in the vicinity of the leaf. Since transpiration is structurally linked with stomata, it is dependent on the number of stomata and their degree of opening. Evidently, transpiration is limited by water availability as well.
Considering the energetic aspects of transpiration, i.e. that the latent heat of vaporization is linearly related to the mass of evaporated water, one can write:
In (3):
- LE is the latent heat to vaporize a specific amount of water, usually expressed in [W m-2];
- ρw is water density [kg m-3];
- λ is the latent heat of vaporization (2,260 at 100 °C) needed to transfer water from its liquid to its vapour phase [kJ kg-1];
- E is the amount of evaporated water (flux) expressed in [m3 m-2 s-1] or [m s-1].
After substitution of (3) into the mass transfer (2), the expression for latent heat can be written as:
The temperature difference between a water surface and the atmospheric space above it also induces heat transfer (sensible heat flux).
Evaporation and transpiration are difficult to measure directly and separately. Hence, usually models are applied for the estimation of cited water mass fluxes. Evaporation models are based on laws of mass conservation such as those applied in water and energy balances, in mass transfer, or in a combined approach.
More information on evapotranspiration quantification can be found in [23] and other sources.
2.3. Crop water relationships
Available water is defined as the difference between the amount of water in a soil at field capacity and the amount of water in a soil at permanent wilting point. Permanent wilting point is (more or less arbitrarily) set at a pF (force of soil water suction) of 4.2 (i.e. log10 |-15849| in [cm]). Field capacity corresponds with water held in a soil against the forces of gravity (sometimes set at a pF value of 2.3). Permanent wilting point is the percentage of soil moisture which induces wilting in a plant system. This wilting is irreversible, i.e. the plant system does not recover, even when placed in an atmosphere with a relative humidity of 100%. Some basic factors affecting water uptake of plants are summarized in Table 1.

Table 1.
Some basic meteorological and plant factors affecting water uptake of plants.
Water stress affects plant yield by a reduction of leaf area, a reduction of stomatal conductance, by a reduction of CO2 uptake and hence photosynthesis and by a slow down of root elongation and development. Water stress also affects proper seed development (starch filling). Yield and water stress can be quantified with the concept of Water Use Efficiency (WUE). The physiological definition of WUE is: “The amount of carbon in milligrams of assimilated carbon per gram of H2O transpired”. The agronomist defines WUE as: “The ratio of dry matter produced (yield) to water consumed”. Crassulacean Acid Metabolism (CAM) plants are metabolically optimized for the highest WUE compared to C3 and C4 metabolism plants. CAM plants can close their stomata during daytime and open them at night. This strategy ensures a significant reduction of water loss by reduced transpiration. CAM plants have a low and variable productivity but a very high WUE.
In general C4 species elicit a higher WUE than C3 plants. Typically C4 plants can close their stomata (less CO2 and less water loss) during daytime, while still carrying out a high level of photosynthesis. Evidently this leads to a higher WUE than C3 plants, which do not have this capacity.
3. Evapotranspiration assessment techniques at different scales of observation
As a result of the spatial heterogeneity of soils, vegetation type and cover, soil moisture status and plant water availability varies spatially [24]. Furthermore, the dependency of hydrological processes on meteorology and climate makes ET, spatially and temporally variable. The interaction between the spatial and temporal dimension of evaporation processes result in a complex methodology for ET assessment [25].
ET estimations can be performed at the scale of a leaf (porometer), an individual plant (i.e. sap-flow, lysimeter), at the field scale (i.e. field water balance, Bowen ratio, scintillometer) and at landscape scale (i.e. eddy correlation and catchment water balance). The assessment of ET always involves the laws of mass or energy conservation or a combination of both. For regional to continental scales, the use of earth observation (EO) data or models assimilating remote sensing data, is a strong requirement [26] [27]. A large number of measuring techniques and modelling approaches have been published in this respect [25]. Without claiming completeness, Table 2 gives an overview of a variety of ET retrieval techniques, frequently encountered in the literature. ET retrieval techniques can be classified according to the spatial scale of application and the conservation law applied. Several earth observation approaches can be found in i.e. [57] [58] [59] [60] [61] [62] [25] [55] [54] [63] [64] [65] [66] [67] [68] [69] [70]. Before briefly discussing the assessment of evapotranspiration, the laws of mass and energy conservation are formally defined, since they are the basis of the assessment methodologies of many variables in this application field.

Table 2.
Different scales of observation to assess evapotranspiration using a variety of techniques.
3.1. The conservation laws
A typical, daily one-dimensional water (mass) balance equation can be defined as follows:
In (5):
- P is the amount of rainfall [mm d-1];
- CR is the capillary rise from the groundwater table [mm d-1];
- Irr is the irrigation dose [mm d-1];
- ET is evapotranspiration [mm d-1];
- R is runoff [mm d-1];
- D is drainage [mm d-1];
- and S is the storage of water in the soil compartment [mm d-1].
A typical, daily one-dimensional energy balance omits (or ignores) energy storage in the canopy due to photosynthesis. For a vegetated land surface, the energy balance equation can be written as:
In (6):
- Rn is net radiation (net short and net long wave) [W m-2];
- G0 is the subsurface heat flux [W m-2];
- S is the rate of heat storage in the plant canopy [W m-2];
- H is the sensible heat flux [W m-2];
- λE is the latent heat flux [W m-2];
- λ is the latent heat of vaporization of water, approximately 2,450 J g-1 H2O at 20°C;
- and E is evapotranspiration [g H2O m-2 s-1].
The energy storage due to photosynthesis is generally estimated to be less than a few percent of land surface net radiation [71]. Hence, generally the energy storage term S in the equation of the land surface energy balance is omitted. However, heat storage in plant canopies can become a substantial part of the energy balance for periods less than a day, particularly for massive canopies such as those of forests. Quantitative information on S is rare in the literature however and moreover difficult to obtain [49]. Both mass and energy balances can be combined, for example by estimating ET using the energy balance, it is possible to better estimate the other terms of the water balance like for example water drainage.
3.2. Point / leaf / plant and field scale transpiration and evapotranspiration estimation
The execution of field measurements represents a labour intensive endeavour. Moreover, it is a time consuming activity, which generally requires expensive equipment. In situ, potentially everything can go wrong. Despite these caveats, field measurements are the very touchstone to confront a modelling approach with the physical reality of the environment. Field measurements provide a treasure of information for the validation of models and for accurate quantitative information needed and asked for by policy and decision makers. Models without accompanying measurements, i.e. calibration and validation (cal/val) data, may be sophisticated mind constructions but they are worthless for sure in underpinning land management policy making. In the next chapter, we give a short overview of sap-flow sensors, the porometer, the lysimeter and field water balance approaches. These techniques produce consistent temporal profiles of ET data with a local outreach.
3.2.1. Estimation of transpiration based on Sap-flow measurements
A sap-flow sensor involves heater and temperature probes which are inserted into stems or branches. Sap-flow absorbs heat thereby inducing a temperature drop. Different type of sap-flow measurement principles exist. For instance the Heat Pulse Velocity principle is applied with a heater probe inserted into the sapwood, with thermocouples inserted downstream and sometimes upstream of the sensor to measure temperature change due to the heat pulse. The Thermal Dissipation Probe is applied by insertion of an upper needle containing a heater element and a thermocouple which is referenced to a second needle downwards in the sapwood stream. The Heat Field Deformation Method is applied by the use of a heater and two atmospherics of a thermocouple implanted symmetrically and asymmetrically into the stem. The Heat Balance Method is based on the ratio between heat input and temperature rise in a pre-defined space. Finally, the Stem Heat Balance method is applied by external heating with a soft and flexible heater and a couple of thermo-sensors.
These techniques allow, to measure plant effective water streams. In that respect sap-flow sensors are very useful for calibration and validation of water and energy balance algorithms whether or not based on remote sensing. They are a very good alternative to lysimeter experiments. Operation of sap-flow sensors though, requires a vast technical input and maintenance effort. Power supply in areas without electricity distribution is an evident problem. Signal conversion (from temperature to sap-flow) involves a (semi)-empirical approach and is based on a priori knowledge of the sapwood basal area. Sapwood basal area is required to convert flow velocities to transpiration rates. Moreover, water storage in the stem must be considered. Tree dimensions are needed for the up-scaling from stem at breast height to the tree level (hence, tree characteristics must be known). More information on the techniques described can be found in: [72] [30 [31] [28] [29] [32] [14].
3.2.2. Estimation of transpiration based on Porometer measurements
A porometer measurement estimates transpiration of a leaf or twig by measuring:
- (i)
- the increase of humidity within a closed chamber attached to the leaf, or;
- (ii)
- with a steady state porometer that maintains a constant humidity in a measuring chamber by matching a flow of dry atmospheric to balance water vapour loss from the enclosed leaf. Water vapour loss from the chamber by atmospheric flow equals the gain in water vapour by transpiration (mass conservation principle). The instrument calculates the amount of water vapour outflow from measured atmospheric flow, relative humidity, and temperature and corrects for the known leaf area in the cuvette to give transpiration per unit leaf area. Porometers are used to determine leaf stomatal conductance but one may also be tempted to extrapolate measurements on a single leave to a whole canopy, when knowing total leaf area.
A porometer measurement provides direct estimates of water loss from leaves. It suffers however from the requirement that the estimations at leaf level must be extrapolated to a whole canopy. This type of up-scaling is not straightforward. Transpiration rates measured with a porometer do not correspond with those measured in undisturbed natural conditions. This is due to differences in boundary layer conductance. A more rigorous approach is the independent determination of atmospheric saturation deficit and the transpiration rate by porometry [73] thereby taking boundary layer conductance into account. Porometers are useful for conductance-based models since leaf stomatal conductance and transpiration can be measured. More specific information on this topic can be found in [46] [47] [14].
3.2.3. Estimation of evapotranspiration based on a lysimeter
The lysimeter is widely used in laboratories and for field work, mainly for agronomic research. The weighing lysimeter technique can be extended if there is a requirement for measurements of tree transpiration. An undisturbed vegetated soil sample is taken with cylinders of different diameters (up to 3.14 m2). ET is estimated from the mass balance of water of initial minus final weight plus rainfall minus drainage.
The main advantage of lysimeter in situ measurements is that water consumption of vegetation can be performed under approximately realistic field conditions. However, a lysimeter measurement requires elaborate preparation in fact intrinsic to field measurements. Moreover it is typically limited to only few individual trees or a small surface area of agricultural crops. Additionally only young trees can be measured, hence this type of measurement is not representative for aged or mixed age forest stands. Moreover, the installation of lysimeters can cause disturbances compared to surrounding vegetation and agricultural crops in a lysimeter may suffer from a different treatment than crops in the field. A more realistic approach is the ‘natural lysimeter’ [74]. In this type of lysimeter, a barrier to lateral water flow in and above the soil is installed and measurements of precipitation and soil water content are made while the rate of deep drainage is approximated.
The lysimeter is very useful for data collection and for modelling water use and growth of agricultural crops. Also known is chemical solute transport research. More specific information can be found in [33] [31] [75].
3.2.4. Estimation of evapotranspiration based on the Bowen ratio
The Bowen ration (BR) is a micrometeorological variable evaluated for a height of a few meters to a few tens of meters above a surface, representative for the surface sub-layer of the atmospheric boundary layer. Under steady state conditions and in absence of horizontal gradients of vertical fluxes of momentum, heat, and water vapour flux, the vertical fluxes of heat and water vapour within a fully turbulent surface sub-layer are not appreciably different from these fluxes at the earth's surface [76]. The scalar vertical fluxes of heat and water vapour of land or water surfaces are estimated within the surface sub-layer. Typically, the Bowen ratio is an energy balance method and represents the ratio of the sensible and latent heat fluxes. The BR is variable used in a widespread approach for ET determination at the local scale. An important boundary condition, however for the evaluation of a one-dimensional BR, is the absence of horizontal energy fluxes. Hence, it cannot be used inside canopies. Furthermore, net radiation and soil heat fluxes must be measured simultaneously. With the BR approach, ET can be estimated beyond the point scale and can therefore be used to compare and classify vegetation types. More specific information about this approach can be found in [35] [37] [14] [36].
3.2.5. Estimation of evapotranspiration based on meteorological datasets
Estimation of ET can be based on energy balance schemes and the Penman-Monteith [56] equation in one of its many varieties. ET estimation can be based as well on the parameterization of energy balance components. Both the Penman-Monteith (PM) equation and the parameterization can be implemented in combination with EO assimilation techniques. In many approaches ETact is estimated from ETpot (i.e. obtained from water balance models such as WAVE see next section); energy balance models such as Penman-Monteith and derivates. A formal definition of ETpot was already given in section 1.2. The formulae to estimate ETpot for other vegetation than lawns is based on ETref and (Kc) as mentioned below (FAO-56 procedure).
The Penman-Monteith equation is applied within the concept of a ‘big-leaf’ approach and evaluates ET from the energy balance, combined with mass transfer. Since in the 1950's and 60's surface temperature could not be measured accurately, hence atmospheric-surface temperature differences could not be applied to calculate sensible heat fluxes. The Penman equation for open water however does not pose problems, since for this surface type atmospheric and water surface temperatures are assumed to be quasi equal. This is in contrast with the case of vegetation and bare soils.
Under the boundary condition mentioned here above, the amount of water to saturate dry atmospheric at a given pressure is temperature dependent (saturated vapour pressure) and is written as expressed in (7).
Saturated vapour pressure is the maximal partial pressure of water vapour in atmospheric at a given temperature. This expression contains, after a linearization with a Taylor expansion, the atmospheric-surface temperature difference. This temperature difference can be inserted in the energy balance equation to lead us to the sensible heat component. The Penman-Monteith equation can then be written as expressed in (8).
In (7) & (8):
- Ta is atmospheric temperature [°C];
- es is saturated vapour pressure at temperature T [mbar];
- Δ is the slope of the vapour pressure curve [mbar K-1];
- γ* equals γ (1+rc rah-1);
- γ is the psychrometric constant [mbar K-1];
- (es(T0)-ea) is saturated vapour pressure deficit [mbar];
rah and rc respectively are the aerodynamic and canopy or surface resistances according to the ‘big leaf’ concept expressed in [s m-1]; Generally rc is defined as rs LAI-1 where rs is the stomatal resistance of leaves.
A simplification of the Penman-Monteith equation is the Priestley-Taylor equation [77]. These authors stated that the atmospheric drying power over a wet surface is a constant, multiplied with Δ(Rn-G0) as expressed in (9).
- α is a constant [-] ranging from 1 to 1.35 for wet surfaces [78];
- γ is the psychrometric constant [mbar K-1];
- Δ is the slope of the vapour pressure curve [mbar K-1].
Choisnel et al. [19] mentions an expression derived from the Penman-Monteith equation, Makkink (1957). It is used in the Netherlands with a taking a value of 0.65 (or 0.8 times of its value in the Penman expression in (9). Brochet-Gernier used the same expression for France [19].
For sparse canopies, the Penman-Monteith ‘big-leaf’ approach no longer holds. Under these boundary conditions, soil evaporation must be incorporated in the modelling approach. Shuttleworth & Wallace [79] suggested the use of a resistance model. In that approach, the energy available for evaporation from the canopy and soil compartments is calculated first and subsequently a resistance model is used to estimate the fluxes between soil and vegetation.
Insertion of the parameters of a hypothetically well watered lawn (height: 0.12 m; surface resistance: 70 s m-1; albedo: 0.23) into the Penman-Monteith equation, allows to evaluate ETref. With ETref, ETpot and ETref for a specific crop is calculated according to crop factors (Kc) used in (10). A typical Kc value during the mid-summer season for many cereal crops is 1.15 [21]). For forest trees between it is situated between 0.7 and 1.1 (as derived with the WAVE model, [80]).
In the FAO-56 approach [21], a dual crop coefficient is use, which takes a dry soil surface layer and adequate soil water content (SMC) in the root compartment into account for full transpiration evaluation. Root zone moisture depletion is evaluated as the difference between SMC at field capacity (pF = 2.3) and actual SMC. The Ks value (which is a water stress factor) equals 1.0 as long as SMC is higher than readily available water (a fraction of the total available water). If SMC is lower than readily available water (RAW), Ks decreases linearly from one to zero according to total available soil water consumed. The FAO-56 procedure is a revised FAO-24 version [20].
In (10) & (11):
- Kc is a crop factor [-];
- ETref is reference crop ET [mm d-1];
- ETpot is potential crop ET [mm d-1];
- Tactcrop is crop ET under water stress conditions [mm d-1];
- Ks is a stress factor [-].
Xu & Singh [81] evaluated and generalized temperature and radiation based methods for ETpot estimation. Most equations adopting this methodology, take the same shape as (10) & (11). The following methods have been evaluated (see [81]): Thornthwaite (1948), Linacre (1977), Blaney and Criddle (1950), Hargreaves (1975), Kharrufa (1985), Hamon (1961) and Romanenko (1961). Singh & Xu [82] evaluated and compared 13 ET equations belonging to the category of the mass transfer methods and developed a generalized model. They also examined the sensitivity of the equations to errors in daily and monthly input data [81].
In (12), (13) & (14):
- ETpot is the potential evapotranspiration [mm d-1];
- Ta is atmospheric temperature [°C];
- h is a humidity term [-];
- d1 is day length [hours];
- c, a, b, c1, c2, c3 are coefficients [-].
- Rg is daily global radiation [MJ d-1 m-2].
3.2.5. Estimation of evapotranspiration based on field water balance methods
Field water balance methods are based on in situ measurements of hydrological mass fluxes. ET in this approach is calculated as a residual of all the other terms of the field mass balance equation. With pluviometers rainfall rate is measured, Time Domain Reflectometry [83] or other sensors (see section 4, Table 4) when inserted into different soil layers are used to determine soil moisture dynamics. Tensiometers or groundwater level tubes, give an estimate of the lower boundary of the soil compartment.

Table 4.
An overview of methods to determine soil moisture content for point and area scales.
Note that the results obtained are very sensitive to measurement frequency differences and the amount of measurement locations, especially for the field scale spatial level. Field water balance methods are useful typically to obtain tree crop factors (popular [48]). More specific information about this approach can be found in [48] [49].
In addition to the measurement of hydrological components to estimate ET, 1D models can be used to simulate vertical water flow. The Darcian flux law for example states that a water flux in a homogeneous porous medium equals the product of the hydraulic gradient and hydraulic conductivity. When combined with the law of mass conservation, the well know Richard's equation is obtained. This equation can even be extended to 3D conditions and describes the water flux into soils. Typical 1D models are WAVE (Water and Agrochemicals in the Vadose Environment [50]) and SWAP [51]. ET is modelled using inputs like rainfall, interception capacity and a (grass) reference potential evapotranspiration as the upper boundary condition. The major lower boundary condition is the groundwater table or the drainage flux. Additional inputs are crop factors, root distribution, leaf-area-index and critical pressures for water uptake. The soil system is described using its soil physical properties like the hydraulic conductivity and retention curves according to the corresponding soil layer. Obviously, 1D modelling corresponds with the field water balance method discussed earlier.
To estimate ET with a 1D water balance model, canopy interception is calculated first using interception capacity. When the amount of gross rainfall is larger than canopy capacity, excess rainwater will reach the soil surface. Rainwater mass equal or smaller than interception capacity is assumed to evaporate. Depending on the maximum infiltration rate of the upper soil, runoff may occur while the remainder of rainwater infiltrates into the lower soil layers of the soil compartment. The product of ETref and the crop factor (Kc) of the vegetation considered results in ETpot, i.e. the maximum rate of water consumption under a non-stress boundary condition. Using leaf-area-index (LAI) in Beer's law, ETpot is split into potential soil evaporation and crop transpiration. This potential crop water use in combination with crop root distribution and SMC, determines the amount of water extracted from the soil compartment. If SMC is smaller than the moisture amount required according to potential water use, then the actual water use is obtained. Actual soil evaporation is calculated from water stress in the topsoil. Non evaporated water is stored in the soil while excess water (not stored), will drain into the deeper under-field. In case of capillary rise, more water will reach the root zone and less water stress occurs.
Although ETact is determined using a water balance approach, ETpot must be calculated first, generally by applying the Penman-Monteith relationship or its derivates. A description and implementation of the WAVE model to estimate ET of Flemish forest can be found in [80]. The spatial up-scaling of 1D models is possible by input of the upper and lower boundaries in a spatially explicit mode. In that case, soil physical properties are required to be input in 3D mode. 3D models must also be able to account for unforeseen water fluxes.
3.3. Evapotranspiration estimation at the field, landscape, regional and continental scales
Where local estimates of ET are satisfactory needed, typically for validation purposes or where detailed small scale application, many applications require spatially up-scaled ET maps. Rather well adapted techniques for this objective are the Bowen ratio, eddy correlation, the scintillometer and field water balance methods.
3.3.1. Scintillometer measurements
A scintillometer measurement is based on the physical principle of the propagation of electromagnetic waves in atmospheric and their disturbance by atmospheric turbulence. This turbulence effect induces the so-called scintillation of the electromagnetic wave. It is the result of fluctuations of atmospheric temperature, moisture, pressure and their interactions. Basically a scintillometer measures the variance of radiation intensity fluctuations. An area-averaged sensible heat flux can be derived from this type of measurements. The scintillometer consists of a transmitter equipped with disc shaped arrays of light emitting diodes and a receiver, which records the perturbed light at a distance up to 5 km. Latent heat is to be derived from the energy balance.
Scintillometers are applied to estimate turbulence as well. Typically the turbulence parameters are the turbulent heat and momentum fluxes, the Monin Obukhov length (see also, the chapter on energy flux based ET assessment method), the dissipation rate of energy, and the vertical distribution of atmospheric temperature and finally refractive index. More specific information on the approach described is found in [38] [39] [40] [41] [42] [43] [44].
3.3.2. Eddy covariance (EC) methodology
Basically, wind vector fluctuations in the three dimensions and in the constant flux region (lowest section of the inertial sub-layer where the fluxes of momentum and heat, water vapour, and other gases are constant with height) of the atmospheric surface boundary layer are measured with very short time intervals. Combined with the associated fluctuations in atmospheric temperature, humidity, or mixing ratios of typically, water vapour or carbon dioxide, the average net flux of the physico-chemical variables mentioned is obtained by integrating their instantaneous fluxes. These fluxes are obtained by evaluating the means, variances and co-variances of the vertical wind vector with its horizontal wind counterpart, with sonic temperature (which is approximately equal to virtual temperature), with water vapour as well as carbon dioxide mixing ratios.
A 3D sonic anemometer is used to obtain the orthogonal wind vectors and sonic temperature. A folded, open path H2O/CO2 infrared gas analyzer is used to measure water vapour and carbon dioxide mixing ratios. The application of footprint theory is required to produce a spatial representation of evapotranspiration. Spatially explicit carbon dioxide fluxes can be derived accordingly. Needless to stress the importance of this type of output for the calibration and validation of carbon balance models. Eddy covariance is a very accurate method. It requires delicate planning with respect to obtaining reliable instrumentation, calibration procedure, the determination of the exact measurement height above the surface exchanging water vapour and carbon dioxide in relation to the required fetch, the length of the sampling period etc. [84]. EC system management and logistical support is expensive and time consuming, both from the point of infrastructure as human resources needed. The technique however due to its accuracy and importance is widely applied for the determination and monitoring of energy components and carbon dioxide and water vapour mass fluxes. Tower networks include for instance the EUROFLUX towers in Europe [49], united at the global scale with other continental scale networks in FLUXNET, the global eddy covariance tower network. More specific information is found in [45] [35] [14] [36] [37].
3.3.3. Catchment scale water balance methodology
With a hydrograph, instantaneous discharge can be measured and consequently, this enables the calculation of annual runoff by dividing the total annual discharge with the surface area of the entire watershed. Annual ET, integrated over the entire water catchment surface area, is then estimated as the residual of total annual rainfall and total runoff. Although this method appears to lead to rather rough EF estimates, Wilson et al. [49] for example found that the magnitude of annual ET estimated over 5 years (1995-2000) is in good agreement between the EC and the catchment water balance methods for a catchment in the South-East of the USA. A major advantage of the catchment scale approach is that only a limited amount of information sources (annual discharge, precipitation, area) is needed. However, some other boundary conditions for use of this method are less favourable. For example, the approach is only applicable for coarse time resolutions such as one year. Moreover an area-averaged estimate is obtained. The field water balance method is typically used in combination with physical and empirical (regression) computer models. More specific information is found in [85] [49].
3.4. Introduction of Earth Observation technology to quantify evapotranspiration
3.4.1. Energy flux measurements
A primordial observation from earlier sections in this paper is, that both SMC and ET, as spatially as well as temporally variable processes, are measured and/or modelled based on the law of mass and/or energy conservation. Since EO provides spatially explicit as well as multi-temporal information on reflected or emitted electromagnetic radiation from the earth's surface, appropriate techniques to assess area ET and SMC is based on remote sensing [11].
The Planetary Boundary Layer (PBL) is that part of the atmosphere where the influence of land surface densities is elicited. Considering the Planetary Boundary Layer (PBL) and especially its lower atmospheric part or Atmospheric Surface Layer (ASL), the estimation of energy balance components are related to the flux-profile as for instance measured with the eddy covariance. The different fluxes under consideration are:
In Eqs. (15) to (19):
- H, λE, G0 and Rn are sensible and latent heat, the soil flux and the net radiation flux respectively [W m-2];
- ρa and ρs are respectively the atmospheric and soil bulk densities [kg m-3];
- cp, cs are the specific heat of atmospheric at a constant pressure and soil specific heat [J kg-1 K-1];
- rah and rsh are the resistance to heat transfer for atmospheric and soil respectively [s m-1];
- Ta, Tz0h, Ts and LST0 are respectively atmospheric, heat source, soil and land surface temperatures [°C];
- qa and qz0h are respectively atmospheric humidity and humidity at reference height [-];
- K↓ and K↑ are incoming and outgoing short wave radiation [W m-2];
- L↓ and L↑ are incoming and outgoing long wave radiation [W m-2];
- α0 is surface albedo [-];
- ε0 is surface emissivity [-];
- σ is the Stefan – Boltzmann constant [W m-2 K-4].
For homogeneous land surfaces flux-profile relationships are introduced using the similarity hypothesis for wind, temperature and humidity vertical profiles.
The similarity hypothesis implies that:
- (i)
- Flux densities are linearly related to the gradients of these parameters;
- (ii)
- Flux densities of momentum, moisture and heat vary less than 10% with height and finally;
- (iii)
- Buoyancy effects on before mentioned densities can be accounted for by one dimensionless variable.
Shear stress is induced when a land surface is not smooth. Since kinetic (wind) energy is lowered by surface friction, a compensating energy flux originates, which is the vertical flux density of momentum. The typical shape of a wind speed profile e.g. according to the natural logarithmic of height in a neutral atmosphere is well known. Of course, both forced and thermal convection do occur, hence mixed convection occurs as well. At this point the Monin-Obukhov length scaled for mixed convection is introduced. An equivalent temperature profile can also be derived. This profile generates the scaling parameters for momentum and heat, in relation to their flux densities. This makes it possible to convert measured wind speed and/or atmospheric temperature under given environmental conditions into scaling parameters and their respective flux densities.
A typical approach for the representation of the scaling parameter of a wind profile is determined by the use of resistance schemes for homogeneous individual land surface elements. For the sensible heat flux density the resistance rah to heat transfer between zoh and a reference height zsur is related to the eddy diffusion coefficient and more explicitly to wind speed. Analogous, the resistance to sensible heat transport in the soil can be written as rsh. For latent heat, resistance parameters can be implemented as well, but an appropriate choice of their values is problematic. Since land surfaces are generally not homogeneous, resistance schemes have to be adjusted to represent surface heterogeneity, either by implementing a one-layer scheme with effective system parameters or a multi-layer scheme with separate parameters according to land surface characteristics. The second solution requires many additional coefficients, difficult to obtain. Bastiaanssen [86] concluded from a literature review, that a one layer resistance scheme is quite convenient to be applied.
A theoretical link between evapotranspiration derived from the energy balance equation and EO can be made assuming the next boundary conditions [86]. Based on equations 15-19 and when Tz0h equals LST0, the surface energy balance for a specific location at a pre-defined moment in time can be combined as follows, to obtain:
After the application of a first order Taylor expansion on the term ε0σLST04 and after re-expressing the equation into LST0 [86] we obtain:
Further reductions lead to (22):
(22) implies that evaporation is a linear combination of surface temperature. The different coefficients ci can be derived using basic mathematical rules. The art of remote sensing is in this specific case, the identification of the spatial patterns of c3 and c4 during a satellite (or aircraft) overpass. (22) is the basis of quite a few methods applied to model the spatio-temporal patterns of evapotranspiration.
3.4.2. Remote sensing based assessment of evapotranspiration
To exhaustively review existing remote sensing (RS) or field scale based approaches to determine ET is a time consuming task indeed. We gladly refer to [87] and other authors for their evaluations of remote sensing applications in the field of water resources management. Since a review on ET will hardly ever be complete, this paper covers a limited list of remote sensing techniques assessing ET as listed in Table 3. The advantages as well as disadvantages of the methods considered are indicated in Table 3. Apart from the parameterization of the surface energy balance, other approaches are based on a combination of the water balance approach, remotely sensed surface temperature and vegetation retrievals. Another frequently applied approach is based on a combination of the Penman-Monteith equation and RS data assimilation. Hence, the methods listed in Table 3 can be classified according to whether they are based on:
- (i)
- the parameterization of the surface energy balance;
- (ii)
- the Penman-Monteith equation;
- (iii)
- the water balance approach, or;
- (iv)
- relationships between vegetation indices and land surface temperature assessed with remote sensing.

Table 3.
A limited list of evapotranspiration assessment methods based on Earth Observation techniques. A summary of (some) model parameters is given, as well as model (dis-)advantages.
A short description of the methods is given in the text below. From Table 3, one can conclude -when generalizing - that most methods to assess ET with remote sensing require non-uniform surfaces in the region of interest (ROI).
As indicated in Table 3, many methods are based on the use of the remote sensing criteria of dry and wet pixels or vegetated and bare soils. Hence, spatially heterogeneous ROI 's favours the application of EO techniques. A rather trivial conclusion since otherwise point techniques would be sufficient for the assessment of ET.
(i) Parameterization of the surface energy balance
Bastiaanssen et al. [25] [55] developed the model, “Surface Energy Balance Algorithm for Land” (SEBAL), which estimates energy partitioning at the regional scale with a minimal requirement for field data. This algorithm is based on the use of surface albedo, a vegetation index and land surface temperature and provides enough information for the parameterization of the energy balance fluxes, e.g., radiation, sensible and soil heat as shown by [25] [55]. This algorithm has been applied in many studies [88] to estimate ET, but also as a tool to estimate other components of the water balance at large scales [97]. It is based on the parameterization of energy fluxes as indicated in this section. The terms of the incoming radiation equation are based on field data and the outgoing terms on RS estimated surface albedo, surface emissivity and land surface temperature. The soil heat flux is estimated empirically, taking surface heating, soil moisture and intercepted solar radiation into consideration. Sensible heat is computed from flux inversions for dry non-evaporating land units and wet evaporating land surfaces. Roughness length is derived from an empirical vegetation index based relation. ET is the residual of the energy balance. Lagouarde et al. [89] implemented the SEBAL model over an agricultural area in the South–East of France. Eddy covariance (EC) measurements were available. Large discrepancies between the reference sensible heat flux from EC and the SEBAL derived flux were observed. This was attributed to errors in the estimates of roughness length based on the use of a semi-empirical NDVI relationship. SEBAL estimates elicited a much closer fit with EC-measurements using a prescribed roughness length for momentum.
Gellens-Meulenberghs [64] assessed ET as a residual of the energy balance using METEOSAT imagery (albedo and land surface temperature) and meteorological and vegetation data. The energy fluxes are parameterized. The soil heat flux is a fraction of the net radiation flux and sensible heat. A terrain dependent aerodynamic roughness parameter and displacement height values are both derived from a digital land use map.
Regional Evapotranspiration through Surface Energy Partitioning (RESEP) has been proposed by Ambast et al. [67] using boundary layer theory. ETact is estimated using the evaporative fraction (EF) and 24 hourly net radiation. EF is also used in the Surface Energy Balance System SEBS [68]. For the calculation of this fraction the concept of sensible and latent fluxes under dry-limited and wet-limited conditions is used.
Verstraeten et al. [69] used evaporative fraction (EF) as a measure for ET. They derived EF from remotely sensed albedo and land surface temperature. EF is the ratio of latent heat over the available energy which indicates the amount of surface energy available for the evaporation of water [98].
García et al. [99] estimates EF with ASTER reflective and thermal data to estimate surface water deficit. Senay et al. [70] developed and implemented a Simplified Surface Energy Balance (SSEB) model to monitor and assess ETact and the performance of irrigated agriculture land using MODIS, ASTER and Landsat imagery. Kimura [100] estimated moisture availability using a combination the NDVI and land surface temperature in a Modified Temperature-Vegetation Dryness Index (MTVDI).
(ii) Penman-Monteith combined with RS
Moran et al. [92] combined the Penman-Monteith equation with land surface temperature and spectral reflectance to estimate evaporation rates for a semi-arid grassland. This method is based on (a hypothetical) trapezoidal shape of the relationship existing between the vegetation index and the atmospheric-soil temperature difference (four vertices occur: 1. well-watered vegetation; 2. water-stressed vegetation; 3. dry bare soil and 4. saturated bare soil). ET is assumed to be linearly associated with temperature difference variations.
The PROMET model family assesses ET at field (1 ha), micro (100 km2) as well as meso-scale (10.000 km2) [54] applying the Penman-Monteith algorithm and RS data assimilation. The PROMET models combine a kernel (Penman-Monteith based SVAT) and a plant-physiological model (to take environmental parameters and canopy resistance into account) and a spatial model. Surface resistance is derived using a coupled plant physiological and soil hydraulic model. Stomatal resistance is determined as a function of intercepted PAR. The 1st micro-scale model layer uses LANDSAT imagery to determine land cover. The 2nd layer consists of spatially explicit soil information. The 3rd layer is a meteorological time series and the final 4th layer contains plant developmental data (LAI, height). For each image pixel a single set of parameters is implemented. The meso-scale model requires NOAA/AVHRR imagery for sub-pixel information collection, with the boundary condition that multi-temporal courses of reflectance and (thermal) emission as measured for each pixel are linearly composed of reflectances and emissions for all land cover types, represented in the pixel.
Granger [65] used a mass transfer method with has its origin in the Penman-Monteith equation applied within a remote sensing framework. He successfully used feedback mechanisms between land surface and the atmospheric layer, so that the observed surface temperature is a sufficiently reliable indicator of atmospheric humidity. A relationship between daily atmospheric vapour pressure deficit and the saturated vapour pressure at the mean daily surface temperature was derived by this author. A long-term mean atmospheric temperature site component is introduced to account for seasonal and latitudinal effects.
Cleugh et al. [94] used the Penman-Monteith algorithm with LAI derived from MODIS satellite data to model leaf conductance.
(iii) Water balance combined with RS
With the integration of agro-hydrological and hydraulic simulation models as well as EO and GIS techniques, D'Urso [66] developed a spatio-temporal irrigation management tool based on the water balance. SWAP is a combination of spatially extended upper and lower boundaries and soil system conditions. For the upper boundary, meteorological data are assumed to be uniform and their spatial distribution governed by canopy variables such as LAI, crop height, Kc and albedo. Kc coefficients are mapped using satellite observations either using classification approaches (supervised and unsupervised) validated with field observations or by formally defined analytical functions relating reflectance to LAI, albedo and crop height. LAI is related to a vegetation index. The lower boundary is spatially extended using functions relating water flux at the bottom of the soil profile and the depth of the groundwater table. The spatial distribution of soil hydraulic characteristics is obtained by calibration of pedo-transfer-functions for the soil type units in a soil map and the functional properties of the soil type. For example, the time required to reach a specified value of pressure head at a certain soil depth. ETpot is calculated using Penman-Monteith.
The ALiBi model [101] is based on the mass transfer method as well. It makes use of vapour pressure deficit in combination with a turbulent exchange coefficient and vegetation surface conductance which depends on leaf stomatal conductance. Inversion of the model was performed by Olioso et al. [102], with the retrieval of canopy ET from RS data including thermal infrared, spectral reflectances and microwave data.
(iv) Direct relationships with remotely-sensed vegetation indices and land surface temperatures
Based on (22), ET is linearly related to land surface temperature. Jackson et al. [57] introduced a simplified equation variant to estimate latent heat ((23):
In (22):
n (close to one) and B are parameters dependent on land surface roughness and wind speed and can be written as a function of a VI [103].
Moran et al. [104] applied the Temperature Vegetation Trapezoid (TVT) type of relationship. Qi et al. [63] used the same approach combined with in situ measurements. Some years before [62], Price [58] applied a relationship between a vegetation index and surface temperature to spatially upscale ET. For heterogeneous land cover and based on the NDVI surface temperature relationship, three different assumedly homogeneous terrestrial functional types (TFT) were defined. Well watered vegetated pixels, dry and wet bare soils. Apart from the assumedly homogeneous TFT pixels, other pixel types are assumed to be composed of a linear combination of the fractions of the three homogeneous cover types, as previously defined. Similarly, Carlson et al. [59] [60] [61] combined a planetary boundary layer model with surface temperature and NDVI measurements, to map soil moisture for the surface and root zone.
4. Soil moisture content assessment techniques at different spatial observation scales
Despite the importance of soil moisture content, its accurate regional assessment is a complex issue. This is mainly due to the fact that the standard estimation protocol, i.e., the gravimetric method, is essentially a point measurement. To map local scale variations in soil moisture requires a high spatial density of observation locations. Obviously point measurements performed in the context just described is labour intensive and quite costly.
Other measuring techniques such as Time Domain Reflectometry (TDR) [83] are local measurements as well, but not very suitable for the determination of the soil water status at field and regional scale as well. Earth observation based up-scaling techniques are a compromise since they are spatially explicit and of relatively low cost [11] [13]. For instance, the spatial resolution of most spaceborne sensors ranges from ± 30 m (Landsat ETM) to ± 250-500 m (MODIS) to ± 1100 m (NOAA/AVHRR, MODIS) to ± 5000 m (METEOSAT) and even to ± 50000 m (ERS Scatterometer) and more.
A general non-exhaustive list of methods to determine soil moisture at point and spatially explicit scales, is given in Table 4, with a short description. According to the discussion of [105], well known techniques to determine soil moisture content are
- (i)
- Gravimetric techniques;
- (ii)
- Nuclear (neutron scattering, gamma attenuation, nuclear magnetic resonance);
- (iii)
- Electromagnetic (resistive and capacitive sensors, time and frequency domain reflectometer);
- (iv)
- Tensiometric;
- (v)
- Hydrometric;
- (vi)
- Remote sensing (passive and active microwave, thermal infrared) and;
- (vii)
- Optical techniques (polarized light, fibre optic sensors, near-infrared);
- (viii)
- An additional technique, is the heat dissipation method [106] where heating or cooling of a porous block is measured after a heat pulse;
- (ix)
- Another, more basic field method is the ‘Feel and Appearance method’, using a soil moisture interpretation chart based on texture classification and squeezing of soil samples [107].
Apart from RS techniques, all given techniques are point measurements. A summary of the advantages and limitations of optical and microwave soil moisture remote sensing is provided by [3]. They made a discussion on spectral measurements such as visible, NIR and SWIR reflectances, thermal infrared emittance, microwave emission and radar measurements. Other methods to assess soil moisture content are the implementation of calibrated and validated hydrological and SVAT models. Both one-dimensional field (WAVE, SWAP see also Table 1) and distributed catchment models (SWAT [53]; MIKE-SHE [52], among others) can provide useful information. Gaps in time series of measured soil moisture content can for example be reconstructed using the validated type of models, cited.
With respect to the production of spatial distributions of SMC, can spaceborne microwave RS be compared with optical and thermal RS? Briefly, microwave based spaceborne RS demonstrates a quantitative capacity to estimate soil moisture under a variety of topographic and vegetation cover conditions so that it can be implemented as measurement technique [3]. Spatial resolution however is problematic with this technique.
The main disadvantage of spaceborne microwave RS is that it is currently not operationally applied. Moreover, the spatial resolution is very coarse (e.g. 50 × 50 km spatial resolution of the ERS Scatterometer). A second important limitation of passive microwave RS is the perturbation of the signal by surface roughness and vegetation biomass, its irregular revisit frequency, and quite importantly as well, water bodies are major obstructions (e.g. coastlines) in terrestrial applications. A disadvantage of optical and thermal RS approaches is their limited soil surface penetration depth. Additionally, optical RS suffers from a high perturbation by clouds and vegetation and a significant signal perturbation by the earth's atmosphere.
4.1. Local scale soil moisture approaches
The most accurate method to estimate SMC is gravimetric sampling. Essentially, it is a destructive method since soil samples must be removed from the pedon mass. The procedure of the gravimetric method starts by taking a soil sample in the field, of which sample mass is immediately measured by putting the sample for 24 to 48 hours in a drying oven at 105 °C, to measure the mass of the dry soil. Soil bulk densities are required to convert gravimetric (water mass per soil mass) to volumetric values (water volume per soil volume).
Other accepted non-destructive (soil structure is conserved) in situ methods to measure SMC are methods based on neutron scattering [109] and gamma ray attenuation [110]. These methods are quite accurate and non-destructive, but require calibration for each soil sample and special attention to avoid health hazard [111].
A more flourishing non-destructive method is based on the measurement of soil electrical conductivity, which is sensitive to SMC. Time domain reflectometry (TDR) for example is widely applied to measure soil electrical conductivity to infer SMC. With a minimum of soil disturbance, TDR enables to simultaneously estimate soil moisture content as well as electrical conductivity and is frequently applied as well in studies of solute transport in porous media [112].
An overview of conceptual dielectric models for TDR application can be found in [113]. A short description of the principles of TDR measurement is given below.
TDR estimates the dielectric constant, κ, in a soil matrix by measuring the propagation time of an electromagnetic wave (EM) sent from an EM pulse generator mounted on top of a coaxial cable, inserted into a soil matrix. EM waves propagate through the coaxial cable to the TDR probe, which is a rod made of stainless steel or brass. Part of the incident electromagnetic waves is reflected at the top of the probe because of the difference in impedance between cable and probe. The remainder of the wave propagates through the probe until it reaches the end of the probe, where the wave is reflected. The round-trip time of the wave, from the beginning to the end of the probe is measured with an oscilloscope branched on the cable tester (see also [111]). For a homogeneous soil, volumetric water content θ (m3 m-3) is calculated by using a calibration curve which was established empirically by [83]. The curve is mathematically formulated in (23):
In (23):
- θ is volumetric soil moisture content (m3 m-3)
- κ is the dielectric constant [-].
The authors found that the apparent soil dielectric constant is rather insensitive to temperature in the range of 10 to 36°C. Identically it is quite insensitive to soil texture (clay to sandy loam), bulk density of soil (1.14–1.44 mg m-3, for non-swelling soils) and soluble salt content (moistened with salt-free water, 0.01 N CaSO4, or 2000 ppm NaCl solution). A physically based model making a causal link between SMC and the dielectric constant, κ, is the model of [114]. These authors used a linear model with parameters including an empirically determined factor γ representing a quantity of initially absorbed water ((24)):
In (23), (24) and (25):
- κx, κa, κh, κw, κb and κi are relative permittivities of the initially absorbed water, atmospheric, solids (or host) fractions, water, ice and inclusion water respectively;
- θt is the transition water content marking a change from a slowly to a more rapid increasing relative permittivity value;
- P is the porosity of the dry soil;
Another technique applied at the local scale is the ground penetrating radar (GPR). This instrument is based on similar techniques as reflection seismics and sonar techniques [115]. The radar produces a high-frequency electromagnetic wave (10–1000 MHz), which transmits through the soil from a source antenna positioned at the earth's surface. The propagation velocity of the radar waves in the soil, mainly depend on soil dielectric permittivity. This in turn, is strongly related to SMC [83]. Any subsurface contrast in dielectric properties reflects part of the wave energy to the soil surface. The reflected wave is detected by the receiving antenna as a function of time [116].
Another non-destructive method to determine SMC is the use of gamma-ray beams. Though the soil structure remains intact, undisturbed soil samples must be collected in the field. Gamma-ray beams can be used to determine the soil water retention curve [117]. The principle of gamma-ray application for SMC determination is briefly given below.
When a gamma-ray beam passes through a soil sample of thickness × (in cm), photons are transmitted following the Lambert - Beer law. Considering two phases in soil samples, solid material and water, the Lambert - Beer law can be written as follows:
In (26):
- I and I0 are respectively the rates of the emerging and incident photon beams;
- μs and μw [cm2 g-1] are soil and water mass attenuation coefficients;
- ρs, is soil bulk density [kg m-3] and;
- θ is volumetric soil water content.
Note that, apart from directly measuring SMC, water balance models can be applied to estimate SMC as well, using meteorological and vegetation input data (e.g. the models WAVE and SWAP). The soil-vegetation-atmosphere water balance model WAVE was developed by Vanclooster et al. [50] and extensively calibrated and validated for the climatic conditions of Flanders and crops like wheat, barley, maize, potato, sugar beet as well as grassland vegetation [118] [119]. WAVE is a conceptual physically based model simulating 1D transport of water and energy in the variably water saturated root zone of a soil profile. For the crops cited earlier in this paragraph, the model contains modules to simultaneously simulate the nitrogen balance and crop responses to water and nitrogen availability in the root zone. In Flanders, until recently [80] the model has only sporadically been used for the simulation of forest water fluxes of a poplar [32] and Scots pine stand [120]. Both applications have been validated with the use of sap-flow measurements. Conceptual models such as WAVE are very useful for gap filling purposes in SMC measurements or to estimate SMC forward or backward in time in a SMC time series, in absence of measurements for certain intervals in time.
4.2. Large scale soil moisture approaches
To address different spatial scales in the estimation of SMC, temporal and spatial stability analysis was performed. Grant et al. [121] provides a backbone for temporal stability analysis, which was first introduced by [122]. Temporal stability of SMC is a reflection of the temporal persistence of spatial SMC patterns. A SMC field is temporally stable if its temporal fluctuations in soil moisture are similar to those of the catchment average [123]. The goal of temporal stability analysis is to provide a methodology that reduces the number of measuring sites required for the analysis of the behaviour of a given soil. The question is whether or not time-stable SMC sites can be considered representative of the area1 mean soil moisture. Field measurement sites have their merit for the direct measurement of mean area1 responses. Grayson et al. [123] names them “Catchment Average Soil Moisture Monitoring sites”, or CASMM sites. Vachaud et al. [122], studying three European agricultural plots, found that soil texture is responsible for an observed high degree of temporal stability. These authors also demonstrate that SMC time-stable sites, representative for both mean and extreme soil moisture contents, exist in a landscape with small to insignificant slope angles. Hence, only a few low slope angle sites are needed for a specific landscape need to be representative for the SMC for the landscape as a whole. Some locations may represent statistical parameters of a normal probability distribution, such as the mean and standard deviation of landscape level SMC, potentially reducing the number of measurements required to characterize landscape SMC distribution. Kachanoski & de Jong [124] expanded the definition of temporal stability as the degree of linear correlation between SMC measured at consecutive times. These authors also discovered a scale dependency of the temporal stability of soil water recharge at their site. Moreover they demonstrated that dry periods show scale independence and wet periods scale dependence. To minimize the bias of SMC estimates when inferring the location of catchment characteristic soil moisture monitoring sites [125] two basic requirements have to be met:
- (i)
- randomness and;
- (ii)
- independence of individual observations.
Apart from the temporal variability, spatial variability or the variability of point measurements at a given time, plays as well. The amount of spatial variability as well as the spatial distribution of SMC can have a critical impact on hydrological processes such as stream-flow generation. A starting point to characterize the structure and heterogeneity of SMC fields is an examination of the spatio-statistical structure [126]. Detailed analyses of TDR determined soil moisture patterns collected in a 10.5 ha Tarrawarra catchment (south-eastern Australia) allows the derivation of variograms with a high degree of reliability [127]. Exponential variogram models, including a nugget, fit soil moisture data variograms closely. Geostatistical structure evolves seasonally with high sills (15–25 m3 m-3) and low correlation lengths (35–50 m) during the wet winter period and smaller sills (5-15 m3 m-3) and longer correlation lengths (50–60 m) during dry summer periods. This seasonality is due to a different lateral redistribution of soil moisture during summer.
In accordance with [124], [125] describe that during the transition from a dry to a wet period, uncertainty (temporal instability) is larger than when a soil is dry (semi-arid Duero basin in Spain). For dry soils a good correlation between mean SMC and the variance for the whole measurement range considered, exists. This is in contrast with results from [121] indicating that soil moisture temporal variability does not appear to be preferential for more wet or dry locations (Reynolds Mountain East, Idaho). Yet, when indirect methods are used to estimate SMC for larger areas (i.e. with earth observation) it is necessary to perform a careful selection of the periods selected for calibration and validation purposes [125].
4.3. Large scale soil moisture estimation based on remote sensing
Researchers of the Vienna University of Technology developed a change detection method to retrieve soil moisture based on the active microwave ERS-Scatterometer sensor [13] [126] [128] [129]. They consider soil surface moisture as a relative measure of soil moisture in the first centimetres of the soil profile. They represent SMC as being the degree of water saturation of the soil with a value scaled between zero and one e.g., the Soil Water Index (SWI). However, SWI cannot be retrieved for snow covered or frozen soil conditions and for dense tropical forest. These land use and cover types do represent a large area of the globe. Moreover, for some dry and arid regions, strong azimuthal effects can occur. These effects are currently not corrected for and hence treated in the retrieval. Therefore they are masked.
The algorithm developed by Vienna University, accounts for heterogeneous land cover and for the effects of vegetation growth and senescence on the remotely sensed signal. It is assumed that the time series of surface wetness observations from the ERS Scatterometer gives an indication of the wetting and drying trend for moisture content in a soil profile. This is because the moisture content profile is affected by weather patterns during the few days to weeks preceding the observation. Since soil moisture content integrated over the deeper soil layers exhibits much smaller variations than in the top layer, it is logical to apply a temporal filter for SMC series smoothing, thereby reproducing the temporal SMC trend in the deeper soil layers. To define an appropriate low-pass filter, a simple two-layer water balance model has been considered. The first soil layer represents remotely sensed topsoil. The second layer, e.g., the reservoir, extends down to the reservoirs bottom and is assumed to be isolated from the outside world via the surface layer. In this model, the water content dynamics in the reservoir is fully explained by past dynamics of surface soil moisture content. Typically, the most recent precipitation events have a stronger impact on the reservoir water as opposed to older ones, because of the use of an exponential weighting function. The time dependency of water content is controlled by the parameter T, which represents a characteristic time length and increases in function of the depth of the soil moisture reservoir L. Though simple, this model is useful as a general concept for the estimation of the soil moisture content profile. It accounts as well for a decreasing impact of measurements with increasing time lag.
The SWI is a soil moisture time trend indicator ranging from zero to one. To estimate water content in deeper soil layers, auxiliary information about soil geophysical properties is required. Again, the rationale is to define calibration points covering dry and wet conditions. It thereby assumed that Wmin and Wmax are the minimum and maximum soil moisture values that can possibly occur in a particular soil. Furthermore a linear relationship is assumed. The profile of SMC at time t can be estimated from SWI according to (Eq. 27):
The soil parameters commonly used to define critical SMC values are the wilting level WL, the field capacity FC, and the total water capacity TWC. The method has quite some application potential. Methods describing large-scale soil moisture fields are of great importance for land-surface parameterization of global circulation models. The disadvantage of the SWI is its coarse spatial resolution (2500 km2) and the absence of long term ERS Scatterometer imagery. This promising methodology was applied by [130] to assess SMC for Europe using optical and thermal coarse resolution spaceborne information and the concept of the thermal inertia of surface bodies.
5. Measurements, models and model selection
5.1. Evapotranspiration across different scales of observation
5.1.1. Scale issues and evapotranspiration retrieval
One of the key issues in hydrological applications is scale and spatial resolution (pixel size) [126]. Ideally the scales of field measurements, modelled variables and EO acquired variables should be similar. Variability in ET (and SMC) is driven by vegetation, soil, climate and topography. Hence, one must consider local (e.g. soil, topography, vegetation) and large scale (e.g. precipitation, radiation) variability. It is clear that understanding the role of landscape heterogeneity and its influence on the scaling behaviour of surface fluxes is critical. The up-scaling of ET fluxes involves capturing land– atmosphere feedbacks and effects of land surface heterogeneity on the surface fluxes and the atmospheric boundary-layer dynamics that play at larger spatial scales. When downscaling ET fluxes, appropriate parameterization of sub-grid scale phenomena within large-scale frameworks is required [131].
Scale differences between field measured and earth observed ET (and also SMC) are not always taken into account. This is partly due to the knowledge gap on uncertainty of scaling parameters and the complexity of data acquisition. One approach to scale up from field level to remotely sensed measurements is the quantification of scale uncertainty conducting VALERI type campaigns [132] [133].
The influence on the scaling behaviour of ET as observed by satellite sensors with different spatial resolutions was studied by McCabe and Wood [134]. They have used data from in-situ tower measurements, Landsat-ETM (60 m), ASTER (90 m), and MODIS (1000 m) satellite platforms over the Walnut Creek watershed in Iowa and applied the SEBS model. From comparisons of high-resolution satellite data, a consistent level of agreement of ET fluxes across a small watershed was obtained. Estimates of ET at high resolutions agreed well with spatially distributed flux towers. Coarser resolution satellite data such as MODIS are useful to estimate averaged ET values at the catchment level. In general, the finer the spatial resolution of the satellite, the better the agreement between the resulting ET estimates and tower measurements. Compared to flux tower measurements Landsat slightly underestimates ET by -6 W m-2, ASTER overestimated ET by 18 W m-2 and MODIS underestimated ET by -57 W m-2. This resulted in errors of 2, 5 and 15% respectively.
In Iowa Kustas et al. [135] studied the effect of spatial resolution (from 60 m to 120, 240, and 960 m) on soybean and corn crops. When the input resolution is on the order of 1000 m, variation in ET fluxes between corn and soybean fields is no longer discernible.
When crop types are not determined, due to too low spatial resolution, the plants are decoupled from the free atmosphere by both the bulk leaf boundary-layer resistance and the aerodynamic resistance through the surface layer (which is the control layer). At the plant level, the leaf (and the stomatal conductance) is decoupled using a leaf cluster boundary condition [131].
Comparison of satellite-based retrievals with field-based evaluation data leads to imperfect assessments of satellite derived variables due to the representativeness between site, pixel scale, sensor accuracy, and the physical equivalence of the measured versus the observed variables (differences in the time averaging, differences between atmospheric boundary-layer measurements compared with instantaneous, largely empirically based predictions) [136]. Since the impact of heterogeneity on ET estimates is crucial, flux tower the positioning and height is critical, particularly where source areas extend beyond the scale of the field being measured. Although the positioning of towers is not arbitrary, non-scientific constraints on their location play as well, such as their accessibility in fields or to equipment, maintenance, energy resources, etc.
5.1.2. Uncertainty in assessing evapotranpiration using Earth Observation techniques
The accuracy to estimate ET with remote sensing methods for different sources is fairly uniform. Nagler et al. [96] reports an uncertainty of 20–30% on ET in western riparian corridors of cottonwood due to inaccuracies in measuring and scaling. Su [68] conducted an error analysis for SEBS and a mean error of 20% relative to the sensible heat flux reported. An uncertainty of 25% on the mean annual ET was estimated by Nagler et al. [95]. Especially, the estimation error due to the uncertainty on roughness length for heat transfer is important, even more so than the uncertainty on temperature, wind speed and stability correction. Cleugh et al. [94] also observed an error on ET between 20 and 25%.
An uncertainty analysis of the evaporative fraction (EF) [137] revealed that EF estimates suffer errors between 8 and 54%. Error scenarios of ET derived from NOAA/AVHRR imagery led to uncertainties between 27 and 66% [69]. The effect on iNOAA-Chain derived ET - of errors due to remotely sensed parameter inputs (LST, albedo) - is small (less than 3%). Errors on meteorological parameters such as Ta of 1 K compared to 0.5 K affect the relative ET uncertainty only with 3% (from a relative error of 50% to 52% as a typical example). In contrast to this, model parameters describing the sensible heat line of the LST-albedo phase space, result in major impacts on ET estimation. Doubling these parameters error values almost doubles the error on the ET finally retrieved. A typical example is an error transfer from a relative parameter error of 50% towards a 93% on ET. McCabe et al. [136] reports the large sensitivity of surface resistance in the estimation of spatially distributed ET.
5.1.3. The performance of Earth Observation techniques to assess evapotranspiration
Several authors have compared remote sensing based ET estimations with different other measuring techniques such as EC, BR, sap-flow etc. for a specific region of interest. In this section authors are briefly cited that have used EO based approaches.
Qi et al. [63] conducted sap-flow, BR, scintillometer and 3D Sonic measurements to estimate seasonal riparian ET using remote sensing and in situ measurements in South-Eastern Arizona, USA. A Sacaton grassland and a Mesquite site were selected. The latent heat values inferred from measurements with before mentioned devices at the Sacaton site were very comparable: 64 W m-2 with the BR, 82 W m-2 with the scintillometer and 78 W m-2 with the 3D device. At the Mesquite site latent heat estimated with the BR amounted to 123 W m-2, the scintillometer estimate gave 124 W m-2. At the same location as [63], Goodrich et al. [138] carried out a riparian corridor water balance estimate. ET estimates were given for a transient groundwater model only and for the BR and a Penman-Monteith-based model, calibrated using sap-flow measurements. The PM model ET estimate amounts up to 86% of the estimates simulated with the groundwater model.
Ambast et al. [67] did show for a well-watered crop in Haryana (India) that the average ET estimated with RESEP is 2.1 mm d-1, whereas using the PM relationship daily ET is estimated to be 1.9 mm. The error involved is 10% and acceptable in most cases.
Lagouarde et al. [89] compared SEBAL and scintillometer sensible heat fluxes over an agricultural area in the South–East of France. Eddy covariance (EC) measurements were available as well. The result of this study was that large discrepancies between the reference sensible heat flux from EC and the SEBAL derived flux were observed. This was attributed to errors in the estimates of roughness length arising from the inadequacy of the semi-empirical NDVI relationship applied.
Jacob et al. [139] validated the SEBAL model for the same area as mentioned by [89]. They verified the model assumption of hydrological contrast and the resulting evolution of land surface temperature versus albedo. Moreover the model estimates agreed with the field references when validating wind speed and atmospheric temperature. However, a significant underestimation of the soil heat flux was observed. Large discrepancies were observed as well when validating the convective fluxes.
Li & Lyons [140] compared three remote sensing based ET approaches applied on native and agricultural vegetation: the extra-resistance model of [141]; the above mentioned model of [104] [142] and a two-source resistance model of [143] [144]. Models 1 and 2 exhibited similar performances and provided better estimates than the more sophisticated model 3.
Nagler et al. [96] compared sap-flow measurements with ET derived from MODIS imagery for a cottonwood restoration plantation in the USA. The cottonwood monitored ET values by remote sensing method and calibrated with ground measurements have an accuracy or uncertainty of 20–30%.
Extensive ET model comparisons are not frequently encountered in the literature. Rarely a large suit of models is applied in comparative campaigns at the same measurement location, this in contrast with ET measurements. We mention one study, where temperature-based potential evaporation methods are compared to pan evaporation values and one very detailed study where models were compared with measurements made in the Gediz basin, Turkey.
Kite & Droogers [145] evaluated ET estimates based on satellite observations, hydrological models and field data for western Turkey (Gediz). The following methods were applied: the FAO-24 and FAO-56 procedures, a large aperture scintillometer, the hydrological models SWAP and SLURP [146]; a satellite derived feedback mechanism; a biophysical model assimilating remote sensing data; and the SEBAL model. The results elicit a wide range of ET estimates without an evident pattern of variability between the different methods. The assumption, that field methods are probably more reliable than other methods, is hard to justify in the framework of cited experiment, since the three methods used give rise to considerably different estimates. Furthermore, [145] remarks that a clear-cut conclusion cannot be drawn for the three groups of results: field measurements, hydrological models and RS-based models. However, when assumptions on the uncertainties involved are made, it can be observed which methods lead to estimates within a reasonable confidence limit. For one field site only, the biophysical model did not meet the requirements. For other field sites as well, the SLURP-model did not give results with a high enough confidentiality. The different spatial and temporal capacities of the methods used, maybe due to differences in ET estimation. Hence, other factors than the ET estimates must be considered, i.e., data requirements, complexity of data assimilation, temporal and spatial scale effects and prognostic capabilities must be reviewed before drawing conclusions which can go more in depth.
5.1.4. Evapotranspiration estimates not based on remote sensing
ET estimates based on meteorological relationships
Xu & Singh [81] developed a generalised model based on seven temperature-based equations to calculate ETpot for Ontario and Canada. Underestimations are a common problem. The Blaney-Criddle equation agreed most closely with the pan values. With recalibrated constants the Blaney-Criddle, Hargraeves-Thornthwaite methods came out as the most suited to estimate ET.
Beyazgül et al. [147] compared six estimation methods for crop requirements in the Gediz Basin in western Turkey. In terms of ETref the FAO-24 methods (Blaney-Criddle, FAO Radiation, FAO Penman and Pan Evaporation) delivered the highest ET values and the Hargreaves and Penman-Monteith delivered the lowest values ranging from 885 mm for Blaney-Criddle down to 697 mm for Penman-Monteith. Differences between ETact and ETpot, including capillary rise (incorporating measured soil moisture contents in a water budget model), were situated between 121 and 216 mm. The differences observed in ETref estimates are striking.
ET estimates based on sap-flow, Bowen ratio, Scintillometer, Eddy Covariance techniques
Samson [148] conducted BR and sap-flow measurements in the Aelmoeseneie forest in Flanders (plant & field/stand scale). The observed diurnal behaviour of the estimates obtained with two methods was not similar. Moreover the sap-flow measurements underestimated the BR value by more than 50%. A possible explanation is that sap-flow measurements do not take herb layer transpiration and soil evaporation into account. Species composition, measurement and up-scaling errors may explain the differences observed.
German [36] evaluated regional ET for the Everglades in Florida using BR and EC measurements (field & landscape scale). The Bowen ratios estimated with EC and BR were comparable, though the mean total heat fluxes estimated with EC were 20% lower than the corresponding energy flux measured with the BR method. Probably the observed difference is related to friction velocity.
Frühauf et al. [85] concluded that the ET of forest stands in a catchment near Dresden (Germany) and EC measurements elicit a good agreement, though different forest stands had a different age, and though different scales of measurement were compared.
Wilson et al. [49] used sap-flow measurements, a soil water budget, eddy covariance and a catchment water balance to compare forest water use in South-Eastern USA (from plant to stand to catchment scale). These authors concluded that EC and catchment methods performed well in estimates of annual ET. They do not require elaborate scaling considerations. In their case study, sap-flow and EC estimates were qualitatively similar over much of the season. Sap-flow estimates however were lower than the results obtained with EC and lower than expected when estimated with the catchment method. These differences may be due to errors associated with the up-scaling of single tree estimates or due to measurement errors associated with ring-porous water conducting elements. The authors concluded that the soil water budget shows significant correlation with sap-flow and EC. Rapid water movement within the soil profile severely limits soil water budget method applicability for the estimation of annual evapotranspiration.
Ezzahar et al. [44] report a RMSE value of 18.25 W m-2 between the latent heat fluxes derived from the scintillometer and Eddy correlation tower measurements. They also observed that the scintillometer underestimates ET by 14%.
5.2. Soil moisture across different scales of observation
At the laboratory scale Liu et al. [149] used optical remote sensing to estimate SMC and reported RMSE values of 0.026-0.056 m3 m-3. Walker et al. [150] compared different automated techniques for point measurement of soil moisture content. Connector-type TDR sensors produced soil moisture measurements within the 0.0250 m3 m-3 accuracy. RMSE values obtained after calibration validation of hydrological models HYDRUS 2D are in the order of 0.075 m3 m-3 [151]. Heathman et al. [10] modelled the soil water profile content with RMSE values between 0.016 up to 0.097 m3 m-3.
Weihermüller et al. [152] used two ground penetrating radar techniques to estimate shallow soil water content at field scale. The RMSE values of the first field wave technique are 0.076 m3 m-3 when compared to the TDR measurements and 0.102 m3 m-3 when compared with volumetric soil samples. The RSME values of the other techniques are 0.053 m3 m-3 when compared with the TDR measurements and an error of 0.051 m3 m-3.
Saleh et al. [153] estimated soil surface moisture for grassland using L-band radiometry and Microwave Emission of the Biosphere model. They report RMSE values between 0.015 and 0.120 m3 m-3 when retrieving soil moisture. Field observations of SMC ranges approximately from 0.050 to 0.450 m3 m-3.
At regional to continental scales the ERS Scatterometer was successfully applied. RMSE values of SMC retrieved varies between 0.022 and 0.158 m3 m-3 for a wide range of soil types and climatic regions (global, Mongolia, Russia, Spain, Ukraine) [13] [128] [129]. Other microwave remote sensing applications (SSM/I, ERS-SAR, PALS) report RMSE values smaller than 0.100 m3 m-3 [154] [155] [156]. Using thermal inertia values derived from METEOSAT, errors on SMC can easily reach 18% [69] [137].
5.3. Selection of the appropriate ET and SMC assessment approaches
The important advantage of modelling, especially with conceptual physical models, is that insight can be obtained in the different mechanisms of the processes involved in water, nitrate and carbon cycling. The complexity of in situ events, induced by different interaction types, can partly be elicited by modelling and by incorporating the spatial as well as temporal dimensions. Moreover, scenario analysis, offering helpful information to decision makers, can be carried out. Some (carefully interpreted) predictions can be made. Nevertheless models are subject to (large) errors and uncertainties due to low quality or lacking input data (noise, gaps, inappropriate measuring dynamics etc), due to modelling assumptions (such as simplifications, linearization), or due to model structure (coupling between sub-processes) and computer coding (programming).
How to select the appropriate measurement and/or modelling tool? Much depends on the assumed objectives and criteria applied as well as on their relative importance. However some general criteria are valid. If the objective is the calibration and validation of a model, the acquisition of field data is crucial. The choice of the measurement methods will depend on the calibration data required. For instance, if a water balance model is to be calibrated for a forest site, the monitoring of the soil water balances together with sap-flow data can provide enough data. When, calibration and validation of a RS model is the objective, then EC equipment is indispensable. Indirect validation may be achieved by using catchment hydrological models as well. If the objective is scenario analysis, then a prognostic model is required. The required spatial and temporal scales strongly limit the possibilities for application. For instance, if the objective is the assessment of land-use change impacts on water consumption, a hydrological model and a historical meteorological dataset are needed. If an EO based carbon balance model for a semi-arid land cover type must be revised and validated, the incorporation of spatial and temporal water consumption values and EC measurements have to be used.
A general procedure to match with objectives, models and logistics is as follows:
- 1)
- Start with a specific scientific objective, check the assessment techniques for their limitations, and check the financial limitations. The method you have is easy to obtain.
- 2)
- Then feed this back into the methods, and subsequently also into the objectives etc.
Many criteria implemented are both scientific as well as non-scientific. For instance Kite and Droogers [145] indicate that a wide range of ET estimates has shown that there is no evident pattern of variability between the different methods. The assumption of the reliability of field methods is hard to scrutinize.
Cutting edge conclusions can be drawn only between the results of field measurements, hydrological models and RS-based models. When model and measuring uncertainty is involved, Kite and Droogers [145] indicated that all ET retrieval techniques fall within a reasonable interval of confidence. From an error study based on error propagation theory and Monte-Carlo techniques in remote sensing, it seems that the error on EF easily reaches 54% and on SMC 18% [137]. Nonetheless, other factors than the ET estimates must be considered such as the available project financial resources, data requirements, problem area complexity, temporal and spatial scale to be addressed, human resources, time frame, models etc. To make a good compromise between the issues raised is an interactive and dynamic process. It is a process of weighing all the pros and cons to be able to ultimately make a sound compromise. Past experience is invaluable in this type of decision making.
6. Conclusions
An extensive survey of international literature describing different methods to estimate land surface and ecosystem related evapotranspiration (ET) and soil moisture content (SMC) with emphasis on ET, has been conducted. The generally accepted theory of plant water uptake has been summarized and a shortlist of meteorological and plant factors influencing plant transpiration has been presented. ET assessment approaches at different s spatial scales (sap-flow, porometer, lysimeter, field water balance, Bowen ratio, scintillometer, eddy correlation and catchment water balance and models) have been the topic of discussion. We summarized SMC assessment techniques at different spatial scales and we suggested that scale is a key issue in hydrological applications. Ideally the scale for measurement, modelling and processing should be identical or at least similar.
It can be concluded that most assessment methods for the estimation of ET and SMC are point/plant/stand scale approaches. Assessment of hydrological impacts can be implemented using remote sensing and spatially distributed hydrological models. Extended networks of (field) sensors [157] have a large potential for ET and SMC estimation across scales as well. Typically, regional to continental scale information required for hydrological applications, is typically obtained with the application of EO techniques, although thermal and optical techniques require clear sky imagery. Clearly, at these large scales, essentially monitoring rather than climate scenario based predictions is possible. Validation and calibration is a strong requirement both in predictive modelling as in spatially distributed approaches. The statement that field methods are probably the most reliable is hard to justify for large scale applications, since three methods (field measurements, hydrological models and RS-based models) give considerably different results. Based on assumptions about uncertainties involved, the different methods elicit a reasonable confidence interval. Hence, other factors than ET or SMC estimates must be taken into consideration, i.e., data requirements, complexity, temporal and spatial scale and the prediction capabilities must be reviewed before further conclusions can be drawn with respect to accuracy issues.
Acknowledgments
The authors wish to thank the Flemish Institute for Technological Research (VITO) for the scholarship and financial support for this study, as well as the support offered by the GLOVEG contract (VG/00/01) and ARCHIMOD project.
References
- Bastiaanssen, W.G.M.; Bos, M.G. Irrigation performance indicators based on remotely sensed data: a review of literature. Irrigation and Drainage Systems 1999, 13, 291–311. [Google Scholar]
- Vinnikov, K.Y.; Robock, A.; Qiu, S.; Entin, J.K.; Owe, M.; Choudhury, B.J.; Hollinger, S.E.; Njoku, E.G. Satellite remote sensing of soil moisture in Illinois, USA. Journal of Geophysical Research 1999, 104, 4145–4168. [Google Scholar]
- Moran, M.S.; Peters-Lidard, C.D.; Watts, J.M.; McElroy, S. Estimating soil moisture at the watershed scale with satellite-based radar and land surface models. Canadian Journal of Remote Sensing 2004, 30(5), 805–826. [Google Scholar]
- Veroustraete, F. On the use of ecosystem modelling for the interpretation of climate change effects at the ecosystem level. Ecological Modelling 1994, 75-76, 221–237. [Google Scholar]
- Veroustraete, F.; Sabbe, H.; Eerens, H. Estimation of carbon mass fluxes over Europe using the C-Fix model and Euroflux data. Remote Sensing of Environment 2002, 83, 376–399. [Google Scholar]
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. On temperature and water limitation of net ecosystem productivity: Implementation in the C-Fix model. Ecological Modelling 2006, 199(1), 4–22. [Google Scholar]
- Field, C.B.; Randerson, J.T.; Malström, C.M. Global net primary production: combining ecology and remote sensing. Remote Sensing of Environment 1995, 51, 74–88. [Google Scholar]
- Verstraeten, W.W.; Veroustraete, F.; Wagner, W.; Van Roey, T.; Heyns, W.; Verbeiren, S.; van der Sande, C.J.; Feyen, J. Impact assessment of remotely sensed soil moisture on ecosystem carbon fluxes across Europe. 2nd International Workshop on Uncertainty in Greenhouse Gas Inventories, IIASA, Austria, 27-28 Sep., 2007.
- Woodwell, F.G.M. The role of terrestrial vegetation in the global carbon cycle, measurement by remote sensing.; SCOPE/ICSU, Wiley & Sons: Chichester; p. 247. 1984. [Google Scholar]
- Heathman, G.C.; Starks, P.J.; Ahuja, L.R.; Jackson, T.J. Assimilation of surface soil moisture to estimate profile soil water content. Journal of Hydrology 2003, 279, 1–17. [Google Scholar]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sensing of Environment 2002, 79, 213–224. [Google Scholar]
- Fen-Li, Z. Effect of vegetation changes on soil erosion on the loess plateau. Pedosphere 2006, 16(4), 420–427. [Google Scholar]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sensing of Environment 1999, 70, 191–207. [Google Scholar]
- Schelde, K. Modelling the forest energy and water Balance. In ISVA; Series Paper 62; Technical University of Denmark, 1996. [Google Scholar]
- Ladekarl, U.L. Estimation of the components of soil water balance in a Danish oak stand from measurements of soil moisture using TDR. Forest Ecology and Management 1998, 104, 2327–238. [Google Scholar]
- Dixon, H.H.; Joly, J. On the ascent of sap. Philosophical Transactions of the Royal Society London 1894, 186, 563–576. [Google Scholar]
- van den Honert, T.H. Water transport in plants as a catenary process. Discussion of the Faraday Society 1948, 3, 146–153. [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geographical Review 1948, 38, 55–95. [Google Scholar]
- Choisnel, E.; de Villele, O.; Lacroze, F. Une approche uniformisée du calcul de l'évapotranspiration potentielle pour l'ensemble des pays de la communauté européenne; Commission de Communautés Européennes: Brussel-Luxemburg; p. 176. 1992. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Crop water requirements. In FAO Irrigation and Drainage Paper 24; FAO: Rome, 1984. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration. Guide-lines for computing crop water requirements. In FAO Irrigation and Drainage Paper 56; FAO: Rome, 1998. [Google Scholar]
- Tyree, M.T. The cohesion-Tension theory of sap ascent: current controversies. Journal of Experimental Botany 1997, 48(315), 1753–1765. [Google Scholar]
- Parodi, G.N. AVHRR Hydrological analysis system: Algorithms and theory-version 1.0. WRES-ITC 2000. [Google Scholar]
- Makkeasorn, A.; Chang, N.-B.; Beaman, M.; Wyatt, C.; Slater, C. Soil moisture estimation in a semiarid watershed using RADARSAT-1 satellite imagery and genetic programming. Water Resources Research 2006, 44. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. Journal of Hydrology 1998, 212-213, 198–212. [Google Scholar]
- Li, J.; Islam, S. On the estimation of soil moisture profile and surface fluxes partitioning from sequential assimilation of surface layer soil moisture. Journal of Hydrology 1999, 220, 86–103. [Google Scholar]
- Verhoef, W.; Bach, H. Remote sensing data assimilation using coupled radiative transfer models. Physics and Chemistry of the Earth 2003, 28, 3–13. [Google Scholar]
- Granier, A. Une nouvelle méthode pour la mesure du flux de sève brute dans le tronc des arbres. Annales des Sciences Forestières 1985, 42, 81–88. [Google Scholar]
- Granier, A.; Bobay, V.; Gash, J.H.C.; Gelpe, J.; Saugier, B.; Shuttleworth, W.J. Vapour flux density and transpiration rate comparisons in a stand of maritime pine (Pinus pinaster Ait.) in Les Landes forest. Agricultural and Forest Meteorology 1990, 51, 309–319. [Google Scholar]
- Cermàk, J.; Nadezhdina, N. Sapwood as the scaling parameter–defining according to xylem water content or radial pattern of sap flow? Annales des Sciences Forestières 1998, 55, 509–521. [Google Scholar]
- Dugas, W.A. Sap flow in stems. Remote Sensing Reviews 1990, 5(1), 225–235. [Google Scholar]
- Meiresonne, L.; Nadezhdina, N.; Cermàk, J.; Van Slycken, J.; Ceulemans, R. Measured sap flow and simulated transpiration from a poplar stand in Flanders (Belgium). Agricultural and Forest Meteorology 1999, 96, 165–179. [Google Scholar]
- Edwards, W.R.N. Precision weighing lysimetry for trees, using a simplified tarred-balance design. Tree Physiology 1986, 1, 127–144. [Google Scholar]
- Verma, S.B. Micrometeorological Methods for Measuring Surface Fluxes of Mass and Energy. Remote Sensing Reviews 1990, 5(1), 99–115. [Google Scholar]
- Bidlake, W.R.; Woodham, W.M.; Lopez, M.A. Evapotranspiration from areas of native vegetation in West-Central Florida. U.S. Geological Survey Water-Supply Paper 1996, 2430. [Google Scholar]
- German, E.R. Regional evaluation of evapotranspiration in the Everglades. U.S. GEOLOGICAL SURVEY; In Water-Resources Investigations Report 00–4217; Tallahassee, Florida, 2000. [Google Scholar]
- Bidlake, W.R. Evapotranspiration from selected fallowed agricultural fields on the Tule Lake National Wildlife Refuge, California, During May to October 2000. U.S. GEOLOGICAL SURVEY; In Water-Resources Investigations; Report 02-4055; Tacoma, Washington, 2002. [Google Scholar]
- de Bruin, H.A.R.; van den Hurk, B.J.J.M.; Kohsiek, W. The scintillation method tested over a dry vineyard area. Boundary Layer Meteorology 1995, 76, 25–40. [Google Scholar]
- McAneney, K.G.; Green, A.E.; Astill, M. Large-aperture scintillometry: the homogeneous case. Agricultural and Forest Meteorology 1995, 76, 149–162. [Google Scholar]
- Green, A.E.; Hayashi, Y. Using the scintillometer technique over a rice paddy. Japanese Agricultural Meteorology 1998, 53(3), 225–231. [Google Scholar]
- Nieveen, J.P.; Green, A.E. Measuring sensible heat flux over pasture using the CT2 –profile method. Boundary-Layer Meteorology 1998, 91, 23–35. [Google Scholar]
- Nieveen, J.P.; Jacobs, C.M.J.; Jacobs, A.F.G. Diurnal and seasonal variation of carbon dioxide from a former true raised bog. Global Change Biology 1998, 4(8), 823–834. [Google Scholar]
- Meijninger, W.; de Bruin, H.A.R. The sensible heat fluxes over irrigated areas in western Turkey determined with a large aperture scintillometer. Journal of Hydrology 2000, 229, 42–49. [Google Scholar]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.C.B.; Er-Raki, S.; Chehbouni, Ah.; Boulet, G.; Bonnefond, J.-M.; De Bruin, H.A.R. The use of the scintillation technique for monitoring seasonal water consumption of olive orchards in a semi-arid region. Agricultural Water Management 2007, 89, 173–184. [Google Scholar]
- Leuning, R.; Moncrieff, J. Eddy covariance CO2 flux measurements using open-path and closed-path CO2 analyzers-corrections for analyzer water vapour sensitivity and damping of fluctuations in air sampling tubes. Boundary-Layer Meteorology 1990, 53, 63–76. [Google Scholar]
- Dolman, A.J. Transpiration of an oak forest as predicted from porometer and weather data. Journal of Hydrology 1988, 97, 225–234. [Google Scholar]
- McNaughton, K.; Jarvis, P.G. Effects of spatial scale on stomatal control of transpiration. Agricultural and Forest Meteorology 1991, 54, 279–302. [Google Scholar]
- Gochis, D.J.; Cuenca, R.H. Plant water use and crop curves for hybrid poplars. Journal of Irrigation and Drainage Engineering 2000, 126, 206–214. [Google Scholar]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: sap-flow, soil water budget, eddy covariance and catchment water balance. Agricultural and Forest Meteorology 2001, 106, 153–168. [Google Scholar]
- Vanclooster, M.; Viaene, P.; Christiaens, K.; Ducheyne, S. WAVE, a mathematical model for simulating water and agrochemicals in the soil and the vadose environment. In Reference and user's manual, release 2.1; Institute for Land and Water Management, Katholieke Universiteit Leuven: Belgium, 1996. [Google Scholar]
- van Dam, J.C.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; van Walsum, P.E.V.; Groenendijk, P.; van Diepen, C.A. Soil Water Atmosphere Plant (SWAT). In Technical Document; Volume 45, DLO Winand Staring Centre: Wageningen, the Netherlands, 1997. [Google Scholar]
- Refsgaard, J.C.; Storm, B. MIKE SHE. Singh, V.P., Ed.; In Computer models of watersheded hydrology; Water Resources Publications: Colorado, USA; pp. 809–846. 1995. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool, Theoretical documentation, Version 2000; Texas Water Resources Institute: College Station, Texas, TWRI Report TR-191; 2002. [Google Scholar]
- Mauser, W.; Schädlich, S. Modelling the spatial distribution of evapotranspiration on different scales using remote sensing data. Journal of Hydrology 1998, 212-213, 250–267. [Google Scholar]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; van der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL). 2. Validation. Journal of Hydrology 1998, 212-213, 198–212. [Google Scholar]
- Monteith, J.L. Evaporation and the environment. In The State and Movement of Water in Living Organisms, 19th Symposium of the Society for Experimental Biology; London; Cambridge University Press; pp. 205–234. 1965. [Google Scholar]
- Jackson, R.D.; Reginato, R.J.; Idso, S.B. Wheat canopy temperature: a practical tool for revaluating water requirements. Water Resources Research 1977, 13, 651–656. [Google Scholar]
- Price, J.C. Using spatial context in satellite data to infer regional scale evapotranspiration. IEEE Transactions on Geoscience and Remote Sensing 1990, 28(5), 940–948. [Google Scholar]
- Carlson, T.N.; Perry, E.M.; Schmugge, T.J. Remote estimation of soil moisture availability and fractional vegetation cover for agricultural fields. Agricultural and Forest Meteorology 1990, 52, 45–69. [Google Scholar]
- Carlson, T.N.; Gillies, R.R.; Perry, E.M. A method to make use of thermal infrared temperature and NDVI measurements to infer surface soil water content and fractional vegetation cover. Remote Sensing Reviews 1994, 9, 161–173. [Google Scholar]
- Carlson, T.N. An overview of the so-called “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Moran, M.S.; Hymer, D.C.; Qi, J.; Sano, E.E. Soil moisture evaluation using multi-temporal Synthetic Aperture Radar (SAR) in semiarid rangeland. Agriculture and Forest Meteorology 2000, 105, 69–80. [Google Scholar]
- Qi, J.; Moran, M.S.; Goodrich, D.C.; Marsett, R.; Scott, R.; Chehbouni, A.; Schaeffer, S.; Schieldge, J.; Williams, D.; Keefer, T.; Cooper, D.; Hipps, L.; Eichinger, W.; Ni, W. Estimation of evapotranspiration over the San Pedro riparian area with remote and in situ measurements. American Meteorological Society, Special Symposium on Hydrology, Phoenix, Arizona, 11-16 January 1998.
- Gellens-Meulenberghs, F. Evapotranspiration and surface heat fluxes over Belgium: outcome and perspectives. Agronomie 2000, 20(8), 857–868. [Google Scholar]
- Granger, R.J. Satellite-derived estimates of evapotranspiration in the Gediz basin. Journal of Hydrology 2000, 229, 70–76. [Google Scholar]
- D'Urso, G. Simulation and management of on-demand irrigation systems. A combined agrohydrological and remote sensing approach. PhD Thesis, Wageningen University, 2001; p. 173. [Google Scholar]
- Ambast, S.K.; Keshari, A.K.; Gosain, A.K. An operational model for estimating regional evapotranspiration through surface energy partitioning (RESEP). International Journal of Remote Sensing 2002, 23(22), 4917–4930. [Google Scholar]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrology and Earth System Sciences 2002, 6(1), 85–99. [Google Scholar]
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. Estimating evapotranspiration of European forests from NOAA-imagery at satellite overpass time: Towards an operational processing chain for integrated optical and thermal sensor data products. Remote Sensing of Environment 2005, 96(2), 256–276. [Google Scholar]
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.F. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar]
- Meyers, T.P.; Hollinger, S.E. An assessment of storage terms in the surface energy balance of maize and soybean. Agricultural and Forest Meteorology 2004, 125, 105–115. [Google Scholar]
- Cermàk, J.; Kucera, J. Scaling up transpiration data between trees, stands and watersheds. Silva Carelica 1990, 15, 101–120. [Google Scholar]
- Pearcy, R.W.; Schulze, E.-D.; Zimmermann, R. Measurement of transpiration and leaf conductance. In Plant Physiological Ecology, Field measurements and instrumentation; Pearcy, R.W., Ehleringer, J., Mooney, H.A., Rundel, P.W., Eds.; Chapman and Hall: London, New York; pp. 137–160. 1989. [Google Scholar]
- Calder, I.R. The measurement of water losses from a forested area using a “natural” lysimeter. Journal of hydrology 1976, 30, 311–325. [Google Scholar]
- Yang, J.; Li, B.; Liu, S. A large weighing lysimeter for evapotranspiration and soil water-groundwater exchange studies. Hydrological Processes 2000, 14, 1887–1897. [Google Scholar]
- Brutsaert, W.; Hsu, A.Y.; Schmugge, T.J. Parameterization of surface sensible heat fluxes above forest with satellite thermal sensing and boundary layer soundings. Journal of Applied Meteorology 1993, 32(5), 909–917. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large scale parameters. Monthly Weather Reviews 1972, 80, 81–92. [Google Scholar]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulation. Remote Sensing of Environment 1994, 50, 1–17. [Google Scholar]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops- an energy combination theory. Quarterly Journal of the Royal Meteorological Society 1985, 111(469), 839–855. [Google Scholar]
- Verstraeten, W.W.; Muys, B.; Feyen, J.; Veroustraete, F.; Minnaert, M.; Meiresonne, L.; De Schrijver, A. Comparative analysis of the actual evapotranspiration of Flemish forest and cropland, using the soil water balance model WAVE. Hydrology and Earth System Sciences 2005, 9, 225–241. [Google Scholar]
- Xu, C.Y.; Singh, V.P. Evaluation and generalization of temperature-based methods for calculating evaporation. Hydrological Processes 2001, 15, 305–319. [Google Scholar]
- Singh, V.P.; Xu, C-Y. Evaluation and generalization of 13 equations for determining free water evaporation. Hydrological Processes 1997, 11, 311–323. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resources Research 1980, 16, 574–582. [Google Scholar]
- Baldocchi, D.D.; Hicks, B.B.; Meyers, T.P. Measuring biosphere-atmosphere exchanges of biologically related gases with micrometeorological methods. Ecology 1988, 69, 1331–1340. [Google Scholar]
- Früchauf, C.; Zimmerman, L.; Bernhofer, Ch. Comparison of forest evapotranspiration from ECEB-measurements over a spruce stand with the water budget of a catchment. Physics and Chemistry of the Earth (B) 1999, 24(7), 805–808. [Google Scholar]
- Bastiaanssen, W.G.M. Regionalization of surface flux densities and moisture indicators in composite terrain: a remote sensing approach under clear skies in Mediterranean climates. PhD thesis, Wageningen, University, the Netherlands, 1995. [Google Scholar]
- Bastiaanssen, W.G.M. Remote sensing in water resources management: the state of the art.; Colombo, Sri Lanka; International Water Management Institute; p. 118. 1998. [Google Scholar]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the surface energy balance algorithm for land (SEBAL) and the two-source energy balance (TSEB) modeling schemes. Remote Sensing of Environment 2007, 108, 369–384. [Google Scholar]
- Lagouarde, J-P.; Jacob, F.; Gu, X.F.; Olioso, A.; Bonnefond, J-M.; Kerr, Y.; McAneney, K.J.; Irvine, M. Spatialization of sensible heat flux over a heterogeneous landscape. Agronomie 2002, 22, 627–633. [Google Scholar]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual. Journal of Irrigation and Drainage Engineering-ASCE 2005, 131(1), 85–93. [Google Scholar]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Physics and Chemistry of the Earth 2000, 25, 147–157. [Google Scholar]
- Moran, M.S.; Rahman, A.F.; Washburne, J.C.; Goodrich, D.C.; Weltz, M.A.; Kustas, W.P. Combining the Penman-Monteith equation with measurements of surface temperature and reflectance to estimate evaporation rates of semiarid grassland. Agricultural and Forest Meteorology 1996, 80, 87–109. [Google Scholar]
- Wang, K.; Li, Z.; Cribb, M. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: A new method to determine the Priestley–Taylor parameter. Remote Sensing of Environment 2006, 102, 293–305. [Google Scholar]
- Cleugh, H.A.; Leuning, R.; Mu, Q.Z.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sensing of Environment 2007, 106(3), 285–304. [Google Scholar]
- Nagler 2005. RSE Predicting riparian evapotranspiration from MODIS vegetation indices and meteorological data. Remote Sensing of Environment 2005, 94, 17–30. [Google Scholar]
- Nagler, P.; Jetton, A.; Fleming, J.; Didan, K.; Glenn, E.; Erker, J.; Morino, K.; Milliken, J.; Gloss, S. Evapotranspiration in a cottonwood (Populus fremontii) restoration plantation estimated by sap flow and remote sensing methods. Agricultural and Forest Meteorology 2007, 144, 95–110. [Google Scholar]
- Mohamed, Y.A.; Savenije, H.H.G.; Bastiaanssen, W.G.M.; Hurk, B.J.J.M. New lessons on the Sudd hydrology learned from remote sensing and climate modeling. Hydrology and Earth System Science 2006, 10(4), 507–518. [Google Scholar]
- Shuttleworth, W.J.; Gurney, R.J.; Hsu, A.Y.; Ormsby, J.P. FIFE: The variation in energy partitioning at surface flux sites. Rango, A., Ed.; In Remote Sensing and Large-Scale Global Processes; IAHS Publication, 186, International Association of Hydrologic Science: Wallingford, Oxfordshire, England; pp. 67–74. 1989. [Google Scholar]
- García, M.; Villagarcía, L.; Contreras, S.; Domingo, F.; Puigdefábregas, J. Comparison of three operative models for estimating the surface water deficit using ASTER reflective and thermal data. Sensors 2007, 7, 860–883. [Google Scholar]
- Kimura, K. Estimation of moisture availability over the Liudaogou river basin of the Loess Plateau using new indices with surface temperature. Journal of Arid Environments 2007, 70, 237–252. [Google Scholar]
- Olioso, A. Simulation des échange d'énergie et de masse d'un couvert végétal, dans le but de relier la transpiration et la photosyntèse aux mesures de réflectance et de température de surface. Thèse de doctorat, Université Montpellier, 1992. [Google Scholar]
- Olioso, A.; Chauki, H.; Wigneron, J.-P.; Bergaoui, K.; Bertuzzi, P.; Chanzy, A.; Bessemoulin, P.; Calvet, J.-C. Estimation of Energy Fluxes from Thermal Infrared, Spectral Reflectances, Microwave Data and SVAT Modelling. Physis and Chemitry of the Earth (B) 1999, 24(7), 829–836. [Google Scholar]
- Carlson, T.N.; Capehart, W.J.; Gillies, R.R. A new look at the simplified method for remote sensing of daily evapotranspiration. Remote Sensing of Environment 1995, 54, 161–167. [Google Scholar]
- Moran, M.S.; Clarke, T.R.; Kustas, W.P.; Weltz, M.; Amer, S.A. Evaluation of hydrologic parameters in a semiarid rangeland using remote sensed spectral data. Water Resources Research 1994, 30(5), 1287–1297. [Google Scholar]
- Zazueta, F.S.; Xin, J. Soil Moisture Sensors. Bulletin 292; Florida Cooperative Extension Service, Institute of Food and Agricultural Sciences, University of Florida, 1994. [Google Scholar]
- Starks, P.J. A general heat dissipation sensor calibration equation and estimation of soil water content. Soil Science 1999, 164, 655–661. [Google Scholar]
- Miles, D.L. Estimating Soil Moisture; Crop series, irrigation; no. 4.700; Colorado State University Cooperative Extension; p. 9/98. 1999. [Google Scholar]
- Schwank, M.; Green, T.R. Simulated effects of soil temperature and salinity on capacitance sensor measurements. Sensors 2007, 7, 548–577. [Google Scholar]
- Gardner, W.; Kirkham, D. Determination of soil moisture by neutron scattering. Soil Sciences 1952, 73, 391–401. [Google Scholar]
- Reginato, R.J.; van Bavel, C.H.M. Soil measurementwith gamma attenuation. Soil Science Sot. Amer. Proc 1964, 28, 721–724. [Google Scholar]
- Noborio, K. Measurement of soil water content and electrical conductivity by time domain reflectometry: a review. Computers and Electronics in Agriculture 2001, 31(3), 213–237. [Google Scholar]
- Vanderborgt, J.; Vanclooster, M.; Timmerman, A.; Seuntjens, P.; Mallants, D.; Kim, D.J.; Jacques, D.; Hubrechts, L.; Gonzalez, C.; Feyen, J.; Diels, J.; Deckers, J. Overview of inert tracer experiments in key Belgian soil types: Relation between transport and soil morphological and hydraulic properties. Water Resources Research 2001, 37(12), 2873–2888. [Google Scholar]
- Woodhead, I.M.; Buchan, G.D.; Christie, J.H.; Irie, K. A general dielectric model for time domain reflectometry. Biosystems Engineering 2003, 86(2), 207–216. [Google Scholar]
- Wang, J.R.; Schmugge, T.J. An empirical model for the complex dielectric permittivity of soils as a function of water content. IEEE Transactions on Geoscience and Remote Sensing 1980, 18, 288–295. [Google Scholar]
- Huisman, J.A.; Snepvangers, J.J.J.C.; Bouten, W.; Heuvelink, G.B.M. Mapping spatial variation in surface soil water content: comparison of ground-penetrating radar and time domain reflectometry. Journal of Hydrology 2002, 207, 194–207. [Google Scholar]
- Davis, J.L.; Annan, A.P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophysical Prospecting 1989, 37(5), 531–551. [Google Scholar]
- Pires, L.F.; Bacchi, O.O.S.; Reichardt, K. Soil water retention curve determined by gammaray beam attenuation. Soil & Tillage Research 2005, 82, 89–97. [Google Scholar]
- Vanclooster, M.; Viaene, P.; Diels, J.; Feyen, J. A deterministic evaluation analysis applied to an integrated soil-crop model. Ecological Modelling 1995, 81, 183–195. [Google Scholar]
- Ducheyne, S.; Schadecka, N.; Vanongeval, L.; Vandendriessche, H.; Feyen, J. Assessment of the parameters of a mechanistic soil–crop–nitrogen simulation model using historic data of experimental field sites in Belgium. Agricultural Water Management 2001, 51, 53–78. [Google Scholar]
- Meiresonne, L.; Sampson, D.A.; Kowalski, A.S.; Janssens, I.A.; Nadezhdina, N.; Cermák, J.; Van Slycken, J.; Ceulemans, R. Water flux estimates from a Belgian Scots pine stand: a comparison of different approaches. Journal of Hydrology 2003, 270, 230–252. [Google Scholar]
- Grant, L.; Seyfried, M.; McNamara, J. Spatial variation and temporal stability of soil water in a snow-dominated, mountain catchment. Hydrological Processes 2004, 18, 3493–3511. [Google Scholar]
- Vachaud, G.; Passerat de Silans, A.; Balabanis, P.; Vauclin, M. Temporal stability of spatially measured soil water probability density function. Soil Science Society of America Journal 1985, 49, 822–828. [Google Scholar]
- Grayson, R.B.; Western, A.W. Towards area1 estimation of soil water content from point measurements: time and space stability of mean response. Journal of Hydrology 1998, 207, 68–82. [Google Scholar]
- Kachanoski, R.G.; De Jong, E. Scale dependence and the temporal persistence of spatial patterns of soil-water storage. Water Resource Research 1988, 21(1), 85–91. [Google Scholar]
- Martinez-Fernandez, J.; Ceballos, A. Temporal stability of soil moisture in a large-field experiment in Spain. Soil Science Society of America Journal 2003, 67(6), 1647–1656. [Google Scholar]
- Grayson, R.B.; Blöschl, G.; Western, A.W.; McMahon, T.A. Advances in the use of observed spatial patterns of catchment hydrological response. Advances in Water Resources 2002, 25, 1313–1334. [Google Scholar]
- Western, A.W.; Grayson, R.B. The Tarrawarra data set: Soil moisture patterns, soil characteristics, and hydrological flux measurements. Water Resources Research 1998, 34(10), 2765–2768. [Google Scholar]
- Ceballos, A.; Scipal, K.; Wagner, W.; Martínez-Fernández, L. Validation of ERS Scatterometer-derived soil moisture data in the central part of the Duero Basin, Spain. Hydrological Processes 2005, 19(8), 1549–1566. [Google Scholar]
- Scipal, K.; Scheffler, C.; Wagner, W. Soil moisture-runoff relation at the catchment scale as observed with coarse resolution microwave remote sensing. Hydrology and Earth System Sciences 2005, 9, 173–183. [Google Scholar]
- Verstraeten, W.W.; Veroustraete, F.; van der Sande, C.J.; Grootaers, I.; Feyen, J. Soil moisture retrieval using thermal inertia, determined with visible and thermal spaceborne data, validated for European forests. Remote Sensing of Environment 2006, 101(3), 299–314. [Google Scholar]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M. Up scaling and downscaling—a regional view of the soil–plant–atmosphere continuum. Journal of Agronomy 2003, 95, 1408–1423. [Google Scholar]
- Justice, C.; Belward, A.; Morisette, J.; Lewis, P.; Privette, J.; Baret, F. Developments in the ‘validation’ of satellite sensor products for the study of the land surface. International Journal of Remote Sensing 2000, 21(17), 3383–3390. [Google Scholar]
- Weiss, M.; de Beaufort, L.; Baret, F.; Allard, D.; Bruguier, N.; Marloie, O. Mapping leaf area index measurements at different scales for the validation of large swat satellite sensors: first results of the VALERI project. In Physical Measurements and Signatures in Remote Sensing; Guyot & Phulpin, 2001; pp. 125–130. [Google Scholar]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sensing of Environment 2006, 105, 271–285. [Google Scholar]
- Kustas, W.P.; Li, F.; Jackson, T.J.; Prueger, J.H.; MacPhersonc, J.I.; Wolde, M. Effects of remote sensing pixel resolution on modeled energy flux variability of croplands in Iowa. Remote sensing of Environment 2004, 92, 535–547. [Google Scholar]
- McCabe, M.F.; Kalma, J. D.; Franks, S.W. Spatial and temporal patterns of land surface fluxes from remotely sensed surface temperatures within an uncertainty modelling framework. HESS 2005, 9, 467–480. [Google Scholar]
- Verstraeten, W.W.; Veroustraete, F.; Heyns, W.; Van Roey, T.; Feyen, J. On uncertainties in carbon flux modelling and remotely sensed data assimilation: the Brasschaat pixel case. Advances in Space Research 2008, 41, 20–35. [Google Scholar]
- Goodrich, D.C.; Scott, R.; Qi, J.; Goff, B.; Unkrich, C.L.; Moran, M.S.; Williams, D.; Schaeffer, S.; Snyder, K.; MacNish, R.; Maddock, T.; Pool, D.; Chehbouni, A.; Cooper, D.I.; Eichinger, W.E.; Shuttleworth, W.J.; Kerr, Y.; Marsett, R.; Ni, W. Seasonal estimates of riparian evapotranspiration using remote and in situ measurements. Agricultural and Forest Meteorology 2000, 105(1-3), 281–309. [Google Scholar]
- Jacob, F.; Olioso, A.; Gu, X.F.; Su, Z.; Seguin, B. Mapping surface fluxes using airborne visible, near infrared, thermal infrared remote sensing data and a spatialized surface energy balance model. Agronomie 2002, 22, 669–680. [Google Scholar]
- Li, F.; Lyons, T.J. Estimation of regional evapotranspiration through remote sensing. Journal of Applied Meteorology 1999, 38, 1644–1654. [Google Scholar]
- Kustas, W.P.; Choudhury, B.J.; Moran, M.S.; Reginato, R.J.; Jackson, R.D.; Gay, L.W.; Weaver, H.L. Determination of sensible heat flux over sparse canopy using thermal infrared data. Agricultural and Forest Meteorology 1989, 44, 197–216. [Google Scholar]
- Moran, M.S.; Humes, K.S.; Pinter, P.J. The scaling characteristics of remotely-sensed variables for sparsely-vegetated heterogeneous landscapes. Journal of Hydrology 1997, 190, 337–362. [Google Scholar]
- Lhomme, J-P.; Monteny, B.; Amadou, M. Estimation sensible heat flux from radiometric temperature over sparse millet. Agricultural and Forest Meteorology 1994, 68, 77–91. [Google Scholar]
- Lhomme, J-P.; Chehbouni, A.; Troufleau, D. Determination of sensible heat flux over Sahelian fallow savannah using infrared thermometry. Agricultural and Forest Meteorology 68, 93–105.
- Kite, G.W.; Droogers, P. Comparing evapotranspiration estimates from satellites, hydrological models and field data. Journal of Hydrology 2000, 229, 3–18. [Google Scholar]
- Kite, G.W. Manual for the SLURP hydrological model; NHRI: Canada; p. 111. 1997. [Google Scholar]
- Beyazgül, M.; Kayama, Y.; Engelsman, F. Estimation methods for crop water requirements in the Gediz Basin of western Turkey. Journal of Hydrology 2000, 229, 19–26. [Google Scholar]
- Samson, R. An experimental and modelling approach to the actual evapotranspiration in a mixed forest ecosystem (Experimental forest Aelmoeseneie at Gontrode). PhD, Universiteit Gent, 2001; p. 294. [Google Scholar]
- Liu, W.; Baret, F.; Gu, X.; Zhang, B.; Tong, Q.; Zheng, L. Evaluation of methods for soil surface moisture estimation from reflectance data. International Journal of Remote Sensing 2003, 24(10), 2069–2083. [Google Scholar]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. In situ measurement of soil moisture: a comparison of techniques. Journal of Hydrology 2004, 293, 85–99. [Google Scholar]
- Joris, I.; Feyen, J. Modelling water flow and seasonal soil moisture dynamics in an alluvial groundwater-fed wetland. Hydrology and Earth System Sciences 2003, 7(1), 57–66. [Google Scholar]
- Weihermüller, L.; Huisman, J.A.; Lambot, S.; Herbst, M.; Vereecken, H. Mapping the spatial variation of soil water content at the field scale with different field penetrating radar techniques. Journal of Hydrology 2007. In Press. [Google Scholar]
- Saleh, K.; Wigneron, J.-P.; Waldteufel, P.; de Rosnay, O.; Schwank, S.; Calvet, J.-C.; Kerr, Y.H. Estimates of surface soil moisture under grass covers using L-band radiometry. Remote Sensing of Environment 2007, 109, 42–53. [Google Scholar]
- De Ridder, K. Quantitative estimation of skin soil moisture with the Special Sensor microwave/Imager. Boundary-Layer Meteorology 2000, 96, 421–432. [Google Scholar]
- Quesney, A.; Le Hégarat-Mascle, S.; Taconet, O.; Vidal-Madjar, D.; Wigneron, J.P.; Loumagne, C.; Normand, M. Estimation of watershed soil moisture index from ERS/SAR data. Remote Sensing of Environment 2000, 72, 290–303. [Google Scholar]
- Narayan, U.; Lakshmi, V.; Njoku, E.G. Retrieval of soil moisture from passive and active L/S band sensor (PALS) observations during the Soil Moisture Experiment in 2002 (SMEX02). Remote Sensing of Environment 2004, 92, 483–496. [Google Scholar]
- Delin, K.A. The Sensor Web: A macro-instrument for coordinated sensing. Sensors 2002, 2(7), 270–285. [Google Scholar]
© 2008 by MDPI Reproduction is permitted for non-commercial purposes.