Soil Moisture Profile Effect on Radar Signal Measurement
Abstract
:1. Introduction
2. Modelling backscattering with a multi-layer permittivity profile
3. Experimental measurements
- -
- The first one of these was obtained at the Avignon site in the south of France, in 1995. It comprises ground measurements only, without satellite acquisitions.
- -
- A second database was obtained at the Villamblain site in 2006, with a large number of experimental campaigns detailed in the next section.
3.1 Description of Avignon Site
3.2 Description of the Villamblain Site
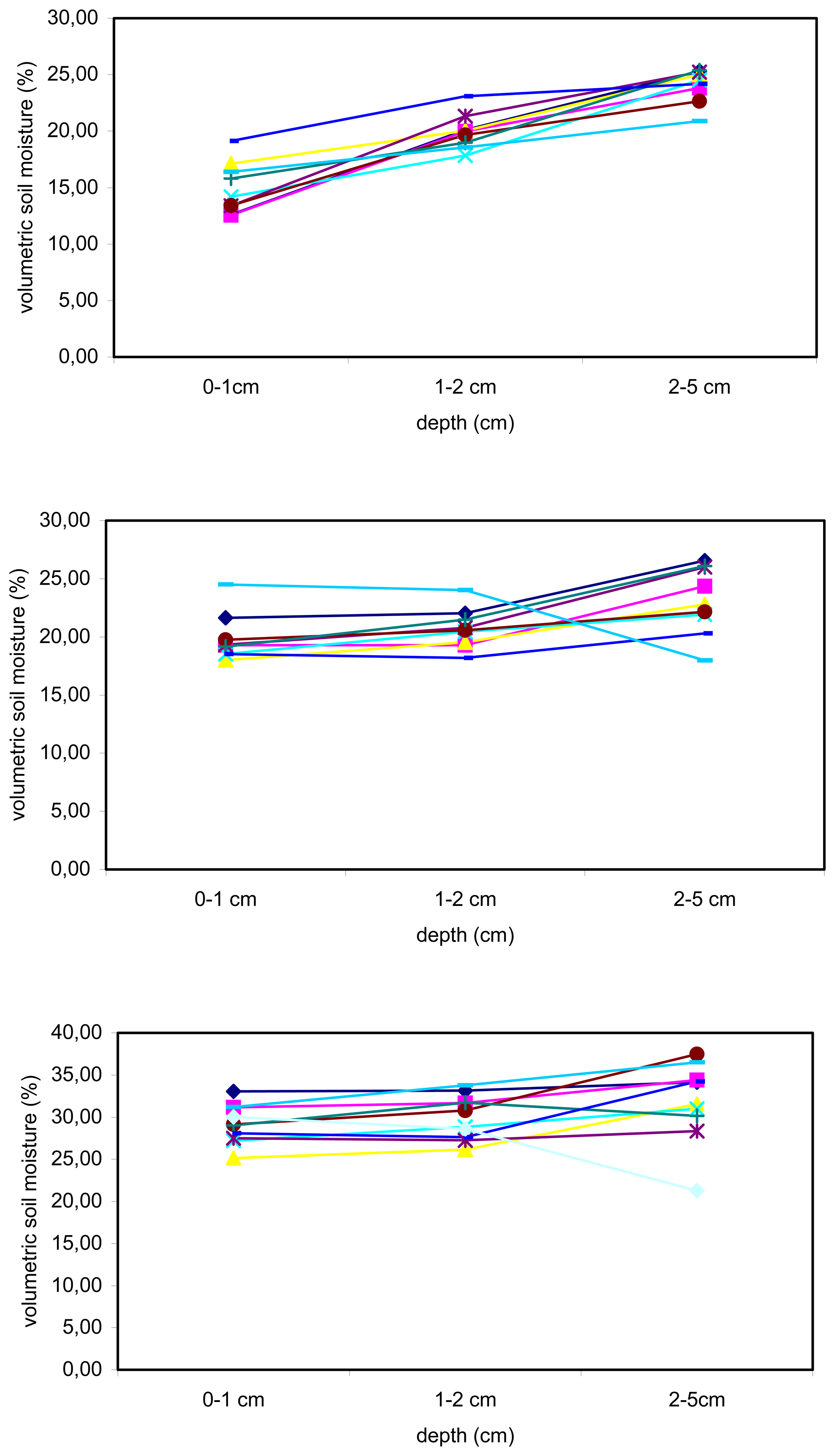
- Soil moisture measurements
- Roughness measurements
3.3 Satellite measurements
4. Application and results
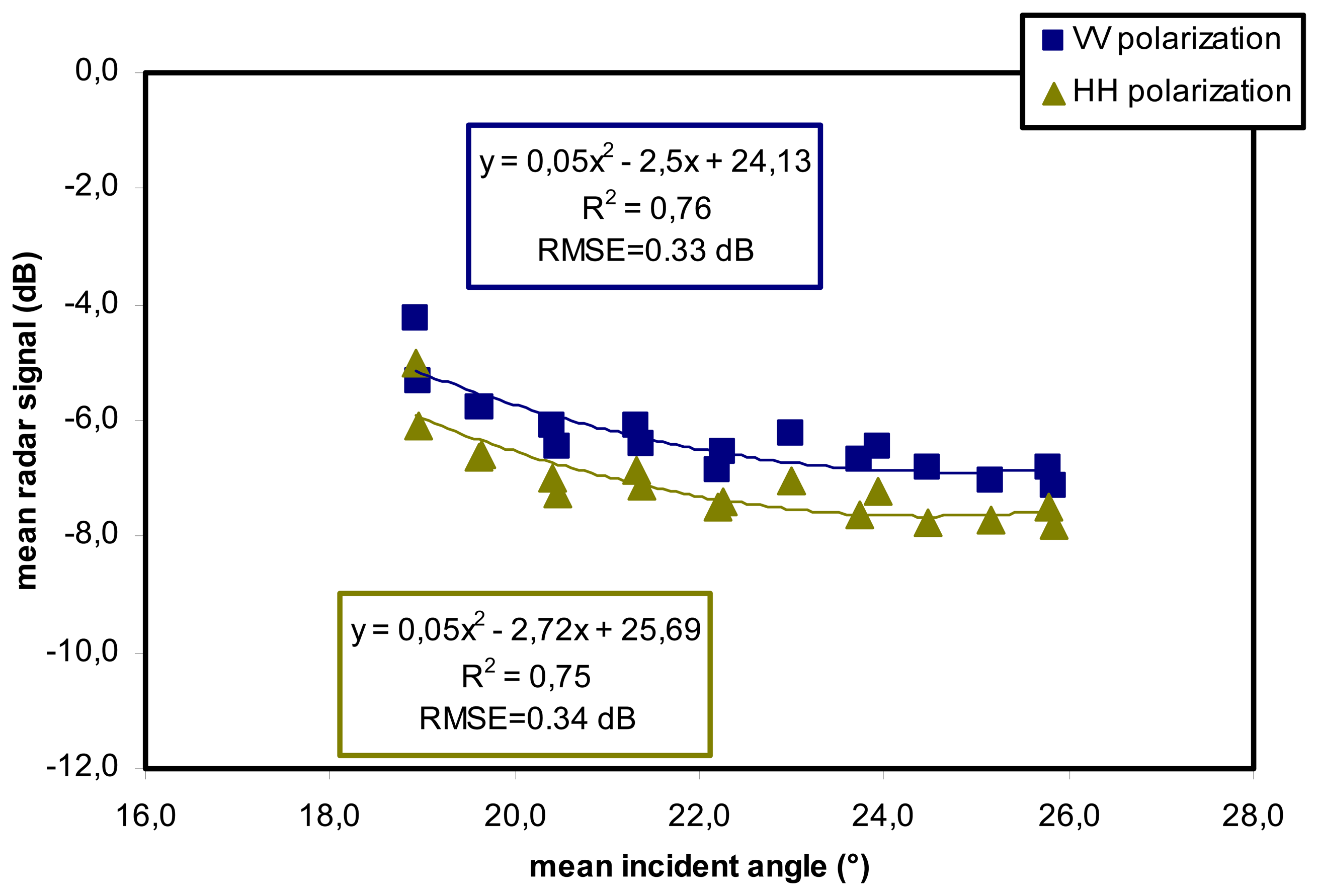
4.1 Analysis of correlation between moisture and radar measurements
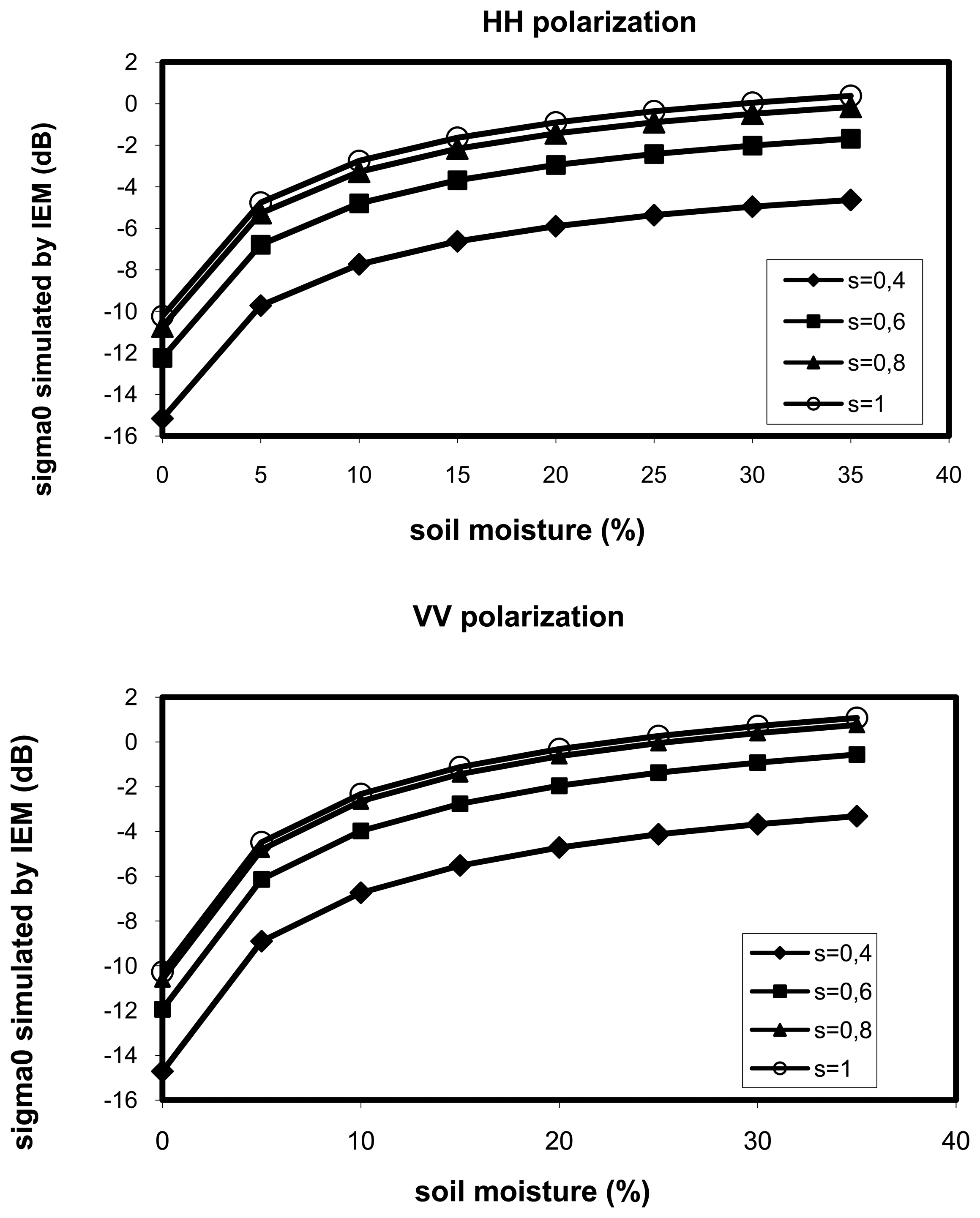
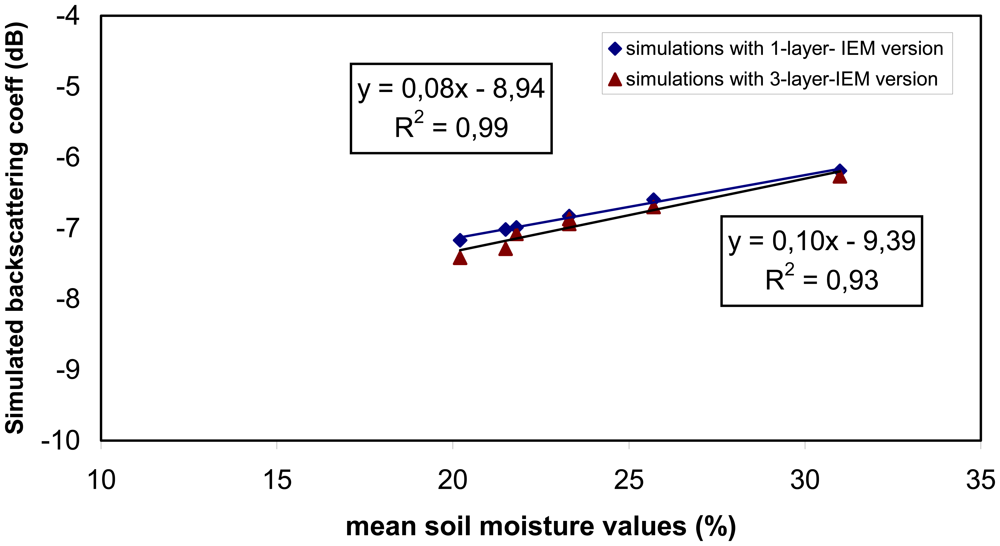
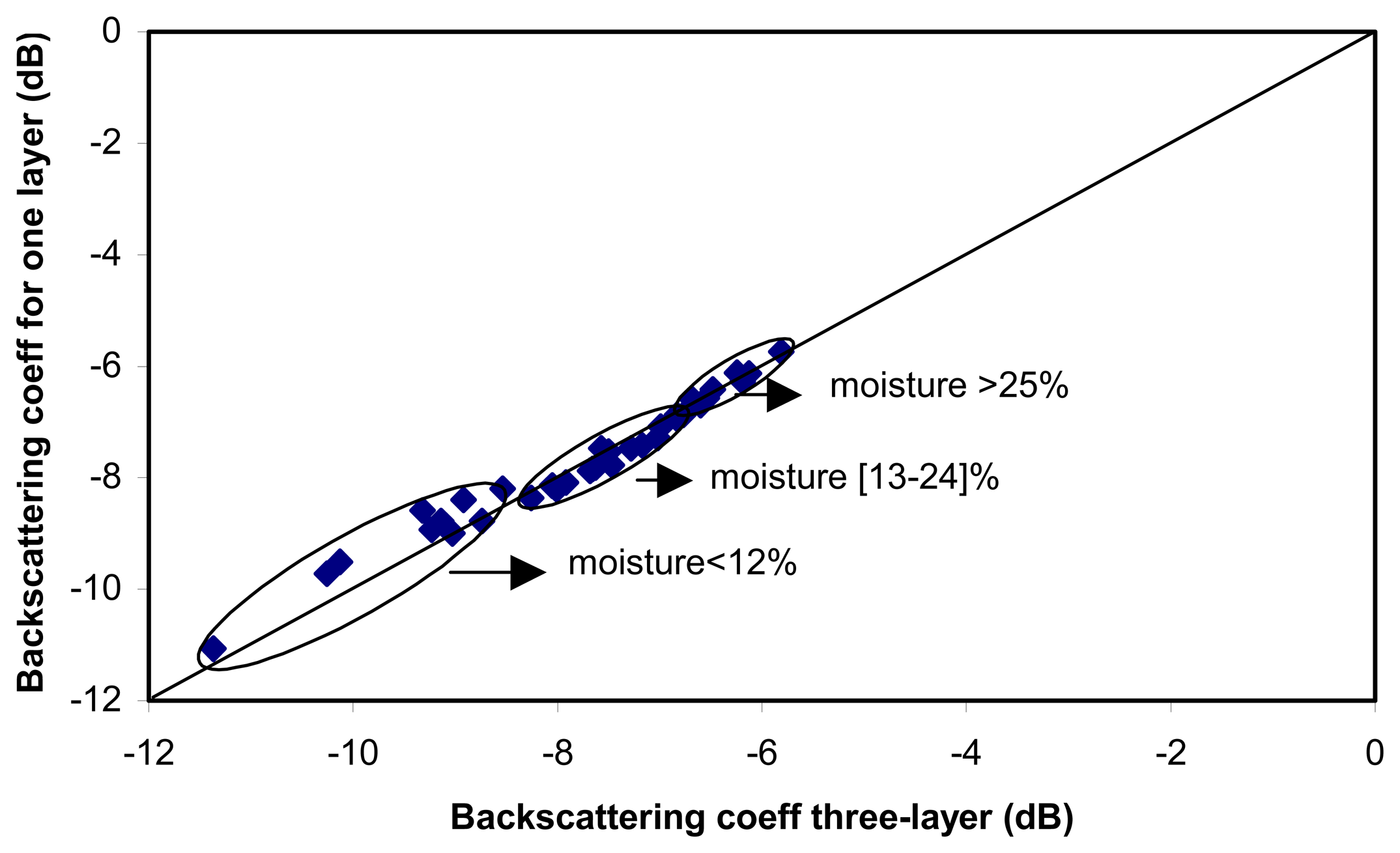
4.2 Analysis of the multi-layer profile effect using the IEM model
5. Conclusions
Acknowledgments
References and Notes
- Bruckler, L.; Wittono, H.; Stengel, P. Near surface moisture estimation from microwave measurements. Remote Sens. Environ 1988, 26, 101–121. [Google Scholar]
- Zribi, M.; Taconet, O.; Le Hégarat-Mascle, S.; Vidal-Madjar, D.; Emblanch, C.; Loumagne, C.; Normand, M. Backscattering behavior and simulation comparison over bare soils using SIRC/XSAR and ERASME 1994 data over Orgeval. Remote Sens. Environ 1997, 59. [Google Scholar]
- Cognard, A.L.; Loumagne, C.; Normand, M.; Olivier, P.; Ottlé, C.; Vidal-Madjar, D.; Louahala, S.; Vidal, A. Evaluation of the ERS-1/synthetic aperture radar capacity to estimate surface soil moisture: Two-year results over the Naizin watershed. Wat. Resour. Res 1995, 31(4), 975–982. [Google Scholar]
- Le Hégarat-Mascle, S.; Zribi, M.; Alem, F.; Weisse, A. Soil moisture estimation from ERS/SAR data: Toward an operational methodology. IEEE Trans. Geosci. Remote Sens 2002, 40. [Google Scholar]
- Zribi, M.; Baghdadi, N.; Holah, N.; Fafin, O. New methodology for soil surface moisture estimation and its application to ENVISAT-ASAR multi-incidence data inversion. Remote Sens. Environ 2005, 96, 485–496. [Google Scholar]
- Baghdadi, N.; Holah, N.; Zribi, M. Soil moisture estimation using multi-incidence and multi-polarization ASAR SAR data. Int. J. Remote Sens 2006, 27. [Google Scholar]
- Boisvert, J.B.; Gwyn, Q.H.J.; Chanzy, A.; Major, D.J.; Brisco, B.; Brown, R.J. Effect of surface soil moisture gradients on modeling radar backscattering from bare fields. Int. J. Remote Sens 1997, 18(1), 153–170. [Google Scholar]
- Fung, A.K.; Boisvert, J.; Brisco, B. Interpretation of radar measurements from rough soil surface with a permittivity profile. IGARSS'97 1997, 3, 1376–1378. [Google Scholar]
- Walker, J.P.; Troch, P.A.; Mancini, M.; Willgoose, G.R.; Kalma, J.D. Profile soil moisture estimation using the modified IEM. IGARSS'97 1997, 3, 1263–1265. [Google Scholar]
- Crosson, W.L.; Laymon, C.A.; Inguva, R.; Bowman, C. Comparison of the two microwave radiobrighthness models and validation with field measurements. IEEE Trans. Geosci. Remote Sens 2002, 40, 143–152. [Google Scholar]
- Lu, T.; Shi, C.; Li, Z. Electromagnetic scattering and emission from rough surfaces of soil with inhomogeneous moisture profile. 4th ICMMWTP; 2004; pp. 940–944. [Google Scholar]
- Ulaby, F.T.; Moore, M.K.; Fung, A.K. Microwave Remote Sensing, Active and Passive; Volume 3, Artech House: Norwood, MA, 1986. [Google Scholar]
- Wu, T.D.; Chen, K.S.; Shi, J.; Fung, A.K. A transition model for the reflection coefficient in surface scattering. IEEE Trans. Geosci. Remote Sens 2001, 39. [Google Scholar]
- Hallikanen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.; Wu, L. Microwave dielectric behavior of Wet Soil- Part I: Empirical Models and Experimental Observations. IEEE Trans. Geosci. Remote Sens. 1985, GE-23(1), 25–34. [Google Scholar]
- Macaire, J. M. Etude sédimentologique des formations superficielles sur le tracé de l'autoroute A10 entre Artenay et Meung/Loire. Thèse 3ecycle, Université d'Orléans, 1971; p. 104 pp. [Google Scholar]

| Date (dd/mm/yy) | Density 0-2.5 cm | Density 2.5-5 cm | Density 5-10cm |
|---|---|---|---|
| 10/10/2006 | 1.02 | 1.11 | 1.114 |
| 20/10/2006 | 1.05 | 1.16 | 1.13 |
| 26/10/2006 | 1.05 | 1.10 | 1.14 |
| 08/11/2006 | 1.04 | 1.11 | 1.13 |
| 14/11/2006 | 1.05 | 1.08 | 1.16 |
| 24/11/2006 | 1.03 | 1.12 | 1.21 |
| 19/12/2006 | 1.05 | 1.09 | 1.19 |
| Date (dd/mm/yy) | Incidence angle | Sensor/mode | Polarization | Pixel spacing | Mean soil moisture“Ws”(%) |
|---|---|---|---|---|---|
| 10/10/2006 | 16.6° | ASAR/IS1 | HH/VV | 12.5 m by 12.5 m | 23.3 |
| 20/10/2006 | 16.4° | ASAR/IS1 | HH/VV | 12.5 m by 12.5 m | 23.3 |
| 26/10/2006 | 20.5° | ASAR/IS2 | HH/VV | 12.5 m by 12.5 m | 21.5 |
| 08/11/2006 | 20.3° | ASAR/IS2 | HH/VV | 12.5 m by 12.5 m | 20.2 |
| 14/11/2006 | 16.7° | ASAR/IS1 | HH/VV | 12.5 m by 12.5 m | 21.8 |
| 24/11/2006 | 16.4° | ASAR/IS1 | HH/VV | 12.5 m by 12.5 m | 31 |
| 27/11/2006 | 24° | ASAR/IS2 | HH/VV | 12.5 m by 12.5 m | 25.7 |
| 19/12/2006 | 16.6° | ASAR/IS1 | HH/VV | 12.5 m by 12.5 m | 27.7 |
| depth | HH polarization | VV polarization | ||
|---|---|---|---|---|
| F | significance | F | significance | |
| 1 cm | 25.45 | 0.0023 | 11.60 | 0.014 |
| 2 cm | 26.60 | 0.0021 | 11.1 | 0.016 |
| 5 cm | 38.89 | 0.00078 | 21.1 | 0.0037 |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Le Morvan, A.; Zribi, M.; Baghdadi, N.; Chanzy, A. Soil Moisture Profile Effect on Radar Signal Measurement. Sensors 2008, 8, 256-270. https://doi.org/10.3390/s8010256
Le Morvan A, Zribi M, Baghdadi N, Chanzy A. Soil Moisture Profile Effect on Radar Signal Measurement. Sensors. 2008; 8(1):256-270. https://doi.org/10.3390/s8010256
Chicago/Turabian StyleLe Morvan, Aurélie, Mehrez Zribi, Nicolas Baghdadi, and André Chanzy. 2008. "Soil Moisture Profile Effect on Radar Signal Measurement" Sensors 8, no. 1: 256-270. https://doi.org/10.3390/s8010256
APA StyleLe Morvan, A., Zribi, M., Baghdadi, N., & Chanzy, A. (2008). Soil Moisture Profile Effect on Radar Signal Measurement. Sensors, 8(1), 256-270. https://doi.org/10.3390/s8010256




