1. Introduction
Microcantilevers (MC) are micromechanical sensors, which are typically hundreds of μm long, about tens of μm broad and approximately 1 μm thick. Applications for MCs are known primarily from the AFM/SFM field, but examples of the use of MCs as chemo- and biosensor devices have become increasingly frequent in recent years [
1-
5]. As a result, a large variety of materials and shapes have been employed in typical semiconductor etching techniques in the MC fabrication processes, providing devices with broad ranges of the principal parameters used to characterize a MC. Said principle parameters allow to calculate the differential surface stress of a MC from its radius of curvature through Stoney's
Equation (1) [
6].:
Where ν and E are Poisson's ratio and Young's modulus for the substrate, respectively and t is the thickness of the cantilever.
Depending on its spring constant, which may vary from several nN/m to μN/m, and the degree of differential surface stress caused e.g. by adsorption of molecules on one surface, a MC bends in order to balance out the exerted force. This deflection can be measured and qualifies MCs as probes for various (bio)analytes.
In such sensor applications, one side of the MC is coated with a sensing layer, e.g. DNA. Differential interaction of analytes in solution with the sensing layer and the surface of the opposing MC surface cause differential surface stress and thus MC bending. Comparison to a standard is often used to verify if the interaction of analyte and sensing layer is specific.
Microcantilevers can also be used to investigate light absorption in the IR range [
3,
7,
8]. Molecules adsorbed on the microcantilever surface absorb photons from incident infrared light and transfer the energy to the MC as heat, which causes bending due to a bimetallic effect.
MCs are also used as detectors for infrared light based on a different mechanism, which involves bending due to charge carriers in the semiconductor material. Numerous studies by Datskos
et al. describe electronic stress as the result of absorption of photons by the semiconductor material [
9,
10,
11]. Photons of sufficient energy promote electrons across the Schottky barrier to the conductivity band, thus creating free charge carriers, which induce a mechanical strain and result in bending of the cantilever.
In the case of a bimaterial microcantilever, one can observe a deflection due to differential stress Δs. The corresponding change in the radius can be described by the following
Equation (2) [
12,
13]:
In
Equation (2), the thickness of the coating and substrate is represented by t
1 and t
2, respectively. l is the length of the cantilever, E
1 and E
2 are Young's moduli of the coating and the microstructure. E* is the effective Young's modulus of the microcantilever with E* = E
1*E
2/(E
1+E
2). Δs is the change in total surface stress, which, if exclusively caused by the photon irradiation above band gap energy, equals the photo-induced stress Δs
pi.
In a semiconductor structure with an energy band-gap ε
g, Δs
pi is the change in total surface stress due to a change in charge carriers, Δn, and is described by
Equation (3) [
14], [
15],
where Δn is the charge carrier density of the photogenerated electrons, E
1 equals the Young's modulus of the coating and dε
g/dP is the pressure dependence of the energy band gap. In the case of a negative values of dε
g/dP, the photoinduced stress is of opposite sign than that of the thermal stress and will cause the semiconductor to contract. By replacing Δs in
Equation (2) with the expression for Δs
pi in
Equation (3), using z
max = l
2/(2R), and approximating the reciprocal of the radius of curvature with d
2z/dy
2,
Equation (2) becomes
Equation (4) [
16]:
A power Φ
e, resulting from absorbed photons of a wavelength λ lower than the cutoff wavelength λ
C, will produce a number density of excess charge carriers Δ
n, given by [
9]:
where η is the quantum efficiency,
h is Planck's constant,
c is the speed of light, and
τL is the lifetime of the free charge carriers in the semiconductor. The quantum efficiency η for a Schottky barrier can be described by
Equation (6) [
17]:
As developed by Datskos
et al.,
Equation (7) provides a measure of the cantilever deflection as a function of the power of the incident light at a given wavelength. Alternatively, at constant power Φ
e, measurement of z
max at different wavelengths provides an avenue to fit the C
0 parameter and the cut-off wavelength λ
C.
This paper reports on the measurement of a fast deflection of blank gold cantilevers upon irradiation with light in the UV and visible wavelength range. Such events have been previously described based on measurements of microcantilever bending in response to infrared light of fixed wavelength at various power settings. Here, the wavelength dependence as proposed by Datskos
et al. (compare
Equation (7)) was used to extrapolate the cut-off wavelength in the infrared range from measurements in the UV-VIS range. The data suggest that measurements of photo-induced immediate bending of cantilevers may be used for quality control purposes in the fabrication and sensor coating processes of cantilevers.
2. Results and Discussion
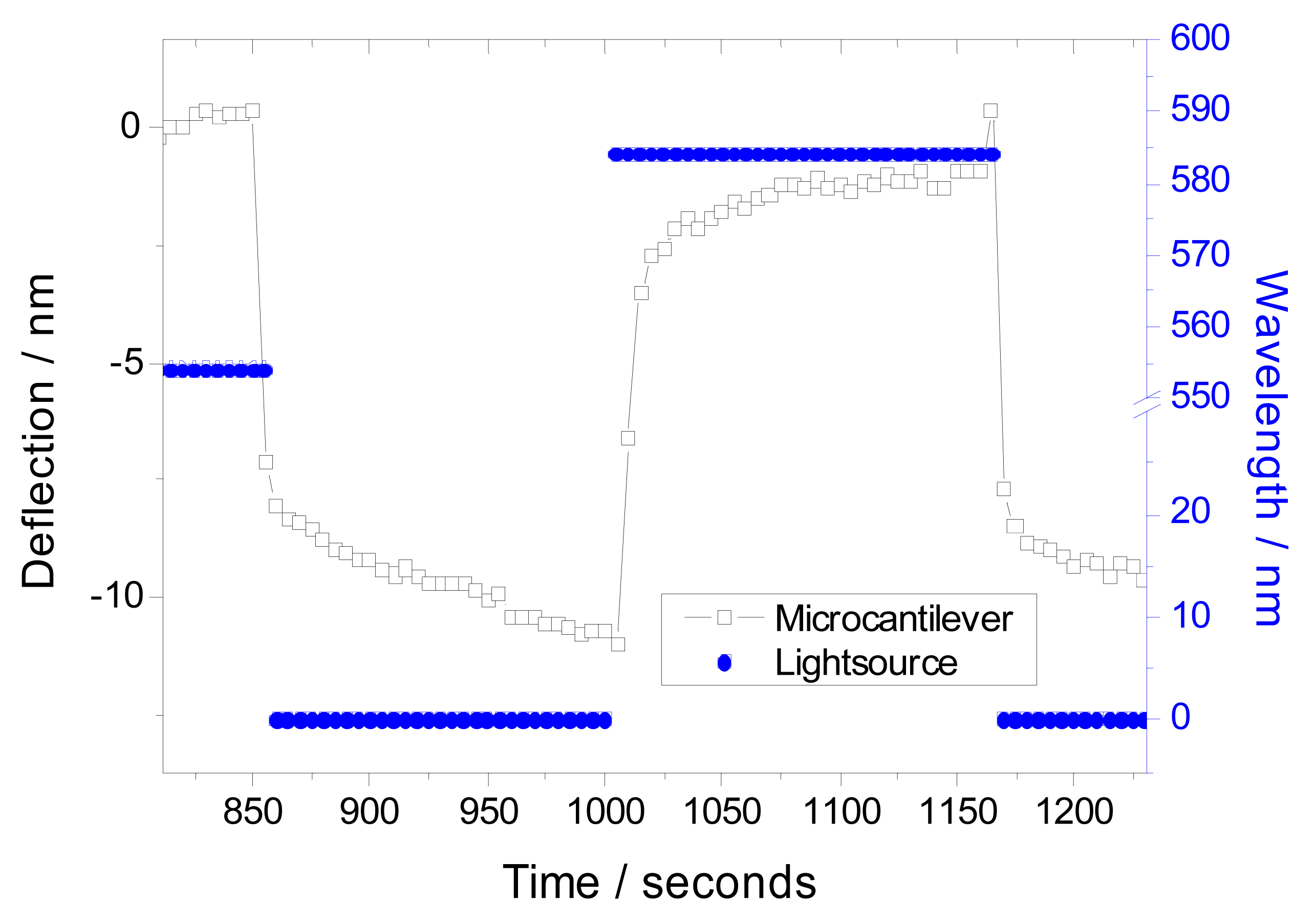
Upon irradiation of freshly cleaned, gold-coated silicon-nitride MCs with visible light with an irradiance of about 200 microwatt/cm
2, a fast MC bending in the upper single-digit nanometer range was observed. The fabry-perot interferometer setup employed here operates on a 5 sec scale, during which the interferometry beam is modulated by a piezo device [
18]. On this time scale, as shown in
Figure 1, a near instantaneous microcantilever bending, hereafter referred to as jump-bending, is followed by a slower bending with relaxation-like characteristics, which may be attributed to thermal processes, including also normal drift. Termination of irradiation results in fast reversal of the jump, again followed by a slow relaxation.
While the chosen setup does not permit fast measurements as previously conducted on Si and SiPt cantilevers irradiated with laser light at 780 and 1550 nm [
9,
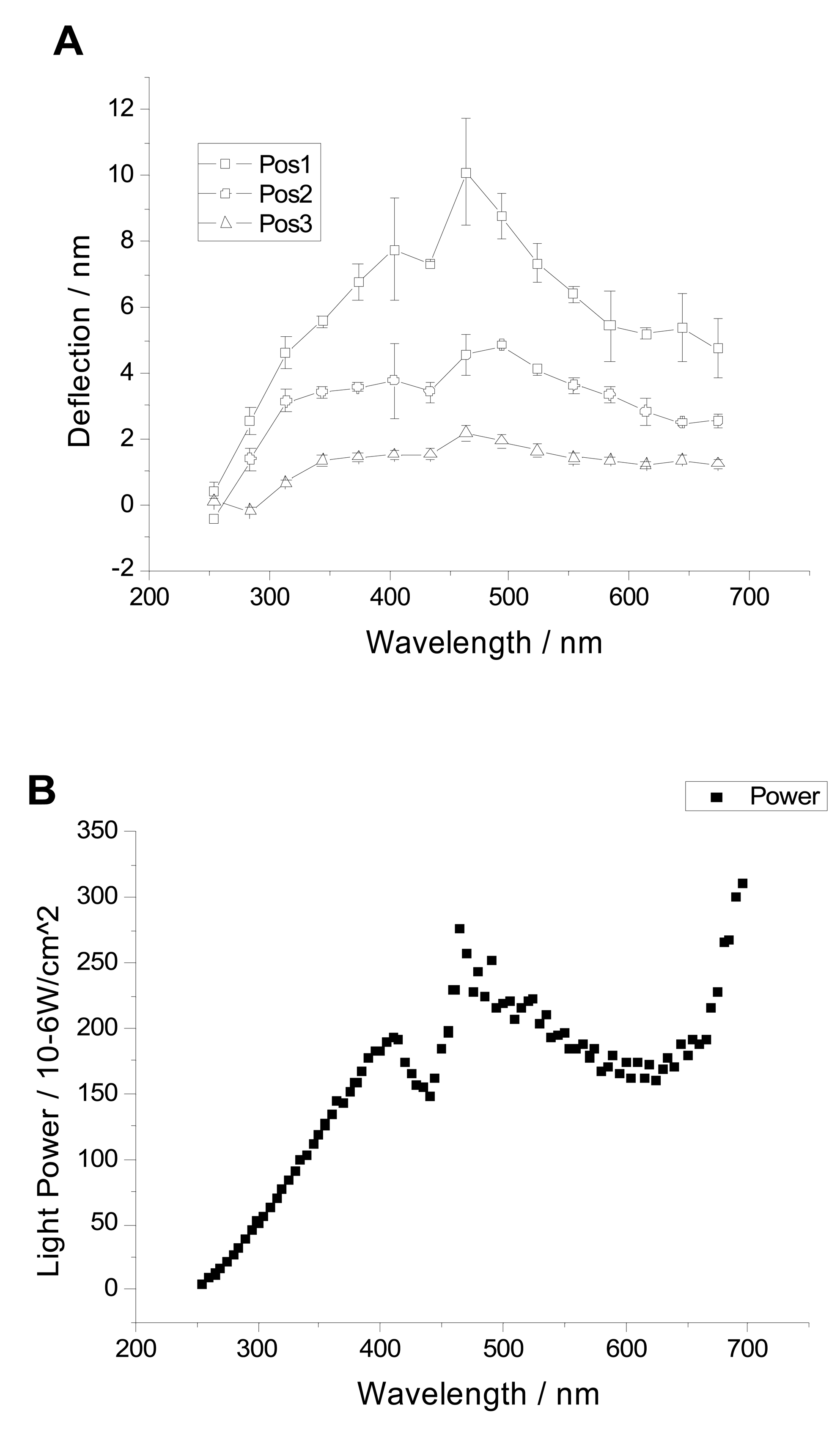
10], wavelength variations are possible across a wide range of the UV and VIS spectrum. Such a wavelength scan was conducted in 5 nm steps (bandwidth of 20 nm) and revealed a pronounced wavelength dependence of the jump-bending amplitude, which is shown in
Figure 2. These measurements were taken at the apex of the MC,
i.e. 450 μm from the support chip. To exclude that the observed signals were artifacts arising from disturbance of the interferometry beam by incident light from the UV-VIS lamp, the scan was repeated at two other positions on the cantilever beam.
The observed jump amplitudes were correspondingly smaller, as shown in
Figure 2A, where the curves denoted Pos1, Pos2, and Pos3 correspond to the distances of 450, 345, and 245 μm, respectively, from the base of the chip. The dependence of bending on the distance from the microcantilever base is a characteristic of a change in curvature and thus of a real microcantilever bending, ruling out optical artifacts related to the interferometer beam. Also, the biphasic nature of the observed deflections suggests that the fast jump-bending is due to photoelectronic stress, while thermal effects may be causative of the slower relaxation-shaped bending. Since
equation 7 clearly shows a dependence of microcantilever bending not only on the wavelength, but also on the power of the incident light, the irradiance of the employed lamp was measured both with a powermeter and the photomultiplier (PMT) of a fluorescence spectrophotometer. For the spectral range of 250-700 nm the relative readings of both methods were in good agreement. Strikingly, the corresponding plot in
Figure 2B shows an obvious resemblance to the deflection plot in
Figure 2A, in particular to the characteristic peaks around 400 nm and 460 nm. These findings provide strong experimental support for the dependence of deflection of incident light power as in
equation 7. However, approaching the cut-off limit at higher wavelengths, the power output clearly increases, while the measured deflection values drop, reflecting the wavelength-containing term in
equation 7. To eliminate the power term, the values of Pos3 in
Figure 2A were normalized to lamp power output using the values plotted in
Figure 2B, and the resulting values are plotted in
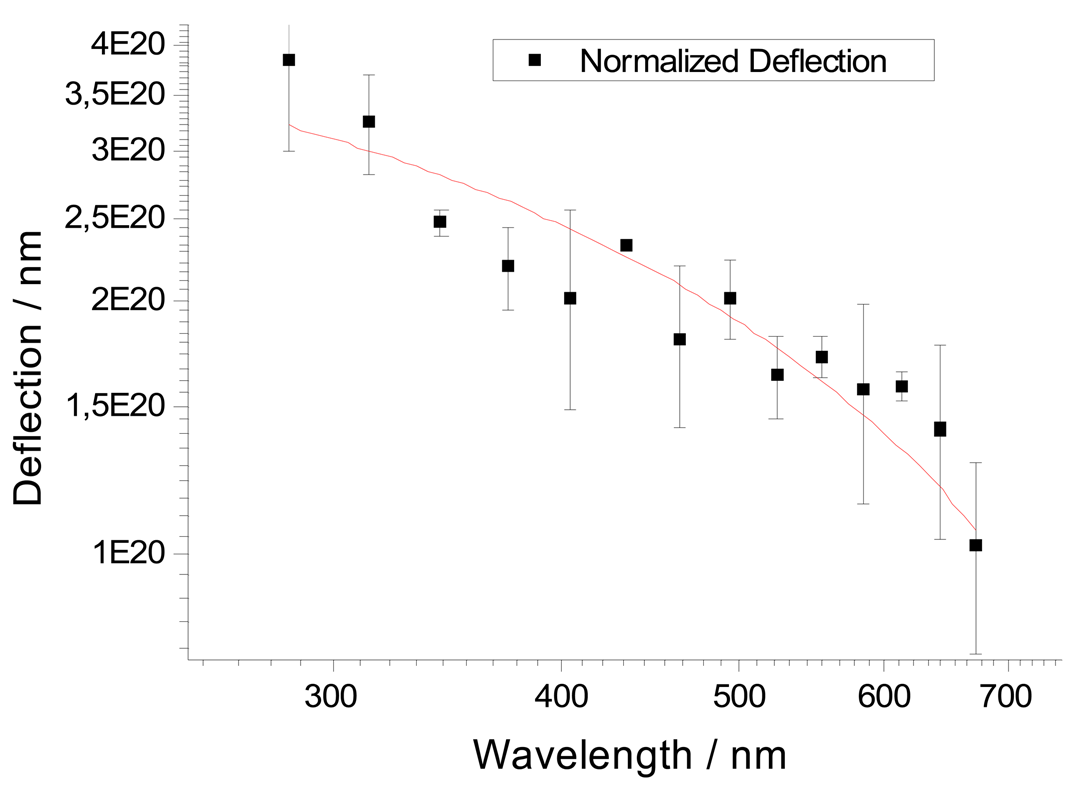
Figure 3.
After rewriting
equation 7 to
equation 8 as follows:
C
0 and λ
C were fitted from
equation 8, using values found in the literature: 78 GPa for the Young modulus of gold (E
2), 150 GPa for silicon nitride (E
1) and -2,9·10
-24 cm
3 for dε
g/dP [
9,
20]. τ
L was approximated as 10
-4 s, which is the lifetime of photo-generated free charge carriers in Si [
9]. Fitting of the values in
Figure 3 to
equation 8 yielded values of 6.3·10
19 J
-1 ± 6.1·10
18 J
-1 for C
0 and 1206 nm ± 100.0 nm for the cut-off wavelength λ
C. The latter value is in reasonable agreement with values found in the literature, ranging from 1100 nm for pure silicon cantilevers to 5500 nm for SiPt cantilever [
9,
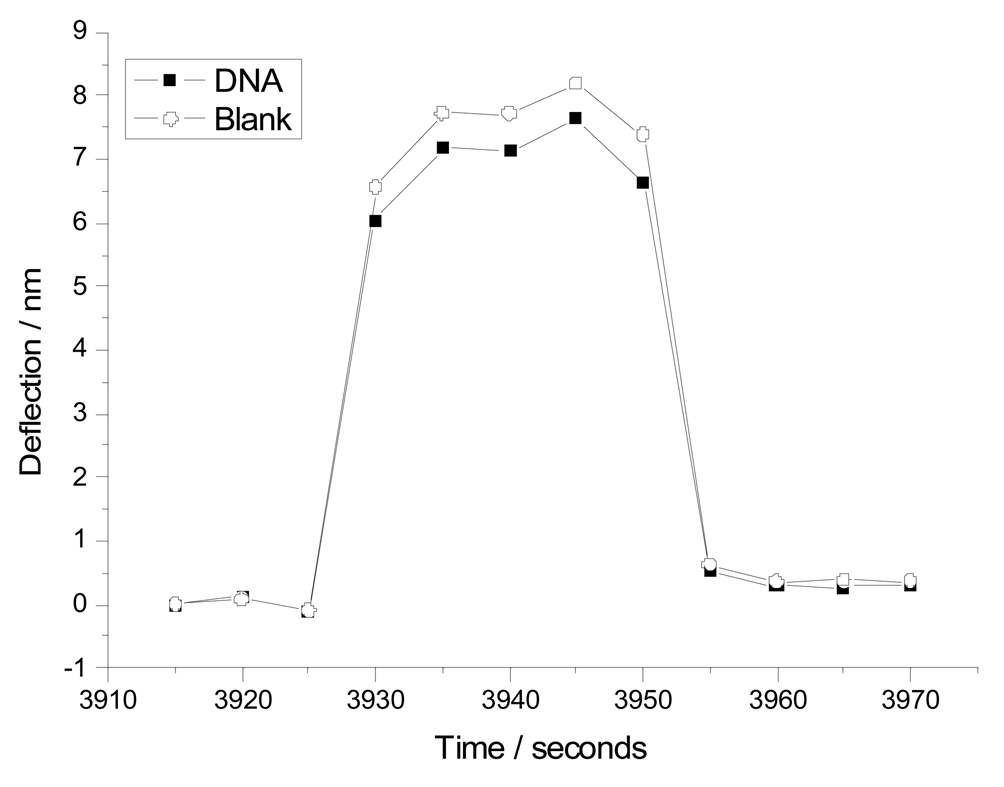
10]. Interestingly, omitting values above 650 nm or even above 600 nm from the fit routine did not significantly change the predicted cut-off wavelength (1112 nm and 1215 nm, respectively), nor were the quality parameters of the fit affected. This suggests, that a small set of measurements at selected wavelengths, ideally employing laser light of higher irradiance in the experimental setup, may be sufficient to measure and compare material properties of different microcantilevers. As an application example of the present setup, we have compared the jump-bending properties of blank gold-coated silicon-nitride cantilevers with DNA-coated MCs of the same fabric on the same support chip. Preliminary experiments, in which microcantilevers and the corresponding support chip had either been left completely untreated, or had been completely DNA coated as detailed in the Experimental Section, had shown very similar jump-type deflection values (data not shown). For a direct comparison, one of two microcantilevers on the same substrate chip was submitted to the coating procedure using glass capillaries. A typical comparative deflection measurement upon irradiation with visible light is shown in
Figure 4. While the deflection of the DNA coated MC was marginally lower than that of the uncoated reference, the difference is clearly within the range of experimental error.
Datskos
et al. [
7,
8] have reproduced the IR-spectrum of small organic molecules and large bacterial spores
via MC bending as a function of the wave number of the incident light. In these cases, the photon energy absorbed by the MC sensor coating is thought to be converted to heat, which induces MC bending through differential thermal expansion. Similarly, excitation of the aromatic nucleobases in DNA by UV-light might give rise to heat transfer and resulting MC bending. Noteworthy however, using the described setup, we were unable to detect any differential deflection between uncoated and DNA-coated MCs at 254 nm, a wavelength where nucleic acids show maximum absorption. This suggests that thermal effects resulting from photon absorption through sensor coating or the microcantilever material itself are much less pronounced than the effects of photoelectronic stress. Since the hypothetic heat transfer from the DNA to the MC surface is expected to be mediated by molecules or residues directly involved in the linkage of DNA to the surface, we have chosen an immobilization method using thiopropionic acid and aluminum chloride. The thiol moiety of thiopropionic acid binds to the gold surface while the acid functionality provides a coordination site for the lewis acid aluminum, which can then coordinate oligonucleotide without any further modifications of the DNA. This chemistry yields DNA surface coverage of about 10 fmol/mm
2, similar to other methods e.g. thiol-linker modified DNA, while providing multiple attachment points for each DNA molecule on the surface, thus maximizing the possible avenues of heat transfer. The failure to detect a thermal bending effect of the DNA coating may be exploited to verify the MC properties at different stages of a DNA sensor layer coating process. In the present case, the lack if differential bending indicates that the mechanical properties of the sensor MC have not suffered during the coating procedure in comparison to the reference MC.
In conclusion, the presented measurements of MC bending due to photoinduced stress as a response of irradiation with light from the UV-VIS range allowed experimental verification of a wavelength dependence proposed by Datskos
et al. [
10] based on measurements at a few selected wavelengths in the IR-spectrum, and provides an alternative experimental avenue to the determination of the cut-off wavelength, above which the photon energy is insufficient to promote electrons across the Schottky barrier.
Our experimental observation that visible light causes measurable and non negligible deflection of cantilevers should promote further research into the influence of ambient light on experimental noise in any type of microcantilever application, including AFM as well as sensor applications. Although such behavior has, in principle, been predicted by the equations of Datskos, they have not, to this point, been experimentally verified.
Light induced jump-type deflection is fast, reversible, and non-invasive. In combination with new interferometry-based imaging techniques of microcantilever bending [
21], this may provide a very fast and efficient means for comparing micromechanical properties such as Young's moduli and/or spring constants of an entire set of microcantilevers
e.g. on the same waver. Further, our data suggest that neither the jump-bending characteristics nor other micromechanical properties of microcantilevers are significantly affected by sensor coatings like DNA oligomers, indicating yet another potential application of this effect
e.g. in quality control of biosensors.
3. Experimental Section
Gold-coated silicon nitride (Si3N4) microcantilevers were purchased from Surface Imaging Systems (Herzogenrath, Germany). Each chip was covered with a 30 nm thick gold layer and contained two cantilevers separated by a pitch of 250 μm. Each cantilever was 500 μm long, 100 μm broad and 0.5 μm thick. Prior to coating or blank measurements, the cantilevers were submerged in pure ethanol for at least 10 minutes and cleaned from organic contaminations under a UV lamp for 10 minutes. The cantilevers were then again submerged in ethanol for at least 10 minutes, rinsed with Millipore water and mounted for deflection measurement.
For certain experiments, DNA was immobilized on the microcantilever gold surface. To this end, the cantilever was first treated with a 1 mM solution of thiopropionic acid in ethanol, followed by washing with ethanol. Subsequently, the functionalized cantilever was incubated in an aqueous solution of 1 mM aluminum trichloride. This treatment is reported to immobilize aluminum ions by coordination to the carboxyl groups of thiopropionic acid. Free coordination sites of the aluminum will then immobilize DNA strands in the subsequent incubation of the cantilever in a 1 μM DNA solution for one hour [
18]. The employed DNA oligomer of the sequence 5′– GGATCCACCTGGAGGAAGGT–3′ was from IBA, Göttingen, Germany. Immobilization efficiency of this procedure was determined by measuring the amount of
32P-labelled DNA on gold-coated Si
3N
4 wavers against a dilution series of [γ-
32P]-ATP (GE Healthcare, Freiburg, Germany) by phosphor-imaging on a Typhoon 9400 (GE Healthcare). Under the described conditions, about 10 fmol of DNA oligomer per mm
2 were immobilized. Omission of treatment with either thiopropionic acid or aluminum trichloride resulted in at least 100-fold lower activity on the waver.
The deflection was measured with a Fabry-Perot interferometer setup (SIS-GmbH, Herzogenrath, Germany) equipped with a 5 mW aluminum- gallium- arsenic semiconductor laser diode with a wavelength of 780 nm [
19]. The system was flooded with argon gas and sealed for the duration of the experiment to prevent formation of ozone. The microcantilever experiment was started after the system was at equilibrium in the temperature range of 25 +/- 0.01 C.
Irradiation was performed with the excitation element of a JASCO fluorescence spectrophotometer integrated in a MOS-250 stopped flow from BioLogic (Claix, France). The wavelength of the incident light was varied from 230 to 700 nm with a bandwidth of 20 nm. Light from a Hamamatsu lamp (150 W) was routed to the cantilever by means of a glass fiber cable, the output of which was fixed perpendicularly to the cantilever at a distance of 2 cm. The power output from the glass fiber cable was measured with an ORION/PD powermeter (Ophir, North Logan, Utah, USA) at 5 nm intervals. The built-in PMT of a wavelength-calibrated JASCO fluorescence spectrometer was used to compare power output at different wavelength settings. At wavelengths 230-700 nm, the relative intensities of power output determined by the powermeter on one hand and by the PMT on the other hand, were in good agreement. Measurements above 700 nm were not included in the analysis, because the measurements of relative power output diverged between the two methods.