1. Introduction
Noises usually play a negative role on the detection of useful signals, and faint signal detection is a challenge work, especially detecting faint signals submerged in strong noise. Traditional filter is used to separate the signals of interest and their noise by restraining noises rather than using of them. For example, Fourier transforms and Wavelet transforms are the widely used idea which performs the filtering operation by projecting the signal into another space, then transforms back into the original space. But the approaches from this idea are effective only when the signals and the noise are not strongly mixed with each other in frequency spectrum. The phase-locked loop (PLL) is a typical approach to detect the faint signals by coherency modulating and demodulating. However, there is the limitation to this approach that is required to provide the reference signal with the same frequency as the detected signal. Other approaches are the application of statistical ideas to filtering problems, such as Kalman filter can make use of imprecise data on a linear (or nearly linear) system with Gaussian errors to continuously update the best estimate of the system's current state[
1]. Least mean squares (LMS) filter is the adaptive filter which adjusts its coefficients to minimize the mean-square error between its output and that of an unknown system[
2]. Another adaptive filter to minimize the least squares criterion is the recursive least squares (RLS) filter [
3] and the QR-RLS filter[
4] which perform QR decomposition and RLS algorithm. These adaptive filters can provide satisfactory solutions to linear or nonlinear problems. However, they focus on model description, optimal process, algorithm convergence and decreasing complexity. The properties of the signals and their noises are not used as the participator to improving filtering process. Especially, the noises mixed in the signals are always considered as the boring and unvalued factor in these approaches. In this paper, different from this traditional idea, we will utilize the noises to enhance the intensity of signals by nonlinear energy transition mechanism. In addition, there is a drawback among these filters that the signals of interest will inevitably be weakened in the process of suppressing noises, especially when the frequencies of noises and faint signals are very close.
However, noises are not always suppressed passively. They can be utilized to suppress themselves. In some systems increasing the amount of ambient noise actually enhances (up to a certain point) the SNR through a complicated nonlinear cooperation between the system and detector. This effect, known to operate in neurons [
5], lasers [
6], and analogue electrical circuits [
7], is called SR, which is a counter intuitive nonlinear phenomenon wherein transmission or detection of a signal can be enhanced by addition of a non-zero level noise [
8-
10]. The noise fluctuations might be stochastic (meaning totally random) but the detection of a desired signal can be maximized by tuning the noise.
For SR, most of the studies were carried out using a dynamical system with bistability, modelled by a double well potential. Here SR is realised due to the shuttling between the two stable states at the frequency of the subthreshold signal (i.e. faint signal) with the help of noise. When the signal (faint signal with noises) is applied into a SR system, the potential barrier height of bistable system is adjusted to meet the condition of SR phenomenon. If SR occurs, the output spectrum of SR system would produce a sharp peak at the faint signal frequency superimposed on a smooth background spectrum [
11]. This means that the output SNR is improved and faint signal is enhanced. Naturally, the adjusting process can be used as a useful procedure to process the receiving signal from the sensor or sensor arrays which need enhance the sensitivity in noisy environment.
This paper discusses how to use SR to detect faint signals with strong noises. Based on the bistable system, we combine SR phenomenon and Fast Fourier Transform (FFT) spectrum analysis together to detect faint signal mixed with noises. Note that the approach presented here is different from the aforesaid adaptive filter in design idea. Though those adaptive filters are in reality a non-linear system and can solve the nonlinear filtering problem, the nonlinear system need be translated into the linear system by various skills in the actual application process. The approach in this paper uses directly the nonlinear mechanism to construct filter and avoids the linearization process. Finally, an adaptive filtering procedure is added to the detection scheme to provide the possibility of application. The procedure resembles an executable program and its performance only depends on the adjustment strategy and evaluation index for SR from the angle of real application. In this sense, our approach is not a well-defined numerical algorithm indeed and is only an application scheme.
3. Adaptive Filtering Procedure by SR
For measurement of real signals, the pre-knowledge about signals is often lack; hence the above-mentioned SR system can not be directly used. The practicable approach requires that the SR can adapt different input signals. Therefore, an adaptive stochastic resonance scheme based on bistable system is presented as follows.
We adopt the power spectrum as the evaluation tool of SR. Here the power spectrum can be obtained by the fast Fourier transform (FFT). Furthermore, we introduce the adaptive filtering scheme to realize signal processing automatically. The key of the scheme is how to adjust the barrier height to satisfy the optimal condition of SR in the presence of any input. A simple idea is to estimate the shift and rise of the power spectrum peak when the barrier height is modulated. If the spectrum peak at a certain frequency is significant relative to the rest frequency components, then we can conclude that SR occurs and the detected signal takes on this frequency feature.
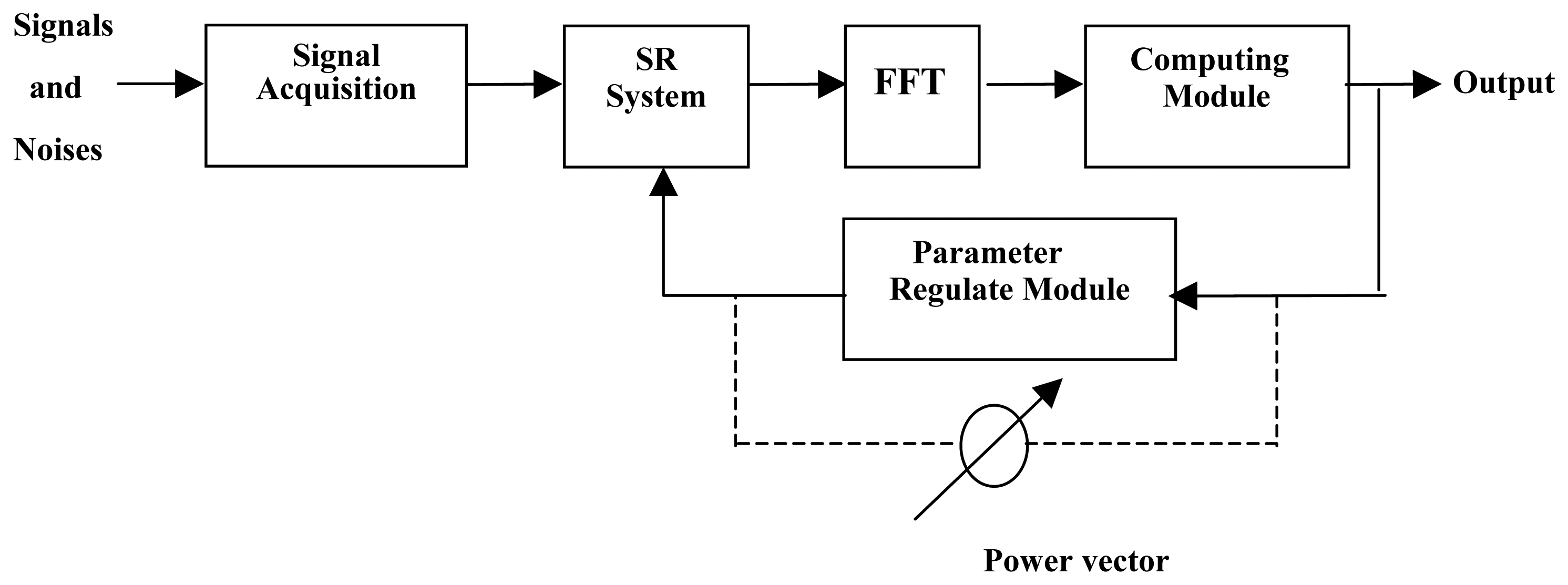
Fig.3 shows the basic scheme which is composed of the adaptive filtering system. Firstly, the original signals from the transducer are applied to a SR system through the acquisition module where the preprocessing such as amplifying and filtering are completed. Then, the processed signals enter the adaptive part. In this part, SR system module can be represented by function (1). FFT module plays a role in evaluating the spectrum features of the output from SR system. In computing module, these spectrum features are used as the variable to estimate optimal condition. According to computing results, a regulating module is introduced to execute the feedback adjustment. On the collective effect of these modules, the parameter of SR system is gradually adjusted to the appropriate barrier potential and the critical value. When a system satisfies the condition of SR, the output contains the information of the detected signal.
The signal noise ratio (SNR) is defined as the ratio of the spectrum value at a frequency
fi (the frequency feature of input signal) to the mean spectrum value of the entire frequency range, respectively. It can be written as follows:
where
S(
fi) represents the spectrum of input signal, and
mean[
S(
f1), …,
S(
fi), ….] represents the mean spectrum value. According to SR definition, a maximum value of
SNR will occurs with the increase of noise intensity in bistable system. This can be considered as the optimal condition for computing module. Note that SR is produced by adjusting the parameters of SR system in computing module since the input signal and noise is fixed. Though the procedure is different from the SR via changing the noise, the essential mechanism is uniform.
Our approach is not a well-defined numerical algorithm indeed and does not exist cost function or transfer function, although it resembles the control algorithm in the form of block diagram. Optimal condition is set up not according to mathematical deduction but according to phyical property of SR systmen. Therefore, we present only an application scheme as follow.
For the given input signal, we will present an operable procedure to execute the adjustment scheme. During this procedure, the optimal condition will be transformed into two in
equation (5) and
(6). If the spectrum features of detected signal satisfies the in
equation (5) and
(6), then it will be concluded that the signal is optimally detected by SR. The frequency component near the maximum value of SNR is estimated by the in
equation (5).Further, the estimation precision is determined by the in
equation (6). This inequation restricts the possible spectrum range and feature of the unknown signal. The parameter
θ at the right of in
equation (5) denotes the relative threshold which evaluates the significance of a certain frequency in power spectrum. Larger the relative threshold is, more precise the estimation value is.
The estimation value for a certain frequency is expressed by the parameters
Afi and
Amean . The former represents the amplitude at a certain frequency
fi and the latter is the mean amplitude of all frequency in power spectrum. The parameter
fi is a frequency of power spectrum,
i=0, 1,…, n. The parameter
Cfi in in
equation (6) denotes the amount of the case that estimation value for a frequency is greater than or equal
θ at a series of power spectrums. Suppose
j the values of power spectrum to be taken,
Cfi may be a value range from 0 to
j. The parameter
K represents the amount of the different frequencies satisfying in
equation (5). Therefore,
P(
f =
fi ) represents the probability that the significant frequency
fi occurs relative to other frequency.
The detail of the procedure is described as follows:
- Step1
For conveniently regulating the SR system, we change one of parameters in the system and fix the rest parameters. It is assumed that the parameter
b in
Equation (3) is constant. For example, it is taken as 1. Correspondingly, we can adjust the potential barrier only by parameter
a.
We take parameter a as different values and observe whether SR system with the corresponding parameter a induces the response. If there are responses of SR system for m parameter a, then we will obtain m spectrum values (e.g., S1…Sm) by FFT module. Obviously, these spectrums have the same frequency range and resolution. Assuming each spectrum consists of n points, then the values of frequency can be taken as f0 , f1 ,…, fn.
- Step2
Choose the appropriate threshold
θ. We can conclude from the in
equation (5) that if the inequation is meaningful then threshold will be always less than one. We can also find the larger threshold can induce higher estimation precision. Therefore, we can restrict the threshold in a certain range. Here we set the initial value
θ = 0.95 .
- Step3
For any frequency
fi (
i =0,1, …,n) corresponding to a certain parameter
a, we record the total number of which frequency amplitude satisfy in
equation (5) at spectrum
S1,
S2, …,
Sm, and obtain the corresponding
Cfi (i=0,1 … n) and
K according to in
equation (6).
- Step 4
Find out the parameter
fi satisfying in
equation (6) and continue the next step. If
fi does not exist, then the parameter
θ will be decreased. Return the step 3.
- Step5
If the threshold θ is less than or equal the given lower limit (e.g., 0.5), then the other parameter a and its spectrum values will be considered. Return step2 .
- Step6
For the parameter a, if the above two inequation is meaningful at limiting threshold range, we will conclude that the output reflect the feature of input signal via the SR effect. Recording the output and ending the procedure.
4. Fault Test by Audio Sensor
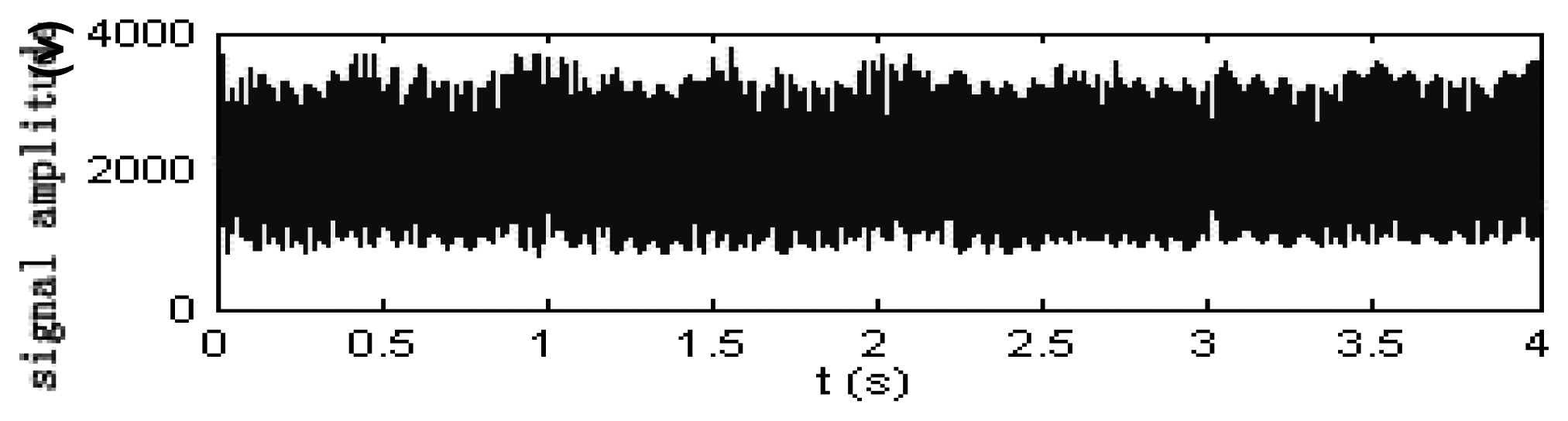
Figure 4 shows the audio signal from a power supply with fault, which is collected and transformed into electrical signal by the audio sensor. Here we use a electret test microphone as the audio sensor. For this microphone, frequency response ranges from 10Hz to 5000Hz and standard sensitivity is 25mV/Pa. It can be used as noise monitor for measure of ambient noise machine noise, vehicle noise, electrical machinery noise, architecture acoustics and electroacoustics.
In normal work status, a power supply emits the audio signal with range of frequency from 0 to 4000Hz. But the frequencies of fault signals, which directly relates with the degree of fault, are about tens of hertz. Obviously, “noise” is mixed with the fault signal to be detected.
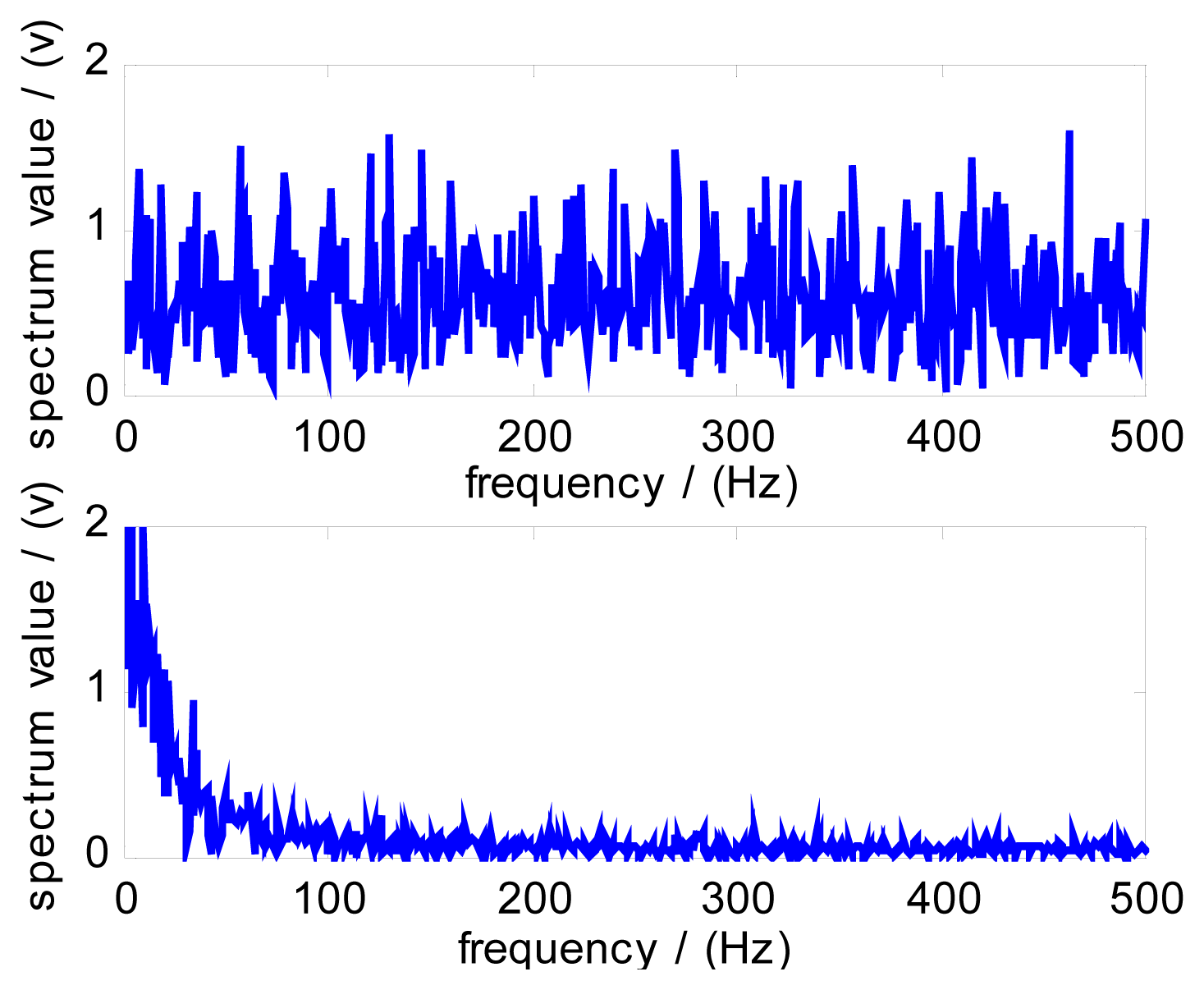
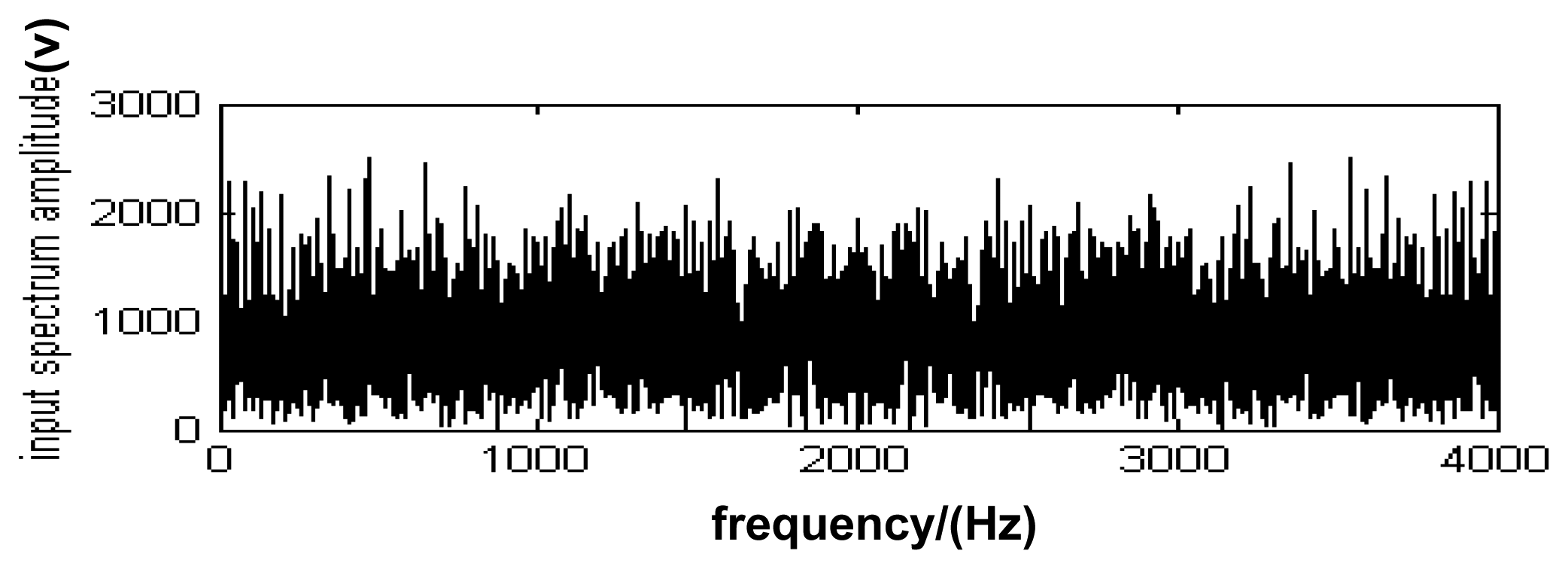
Fig. 5 shows the power spectrum of the signal in
Fig.4. It can be found that the information relevant to fault cannot be directly distinguished by the power spectrum (as shown in
Fig.5). In order to improve the sensitivity of fault detection, the adaptive SR approach has to be used to process the detected signal from audio sensor.
According to the abovementioned procedure, the fault signal with noise is considered as the input of the system in
Fig.3. The parameter b is taken as the fixed value 1 and
θ is equal to 0.9. The parameter
a is changed from 0.1 to 1 by the step length 0.1, so the
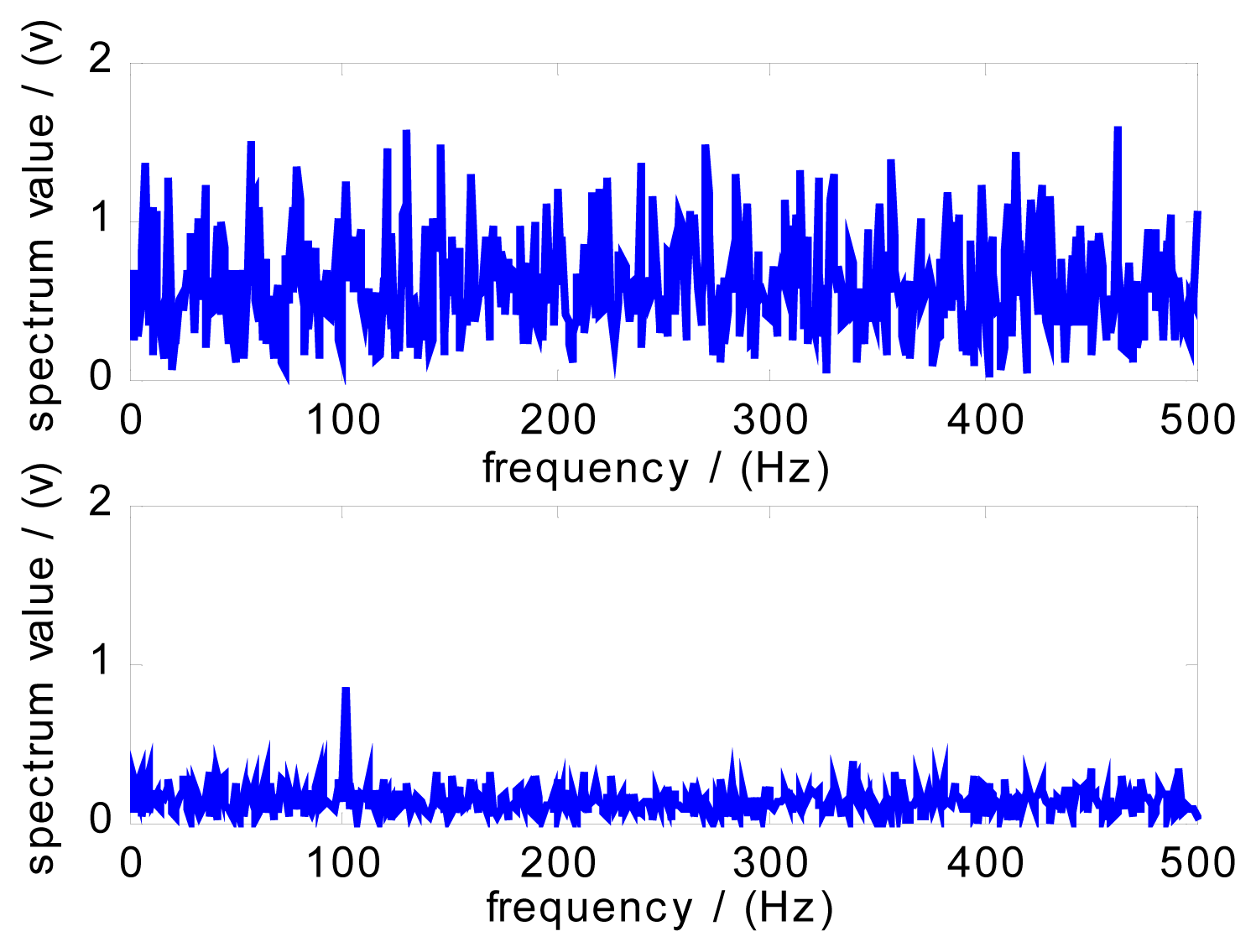
m is set as 10. Because the sample frequency is 500Hz, there are 2000 sample points during the signal of 4 seconds. Correspondingly, n is taken as 2000. The simulation of algorithm is performed by the simulation tool of Matlab software. After adjusting the parameter, the optimal SR can be obtained.
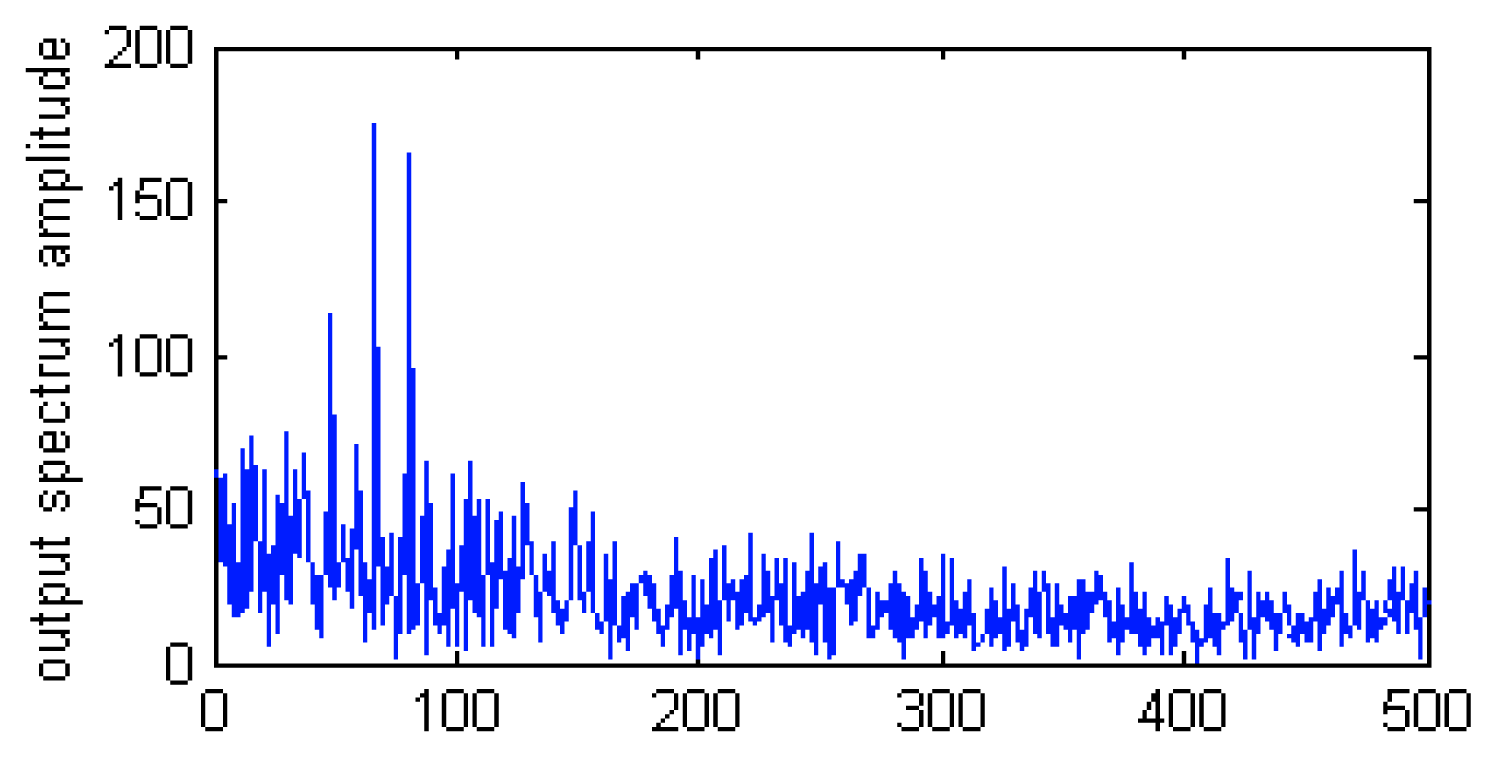
Fig.6 shows the power spectrum of the corresponding output when SR occurs. The signals with frequency component 65Hz and 80Hz can be clearly recognize. According to experience, these signals belong to the fault information.