Electrochemical characterization and electron transfer dynamics at SWCNT modified gold and glassy carbon electrodes
Single walled carbon nanotubes may be deposited either as random dispersions or ordered arrays. We expect that the redox response exhibited by carbon nanotube modified electrodes will depend to a large extent on the manner in which the nanotubes are aligned with respect to the support electrode surface. The oxidation of ferrocyanide to ferricyanide in aqueous solution has served as a benchmark reaction in fundamental electrochemistry since the Fe(CN)64-/3- reaction involves the transfer of a single electron and exhibits close to ideal quasi-reversible outer sphere kinetic behaviour, especially at electrodes such as carbon where there is minimum bonding (or adsorption) interaction between the electrode material and the reactant (and indeed spectator) ions in solution.
The cyclic voltammetric response profile for a quasi-reversible electron transfer reaction has been the subject of quantitative mathematical analysis, especially in a classic paper by Nicholson [
14]. The net shape of the voltammetric curves have been shown to depend on a kinetic parameter ψ which is given by the expression :
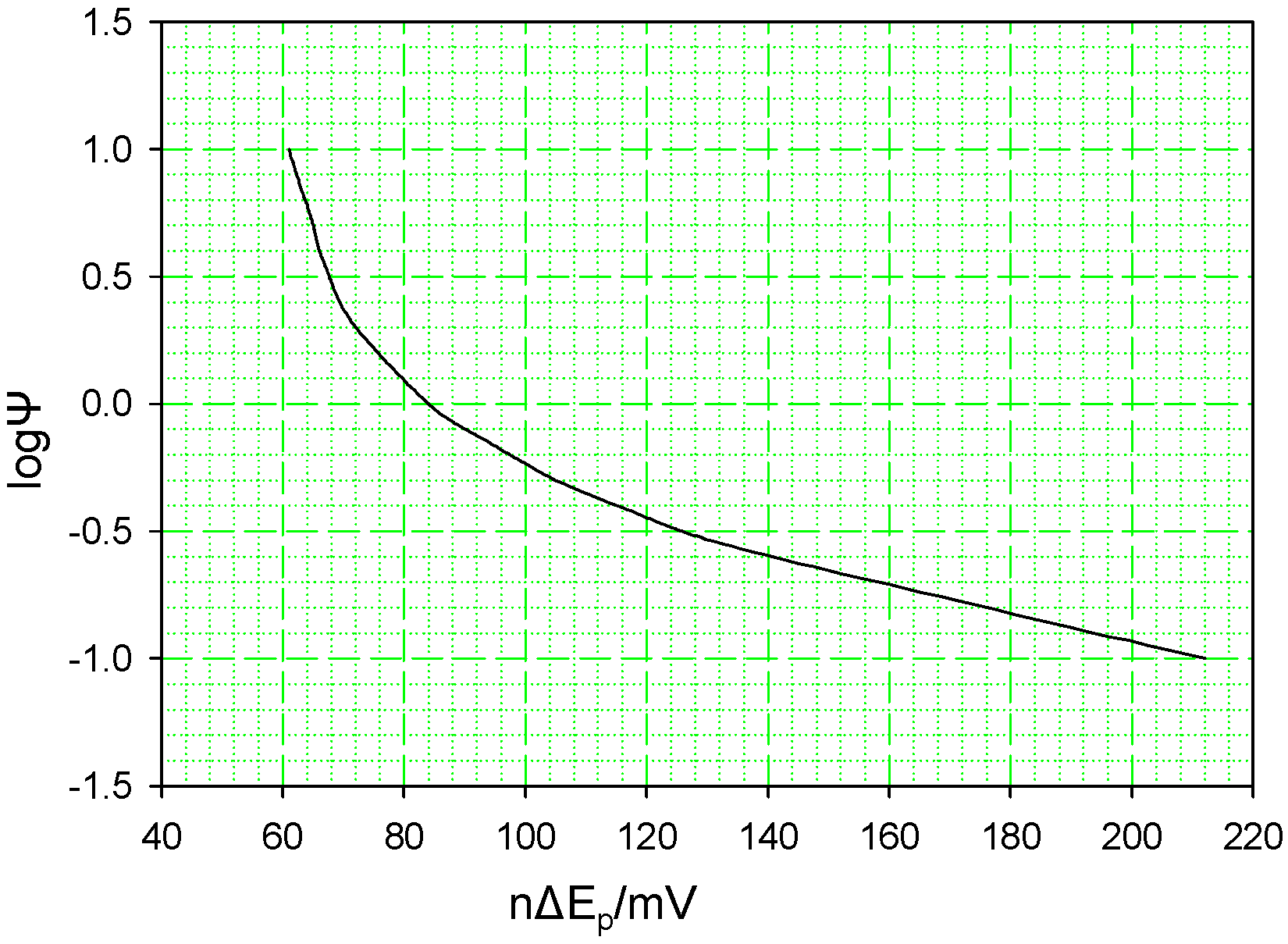
where we have assumed for simplicity that the diffusion coefficient for the oxidized (O) and reduced (R) forms of the solution phase probe redox couple are equal and that the transfer coefficient α is ½. A numerical analysis of the diffusion boundary value problem for cyclic voltammetry has established a quantitative analysis of the relationship between the kinetic parameter Ψ and the voltammetric peak separation ΔE
p. This is illustrated as a working curve in
figure 2 below. For nΔE
p ≥ 140 mV this plot is essentially linear, and Ψ may be calculated by using the following equation:
Figure 2.
The variation of the kinetic parameter Ψ with voltammetric peak separation .
Figure 2.
The variation of the kinetic parameter Ψ with voltammetric peak separation .
Hence it is straightforward to determine the standard heterogeneous rate constant k
0 for an interfacial electron transfer reaction, by noting the voltammetric peak separation at a given scan rate ν, and using the working curve outlined in
figure 1 to determine the corresponding value of the parameter Ψ. The heterogeneous rate constant k
0 may then be determined provided that the diffusion coefficient D of the redox reactant species is known. We note that the smaller the peak separation ΔE
p observed, the larger is the rate constant k
0 , and consequently the more facile are the ET kinetics.
It has been established that the cyclic voltammetry response for the Fe(CN)64-/3- probe reaction at the basal plane of highly ordered pyrolytic graphite (HOPG) is quasi-reversible with very large peak potential separation ΔEp typically greater than 700mV (although with surface treatment these values can be reduced to ca. 100 mV), indicative of very sluggish electron transfer kinetics. On graphite edge planes, interfacial Electron transfer occurs much more rapidly with ΔEp values of 70 mV (recorded at the same sweep rate) being typical.
In our experiments, cyclic voltammetry for ferricyanide reduction was performed using 1 mM ferricyanide reagent in 50 mM KCl / 50mM phosphate buffer solution (pH 7). The scan rates employed (the latter determining the range of experimental timescales) were in the range 5 – 1000 mVs-1.
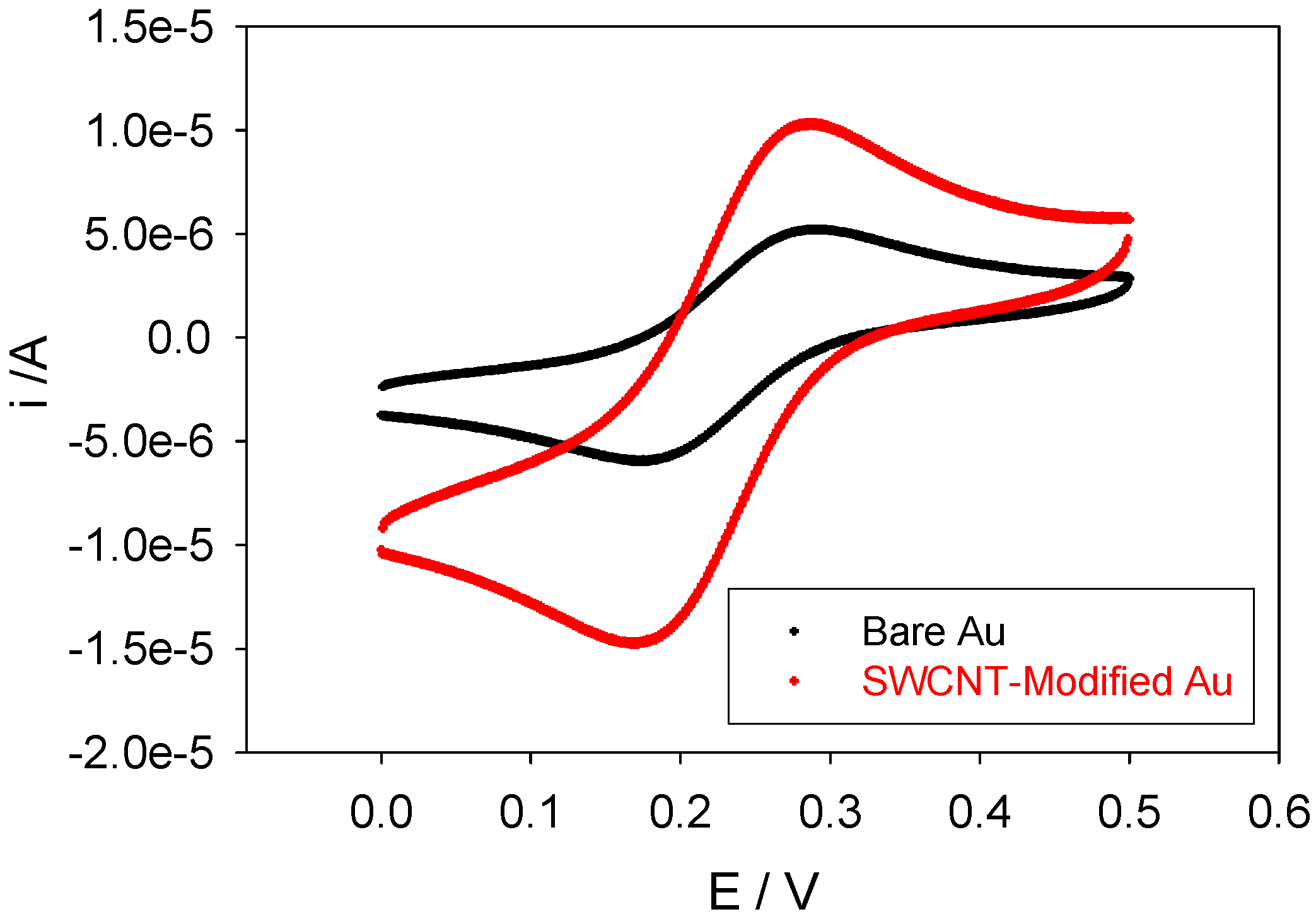
In
figure 3 we outline a comparison between voltammograms obtained using a bare and SWCNT-modified gold working electrodes. Clearly, the SWCNT-modified electrode gives rise to larger ferricyanide reduction peak currents. It is immediately obvious that the peak current for the reduction of ferrocyanide ion is greater for the SWCNT modified electrode than for the unmodified gold electrode. This probably reflects the greater surface area of the nanotube modified electrode. It may also be due to the increased rate of diffusive mass transport of the ferrocyanide reactant to the nanotube surface (the latter being considered as a supported nanoelectrode).
Figure 3.
Comparison between voltammograms obtained using a bare and SWCNT-modified gold working electrode. The scan rate employed was 100 mVs-1. The electrolyte used was 1mM potassium ferricyanide in 50 mM KCl in 50 mM phosphate buffer (pH 7).
Figure 3.
Comparison between voltammograms obtained using a bare and SWCNT-modified gold working electrode. The scan rate employed was 100 mVs-1. The electrolyte used was 1mM potassium ferricyanide in 50 mM KCl in 50 mM phosphate buffer (pH 7).
The peak heights recorded from the cyclic voltammogram for oxidation and reduction should vary in a linear manner with the square root of the scan rate according to the Randles-Sevcik (RS) equation:
Here, n is the number of electrons lost or gained in the redox process (for this system n = 1), A is the surface area of the electrode in m
2 (for a macroelectrode of radius 1mm, A = 3.14 × 10
-6 m
2), c
∞ is the concentration of the electroactive species (molm
-3) and ν is the sweep rate (Vs
-1).
Figure 4(a) shows a comparison between Randles-Sevcik plots obtained for the reduction of ferricyanide using a bare and SWCNT-modified Au working electrode.
Figure 4(b) shows the corresponding comparison for the oxidation of ferrocyanide. In both cases we note that the Randles-Sevcik slopes for the nanotube modified gold surface are greater than the same parameter recorded for the unmodified electrode. In the case of ferricyanide reduction, the RS slopes were 2.0 × 10
-5 (r
2 = 0.9991) and 4.5 × 10
-5 (r
2 = 0.9997) As
1/2V
-1/2 for the bare and SWCNT-modified electrodes respectively. Using the RS equation, the slope of these plots (m
R-S) is related to the diffusion coefficient according to:
. Since the slope is proportional (for a given bulk concentration of reactant species) both to the surface area of the working electrode and to the diffusion coefficient of the electroactive reactant, it is clear that the larger slope found for the SWCNT-modified electrode was due to increased surface area, since the diffusion coefficient is a parameter characteristic of the solution phase reactant and not the nature of the electrode.
Figure 4.
Randles-Sevcik Plots for (a) ferricyanide reduction and (b) ferrocyanide oxidation at bare and SWCNT modified gold electrodes. The upper curve denotes the SWCNT modified electrode data in each case.
Figure 4.
Randles-Sevcik Plots for (a) ferricyanide reduction and (b) ferrocyanide oxidation at bare and SWCNT modified gold electrodes. The upper curve denotes the SWCNT modified electrode data in each case.
The bare Au data were used to calculate the diffusion coefficients for the oxidized [Fe(CN)6]2- and reduced [Fe(CN)6]3- species. From the plots, the respective Randles-Sevcik slope values are mO = 1.9 × 10-5 and mR = 2.0 × 10-5 As1/2V-1/2 respectively. These were used to calculate the corresponding diffusion coefficients DO = 5.1 × 10-6 and DR = 5.6 × 10-6 cm2s-1. The diffusion coefficients for ferrocyanide and ferricyanide are approximately equal. This is to be expected since both complex ions are approximately the same size , are both octahedral, and do not differ very much in solvated environment. In further experiments we have shown that linear RS behaviour is not observed at higher sweep rates which suggests that the ET reaction becomes quasi-reversible under such conditions.
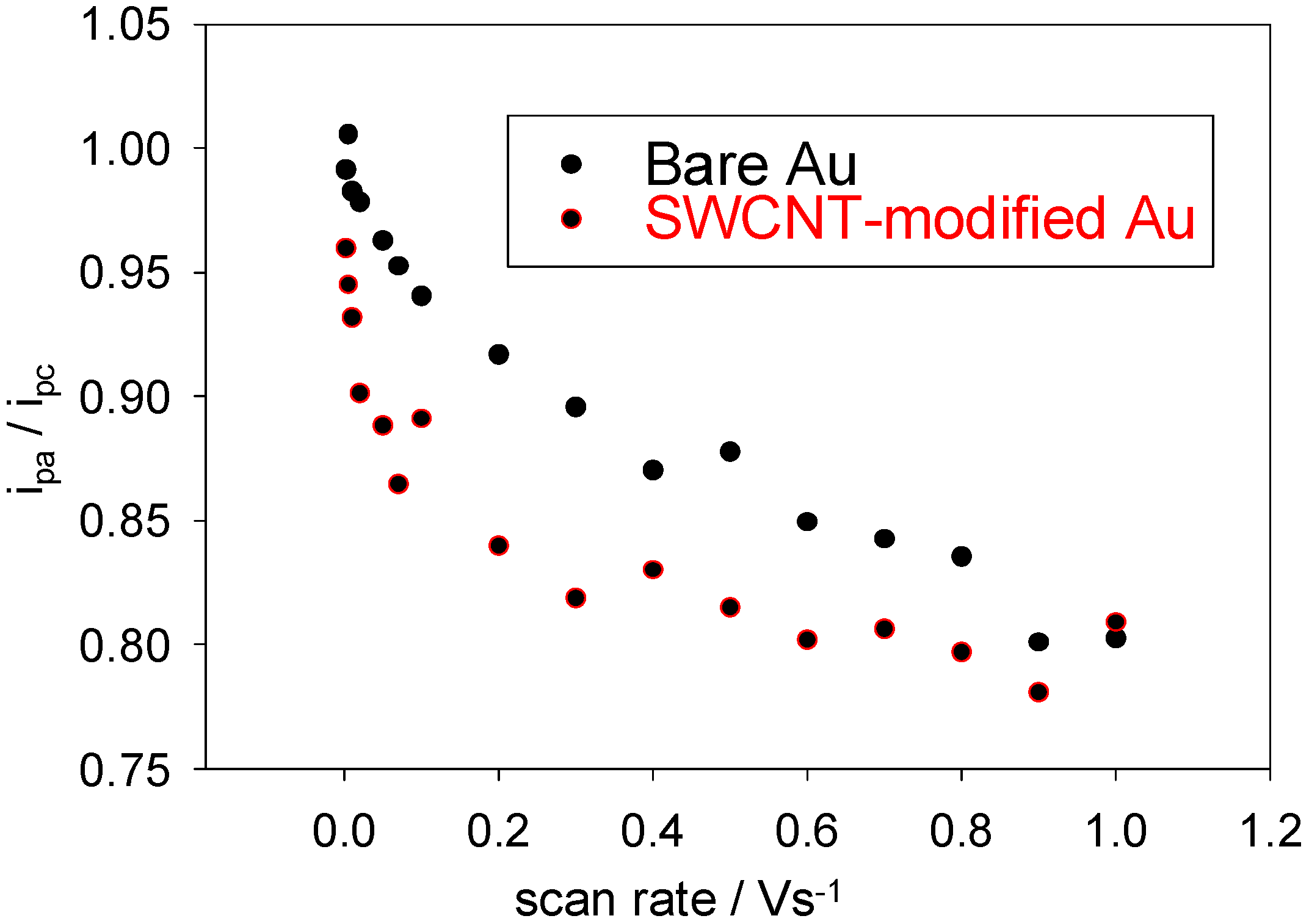
Further evidence for the decrease in reversibility at higher sweep rates is provided by the variation of the oxidation to reduction peak ratio i
pa / i
pc with sweep rate ν (see
Figure 5). For a perfectly reversible system, this number should always be unity. As can be seen, for both the bare and modified working electrodes, the observed ratio departs steadily from this value as the scan rate increases. Clearly, the ET is not reversible on the smaller timescales (larger sweep rates). For reversible systems, the ET rates at all potentials are significantly greater than the rate of mass transport and therefore Nernstian equilibrium is always maintained at the electrode surface. At low sweep rates, the ET rate may be greater than the rate of mass transport and a reversible scan may be obtained, even if the process is irreversible.
Figure 5.
The variation of the ratio of the anodic to the cathodic peak currents with scan rate for a bare and SWCNT-modified Au working electrode. The electrolyte used was a 1mM solution of ferricyanide in 50 mM KCl in a 50 mM PBS (pH 7).
Figure 5.
The variation of the ratio of the anodic to the cathodic peak currents with scan rate for a bare and SWCNT-modified Au working electrode. The electrolyte used was a 1mM solution of ferricyanide in 50 mM KCl in a 50 mM PBS (pH 7).
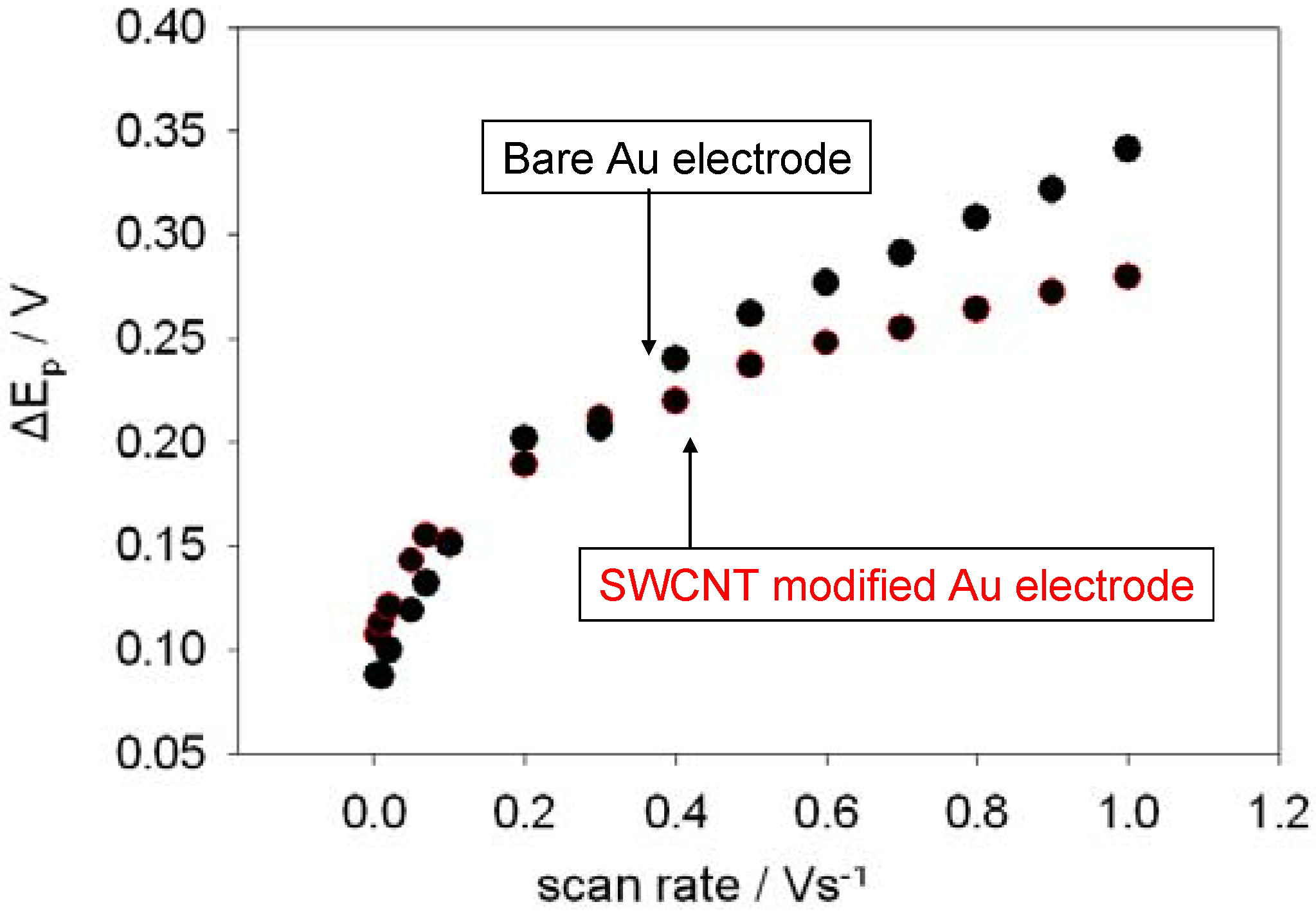
Shown below in
figure 6 is a comparison between the variation of peak separation with scan rate for a bare and a SWCNT-modified gold electrode. It is clear from the plot that the SWCNT modified electrode exhibits more facile ET kinetics compared with the unmodified gold surface at higher scan rates since the peak separation values are considerably smaller under these conditions. However, littler difference was observed at lower scan rates. The ΔE
P data over a wide range of sweep rates was analysed using the theory discussed previously in conjunction with the working curve presented in
figure 3 .This protocol was used to calculate the Ψ parameter appropriate for a given peak separation value and scan rate and hence to evaluate heterogeneous ET rate constants for each scan rate used. The average k
0 values were found to be (6.2 ± 1.4) × 10
-3 and (10.2 ± 5.1) × 10
-3 cms
-1 for the bare and SWCNT-modified Au electrodes respectively. We note that our SWCNT modified gold electrodes are not as catalytically active as those reported recently by Nugent and co-workers [
15]. The latter reported similar experiments conducted on MWCNT modified platinum electrode surfaces and reported that the ET rate constant for ferrocyanide oxidation is k
0 ≈ 0.5 cm s
-1 .
Similar experiments were carried out using SWCNT dispersed on glassy carbon support electrodes. Here, the rate constants were found to be (2.7 ± 0.6) × 10
-3 and (4.2 ± 0.1) × 10
-3 cms
-1 for the bare and SWCNT-modified GC electrodes, respectively. It is interesting to note that the presence of the nanotubes enhances the rate constant by the same factor, 1.6, for both gold and glassy carbon. This finding indicates that dispersions of SWCNTs display well-defined and reproducible electrochemistry, despite their random arrangement. The better performance of the SWCNT electrodes has been attributed to the NT dimensions, structure, and to topological defects present on the tube surface [
16].
Figure 6.
The variation of peak separation with scan rate. The electrolyte used was a 1mM solution of ferricyanide in 50 mM KCl in a 50 mM Phosphate buffer solution (pH 7).
Figure 6.
The variation of peak separation with scan rate. The electrolyte used was a 1mM solution of ferricyanide in 50 mM KCl in a 50 mM Phosphate buffer solution (pH 7).
The rate constant for heterogeneous ET between a solution phase redox couple and an electrode can be calculated using a number of different approaches. The theories of ET reactions can be classified into two groups. The first are the classical or semi-classical theories derived from the models of Hush and Marcus. These are based on the transition state theory or its modern extensions, and pertain to the adiabatic limit in which the interaction between the electrode and the reactant is strong. The second group are quantum theories based on the work of Levich and Dogonadze which rely on perturbation theory and presume a weak interaction between the electrode and the reactant and so deal with non-adiabatic ET. Both classes of theories have been reviewed recently [
4]. In short the heterogeneous rate constant depends on the product of the density of electronic states in the metal and the transition probability for ET across the interface integrated over all available energies. It is expected that the local density of electronic states of a SWCNT will differ significantly from that of a bare metal. This may well explain the difference in rate constants observed.
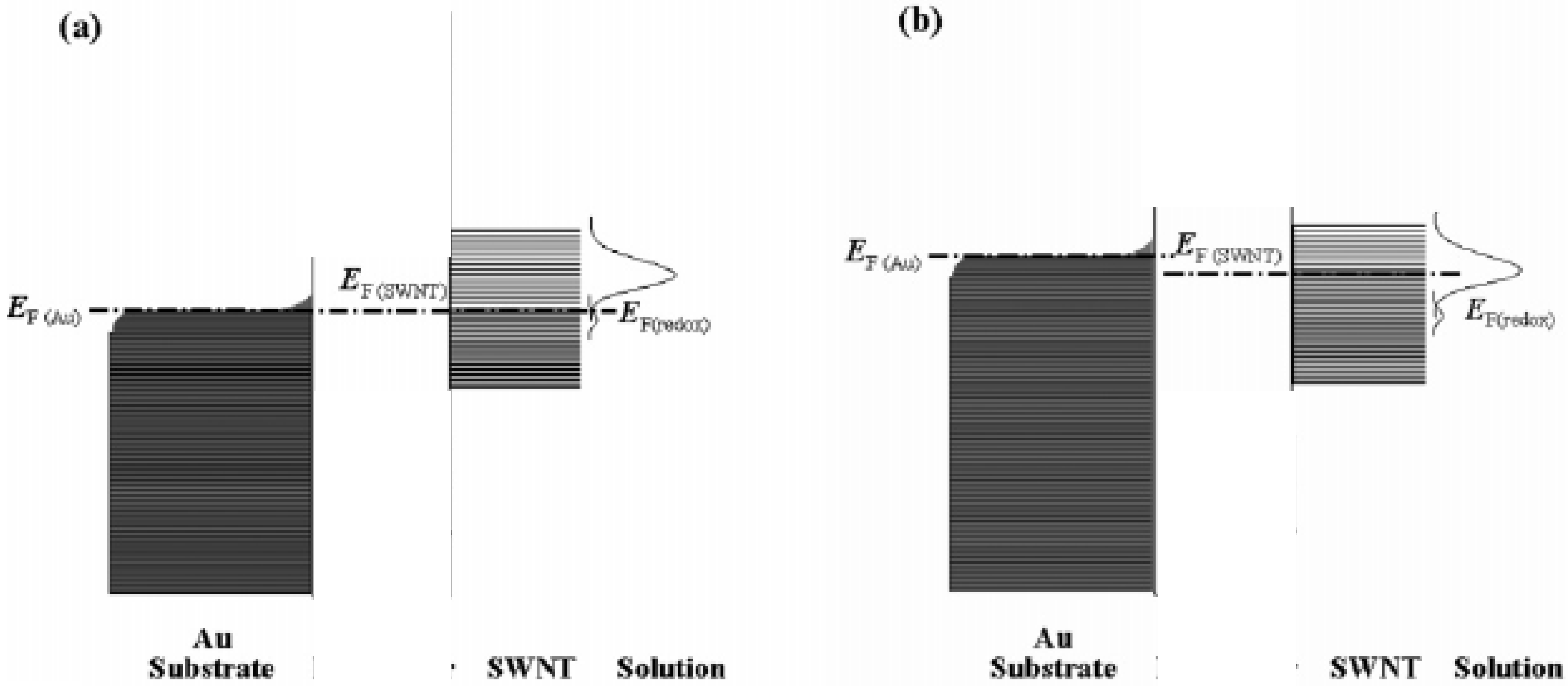
Furthermore it has been suggested [
17] that the immobilized SWCNT species act as electron transfer relay stations and mediate electron exchange between the underlying metal electrode and the redox couple in solution. The density of electronic states distribution diagram for a SWCNT modified gold electrode in contact with an electrolyte solution containing a redox active couple such as ferricyanide is outlined in
figure 7. The filled electronic states are shaded and the situation at equilibrium (
fig.7(a)) and under cathodic polarization (
fig.7(b)) are illustrated. At equilibrium the Fermi levels of Au, SWCNT and redox couple are all located at the same position. When the potential is swept in the negative direction away from the equilibrium value the Fermi level E
F,Au is raised and exceeds E
F,SWCNT. Consequently electrons are injected into the unoccupied energy states of the SWCNT via through space electron tunneling to make E
F,SWCNT = E
F,Au . The increased value for the Fermi energy of the SWCNT species results in a significant overlap between the Gaussian density of states curve for the oxidized form of the redox couple (i.e. ferricyanide) and that of the filled SWCNT levels. Hence the transition probability of electron transfer from the SWCNT to the oxidized form of the redox couple is greatly enhanced . Conversely the degree of overlap between SWCNT filled levels and the Gaussian density of states curve for the reduced form of the redox couple (i.e. ferrocyanide) is significantly reduced and oxidation is disfavoured. Hence an enhanced reduction current is observed. Conversely if the potential is scanned in a direction positive from that corresponding to the equilibrium value the E
F,Au value is decreased, which causes a corresponding fall in the value of E
F,SWCNT. When the potential is such that E
F,Au is less than the equilibrium value, the value of E
F,SWCNT will overlap significantly with the Gaussian maximum density of states of the reduced form of the redox couple and the probability of electron transfer from the reduced species energy levels to the SWCNT will be enhanced and a net oxidation current occurs. Hence this simple energy level picture can explain the voltammetric results illustrated in
figure 3.
Figure 7.
The variation of peak separation with scan rate. The electrolyte used was a 1mM solution of ferricyanide in 50 mM KCl in a 50 mM Phosphate buffer solution (pH 7) (adapted from ref.17).
Figure 7.
The variation of peak separation with scan rate. The electrolyte used was a 1mM solution of ferricyanide in 50 mM KCl in a 50 mM Phosphate buffer solution (pH 7) (adapted from ref.17).
It is reasonable to suppose that the large pi-conjugated system within the SWCNT ‘molecule’ confers properties both of electron acceptor and electron donor to the latter. Under cathodic polarization the adsorbed SWCNT accept electrons from the gold thereby increasing the filled energy levels in the SWCNT, thereby enabling electrons to be donated to acceptor redox couples in solution. Correspondingly during anodic polarization SWCNT molecules donate electrons to the gold electrode and simultaneously accept electrons from donor redox couples in solution. The large number of occupied and unoccupied energy states within the SWCNT allows not only facile ET between the adsorbed SWCNT and the redox couple in solution but also efficient electron tunneling between the SWCNT and the electrode substrate.
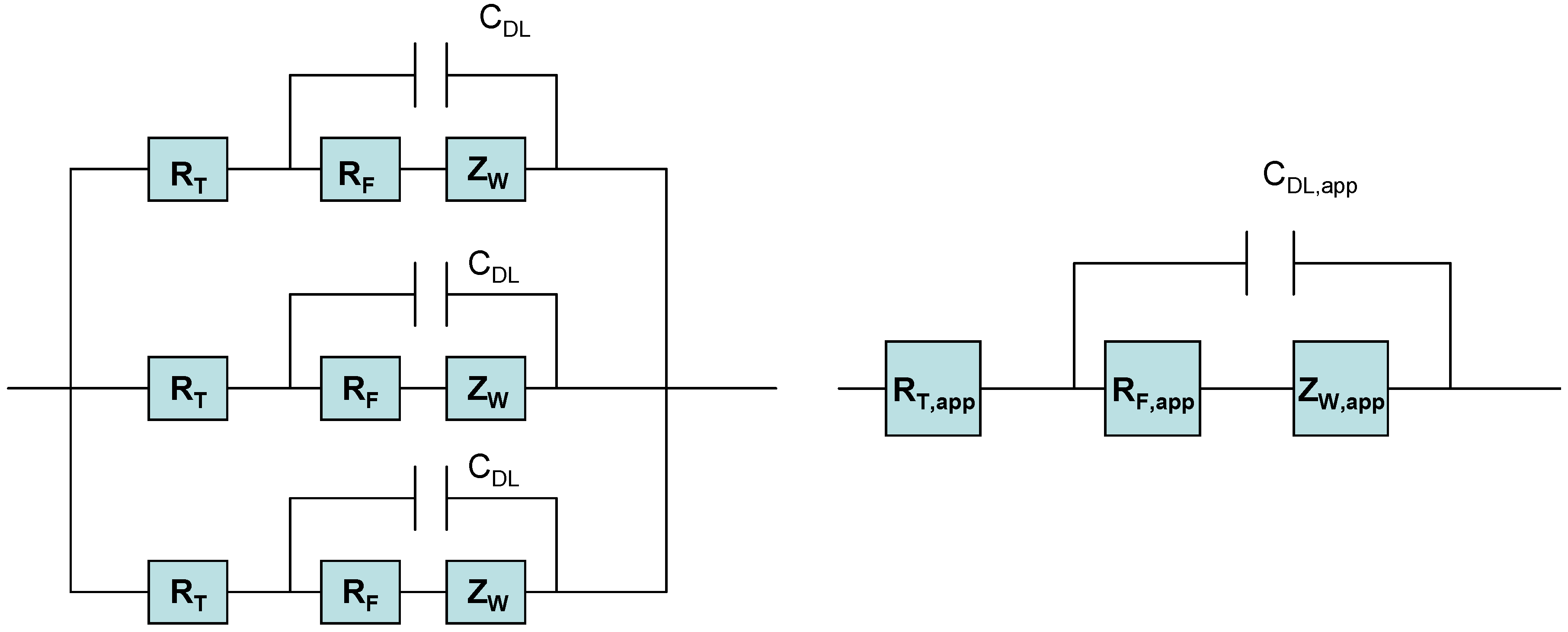
Hence when considering the redox behaviour of SWCNT modified electrodes in contact with solution phase redox couples, three distinct kinetic processes must be considered: (i) electron tunneling from gold/glassy carbon surface to SWCNT ; (2) electron transport within SWCNT and (3) heterogeneous ET from SWCNT ends or sidewalls to Fe(CN)
63- molecules in solution. If it assumed that electron transport through the nanotube is rapid then the observed redox response may be attributed either to electron tunneling from the support electrode surface to the adsorbed nanotube, or to slow electron transfer kinetics of the solution phase redox couple at the sidewalls and ends of the nanotubes. The situation may be represented in terms of a simple electrical equivalent circuit as illustrated in
figure 8.
Figure 8.
Electrical equivalent circuit of ensemble of randomly dispersed SWCNT on metal support surface.
Figure 8.
Electrical equivalent circuit of ensemble of randomly dispersed SWCNT on metal support surface.
In this figure we represent the redox behaviour of the immobilized nanotubes in terms of an electrical equivalent circuit [
17] consisting of a number of parallel branches each consisting of a tunneling resistance R
T in series with another circuit element consisting of a parallel combination of a double layer capacitor C
DL in, a Faradaic charge transfer resistance R
F and a Warburg diffusion impedance Z
W. This equivalent circuit represents an ensemble of SWCNT’s immobilized randomly on the surface of a gold support electrode. We expect that a certain degree of dispersion with respect to energy and kinetic activity will be exhibited by the immobilized ensemble. If no such energy dispersion exits then one can predict that the equivalent circuit illustrated on the right hand side of
figure 8 reduces to the simple set of circuit elements presented on the left hand side of
figure 8 , where the energy distributed elements are replaced by ‘apparent’ or energy averaged quantities. We can readily show that the impedance response of this type of circuit configuration in the complex plane [
18] consisting of an Nyquist plot of Imaginary part Im(Z) = Z’’ of the total impedance versus real part of the impedance Re(Z) = Z’, is a depressed semicircle at high frequencies followed by a linear feature at lower frequency. The high frequency semicircle represents the heterogeneous ET kinetics between the nanotube and the solution phase redox reactant, whereas the low frequency linear feature is associated with the diffusive transport of the solution phase redox couple to the nanotube surface. Furthermore the real axis intercept at high frequency is associated with the sum of tunneling and solution resistance.
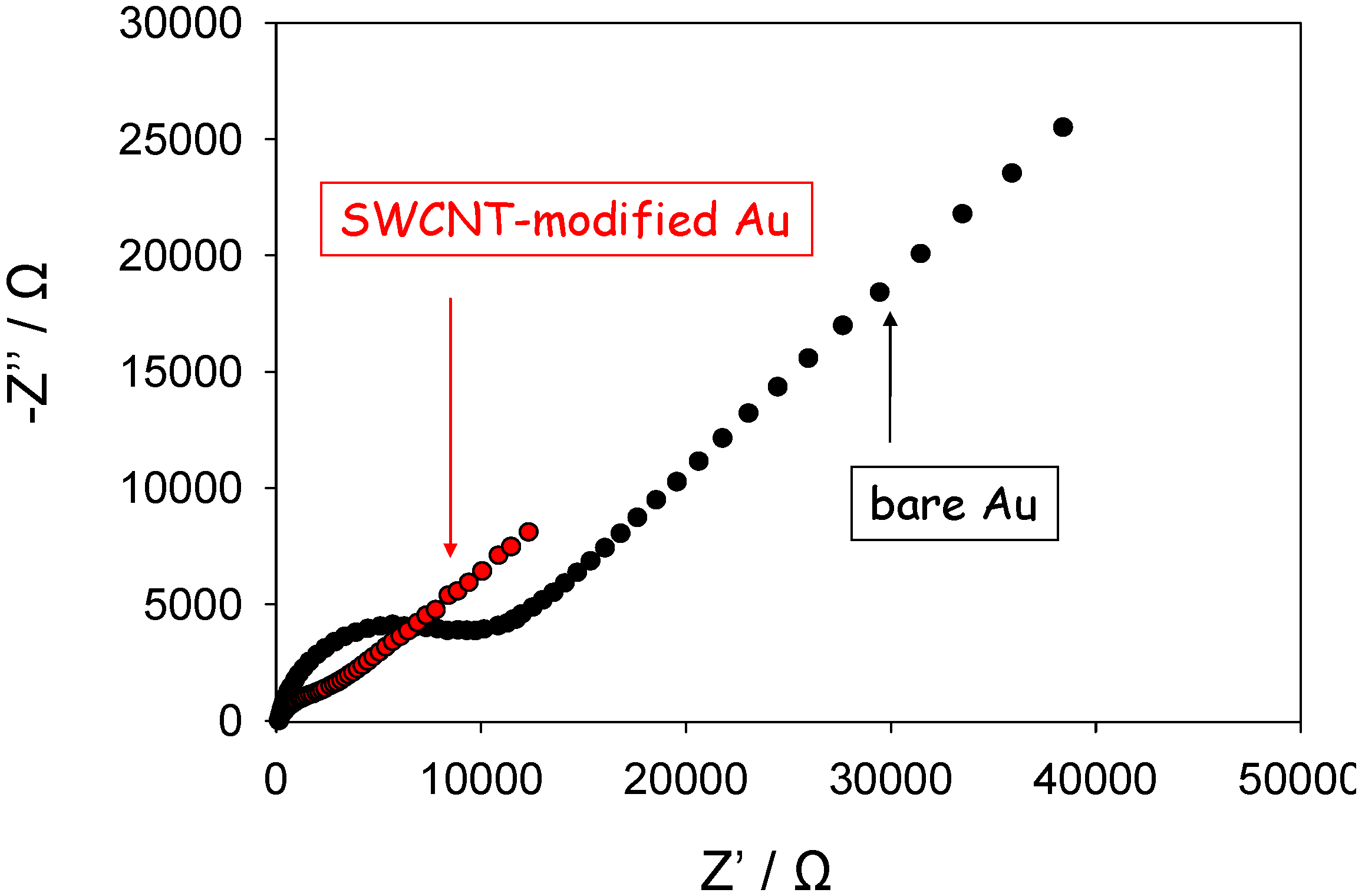
We have performed a series of preliminary experiments to measure the complex impedance response of SWCNT randomly dispersed and immobilized both on gold and glassy carbon electrodes in contact with aqueous solutions containing the ferrocyanide/ferricyanide redox couple, and compared these results with analogous data obtained for the respective unmodified electrodes. We determined the impedance response of both unmodified and SWCNT modified gold electrodes over a wide range of frequencies, typically from an upper limit of 100 kHz to a lower limit of 1 Hz. Typical Nyquist data obtained from such experiments are presented in
figure 9 and
10 below. Each data point corresponds to a discrete frequency measurement. The measurements were obtained when the electrode was polarized at a dc potential of 0.23 V corresponding to that of the standard potential of the Fe(CN)
63-/4- redox couple. We note from
figure 9 that depressed semi-circle features are observed at high frequencies and well defined linear Warbourg diffusive features are present at lower frequencies both for the unmodified gold electrode and the SWCNT modified gold electrode. This is in accordance with the basic equivalent circuit description presented in
figure 8. Furthermore the amplitude of the high frequency semicircle is much smaller for the SWCNT modified electrode indicating the occurrence of faster heterogeneous electron transfer kinetics and electron injection via tunneling at the latter modified electrode compared with the unmodified electrode.
Figure 9.
Complex impedance Nyquist plots recorded for ferricyanide reduction at Au and SWCNT modified Au electrodes.
Figure 9.
Complex impedance Nyquist plots recorded for ferricyanide reduction at Au and SWCNT modified Au electrodes.
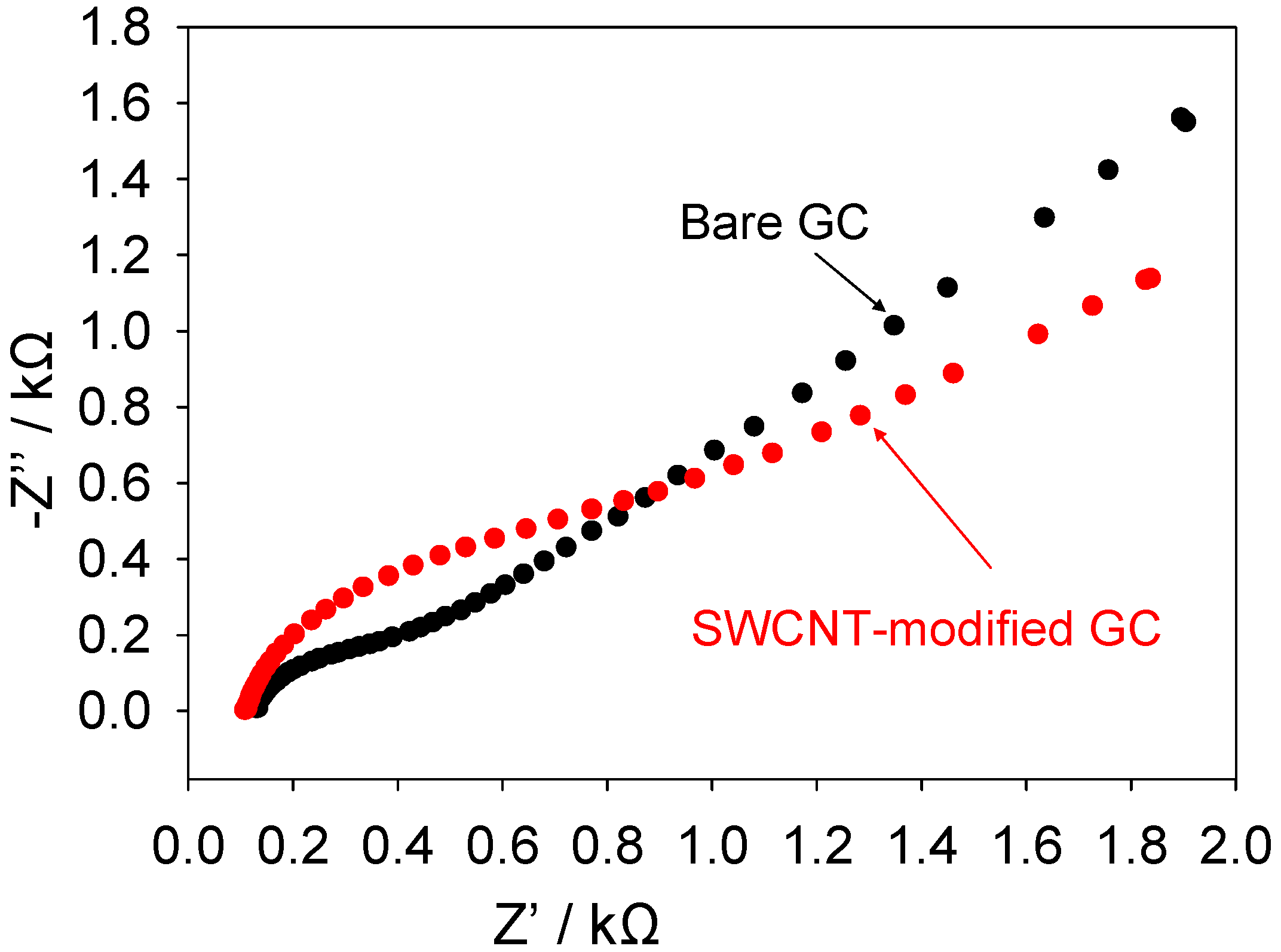
A similar set of impedance experiments were conducted on unmodified glassy carbon and SWCNT-modified glassy carbon electrodes. The results of these experiments are presented in
figure 10 below. Again both a depressed semicircle observed at high frequencies followed by a Warbourg feature at lower frequencies may be noted both for the unmodified and SWCNT modified GC electrodes. In contrast to that seen with gold the high frequency semicircle is larger when the GC electrode is modified with the dispersed nanotube assembly.
General electrochemical properties of SWCNT/GOx-modified electrodes
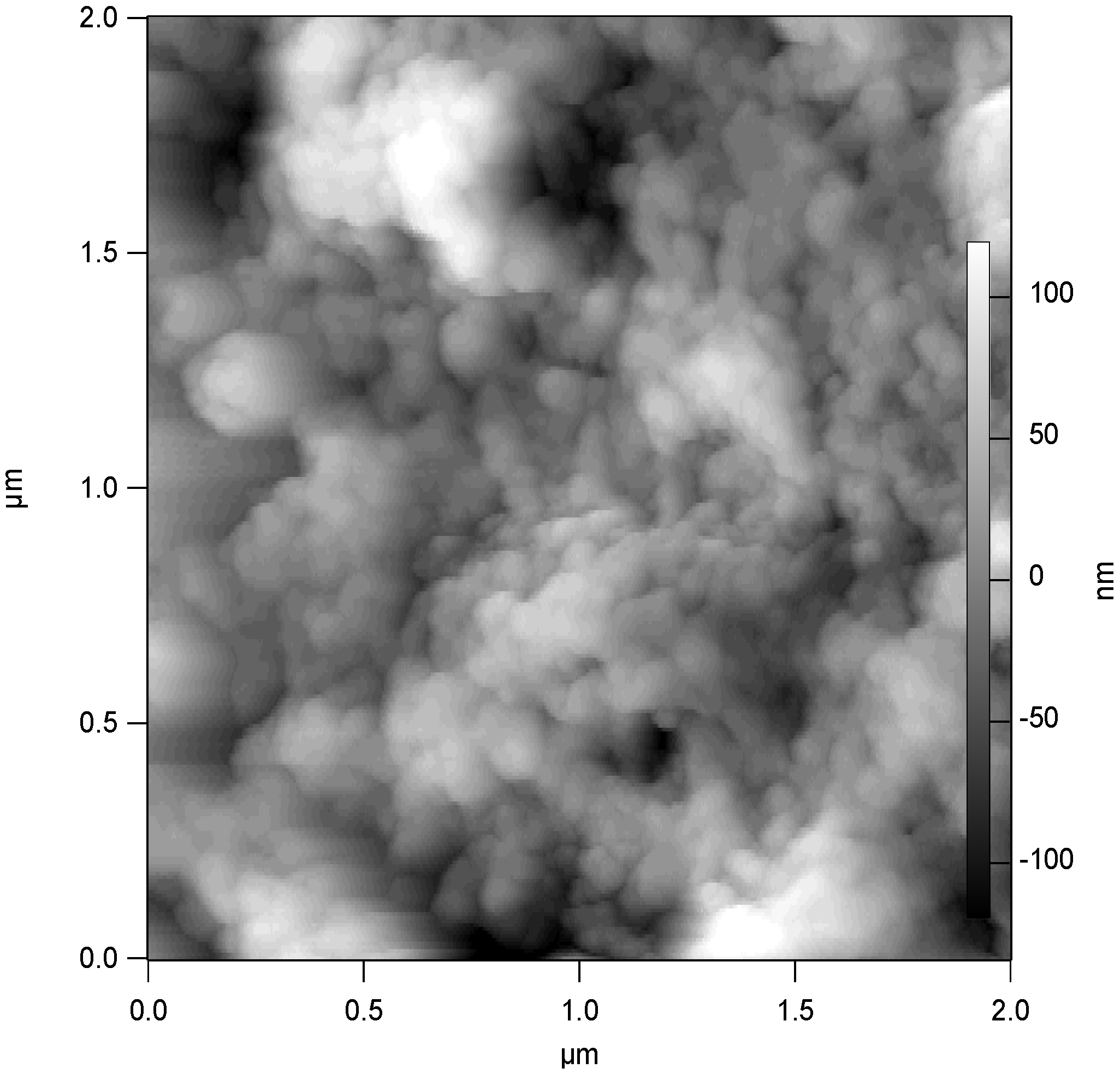
In this section of the paper we concentrate on examining the general electrochemical characteristics of glucose oxidase which has been adsorbed on an assembly of single walled carbon nanotubes randomly dispersed both on gold and glassy carbon support electrode surfaces. A typical AFM image recorded for a nanotube assembly (dispersed in this case on a silicon surface) on which glucose oxidase has been adsorbed is outlined in
figure 11. It is clear from the latter image that the enzyme fills much of the void space between the nanotube fibres. Hence we expect that the enzyme loading should be at a level to ensure good catalytic activity. In our experiments the gold electrodes were initially modified with an assembly of SWCNT as outlined previously. The SWCNT modified Au (or glassy carbon) electrode was then thoroughly washed with water and immersed in a 16 mg mL
-1 GOx in phosphate buffer solution (0.05 M, KH
2PO
4 + Na
2HPO
4, pH 7) at 20
0C for ca. 2.5 hours. Adsorption of glucose oxidase onto the SWCNT occurs within this timescale. In some experiments the enzyme SWCNT composite electrode was further modified by depositing a thin layer of soluble nafion via drop coating. The resulting enzyme modified electrodes were then subjected to electrochemical analysis (largely cyclic voltammetry and potential step chronoamperometry) in phosphate buffer solution.
Figure 10.
Complex impedance Nyquist plots recorded for ferricyanide reduction at GC and SWCNT modified GC electrodes.
Figure 10.
Complex impedance Nyquist plots recorded for ferricyanide reduction at GC and SWCNT modified GC electrodes.
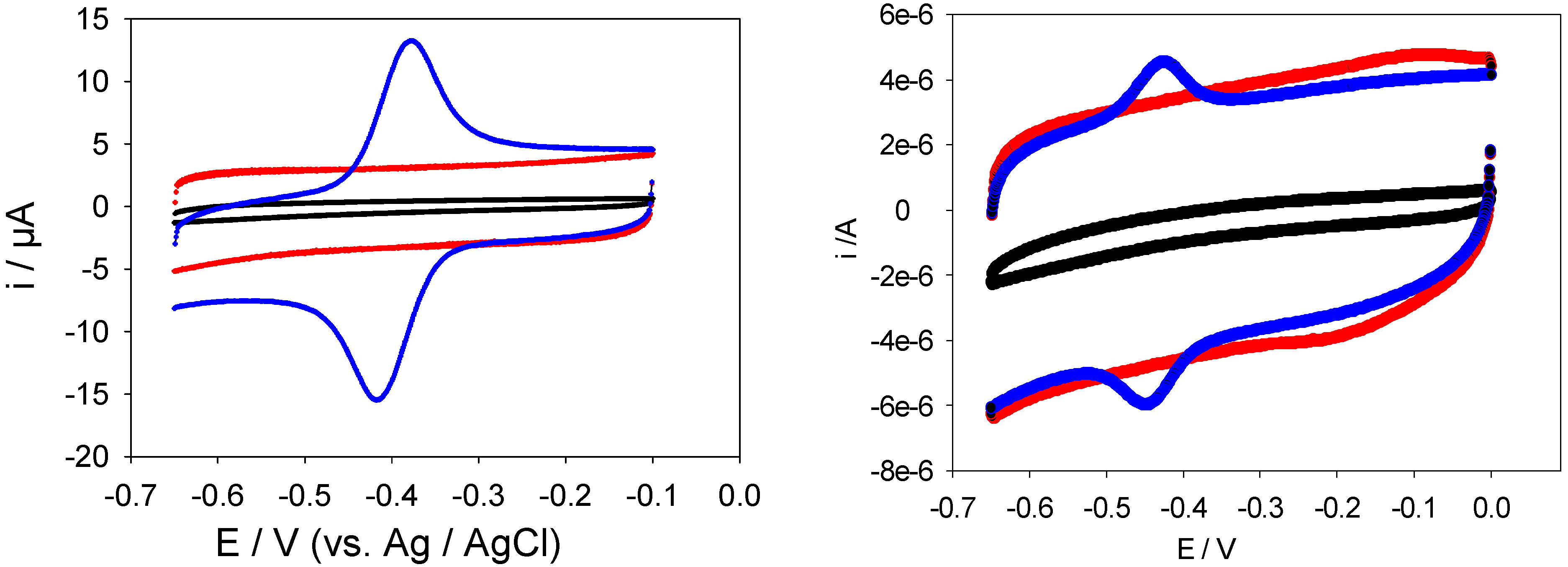
The electrochemical response of the latter enzyme modified SWCNT modified electrode was determined using cyclic voltammetry. The voltammograms presented in
Figure 12 were obtained using a bare, SWCNT-modified and SWCNT/GOx and SWCNT/GOx/Nafion-modified gold working electrodes in a 50 mM phosphate buffer (pH 7). As can be seen, while a bare gold electrode exhibits a virtually flat and featureless voltammetric response, a pair of well-defined redox peaks was observed at the both the SWCNT/GOX and SWCNT/GOx/Nafion-modified electrode. The observed peaks are characteristic of those representing the redox behaviour of an adsorbed species, in this case that of the flavin adenine dinucleotide FAD. The peaks are reasonably symmetrical and exhibit the characteristic bell shape expected for adsorbed redox species [
19]. The absence of any peaks on the SWCNT-modified Au voltammogram suggests that the voltammetric response observed with the latter is essentially capacitive in the absence of any redox active substrates present in the electrolyte solution. It also indicates that the nanotubes are reasonably free from any oxidized functionalities.
Figure 11.
AFM image recorded for a SWCNT assembly dispersed randomly on a silicon surface on which glucose oxidase was adsorbed for a 2.5 hr period at room temperature.
Figure 11.
AFM image recorded for a SWCNT assembly dispersed randomly on a silicon surface on which glucose oxidase was adsorbed for a 2.5 hr period at room temperature.
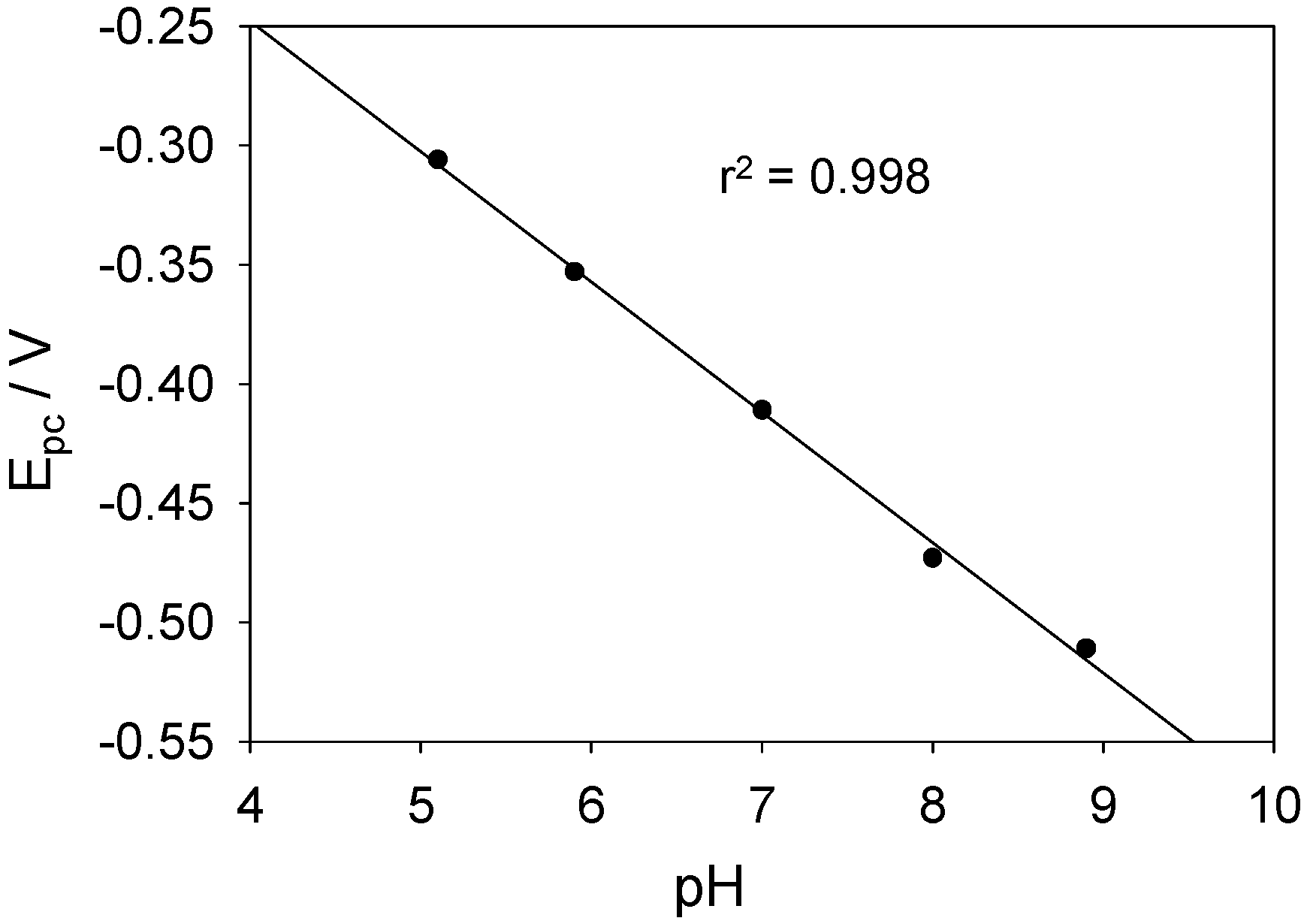
It is interesting to note that the FAD/FADH2 redox peaks are more defined when Nafion is used as an overcoating agent. Without application of the latter the voltammograms are characterized by an ill resolved set of redox peaks superimposed on a rather large capacitive current backgrouns. For the voltammetric response of the SWCNT/GOx/Nafion composite electrode at a sweep rate of 100 mVs-1, the cathodic peak potential (Epc) is -417 mV vs. Ag/AgCl and the peak separation (ΔEp) is 41 mV. The surface coverage of adsorbed redox enzyme can be calculated by integrating the charge Q under the voltammetric peak using the formula : where A denotes the geometric electrode area , n denotes the number of electrons transferred in the redox process (2 in the present case) and F is the Faraday constant. We estimate that Γ = 1.7 nmol cm-2 for the Nafion coated SWCNT/GOx composite electrode. The corresponding data set for the SWCNT/GOx composite without the Nafion overlayer is a cathodic peak potential (Epc)of -449 mV vs. Ag/AgCl and a peak separation (ΔEp) of 24 mV. It is difficult to estimate the surface coverage for the latter system since the resolution between Faradaic and capacitive processes is poor. Consequently we do not provide a numerical estimate for this quantity but merely note that it is certainly less that that recorded for the Nafion coated system.
Figure 12.
LHS Picture: Cyclic voltammograms recorded at a bare (black), SWCNT-modified (red) and SWCNT/GOx -modified (blue) gold working electrode. RHS Picture: Cyclic voltammograms recorded at a bare (black), SWCNT-modified (red) and SWCNT/GOx/Nafion -modified (blue) gold working electrode The electrolyte used in both sets of experiments was a 50 mM phosphate buffer (pH 7) and the scan rate employed was 100 mVs-1.
Figure 12.
LHS Picture: Cyclic voltammograms recorded at a bare (black), SWCNT-modified (red) and SWCNT/GOx -modified (blue) gold working electrode. RHS Picture: Cyclic voltammograms recorded at a bare (black), SWCNT-modified (red) and SWCNT/GOx/Nafion -modified (blue) gold working electrode The electrolyte used in both sets of experiments was a 50 mM phosphate buffer (pH 7) and the scan rate employed was 100 mVs-1.
In a recent communication Wang and co-workers [
20] have reported that SWCNT are readily soluabilised in Nafion solutions made from ethanol or aqueous phosphate buffer. TEM images clearly indicate individual SWCNT ropes when disersed in the latter media. This is in contrast to the high density intertwined aggregates found when SWCNT are dispersed in organic solvents such as chloroform. The structure of Nafion in solution may be viewed as a fluorocarbon backbone with protruding polar sulfonate SO
3- groups . Hence it is similar in nature to other polymers which have been used to wrap and solubilise CNT material. According to Smalley and co-workers [
21] the wrapping of nanotubes by water soluble polymers such as Nafion is a general phenomenon driven by a thermodynamic impetus to eliminate the hydrophobic interface between the tubes and the aqueous medium, thereby reducing the density of the tangled and rather dense tube assembly on the electrode surface. This may well increase the permeability of the void space between the tubes to increased quantities of electrolyte ions which will result in a change in the interfacial potential distribution and hence on the voltammetric response [
22].
Ideally ΔE
p should be zero for surface immobilized redox systems, [
19,
23] . The non zero ΔE
p value observed in both cases above may be attributed to the presence of a potential difference between the electrode and the site of electron transfer (the flavin redox group) [
24]. Such a difference would be attributed to the surrounding protein sheath acting as a dielectric layer. The presence of Nafion, while enhancing the discrimination between current resulting the surface redox reacting and the capacitive background contribution, may well result in a larger potential drop in the interface region. The prominent background current is a consequence of the large, catalytically active surface area of the modified electrode [
25,
26].
The influence of scan rate on the system was investigated within the range of 0.005 to 5.0 Vs
-1 for gold and 0.002 to 13.0 Vs
-1 for glassy carbon.
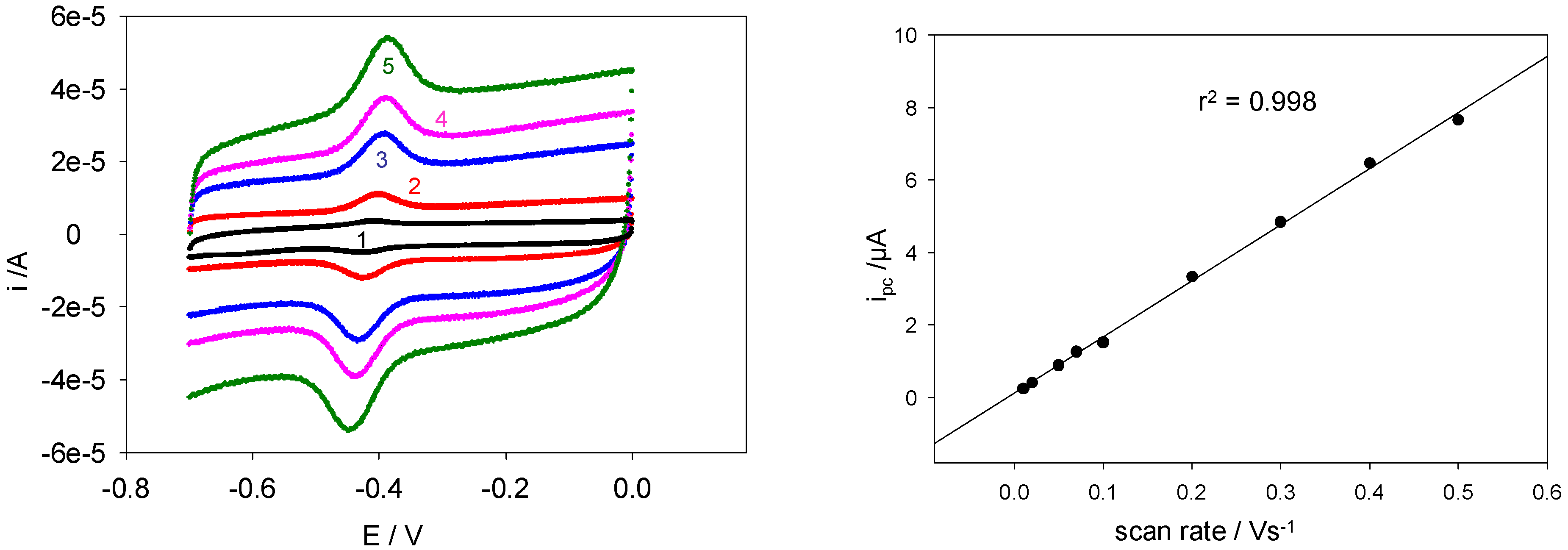
Figure 12 shows a comparison between voltammograms obtained at five different scan rates.
Figure 13.
(a) Cyclic voltammograms obtained using a SWCNT/GOx-modified Au working electrode. The electrolyte used was a 50 mM PBS (pH 7). The scan rates shown are (1) 0.1, (2) 0.3, (3) 0.8, (4) 1.1 and (5) 1.5 Vs-1. (b) The variation of cathodic peak current with scan rate using a SWCNT/GOx-modified Au working electrode. The electrolyte used was a 50 mM PBS (pH 7).
Figure 13.
(a) Cyclic voltammograms obtained using a SWCNT/GOx-modified Au working electrode. The electrolyte used was a 50 mM PBS (pH 7). The scan rates shown are (1) 0.1, (2) 0.3, (3) 0.8, (4) 1.1 and (5) 1.5 Vs-1. (b) The variation of cathodic peak current with scan rate using a SWCNT/GOx-modified Au working electrode. The electrolyte used was a 50 mM PBS (pH 7).
It was found that the peak currents exhibited a linear relationship with the sweep rate, a feature which is characteristic of surface-bound redox processes as outlined in the analytic theory proposed by Laviron [
19,
23].
Figure 13(b) shows the variation of i
pc with ν for lower scan rates. The linearity was reasonably evident over the entire range of sweep rates studied.
Determination of flavin group redox kinetics via lps voltammetry: application of the Laviron Method
Linear potential sweep voltammetry may be used to extract kinetic parameters such as heterogeneous rate constants and transfer coefficients for surface immobilized redox reactions by examining the variation of voltammetric redox peak potential with experimental time scale (i.e. sweep rate). Quantitative data analysis relies on a theoretical methodology originally developed by Laviron [
19]. We will briefly summarise this analysis here.
The degree of kinetic reversibility exhibited by a surface redox reaction depends on the experimental timescale. It is expected that a surface redox reaction will exhibit reversible behaviour (manifested as a sweep rate invariant peak potential) when the sweep rate is small, and irreversible behaviour (indicated by a linear variation of peak potential with natural logarithm of sweep rate) when the sweep rate is large. This general expectation was confirmed in our experiments. When the scan rate is higher than 0.2 Vs
-1, it was observed that E
pc shifts negatively and E
pa shifts positively with increasing sweep rate.
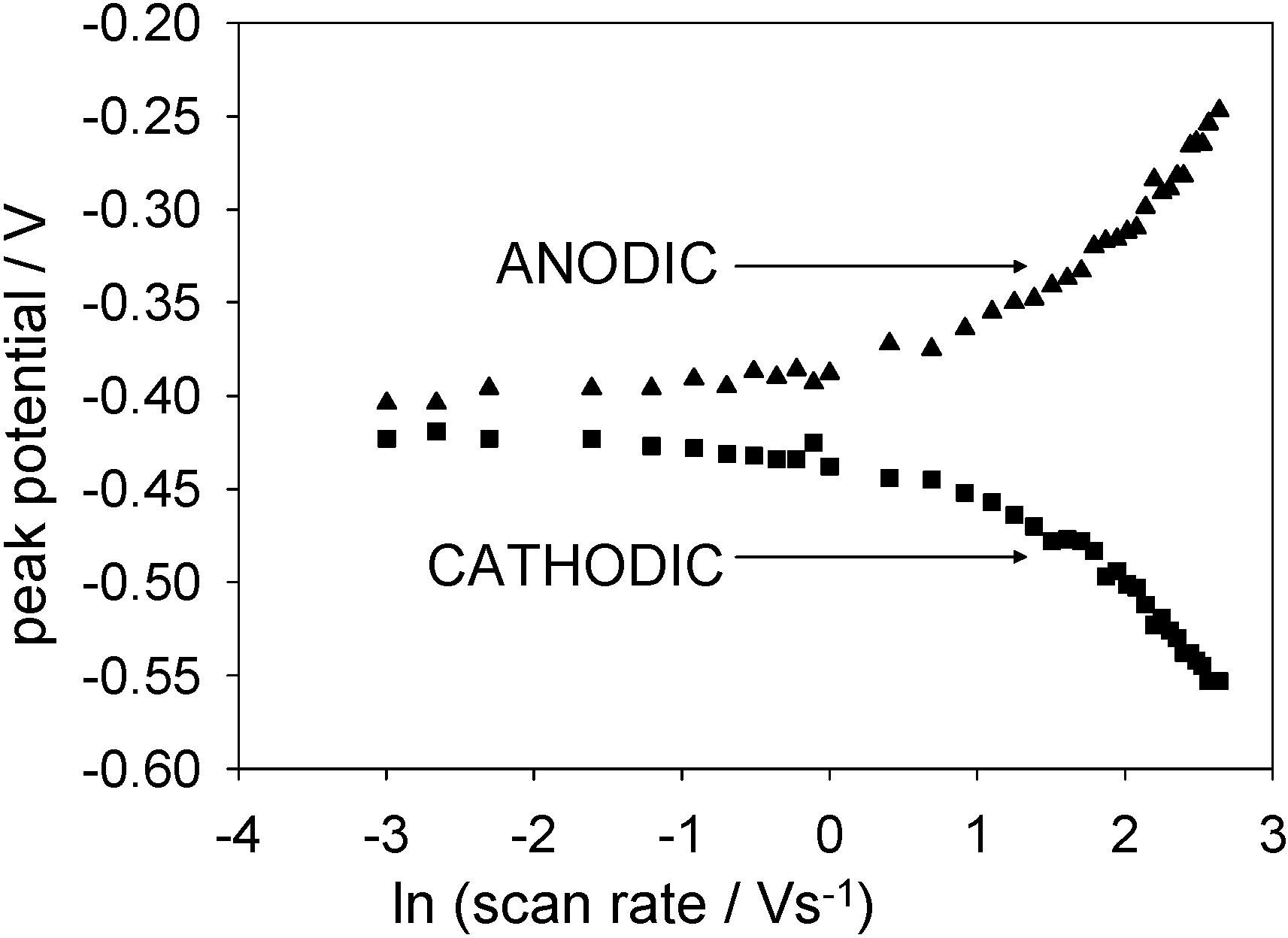
Figure 15 shows plots of anodic and cathodic peak potential as a function of the natural logarithm of the applied scan rate for a SWCNT/GOx/Nafion-modified gold working electrode. It is clear that the peak potentials are practically invariant with sweep rate when the latter is low, and in contrast for high sweep rates, peak potentials are proportional to ln ν.
Figure 16.
Plots of anodic and cathodic peak potentials against the natural logarithm of scan rate for a SWCNT/GOx/Nafion-modified gold working electrode. The electrolyte used was a 50 mM phosphate buffer (pH 7).
Figure 16.
Plots of anodic and cathodic peak potentials against the natural logarithm of scan rate for a SWCNT/GOx/Nafion-modified gold working electrode. The electrolyte used was a 50 mM phosphate buffer (pH 7).
For a surface-bound redox reaction involving redox active enzyme molecules adsorbed on surface immobilized SWCNT meshes, we can show that the following expression holds for the normalized current response for an oxidative potential sweep:
where i denotes the current,
is the total redox group surface coverage (mol cm
-2),
is the voltammetric sweep rate (V/s), A denotes the electrode area (cm
2) and m is a dimensionless parameter which relates the heterogeneous electron transfer rate constant to the experimental time scale and is given by
. Also in eqn.4
represents the symmetry factor (typically ½) and
, where the normalized potential is given by:
. Finally the mole fraction
of reduced enzyme sites adsorbed on the SWCNT mesh is given by the solution to the following differential equation:
This equation may be readily solved for suitable limiting values of the Laviron reversibility parameter m. First when the redox reaction is totally irreversible when
. Under these circumstances
and eqn.5 reduces to:
which can be readily integrated to yield
and also for totally irreversible conditions we have
and so the expression for the normalized current response presented in eqn.4 reduces to
This function exhibits a maximum or peak value designates as
when
. We can readily show that under such conditions
which is a maximum value, and
Hence simplifying we obtain
which simplifies to
Substituting eqn.11 into eqn. 8 we end up with the following simple result
In terms of currents we obtain
We also note that the normalized peak potential function is given by
where we have written
and we note that
represent normalized potentials. Hence we end up with a useful diagnostic expression for an irreversible surface oxidation reaction
where a plot of peak potential versus the natural logarithm of the inverse sweep rate parameter is linear.
It is possible to derive similar expressions for a reductive surface process and we can show that in such a situation:
and the corresponding peak currents and potentials are given by
Furthermore we define
as the normalized peak potential difference. This parameter can be used to derive useful kinetic information. We can show that
Specifically when the transfer coefficient β = 0.5, eqn.18 becomes
. This expression will be valid with less than 2% error for m
-1 > 12 which occurs for ΔE
P > 200 mV. We can simplify eqn.18 to obtain the following expression from which the standard rate constant
can be derived provided that the transfer coefficient β can be evaluated:
wheres
Furthermore from eqn.15 and eqn.17 we note that the normalized peak potential
will vary in a linear manner with the natural logarithm of the inverse scan rate parameter
. Now if the linear portion of the
versus
curve is extrapolated to the point where
, then at this specific value of the parameter m which we designate as m
ox* we note that
or
. This translates to
. Similarly we can show that
. Now we can readily evaluate an expression for the transfer coefficient β by noting that
We conclude therefore that from eqn.21 and eqn.19 the fundamental kinetic parameters for an irreversible surface process may be determined via measurement of peak potential and peak potential difference as a function of sweep rate.
Transforming eqn.18 we obtain [
19]:
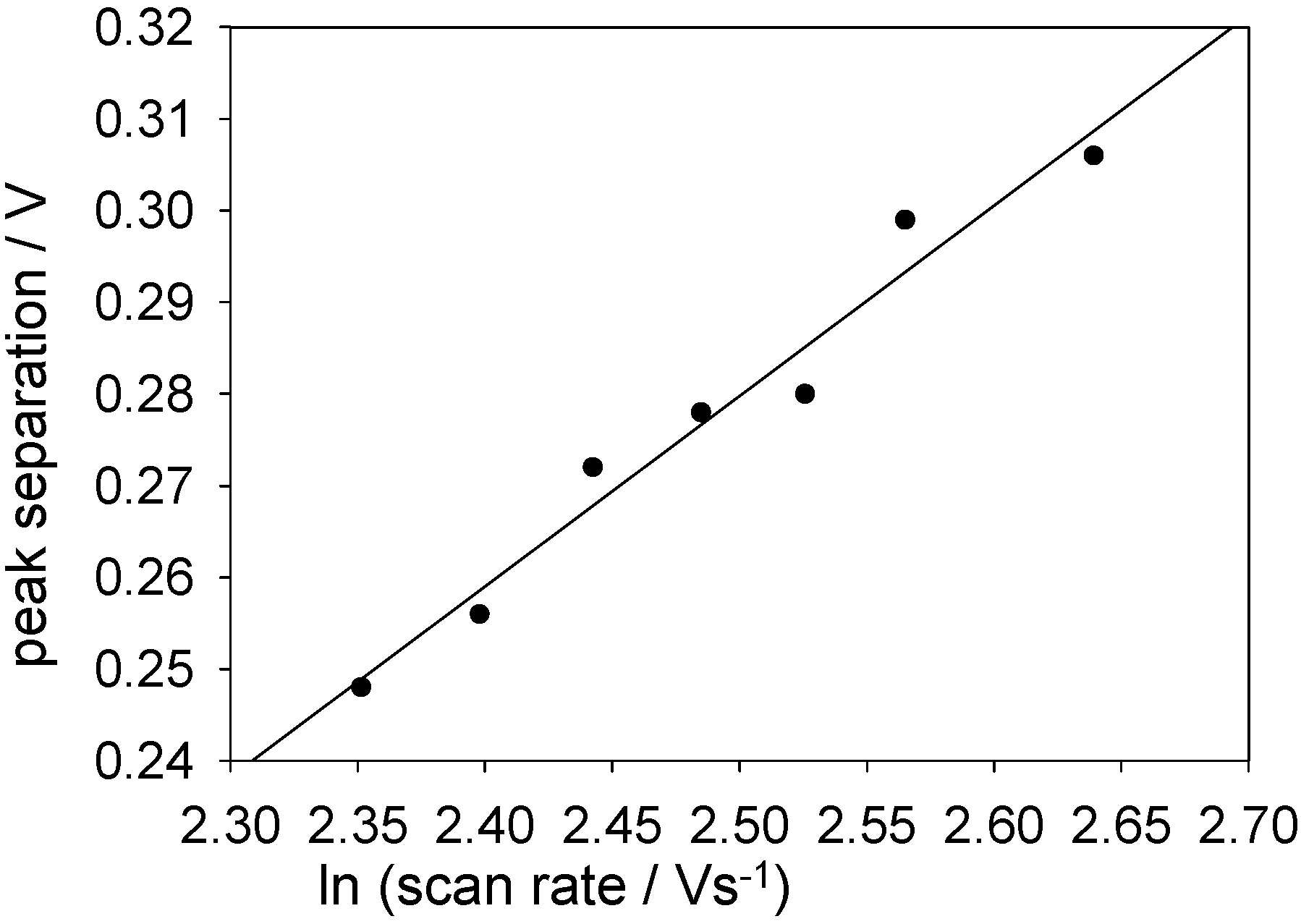
Peak separations were plotted against lnν for high scan rates (at which the redox process exhibits quasi-reversible/totally irreversible behaviour).
Figure 17 shows such a plot for a SWCNT/GOx/Nafion-modified gold electrode. The slope of this graph was found to be 208 mV, with a y-intercept of -234 mV. For the glassy carbon working electrode these values were 122 and -42 mV, respectively. From the slopes, α values of 0.11 and 0.10 were calculated for gold and glassy carbon respectively. These values were used along with the intercepts to calculate a rate constant of 19 s
-1 for the FAD/FADH
2 transformation on gold and 18 s
-1 for the same process on glassy carbon.
Figure 17.
Peak separation against the natural logarithm of scan rate for a SWCNT/GOx/Nafion-modified gold working electrode. The electrolyte used was a 50 mM phosphate buffer (pH 7).
Figure 17.
Peak separation against the natural logarithm of scan rate for a SWCNT/GOx/Nafion-modified gold working electrode. The electrolyte used was a 50 mM phosphate buffer (pH 7).
These results may be compared with data previously reported in the literature [
27,
28]. In this work the apparent heterogeneous electron transfer rate constants for redox proteins and enzymes such as hemoglobin (Hb), horseradish peroxidase (HRP) and Glucose Oxidase (GOx) were determined using linear potential sweep voltammetry at SWCNT modified glassy carbon electrodes to be in the range 1-2 s
-1. In contrast Dong and co-workers [
29] have examined the kinetics of the microperoxidase 11 redox transformation at glassy carbon electrodes modified with MWCNT meshes. For a microperoxidase loading of 0.84 nmol cm
-2 a standard rate constant of 38 s
-1 was determined. It is clear that the standard heterogeneous rate constant for adsorbed redox proteins and enzymes can vary somewhat and lie between 1-40 s
-1 when cyclic voltammetry measurements are made in phosphate buffer solution on CNT meshes. We should note however that molecular oxygen, the natural co-substrate of the enzyme glucose oxidase, accepts electrons from native GOx at a rate of around 700 s
-1 [
30]. This may suggest that the rate constants measured using simple Laviron theory may
underestimate the facility of redox protein turnover at a nanotube modified electrode. This idea is pursued in the next section where the intrinsically dispersive nature of the adsorbed enzyme system is emphasized. This dispersive spread in kinetic activity is not recognised by the Laviron model, which predicts a linear variation of peak separation with lnν, and a single value for the rate constant. In the next section we suggest that the technique of potential step chronoamperometry provides a convenient method to both identify, and monitor the extent of, kinetic dispersion in a surface adsorbed redox system and we examine the response of the GOx immobilized on SWCNT /Nafion modified glassy carbon and gold electrodes.
Determination of flavin group redox kinetics via Potential Step Chronoamperometry: the effect of kinetic dispersion
Cyclic voltammetry does not always provide the optimum route to kinetic parameters. It can be difficult to distinguish between Ohmic drop and kinetic effects when investigating the variation of the voltammetric response with sweep rate. Potential step techniques may be used to calculate electron transfer rate constants for redox systems immobilised on electrodes.
For both gold and glassy carbon, the potential was stepped from a value just before the cathodic peak to a value just after the anodic peak and back again. Hence the potential was stepped from -0.5 to -0.3 V to investigate oxidation, and then from -0.3 to -0.5 V to analyse the reduction process.
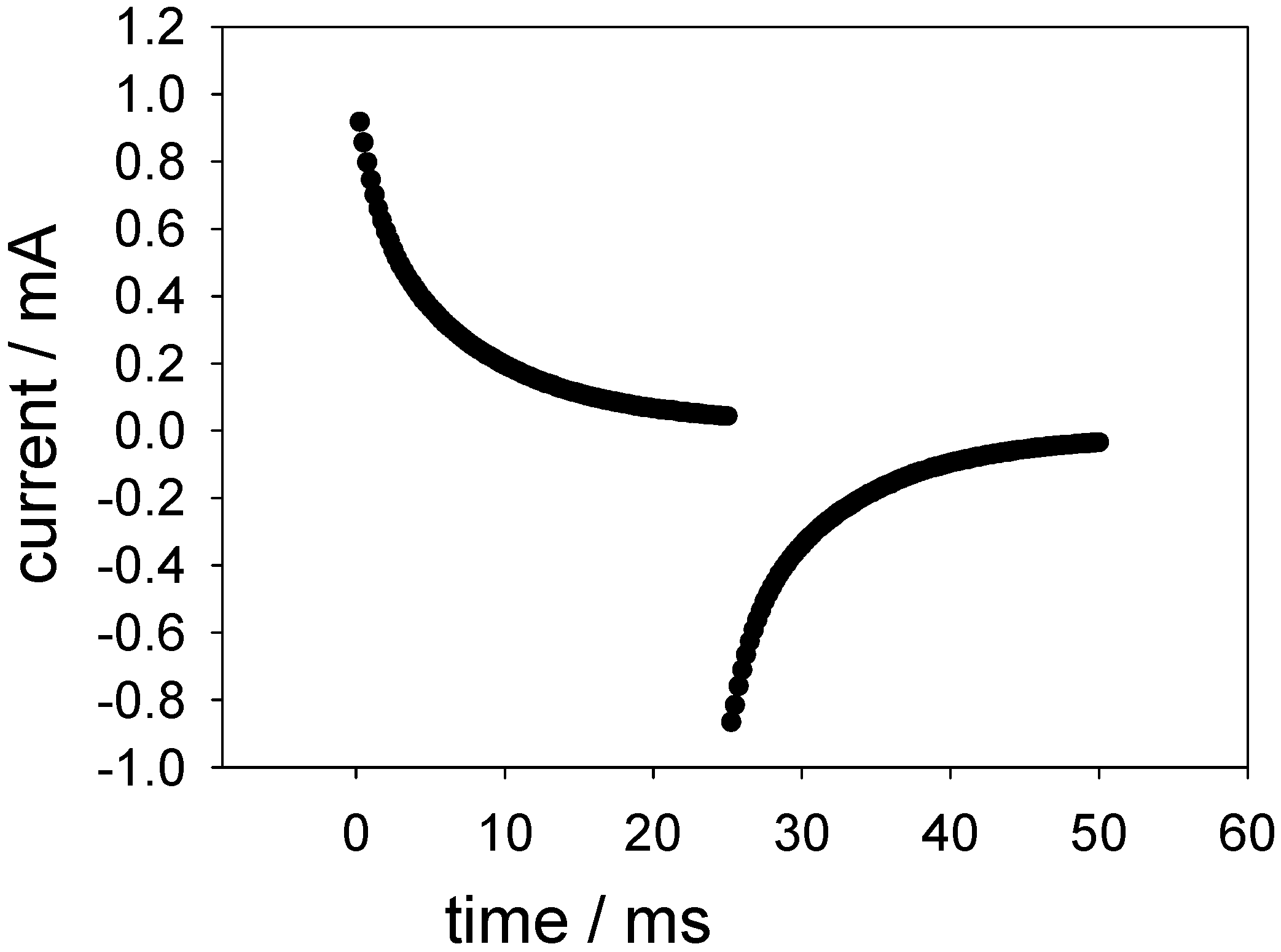
Figure 18 shows a typical outcome of such an experiment.
Figure 18.
Typical outcome of a potential step experiment across the FAD oxidation and reduction potentials for a SWCNT/GOx/Nafion-modified gold electrode. The electrolyte used was a 50 mM phosphate buffer (pH 7).
Figure 18.
Typical outcome of a potential step experiment across the FAD oxidation and reduction potentials for a SWCNT/GOx/Nafion-modified gold electrode. The electrolyte used was a 50 mM phosphate buffer (pH 7).
The analysis of the current versus time response to a potential step of arbitary magnitude has been recently described by Lyons [
30]. We review this material for convenience here. We initially consider the transient current response obtained to a large amplitude potential step perturbation applied to a surface immobilized redox couple A/B. We let Γ
j (j = A,B) represent the surface coverage (units: mol cm-2) of component j of the redox couple, and define the total surface coverage as
. We initially assume that the surface redox reaction is irreversible with a rate equation given by:
where the heterogeneous electrochemical rate constant (units: s
-1) is of the Butler-Volmer type and is given by
where k
0 denotes the standard rate constant, β is the symmetry factor and ξ denotes a normalized potential given by
. The current response to the applied potential step is given by
where f
Σ denotes the net flux (units: mol cm
-2 s
-1), n denotes the number of electrons transferred in the surface redox process, A denotes the geometric area of the electrode and F is the Faraday constant.
The variation of surface coverage with time is obtained via integration of eqn.1 subject to the initial condition that at
. Hence integration of eqn.23 immediately yields that
and the surface redox transition obeys first order kinetics. Hence the current response is expected to follow a simple exponential decay and is given by
where the charge Q is related to the surface coverage of electroactive groups via the expression
. This expression has been used by Finklea [
31], Chidsey [
32] , Miller and co-workers [
33] and by Forster and Faulkner [
34] to examine the dynamics of self assembled monolayer systems. Hence we conclude that the variation of current with time for a simple surface redox transformation is described by simple first-order kinetics. This means that, ideally, a plot of natural logarithm of the current against time should be linear, with a slope giving directly the heterogeneous electrochemical rate constant k
ET.
We can readily extend the analysis to consider a quasi-reversible surface reaction. In this case the rate equation for the surface redox reaction is given by
where the heterogeneous rate constant for the reverse step is given by
. We can integrate eqn.28 using the initial condition
to obtain
where we note that
. At any time t we also note that
and so we also obtain that
The net current response is therefore given by
From eqn.29, eqn.30 and eqn.31 we immediately obtain
Again a simple exponential decay in current with time is predicted. A plot of ln i versus t is linear with intercept given by
and a slope given by
. Hence the surface redox kinetics can be completely resolved using the potential step technique.
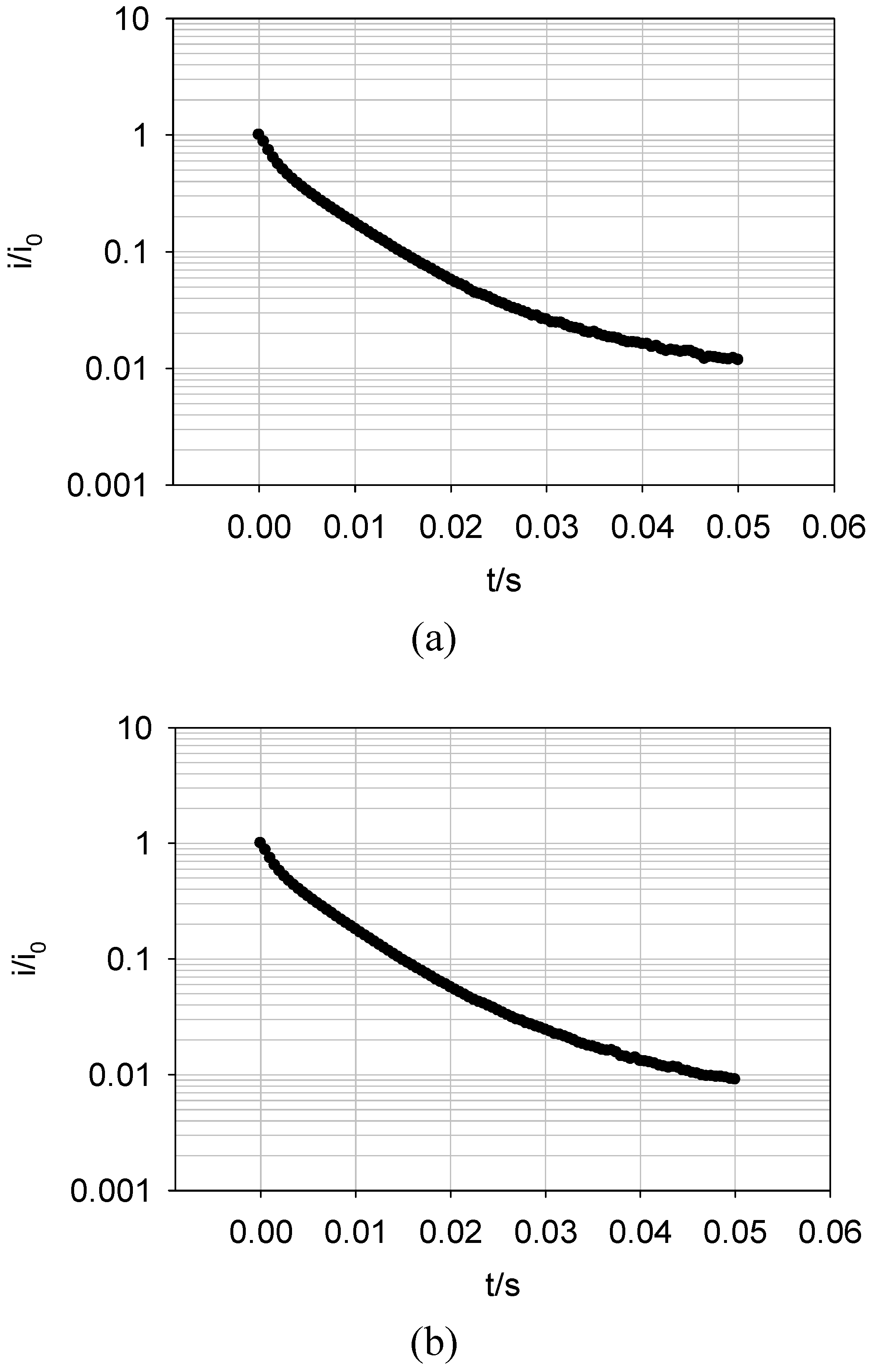
Figure 19 shows a plot of the logarithm of the normalised current against time obtained for the oxidation of FADH2 and the reduction of FAD at a SWCNT/GOx/Nafion-modified gold electrode. The current at zero time (i0) is simply estimated using
Figure 18. It can be seen that the chronoamperometric transients displayed in
Figure 19 are not linear. Consequently the prediction of a simple first order kinetic situation is not maintained experimentally, and the modellistic analysis must be adjusted accordingly. It is also clear that the deviation of the semilogarithmic plot from simple linear first order kinetic behaviour presents in a very direct way the fact that the surface redox kinetics are more complex than expected . This is a compelling reason why the technique of potential step chronoamperometry is to be preferred over that of cyclic voltammetry.
This discrepancy is attributed to the energetic non- equivalence of the GOx molecules on the nanotubes. It is safe to assume that the orientation of the protein structure with respect to the nanotube platform is not uniform. This means that the FAD sites in each molecule are various distances from the nanotubes, so a variation in the magnitude of the rate constant quantifying the ET kinetics between the flavin active site and the nanotube surface is observed. There exists an undefined spatial relationship between the protein and the SWCNTs. Furthermore, some sites on the nanotubes are more active than others due to the presence or absence of oxygenated defects. Also, it has been established that SWCNTs show a range of conductivity [
1]. These factors all serve to increase the spread of observed rate constants.
Figure 19.
Semi – logarithmic chronoamperometric plot recorded for (a) the oxidation of FADH2 and (b) the reduction of FAD at a SWCNT/GOx/Nafion-modified gold electrode. The electrolyte used was a 50 mM phosphate buffer (pH 7).
Figure 19.
Semi – logarithmic chronoamperometric plot recorded for (a) the oxidation of FADH2 and (b) the reduction of FAD at a SWCNT/GOx/Nafion-modified gold electrode. The electrolyte used was a 50 mM phosphate buffer (pH 7).
The Gaussian Model
Typically when heterogeneous systems such as hydrated oxide thin films, fluorescence decay in membranes, semiconductor nanoparticle dispersions are subjected to a kinetic analysis, curved semilogarithmic plots are often observed (as presented in
figure 19) when the data is tested for first order kinetics. Albery and co-workers [
37] have proposed that it is possible to present an alternative model for kinetics in these dispersed systems. In this approach one assumes a Gaussian distribution in the
free energy of activation for the kinetic process and consequently in the
logarithm of the rate constant about some mean value. In short a log-normal distribution is assumed [
38]. Hence one single adjustable parameter is only introduced- the width γ of the distribution. When γ = 0 there is no dispersion and the system behaves in a classical homogeneous fashion and first order kinetics are observed.
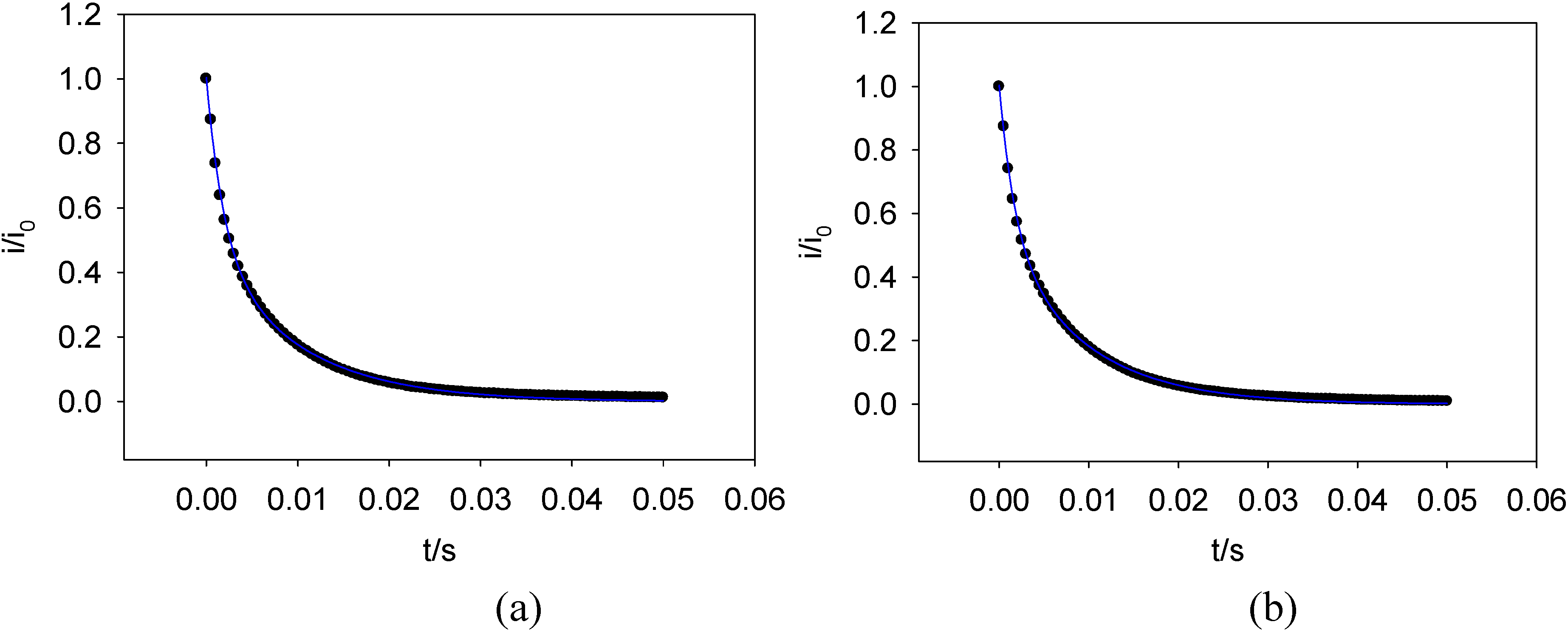
Figure 20.
Potential step chronoamperometry transients recorded for (a) GOx oxidation (potential step -500 to - 300 mV ) and (b) GOx reduction (potential step from – 300 to – 500 mV) fit via SIGMAPLOT to the four parameter biexponential model. Phosphate buffer solution pH 7.
Figure 20.
Potential step chronoamperometry transients recorded for (a) GOx oxidation (potential step -500 to - 300 mV ) and (b) GOx reduction (potential step from – 300 to – 500 mV) fit via SIGMAPLOT to the four parameter biexponential model. Phosphate buffer solution pH 7.
We assume that the free energy of activation for the enzyme redox process is given by the following expression
where
denotes the mean free energy of activation and γ denotes the spread parameter. The quantity χ denotes the co-ordinate characterizing the Gaussian Distribution. Note that when γ = 0
and there is no dispersive spread. The kinetics are simple first order. We define
to be the heterogeneous electron transfer rate constant for the most probable state and write that the dispersion in first order rate constants is
We also define a normalized time
related to the mean rate constant
via
. Now the first order rate equation for surface adsorbed enzyme is given by
Integrating we obtain
and so simplifying we obtain
We now integrate across the Gaussian distribution and note that the decay of the surface concentration of species Γ from their initial value Γ
0 is given by
where we note that the Gaussian integral takes the following form
It is satisfactory to note that when γ = 0 corresponding to the absence of kinetic dispersion, eqn. 39 reduces to
corresponding to simple first order exponential decay.
Now the net current i is given by
The integral
on the rhs of eqn.42 must be solved numerically. We note that:
where
To proceed further we follow the procedure first outlined by Albery and co-workers [
37] and utilize the following transformation:
Hence when
and so the integrals outlined in eqn.44 reduce to
where we have used the following identities
Hence we obtain that
where we define
Hence the current transient may be computed from eqn.42 using eqn.49 and eqn.50. Similarly, the integral outlined in eqn.39 may be integrated in a similar manner
where
The population of Gaussian distributed redox states computed numerically via the extended Simpsons rule [
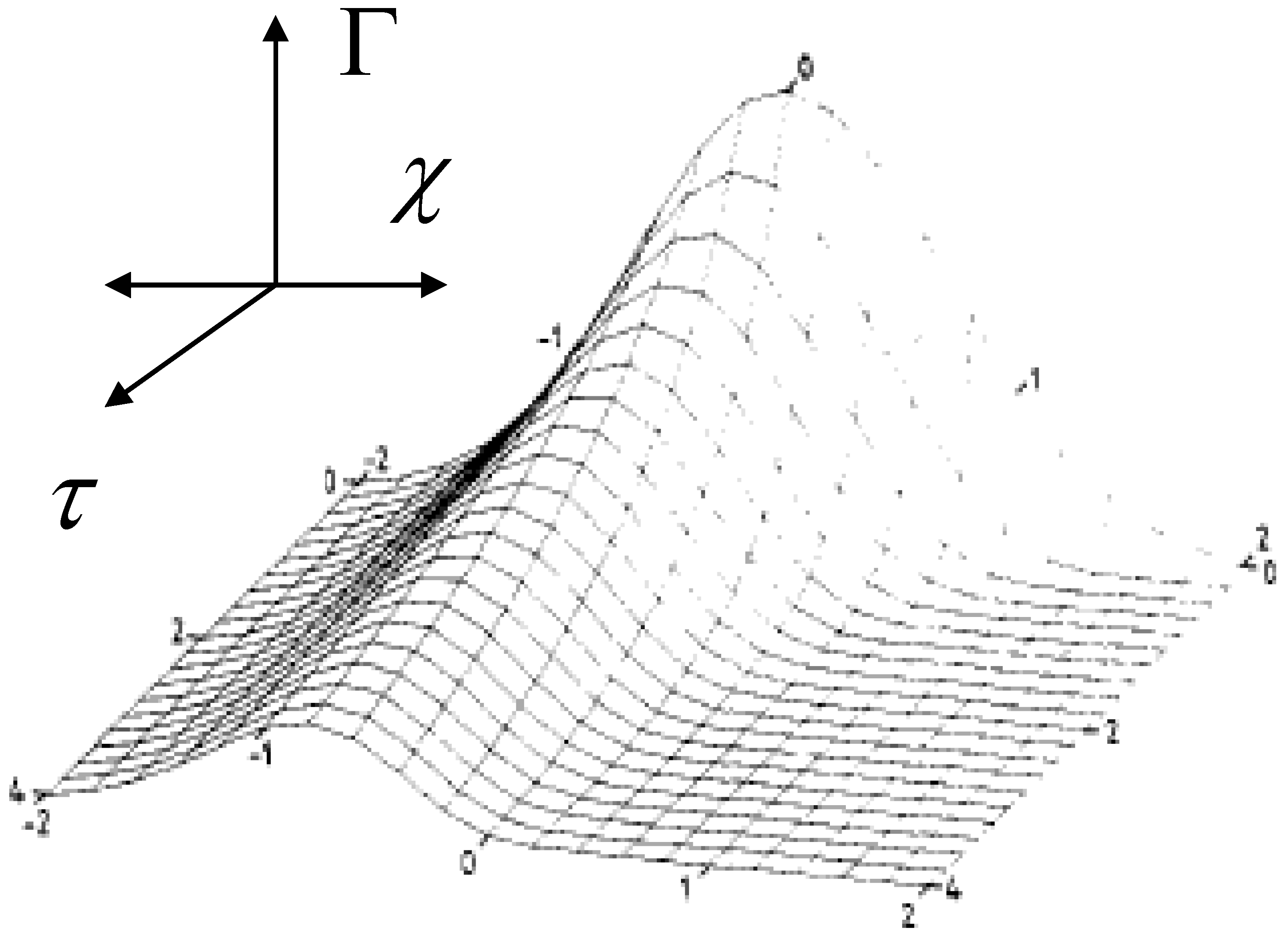
37] with γ = 2 is outlined in
figure 21.
Figure 21.
The decay of the Gaussian population calculated using eqn.51 with spread parameter γ = 2.
Figure 21.
The decay of the Gaussian population calculated using eqn.51 with spread parameter γ = 2.
We note from this 3D surface plot calculated from eqn.51 that as the reaction proceeds (as τ increases) the original symmetrical Gaussian profile becomes skewed to those species with lower rate constants. These slower species predominate in the latter stages of a chronoamperometric experiment giving rise to the type of curvature seen in the semi-logarithmic plots presented in
figure 20. It also indicates why a simple bi-exponential model is not the best method for analysis of chronoamperometric transients. The values for the fast and slow rate constants extracted from the latter type of analysis will depend on the magnitude of the time window over which the potential pulse is applied. Hence the Gaussian model with the derivation of an average rate constant along with a measure of the dispersive spread γ is a much better approach. It should be noted that when analyzing current transients the faster redox sites make a greater contribution to the observed redox current.
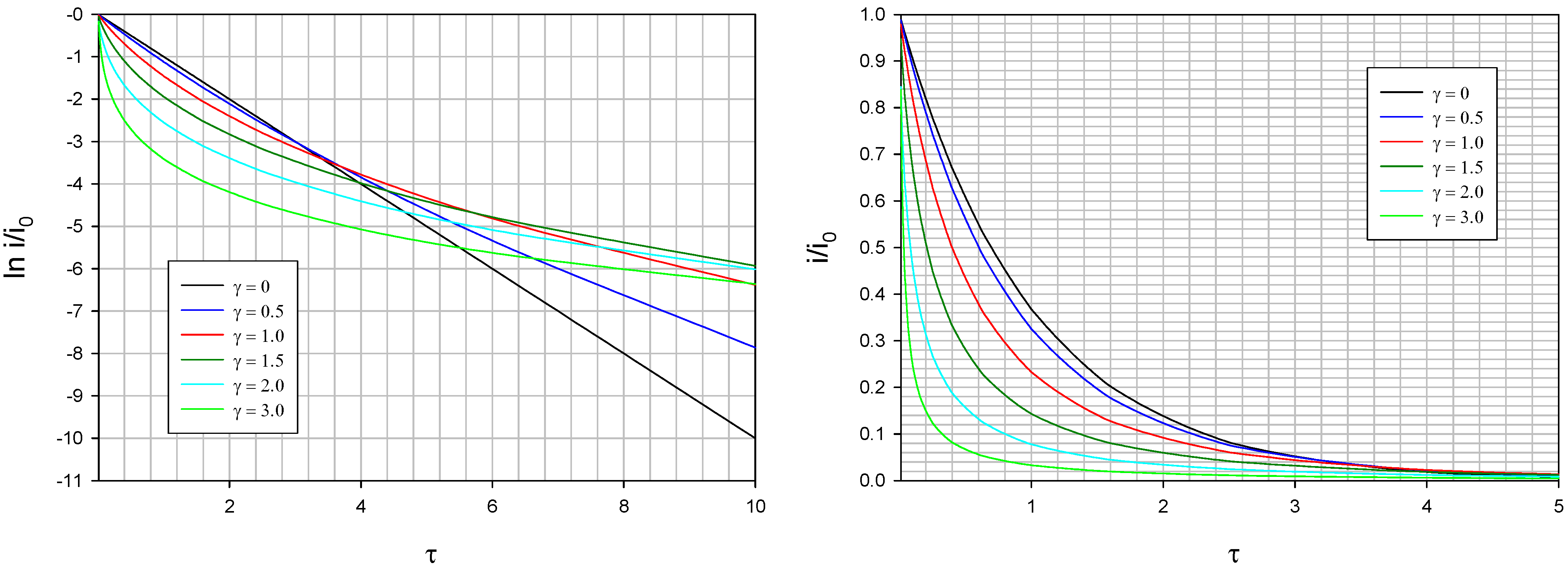
Typical theoretical current transients computed via eqn.42 using eqn.49 and eqn.50 are presented below in
figure 22. We note that the current decays more rapidly as the value of the Gaussian spread parameter γ increases. We also note that the deviation from linearity in the semi logarithmic plot presented in
figure 22b also increases significantly when the dispersive spread parameter γ increases.
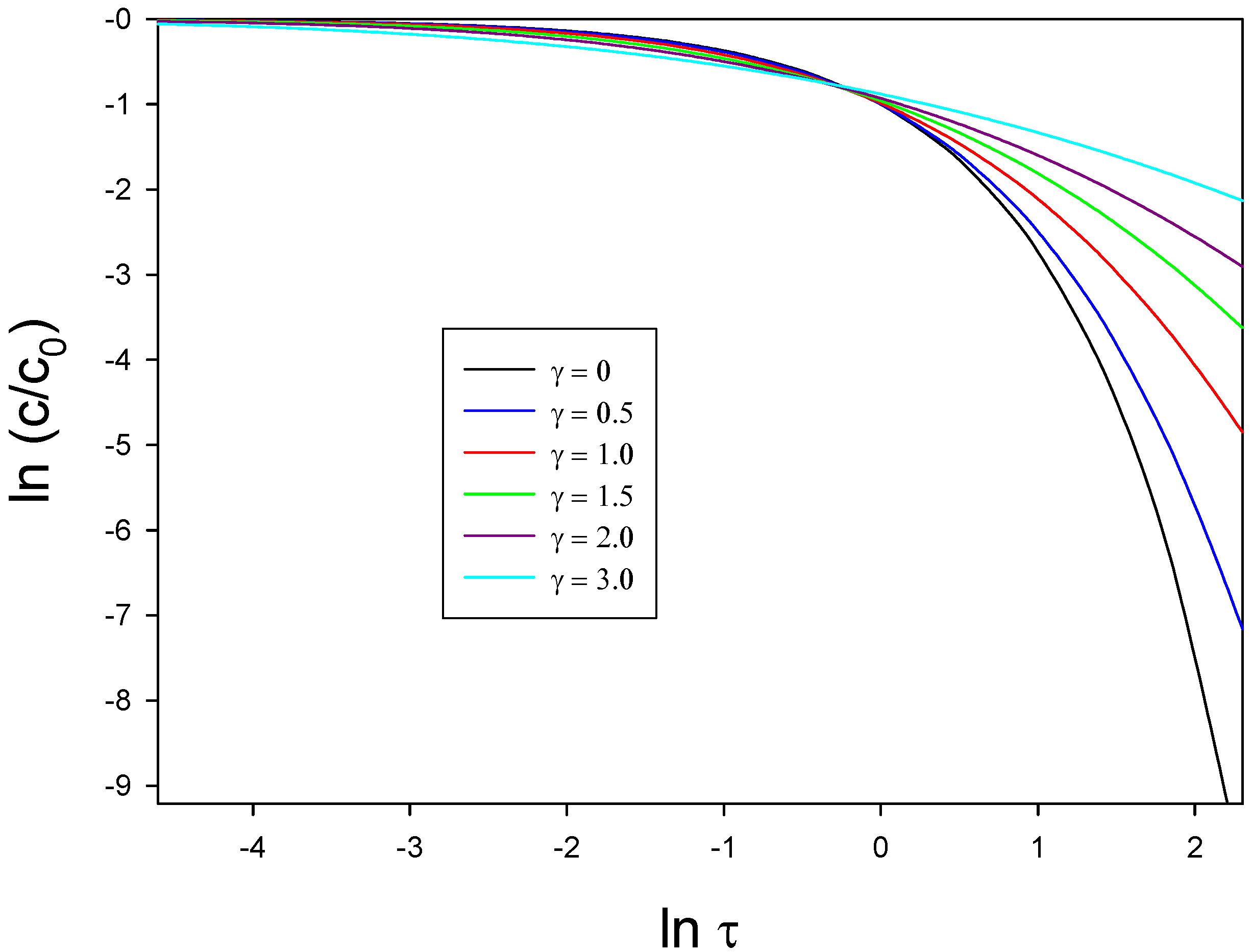
The calculations derived using eqn.51 are also presented in terms of a double logarithmic plot in
figure 23. The latter form a working curve of
versus
. Experimentally derived data may be readily recast into equivalent format and the experimental curve can then be matched to the theoretical curve by adjusting the displacements on both the x and y axes. In this way the Gaussian spread parameter may be determined.
Alternatively, to determine a value of the spread parameter from experimental data one can follow the procedure originally suggested by Albery and co-workers [
37]. In this work it was suggested that the ratio of
to
be measured where
defined the half life of the reaction and
defines the time when one eight of the original reactant species remains. The following empirical relationship between γ and the latter parameters has been proposed:
It was also suggested that the mean rate constant could be evaluated from the latter relationship
where
is the time when the current has decayed to 1/e (~0.37) of its initial value. In practical terms, this is simply the time when the ratio i / i
0 is approximately 0.63, or ln (i /i
0) is around -0.46. Our experimental findings, measured at pH 7 are summarized in
Table 2. It is clear from this data that the rate constant as estimated from the simple Laviron analysis is considerably less than that estimated using the Gaussian model. Hence we conclude that the neglect of kinetic dispersion will result in a serious under-estimation of the heterogeneous electrochemical rate constant for the redox transformation of an immobilized redox active moiety.
Figure 22.
(a) Typical normalized current transients calculated for various values of the Gaussian spread parameter γ. (b) Semi-logarithmic representation of the data presented in fig.22(a), again as a function of spread parameter.
Figure 22.
(a) Typical normalized current transients calculated for various values of the Gaussian spread parameter γ. (b) Semi-logarithmic representation of the data presented in fig.22(a), again as a function of spread parameter.
It is well established that the redox chemistry of the FAD/FADH
2 reaction is pH dependent. We therefore measured the heterogeneous electron transfer rate constant for the latter process as a function of solution pH via analysis of the potential step chronoamperometric response and using the Gaussian dispersive spread model. Our findings are presented in
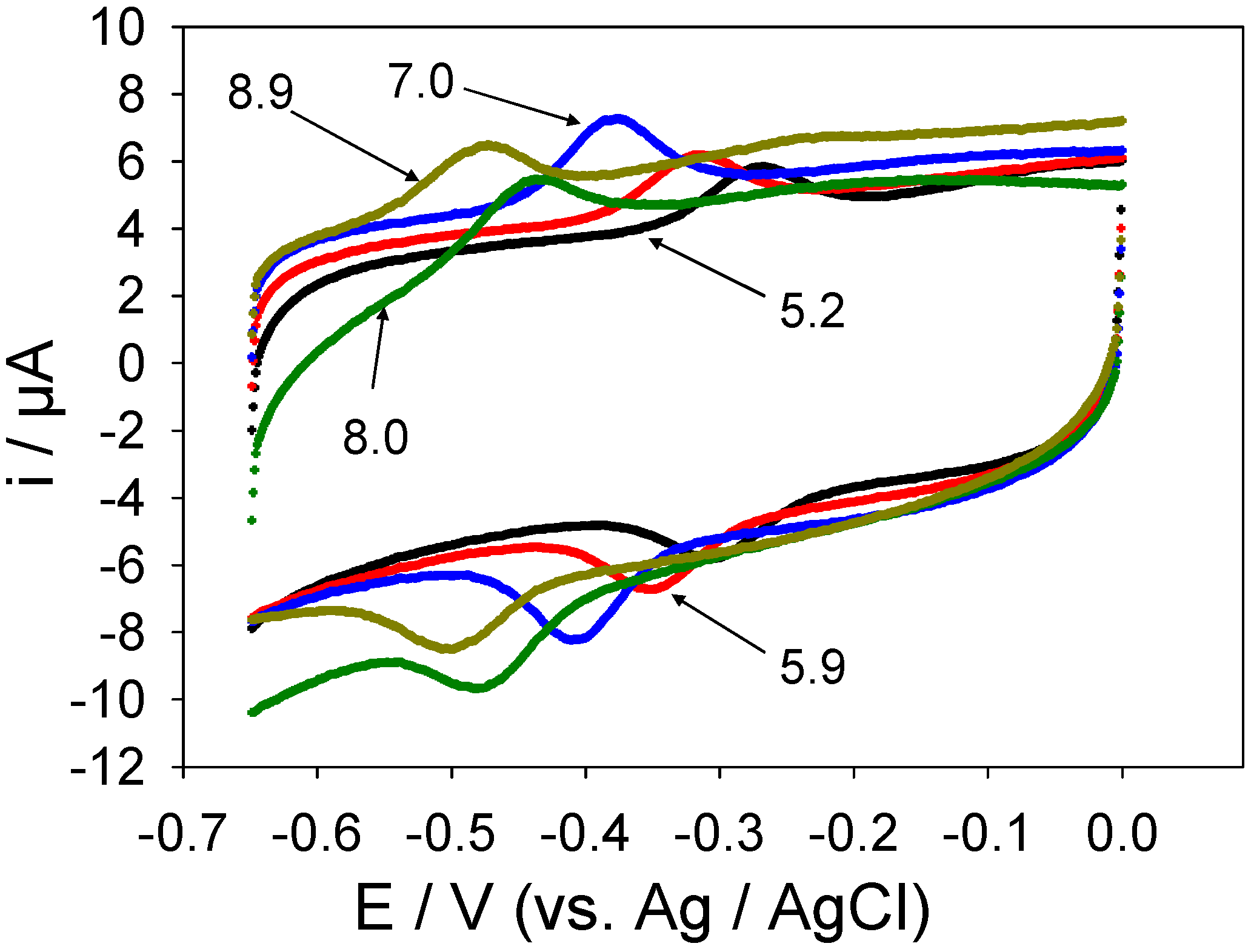
table 3. Over the pH range studied, it is clear that the rate of the redox transition increases with increasing pH, whereas the latter does not influence the degree of kinetic dispersion to any appreciable extent. The values determined for the rate constants are quite large and imply an efficient turnover of the redox enzyme oxidation state at the carbon nanotube surface. This observation augers well for biosensor applications.
Figure 23.
Typical double logarithmic plots calculated for various values of the Gaussian spread parameter γ.
Figure 23.
Typical double logarithmic plots calculated for various values of the Gaussian spread parameter γ.
Table 2.
Analysis of chronoamperometric transients viathe simple Laviron model and via the Gaussian spread model.
Table 2.
Analysis of chronoamperometric transients viathe simple Laviron model and via the Gaussian spread model.
| Working Electrode | Laviron
model
kET / s-1 | Gaussian
model
<kET>/ s-1 | Spread
Parameter
γ |
| Au/SWCNT/GOx/Nafion | 19 | 830 | 0.9 |
| GC/SWCNT/GOx/Nafion | 18 | 950 | 1.2 |
Table 3.
Analysis of the FAD/FADH2 ET kinetics as function of solution pH.
Table 3.
Analysis of the FAD/FADH2 ET kinetics as function of solution pH.
| Solution pH | mean rate constant
<kET> / s-1 | Gaussian
spread parameter
γ |
|---|
| 5.2 | 500 | 0.8 |
| 5.9 | 625 | 0.8 |
| 7.0 | 830 | 0.9 |
| 8.0 | 1250 | 1.0 |
| 8.9 | 1600 | 1.0 |