1. Introduction
Remote detection and identification of chemical plumes using airborne passive infrared (IR) sensors is a challenging problem. Our goal is to detect weak gaseous chemical plumes in cluttered scenes that contain a mixture of background types, such as water, vegetation, asphalt, concrete, buildings, etc. Data from a typical scene consists of the measured, calibrated radiance r for each of many wavelengths (covering some subset of the visible to the long-wave IR regions using approximately 128 to 256 spectral channels spanning wavelengths from approximately 0.5 to 15 μm) in each of approximately 500 x 500 spatial pixels (in both the cross-tracking direction and the with-tracking direction of the airplane carrying the IR sensor). The measured signal at each pixel depends on the atmosphere and ground radiance, atmospheric transmission, instrument noise, and whether a chemical plume lies between the ground and the detector. The relative contributions of these various factors changes with wavelength, so that in principle, the composition of the background and the plume can be estimated.
We seek to determine whether small (up to a few or a few tens of pixels out of tens or hundreds of thousands of pixels) and weak (both in terms of temperature contrast and chemical strength, see
section 3) plumes from a known library of possible chemicals might be present in the scene. These chemicals have effects on the measured at-sensor radiance that we refer to as “chemical signatures,” which are based on “known” spectra (the spectral library values are not known perfectly) that must be transformed (introducing an error source). Therefore, the “chemical signatures” are also not known perfectly.
Most real scenes look to the human eye like a mixture of components (Scene A, in
Figure 1, [
1,
2]) and this background mixture is called “clutter.” However, whether formal mixture models consisting of mixing multiple components such as water, asphalt, vegetation, etc. (which each have multivariate distributions) are effective for analysis depends on the goals. A single-component multivariate Gaussian (SCMG) refers to a Gaussian distribution having a single mean vector and covariance matrix. Although modeling clutter as a SCMG may seem too simplistic, it has proven to be surprisingly effective for weak chemical plume detection (see
section 7) when compared to other approaches that have been proposed for IR data [
3,
4,
5,
6,
7,
8,
9,
10].
This paper emphasizes issues that impact performance in detecting weak plumes and quantifying the chemicals in a weak plume. Performance is typically defined as the probability of detecting a plume for a given, fixed, and small false alarm probability.
Section 2 gives additional background.
Section 3 describes the physical model for calibrated, measured IR radiance at aircraft elevation including atmospheric, ground, plume, and sensor effects.
Section 4 and
Section 5 describe model simplifications involving background (nonplume) clutter and linearization of nonlinear plume effects (including the well-known temperature-emissivity separation challenge). This description clarifies inherent error sources and error sources introduced by model simplifications.
Section 6 is a problem and solution taxonomy.
Section 7 describes current inferences algorithms (linear and nonlinear), associated statistical issues, and factors impacting performance and performance indicators.
Section 8 includes related topics and provides addition detail including research areas for some of the topics discussed in previous sections.
Section 8 lists key definitions.
Section 9 summarizes.
2. Background
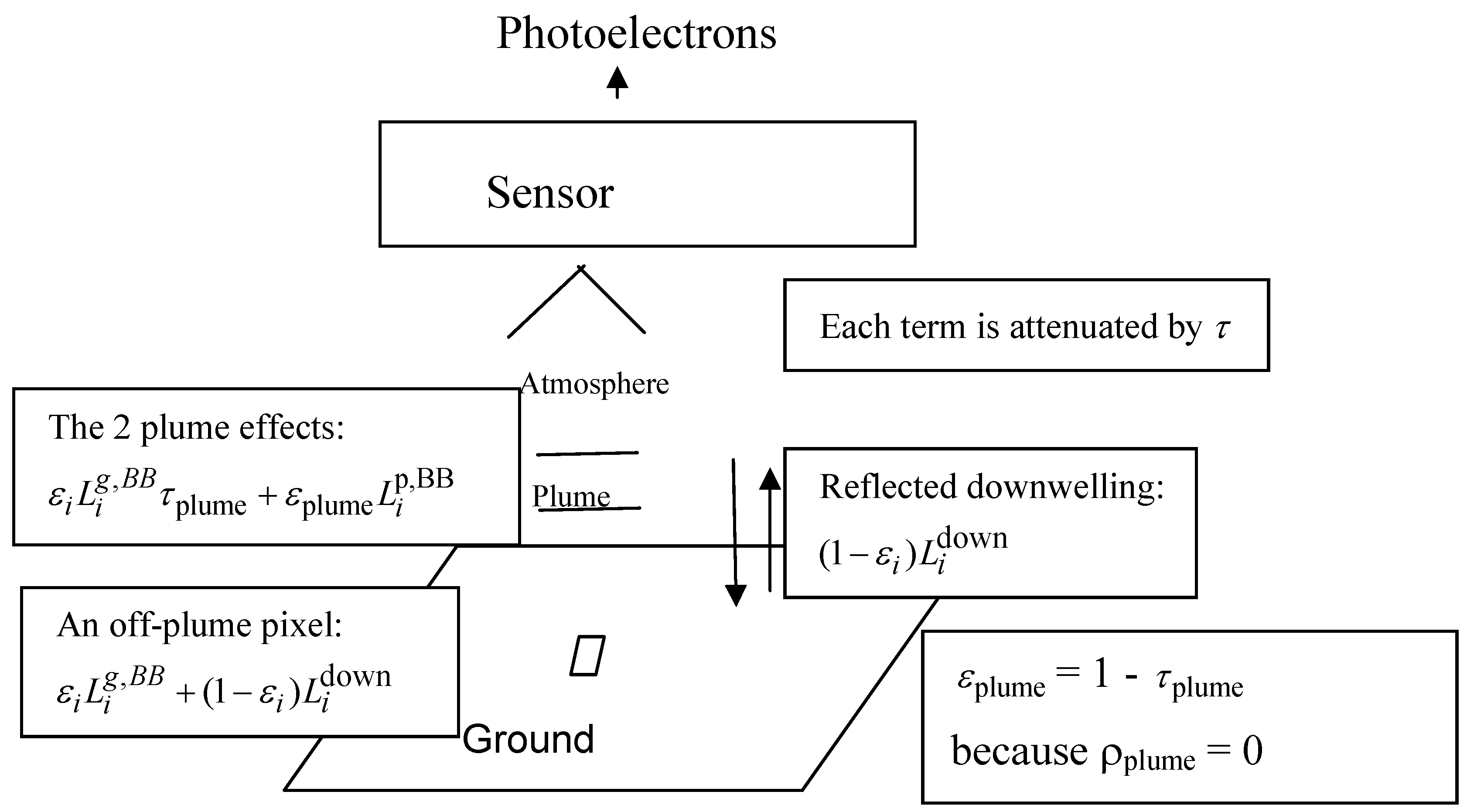
Figure 2 is a simple schematic of the basic sensor and scene setting. Typically, each pixel represents a ground area covering ~10 to ~100
m2. Plume-like pixels are those thought to have a gas plume influencing the signal; background pixels are those thought not to have a plume influencing the signal.
Section 3 describes the terms used in the physical models that are indicated in
Figure 2.
Detecting gaseous plumes in cluttered scenes using hyperspectral images has received growing attention, dating to approximately 1995 when hyperspectral (having relatively many spectral channels) imaging systems were deployed and analysts began to develop detection and quantification methods [
1,
2]. This review focuses on identifying weak, rare, but approximately known targets (chemical signatures) in cluttered backgrounds of varying radiance values using one (or one time-averaged) image consisting of
p wavelengths (spectral channels) in the IR region. Applications include detection of chemical and biological weapons as they are being developed and/or being used, and environmental monitoring. Qualitatively, the main task is to look for evidence of one or more chemical signatures from a “known” library in a scene that is cluttered due to variation in ground materials, ground temperatures and shading, atmospheric effects, viewing angle, and sensor noise. An associated task is to assess our confidence in finding and quantifying such signatures. Confidence assessments often rely on model assumptions and/or computationally-intensive empirical studies.
Figure 1.
Scene A. Typical broadband image of a scene that is cluttered because it includes mountains, buildings, and water, but contains no plumes. Similar images are available from the Jet Propulsion Lab’s AVIRIS website [
1]. The two white ovals are hypothetical results of a plume-detection method, indicating either false alarms or the presence of gaseous plumes along the lake shore.
Figure 1.
Scene A. Typical broadband image of a scene that is cluttered because it includes mountains, buildings, and water, but contains no plumes. Similar images are available from the Jet Propulsion Lab’s AVIRIS website [
1]. The two white ovals are hypothetical results of a plume-detection method, indicating either false alarms or the presence of gaseous plumes along the lake shore.
IR hyperspectral imagery can be used to characterize plumes. By “characterize,” we mean either to detect (locate pixels that contain a plume), to detect and identify (identify the chemical components), or to detect, identify, and quantify the plume components (and possibly plume temperature), depending on the context. In addition, background scenes can be segmented using various clustering methods; only when such clustering is part of the plume-characterization [
11] will it be within our scope (
section 8). More broadly, other targets (including solid or liquid targets) can be discovered using IR, but our scope is gaseous plume characterization [
3,
4,
5,
6,
7,
8,
9,
10].
IR is challenging, because nearly everything (solids, liquids, and gases) emits and/or absorbs in the IR region of the spectrum. The visible, near IR, short-wave IR, mid-wave IR, and long-wave IR regions each have unique challenges and opportunities, but we consider broad issues that apply generally for the entire near IR and IR regions. We consider only one (or one time-averaged) IR image. Other approaches become available if the ground pixels are viewed more than once or if specific regions of the spectrum are used. For example, it is believed that mid-wave IR data might allow the opportunity to observe plume effects twice, allowing for improved inference and confidence assessments. Using mid-wave IR, the first observed plume effect is explained as in
section 3 (
Figure 2) when the plume lies in the direct line of sight between the sensor and the corresponding ground pixels. The second observed plume effect is a shadow effect whereby certain pixels when viewed from directly above will be in the shadow from the sun of a small off-the-ground plume that is some distance removed from the direct line of sight to the sensor.
Figure 2.
Simple description of on-plume and off-plume pixels. Off-plume pixels contribute where is the term describing Planck’s radiation law for an ideal black body, is the ground emissivity, which is less that 1 for real surfaces, and is the reflected downwelling atmospheric radiation. A plume has two effects: it absorbs some of the emitted ground radiation, and it emits radiation. The emitted ground radiation that transmits through the plume is described using and the plume emission is All terms are attenuated by transmission through the atmosphere, . This paper focuses on small (impacting up to tens of pixels among tens of thousands of pixels) and weak gaseous plumes. Weak plumes in this context are also called optically thin plumes, meaning that where Ck is the concentration of chemical k integrated over the pathlength through the plume and σk is the chemical spectra for chemical k. This results in approximately a linear relation between plume absorption (or emission) and either of plume thickness, chemical concentration, or the temperature contrast between the ground and plume.
Figure 2.
Simple description of on-plume and off-plume pixels. Off-plume pixels contribute where is the term describing Planck’s radiation law for an ideal black body, is the ground emissivity, which is less that 1 for real surfaces, and is the reflected downwelling atmospheric radiation. A plume has two effects: it absorbs some of the emitted ground radiation, and it emits radiation. The emitted ground radiation that transmits through the plume is described using and the plume emission is All terms are attenuated by transmission through the atmosphere, . This paper focuses on small (impacting up to tens of pixels among tens of thousands of pixels) and weak gaseous plumes. Weak plumes in this context are also called optically thin plumes, meaning that where Ck is the concentration of chemical k integrated over the pathlength through the plume and σk is the chemical spectra for chemical k. This results in approximately a linear relation between plume absorption (or emission) and either of plume thickness, chemical concentration, or the temperature contrast between the ground and plume.
![Sensors 06 01721 g002]()
Figure 1 is the broadband image (the average radiance over all
p = 224 spectral channels) of an example scene (614 vertical by 512 horizontal pixels) that is cluttered because it contains mountains, buildings, and water, but contains no plumes. This scene is in the visible/near IR region [
1,
2], and for our purposes can be considered to have the save features as do IR images. IR images are typically displayed for the human eye using gray scale to represent scalar-valued radiance magnitude at each pixel. The scalar value is typically the broadband image or an average of a subset of the spectral channels.
4. Background Clutter
Several studies have investigated the distribution of background clutter [
7,
15,
18,
19,
20,
21,
22,
23,
24,
25] in IR scenes. There is complete agreement that the distribution of
is not accurately described as a SCMG. However, which model is most appropriate depends on the goals. As discussed in
section 7, for the weak plume detection goal, there also is reasonably good agreement that algorithms based on the SCMG model for clutter are surprisingly effective. For example, references [
3,
4,
5,
6,
7,
8,
9,
10] conclude either that the simplistic SCMG approach is the overall best method or is not much worse than other methods.
There are several implications of concluding that an SCMG model is effective in our context. First, it is a simple model-based summary of complicated clutter. Second, decision thresholds could be based on SCMG data, and therefore could be computed analytically (analogous, for example, to claiming that a decision threshold of
standard deviations corresponds to a 5% false alarm probability by appealing to a Gaussian approximation). Third, it would suggest that it might be difficult to find robust methods that improve the GLS plume-detection performance (defined as the false negative rate for a given small fixed positive rate). However, if the SCMG model is inadequate, a scene-specific empirical reference distribution could be used to select decision thresholds and associated confidence measures (see
Section 8.6).
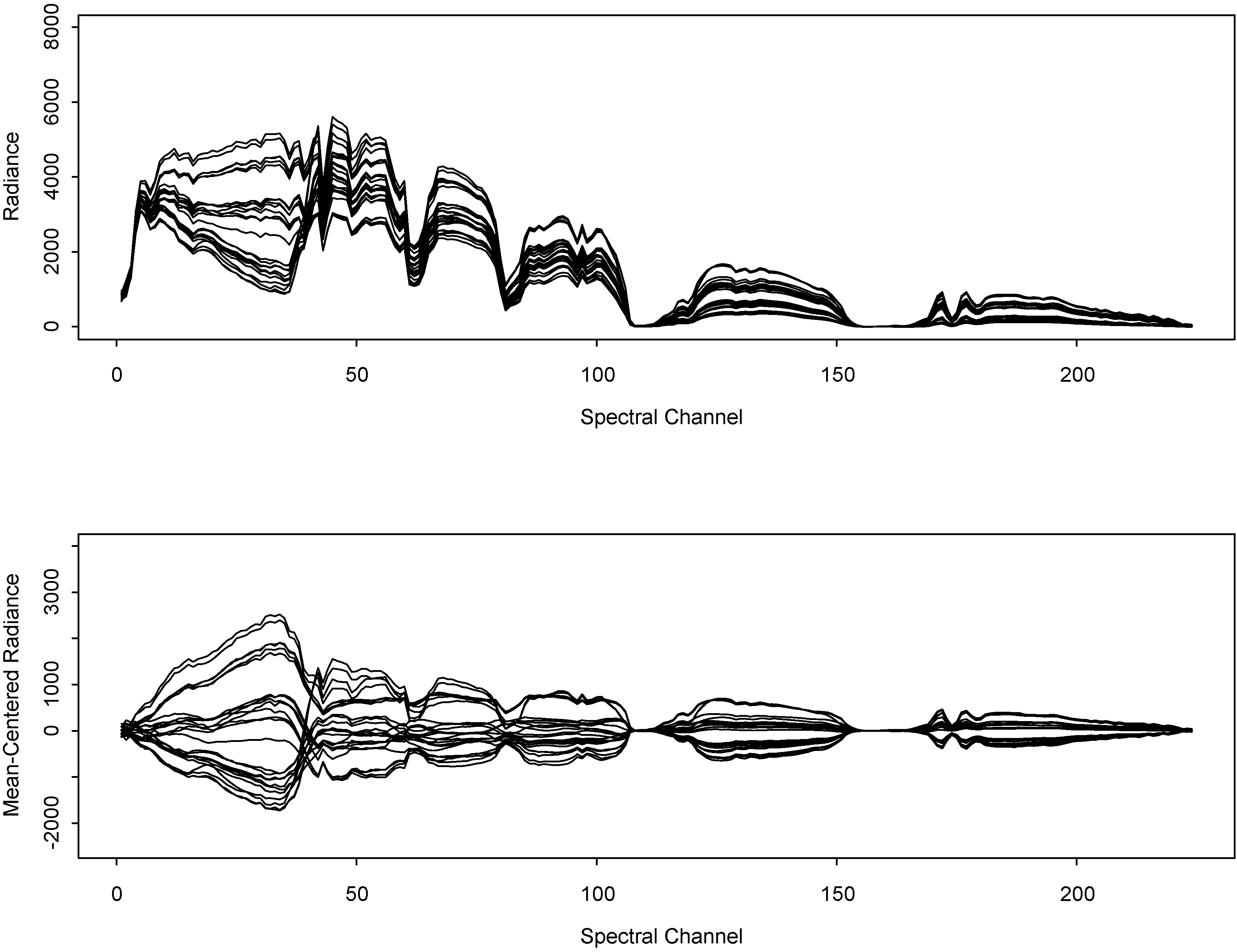
Figure 3 plots the
p = 224 channel response from each of several selected pixels from scene A. The mean-centered radiance (bottom plot) for the selected pixels exhibits long runs of either positive (above the mean) or negative (below the mean) values. This is a type of mixture distribution that might be expected for
on the basis of looking at cluttered scenes such as Scene A, which have contiguous patches of lower-than-average or higher-than-average emissivities and is a clear departure from the one-component multivariate Gaussian assumption.
Figure 3.
Example radiance (top) and mean-centered radiance (bottom) from selected pixelsin scene A.
Figure 3.
Example radiance (top) and mean-centered radiance (bottom) from selected pixelsin scene A.
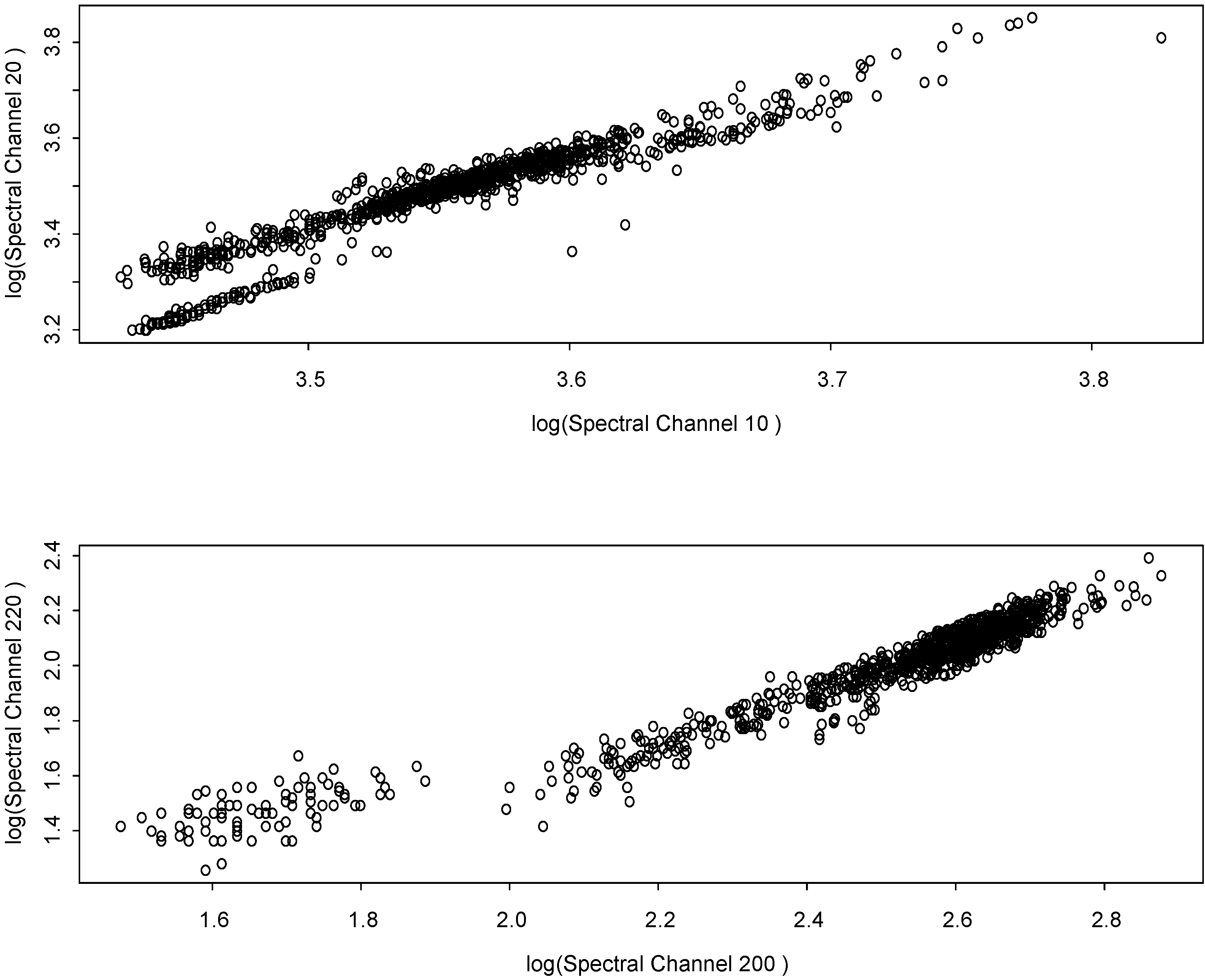
The scatter plots in
Figure 4 are two sets of log-transformed (base 10) values from two pairs of spectral channels from each of 1000 randomly-chosen pixels from Scene A. Both plots appear to have at least two or three distinct clusters (probably corresponding to distinct ground components in the scene), which is another indication of non-Gaussian behavior. If the distribution across pixels were more nearly bivariate Gaussian, these scatter plots would be elliptical, without clusters.
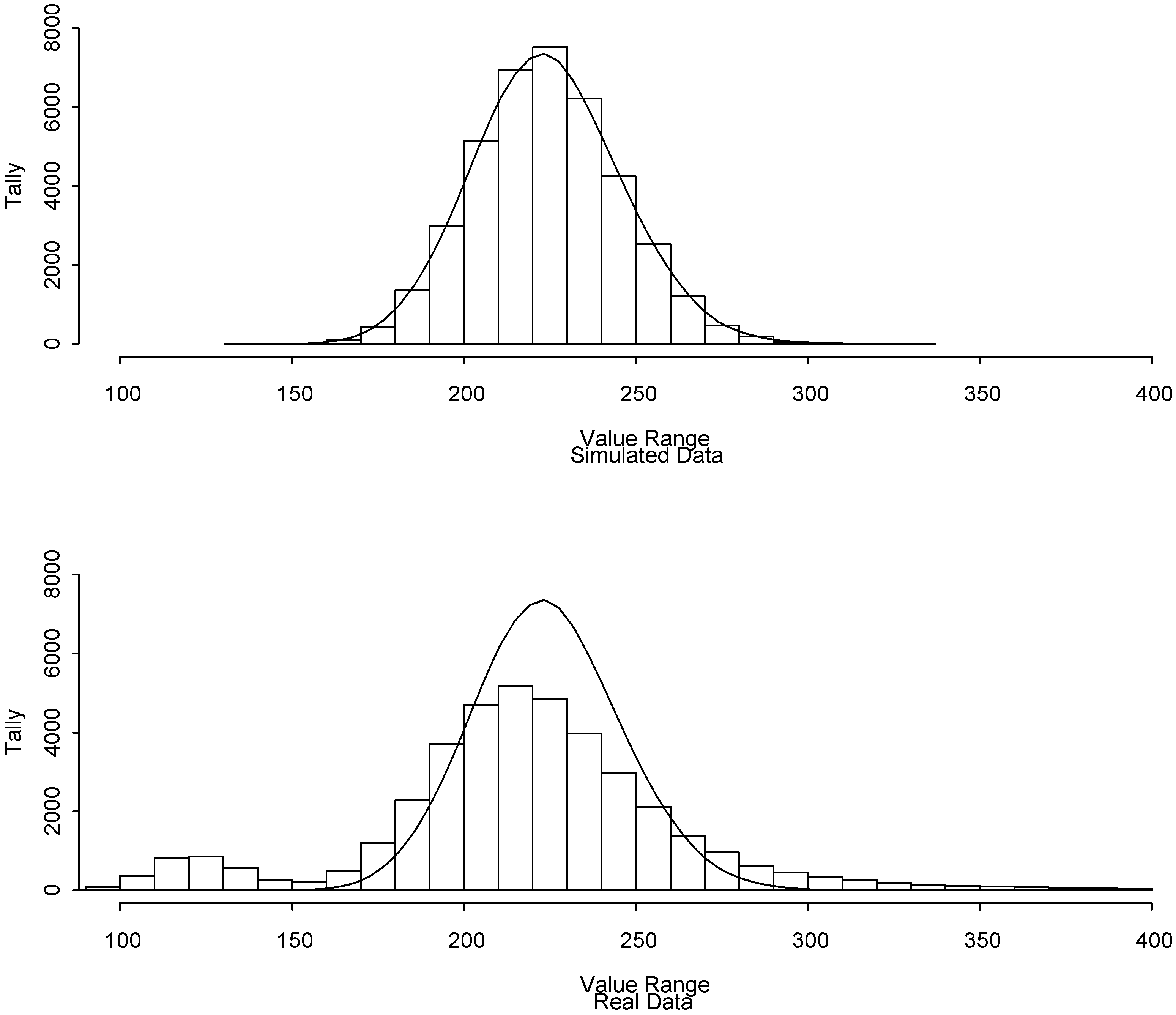
Figure 5 (top plot) is a histogram of 40000 randomly-generated values of the squared Mahalanobis distance defined as
[
21]. The MD
2 values in the top plot are distributed as a χ
2(
p) (chi-squared with
p degrees of freedom) random variable because the radiance
r values were simulated from the N(0,
) distribution with
estimated from Scene A. The top plot is substantially different from the bottom plot, which is 40000 randomly-selected MD
2 values from scene A. This also indicates that the
r values from scene A are not well modeled in this context by the N(0,
) distribution. The corresponding χ
2(
p) probabilities are given by the smooth density function in both the top and bottom plots. It is evident that the χ
2(
p) probabilities fit the top plot but not the bottom plot.
Figure 4.
Scatter plot of two sets of log-transformed (log base 10) spectral channel pairs, each from the same 1000 randomly-selected pixels from scene A.
Figure 4.
Scatter plot of two sets of log-transformed (log base 10) spectral channel pairs, each from the same 1000 randomly-selected pixels from scene A.
Several studies have observed that MD
2 values from IR scenes are not well approximated by a χ
2(
p) distribution. For example, [
21] used plots similar to
Figure 5, and also used four quantitative distances for comparing two distributions to demonstrate departure from χ
2(
p) behavior. Of the four distances, the distance that is most appropriate in our context was the “exceedance metric,” which summed the absolute values of quantiles of the two distributions. The
pth quantile
=
xp of a distribution
F(
x) is the value
xp such that 100
p% of the values generated from
F are less than
xp, and the exceedance metric between two distributions
F and
G (defined as
) was evaluated using
K equally spaced probabilities (on a logarithm scale). The choice of
K and the spacing of the
pi is arbitrary, but provided these are chosen before observing the data, this is a reasonable measure of distance between any two distributions.
Section 8 describes why another appropriate distance measure in our context is to compare one or a few specific quantiles or to compare percentages that exceed specified thresholds.
The observed tendency for
MD2 values from IR scenes to be poorly modeled by a χ
2(
p) distribution has led to consideration of elliptically-contoured (EC) distributions. These EC distributions generalize the multivariate Gaussian in a way that allows for longer and fatter tails; however, as seen in the bottom plot of
Figure 5 (and in the “stair-step” plots in [
21]), the
MD2 values from real scenes also exhibit clustering, which is not predicted by any EC distribution. This has led to various mixture strategies such as fitting the main body of the
MD2 values with one EC distribution (often close to Gaussian) and the tail of the
MD2 values with a second EC distribution (often not close to Gaussian).
Figure 5.
The squared Mahalanobis distances from 40000 (top) simulated r values; (bottom) from randomly-chosen r values from pixels from Scene A. The smooth curve in both plots is based on the χ2(p) distribution.
Figure 5.
The squared Mahalanobis distances from 40000 (top) simulated r values; (bottom) from randomly-chosen r values from pixels from Scene A. The smooth curve in both plots is based on the χ2(p) distribution.
For example, [
21] applied this strategy to relatively homogeneous subsets of pixels (which were located using a clustering algorithm applied to the
r values). Somewhat surprisingly, even these relatively homogeneous subsets of pixels appear to arise from a mixture distribution. This was also observed in [
26] which proposed a combination of local mean subtraction and nonparametric density estimation to estimate the distribution of
r values (Eq. (5)) for AHI (advanced hyperspectral imager) data [
27].
Nonparametric density estimation is often effective, but usually only in small dimensions; in large dimensions such as our
p = 224 case, the well-known curse of dimensionality [
28] suggests that nonparametric density estimates will be low quality. The approach in [
26] was in the context of building a model for the background data so that a potential target could be identified on the basis of being anomalous compared to the background model, without having a library of targets. It is not yet known whether the approach in [
26] is competitive when a target library is available. In addition, we point out that the simplified model that assumes
together with an estimate of
is a parametric density estimation approach because it assumes a parametric form for the density (multivariate Gaussian), and the density estimation task reduces to estimation of Σ. This mitigates the well-known curse of dimensionality, but is effective only if the multivariate normality assumption leads to acceptable target detection schemes and associated confidence measures.
Section 7 includes more detail involving the number of observations (pixels) required to estimate Σ effectively. For comparison, note that [
28] reports that to estimate the density at the mean value of a 10-parameter normal distribution requires 842,000 samples to achieve an average squared error of approximately 0.1.
One motive for fitting any distribution to real data is that it provides insight, as well as a model-based summary. Also, if the model approximates the relevant aspects of
r sufficiently well, it could provide both a way to optimize plume detection and to quantify the confidence in detected plumes. To date, there has been no fully successful demonstration of sufficiently accurate fitting of
r values across a scene using any model ([
18,
21,
22] and
section 7). In addition, fitted EC distributions focus exclusively on the scalar-valued MD
2 arising from
r values, which only partly captures the relevant aspects of
r values in the context of plume detection. Work in this area is ongoing, and a recent reference [
29] developed a method to detect outliers in EC-distributed data. It is currently unknown whether a weak chemical plume would be a sufficiently large outlier to be detected by this outlier-detection approach.
In summary, it is known that one would not choose a SCMG to describe
on the basis of the clutter (mixture distribution) that our eyes see in real scenes. However, the appropriate model depends on the goals, and we indicate in
section 7 that modeling
as a SCMG remains competitive for our plume characterization goals. There has been considerable interest in fitting EC distributions in our context, although EC distributions also do not fit the
r data particularly well. However, individual EC distributions or mixtures of EC distributions fit the distributions of MD
2 values much better than does a χ
2(
p) distribution, which arises from assuming the
r values arise from a SCMG model. Finally, it is not yet clear whether it will be useful to fit a mixture of EC distributions for the purpose of plume detection [
8,
15,
29].
5. The Target Signature
The terms
and
in the target signature
involve Planck’s blackbody function,
. The frequency ν corresponding to each wavelength channel can be known to high accuracy, although instrument resolution and drift in sensor calibration imply that the wavelengths and corresponding frequencies are not known exactly (see
section 8.11). The temperature
T is unknown, and can vary across pixels. The emissivity
is a vector of
p unknowns, although
can generally be assumed to vary slowly with frequency (see
Figure 3). Recall that the term
is sometimes neglected, depending on the wavelength region (
is small in the LWIR), but generally it contributes to the target signature in varying amounts, thus adding uncertainty to
The atmospheric transmission τ must be estimated (see
section 8.5), and the spectral library σ is also estimated (see
section 8.11) Because the number of unknowns per pixel exceeds the number of observations (wavelengths) per pixel, various approximations are used for the target signature
as we now describe.
One common approximation is based on the assumption that the plume temperature is nearly equal to the ground temperature,
, so that, for example,
can be accurately approximated using only the linear term in a Taylor series expansion [
15,
16,
17]. Then,
where
is the “temperature contrast” between the plume and ground, which can be positive or negative. It is important to recognize that the target signature can also be positive or negative, and sometimes can switch from positive to negative in the same scene even if the multiple plumes consist of the same chemical. Whether the temperature contrast can switch signs (positive to negative or negative to positive) among pixels of the same plume is another unknown that is scene-specific. This implies that inference options that impose constraints on parameter signs via prior information cannot always assume the target signature is nonnegative. Assuming the linear approximation to Planck’s function is adequate, the target signature can be approximated as
which depends on both pixel and frequency. If the target signature depends on both pixel and frequency in unknown ways due to the dependence on the emissivity
and on
then performance claims regarding target detection are difficult.
As a rough approximation, one approach is to assume
=1 for all pixels [
17], so the approximation for
Ai becomes
implying that
Ai is linear in
, and the target signature depends on
and on
.
Depending on the particular wavelength, most objects’
values vary in a non-negligible way. For example, in the long-wave IR, most
values are in the range 0.90 to 1.0 [
17]. Therefore, more correctly,
varies among pixels, as does the temperature, so there are often attempts to separately estimate temperature and emissivity. Define
and
. Then,
and
are the “signatures” that we seek evidence for, which are not dependent on
Tp, but which can be nearly collinear, leading to poor estimation performance.
Another compromise is to let
(but not temperature) vary among pixels, and then seek evidence for the “signature”
Ai as approximated in Eq. (6). Because there are more unknowns than observations, various assumptions must be made regarding
, such as spatial and/or spectral smoothness. Spatial smoothness assumes that nearby pixels have similar
values. Spectral smoothness assumes that
varies slowly with wavelength. Various “fit background” methods (
section 7) explicitly or implicitly make similar assumptions.
Although it is not necessary to separately estimate emissivity and temperature to estimate
Ai, this section illustrates that errors in
Ai are pixel-dependent because of varying temperature and background emissivity. A referee has pointed out that an effective way to reduce the errors in an estimate of
Ai that does not require separate estimates of temperature and emissivity is as follows. First estimate
Ai and the corresponding β via Eq. (4) using
where
can initially be estimated using any rough estimate of the background clutter (see
section 6.2). This leads to a refined estimate of the background clutter
, which can then be used to improve the initial estimate of
Ai.
Obtaining high-quality estimates of β using any of these methods is difficult; accuracy depends strongly on the chemicals in the plume and on
. Each of the above approaches has merit and has been applied to real and simulated data, particularly in the context of temperature-emissivity separation (TES) which is often treated separately from plume characterization (
section 7). However, a tentative finding is that more elaborate methods that account for the error in
Ai are difficult to implement (too many pixels for routine fitting) and do not substantially outperform methods that ignore errors in predictors [
6,
7,
8,
16]. Strategies to deal with these predictor errors (misspecification of the target signature) is the subject of ongoing work, and TES-related issues such as those presented here help to quantify the anticipated errors in
Ai.
To summarize, Eq. (5) is
r =
Aiβ +
z, where
r is the mean-centered measured radiation at pixel
i, β is the amount of target
Ai (
Ai is defined in Eq. (3), but various approximations are typically used, such as the approximation in Eq. (6)) present in the pixel, and
z is the mean-centered background effect (z =
) [
16]. Regardless of the approach, note that the chemical signature depends on the temperature contrast
. This is a characteristic of passive (not active) sensors [
17].
7. Inference Approaches
The inference tasks are to first locate pixels that exhibit plume-like behavior and then to select which chemicals from a chemical library are thought to be present in these plume-like pixels. Some approaches [
4,
5,
7,
8,
16] combine these tasks by first estimating β in Eq. (5) (or some version of repeated application of Eq. (5) such as the model averaging option described below) for each pixel. This requires an estimate of
.
The estimate
can be based on all pixels or on all pixels except the pixel(s) being evaluated via Eq. (5). For small plumes, there should be little difference in performance arising from using either all pixels or on all pixels except for the one(s) being evaluated. In practice, it is not known whether a real scene contains any plumes, so there is typically an iterative procedure that first assumes there are no plumes, then looks for plumes using
from the “off-plume” pixels, then removes “plume-like” pixels and re-estimates the “off-plume”
. As a practical issue, it might require too much time to re-estimate
if each pixel is to be examined individually via Eq. (5). However, plume-detection performance is expected to degrade when on-plume pixels are used to estimate the background
and
Performance also degrades if the chemical target directions are similar to the clutter directions (as defined, for example, by the eigenvector directions in the spectral decomposition of the background
[
5] ).
Another approach [
6,
19] applies the two tasks in distinct steps, although iterative estimation of Σ is still required if plume-like pixels are to be omitted from
. First there is a rapid screening to identify contiguous groups of atypical pixels and then there is an attempt to identify which chemicals are in these plume-like pixel regions. The rapid but computationally demanding screening could use a library of chemical signatures one at a time to identify contiguous pixels that all have evidence of one or more chemical signatures impacting the radiance
r. The white ovals in
Figure 1 are a hypothetical depiction of this approach. Because of background clutter and possible overlap between background radiance and chemical (target) signatures, these white ovals could be false positives. This two-step approach will fail to detect single-pixel plumes, but fitting to the pixel-group average has been shown to be effective for finding multiple-contiguous-pixel plumes [
6,
19].
The remainder of this section describes five inference options for the task of selecting which chemicals from a chemical library are thought to be in a pixel or in a “super-pixel” (a collection of contiguous pixels that was found by the rapid screening for groups of plume-like pixels). A super-pixel radiance is typically the average radiance of contiguous pixels. The contiguous pixels are chosen because they all exhibit departure in the same direction from the background model in Eq. (5), thus providing evidence that the β valuẹ for at least one chemical in the library is nonzero. If size of the chemical library is relatively small, say 20 chemicals or less, then Eq. (5) can be fit directly to a pixel or super-pixel allowing the full library to be used in one step. Alternatively, any of the techniques in the variable selection literature [
35,
36] could be considered (
section 8). However, recall that we are focusing on the case where the chemical library is larger than the number of spectral channels, so Eq. (5) is underdetermined without imposing constraints. The constraint we discuss is to assume any plume of interest will contain no more than three chemicals.
7.1 GLS and maximum penalized likelihood
The GLS solution to Eq. (5) for a given pixel is
as given in Eq. (8), which is an
p-by-k dimensional matrix consisting of
p rows (1 row per spectral channel) of
k concentration estimates [
35]. If we assume that real plumes contain at most three chemicals, then
. However, we typically must evaluate many or all possible subsets of 1, 2, or 3 chemicals. Because the number of spectral channels is typically at least 100 or more, this approach restricts attention to the overdetermined
p >
k case.
The GLS solution is also a likelihood ratio (LR) solution provided the SCMG assumption holds, so that
in Eq. (5). According to the Neyman Pearson lemma [
37], LR solutions have the desirable property of being optimal in the sense of having the smallest false negative rate for a given false positive rate. Furthermore, the
assumption leads to a convenient analytical way to quantify performance without resorting to empirical testing.
Regarding the need to estimate
, the signal processing literature [
37] refers to a constant false alarm rate detector (CFAR) as one that has a fixed and known false alarm rate. Student’s-
t distribution was developed for the case of having to estimate the variance in order to test with a CFAR statistic whether a scalar-valued mean was equal to a hypothesized value [
35]. Analogously, the need to estimate
and the desire for a CFAR statistic led Kelly [
38] to a small correction factor involving the number of pixels used in the estimate
. This small correction factor is typically ignored in images having many pixels. However, it is also known that the estimates of the smallest eigenvalues of
tend to be underestimated [
39], and this could impact OSP-like approaches that use the eigenvectors of
.
As a step towards addressing this concern, we evaluated
using varying numbers of pixels (one
r vector per pixel) from Scene A, including 1000, 2000, 3000, 4000, 5000, up to 32000 pixels. We assumed that
based on 40000 randomly selected pixels was the “true” value (having a smallest eigenvalue of approximately 1.48 and a largest eigenvalue of approximately 4.5
x 10
7), and then simulated the varying numbers of pixels. By using simulated pixel values, we could evaluate the impact of sample size alone, without considering pixel heterogeneity. In this case, there was a clear negative bias for the smallest eigenvalue that gradually decreased from approximately 40% relative error for 1000 pixels to approximately 0.5% relative error for 32000 pixels. The mean absolute difference between all
entries and all
entries decreased rapidly as the number of pixels increased from 1000 to 10000 and then very slowly decreased beyond 10000 pixels. Similarly, the sum of the eigenvalues (which equals the sum of the variances) varied erratically with large magnitude that decreased rapidly as the number of pixels increased from 1000 to 10000, and then continued to slowly decrease. The issue of sample size (number of pixels) has not been thoroughly studied in our context, but sample size is nearly always a factor that impacts performance. Qualitatively, we recognize that sample size is made artificially large by pooling heterogeneous pixels to estimate
. Some [
11,
20,
26] have worked with smaller sample sizes of more homogeneous pixels.
The GLS estimate for
must be converted to a decision regarding which chemicals are present. One option for doing so involves the use of a penalized negative log likelihood,
, where RSS
j is the residual sum of squares for subset
j, RSS
min is the minimum RSS over all fitted models, λ is a tuning parameter, and
Sj is the number of predictors (chemicals) in subset
j [
6]. The residual is the error remaining after fitting Eq. (5) using
from Eq. (8) corresponding to subset
j. Readers who are familiar with variable selection literature will recognize that the penalty-for-large-models value λ = 2 corresponds to the well-known Aikike information criterion and λ = ln(
p) corresponds to the Bayesian information criterion [
6,
36]. The “pick winner” method (as we will refer to it below) simply chooses that chemical subset that has the smallest PL value (smallest is best because this is a negative log likelihood). Among the contending models is the null model having no chemicals, so it is possible that the prediction is “no chemical present.” In practice, λ can be chosen empirically, so that a desired false alarm rate is maintained.
7.2 Bayesian Model Averaging
In order to decide which chemicals are present in a candidate plume, GLS can be applied to each subset of 1, 2, or 3 chemicals, and then Bayesian Model Averaging (BMA) [
40] can be used to estimate the probability that each chemical from the library is present. These probability estimates are impacted by nonGaussian behavior [
23,
41], implying that although the BMA outputs are in the 0 to 1 range, they do not necessarily behave as well-calibrated probabilities [
41]. Here we briefly describe BMA for subset selection.
For a given data set
D and probability model for the data, it would be ideal if we could calculate the exact probability of each subset. By Bayes theorem,
where P(
M1) is the prior probability for model (subset)
M1. This calculation requires calculation of the expression
where
is the coefficient vector for the chemicals in model
M1. Such integrals are notoriously difficult in most real problems requiring either numerical integration, analytical approximation, or Markov Chain Monte Carlo methods [
41,
42,
43]. Even if the integral could be computed accurately, we would rarely know the exact subset probabilities because real data never follows any probability model exactly. Therefore, various approximations are in common usage, with the BIC (Bayesian Information Criterion) being perhaps the most common [
40].
Following [
40],
can be approximated using the approximate result that
where
nj is the number of predictor variables in model
j (the number of chemicals from the library that are being fit in model
j),
is the residual sum of squares for model
j,
p is the number of spectral channels per pixel, and
is the ordinary least squares estimate of β
j. The BIC expression is derived using the Laplace method for approximating the integral required to calculate
, and assuming a flat prior (over the region where the integrand is nonnegligible) for the value of β
j. Model
is defined by the subset of chemicals from the full chemical library being used in a particular fit, so we use the terms “model” and “subset” interchangeably here.
The probability that chemical C is present is
, where
equals 1 if its argument is true. That is, to estimate P(C|D), we simply sum the model probabilities for each subset that includes chemical C. Although these probabilities have varying accuracy, depending on the data, BMA is one of the most effective strategies for chemical subset selection, particularly when prior information such as some chemical combinations being highly likely or unlikely is available [
40].
On the basis of one small study [
6], it appears that the “pick-winner” made that uses the penalized likelihood approach performs approximately the same as the BMA method, both with and without “errors in predictors,” in the absence of any prior information. However, because both methods evaluate many subsets (or in some cases, evaluate all subsets), there is almost no computational advantage in using the “pick-winner”
PL method; in addition, BMA performs much better [
40] if there is prior information such as restrictions on the magnitudes and/or signs of the β coefficients. Note that in our case, both methods use the strong prior information that no more than three chemicals are in a plume.
7.3 Fitting the Background Options
Recall that Eq. (5) could be replaced with Eq. (9),
where the background is explicitly modeled by fitting background endmembers rather than using
as estimated from all background pixels. The basis vectors chosen as endmembers can be obtained using principle components or, Foy and Theiler [
46] illustrated promising results using independent components. Regardless of how the endmembers are chosen, this is an OSP-type approach [
44,
45] and Bajorski [
5] provides one of the most definitive treatments of when it should outperform GLS-type approaches based on Eq. (5). If the chemical spectra considered by Bajorski [
5] had been transformed via the “whitening” transform involving multiplication by
, then a more direct comparison of the GLS and OSP approaches using libraries of transformed chemical spectra could have been made. Also, most of the results in Bajorski [
6] are available from the variable selection literature [
35,
36]. This “fit background” approach is the basis for the only currently-implemented nonlinear regression methods as described next.
7.4 Nonlinear Bayesian Regression
Heasler et al. [
7] report mixed results with an elegant nonlinear Bayesian regression (NLBR) approach that has OSP-like features as well as an attempt to estimate pixel temperature, using a library of 20 possible chemicals. This could also be applied in our setting of a large library where many small subsets of chemicals must each be separately evaluated. The OSP-like features essentially try to fit the background emissivity at each pixel. No linearization simplifications are used, so the nonlinear Planck function and plume absorption are retained. Prior mean and variances must be assigned for all parameters. The parameters include temperature, fits to the background (“endmember”) principal components, and fits to the 20 chemicals at each pixel. There has not yet been a published attempt to apply NLBR to superpixels; however, in a small experiment by the authors using known releases with well-characterized chemical ratios, NLBR applied to superpixels did worse than BMA applied to the same superpixels .
Heasler et al. [
7] discuss possible reasons the GLS approach remains competitive compared to this elegant NLBR approach. One reason is the same as mentioned in
section 5 involving TES. That is, TES can lead to highly collinear predictors, which is never good for performance or interpretation. A second reason involves the fact that NLBR must also assume a distribution for the error vector that remains after fitting pixel temperature, and fitting to the background endmembers and to the chemical signatures. Apparently, in the real scenes evaluated, this error distribution exhibits spatial clustering, possibly due to a shortcoming of the “fit background” approach or possibly due to sensor artifacts and/or drifting calibration.
Overall, NLBR should be the best approach if all important effects are well modeled, and it can clearly specify which of the physical effects in the background and/or target signature will be modeled and how. However, it has not yet found wide usage. This is partly due to the mixed results (roughly comparable to GLS results), plus it is more complicated and computationally demanding to implement. If the error distributions are specified approximately correctly, and all important effects are well modeled, then NLBR has the advantage of providing error estimates and associated confidence estimates as part of the inference. At the very least, the NLBR approach might be able to provide realistic input for how to structure the error in the signature
A (an approximation to
A is defined in Eq. (6), and other approximations to
A are also commonly used) to extend the generic errors in predictors study initiated in [
6].
7.5 Machine Learning
Foy et al. [
8] report on “the unreasonable effectiveness of the AMF (GLS)” as compared to a modified support vector machine (SVM) from the machine or statistical learning literature. The experiment involved “matched pairs,” in which chemical signatures were added to each pixel to create data to train the SVM. The experiment ignored error in the chemical signatures because the authors believe that background clutter is the major factor that limits and determines performance. Interestingly, only a two-dimensional vector from each pixel (both with and without the synthetic chemical added) was used to train the SVM, consisting of the GLS estimate
and the associated sum of squared residuals (SSR). Interestingly, the humble GLS estimate
did well compared to the SVM applied to
plus the associated SSR. Other pattern recognition methods could be attempted, using perhaps the entire
r vector rather than a two-dimensional summary.
The use of “matched pairs” in this context is not new, but typically, synthetic chemical is added to a few pixels rather than to each pixel. Adding synthetic chemical effects to each pixel creates a large training set that is useful for characterizing how well one should detect and characterize plumes in a scene that is known to have no plumes. In the analysis of a scene that might contain plumes, some caution regarding this approach is needed, unless it is also assumed as we do here, that any plume of interest is weak and small.
9. Definitions
AMF: adaptive matched filter, which we have written as . The covariance is estimated from the scene.
CFAR: constant false alarm rate
Clutter: spatial heterogeneity in multi-dimensional radiance measurements, as in
Figure 1.
GLS: generalized least squares. This is the same as the AMF.
Optically thin plume: a linear relation exists between plume absorption (or emission) and either of plume thickness, chemical concentration, or the temperature contrast between the ground and plume.
Brightness temperature: the temperature value in Planck’s blackbody radiation function that corresponds to the observed radiance
Radiance: A measure that describes the amount of electromagnetic radiation that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. The SI unit of radiance is watts per steradian per square metre (W·sr-1·m-2).
TES: temperature-emissivity separation is an attempt to separately estimate emissivity and temperature for a given pixel. For example, for a pixel containing grass, the ground radiance is , where is the Planck blackbody radiation, which depends on ground temperature T. Although has as many unknowns as observations (spectral channels), T is a single unknown, so provided various assumptions regarding spectral and/or spatial smoothness in values are adequate, TES can be fairly successful in some situations.
10. Summary
This review focused on cases where real or synthetic plumes contain one, two, or at most three gases from a library of hundreds to thousands of possible chemicals. Typically there are approximately 10000 to 500,000 pixels in a scene that has one to several weak (optically thin), small (impacting only a relatively few pixels) plumes. The number of pixels corresponding to a given plume is tens to hundreds. It is important to recognize that only chemical plumes having nonzero thermal contrast with the ground can be detected using passive IR.
Even in this relatively confined context, many technical issues regarding physical models, simplifying assumptions, and error sources arise that impact inference performance, as discussed. At the time of this review, the humble GLS approach remains surprisingly effective compared to methods having a more explicit “fit background” aspect. Most studies that come to this conclusion regarding GLS have considered one chemical at a time, representing a context where it is known that if a plume is present, then it consists of the chosen chemical.
Many believe that background clutter (arising from emissivity variation corresponding to different ground components such as water, grass, asphalt, trees, etc., and from ground temperature variation among pixels) is the main factor that limits performance. This is the reason that EC distributions have been proposed for hyperspectral IR data. EC distributions do not fit all aspects of the radiance values very well, but do fit the Mahalanobis distances that are based on radiance values better than the multivariate Gaussian does.