Multi-Camera Hierarchical Calibration and Three-Dimensional Reconstruction Method for Bulk Material Transportation System
Abstract
1. Introduction
- A multi-camera measurement theoretical framework centered on the core camera was established. The camera with the optimal field of view is selected as the core camera, a unified measurement coordinate system is constructed, and speckle structured light technology is combined to enhance material surface features, thereby improving the reliability of feature matching.
- A globally optimized hierarchical calibration strategy was proposed. A ‘monocular-binocular-multi-camera association’ hierarchical calibration method is adopted, which fully utilizes geometric constraints between multiple cameras. Through global optimization algorithms, the system calibration accuracy is improved, effectively reducing error accumulation.
- An algorithm based on multi-view depth information fusion was developed. By establishing multi-epipolar geometric constraints, multi-view disparity calculation is achieved, and reconstruction accuracy and completeness are improved through depth information fusion.
2. Materials and Methods
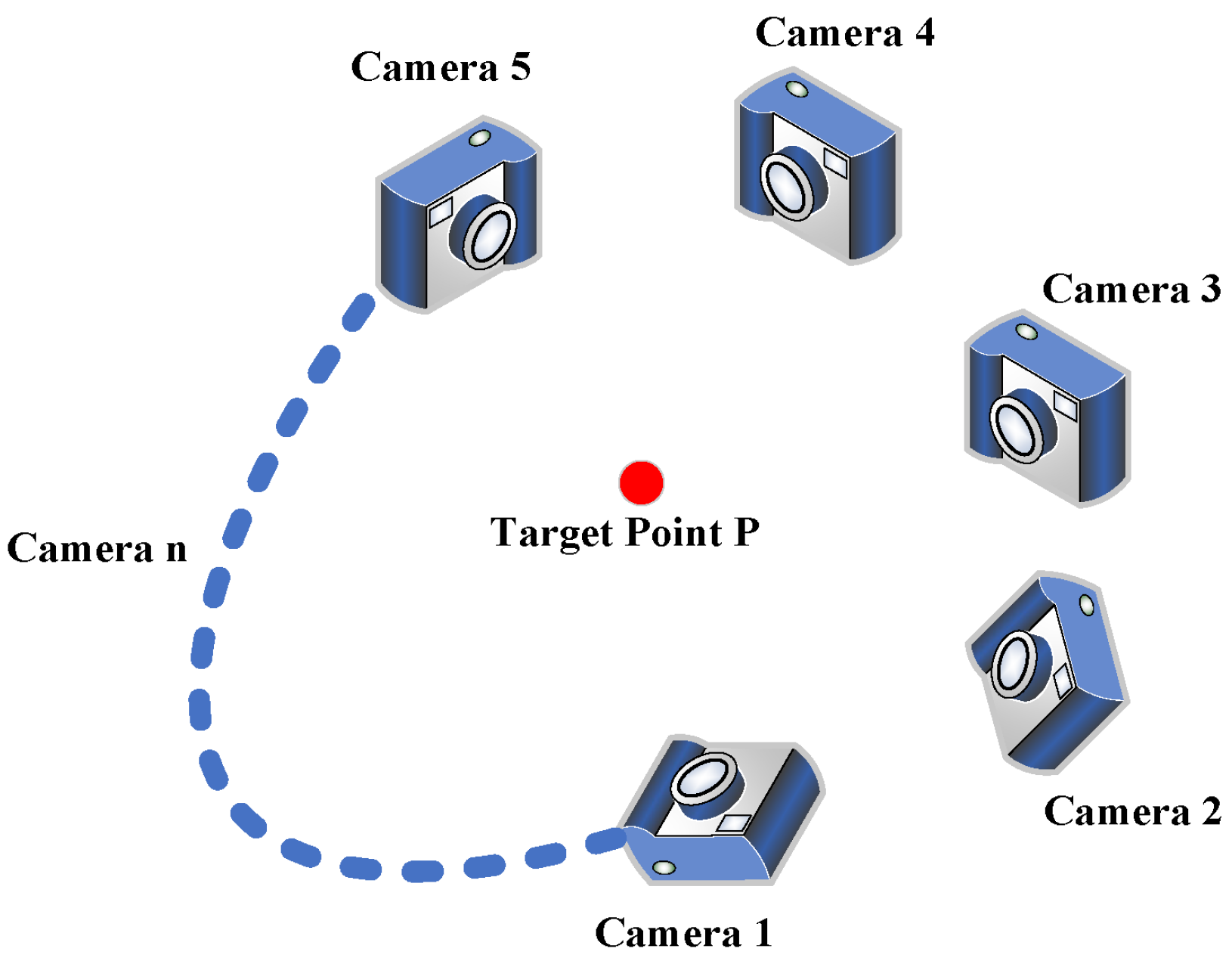
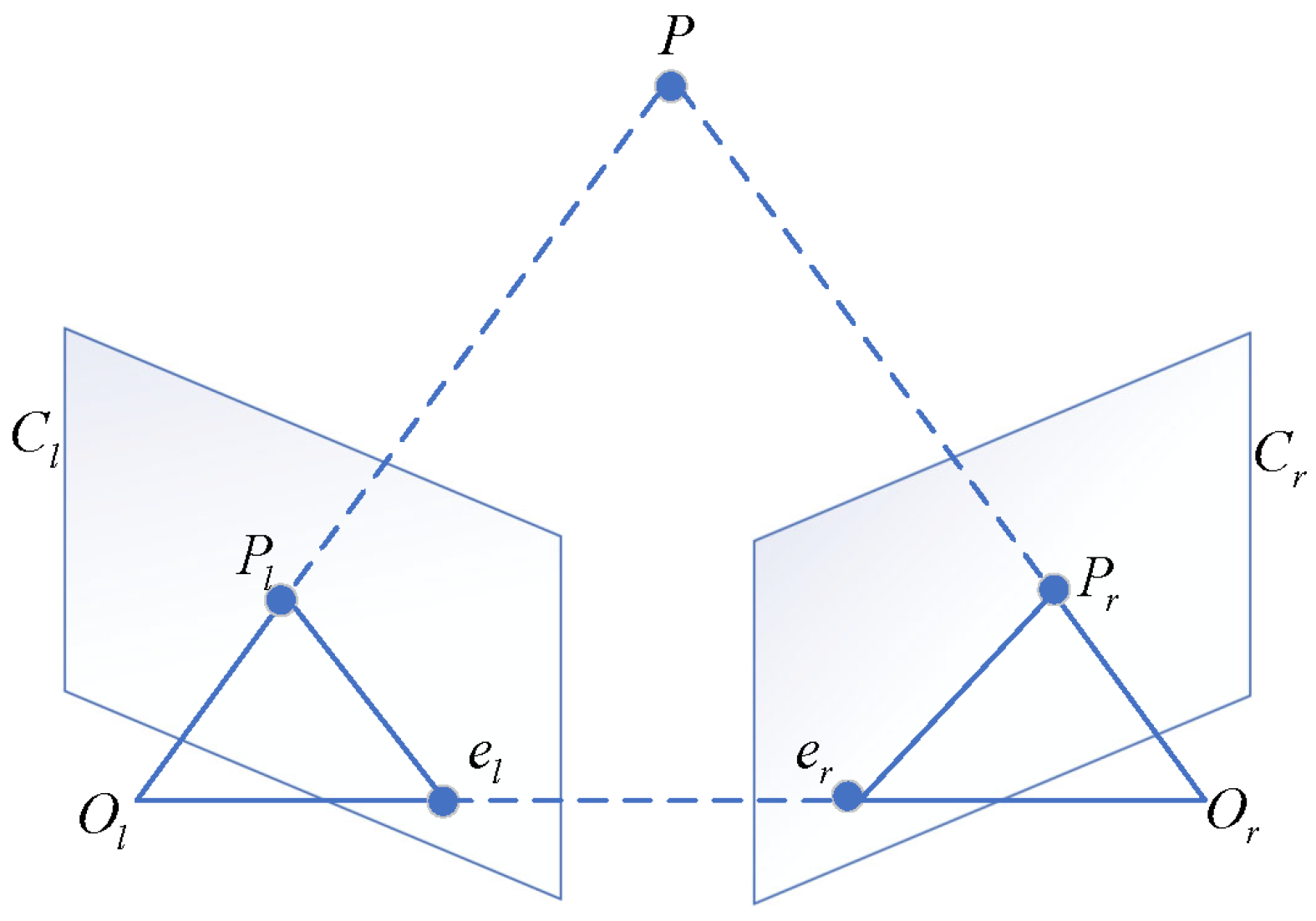
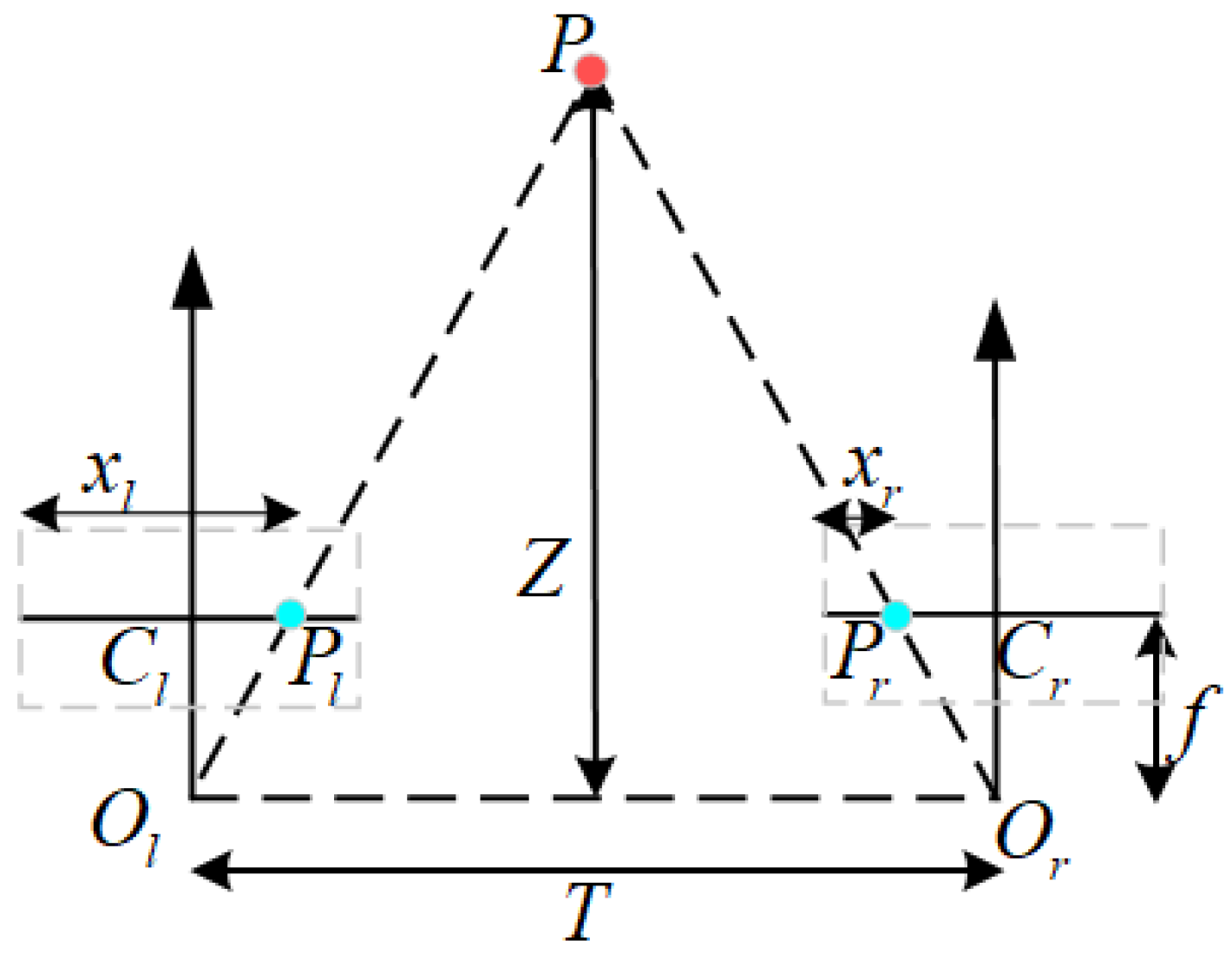
2.1. Multi-Camera Measurement Principles and Imaging Model
2.2. Multi-Camera Hierarchical Calibration and Global Optimization
2.2.1. Monocular Calibration
2.2.2. Binocular Calibration
2.2.3. Multi-Camera Association
2.2.4. Global Optimization
2.3. Multi-View Depth Acquisition and Fusion
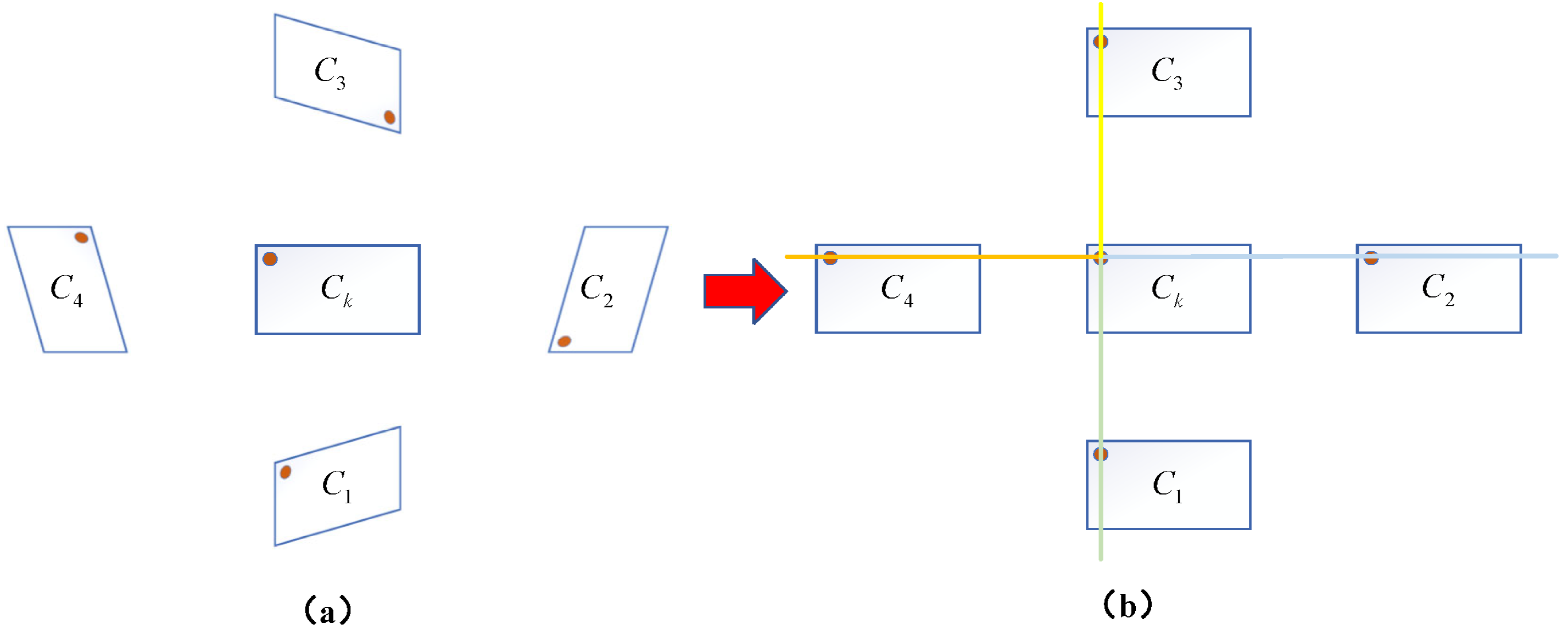
2.3.1. Multi-Epipolar Rectification Based on Core Camera
- Obtain the calibration parameters of the core camera and each auxiliary camera, including the intrinsic matrix and the rotation matrices and translation vectors between the cameras, using the hierarchical calibration method described in Section 2.2.
- Select the core camera and any auxiliary camera, referring to the binocular vision model shown in Figure 4. Use the Bouguet algorithm [44] to compute the new rotation matrix for the core camera and the new rotation matrix for the auxiliary camera. is chosen to minimize distortion in the core camera’s image, while ensures that the auxiliary camera is coplanar with the core camera.
- Calculate projection matrices based on the new rotation matrices and original intrinsic parameters:where and are the original intrinsic parameters of the core camera and auxiliary camera, respectively.
- Perform image transformation to project the original images onto the new image planes.
- Repeat the above steps to complete the epipolar rectification between the core camera and all other cameras. The results of multi-epipolar rectification are shown in Figure 6. In Figure 6b, different colored lines illustrate the binocular epipolar rectification relationships between the core camera and each auxiliary camera.
2.3.2. Multi-View Disparity Calculation and Fusion
3. Experiments and Results Analysis
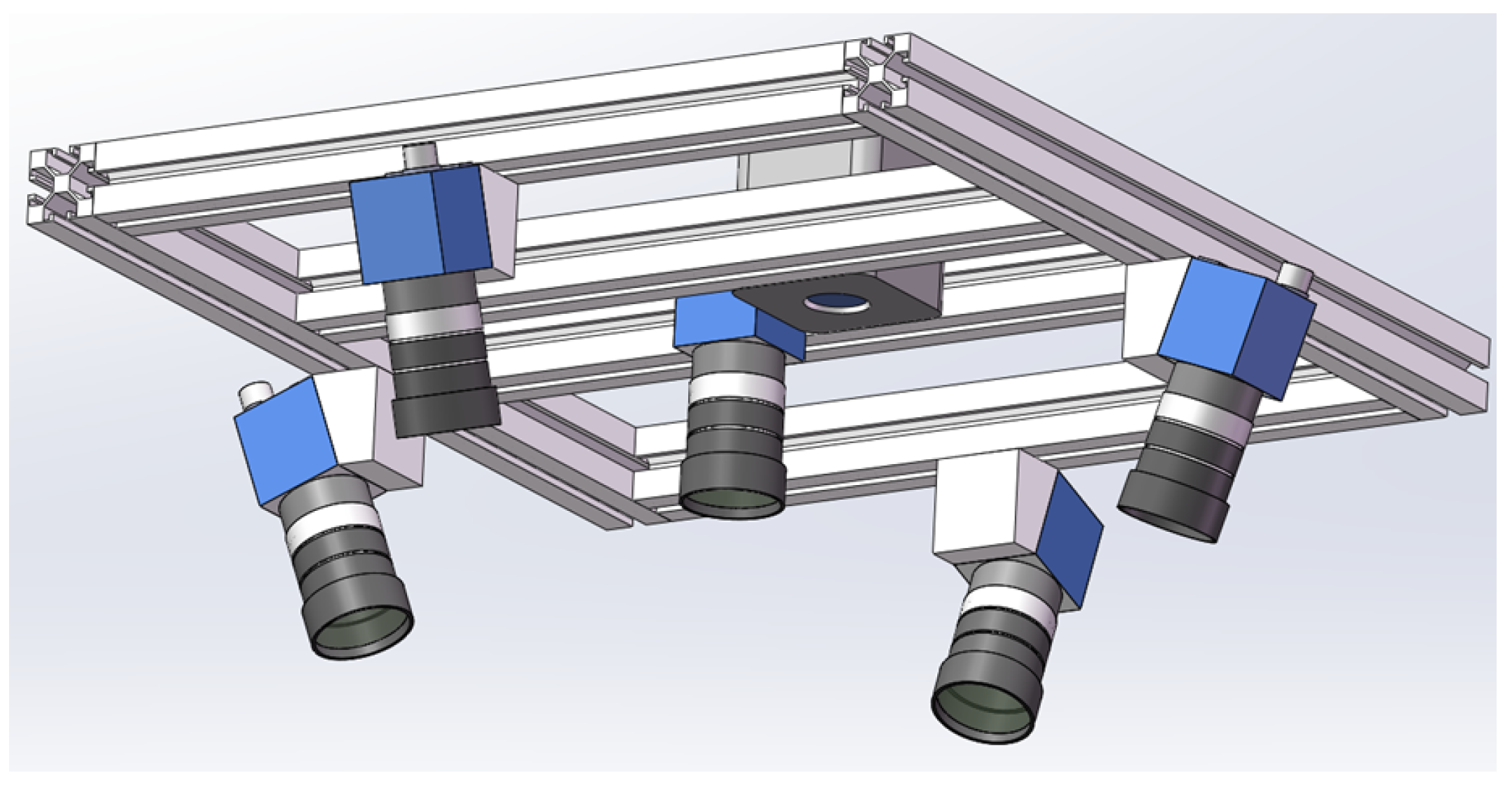
3.1. Setup of the Multi-Camera System
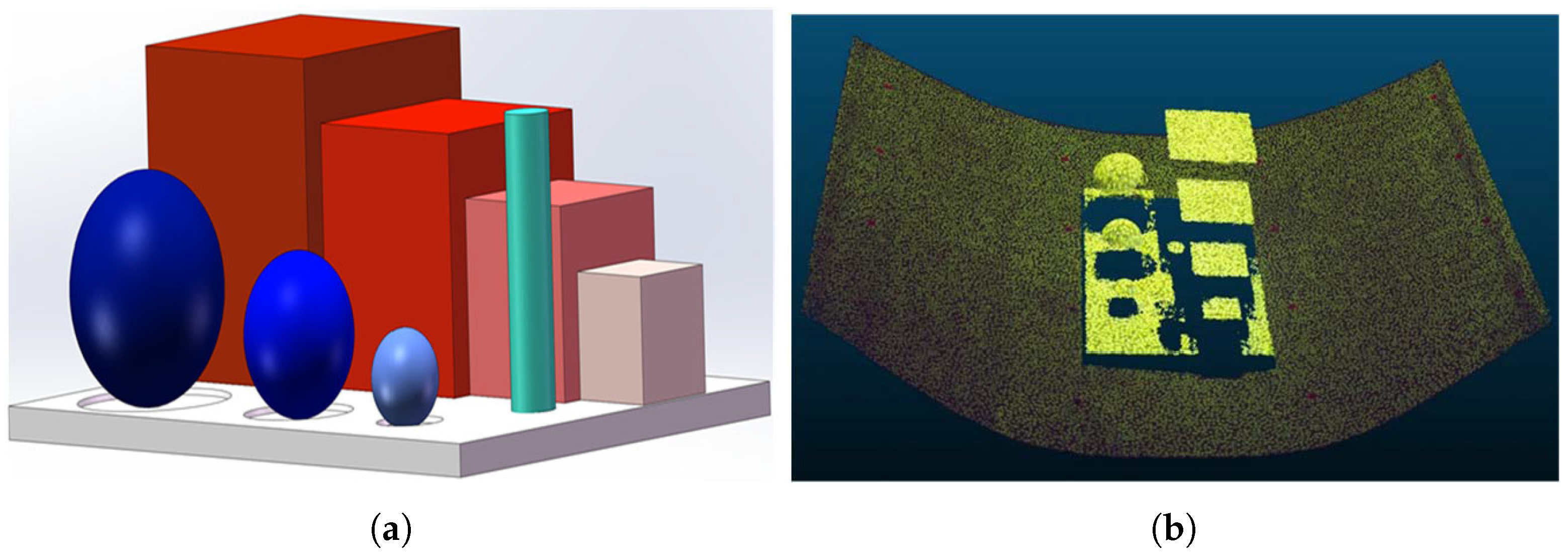
3.2. Multi-Camera 3D Reconstruction Accuracy Measurement Experiment
3.3. Comparison Experiment Between Multi-Camera Vision and Binocular Vision
3.4. Comparison Experiment Between Multi-Camera Speckle Structured Light and Multi-Camera Non-Structured Light
3.5. Comparison Experiment Between Multi-Camera 3D Reconstruction and TOF Camera 3D Reconstruction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.; Yang, S.; Hu, P.; Deng, H. Advances and prospects of vision-based 3D shape measurement methods. Machines 2022, 10, 124. [Google Scholar] [CrossRef]
- Zhao, X.; Yu, T.; Liang, D.; He, Z. A review on 3D measurement of highly reflective objects using structured light projection. Int. J. Adv. Manuf. Technol. 2024, 132, 4205–4222. [Google Scholar]
- Wang, Y.; Guo, W.; Zhao, S.; Xue, B.; Xing, Z. A scraper conveyor coal flow monitoring method based on speckle structured light data. Appl. Sci. 2022, 12, 6955. [Google Scholar] [CrossRef]
- Mao, Z.; Li, D.; Zhao, X. Structured light-based dynamic 3D measurement system for cold-formed steel hollow sections. Int. J. Mechatron. Manuf. Syst. 2022, 15, 203–225. [Google Scholar]
- Hou, C.; Qiao, W.; Gao, X.; Dong, H.; Qiao, T. Non-contact measurement of conveyor belt speed based on fast point cloud registration of feature block. Meas. Sci. Technol. 2024, 35, 125023. [Google Scholar]
- Li, H.; Zou, J.; Li, Y.; Xu, Y.; Xiao, Z. TOF camera array for package volume measurement. In Proceedings of the 2020 7th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 18–20 December 2020; pp. 2260–2264. [Google Scholar]
- Wu, Y.; Wang, Y.; Zhang, S.; Ogai, H. Deep 3D object detection networks using LiDAR data: A review. IEEE Sens. J. 2021, 21, 1152–1171. [Google Scholar]
- Tapia-Zapata, N.; Saha, K.K.; Tsoulias, N.; Zude-Sasse, M. A geometric modelling approach to estimate apple fruit size by means of LiDAR 3D point clouds. Int. J. Food Prop. 2024, 27, 566–583. [Google Scholar]
- Xu, S.; Cheng, G.; Pang, Y.; Jin, Z.; Kang, B. Identifying and characterizing conveyor belt longitudinal rip by 3D point cloud processing. Sensors 2021, 21, 6650. [Google Scholar] [CrossRef]
- Wen, L.; Liang, B.; Zhang, L.; Hao, B.; Yang, Z. Research on coal volume detection and energy-saving optimization intelligent control method of belt conveyor based on laser and binocular visual fusion. IEEE Access 2023, 12, 75238–75248. [Google Scholar]
- Li, J.; Zhang, J.; Wang, H.; Feng, B. Coal flow volume measurement of belt conveyor based on binocular vision and line structured light. In Proceedings of the 2021 IEEE International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Qingdao, China, 2–4 July 2021; pp. 636–639. [Google Scholar]
- Hennad, A.; Cockett, P.; McLauchlan, L.; Mehrubeoglu, M. Characterization of irregularly-shaped objects using 3D structured light scanning. In Proceedings of the 2019 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 5–7 December 2019; pp. 600–605. [Google Scholar]
- Bao, Y.; Tang, L.; Srinivasan, S.; Schnable, P.S. Field-based architectural traits characterisation of maize plant using time-of-flight 3D imaging. Biosyst. Eng. 2019, 178, 86–101. [Google Scholar]
- Wang, L.; Zheng, L.; Wang, M.; Wang, Y.; Li, M. Kinect-based 3D reconstruction of leaf lettuce. In Proceedings of the 2020 ASABE Annual International Virtual Meeting, American Society of Agricultural and Biological Engineers, Omaha, NE, USA, 13–15 July 2020; p. 2000545. [Google Scholar]
- Li, Z.; Han, Y.; Wu, L.; Zang, Z.; Dai, M.; Set, S.Y.; Yamashita, S.; Li, Q.; Fu, H.Y. Towards an ultrafast 3D imaging scanning LiDAR system: A review. Photonics Res. 2024, 12, 1709–1729. [Google Scholar]
- Zhang, L.; Hao, S.; Wang, H.; Wang, B.; Lin, J.; Sui, Y.; Gu, C. Safety warning of mine conveyor belt based on binocular vision. Sustainability 2022, 14, 13276. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, W.; Zhang, L.; Ma, X. Coal weight measurement method of belt conveyor based on binocular stereo vision. In Proceedings of the 2020 7th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS), Guangzhou, China, 13–15 November 2020; pp. 486–492. [Google Scholar]
- Xu, S.; Cheng, G.; Cui, Z.; Jin, Z.; Gu, W. Measuring bulk material flow—Incorporating RFID and point cloud data processing. Measurement 2022, 200, 111598. [Google Scholar]
- Le, K.; Yuan, Y. Based on the geometric characteristics of binocular imaging for yarn remaining detection. Sensors 2025, 25, 339. [Google Scholar] [CrossRef]
- Liao, Z.; Waslander, S.L. Multi-view 3D object reconstruction and uncertainty modelling with neural shape prior. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024; pp. 3098–3107. [Google Scholar]
- Zhou, L.; Wu, G.; Zuo, Y.; Chen, X.; Hu, H. A comprehensive review of vision-based 3D reconstruction methods. Sensors 2024, 24, 2314. [Google Scholar] [CrossRef]
- Pai, W.; Liang, J.; Zhang, M.; Tang, Z.; Li, L. An advanced multi-camera system for automatic, high-precision and efficient tube profile measurement. Opt. Laser Eng. 2022, 154, 106890. [Google Scholar] [CrossRef]
- Lee, K.; Cho, I.; Yang, B.; Park, U. Multi-head attention refiner for multi-view 3D reconstruction. J. Imaging 2024, 10, 268. [Google Scholar] [CrossRef]
- Pan, J.; Li, L.; Yamaguchi, H.; Hasegawa, K.; Thufail, F.I.; Brahmantara; Tanaka, S. 3D reconstruction of Borobudur reliefs from 2D monocular photographs based on soft-edge enhanced deep learning. ISPRS J. Photogramm. Remote Sens. 2022, 183, 439–450. [Google Scholar]
- Wei, Z.; Zhu, Q.; Min, C.; Chen, Y.; Wang, G. AA-RMVSNet: Adaptive aggregation recurrent multi-view stereo network. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 6187–6196. [Google Scholar]
- Liao, J.; Ding, Y.; Shavit, Y.; Huang, D.; Ren, S.; Guo, J.; Feng, W.; Zhang, K. WT-MVSNet: Window-based transformers for multi-view stereo. In Proceedings of the Advances in Neural Information Processing Systems 35 (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; pp. 8564–8576. [Google Scholar]
- Li, J.; Lu, Z.; Wang, Y.; Xiao, J.; Wang, Y. NR-MVSNet: Learning multi-view stereo based on normal consistency and depth refinement. IEEE Trans. Image Process. 2023, 32, 2649–2662. [Google Scholar]
- Yu, J.; Yin, W.; Hu, Z.; Liu, Y. 3D reconstruction for multi-view objects. Comput. Electr. Eng. 2023, 106, 108567. [Google Scholar]
- Wu, J.; Wyman, O.; Tang, Y.; Pasini, D.; Wang, W. Multi-view 3D reconstruction based on deep learning: A survey and comparison of methods. Neurocomputing 2024, 582, 127553. [Google Scholar]
- Jin, D.; Yang, Y. Using distortion correction to improve the precision of camera calibration. Opt. Rev. 2019, 26, 269–277. [Google Scholar]
- Zhang, Z.; Zheng, L.; Qiu, T.; Deng, F. Varying-parameter convergent-differential neural solution to time-varying overdetermined system of linear equations. IEEE Trans. Autom. Control 2020, 65, 874–881. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Feng, S.; Zuo, C.; Zhang, L.; Tao, T.; Hu, Y.; Yin, W.; Qian, J.; Chen, Q. Calibration of fringe projection profilometry: A comparative review. Opt. Laser Eng. 2021, 143, 106622. [Google Scholar]
- Ding, G.; Chen, T.; Sun, L.; Fan, P. In high precision camera calibration method based on full camera model. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; pp. 4218–4223. [Google Scholar]
- Zhao, C.; Fan, C.; Zhao, Z. A binocular camera calibration method based on circle detection. Heliyon 2024, 10, e38347. [Google Scholar]
- Wu, A.; Xiao, H.; Zeng, F. A camera calibration method based on OpenCV. In Proceedings of the 4th International Conference on Intelligent Information Processing (ICIIP), Guilin, China, 16–17 November 2019; pp. 320–324. [Google Scholar]
- Zhang, J.; Sun, D.; Luo, Z.; Yao, A.; Zhou, L.; Shen, T.; Chen, Y.; Quan, L.; Liao, H. Learning two-view correspondences and geometry using Order-Aware Network. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5845–5854. [Google Scholar]
- Chirikjian, G.S.; Mahony, R.; Ruan, S.; Trumpf, J. Pose changes from a different point of view. J. Mech. Robot. 2018, 10, 021008. [Google Scholar]
- Cuypers, H.; Meulewaeter, J. Extremal elements in Lie algebras, buildings and structurable algebras. J. Algebra 2021, 580, 1–42. [Google Scholar]
- Fischer, A.; Izmailov, A.F.; Solodov, M.V. The Levenberg–Marquardt method: An overview of modern convergence theories and more. Comput. Optim. Appl. 2024, 89, 33–67. [Google Scholar]
- Hanachi, S.B.; Sellami, B.; Belloufi, M. New iterative conjugate gradient method for nonlinear unconstrained optimization. RAIRO-Oper. Res. 2022, 56, 2315–2327. [Google Scholar]
- Jaybhaye, L.V.; Mandal, S.; Sahoo, P.K. Constraints on energy conditions in f(R,Lm) gravity. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250050. [Google Scholar]
- Zhou, H.; Jagadeesan, J. Real-time dense reconstruction of tissue surface from stereo optical video. IEEE Trans. Med. Imaging 2020, 39, 400–412. [Google Scholar] [PubMed]
- Zhong, F.; Quan, C. Stereo-rectification and homography-transform-based stereo matching methods for stereo digital image correlation. Measurement 2021, 173, 108635. [Google Scholar]
- Imai, T.; Wakamatsu, H. Stereoscopic three dimensional dissection of brain image by binocular parallax. IEEJ Trans. Electron. Inf. Syst. 1991, 111, 242–248. [Google Scholar]
- Juarez-Salazar, R.; Zheng, J.; Diaz-Ramirez, V.H. Distorted pinhole camera modeling and calibration. Appl. Opt. 2020, 59, 11310–11318. [Google Scholar]











| MER2-502-79U3C | HN-0828-6M-C2/3B | ||
|---|---|---|---|
| Resolution | 2448 (H) × 2048 (V) | Sensor size | 2/3″ |
| Sensor format | 2/3″ | Focal length (mm) | 8 |
| Pixel size | 3.45 m × 3.45 m | F/No | F2.8–F16 |
| Frame rate | 79.1 fps | Angle of view (D × H × V) | 68.5° × 57° × 44.2° |
| Exposure time | UltraShort: 1 s–100 s. | ||
| Standard: 20 s–1 s. | |||
| Synchronization | Hardware trigger, software trigger | ||
| Measurement Parameter | Actual Value (mm) | Measured Value (mm) | Relative Error (%) |
|---|---|---|---|
| 100 mm cube edge length | 100 | 100.6125 | 0.61 |
| 80 mm cube edge length | 80 | 80.6290 | 0.79 |
| 60 mm cube edge length | 60 | 60.0137 | 0.02 |
| 40 mm cube edge length | 40 | 39.1015 | 2.25 |
| 70 mm sphere radius | 35 | 34.1970 | 2.29 |
| 50 mm sphere radius | 25 | 24.5766 | 1.69 |
| 30 mm sphere radius | 15 | 14.6196 | 2.54 |
| Cylinder diameter | 20 | 20.3059 | 1.53 |
| Cylinder height | 90 | 86.2748 | 4.14 |
| Base length | 285 | 281.528 | 1.22 |
| Base width | 200 | 201.987 | 0.99 |
| Height difference between adjacent cubes | 20 | 19.5795 | 2.10 |
| Measurement Parameter | Actual Value (mm) | Measured Value (mm) | Relative Error (%) |
|---|---|---|---|
| 100 mm cube edge length | 100 | 108.1152 | 8.12 |
| 80 mm cube edge length | 80 | 82.5438 | 3.18 |
| 60 mm cube edge length | 60 | 61.6870 | 2.81 |
| 40 mm cube edge length | 40 | 44.4484 | 11.12 |
| 70 mm sphere radius | 35 | 28.1255 | 19.64 |
| 50 mm sphere radius | 25 | 19.2265 | 23.09 |
| 30 mm sphere radius | 15 | 12.0833 | 19.44 |
| Cylinder diameter | 20 | - | - |
| Cylinder height | 90 | 91.978 | 2.20 |
| Base length | 285 | 293.286 | 2.91 |
| Base width | 200 | 205.293 | 2.65 |
| Height difference between adjacent cubes | 20 | 18.6571 | 6.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, C.; Kang, Y.; Qiao, T. Multi-Camera Hierarchical Calibration and Three-Dimensional Reconstruction Method for Bulk Material Transportation System. Sensors 2025, 25, 2111. https://doi.org/10.3390/s25072111
Hou C, Kang Y, Qiao T. Multi-Camera Hierarchical Calibration and Three-Dimensional Reconstruction Method for Bulk Material Transportation System. Sensors. 2025; 25(7):2111. https://doi.org/10.3390/s25072111
Chicago/Turabian StyleHou, Chengcheng, Yongfei Kang, and Tiezhu Qiao. 2025. "Multi-Camera Hierarchical Calibration and Three-Dimensional Reconstruction Method for Bulk Material Transportation System" Sensors 25, no. 7: 2111. https://doi.org/10.3390/s25072111
APA StyleHou, C., Kang, Y., & Qiao, T. (2025). Multi-Camera Hierarchical Calibration and Three-Dimensional Reconstruction Method for Bulk Material Transportation System. Sensors, 25(7), 2111. https://doi.org/10.3390/s25072111





