Clustering and Interpretability of Residential Electricity Demand Profiles
Abstract
1. Introduction
1.1. Contributions of the Paper
- Clustering interpretability through decision trees;
- Comprehensive clustering comparison;
- Impact of dimensionality reduction on clustering performance;
- Evaluation of five Cluster Validity Indices (CVIs) for reliable assessment.
1.2. Outline of the Paper
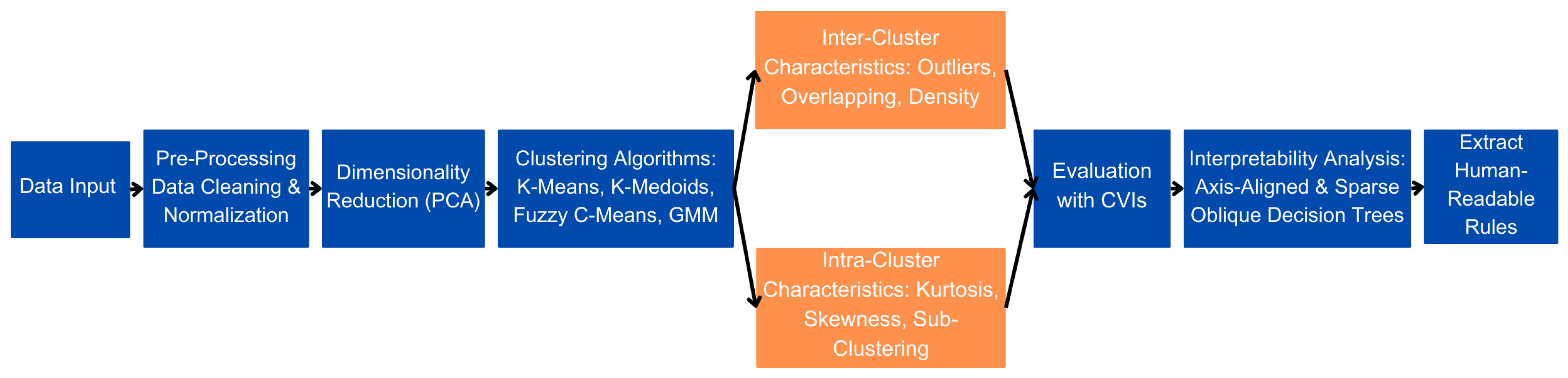
2. Materials and Methods
2.1. Data and Pre-Processing
2.2. Dimensionality Reduction
2.3. Clustering Algorithms
2.4. Intra-Cluster and Inter-Cluster Analysis
2.4.1. Inter-Cluster Analysis
- Outliers are defined as single-point clusters in the clustering results. These points are included in the clustering process but are not expected to significantly influence the CVI scores. To verify this assumption, outliers were identified through manual inspection and subsequently removed. CVI scores were then compared before and after the removal of these single-point clusters to evaluate any potential impact on the clustering validation metrics.
- Overlapping clusters occur when certain data points share characteristics with more than one cluster, making it difficult to assign them definitively to a single cluster. This typically arises when clusters are not well-separated, with some data points located near the boundaries of two or more clusters. To address this issue, overlapping points were removed from the dataset to evaluate whether reducing overlap could improve cluster quality. For Fuzzy C-Means without and with DR, GMM without DR, and K-Means without DR, overlapping points were identified and removed through manual inspection. For GMM with DR, K-Medoids with and without DR, and K-Means with DR, a distance-based approach was applied. This method calculates the Euclidean distance between each data point and the cluster centers. Points found to be close to multiple centers within a specified threshold were considered overlapping and removed. The threshold was manually adjusted to balance effectiveness in reducing overlap while maintaining data integrity.
- Differential density refers to clusters having varying densities, often reflecting natural consumption patterns. Density is defined as the number of data points per unit volume and was calculated as the ratio of points in a cluster to its diameter. It was hypothesized that increasing the density of clusters would improve CVI scores. To evaluate this, the density of the densest cluster was increased by adding additional points while keeping the cluster diameter constant. The effect of this adjustment on CVI scores was then analyzed to assess the relationship between cluster density and clustering quality.
2.4.2. Intra-Cluster Analysis
- Central kurtosis refers to data points being tightly clustered around the center of a cluster, with fewer points near the edges. Statistically, kurtosis measures the peakedness or flatness of a distribution. When more points are concentrated near the center, the distribution becomes leptokurtic, increasing similarity within the cluster. This increased density is expected to enhance CVI scores by making clusters more compact. To evaluate this, k% of the data points in each cluster were shifted closer to the center, where k ∈ {25, 50, 75, 100}. The shifted points were generated on a d-dimensional hypersphere, where d corresponds to the data dimensionality. The radius of the hypersphere was set to the cluster radius divided by m, where m is a discrete value ranging from 5 to 20, depending on the dimensionality of the data. The effect of these adjustments on CVI scores was analyzed to assess the impact of central kurtosis on clustering performance.
- Skewness occurs when the mean is positioned away from the cluster’s center, resulting in an asymmetrical distribution. While kurtosis increases density near the center, skewness shifts the majority of data points toward one side of the cluster, causing the mean to deviate from the geometric center. With the cluster’s diameter remaining constant, increasing skewness is expected to either maintain or improve CVI scores. To evaluate this, k% of the data points in each cluster were rearranged farther from the center and closer to the mean, where k ∈ {25, 50, 75, 100}. To preserve the natural structure of each cluster, no new points were added to empty regions. Adjustments were performed around the mean to introduce skewness without creating artificial patterns inconsistent with real-world data distributions. During implementation, the distance between the mean and the center was calculated for all clusters. If this distance exceeded the cluster radius divided by n, skewness adjustments were applied, where n is a discrete value ranging from 2 to 5, depending on the cluster size. The rearranged points were positioned on a d-dimensional hypersphere, where d corresponds to the data dimensionality. The radius of the hypersphere was set to the cluster radius divided by m, where m is a discrete value ranging from 5 to 20, based on the data dimensionality.
- Subclustering occurs when a cluster splits into two or more smaller clusters. This suggests that the cluster structure is not optimal and that dividing it into smaller, distinct clusters may yield better results. Such a division indicates that the subclusters do not share significant characteristics or features, warranting their distinction as separate clusters. The presence of subclusters is expected to worsen CVI scores due to reduced cohesion and separation within the clusters. To evaluate the impact of subclustering, the mean and center of each cluster were analyzed, as these are considered dense points. The distance between the mean and the center of each cluster was calculated and compared to a threshold defined for each algorithm. If this distance exceeded the threshold, subclustering was identified. In such cases, points were rearranged to move closer to the nearest dense point (mean or center). These rearrangements were performed with adjustments affecting {25, 50, 75, 100} of the points within the cluster.
2.5. Cluster Validity Indices
3. Results and Discussion
3.1. Principal Component Analysis
3.2. Clustering Algorithms
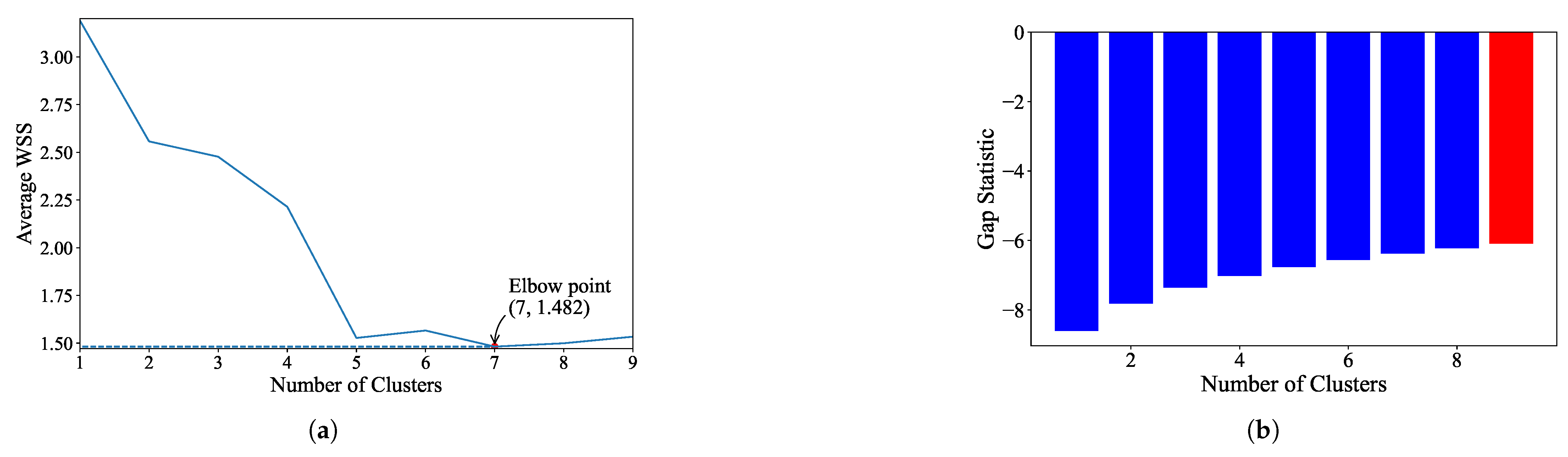
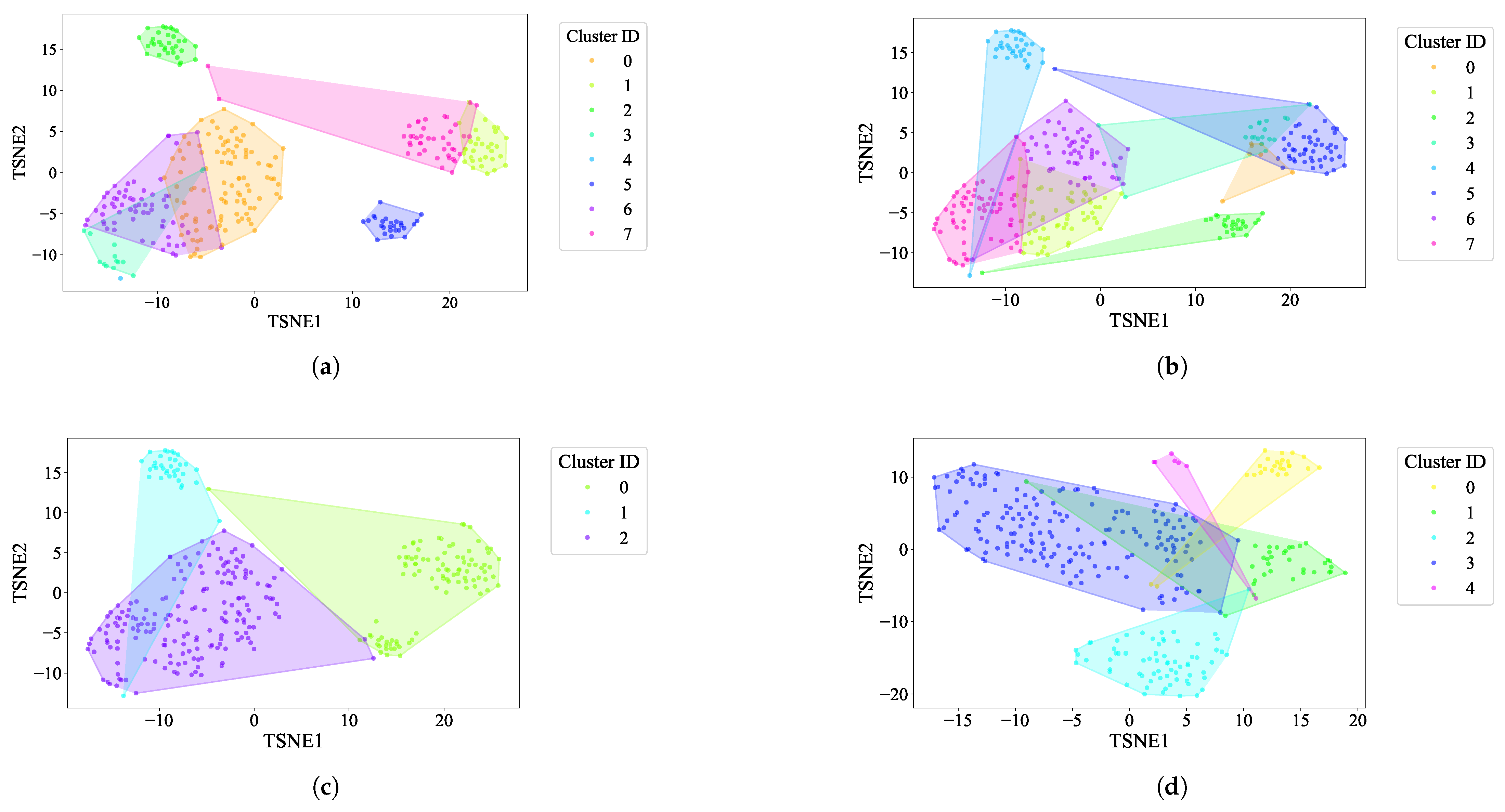
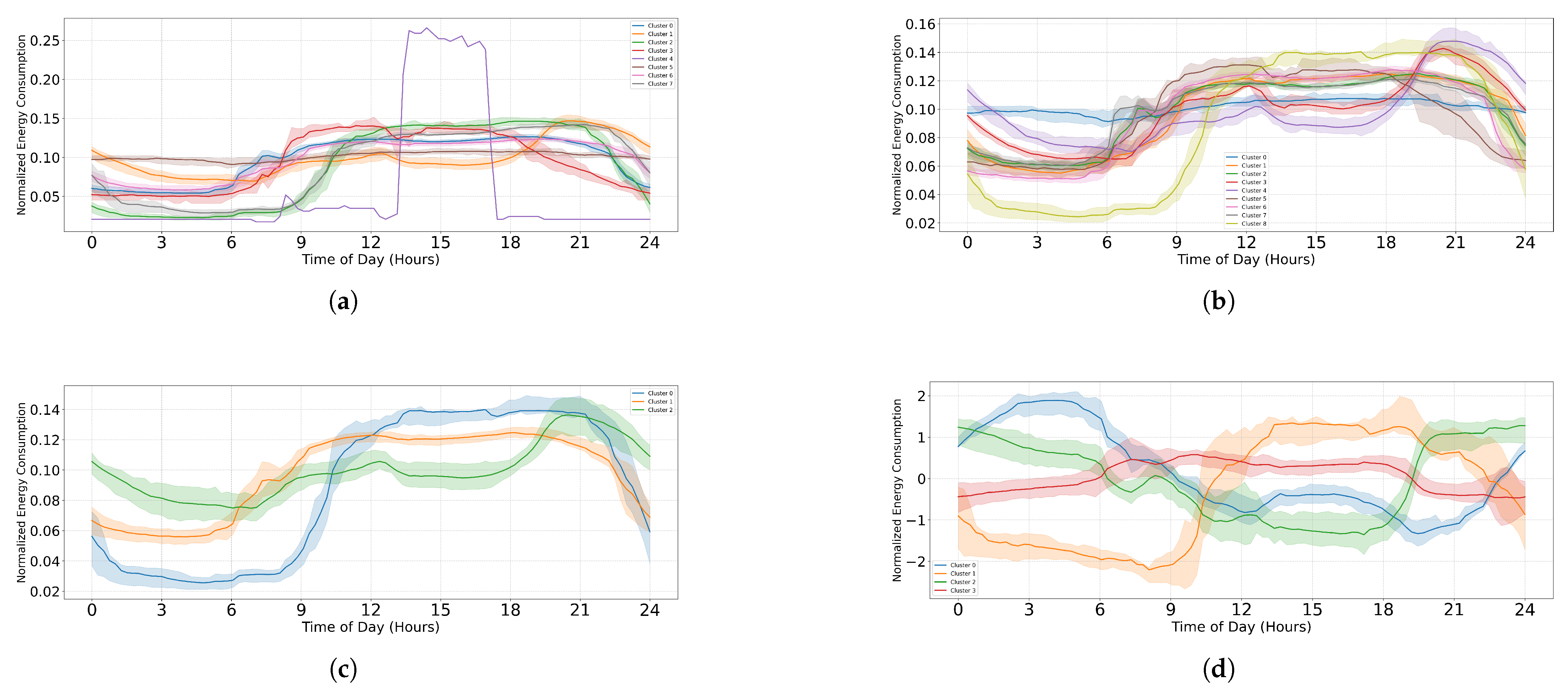
- K-Means: For the EL dataset without DR, the optimal number of clusters was determined using two methods. The elbow heuristic suggested seven clusters while the gap statistic recommended nine clusters, as shown in Figure 4. To correct this difference, eight clusters were selected as the optimal number. Applying K-Means with eight clusters produced the visualization shown in Figure 5, which reveals overlapping clusters and the presence of an outlier. For the EL dataset with DR, the same process was followed. The elbow heuristic again suggested seven clusters while the gap statistic indicated nine clusters, as presented in Figure 6. Based on both methods, eight clusters were again selected as the optimal number. The clustering results, displayed in Figure 7, also show overlapping clusters and the presence of an outlier in cluster 4. K-Means, as a hard clustering algorithm, is known to be sensitive to outliers. This sensitivity is evident in the clustering results presented, where outliers were present alongside overlapping clusters. The reliance on the mean as the cluster center causes outliers to significantly influence the cluster boundaries, resulting in less accurate cluster definitions.
- K-Medoids: To address the identified outlier issue, the K-Medoids algorithm was applied. For the EL dataset without DR, the gap statistic suggested an optimal number of clusters equal to nine while for EL dataset with DR, the gap statistics proposed eight clusters (see Figure 8). After applying K-Medoids clustering with nine clusters and with eight clusters, the results, shown in Figure 5 and Figure 7, respectively, demonstrated effective handling of the outlier. However, overlapping still exists in both cases. K-Medoids, as a hard clustering algorithm, solved the outlier issue. The removal of outliers demonstrates its effectiveness in correcting this limitation of K-Means. However, overlapping clusters persisted, indicating that while K-Medoids can handle outliers, it does not correctly address the challenge of overlapping. This underscores a limitation of hard clustering methods, as they rely on strict boundaries that cannot account for shared characteristics between clusters.
- Fuzzy C-Means: To address the issue of overlapping clusters, the soft clustering algorithm Fuzzy C-Means was applied. For the EL dataset without DR, the Dunn Index identified the optimal number of clusters as 3, with a fuzzifier value of 1.2. The clustering results, presented in Figure 5, show that Fuzzy C-Means minimized overlapping compared to hard clustering techniques. For the EL dataset with DR, the Dunn Index similarly indicated an optimal cluster count of 3, with a slightly adjusted fuzzifier value of 1.1. The clustering results, displayed in Figure 7, show no outliers and minimal overlapping, although the overlap was slightly greater than in the non-DR case.Fuzzy C-Means resulted in a marked reduction in overlap. The probabilistic nature allows it to handle data points that fall near cluster boundaries. This results in smoother transitions between clusters and a better representation of complex data structures. Furthermore, no outliers were observed, which highlight its robustness. Dimensionality reduction had no noticeable effect on these results, as similar improvements were observed for both datasets with and without DR.
- Gaussian Mixture Model: The second soft clustering algorithm applied was the GMM, where the silhouette score was used to determine the optimal number of clusters. For the EL dataset without DR, the SH identified four as the optimal number of clusters. The clustering results, presented in Figure 5, show well-defined clusters with minimal overlap and no outliers, demonstrating the capability of GMM to handle overlapping clusters effectively. For the EL dataset with DR, SH indicated five as the optimal number of clusters, as shown in Figure 7. The clustering results reveal no outliers but show a slightly higher degree of overlap compared to the dataset without DR. The presented results further validate the advantages of soft clustering. Like Fuzzy C-Means, results from GMM demonstrated reduced overlap compared to hard clustering methods and the complete absence of outliers. GMM’s ability to model the data probabilistically improves its flexibility in representing real-world data, particularly in high-dimensional spaces. Dimensionality reduction similarly showed no significant impact on the results, as the improvements in clustering quality were consistent across both datasets.Findings from both the EL datasets, with and without dimensionality reduction, demonstrated that soft clustering is better than hard clustering in terms of outlier and overlapping. While K-Means and K-Medoids struggle with overlapping clusters, soft clustering algorithms, Fuzzy C-Means, and GMM effectively reduce overlap and eliminate outliers. This reinforces the strength of soft clustering approaches in handling complex data distributions, where clusters may share characteristics or where outliers significantly impact results. The absence of a noticeable effect from dimensionality reduction suggests that the algorithms themselves played a more critical role in improving clustering quality than the pre-processing step.



3.3. Inter- and Intra-Cluster Characteristics
3.3.1. Inter-Cluster Characteristics
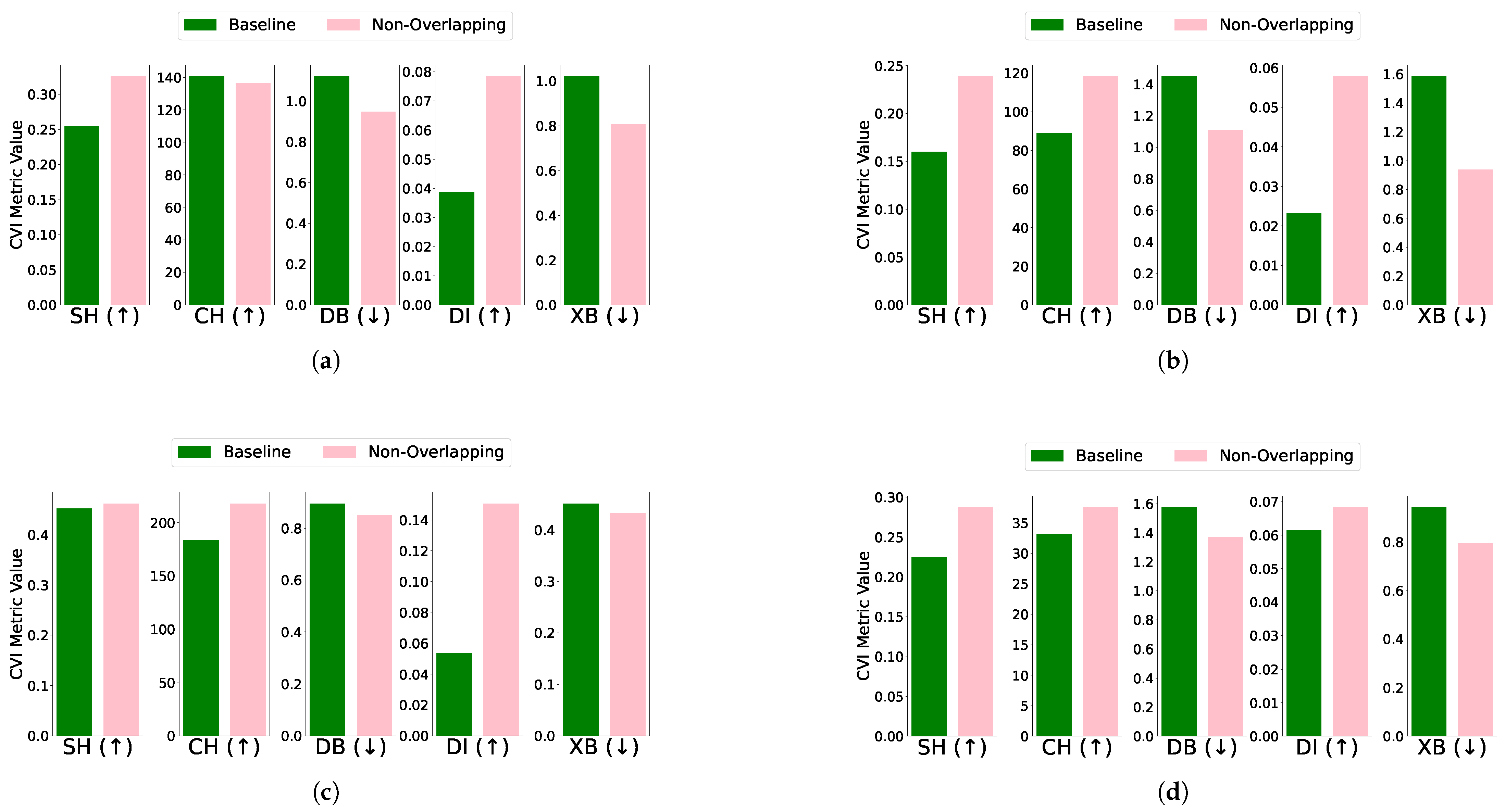
- Outlier: The impact of outlier removal on clustering performance was assessed by comparing CVI metrics for the baseline and outlier-removed cases. Among the algorithms, only K-Means identified outliers. In both the EL dataset without and with DR, SH, DI, and XB metrics remained unchanged after outlier removal. However, the CH score improved, while the DB index deteriorated unexpectedly in both cases (see Figure 10). Most CVIs remained unaffected, except for CH and DB. CH improved due to enhanced inter-cluster dispersion, as outlier removal increased the separation between clusters. Conversely, DB deteriorated unexpectedly, likely because the reduced intra-cluster variance was accompanied by diminished inter-cluster separation. This behavior suggests that SH, XB, or DI are reliable CVIs for datasets with outliers, while DB and CH require careful consideration due to their sensitivity to outlier removal.
- Overlapping: The effect of removing overlapping profiles on clustering performance was evaluated for each algorithm and dataset combination. For the EL dataset without DR, removing overlapping profiles improved clustering performance across algorithms. Specifically, K-Means showed improved CVI metrics, except for the XB index, which worsened; K-Medoids demonstrated enhancements in SH, DB, and DI indices, while CH and XB indices remained unchanged; Fuzzy C-Means exhibited minimal impact on CVIs after the removal of one profile; and GMM showed improvements across all CVIs after removing two profiles. For the EL dataset with DR, the removal of overlapping profiles resulted in more distinct clusters and noticeable improvements across all algorithms. K-Means exhibited substantial improvements in SH, DB, DI, and XB indices, with a slight deterioration in CH; K-Medoids and Fuzzy C-Means showed significant improvements across all CVIs; and GMM achieved better-defined clusters with enhanced CVI performance. The results are summarized in Figure 11 (without DR) and Figure 12 (with DR).Removing overlapping data points improved all CVIs across algorithms, both with and without DR, except for XB in K-Medoids without DR. This inconsistency in XB’s behavior highlights the need for further investigation, as it demonstrated improvements when DR was applied. For overlapping datasets, SH, CH, DI, and DB are recommended, while XB should be used cautiously, particularly in non-DR scenarios.
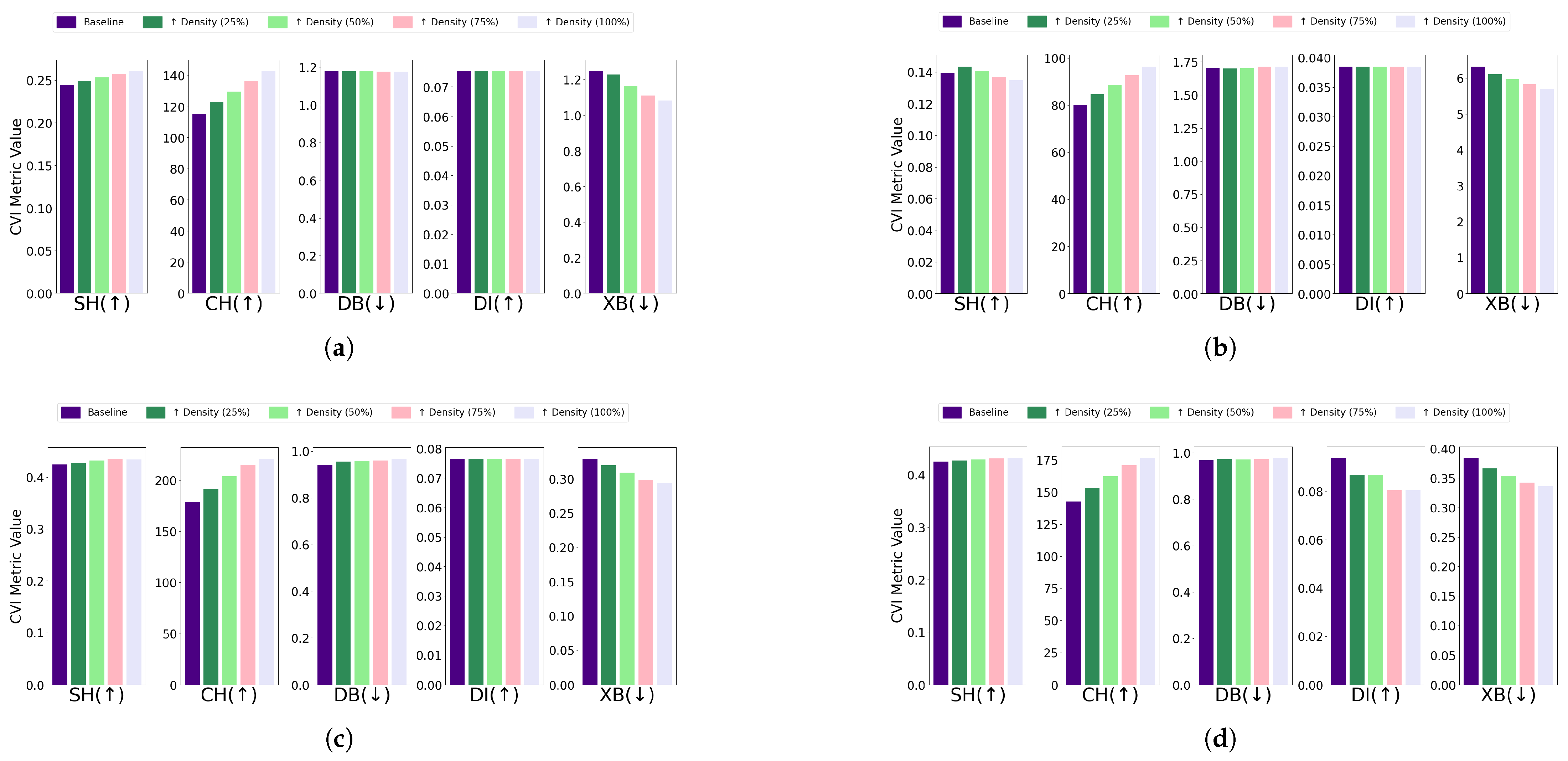
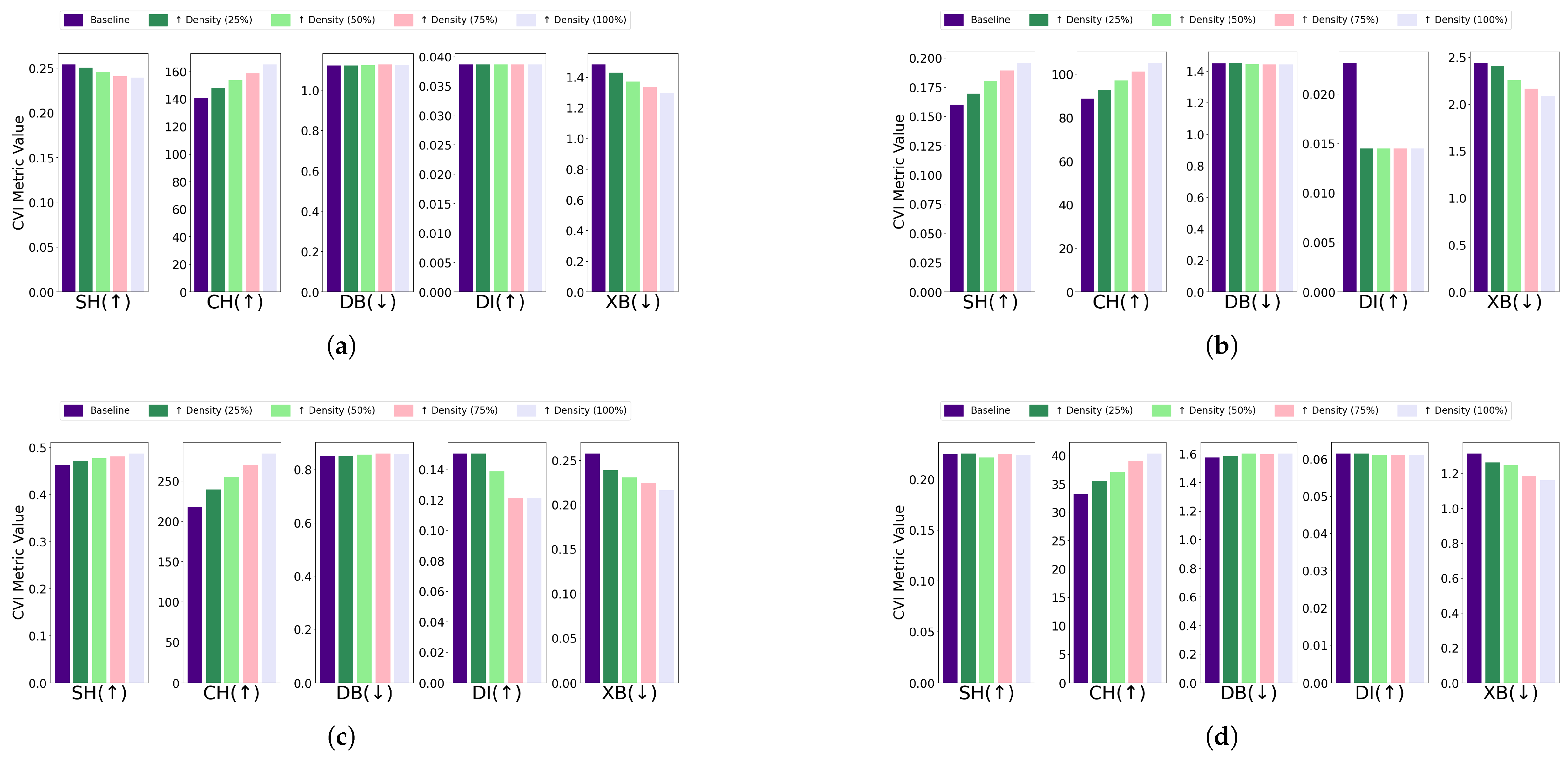
- Differential density: The impact of differential density on CVI metrics varied across clustering algorithms and dataset configurations. Without DR, most algorithms showed improvements in SH, CH, and XB indices, while DB and DI generally remained constant. Notably, GMM exhibited slight decreases in DI despite improvements in CH and XB. With DR, CH and XB consistently improved across all algorithms. However, K-Means and Fuzzy C-Means showed unexpected deterioration in SH, and K-Medoids and Fuzzy C-Means experienced decreases in DI. Full details are visualized in Figure 13 (without DR) and Figure 14 (with DR). Increasing the density of clusters improved most CVIs, except for DI and DB, which remained stable across all algorithms. This stability can be attributed to DI’s reliance on minimum inter-cluster distances, which are unaffected by density changes, and DB’s focus on the average similarity between clusters, which does not capture intra-cluster density variations. For datasets with increasing density, SH, XB, and CH are the most reliable CVIs, while DI and DB may be less informative.
3.3.2. Intra-Cluster Characteristics
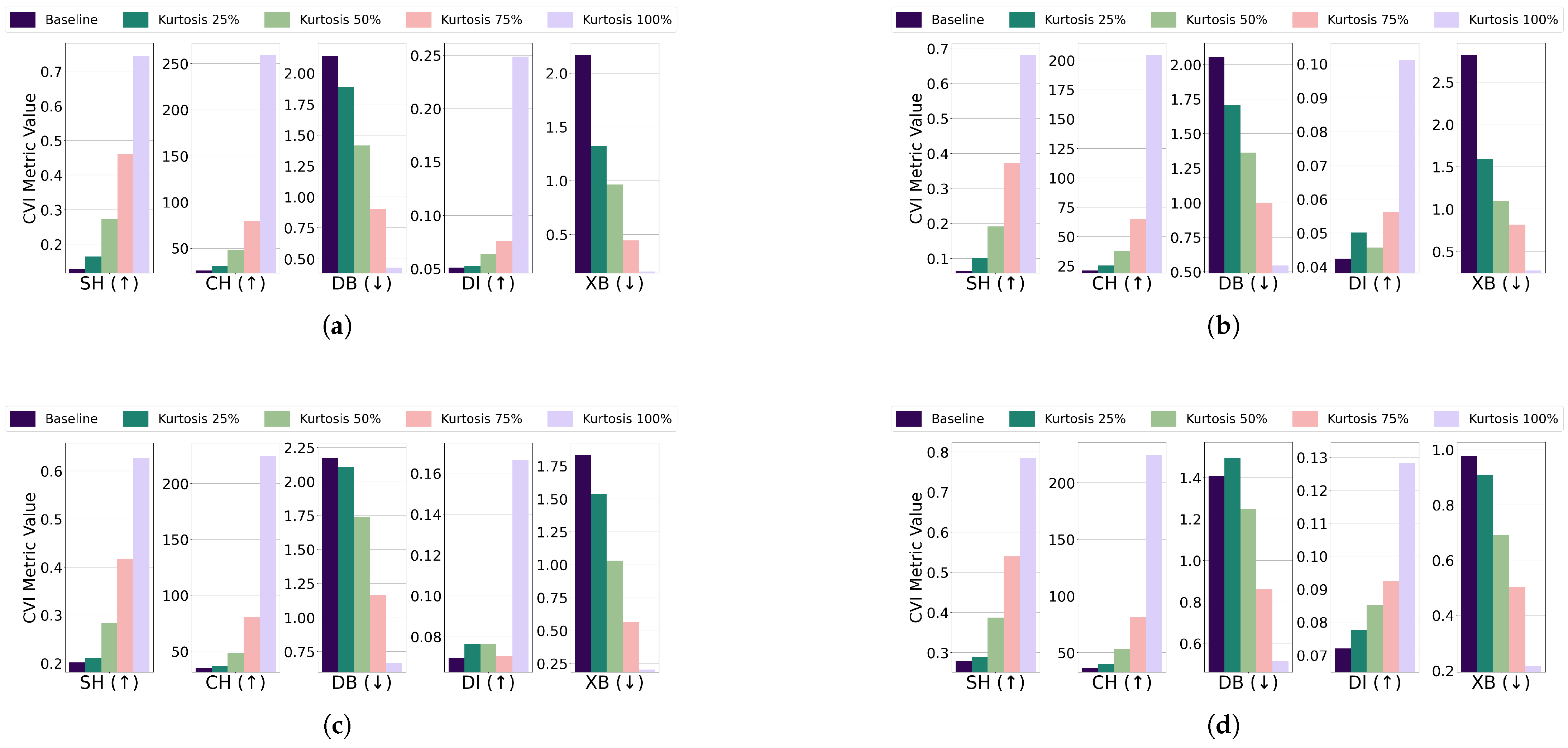
- Central kurtosis: The effect of increasing central kurtosis on clustering performance was evaluated for each algorithm and dataset combination. For the EL dataset without DR, points were adjusted to lie on a 96-dimensional hypersphere with a radius equal to of the cluster size. For the EL dataset with DR, points were shifted to a nine-dimensional hypersphere with a radius equal to of the cluster size. Across all algorithms—K-Means, K-Medoids, Fuzzy C-Means, and GMM—increasing central kurtosis led to improvements in CVI metrics for both versions of the EL dataset. The results for CVIs on the EL dataset without DR are displayed in Figure 15 while the results for the EL dataset with DR are shown in Figure 16. Increasing central kurtosis positively impacted all CVIs, as redistributing points closer to cluster centers enhanced both intra-cluster compactness and inter-cluster separation. This consistent improvement across algorithms suggests that SH, XB, CH, DI, and DB are all effective for datasets with central kurtosis.
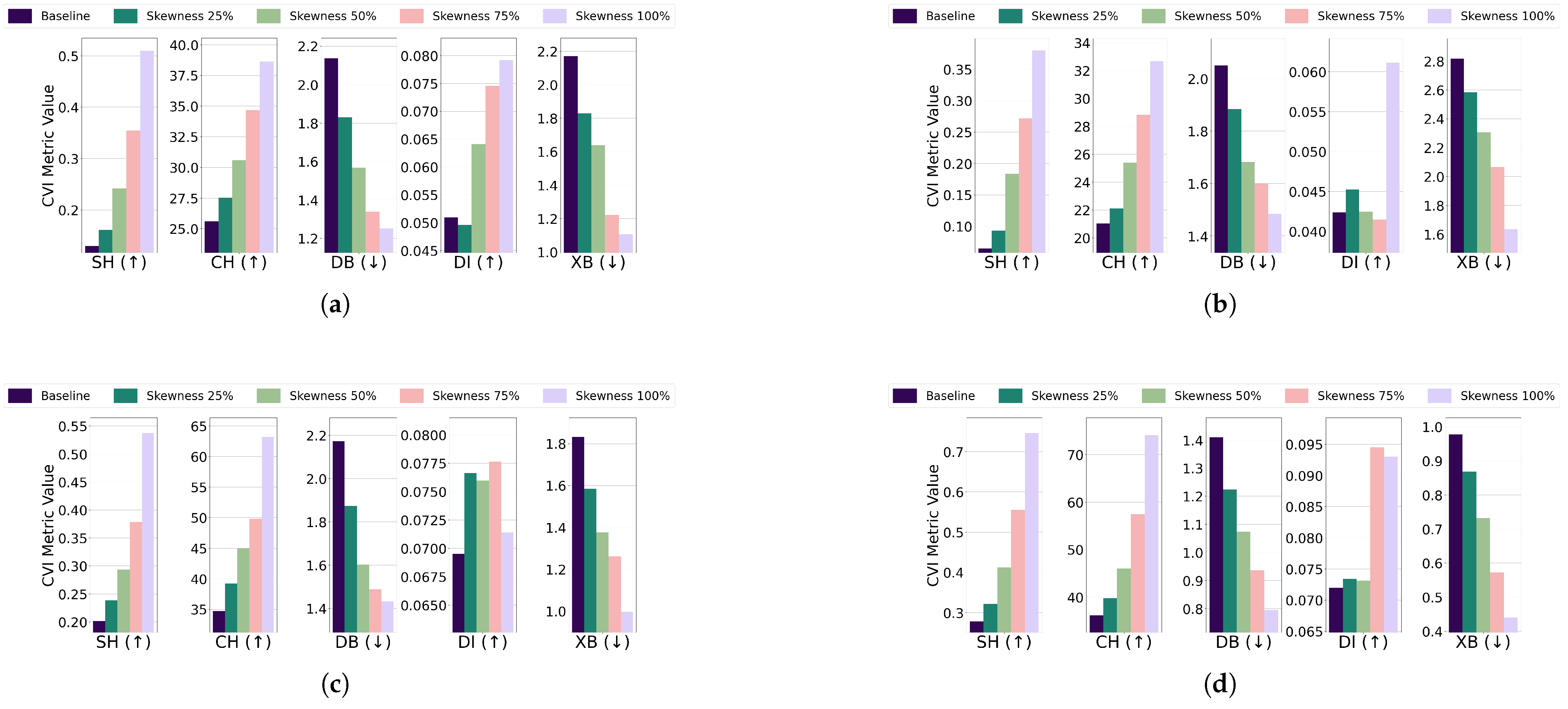
- Skewness: For the EL dataset without DR, points were repositioned on a 96-dimensional hypersphere with a radius equal to of the cluster size. Adjustments led to improvements in CVI metrics across all algorithms. K-Means, K-Medoids, Fuzzy C-Means, and GMM all exhibited enhanced clustering performance with increased skewness. For the EL dataset with DR, points were relocated on a nine-dimensional hypersphere with a radius equal to of the cluster size. Increasing skewness resulted in noticeable improvements in CVI metrics across all algorithms. The results are summarized in Figure 17 (without DR) and Figure 18 (with DR). Skewness adjustments revealed irregular behavior in DI, likely due to its sensitivity to cluster shape distortions. For skewed datasets, it is recommended to avoid DI and instead use SH, XB, CH, or DB.
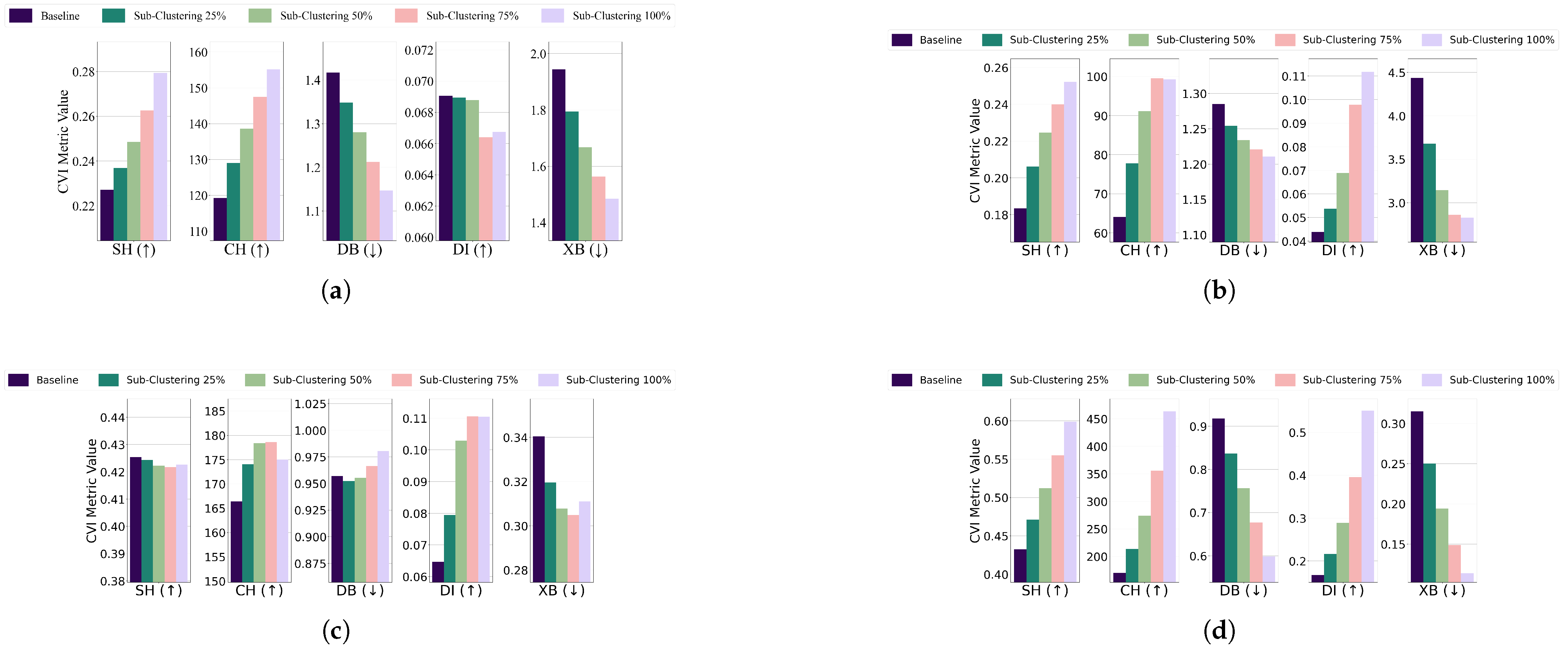
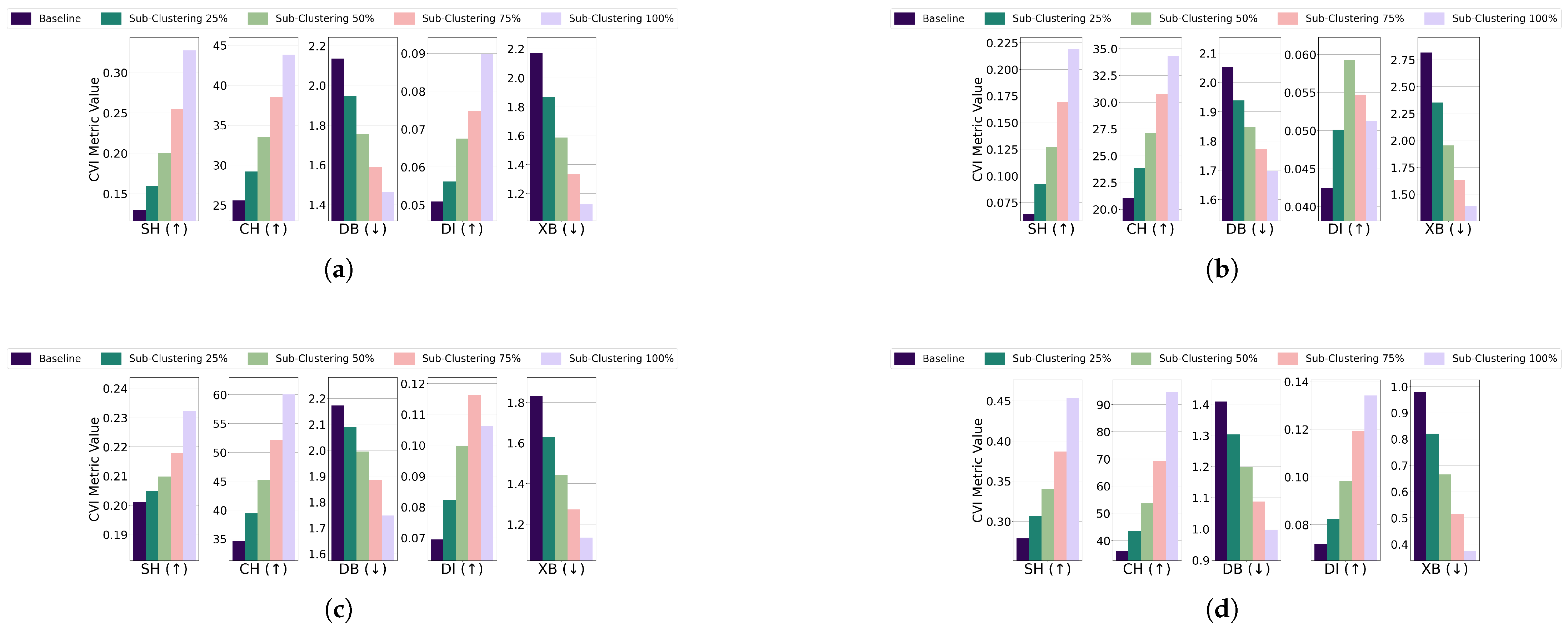
- Subclustering; For the EL dataset without DR, the threshold for all algorithms was set to of the cluster’s radius, except for GMM, which used . K-Medoids and GMM showed unexpected improvements across all CVIs, while K-Means exhibited stable Dunn’s Index initially but a later decline, and Fuzzy C-Means displayed inconsistent CVI behavior. For the EL dataset with DR, thresholds for all algorithms were set to of the cluster’s radius. K-Means and GMM demonstrated improvements across all CVIs, while for K-Medoids and Fuzzy C-Means, Dunn’s Index deteriorated instead of improving. The results are summarized in Figure 19 (without DR) and Figure 20 (with DR).Subclustering affected only DI, which deteriorated as the minimum inter-cluster distance decreased due to the formation of subclusters. This makes DI suitable for datasets with subclustering.
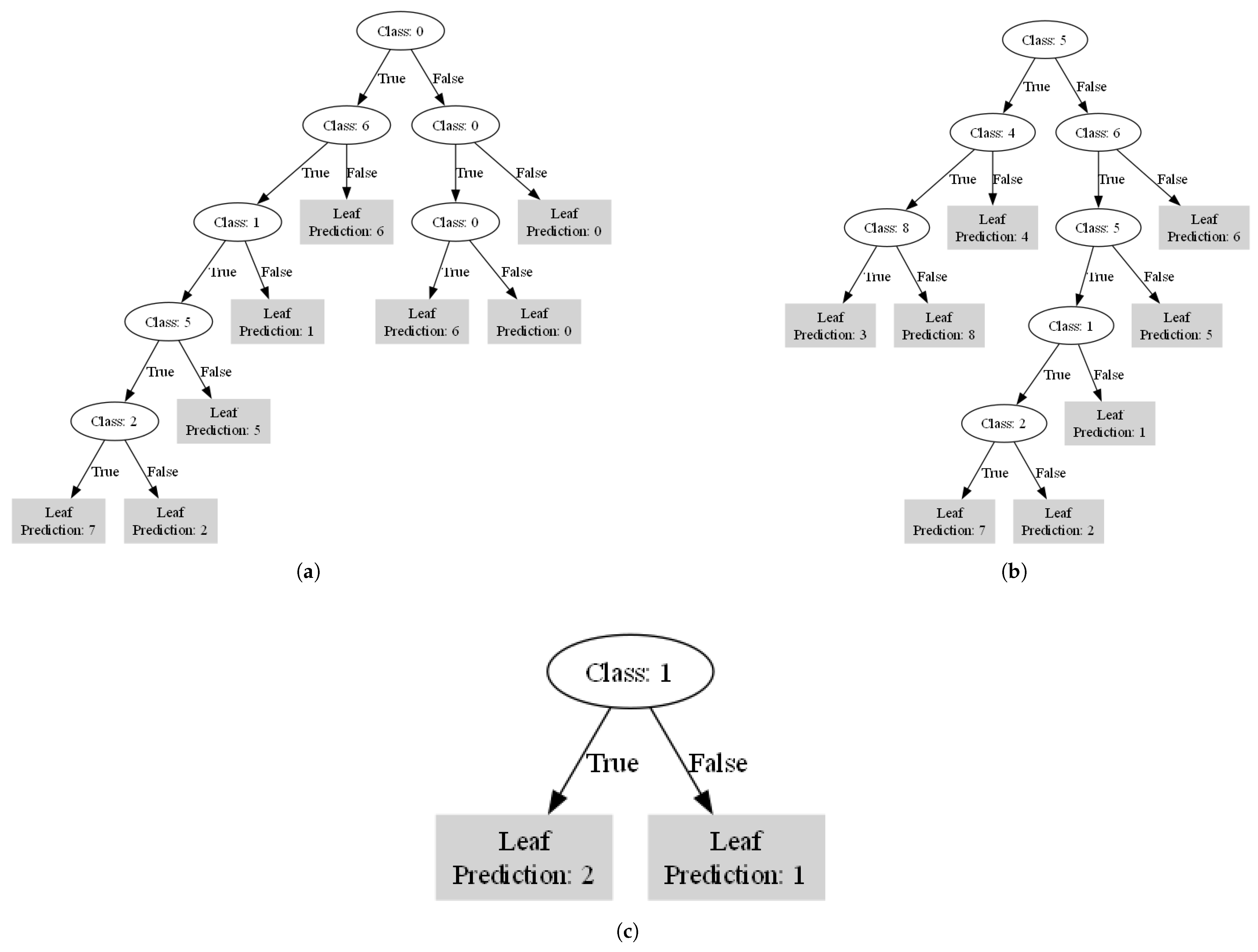
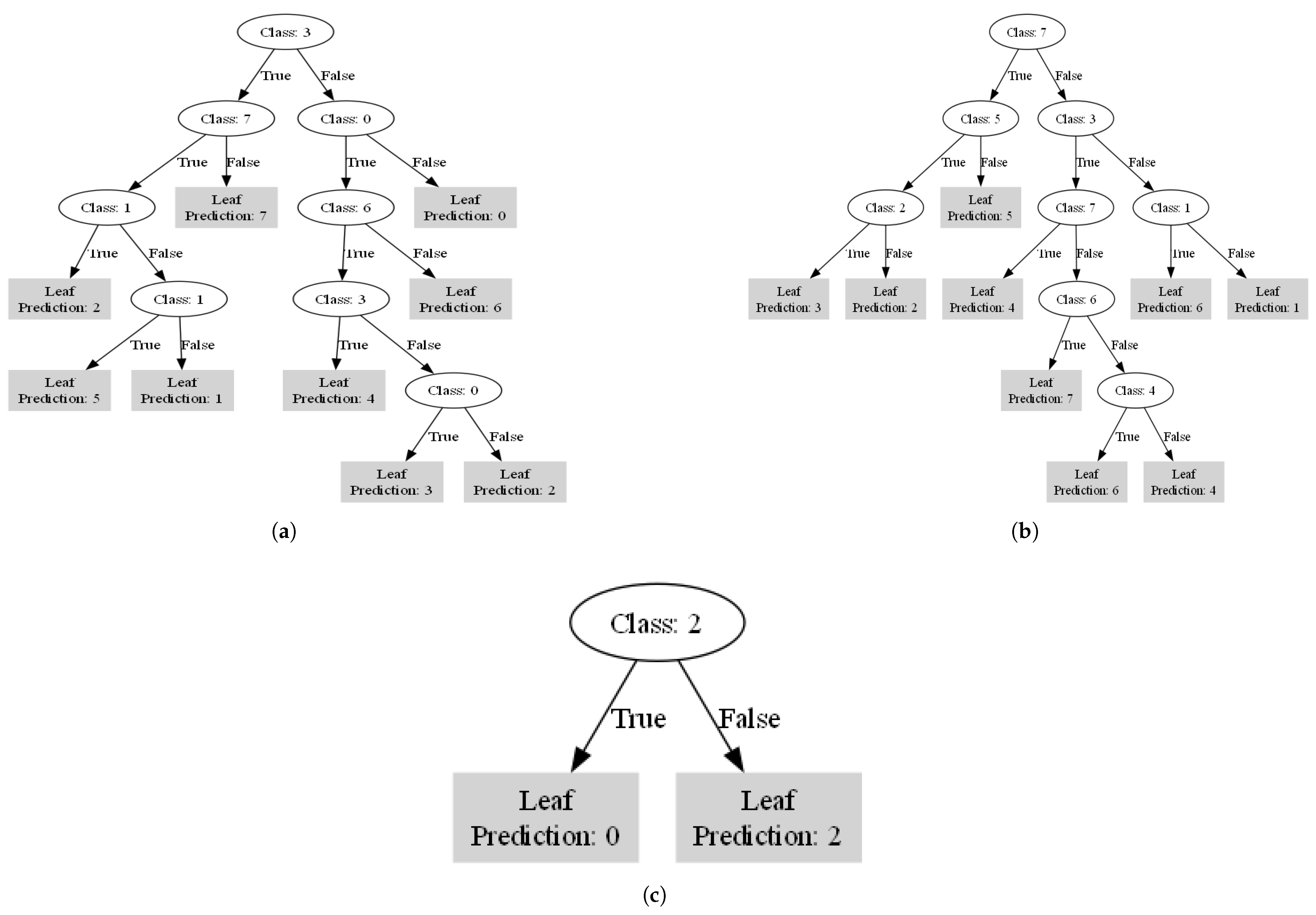
4. Interpretability Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DR | Dimensionality reduction |
| GMM | Gaussian Mixture Model |
| CVI | Clustering validation index |
| PCA | Principal Component Analysis |
Appendix A


References
- International Energy Agency (IEA). World Energy Outlook 2004; OECD Publishing: Paris, France, 2004. [Google Scholar] [CrossRef]
- Sun, X.; Khan, D.; Zheng, Y. Articulating the Role of Technological Innovation and Policy Uncertainty in Energy Efficiency: An Empirical Investigation. J. Knowl. Econ. 2023, 15, 14597–14616. [Google Scholar]
- Liao, S.-H.; Chu, P.-H.; Hsiao, P.-Y. Data Mining Techniques and Applications: A Decade Review from 2000 to 2011. Expert Syst. Appl. 2012, 39, 11303–11311. [Google Scholar]
- Han, J.; Pei, J.; Tong, H. Data Mining: Concepts and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2022. [Google Scholar]
- Mikut, R.; Reischl, M. Data Mining Tools. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 431–443. [Google Scholar]
- Oyewole, G.J.; Thopil, G.A. Data Clustering: Application and Trends. Artif. Intell. Rev. 2023, 56, 6439–6475. [Google Scholar]
- Bertsimas, D.; Orfanoudaki, A.; Wiberg, H. Interpretable Clustering: An Optimization Approach. Mach. Learn. 2021, 110, 89–138. [Google Scholar] [CrossRef]
- Bandyapadhyay, S.; Fomin, F.V.; Golovach, P.A.; Lochet, W.; Purohit, N.; Simonov, K. How to Find a Good Explanation for Clustering? Artif. Intell. 2023, 322, 103948. [Google Scholar] [CrossRef]
- Toussaint, W.; Moodley, D. Clustering Residential Electricity Consumption Data to Create Archetypes That Capture Household Behaviour in South Africa. S. Afr. Comput. J. 2020, 32, 1–34. [Google Scholar] [CrossRef]
- Jain, M.; Jain, M.; AlSkaif, T.; Dev, S. Which Internal Validation Indices to Use While Clustering Electric Load Demand Profiles? Sustain. Energy Grids Netw. 2022, 32, 100849. [Google Scholar]
- Zhou, K.; Peng, N.; Hu, D.; Shao, Z. Industrial Park Electric Power Load Pattern Recognition: An Ensemble Clustering-Based Framework. Energy Build. 2023, 279, 112687. [Google Scholar]
- Damayanti, R.; Abdullah, A.G.; Purnama, W.; Nandiyanto, A.B.D. Electrical Load Profile Analysis Using Clustering Techniques. IOP Conf. Ser. Mater. Sci. Eng. 2017, 180, 012081. [Google Scholar]
- Loyola-Gonzalez, O.; Gutierrez-Rodríguez, A.E.; Medina-Pérez, M.A.; Monroy, R.; Martínez-Trinidad, J.F.; Carrasco-Ochoa, J.A.; Garcia-Borroto, M. An Explainable Artificial Intelligence Model for Clustering Numerical Databases. IEEE Access 2020, 8, 52370–52384. [Google Scholar] [CrossRef]
- Hu, L.; Jiang, M.; Dong, J.; Liu, X.; He, Z. Interpretable Clustering: A Survey. arXiv 2024, arXiv:2409.00743. [Google Scholar]
- Trindade, A. Electricity Load Diagrams 2011–2014 Dataset. Available online: https://archive.ics.uci.edu/dataset/321/electricityloaddiagrams20112014 (accessed on 4 January 2025).
- Verleysen, M.; François, D. The Curse of Dimensionality in Data Mining and Time Series Prediction. In Proceedings of the International Work-Conference on Artificial Neural Networks, Barcelona, Spain, 8–10 June 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 758–770. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal Component Analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar]
- Raykov, T.; Marcoulides, G.A. Population Proportion of Explained Variance in Principal Component Analysis: A Note on Its Evaluation via a Large-Sample Approach. Struct. Equ. Model. Multidiscip. J. 2014, 21, 588–595. [Google Scholar]
- Paparrizos, J.; Gravano, L. Fast and accurate time-series clustering. ACM Trans. Database Syst. (TODS) 2017, 42, 1–49. [Google Scholar]
- De Oliveira, J.V.; Pedrycz, W. Advances in Fuzzy Clustering and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Shrifan, N.H.M.M.; Akbar, M.F.; Isa, N.A.M. An Adaptive Outlier Removal Aided K-Means Clustering Algorithm. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 6365–6376. [Google Scholar]
- Arora, P.; Varshney, S. Analysis of K-Means and K-Medoids Algorithm for Big Data. Procedia Comput. Sci. 2016, 78, 507–512. [Google Scholar]
- Mirkin, B. Clustering for Data Mining: A Data Recovery Approach; Chapman and Hall/CRC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Ghosh, S.; Dubey, S.K. Comparative Analysis of K-Means and Fuzzy C-Means Algorithms. Int. J. Adv. Comput. Sci. Appl. 2013, 4, 1–7. [Google Scholar]
- Patel, E.; Kushwaha, D.S. Clustering Cloud Workloads: K-Means vs. Gaussian Mixture Model. Procedia Comput. Sci. 2020, 171, 158–167. [Google Scholar] [CrossRef]
- Syakur, M.A.; Khotimah, B.K.; Rochman, E.M.S.; Satoto, B.D. Integration K-Means Clustering Method and Elbow Method for Identification of the Best Customer Profile Cluster. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 336, p. 012017. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the Number of Clusters in a Data Set via the Gap Statistic. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 411–423. [Google Scholar]
- Saitta, S.; Raphael, B.; Smith, I.F.C. A Comprehensive Validity Index for Clustering. Intell. Data Anal. 2008, 12, 529–548. [Google Scholar]
- Liu, Y.; Li, Z.; Xiong, H.; Gao, X.; Wu, J. Understanding of Internal Clustering Validation Measures. In Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, Australia, 14–17 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 911–916. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On Clustering Validation Techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar]
- Mary, S.A.L.; Sivagami, A.N.; Rani, M.U. Cluster Validity Measures Dynamic Clustering Algorithms. ARPN J. Eng. Appl. Sci. 2015, 10, 4009–4012. [Google Scholar]
- Liu, G. A New Index for Clustering Evaluation Based on Density Estimation. arXiv 2022, arXiv:2207.01294. [Google Scholar]
- Lamirel, J.-C.; Dugué, N.; Cuxac, P. New Efficient Clustering Quality Indexes. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3649–3657. [Google Scholar]
- Al-Bazzaz, H.; Azam, M.; Amayri, M.; Bouguila, N. Explainable finite mixture of mixtures of bounded asymmetric generalized Gaussian and Uniform distributions learning for energy demand management. ACM Trans. Intell. Syst. Technol. 2024, 15, 1–64. [Google Scholar]
- Al-Bazzaz, H.; Azam, M.; Amayri, M.; Bouguila, N. Enhanced Energy Characterization and Feature Selection Using Explainable Non-parametric AGGMM. In Proceedings of the Recent Challenges in Intelligent Information and Database Systems—15th Asian Conference, ACIIDS 2023, Phuket, Thailand, 24–26 July 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 145–156. [Google Scholar]
- Prabhakaran, K.; Dridi, J.; Amayri, M.; Bouguila, N. Explainable K-Means Clustering for Occupancy Estimation. In Proceedings of the 17th International Conference on Future Networks and Communications/19th International Conference on Mobile Systems and Pervasive Computing/12th International Conference on Sustainable Energy Information Technology (FNC/MobiSPC/SEIT 2022), Niagara Falls, ON, Canada, 9–11 August 2022; Procedia Computer Science: Manchester, UK, 2022; pp. 326–333. [Google Scholar]
- Al-Bazzaz, H.; Azam, M.; Amayri, M.; Bouguila, N. Explainable Robust Smart Meter Data Clustering for Improved Energy Management. In Proceedings of the 2023 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Honolulu, HI, USA, 1–4 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 5194–5199. [Google Scholar]
- Al-Bazzaz, H.; Prabhakaran, K.S.; Amayri, M.; Bouguila, N. Refining Nonparametric Mixture Models with Explainability for Smart Building Applications. In Proceedings of the 2023 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Honolulu, HI, USA, 1–4 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 5212–5217. [Google Scholar]







| PC (Feature Index) | Top Contributing Features | Time Intervals |
|---|---|---|
| PC1 | Features {3,4,5,6,7} | 00:45, 01:00, 01:15, 01:30, 01:45 |
| PC2 | Features {79,80,82,83,84} | 19:45, 20:00, 20:30, 20:45, 21:00 |
| PC3 | Features {39,40,76,77, 78} | 09:45, 10:00, 19:00, 19:15, 19:30 |
| PC4 | Features {69,70,71,72, 73} | 17:15, 17:30, 17:45, 18:00, 18:15 |
| PC5 | Features {27,28,29, 30, 48} | 06:45, 07:00, 07:15, 07:30, 12:00 |
| PC6 | Features {0,1,69, 70, 72} | 00:00, 00:15, 17:15, 17:30, 18:00 |
| PC7 | Features {89,90,91, 92,52} | 22:15, 22:30, 22:45, 23:00, 13:00 |
| PC8 | Features {51,52,50, 49, 88} | 12:45, 13:00, 12:30, 12:15, 22:00 |
| PC9 | Features {23,24,22, 88, 87} | 05:45, 06:00, 05:30, 22:00, 21:45 |
| Algorithm | Model | Clusters Explained | Clusters Unexplained |
|---|---|---|---|
| Without Dimensionality Reduction | |||
| K-Means | Sparse Oblique Tree | 6/8 | 3, 4 |
| Axis-Aligned Tree | All 8 | None | |
| K-Medoids | Sparse Oblique Tree | 7/9 | 0,9 |
| Axis-Aligned Tree | 8/9 | 7 | |
| Fuzzy C-Means | Sparse Oblique Tree | 2/3 | 0 |
| Axis-Aligned Tree | All 3 | None | |
| GMM | Sparse Oblique Tree | 3/4 | 0 |
| Axis-Aligned Tree | All 4 | None | |
| With Dimensionality Reduction | |||
| K-Means | Sparse Oblique Tree | All 8 | None |
| Axis-Aligned Tree | 7/8 | 4 | |
| K-Medoids | Sparse Oblique Tree | 7/8 | 0 |
| Axis-Aligned Tree | All 8 | None | |
| Fuzzy C-Means | Sparse Oblique Tree | 2/3 | 1 |
| Axis-Aligned Tree | All 3 | None | |
| GMM | Sparse Oblique Tree | All 5 | None |
| Axis-Aligned Tree | All 5 | None | |
| Algorithm | Sparse Oblique Decision Tree F1 Score | Axis-Aligned Decision Tree F1 Score |
|---|---|---|
| Without Dimensionality Reduction | ||
| K-Means | 0.692 | 0.913 |
| K-Medoids | 0.766 | 0.739 |
| Fuzzy C-Means | 0.613 | 0.992 |
| GMM | 0.681 | 0.991 |
| With Dimensionality Reduction | ||
| K-Means | 0.907 | 0.846 |
| K-Medoids | 0.655 | 0.902 |
| Fuzzy C-Means | 0.616 | 1.000 |
| GMM | 0.951 | 0.964 |
| Rule | Conditions | Predicted Cluster | Interpretation |
|---|---|---|---|
| 1 | 00:45 ≤ 0.39 08:00 ≤ −1.40 | Cluster 1 | Very low consumption from midnight to early morning and extremely low in the morning.Real-world implication: Households that barely use electricity overnight, possibly indicating no late-night appliances (e.g., washing machines or dishwashers) and minimal morning routines (e.g., inhabitants leave early). |
| 2 | 00:45 ≤ 0.39 08:00 > −1.40 12:15 ≤ −0.66 | Cluster 2 | Slightly higher morning usage, moderate midday usage.Real-world implication: Households with moderate breakfast routines but still low midday activity; could be working families with children who leave by mid-morning. |
| 3 | 00:45 ≤ 0.39 08:00 > −1.40 12:15 > −0.66 09:45 ≤ −0.59 | Cluster 1 | Closer thresholds between morning and midday usage lead back to Cluster 1.Real-world implication: Illustrates how small differences in the 09:45 slot can switch a household between two morning-centric clusters, capturing subtle variations in morning routines. |
| 4 | 09:45 > −0.59 02:00 ≤ −1.80 | Cluster 1 | Extremely low consumption at 02:00 but higher mid-morning consumption.Real-world implication: Possibly households that shut off most devices before bed but wake up with a substantial breakfast or early appliance use (e.g., coffee machines, toasters). |
| 5 | 02:00 > −1.80 | Cluster 3 | Slightly higher overnight usage.Real-world implication: Households that keep some devices running overnight (e.g., fridge plus entertainment devices or charging stations). |
| 6 | 00:45 > 0.39 22:15 ≤ 0.21 | Cluster 0 | More consumption after midnight but low late-evening usage.Real-world implication: Households that shift certain appliance usage to shortly after midnight but reduce activities earlier in the evening, indicating evening routines that end relatively early. |
| 7 | 22:15 > 0.21 08:30 ≤ −2.14 | Cluster 1 | Late-evening changes trigger very low morning usage.Real-world implication: Possibly households with moderate to high consumption around 22:15, but extremely low consumption by early morning, suggesting that nighttime routines end abruptly, reducing load well before 08:30. |
| 8 | 08:30 > −2.14 20:00 ≤ −0.82 | Cluster 0 | Adjusted early-evening consumption leads back to Cluster 0.Real-world implication: Households that may be active enough in the morning to exceed the lower threshold, but remain below the early-evening usage cut-off, indicating little to no significant consumption around 20:00. |
| 9 | 20:00 > −0.82 | Cluster 2 | Slightly higher evening consumption sets Cluster 2.Real-world implication: Households that exhibit more pronounced evening activity (e.g., cooking dinner or using entertainment devices) around or after 20:00, pushing them into a higher-consumption cluster. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kallel, S.; Amayri, M.; Bouguila, N. Clustering and Interpretability of Residential Electricity Demand Profiles. Sensors 2025, 25, 2026. https://doi.org/10.3390/s25072026
Kallel S, Amayri M, Bouguila N. Clustering and Interpretability of Residential Electricity Demand Profiles. Sensors. 2025; 25(7):2026. https://doi.org/10.3390/s25072026
Chicago/Turabian StyleKallel, Sarra, Manar Amayri, and Nizar Bouguila. 2025. "Clustering and Interpretability of Residential Electricity Demand Profiles" Sensors 25, no. 7: 2026. https://doi.org/10.3390/s25072026
APA StyleKallel, S., Amayri, M., & Bouguila, N. (2025). Clustering and Interpretability of Residential Electricity Demand Profiles. Sensors, 25(7), 2026. https://doi.org/10.3390/s25072026








