Few-Mode Erbium-Doped Fiber with Three-Layer Center-Recessed Doping for Gain Equalization
Abstract
1. Introduction
2. Simulation Principle and Design
2.1. Operation Principle
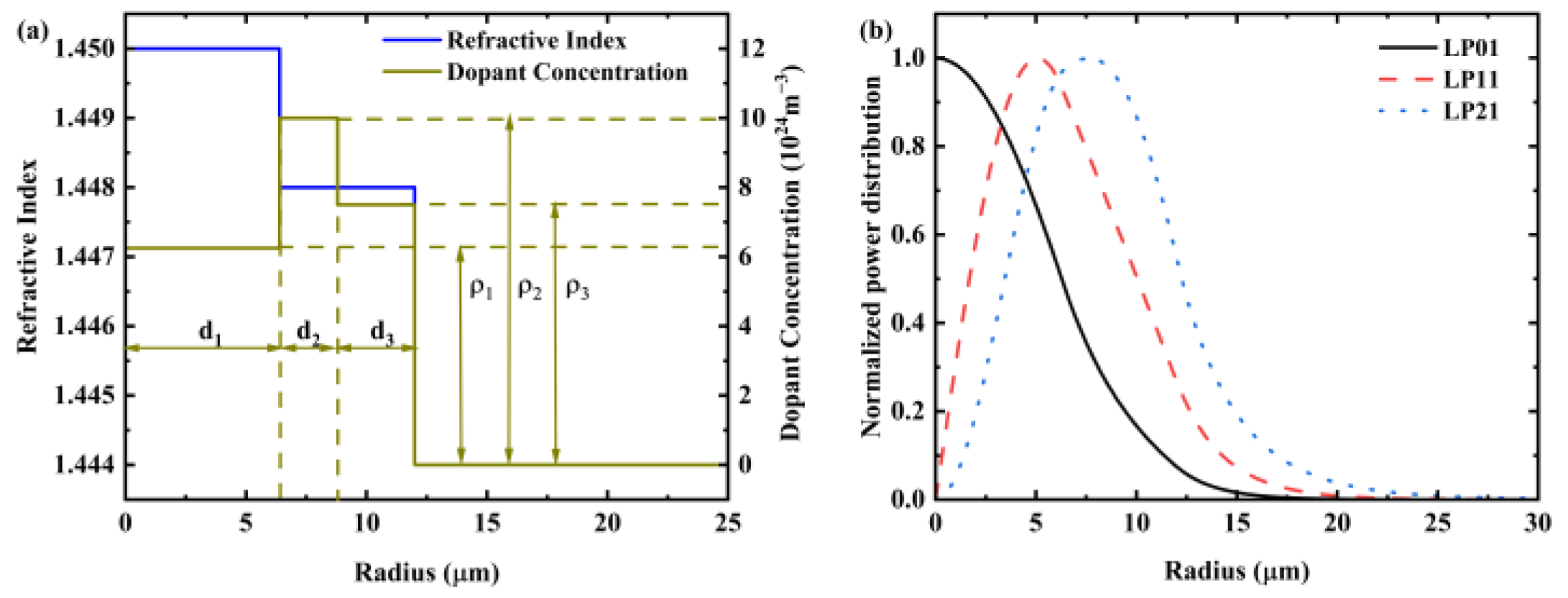
2.2. Design of Few-Mode Erbium-Doped Fiber
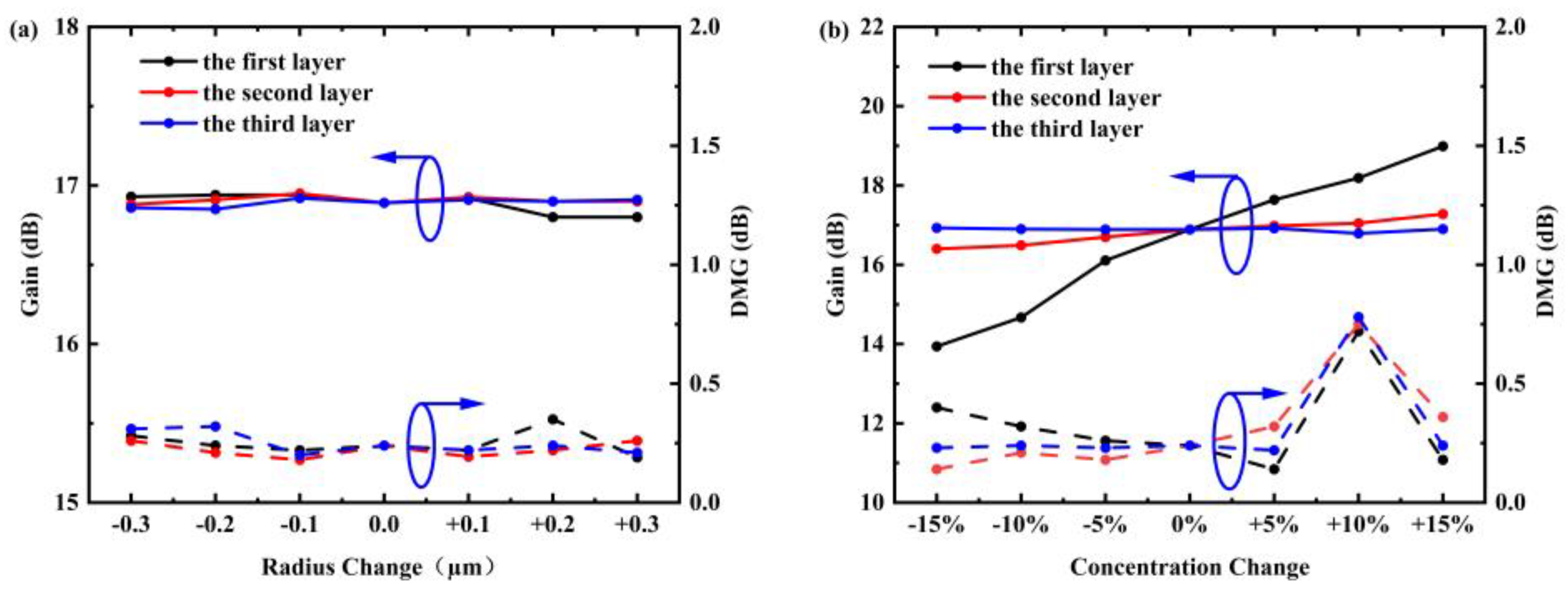
3. Simulation Results and Discussions
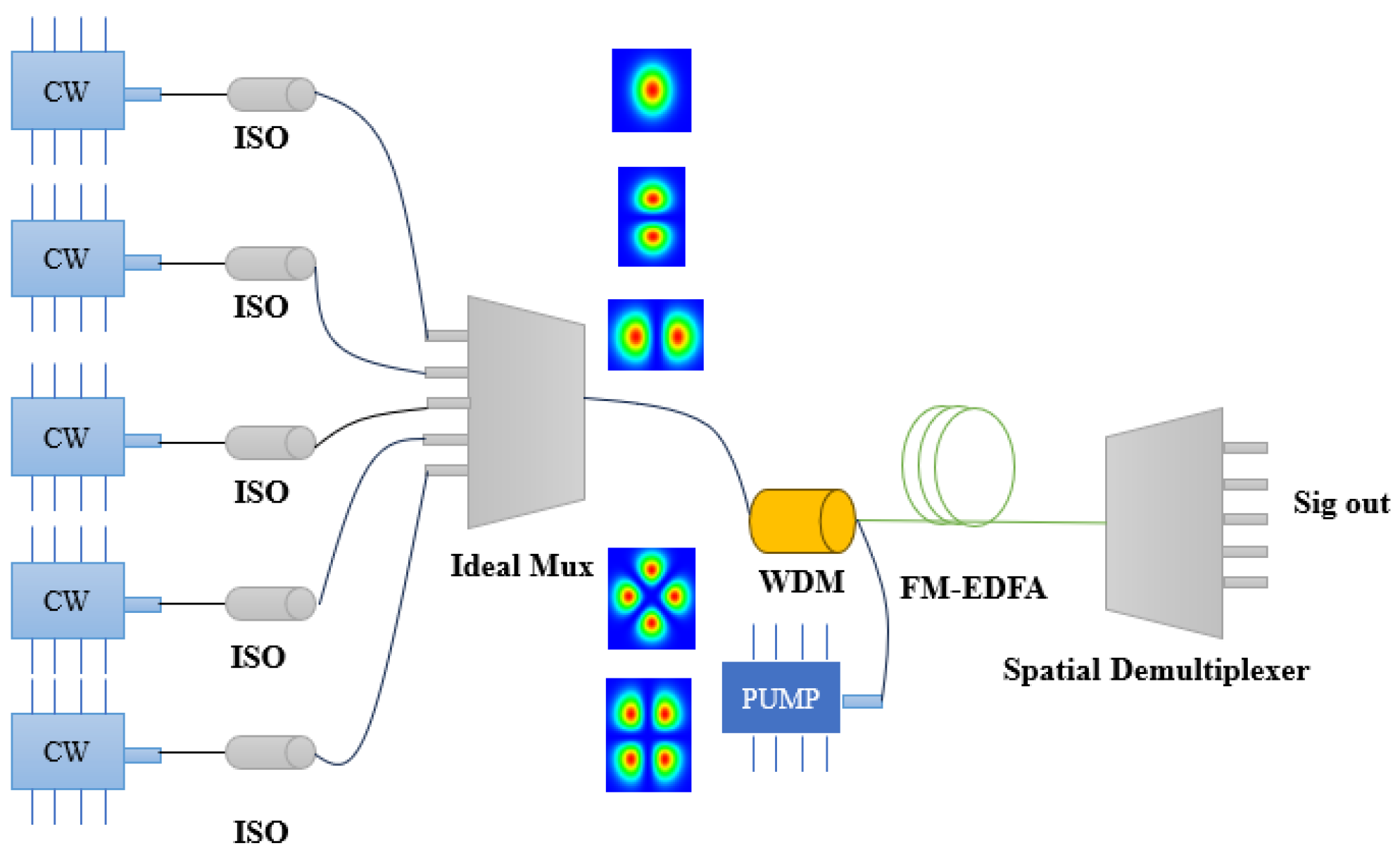
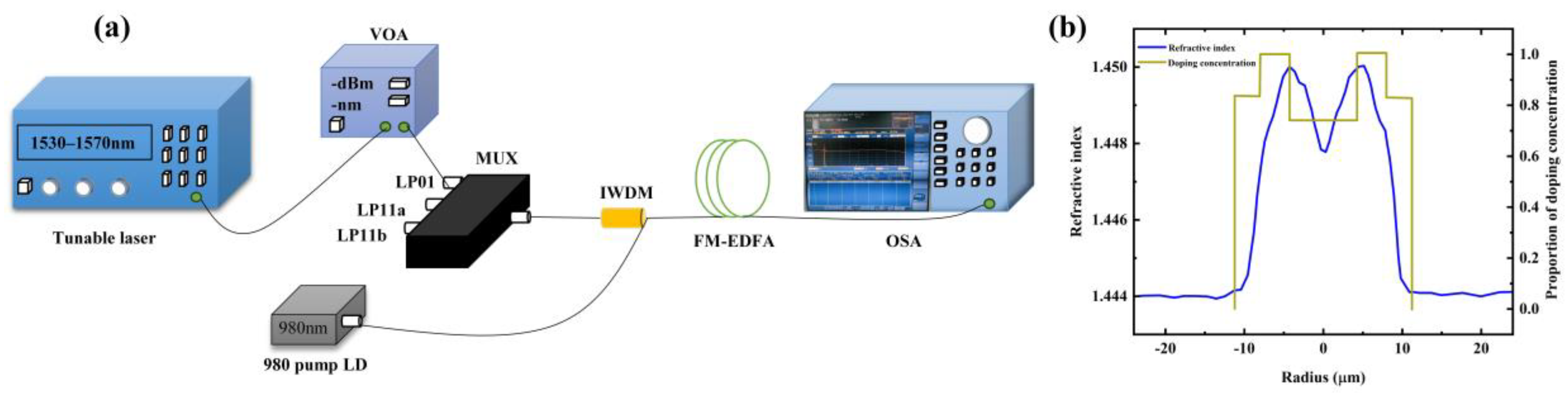
4. Experimental Process and Result Analysis
4.1. Experimental Process
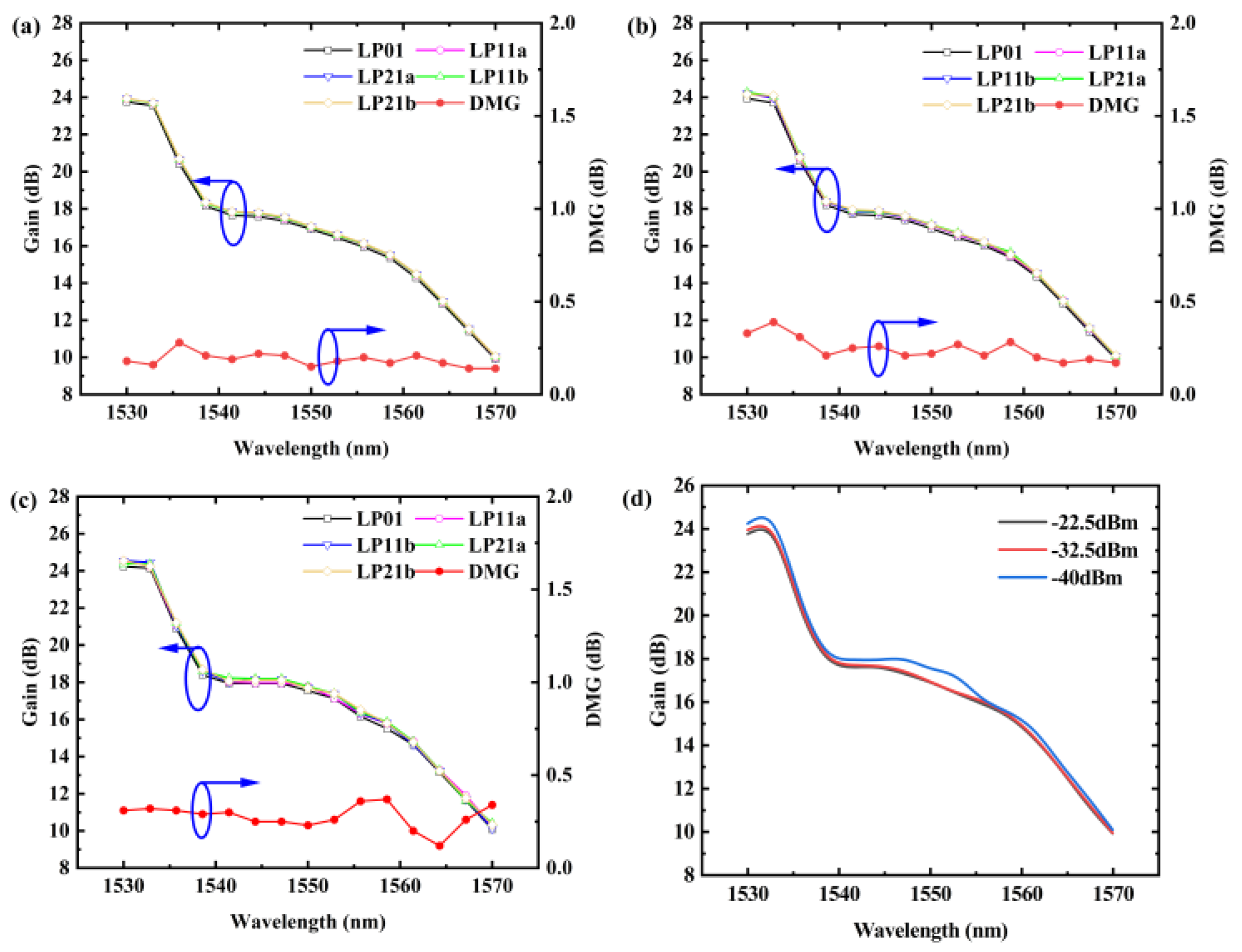
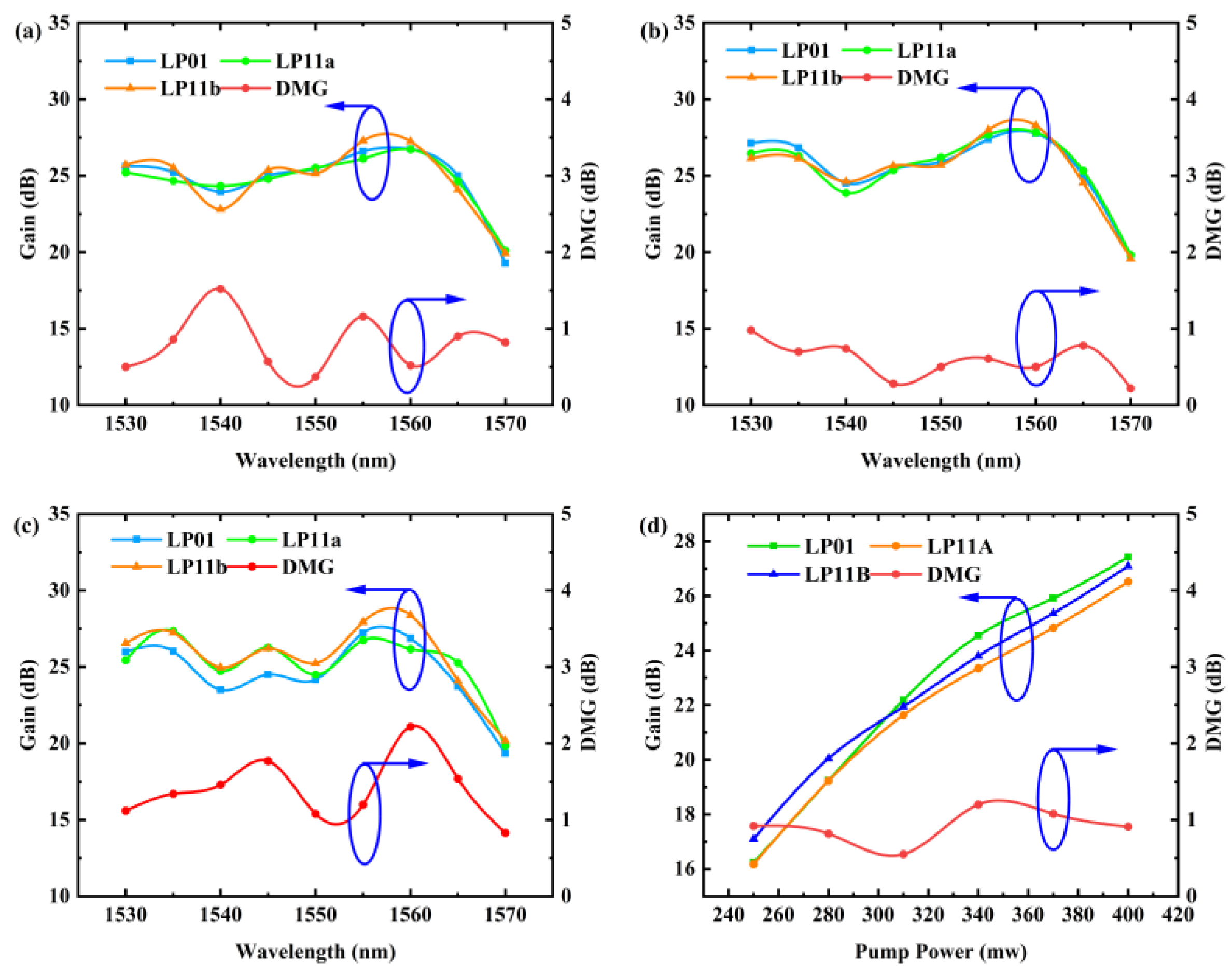
4.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qian, D.Y.; Huang, M.F.; Ip, E.; Huang, Y.K.; Shao, Y.; Hu, J.Q.; Wang, T. 101.7-Tb/s (370x294-Gb/s) PDM-128QAM-OFDM Transmission over 3x55-km SSMF using Pilot-based Phase Noise Mitigation. In Proceedings of the Conference on Optical Fiber Communication (OFC)/National Fiber Optic Engineers Conference(NFOEC), Los Angeles, CA, USA, 6–10 March 2011. [Google Scholar]
- Kobayashi, T.; Sano, A.; Matsuura, A.; Miyamoto, Y.; Ishihara, K. Nonlinear Tolerant Spectrally-Efficient Transmission Using PDM 64-QAM Single Carrier FDM With Digital Pilot-Tone. J. Light. Technol. 2012, 30, 3805–3815. [Google Scholar] [CrossRef]
- Winzer, P.J. Optical Networking Beyond WDM. IEEE Photonics J. 2012, 4, 647–651. [Google Scholar] [CrossRef]
- Wada, N.; Puttnam, B.J.; Luís, R.S.; Sakaguchi, J.; Klaus, W.; Mendinueta, J.M.D.; Awaji, Y. Space Division Multiplexing (SDM) Transmission and Related Technologies. In Proceedings of the 18th International Conference on Transparent Optical Networks (ICTON), Trento, Italy, 10–14 July 2016. [Google Scholar]
- Ryf, R.; Fontaine, N.K.; Chen, H.; Guan, B.; Huang, B.; Esmaeelpour, M.; Gnauck, A.H.; Randel, S.; Yoo, S.J.B.; Koonen, A.M.J.; et al. Mode-multiplexed transmission over conventional graded-index multimode fibers. Opt. Express 2015, 23, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Winzer, P.J.; Foschini, G.J. MIMO capacities and outage probabilities in spatially multiplexed optical transport systems. Opt. Express 2011, 19, 16680–16696. [Google Scholar] [CrossRef]
- Li, Z.Q.; Pei, L.; Zheng, J.J.; Wang, J.S.; Xu, W.X.; Shen, L.; Zhong, L. Amplification and Transmission System with Matching Multi-Layer Ion-Doped FM-EDFA. J. Light. Technol. 2023, 41, 695–701. [Google Scholar] [CrossRef]
- Zhao, Q.; Pei, L.; Tang, J.; Wang, J.; Zheng, J.; Li, J.; Ning, T. Design of few-mode erbium-doped fiber with a low differential modal gain and weak coupling based on layered doping. Appl. Opt. 2023, 62, 1567–1574. [Google Scholar] [CrossRef]
- Yuanpeng, D.; Junjie, Q.; Lei, S.; Guangchong, D.; Rui, Z.; Jun, C.; Zhao, Y.; Lei, Z.; Jie, L. Few-mode erbium-doped fiber amplifier for mode-division multiplexed transmission. In Proceedings Volume 12935, Fourteenth International Conference on Information Optics and Photonics; SPIE: Bellingham, WA, USA, 2023; p. 1293547. [Google Scholar]
- Liu, Y.; Wang, X.; Yang, Z.; Zhang, L.; Li, G. Strongly Coupled Few-Mode Erbium-Doped Fiber Amplifiers with Ultralow Differential Modal Gain. In 2020 Optical Fiber Communications Conference and Exhibition (OFC); Optica Publishing Group: Washington, DC, USA, 2020; pp. 1–3. [Google Scholar]
- Zhang, Z.Z.; Guo, C.; Cui, L.; Zhang, Y.C.; Du, C.; Li, X.Y. All-fiber few-mode erbium-doped fiber amplifier supporting six spatial modes. Chin. Opt. Lett. 2019, 17, 100604. [Google Scholar] [CrossRef]
- Zhang, Z.; Mo, Q.; Guo, C.; Zhao, N.; Du, C.; Li, X. Gain Equalized Four Mode Groups Erbium Doped Fiber Amplifier with LP01 Pump. In Asia Communications and Photonics Conference 2016; OSA Technical Digest (online); Optica Publishing Group: Washington, DC, USA, 2016; p. ATh3B.5. [Google Scholar]
- Jung, Y.; Alam, S.; Li, Z.; Dhar, A.; Giles, D.; Giles, I.P.; Sahu, J.K.; Poletti, F.; Grüner-Nielsen, L.; Richardson, D.J. First demonstration and detailed characterization of a multimode amplifier for space division multiplexed transmission systems. Opt. Express 2011, 19, 952–957. [Google Scholar] [CrossRef]
- Kang, Q.Y.; Lim, E.L.; Jung, Y.M.; Sahu, J.K.; Poletti, F.; Baskiotis, C.; Shaif-ul, A.; Richardson, D.J. Accurate modal gain control in a multimode erbium doped fiber amplifier incorporating ring doping and a simple LP01 pump configuration. Opt. Express 2012, 20, 20835–20843. [Google Scholar] [CrossRef]
- Krummrich, P.M. Optical Amplifiers for Multi Mode Multi Core Transmission. In Optical Fiber Communication Conference; OSA Technical Digest; Optica Publishing Group: Washington, DC, USA, 2012; p. OW1D.1. [Google Scholar]
- Jin, C.; Ung, B.; Messaddeq, Y.; LaRochelle, S. Tailored modal gain in a multi-mode erbium-doped fiber amplifier based on engineered ring doping profiles. In Proceedings Volume 8915, Photonics North 2013; SPIE: Bellingham, WA, USA, 2013. [Google Scholar]
- Kang, Q.Y.; Lim, E.L.; Poletti, F.; Jung, Y.M.; Baskiotis, C.; Alam, S.U.; Richardson, D.J. Minimizing differential modal gain in cladding-pumped EDFAs supporting four and six mode groups. Opt. Express 2014, 22, 21499–21507. [Google Scholar] [CrossRef]
- Zeng, Y.; Fang, Y.H.; Qin, Y.W.; Xu, O.; Li, J.P.; Fu, S.N. Rigorous FM-EDF design with an oversized two-layer erbium ion distribution for C-band DMG mitigation. J. Opt. Soc. Am. B 2021, 38, F1–F7. [Google Scholar]
- Liu, Y.P.; Yang, Z.Q.; Wang, X.T.; Jung, Y.M.; Zhang, L. Gain Equalization for Few-Mode Erbium-Doped Fiber Amplifiers via Strong Mode Coupling. Appl. Sci. 2022, 12, 767. [Google Scholar] [CrossRef]
- Gao, J.; Yan, F.P.; Ren, G.B.; Guo, H.; Wang, B.Y.; Li, G.B.; Zhu, F.X.; Tan, H.Y.; Feng, T. Gain equalization for a few-mode erbium-doped fiber amplifier supporting eight spatial modes. Appl. Opt. 2023, 62, 9274–9282. [Google Scholar]
- Kai, S.; Premaratne, M. Effects of SPM, XPM, and four-wave-mixing in L-band EDFAs on fiber-optic signal transmission. IEEE Photonics Technol. Lett. 2000, 12, 1630–1632. [Google Scholar]
- Giles, C.R.; Desurvire, E. Modeling Erbium-Doped Fiber Amplifiers. J. Light. Technol. 1991, 9, 271–283. [Google Scholar]
- Wang, N.; Kim, I.; Vassilieva, O.; Ikeuchi, T.; Wen, H.; Antonio-Lopez, J.E.; Alvarado-Zacarias, J.C.; Liu, H.Y.; Fan, S.L.; Habib, M.S.; et al. Low-crosstalk few-mode EDFAs using retro-reflection for single-mode fiber trunk lines and networks. Opt. Express 2019, 27, 35962–35970. [Google Scholar] [CrossRef]
- Mizuno, T.; Takara, H.; Shibahara, K.; Sano, A.; Miyamoto, Y. Dense Space Division Multiplexed Transmission Over Multicore and Multimode Fiber for Long-haul Transport Systems. J. Light. Technol. 2016, 34, 1484–1493. [Google Scholar]
- Matte-Breton, C.; Chen, H.; Fontaine, N.K.; Ryf, R.; Essiambre, R.J.; Kelly, C.; Jin, C.; Messaddeq, Y.; LaRochelle, S. Demonstration of an erbium-doped fiber with annular doping for low gain compression in cladding-pumped amplifiers. Opt. Express 2018, 26, 26633–26645. [Google Scholar] [CrossRef]
- Barnes, W.L.; Laming, R.I.; Tarbox, E.J.; Morkel, P.R. Absorption and emission cross section of Er/sup 3+/ doped silica fibers. IEEE J. Quantum Electron. 1991, 27, 1004–1010. [Google Scholar] [CrossRef]
- Kuroda, K.; Nakandakari, M.; Yoshikuni, Y. Metastable-state lifetime of erbium ions measured through delayed absorption in the fiber propagation direction. Appl. Phys. B 2017, 123, 95. [Google Scholar]
- Webb, A.S.; Boyland, A.J.; Standish, R.J.; Yoo, S.; Sahu, J.K.; Payne, D.N. MCVD in-situ solution doping process for the fabrication of complex design large core rare-earth doped fibers. J. Non-Cryst. Solids 2010, 356, 848–851. [Google Scholar] [CrossRef]
- Townsend, J.E.; Poole, S.B.; Payne, D.N. Solution-doping technique for fabrication of rare-earth-doped optical fibres. Electron. Lett. 1987, 23, 329–331. [Google Scholar] [CrossRef]
- Bromage, J. Raman amplification for fiber communications systems. J. Light. Technol. 2004, 22, 79–93. [Google Scholar] [CrossRef]



| Mode | Overlapping Integral | Er Metastable Lifetime |
|---|---|---|
| LP01 | 1.5808 × 1022 | 10 ms |
| LP11 a/b | 2.2434 × 1022 | |
| LP21 a/b | 2.6548 × 1022 |
| Ref. | Structure | Gain (dB) | DMG (dB) | NF (dB) |
|---|---|---|---|---|
| [18] (Simulation) | An oversized two-layer erbium ion distribution | ~25 | <0.64 | 5–7 |
| [20] (Simulation) | Three-layer refractive index with three-layer doping | ~20 | ~0.4 | <5 |
| [8] (Simulation) | Three-layer doping with uniform refractive index | <22 | <0.5 | <5 |
| [9] (Experiment) | ~ | ~26 | ≤0.6 | <11 |
| This paper (Sim) | Three-layer doping with dual-layer refractive index | <25 | <0.5 | ~ |
| This paper (Exp) | ~ | <30 | <0.8 | <8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, S.; Cheng, Y.; Tang, Y.; Chen, M.; Deng, S.; Yuan, L. Few-Mode Erbium-Doped Fiber with Three-Layer Center-Recessed Doping for Gain Equalization. Sensors 2025, 25, 2010. https://doi.org/10.3390/s25072010
Bao S, Cheng Y, Tang Y, Chen M, Deng S, Yuan L. Few-Mode Erbium-Doped Fiber with Three-Layer Center-Recessed Doping for Gain Equalization. Sensors. 2025; 25(7):2010. https://doi.org/10.3390/s25072010
Chicago/Turabian StyleBao, Shengchen, Yu Cheng, Yi Tang, Ming Chen, Shijie Deng, and Libo Yuan. 2025. "Few-Mode Erbium-Doped Fiber with Three-Layer Center-Recessed Doping for Gain Equalization" Sensors 25, no. 7: 2010. https://doi.org/10.3390/s25072010
APA StyleBao, S., Cheng, Y., Tang, Y., Chen, M., Deng, S., & Yuan, L. (2025). Few-Mode Erbium-Doped Fiber with Three-Layer Center-Recessed Doping for Gain Equalization. Sensors, 25(7), 2010. https://doi.org/10.3390/s25072010






