Tool Wear State Identification Method with Variable Cutting Parameters Based on Multi-Source Unsupervised Domain Adaptation
Abstract
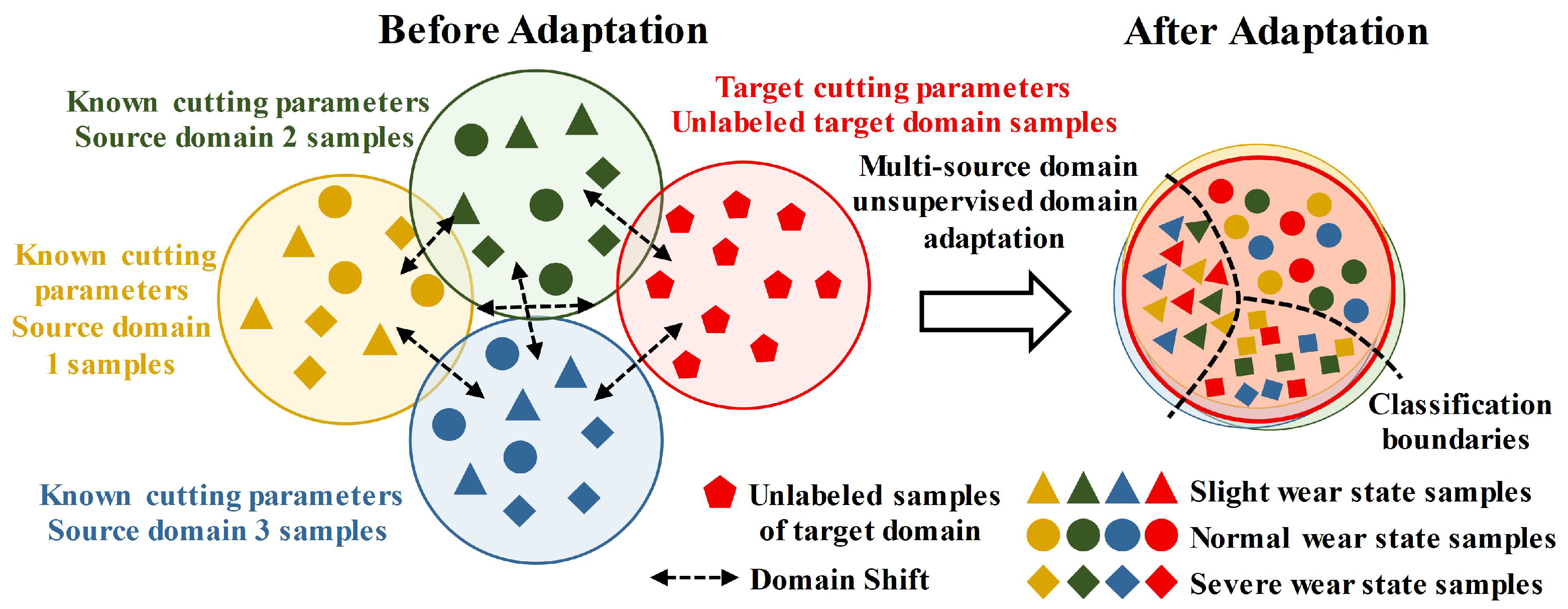
1. Introduction
- (1)
- A novel multi-source domain adaptive tool wear state prediction method based on Multiple Feature Spaces Adaptation Network (MFSAN) architecture is proposed. This method achieves tool wear state prediction under varying cutting parameters by constructing a multi-feature space adaptation network.
- (2)
- A public feature extractor based on a Non-Stationary Transformer Encoder (NSTE) is proposed. This extractor utilizes a sequence stationarization module and NSTE to explore non-stationary input features in multi-channel signals, thereby extracting advanced public features related to wear.
- (3)
- The proposed model incorporates a domain-specific feature distribution alignment module based on sliced Wasserstein distance (SWD) and a domain-specific classifier output alignment module. SWD allows for the measurement of differences in the hidden feature space with low computational cost. These two alignment modules mitigate domain shift and simplify the synchronization of alignment across multiple domain distributions.
2. Proposed Method
2.1. Problem Description
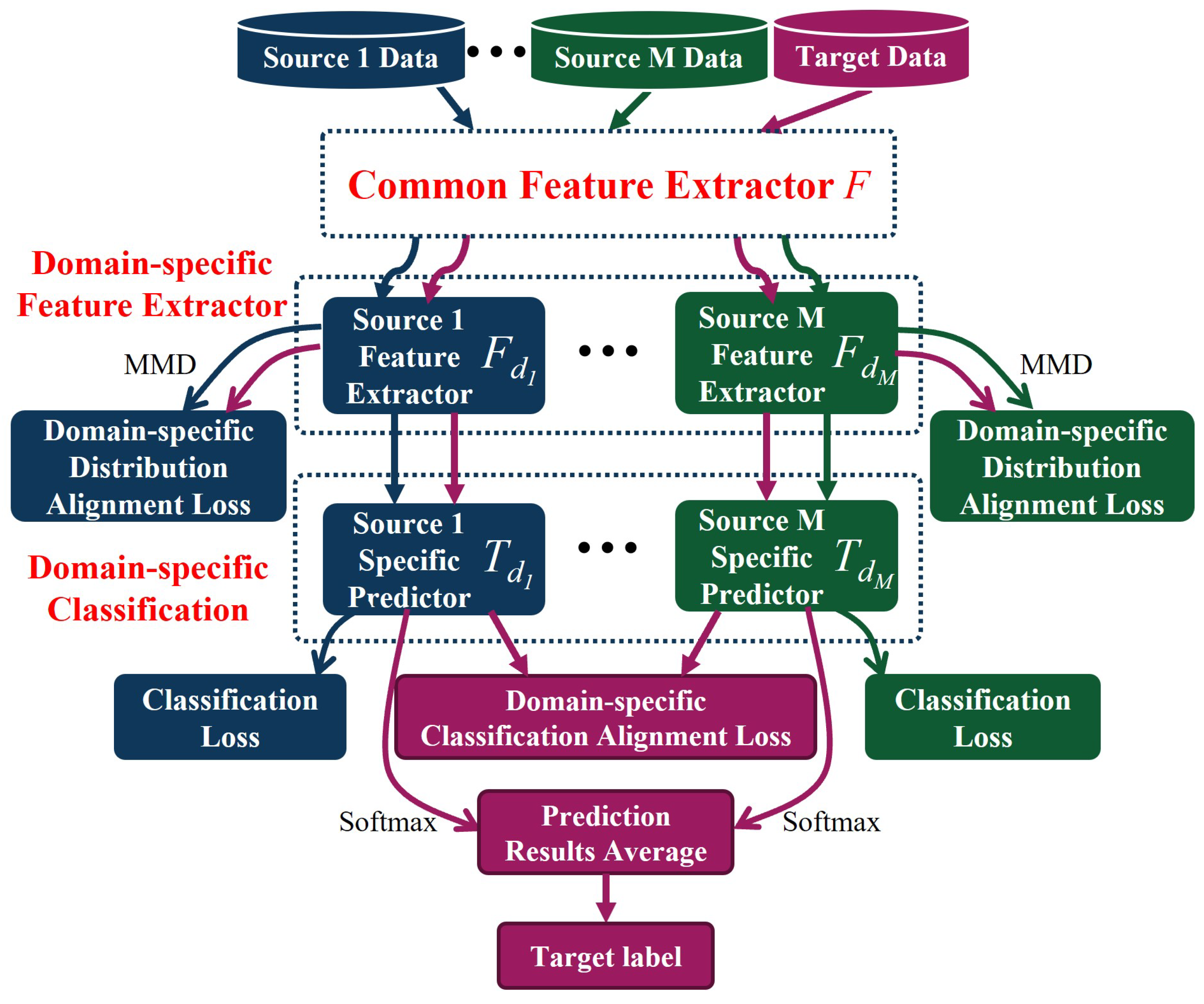
2.2. The Method for Tool Wear State Recognition Based on MFSAN
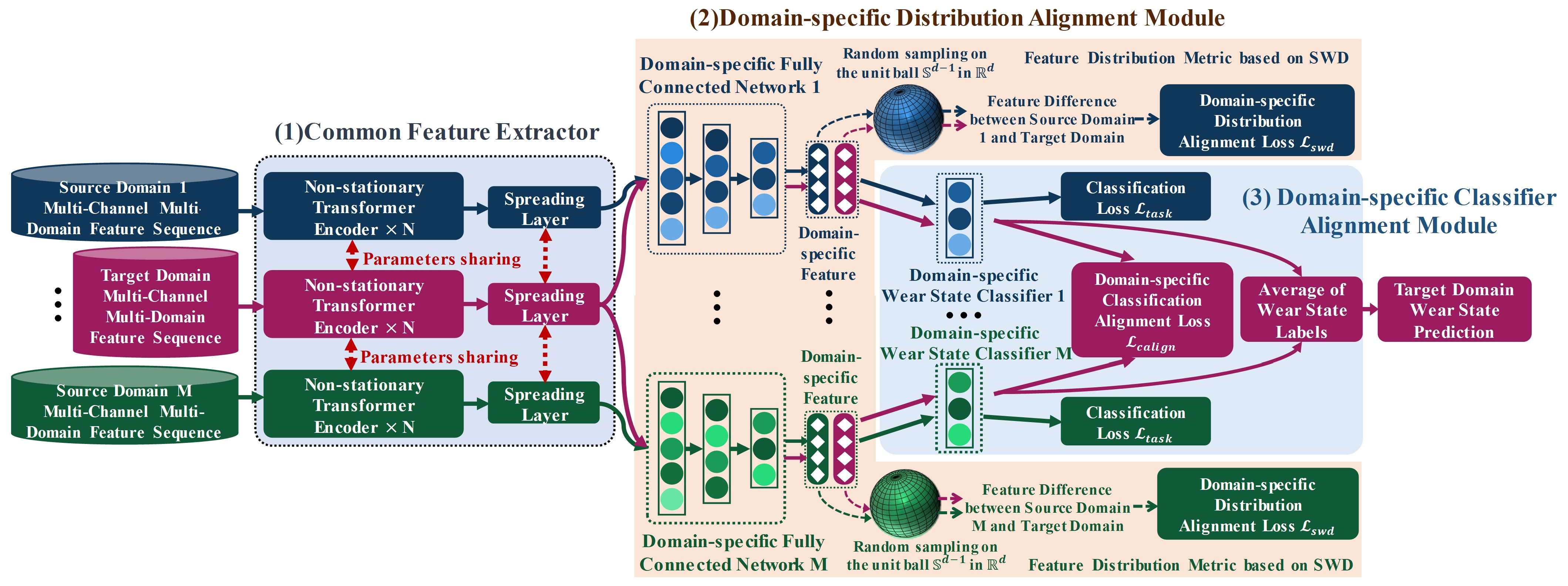
2.3. Common Feature Extractor
2.4. Domain-Specific Distribution Alignment Module
2.5. Domain-Specific Classifier Alignment Module
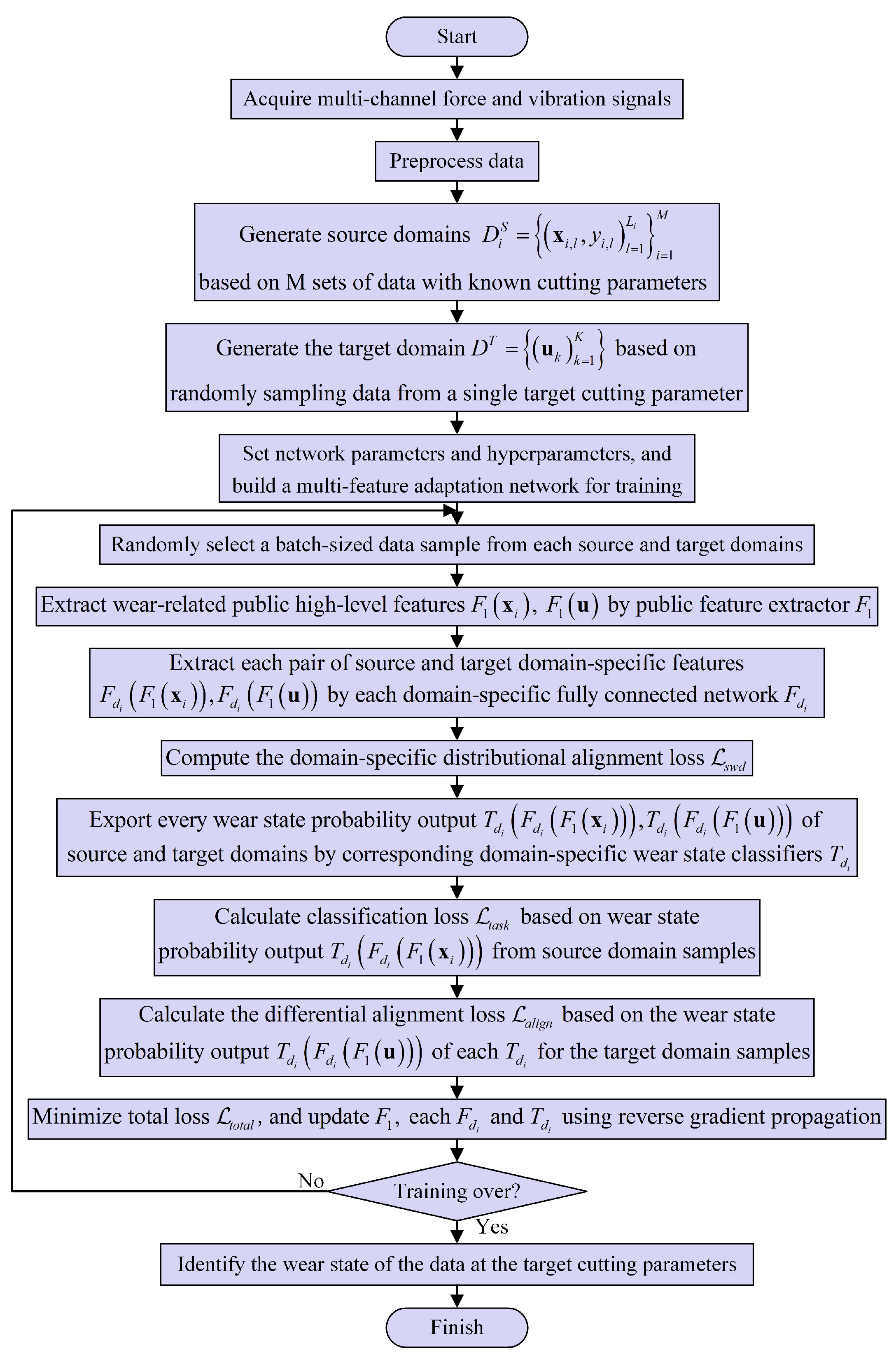
2.6. Training Procedure for the Proposed Method
3. Experimental Research
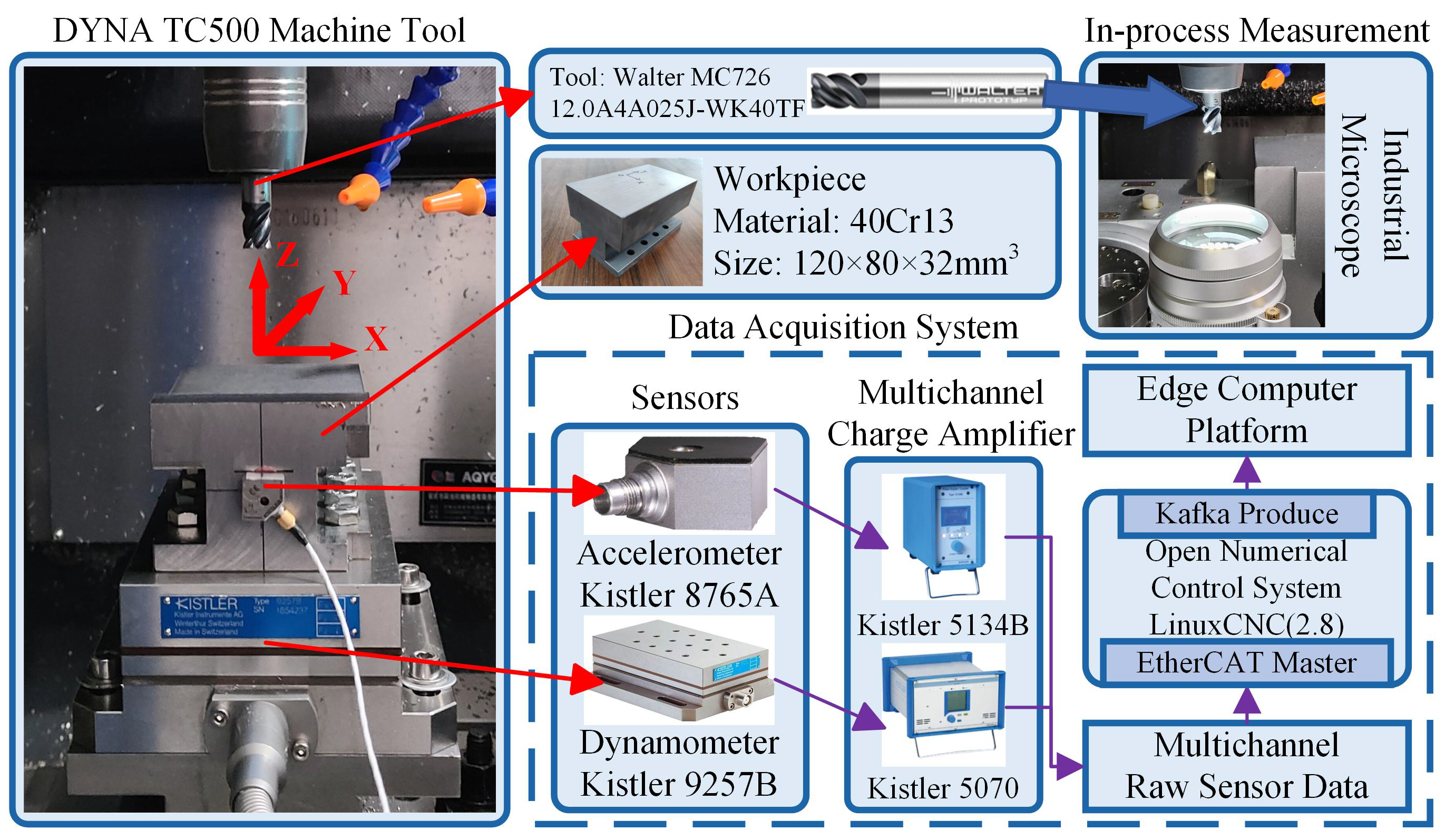
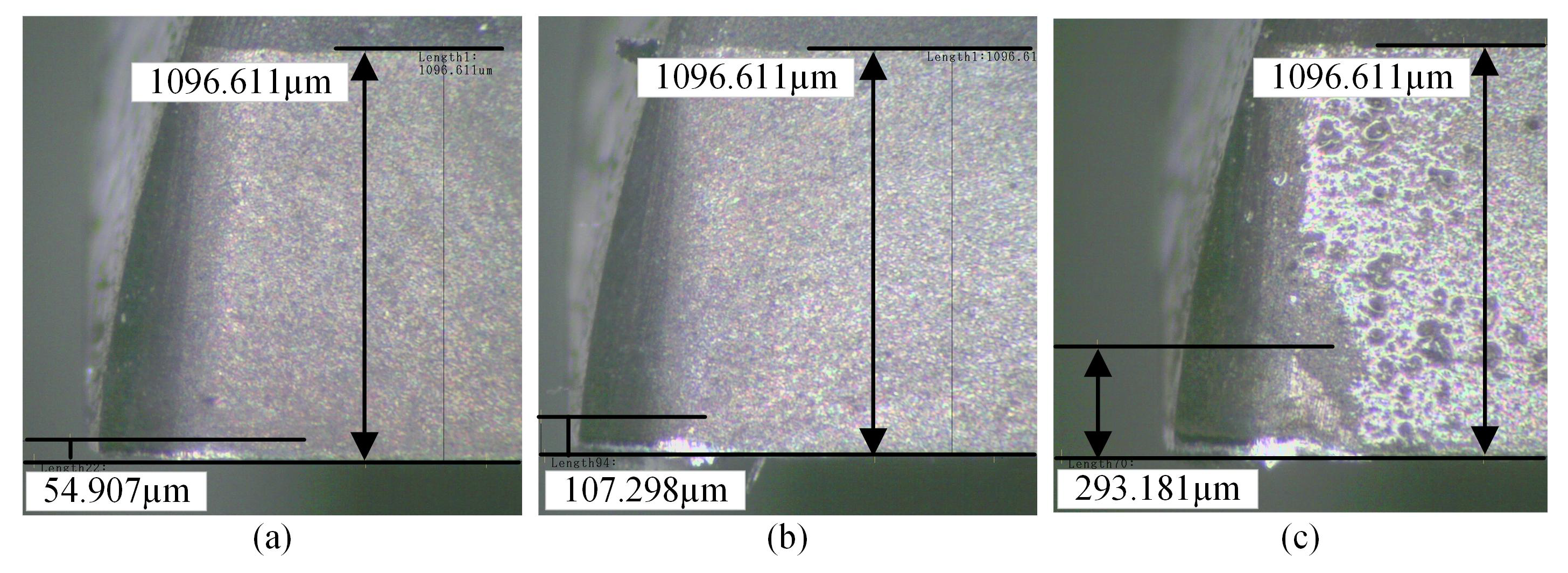
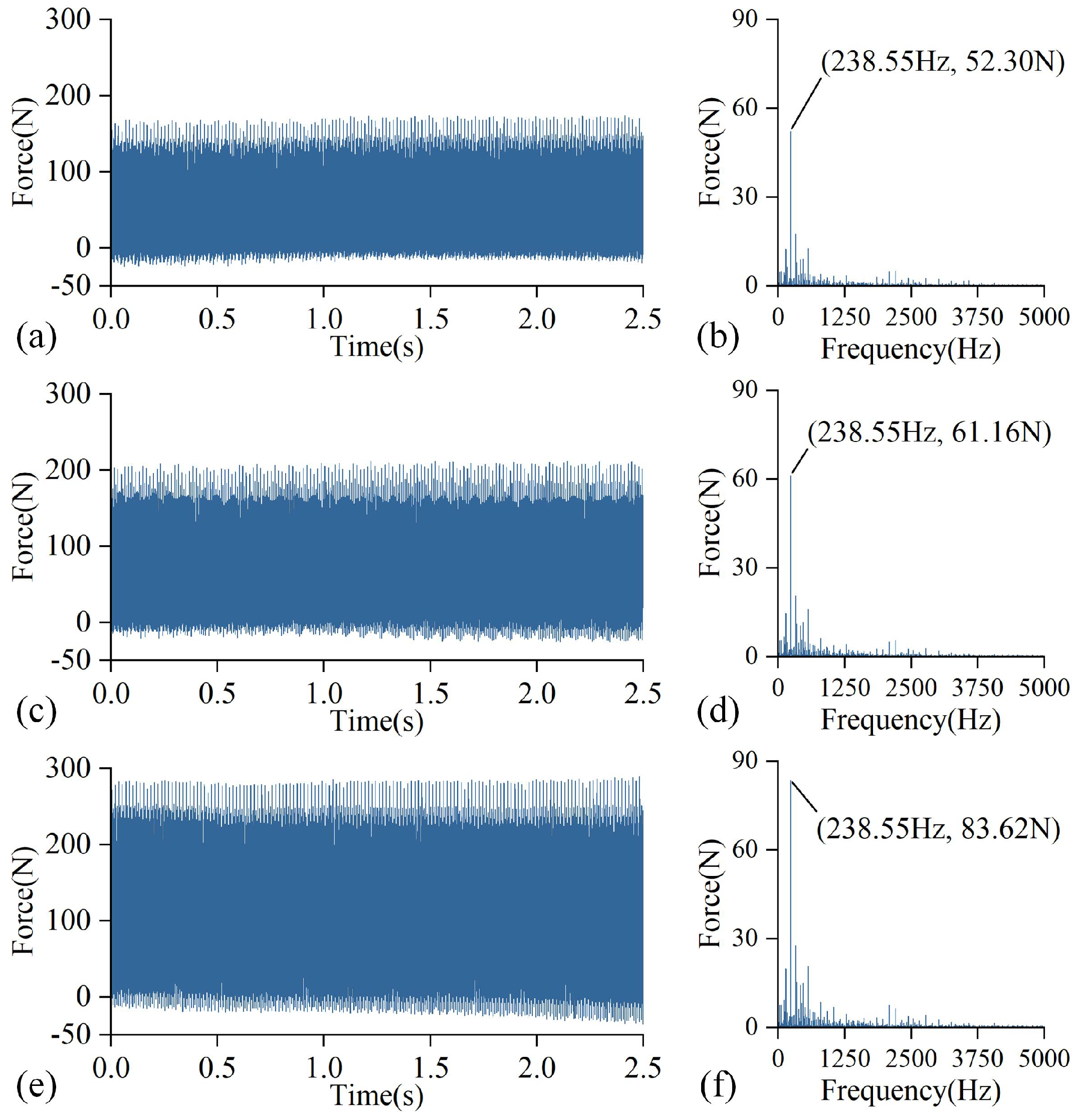
3.1. Experiment Design
3.2. Multi-Source Domain Unsupervised Adaptive Tasks
3.3. Design of Ablation Experiment
4. Analysis and Discussion
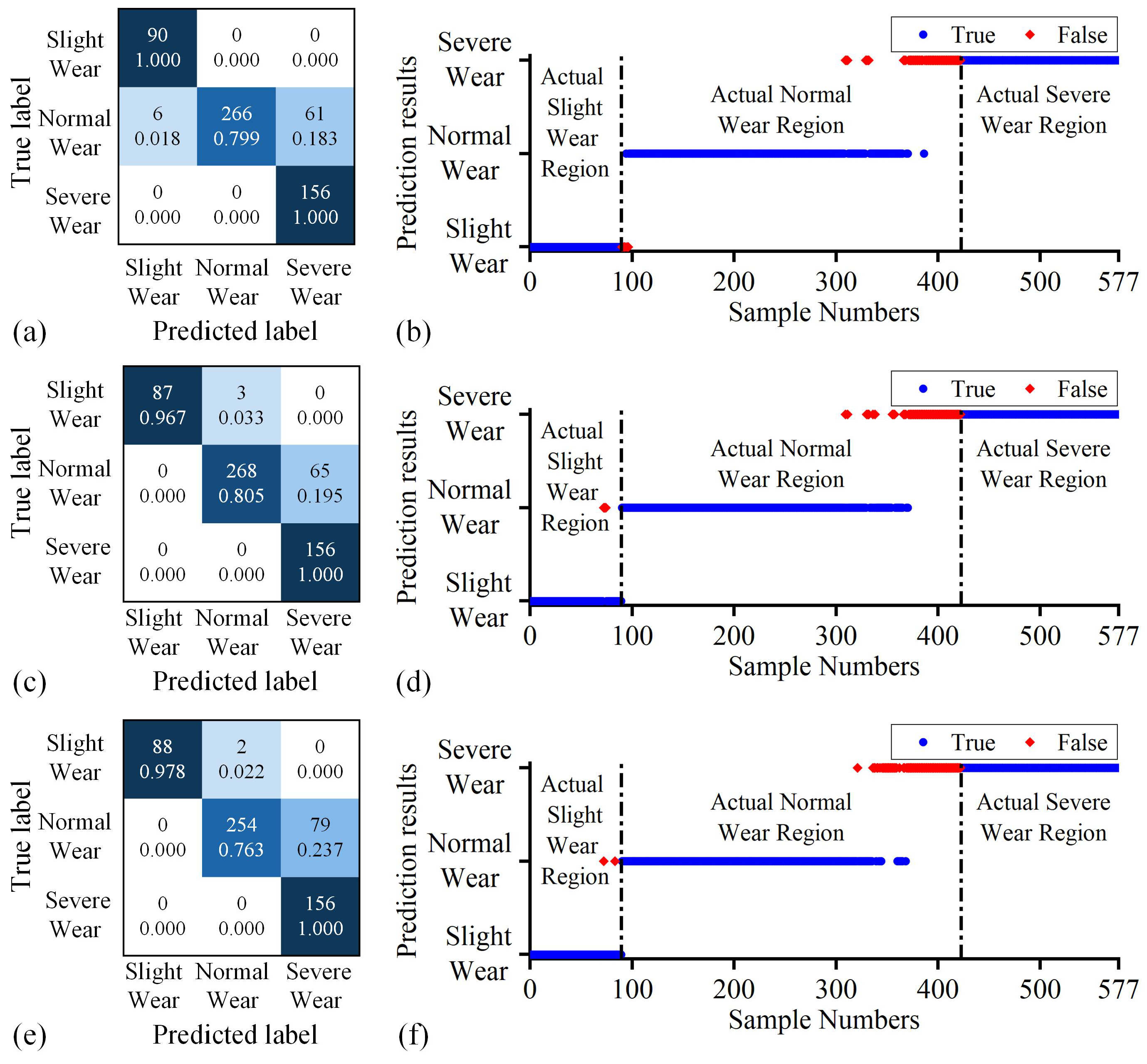
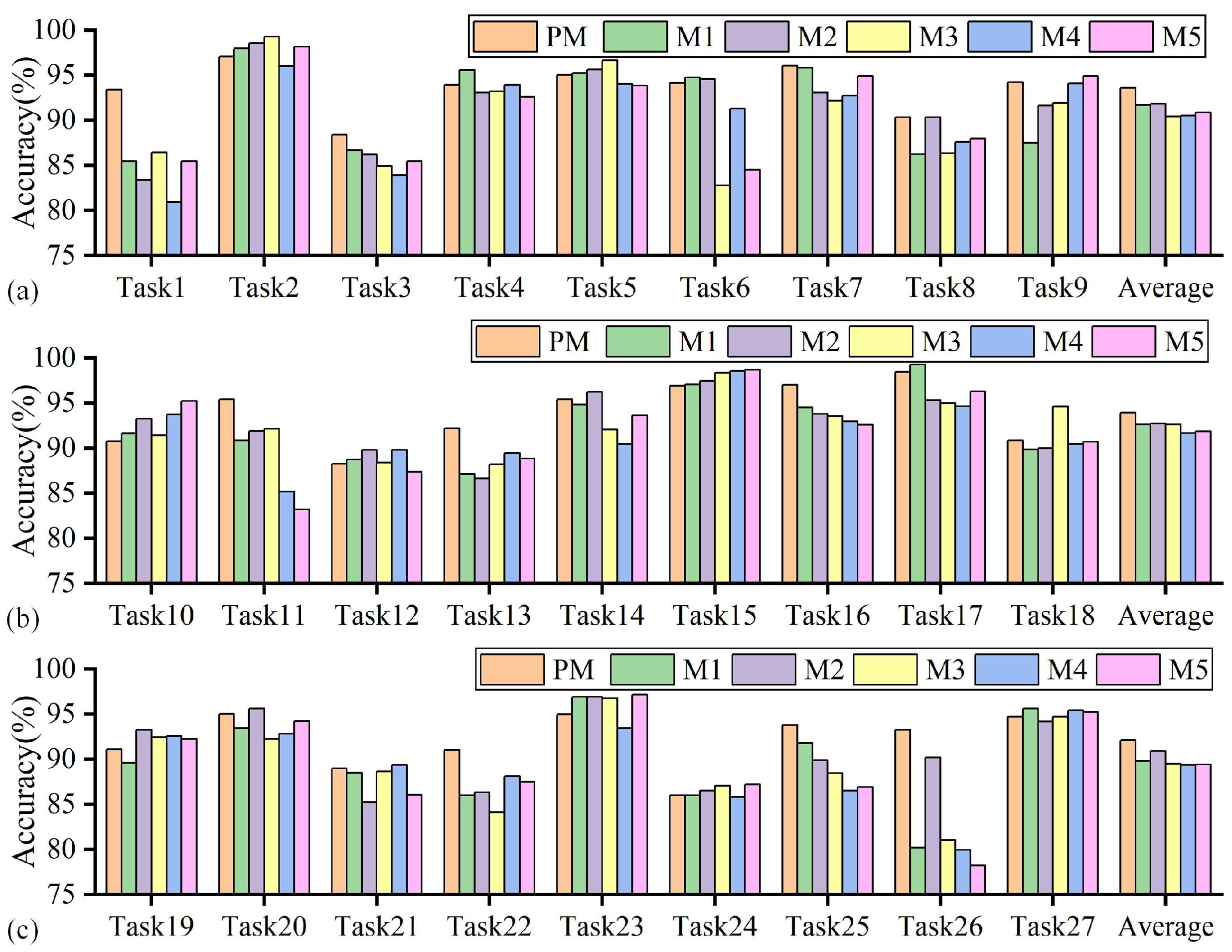
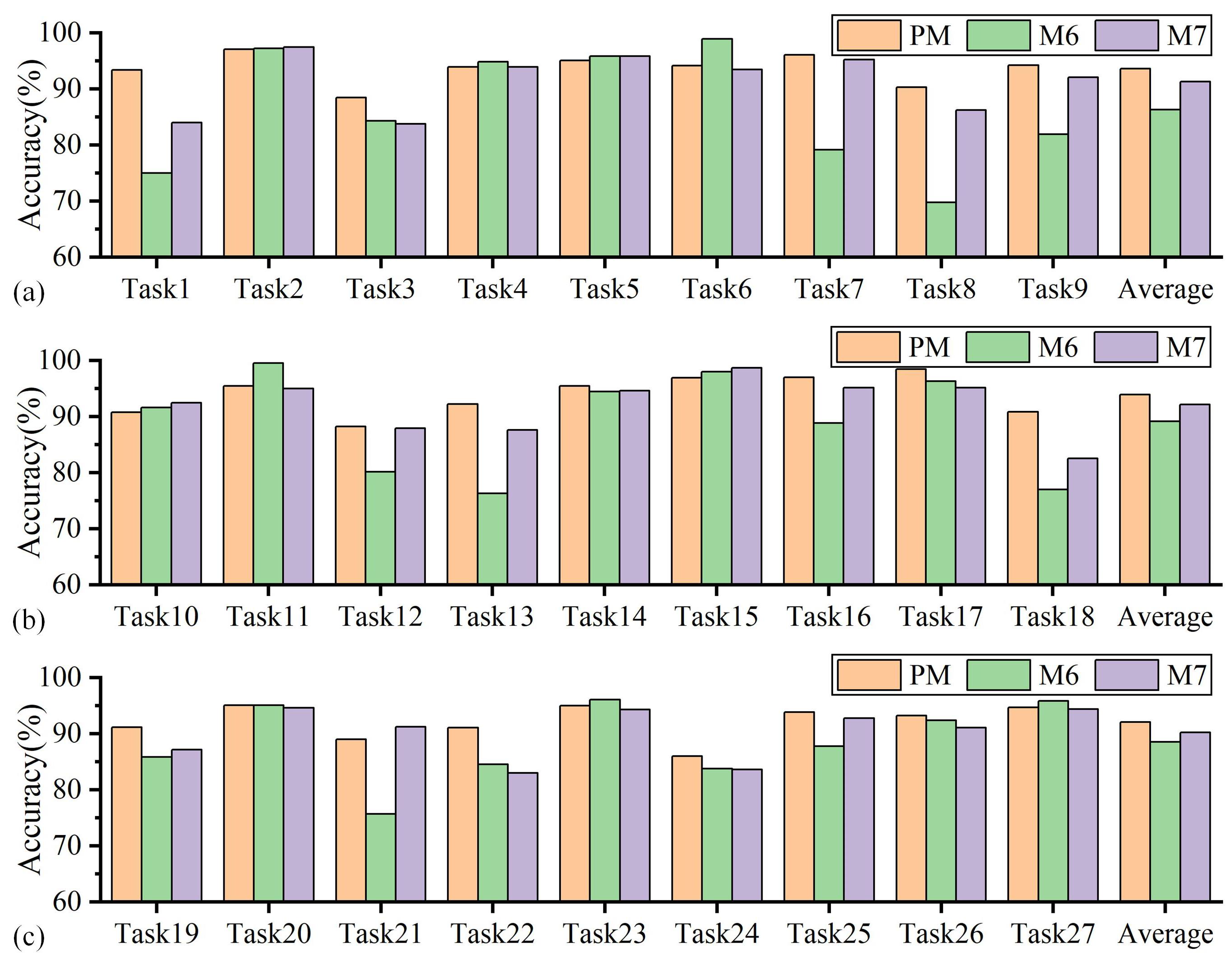
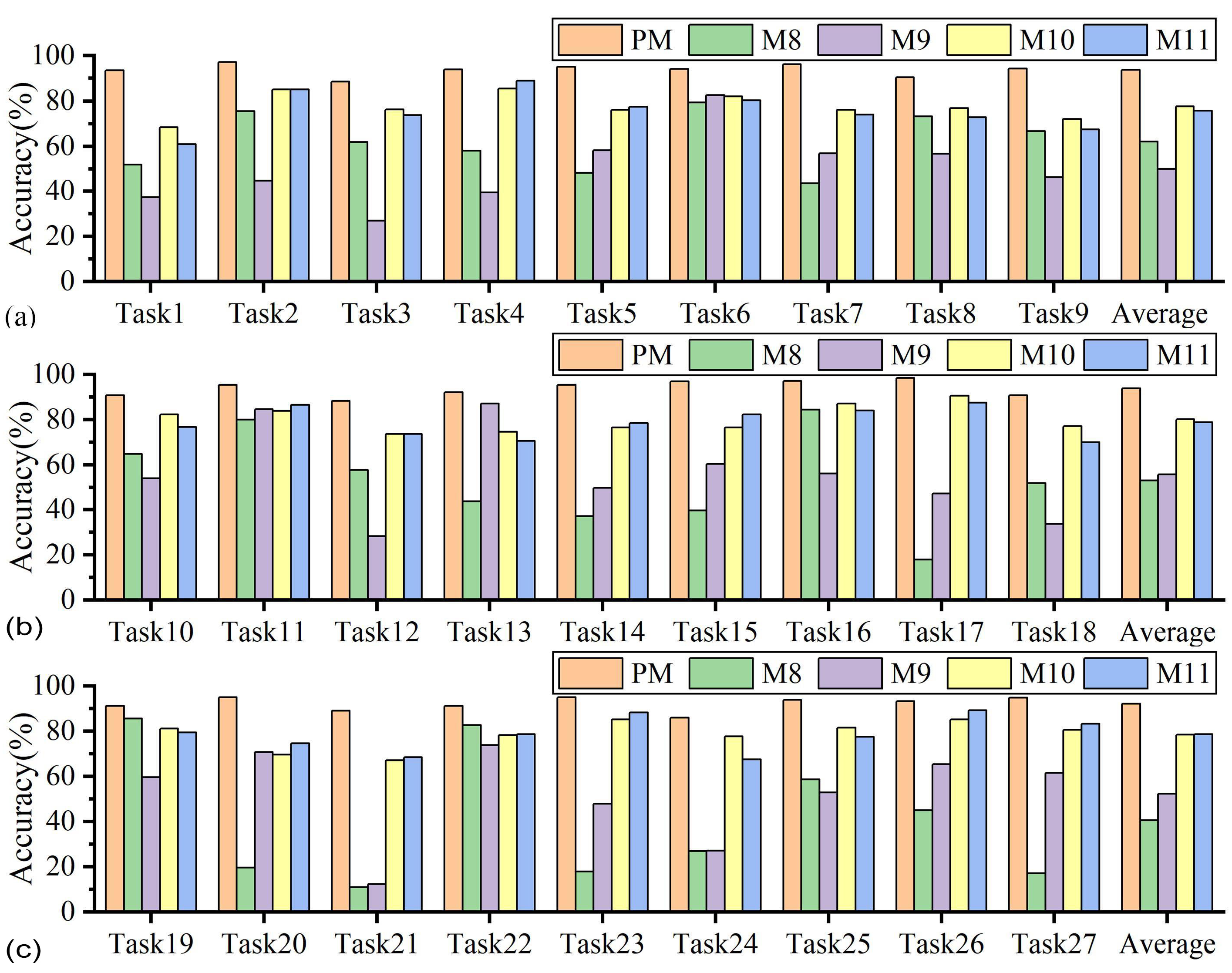
4.1. Results Comparison and Analysis
4.2. Ablation Studies
5. Conclusions and Future Works
- (1)
- A multi-source unsupervised domain adaptive training strategy based on MFSAN boosts tool wear state identification accuracy under variable cutting parameter scenarios. The strategy fully utilizes multiple known cutting parameter data sets and effectively achieves mutual separation of wear states under varied cutting parameters by aligning domain-specific feature distribution and domain-specific classifier output in two stages.
- (2)
- The common feature extractor based on the NSTE and the domain-specific feature distribution measure with SWD assist in improving the wear state classification performance.
- (3)
- The effectiveness of the proposed method is evaluated through the tasks of identifying tool wear status with variable cutting parameters. Among 27 sets of tasks, the proposed method demonstrates an average accuracy of 93.22%, representing a significant enhancement of 14.44% over methods such as DAN and DSAN. The use of NSTE and SWD improves the recognition accuracy of the proposed method by 1.41% and 1.99%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| No. | Source Domain | Target Domain | Accuracy (%) | Average Accuracy (%) | Overall Accuracy (%) |
|---|---|---|---|---|---|
| Task1 | N1, N2, N3, N4, N5, N6 | N7 | 93.41 | 92.97 | 93.63 |
| Task2 | N1, N2, N3, N4, N5, N6 | N8 | 97.09 | ||
| Task3 | N1, N2, N3, N4, N5, N6 | N9 | 88.43 | ||
| Task4 | N1, N2, N3, N7, N8, N9 | N4 | 93.93 | 94.36 | |
| Task5 | N1, N2, N3, N7, N8, N9 | N5 | 95.04 | ||
| Task6 | N1, N2, N3, N7, N8, N9 | N6 | 94.12 | ||
| Task7 | N4, N5, N6, N7, N8, N9 | N1 | 96.07 | 93.55 | |
| Task8 | N4, N5, N6, N7, N8, N9 | N2 | 90.34 | ||
| Task9 | N4, N5, N6, N7, N8, N9 | N3 | 94.24 | ||
| Task10 | N1, N4, N7, N2, N5, N8 | N3 | 90.79 | 91.49 | 93.93 |
| Task11 | N1, N4, N7, N2, N5, N8 | N6 | 95.43 | ||
| Task12 | N1, N4, N7, N2, N5, N8 | N9 | 88.26 | ||
| Task13 | N1, N4, N7, N3, N6, N9 | N2 | 92.19 | 94.84 | |
| Task14 | N1, N4, N7, N3, N6, N9 | N5 | 95.44 | ||
| Task15 | N1, N4, N7, N3, N6, N9 | N8 | 96.91 | ||
| Task16 | N2, N5, N8, N3, N6, N9 | N1 | 97.02 | 95.44 | |
| Task17 | N2, N5, N8, N3, N6, N9 | N4 | 98.45 | ||
| Task18 | N2, N5, N8, N3, N6, N9 | N7 | 90.84 | ||
| Task19 | N1, N6, N8, N2, N4, N9 | N3 | 91.12 | 91.72 | 92.11 |
| Task20 | N1, N6, N8, N2, N4, N9 | N5 | 95.04 | ||
| Task21 | N1, N6, N8, N2, N4, N9 | N7 | 89.01 | ||
| Task22 | N1, N6, N8, N3, N5, N7 | N2 | 91.08 | 90.70 | |
| Task23 | N1, N6, N8, N3, N5, N7 | N4 | 95.00 | ||
| Task24 | N1, N6, N8, N3, N5, N7 | N9 | 86.01 | ||
| Task25 | N2, N4, N9, N3, N5, N7 | N1 | 93.81 | 93.92 | |
| Task26 | N2, N4, N9, N3, N5, N7 | N6 | 93.25 | ||
| Task27 | N2, N4, N9, N3, N5, N7 | N8 | 94.72 |
| No. | Accuracy (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PM | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 | M11 | |
| Task1 | 93.41 | 85.47 | 83.39 | 86.45 | 80.95 | 85.47 | 74.97 | 84.01 | 51.84 | 37.36 | 68.50 | 61.05 |
| Task2 | 97.09 | 98.00 | 98.54 | 99.27 | 95.99 | 98.18 | 97.27 | 97.45 | 75.57 | 44.81 | 85.06 | 85.06 |
| Task3 | 88.43 | 86.70 | 86.18 | 84.97 | 83.94 | 85.49 | 84.28 | 83.77 | 61.98 | 26.98 | 76.34 | 73.92 |
| Task4 | 93.93 | 95.60 | 93.10 | 93.21 | 93.93 | 92.62 | 94.88 | 93.93 | 58.13 | 39.38 | 85.36 | 88.93 |
| Task5 | 95.04 | 95.24 | 95.64 | 96.63 | 94.05 | 93.85 | 95.83 | 95.83 | 48.21 | 58.33 | 76.19 | 77.58 |
| Task6 | 94.12 | 94.77 | 94.55 | 82.79 | 91.29 | 84.53 | 98.91 | 93.46 | 79.44 | 82.52 | 81.92 | 80.39 |
| Task7 | 96.07 | 95.83 | 93.10 | 92.14 | 92.74 | 94.88 | 79.17 | 95.24 | 43.75 | 57.02 | 76.07 | 74.05 |
| Task8 | 90.34 | 86.25 | 90.34 | 86.37 | 87.61 | 87.98 | 69.77 | 86.25 | 73.30 | 56.69 | 76.95 | 72.86 |
| Task9 | 94.24 | 87.50 | 91.61 | 91.94 | 94.08 | 94.90 | 81.91 | 92.11 | 66.75 | 46.36 | 72.20 | 67.43 |
| Task10 | 90.79 | 91.61 | 93.26 | 91.45 | 93.75 | 95.23 | 91.61 | 92.43 | 64.75 | 54.13 | 82.24 | 76.65 |
| Task11 | 95.43 | 90.85 | 91.94 | 92.16 | 85.19 | 83.22 | 99.56 | 94.99 | 79.93 | 84.64 | 83.88 | 86.49 |
| Task12 | 88.26 | 88.77 | 89.81 | 88.43 | 89.81 | 87.39 | 80.14 | 87.91 | 57.68 | 28.28 | 73.58 | 73.58 |
| Task13 | 92.19 | 87.11 | 86.62 | 88.23 | 89.47 | 88.85 | 76.33 | 87.61 | 43.85 | 87.08 | 74.60 | 70.51 |
| Task14 | 95.44 | 94.84 | 96.23 | 92.06 | 90.48 | 93.65 | 94.44 | 94.64 | 37.20 | 49.85 | 76.59 | 78.37 |
| Task15 | 96.90 | 97.09 | 97.45 | 98.36 | 98.54 | 98.73 | 98.00 | 98.73 | 39.63 | 60.38 | 76.50 | 82.33 |
| Task16 | 97.02 | 94.52 | 93.81 | 93.57 | 92.98 | 92.62 | 88.81 | 95.12 | 84.38 | 56.21 | 87.02 | 84.05 |
| Task17 | 98.45 | 99.29 | 95.36 | 95.00 | 94.64 | 96.31 | 96.31 | 95.12 | 17.86 | 47.23 | 90.60 | 87.50 |
| Task18 | 90.84 | 89.87 | 89.99 | 94.63 | 90.48 | 90.72 | 77.05 | 82.54 | 51.84 | 33.61 | 77.17 | 70.09 |
| Task19 | 91.12 | 89.64 | 93.26 | 92.43 | 92.60 | 92.27 | 85.86 | 87.17 | 85.63 | 59.56 | 81.09 | 79.44 |
| Task20 | 95.04 | 93.45 | 95.64 | 92.26 | 92.86 | 94.25 | 95.04 | 94.64 | 19.64 | 70.83 | 69.64 | 74.60 |
| Task21 | 89.01 | 88.52 | 85.23 | 88.65 | 89.38 | 86.08 | 75.70 | 91.21 | 11.03 | 12.27 | 67.16 | 68.50 |
| Task22 | 91.08 | 86.00 | 86.37 | 84.14 | 88.10 | 87.49 | 84.51 | 83.02 | 82.67 | 73.79 | 78.32 | 78.69 |
| Task23 | 95.00 | 96.91 | 96.91 | 96.79 | 93.45 | 97.14 | 96.07 | 94.29 | 17.86 | 47.86 | 85.12 | 88.21 |
| Task24 | 86.01 | 86.01 | 86.53 | 87.05 | 85.84 | 87.22 | 83.77 | 83.59 | 26.95 | 27.11 | 77.72 | 67.53 |
| Task25 | 93.81 | 91.79 | 89.88 | 88.45 | 86.55 | 86.91 | 87.74 | 92.74 | 58.64 | 52.90 | 81.55 | 77.50 |
| Task26 | 93.25 | 80.17 | 90.20 | 81.05 | 79.96 | 78.21 | 92.38 | 91.07 | 45.07 | 65.36 | 85.19 | 89.33 |
| Task27 | 94.72 | 95.63 | 94.17 | 94.72 | 95.45 | 95.26 | 95.81 | 94.35 | 17.05 | 61.61 | 80.51 | 83.24 |
| Average | 93.22 | 91.39 | 91.82 | 90.86 | 90.52 | 90.72 | 88.00 | 91.23 | 51.87 | 52.67 | 78.78 | 77.70 |
References
- Brito, L.C.; da Silva, M.B.; Viana Duarte, M.A. Identification of cutting tool wear condition in turning using self-organizing map trained with imbalanced data. J. Intell. Manuf. 2021, 32, 127–140. [Google Scholar] [CrossRef]
- Kong, D.; Chen, Y.; Li, N. Gaussian process regression for tool wear prediction. Mech. Syst. Signal Process. 2018, 104, 556–574. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, W. A Multisensor Fusion Method for Tool Condition Monitoring in Milling. Sensors 2018, 18, 3866. [Google Scholar] [CrossRef]
- Zeng, Y.; Liu, R.; Liu, X. A novel approach to tool condition monitoring based on multi-sensor data fusion imaging and an attention mechanism. Meas. Sci. Technol. 2021, 32, 055601. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ren, L.; Jia, Z.; Laili, Y.; Huang, D. Deep Learning for Time-Series Prediction in IIoT: Progress, Challenges, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 15072–15091. [Google Scholar] [CrossRef]
- Zhang, X.; Han, C.; Luo, M.; Zhang, D. Tool Wear Monitoring for Complex Part Milling Based on Deep Learning. Appl. Sci. 2020, 10, 6916. [Google Scholar] [CrossRef]
- Loizou, J.; Tian, W.; Robertson, J.; Camelio, J. Automated wear characterization for broaching tools based on machine vision systems. J. Manuf. Syst. 2015, 37, 558–563. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Incecik, A.; Gupta, M.K.; Kroclzyk, G.M.; Gardoni, P. A novel ensemble deep learning model for cutting tool wear monitoring using audio sensors. J. Manuf. Process. 2022, 79, 233–249. [Google Scholar] [CrossRef]
- Wang, J.; Yan, J.; Li, C.; Gao, R.X.; Zhao, R. Deep heterogeneous GRU model for predictive analytics in smart manufacturing: Application to tool wear prediction. Comput. Ind. 2019, 111, 1–14. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, L.; Gao, H.; Liu, Y.; Feng, T. Pareto-Optimal Adaptive Loss Residual Shrinkage Network for Imbalanced Fault Diagnostics of Machines. IEEE Trans. Ind. Inform. 2022, 18, 2233–2243. [Google Scholar] [CrossRef]
- Li, W.; Fu, H.; Han, Z.; Zhang, X.; Jin, H. Intelligent tool wear prediction based on Informer encoder and stacked bidirectional gated recurrent unit. Robot. Comput.-Integr. Manuf. 2022, 77, 102368. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Li, J.; Lu, J.; Chen, C.; Ma, J.; Liao, X. Tool wear state prediction based on feature-based transfer learning. Int. J. Adv. Manuf. Technol. 2021, 113, 3283–3301. [Google Scholar] [CrossRef]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A Survey on Deep Transfer Learning. In Artificial Neural Networks and Machine Learning—ICANN 2018, Part III, Proceedings of the 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Lecture Notes in Computer Science; Kurkova, V., Manolopoulos, Y., Hammer, B., Iliadis, L., Maglogiannis, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11141, pp. 270–279. [Google Scholar] [CrossRef]
- Zhang, N.; Zhao, J.; Ma, L.; Kong, H.; Li, H. Tool Wear Monitoring Based on Transfer Learning and Improved Deep Residual Network. IEEE Access 2022, 10, 119546–119557. [Google Scholar] [CrossRef]
- Bahador, A.; Du, C.; Ng, H.P.; Dzulqarnain, N.A.; Ho, C.L. Cost-effective classification of tool wear with transfer learning based on tool vibration for hard turning processes. Measurement 2022, 201, 111701. [Google Scholar] [CrossRef]
- Shi, Y.; Ying, X.; Yang, J. Deep Unsupervised Domain Adaptation with Time Series Sensor Data: A Survey. Sensors 2022, 22, 5507. [Google Scholar] [CrossRef]
- Zhang, S.; Su, L.; Gu, J.; LI, K.; Zhou, L.; Pecht, M. Rotating machinery fault detection and diagnosis based on deep domain adaptation: A survey. Chin. J. Aeronaut. 2023, 36, 45–74. [Google Scholar] [CrossRef]
- Huang, Z.; Shao, J.; Zhu, J.; Zhang, W.; Li, X. Tool wear condition monitoring across machining processes based on feature transfer by deep adversarial domain confusion network. J. Intell. Manuf. 2024, 35, 1079–1105. [Google Scholar] [CrossRef]
- He, J.; Sun, Y.; Yin, C.; He, Y.; Wang, Y. Cross-domain adaptation network based on attention mechanism for tool wear prediction. J. Intell. Manuf. 2023, 34, 3365–3387. [Google Scholar] [CrossRef]
- Sun, W.; Zhou, J.; Sun, B.; Zhou, Y.; Jiang, Y. Markov Transition Field Enhanced Deep Domain Adaptation Network for Milling Tool Condition Monitoring. Micromachines 2022, 13, 873. [Google Scholar] [CrossRef]
- Li, S.; Huang, S.; Li, H.; Liu, W.; Wu, W.; Liu, J. Multi-condition tool wear prediction for milling CFRP base on a novel hybrid monitoring method. Meas. Sci. Technol. 2024, 35, 035017. [Google Scholar] [CrossRef]
- Li, K.; Chen, M.; Lin, Y.; Li, Z.; Jia, X.; Li, B. A novel adversarial domain adaptation transfer learning method for tool wear state prediction. Knowl.-Based Syst. 2022, 254, 109537. [Google Scholar] [CrossRef]
- Liu, D.; Cui, L.; Wang, G.; Cheng, W. Interpretable domain adaptation transformer: A transfer learning method for fault diagnosis of rotating machinery. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Kim, G.; Yang, S.M.; Kim, S.; Kim, D.Y.; Choi, J.G.; Park, H.W.; Lim, S. A multi-domain mixture density network for tool wear prediction under multiple machining conditions. Int. J. Prod. Res. 2023, 5, 1–20. [Google Scholar] [CrossRef]
- Zhu, Y.; Zi, Y.; Xu, J.; Li, J. An unsupervised dual-regression domain adversarial adaption network for tool wear prediction in multi-working conditions. Measurement 2022, 200, 111644. [Google Scholar] [CrossRef]
- Wilson, G.; Cook, D.J. A Survey of Unsupervised Deep Domain Adaptation. ACM Trans. Intell. Syst. Technol. 2020, 11, 1–46. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhuang, F.; Wang, D. Aligning Domain-Specific Distribution and Classifier for Cross-Domain Classification from Multiple Sources. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 30, pp. 5989–5996. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems 30 (NIPS 2017); Guyon, I., Luxburg, U., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; The MIT Press: Cambridge, MA, USA, 2017; Volume 30. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationary Transformers: Exploring the Stationarity in Time Series Forecasting. In Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein Generative Adversarial Networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70. [Google Scholar]
- Frogner, C.; Zhang, C.; Mobahi, H.; Araya-Polo, M.; Poggio, T. Learning with a Wasserstein Loss. In Advances in Neural Information Processing Systems 28 (NIPS 2015); Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R., Eds.; The MIT Press: Cambridge, MA, USA, 2015; Volume 28. [Google Scholar]
- Chen, P.; Zhao, R.; He, T.; Wei, K.; Yang, Q. Unsupervised domain adaptation of bearing fault diagnosis based on Join Sliced Wasserstein Distance. ISA Trans. 2022, 129, 504–519. [Google Scholar] [CrossRef]
- Nguyen, K.; Nguyen, D.; Ho, N.L. Self-Attention Amortized Distributional Projection Optimization for Sliced Wasserstein Point-Cloud Reconstruction. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Damodaran, B.B.; Kellenberger, B.; Flamary, R.; Tuia, D.; Courty, N. DeepJDOT: Deep Joint Distribution Optimal Transport for Unsupervised Domain Adaptation. In Proceedings of the Computer Vision—ECCV 2018, Lecture Notes in Computer Science, Part IV, Munich, Germany, 8–14 September 2018; Volume 11208, pp. 467–483. [Google Scholar] [CrossRef]
- Helgason, S. Integral Geometry and Radon Transforms; Springer: New York, NY, USA, 2010. [Google Scholar]
- Bonneel, N.; Rabin, J.; Peyre, G.; Pfister, H. Sliced and Radon Wasserstein Barycenters of Measures. J. Math. Imaging Vis. 2015, 51, 22–45. [Google Scholar] [CrossRef]
- ISO 8688-1; Tool Life Testing in Milling. Part 1: Face Milling. ISO: Geneva, Switzerland, 1989.
- Worden, K.; Iakovidis, I.; Cross, E.J. On Stationarity and the Interpretation of the ADF Statistic. In Dynamics of Civil Structures: Proceedings of the 36th IMAC, A Conference and Exposition on Structural Dynamics 2018, Orlando, FL, USA, 12–15 February 2018; Conference Proceedings of the Society for Experimental Mechanics Series; Pakzad, S., Ed.; Springer International Publishing: Cham, Switzerland, 2019; Volume 2, pp. 29–38. [Google Scholar] [CrossRef]
- Kagalwala, A. kpsstest: A command that implements the Kwiatkowski, Phillips, Schmidt, and Shin test with sample-specific critical values and reports p-values. Stata J. 2022, 22, 269–292. [Google Scholar] [CrossRef]
- Li, W.; Fu, H.; Zhuo, Y.; Liu, C.; Jin, H. Semi-supervised multi-source meta-domain generalization method for tool wear state prediction under varying cutting conditions. J. Manuf. Syst. 2023, 71, 323–341. [Google Scholar] [CrossRef]
- Long, M.; Cao, Y.; Cao, Z.; Wang, J.; Jordan, M. Transferable Representation Learning with Deep Adaptation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 3071–3085. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Saenko, K. Deep CORAL: Correlation Alignment for Deep Domain Adaptation. In Proceedings of the Computer Vision—ECCV 2016 Workshops, Amsterdam, The Netherlands, 8–10, 15–16 October 2016; Hua, G., Jégou, H., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 443–450. [Google Scholar]
- Sun, H.; Jin, H.; Zhuo, Y.; Ding, Y.; Guo, Z.; Han, Z. Investigation on a chatter detection method based on meta learning for machining multiple types of workpieces. J. Manuf. Process. 2024, 131, 1815–1832. [Google Scholar] [CrossRef]
- Long, M.; Cao, Y.; Wang, J.; Jordan, M.I. Learning Transferable Features with Deep Adaptation Networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; Volume 37, pp. 97–105. [Google Scholar]
- Zhu, Y.; Zhuang, F.; Wang, J.; Ke, G.; Chen, J.; Bian, J.; Xiong, H.; He, Q. Deep Subdomain Adaptation Network for Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1713–1722. [Google Scholar] [CrossRef]




| Network Modules | Parameters |
|---|---|
| NSTE | Number of encoders: 2, non-stationary self-attention head number: 1 |
| Point-wise Feed Forward | Convolution kernel size of one-dimensional convolutional layer 1:1, padding: 0, input channel dimension: 66, output channel dimension: 264; convolution kernel size of one-dimensional convolutional layer 2:1, padding: 0, input channel dimension: 264, output channel dimension: 64 |
| Projector | Number of hidden layers: 1, dimension of hidden layer: 64, activation function: ReLU |
| Domain-specific fully connected network | Dimensions of each hidden layer: 792-128-64-32, activation function: PReLU |
| Domain-specific classifer | Dimensions of hidden layer: 32-3 |
| Hyperparameters | Value | Hyperparameters | Value |
|---|---|---|---|
| Batch size | 32 | Optimizer | AdamW |
| Training times | 100 | Weight decay in the optimizer | 0.00005 |
| Learning rate (LR) | 0.0008 | Momentum in the optimizer | 0.9 |
| LR scheduler | Cosine Annealing Warm Up | Dropout | 0.1 |
| LR warmup steps | 15 | Number of SWD projection directions | 320 |
| No. | (m/min) | (mm) | (mm) | (mm/r) | n (rpm) |
|---|---|---|---|---|---|
| N1 | 135 | 1.5 | 0.6 | 0.116 | 3580 |
| N2 | 135 | 2 | 0.7 | 0.116 | 3580 |
| N3 | 135 | 2.5 | 0.8 | 0.116 | 3580 |
| N4 | 140 | 1.5 | 0.7 | 0.116 | 3710 |
| N5 | 140 | 2 | 0.8 | 0.116 | 3710 |
| N6 | 140 | 2.5 | 0.6 | 0.116 | 3710 |
| N7 | 150 | 1.5 | 0.8 | 0.116 | 3980 |
| N8 | 150 | 2 | 0.6 | 0.116 | 3980 |
| N9 | 150 | 2.5 | 0.7 | 0.116 | 3980 |
| No. | Feature | Formula |
|---|---|---|
| 1 | Mean | |
| 2 | Root mean square | |
| 3 | Max | |
| 4 | Standard deviation | |
| 5 | Peak value | |
| 6 | Peak-to-peak | |
| 7 | Spectral power | |
| 8 | Frequency centroid | |
| 9 | Root mean square frequency | |
| 10 | Root variance frequency | |
| 11 | Wavelet packet energy |
| No. | Number of Slight Wear Samples | Number of Normal Wear Samples | Number of Severe Wear Samples | Total Number of Samples |
|---|---|---|---|---|
| N1 | 80 | 235 | 248 | 563 |
| N2 | 144 | 272 | 252 | 668 |
| N3 | 96 | 144 | 192 | 432 |
| N4 | 100 | 200 | 304 | 604 |
| N5 | 72 | 192 | 156 | 420 |
| N6 | 44 | 88 | 200 | 332 |
| N7 | 60 | 280 | 224 | 564 |
| N8 | 72 | 164 | 216 | 452 |
| N9 | 60 | 239 | 128 | 427 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.; Li, W.; Song, J.; Jin, H.; Fu, H. Tool Wear State Identification Method with Variable Cutting Parameters Based on Multi-Source Unsupervised Domain Adaptation. Sensors 2025, 25, 1742. https://doi.org/10.3390/s25061742
Cai Z, Li W, Song J, Jin H, Fu H. Tool Wear State Identification Method with Variable Cutting Parameters Based on Multi-Source Unsupervised Domain Adaptation. Sensors. 2025; 25(6):1742. https://doi.org/10.3390/s25061742
Chicago/Turabian StyleCai, Zhigang, Wangyang Li, Jianxin Song, Hongyu Jin, and Hongya Fu. 2025. "Tool Wear State Identification Method with Variable Cutting Parameters Based on Multi-Source Unsupervised Domain Adaptation" Sensors 25, no. 6: 1742. https://doi.org/10.3390/s25061742
APA StyleCai, Z., Li, W., Song, J., Jin, H., & Fu, H. (2025). Tool Wear State Identification Method with Variable Cutting Parameters Based on Multi-Source Unsupervised Domain Adaptation. Sensors, 25(6), 1742. https://doi.org/10.3390/s25061742







