Investigation of Influencing Factors on the Measurement Signal of a CMOS Image Sensor for Measuring Field Emission Currents
Abstract
1. Introduction
2. Theoretical Description of Signal Generation in the Sensor as a Function of the Emission Current
2.1. Description of the X-Ray Signal Generated by the Incident Electrons

2.2. Generation of the Electrical Sensor Signal for One Electron Emission Spot
2.3. Determination of Individual Currents for Field Emission Arrays with Multiple Emission Spots
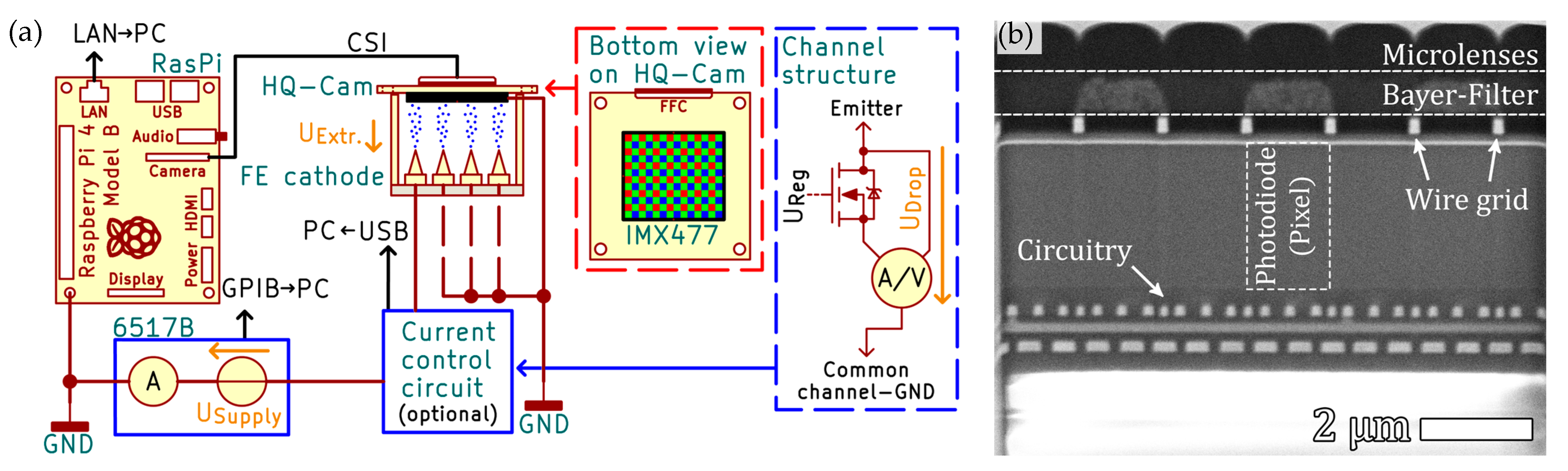
3. Experimental Setup for Carrying out the Experiments to Measure Field Emission Currents with the CMOS Sensor
3.1. Overview over the Experimental Setup
3.2. Acquisition Hardware for the CMOS Image Sensor
3.3. Field Emission Cathode for Generating Several Individually Controllable Emission Spots on the CMOS Sensor
4. Measurement Data Acquisition and Image Post-Processing
4.1. Measurement Data Acquisition
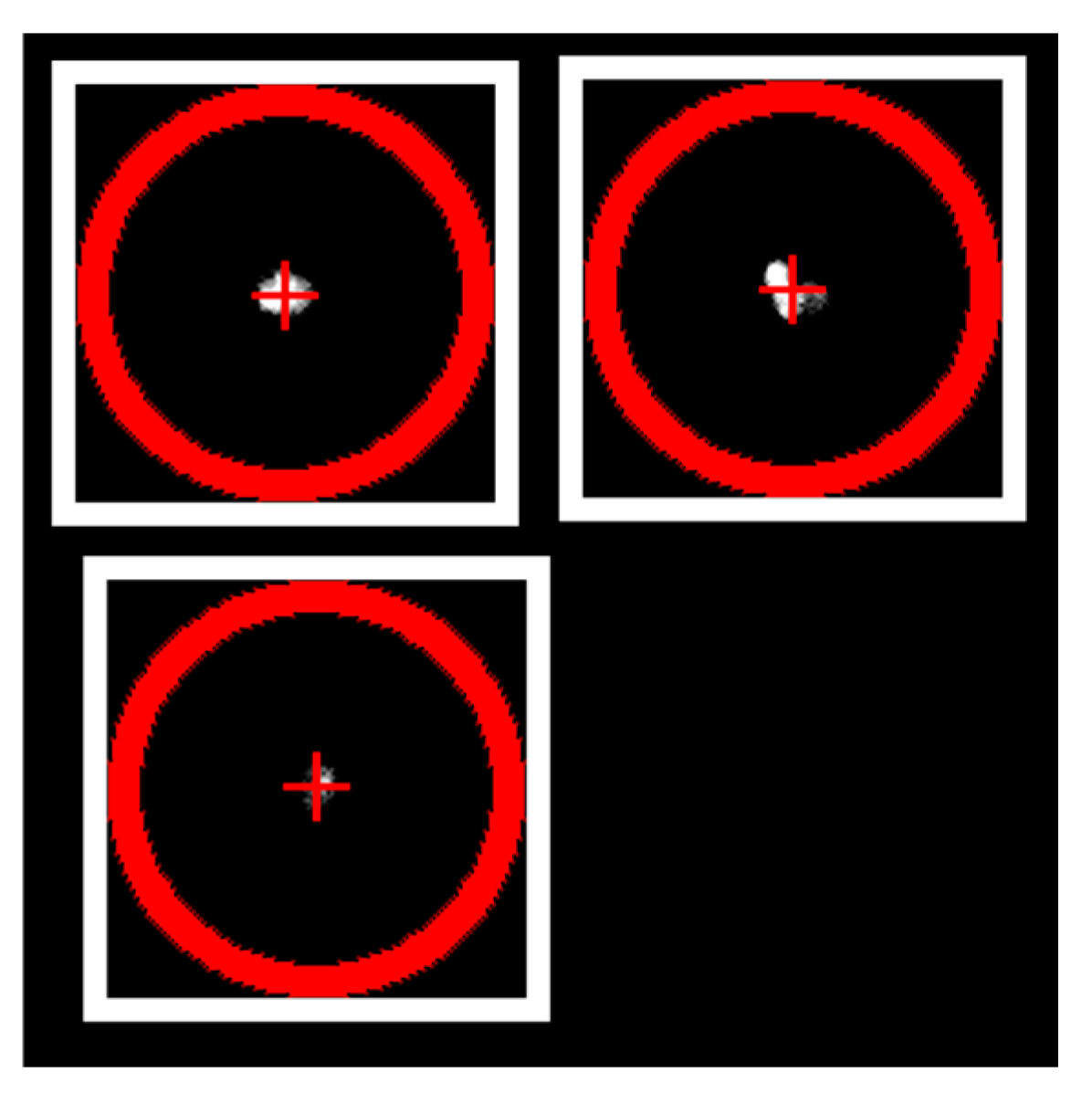
4.2. Image Post-Processing to Obtain the Field Emission Spot Signals from the Images
4.2.1. Conversion of the RAW Bayer-Data to 16-Bit Grayscale PNG
4.2.2. Obtaining the Emission Spot Signals from the Image Data
5. Experiments and Results
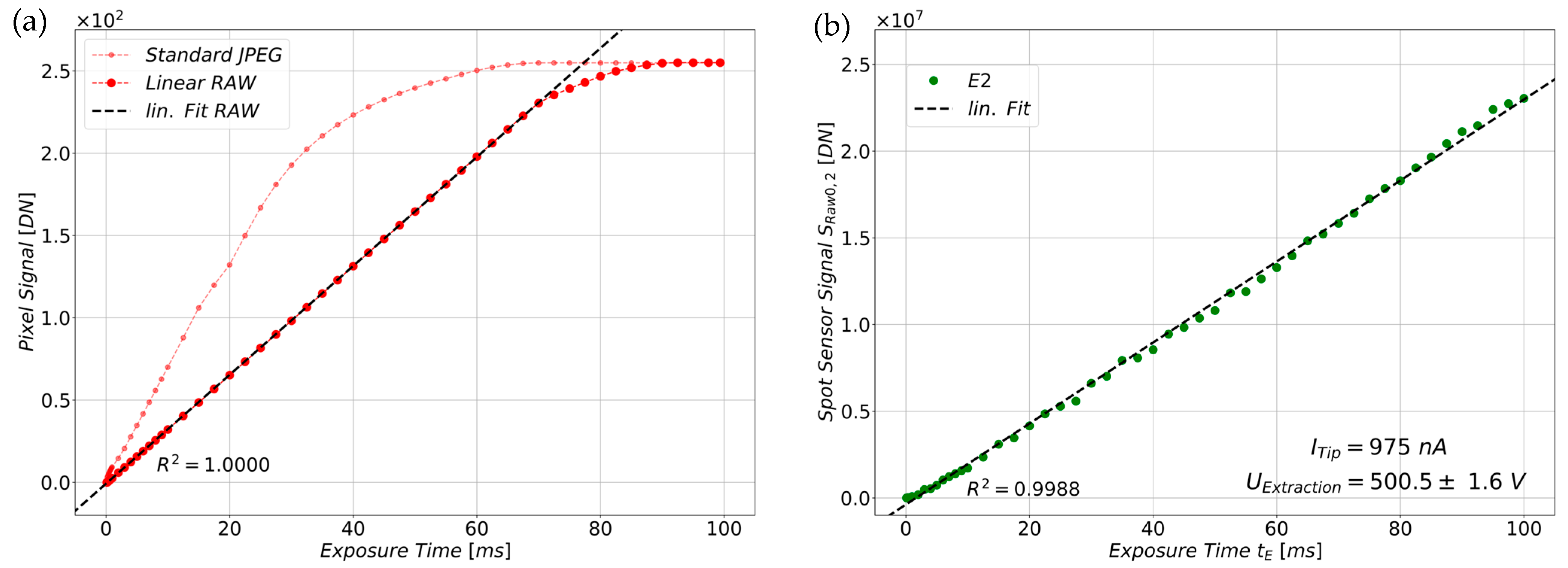
5.1. Influence of the Exposure Time on the Sensor Signal
5.1.1. Investigation of the Dependence of the Sensor Signal on the Exposure Time When Irradiated with Visible Light
5.1.2. Investigation of the Dependence of the Sensor Signal on the Exposure Time Under Constant Electron Irradiation
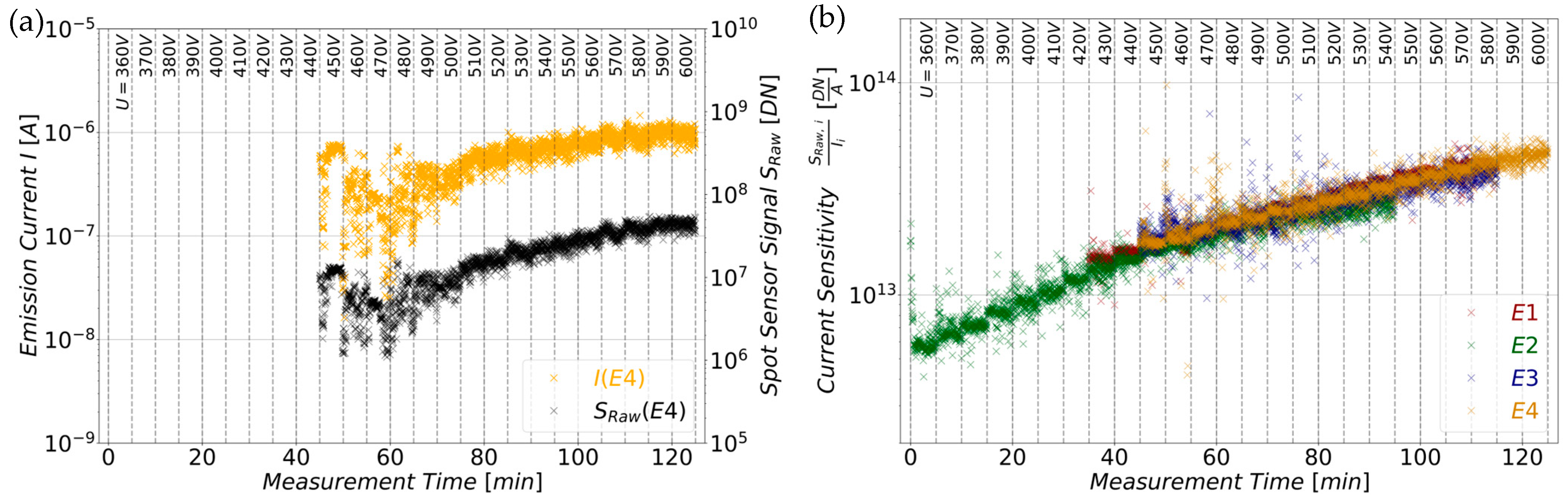
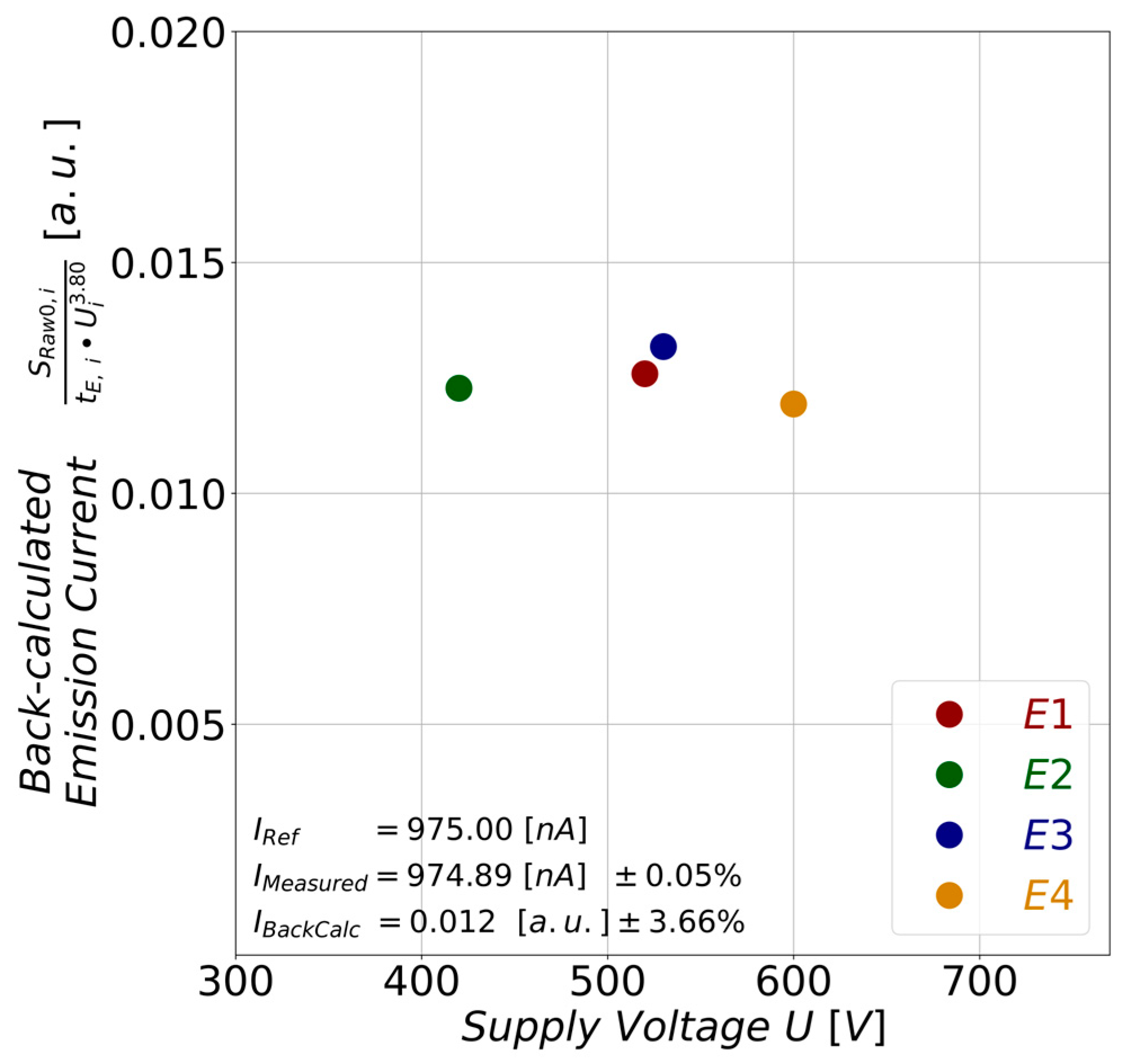
5.2. Influence of the Emission Current on the Sensor Signal at Different Extraction Voltages
6. Conclusions
7. Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Raspberry Pi, Ltd. Buy a Raspberry Pi High Quality Camera. Available online: https://www.raspberrypi.com/products/raspberry-pi-high-quality-camera/ (accessed on 14 February 2025).
- Datasheet IMX477-AACK-C. Available online: https://docs.arducam.com/Raspberry-Pi-Camera/Native-camera/source/IMX477-DS.pdf (accessed on 26 January 2025).
- Schels, A.; Edler, S.; Herdl, F.; Hansch, W.; Bachmann, M.; Ritter, D.; Dudeck, M.; Düsberg, F.; Meyer, M.; Pahlke, A.; et al. In-Situ Quantitative Field Emission Imaging Using a Low-Cost CMOS Imaging Sensor. J. Vac. Sci. Technol. B 2022, 40, 014202. [Google Scholar] [CrossRef]
- Schels, A.; Herdl, F.; Hausladen, M.; Wohlfartsstätter, D.; Edler, S.; Bachmann, M.; Pahlke, A.; Schreiner, R.; Hansch, W. Quantitative Field Emission Imaging for Studying the Doping-Dependent Emission Behavior of Silicon Field Emitter Arrays. Micromachines 2023, 14, 2008. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, L. Cathodoluminescence and Photoluminescence: Theories and Practical Applications; Phosphor Science and Engineering; CRC Press: Boca Raton, CA, USA, 2007; ISBN 978-1-4200-5270-1. [Google Scholar]
- Lee, S.W.; Lee, C.H.; Lee, J.A.; Lee, S.S. Vertically Aligned Carbon Nanopillars with Size and Spacing Control for a Transparent Field Emission Display. Nanotechnology 2013, 24, 025301. [Google Scholar] [CrossRef] [PubMed]
- Senthil, K.; Yong, K. Enhanced Field Emission from Density-Controlled SiC Nanowires. Mater. Chem. Phys. 2008, 112, 88–93. [Google Scholar] [CrossRef]
- Ding, S.; Li, C.; Lei, W.; Zhang, Y.; Qasim, K.; Cui, H.; Zhang, X.; Wang, B. Stable and Uniform Field Emission from Zinc Oxide Nanowires Grown on Carbon Nanotube Mesh Template. Thin Solid Film. 2012, 524, 245–248. [Google Scholar] [CrossRef]
- Hausladen, M.; Schels, A.; Buchner, P.; Bartl, M.; Asgharzade, A.; Edler, S.; Wohlfartsstätter, D.; Bachmann, M.; Schreiner, R. Measurement of Field Emission Array Current Distributions by Metal-Coated CMOS Image Sensors. J. Vac. Sci. Technol. B 2024, 42, 062209. [Google Scholar] [CrossRef]
- Meredith, W.J.; Massey, J.B. Fundamental Physics of Radiology, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1984; ISBN 978-0-7236-0778-6. [Google Scholar]
- Demtröder, W. Emission Und Absorption Elektromagnetischer Strahlung Durch Atome. In Experimentalphysik 3; Springer-Lehrbuch; Springer: Berlin/Heidelberg, Germany, 2016; pp. 215–249. ISBN 978-3-662-49093-8. [Google Scholar]
- Duane, W.; Hunt, F. On X-Ray Wave-Lengths. Phys. Rev. 1915, 6, 166–172. [Google Scholar] [CrossRef]
- Müller-Sievers, K. Intensitätsmessungen an Röntgen-Bremsstrahlung im Energiebereich von 200 bis 10 eV. Biophysik 1973, 10, 163–175. [Google Scholar] [CrossRef] [PubMed]
- Mosorov, V. The Lambert-Beer Law in Time Domain Form and Its Application. Appl. Radiat. Isot. 2017, 128, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Hagemann, H.-J.; Gudat, W.; Kunz, C. Optical Constants from the Far Infrared to the X-Ray Region: Mg, Al, Cu, Ag, Au, Bi, C, and Al2O3. J. Opt. Soc. Am. 1975, 65, 742. [Google Scholar] [CrossRef]
- Hagemann, H.-J. Optical Constants (Data-Tables) from the Far Infrared to the X-Ray Region: Mg, Al, Cu, Ag, Au, Bi, C, and Al2O3. Available online: https://bib-pubdb1.desy.de/record/399463/files/Hagemann%201974%20-%20DESY%20report%20SR-74-7.pdf (accessed on 26 January 2025).
- Lukiyanov, F.A.; Rau, E.I.; Sennov, R.A. Depth Range of Primary Electrons, Electron Beam Broadening, and Spatial Resolution in Electron-Beam Studies. Bull. Russ. Acad. Sci. Phys. 2009, 73, 441–449. [Google Scholar] [CrossRef]
- K Kanaya; S Okayama Penetration and Energy-Loss Theory of Electrons in Solid Targets. J. Phys. D: Appl. Phys. 1972, 5, 43–58. [CrossRef]
- Hausladen, M. FE-PyCam2 (Group-Container). Available online: https://github.com/Dephrilibrium/FE-PyCam2 (accessed on 27 September 2024).
- Hausladen, M. FE-FEAR16v2 (Group-Container). Available online: https://github.com/Dephrilibrium/FE-FEAR16v2 (accessed on 27 September 2024).
- Hausladen, M. FE-FEMDAQv2 (Group-Container). Available online: https://github.com/Dephrilibrium/FE-FEMDAQv2 (accessed on 27 September 2024).
- Raspberry Pi Datasheet—Raspberry Pi 4B. Available online: https://datasheets.raspberrypi.com/rpi4/raspberry-pi-4-datasheet.pdf (accessed on 26 January 2025).
- Libcamera/Libcamera.Git—Libcamera Official Repository. Available online: https://git.libcamera.org/libcamera/libcamera.git/ (accessed on 20 May 2023).
- Unofficial Mirror of Libcamera. Available online: https://github.com/libcamera-org/libcamera (accessed on 20 May 2023).
- New HQ Camera Tuning File—Raspberry Pi Forums. Available online: https://forums.raspberrypi.com/viewtopic.php?p=2057916&hilit=New+HQ+Camera+Tuning+File#p2057465 (accessed on 12 May 2023).
- Bayer, B.E. Color Imaging Array. U.S. Patent US3971065A, 20 July 1976. [Google Scholar]
- Trussell, H.J.; Hartwig, R.E. Mathematics for Demosaicking. IEEE Trans. Image Process. 2002, 11, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Lawrowski, R.; Hausladen, M.; Buchner, P.; Schreiner, R. Silicon Field Emission Electron Source With Individually Controllable Single Emitters. IEEE Trans. Electron Devices 2021, 68, 4116–4122. [Google Scholar] [CrossRef]
- Hausladen, M.; Buchner, P.; Schels, A.; Edler, S.; Bachmann, M.; Schreiner, R. An Integrated Field Emission Electron Source on a Chip Fabricated by Laser-Micromachining and Mems Technology. In Proceedings of the 2023 IEEE 36th International Vacuum Nanoelectronics Conference (IVNC), Cambridge, MA, USA, 10 July 2023; pp. 115–116. [Google Scholar]
- El Gamal, A.; Eltoukhy, H. CMOS Image Sensors. IEEE Circuits Devices Mag. 2005, 21, 6–20. [Google Scholar] [CrossRef]
- Rahman, S.; Rahman, M.M.; Abdullah-Al-Wadud, M.; Al-Quaderi, G.D.; Shoyaib, M. An Adaptive Gamma Correction for Image Enhancement. J Image Video Proc. 2016, 2016, 35. [Google Scholar] [CrossRef]
- Frequently Asked Questions—Libcamera. Available online: https://libcamera.org/faq.html (accessed on 1 February 2025).
- Feature Requirements—Libcamera. Available online: https://libcamera.org/feature_requirements.html (accessed on 1 February 2025).



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hausladen, M.; Schels, A.; Asgharzade, A.; Buchner, P.; Bartl, M.; Wohlfartsstätter, D.; Edler, S.; Bachmann, M.; Schreiner, R. Investigation of Influencing Factors on the Measurement Signal of a CMOS Image Sensor for Measuring Field Emission Currents. Sensors 2025, 25, 1529. https://doi.org/10.3390/s25051529
Hausladen M, Schels A, Asgharzade A, Buchner P, Bartl M, Wohlfartsstätter D, Edler S, Bachmann M, Schreiner R. Investigation of Influencing Factors on the Measurement Signal of a CMOS Image Sensor for Measuring Field Emission Currents. Sensors. 2025; 25(5):1529. https://doi.org/10.3390/s25051529
Chicago/Turabian StyleHausladen, Matthias, Andreas Schels, Ali Asgharzade, Philipp Buchner, Mathias Bartl, Dominik Wohlfartsstätter, Simon Edler, Michael Bachmann, and Rupert Schreiner. 2025. "Investigation of Influencing Factors on the Measurement Signal of a CMOS Image Sensor for Measuring Field Emission Currents" Sensors 25, no. 5: 1529. https://doi.org/10.3390/s25051529
APA StyleHausladen, M., Schels, A., Asgharzade, A., Buchner, P., Bartl, M., Wohlfartsstätter, D., Edler, S., Bachmann, M., & Schreiner, R. (2025). Investigation of Influencing Factors on the Measurement Signal of a CMOS Image Sensor for Measuring Field Emission Currents. Sensors, 25(5), 1529. https://doi.org/10.3390/s25051529




