AIPI: Network Status Identification on Multi-Protocol Wireless Sensor Networks
Abstract
1. Introduction
- (1)
- Active interception identifies topology through interfering node communication with an energy-effective dichotomy;
- (2)
- Local information extraction with self-adaptive error distribution provides extra effective information for active interception;
- (3)
- Passive interception with the Granger causality test is proposed to track topology of WSN with physical layer information.
2. Theoretical Basis
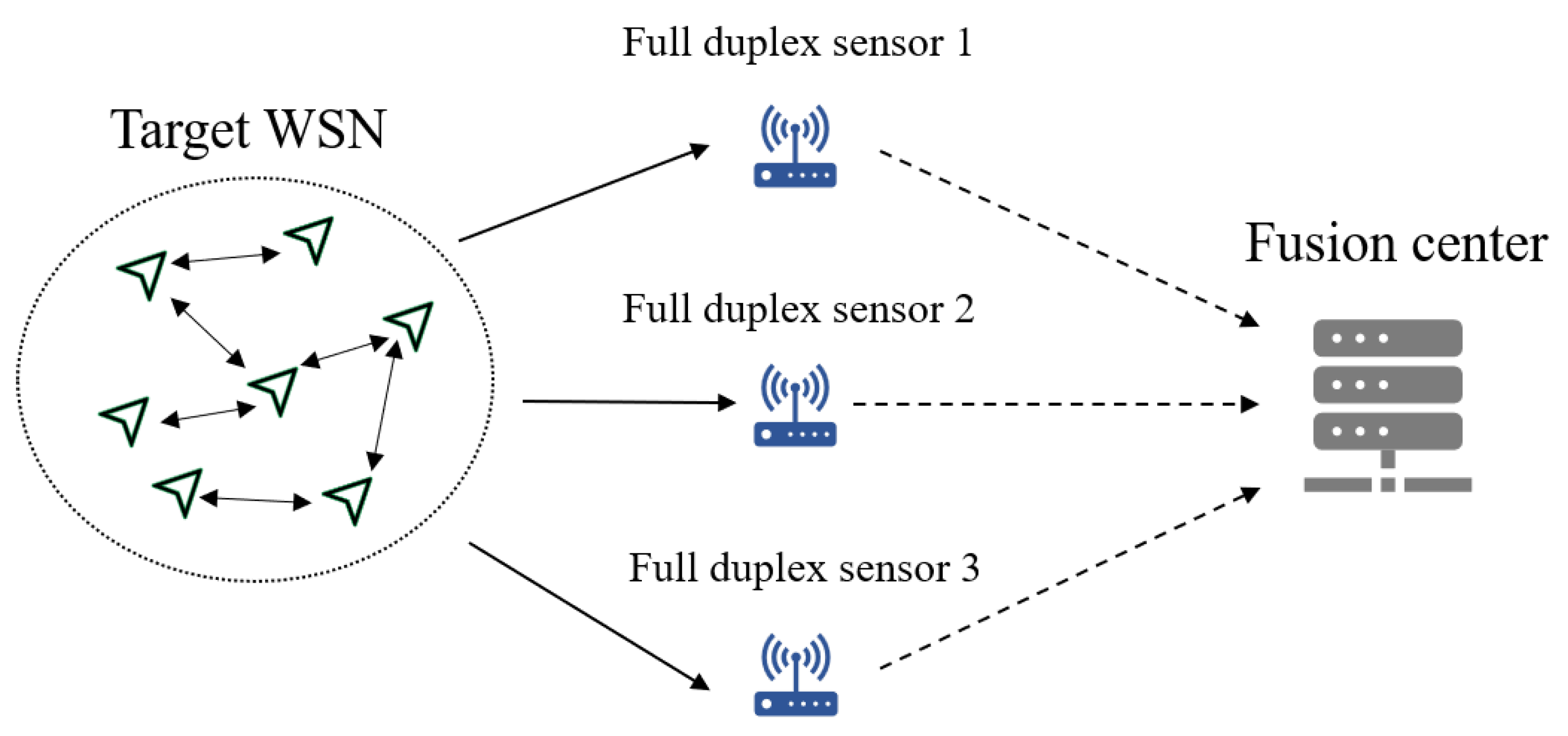
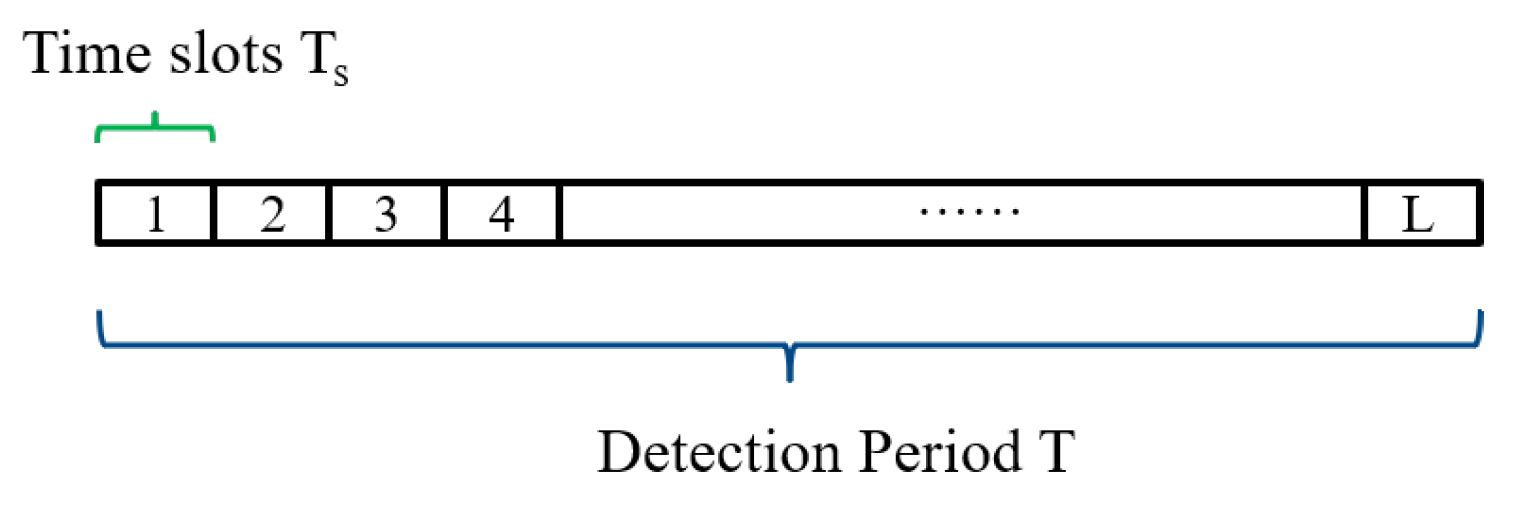
2.1. Problem Formulation
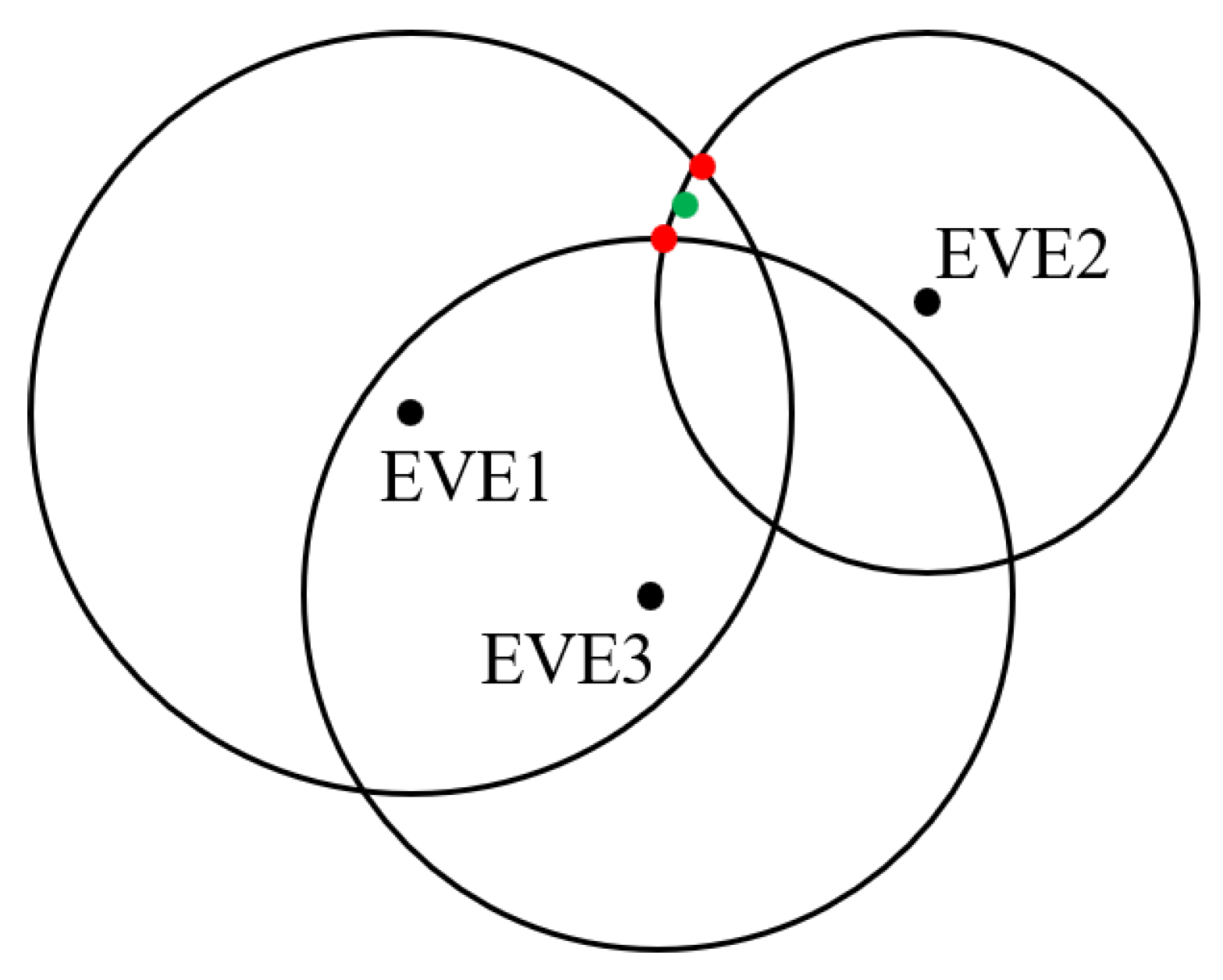
2.2. Active Interception
| Algorithm 1 Interference Strategy of Active Interception. |
|
| Algorithm 2 EM Algorithm for Gaussian Mixture Model Parameter Estimation |
|
2.3. Passive Interception
3. Experiment and Analysis
3.1. Experimental Setup
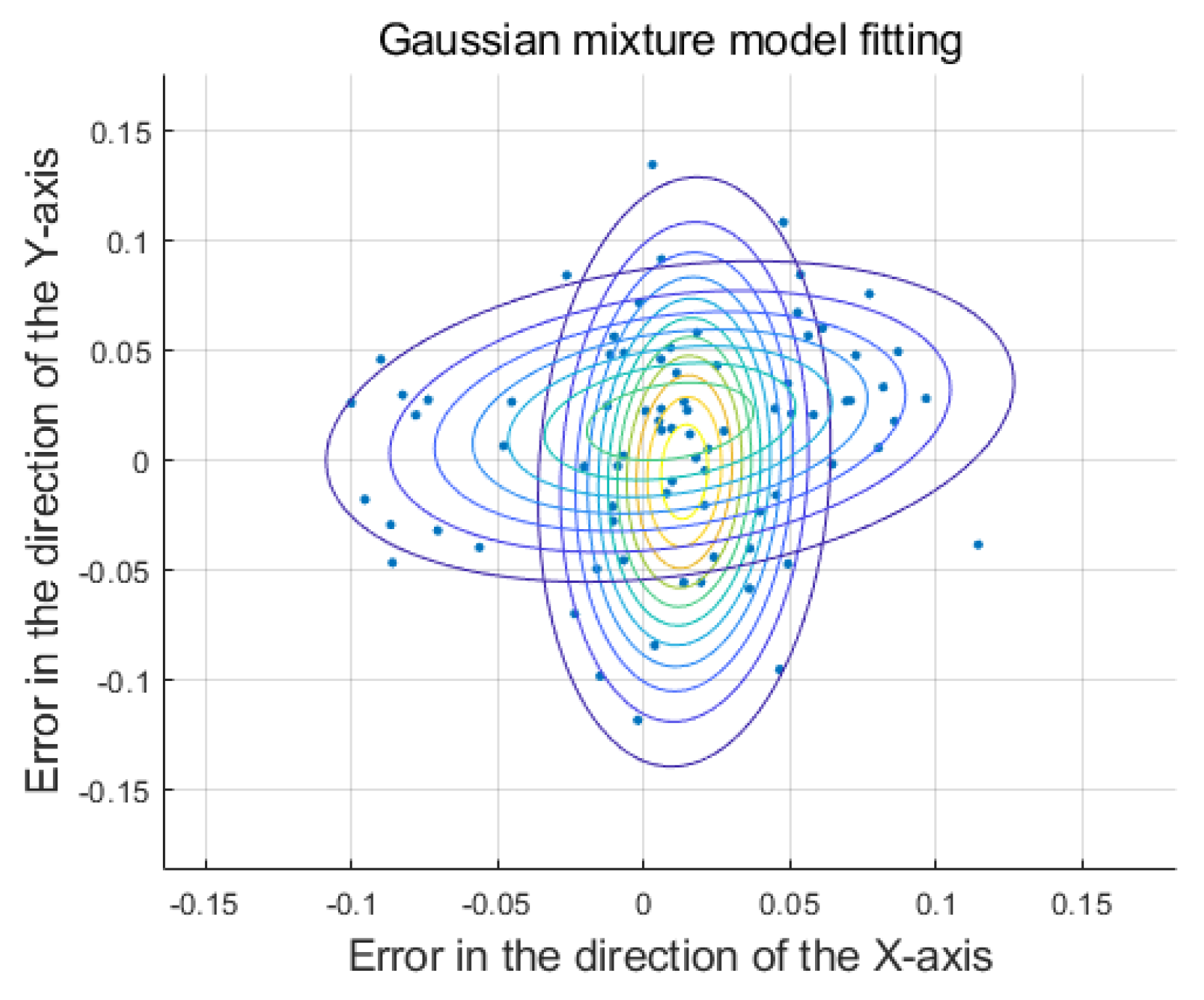
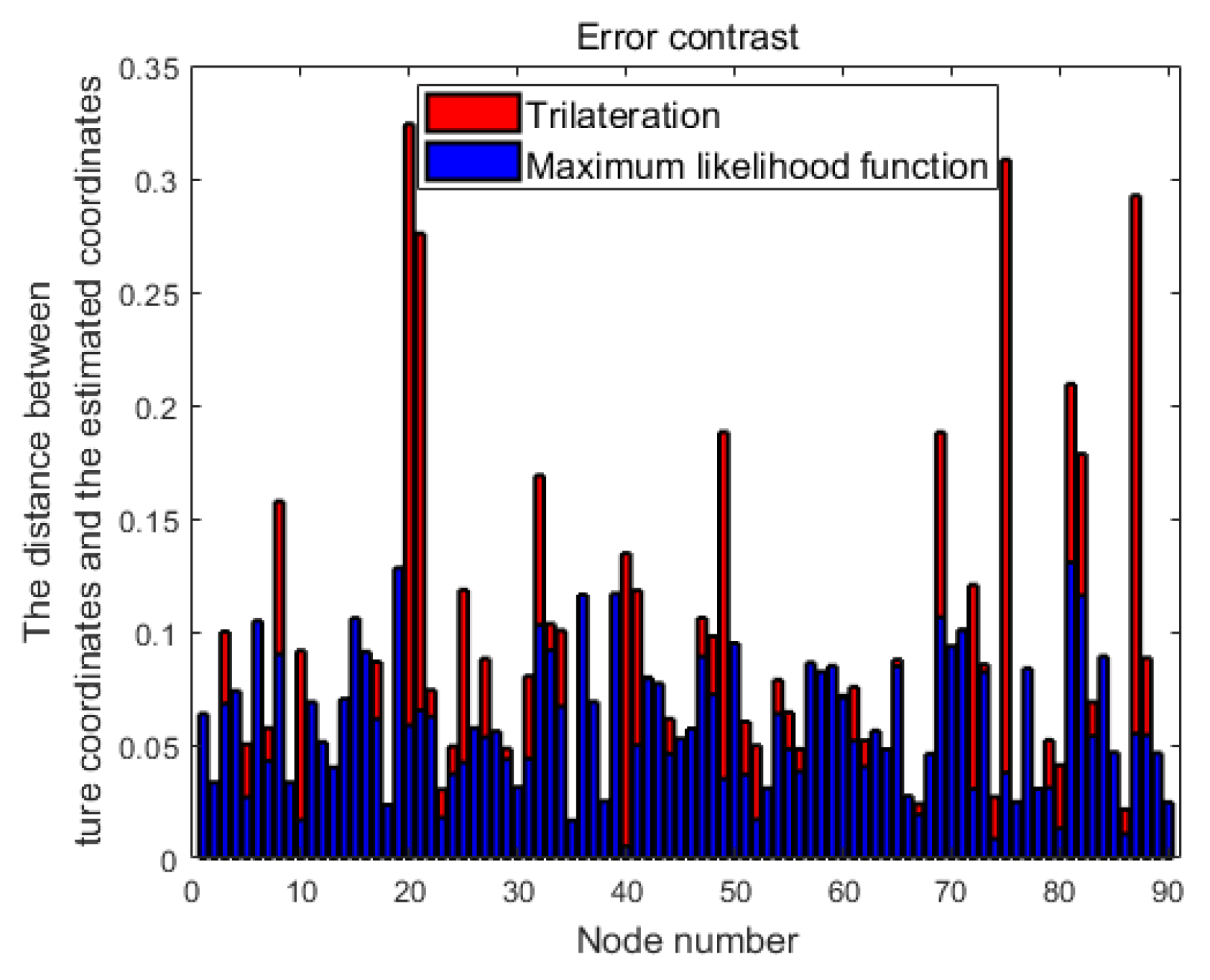
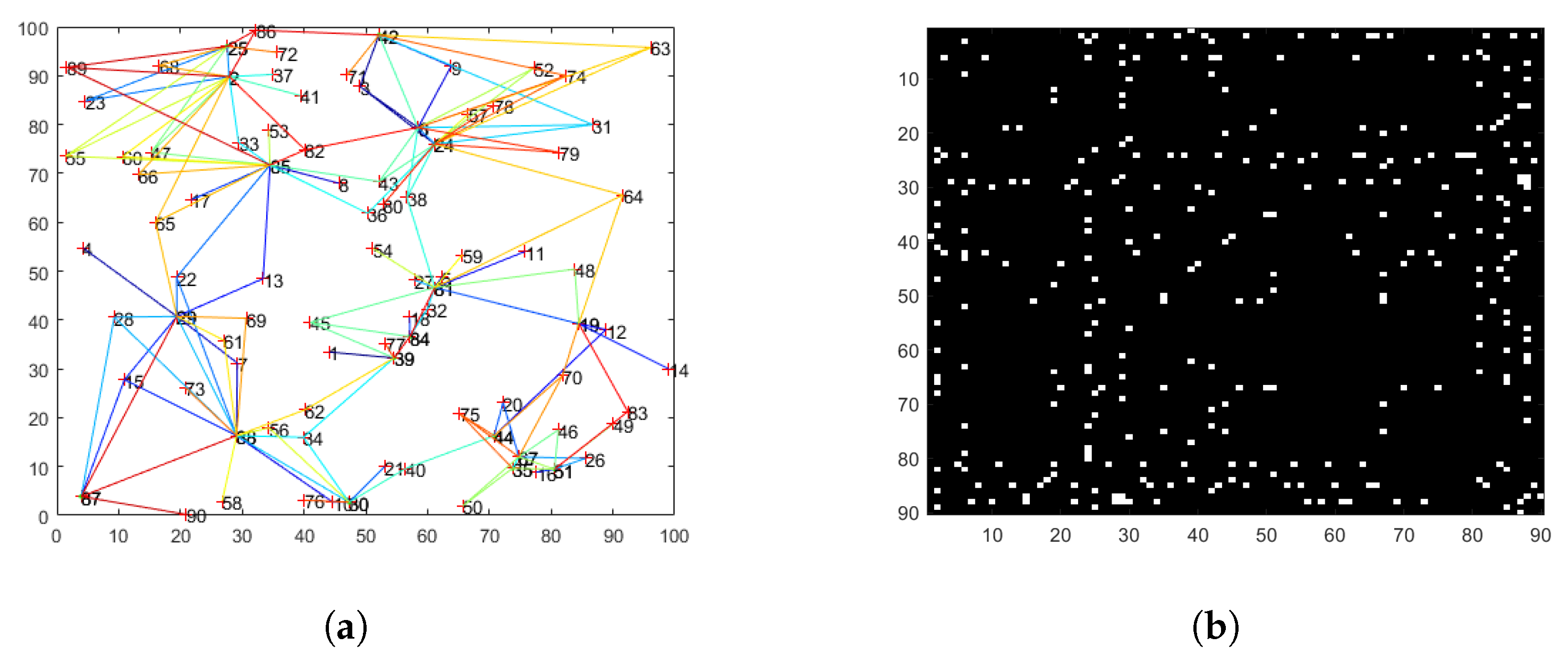
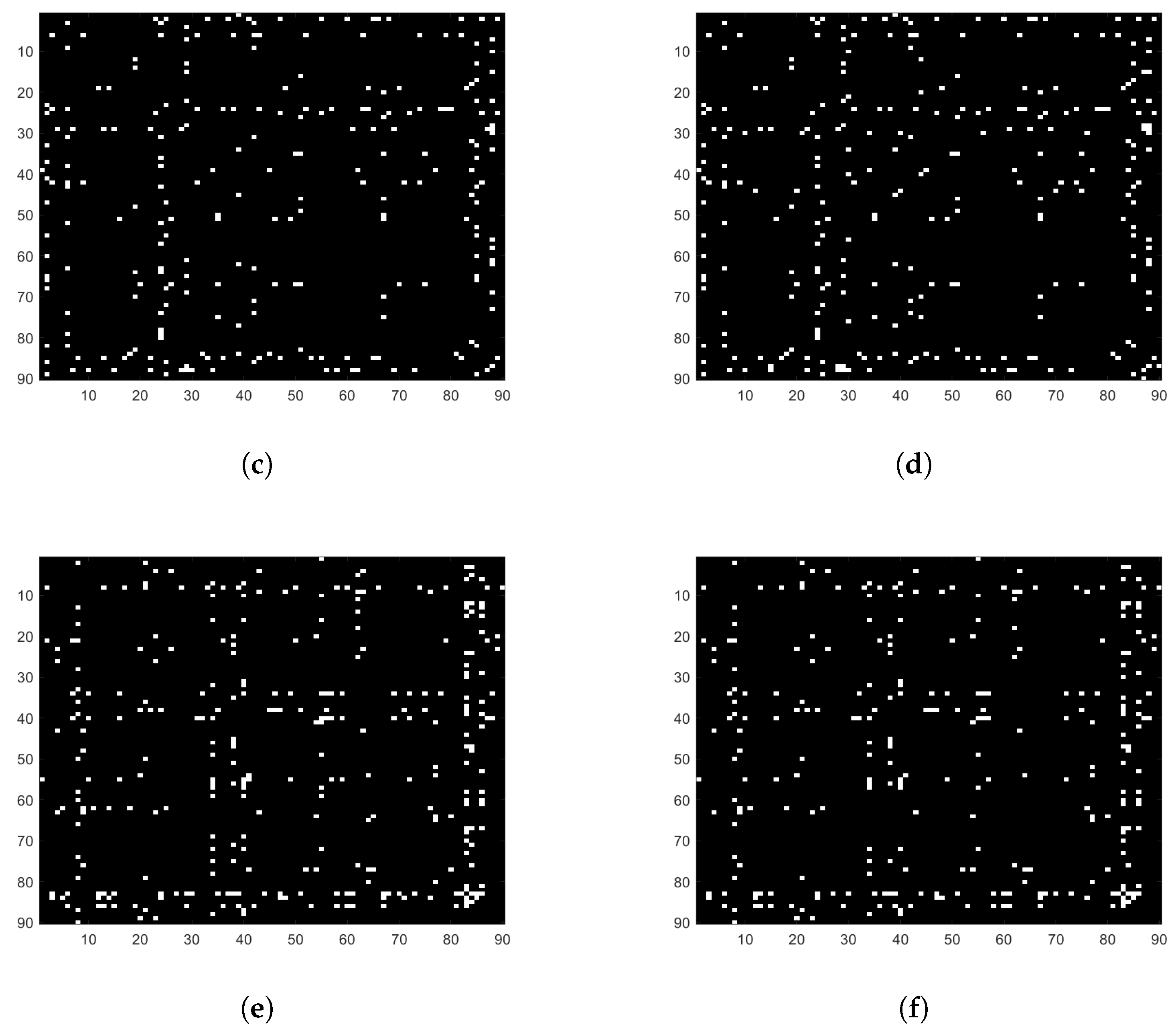
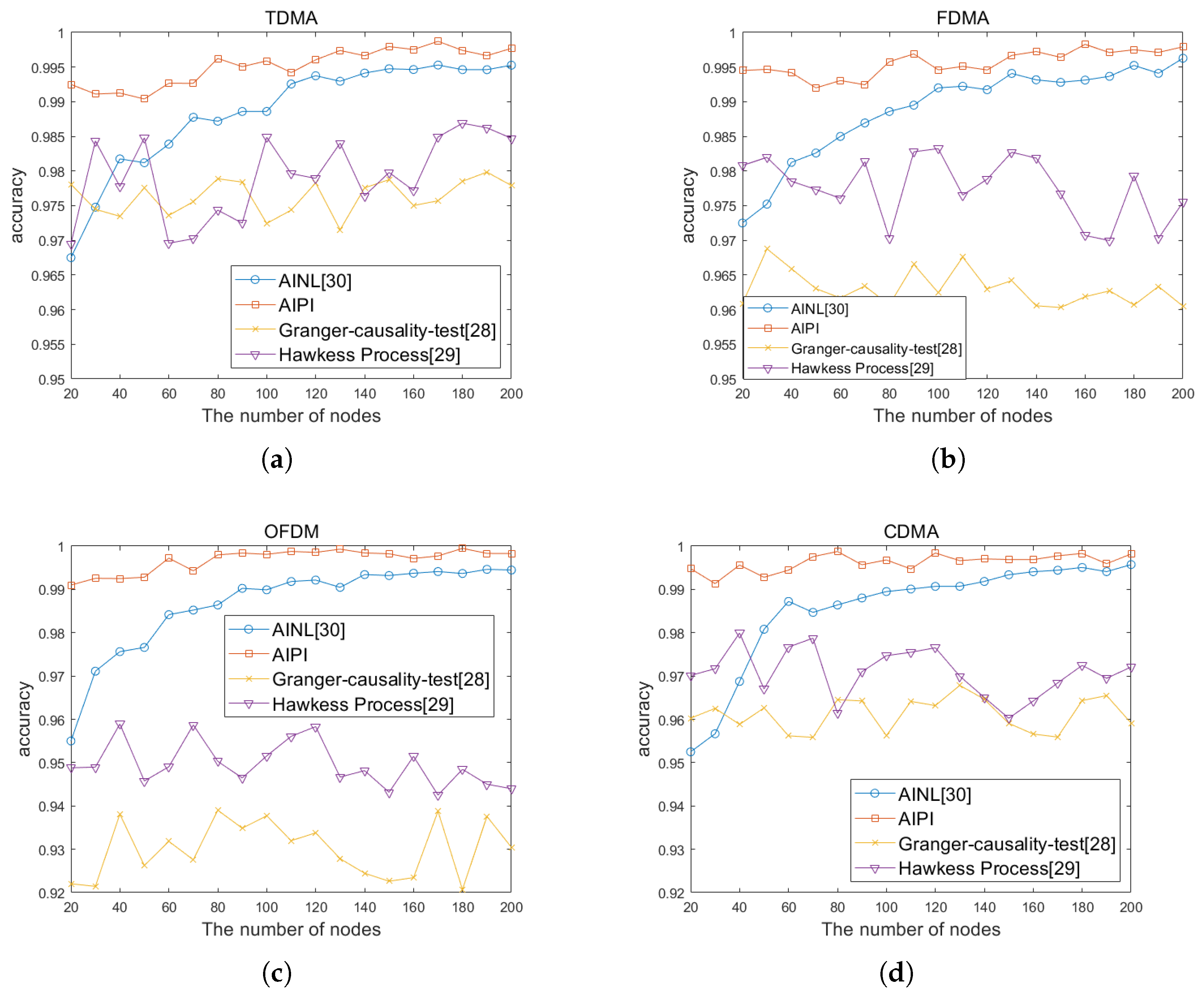
3.2. Comparison Result
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zagrouba, R.; Kardi, A. Comparative Study of Energy Efficient Routing Techniques in Wireless Sensor Networks. Information 2021, 12, 42. [Google Scholar] [CrossRef]
- Kenyeres, M.; Kenyeres, J. Distributed Mechanism for Detecting Average Consensus with Maximum-Degree Weights in Bipartite Regular Graphs. Mathematics 2021, 9, 3020. [Google Scholar] [CrossRef]
- Kullmann, L.; Kertész, J.; Kaski, K. Time-dependent cross-correlations between different stock returns: A directed network of influence. Phys. Rev. E 2002, 66, 026125. [Google Scholar] [CrossRef]
- Stetter, O.; Battaglia, D.; Soriano, J.; Geisel, T. Model-free reconstruction of excitatory neuronal connectivity from calcium imaging signals. PLoS Comput. Biol. 2012, 8, e1002653. [Google Scholar] [CrossRef]
- Runge, J.; Bathiany, S.; Bollt, E.; Camps-Valls, G.; Coumou, D.; Deyle, E.; Glymour, C.; Kretschmer, M.; Mahecha, M.D.; Muñoz-Marí, J.; et al. Inferring causation from time series in Earth system sciences. Nat. Commun. 2019, 10, 2553. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.X.; Lai, Y.C.; Grebogi, C. Data based identification and prediction of nonlinear and complex dynamical systems. Phys. Rep. 2016, 644, 1–76. [Google Scholar] [CrossRef]
- Nitzan, M.; Casadiego, J.; Timme, M. Revealing physical interaction networks from statistics of collective dynamics. Sci. Adv. 2017, 3, e1600396. [Google Scholar] [CrossRef] [PubMed]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Xu, J.; Duan, L.; Zhang, R. Proactive Eavesdropping Via Jamming for Rate Maximization Over Rayleigh Fading Channels. IEEE Wirel. Commun. Lett. 2016, 5, 80–83. [Google Scholar] [CrossRef]
- Cai, H.; Zhang, Q.; Li, Q.; Qin, J. Proactive Monitoring Via Jamming for Rate Maximization Over MIMO Rayleigh Fading Channels. IEEE Commun. Lett. 2017, 21, 2021–2024. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, C.; Shi, Q.; Li, G.Y.; Champagne, B. Joint Beamforming and Jamming Design for mmWave Information Surveillance Systems. IEEE J. Sel. Areas Commun. 2018, 36, 1410–1425. [Google Scholar] [CrossRef]
- Han, Y.; Duan, L.; Zhang, R. Jamming-Assisted Eavesdropping Over Parallel Fading Channels. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2486–2499. [Google Scholar] [CrossRef]
- Hu, G.; Cai, Y. Proactive Eavesdropping Via Jamming for Ergodic Rate Maximization Over Wireless-Powered Multichannel Suspicious System. IEEE Commun. Lett. 2020, 24, 1830–1834. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, Q.; Yang, P.; Qin, J. Proactive Monitoring via Jamming in Amplify-and-Forward Relay Networks. IEEE Signal Process. Lett. 2017, 24, 1714–1718. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, H.; Dai, H.; Wu, W.; Wang, B. Proactive Eavesdropping in UAV-Aided Suspicious Communication Systems. IEEE Trans. Veh. Technol. 2019, 68, 1993–1997. [Google Scholar] [CrossRef]
- Hu, G.; Si, J.; Cai, Y.; Zhu, F. Proactive Eavesdropping via Jamming in UAV-Enabled Suspicious Multiuser Communications. IEEE Wirel. Commun. Lett. 2022, 11, 3–7. [Google Scholar] [CrossRef]
- Li, B.; Yao, Y.; Chen, H.; Li, Y.; Huang, S. Wireless Information Surveillance and Intervention Over Multiple Suspicious Links. IEEE Signal Process. Lett. 2018, 25, 1131–1135. [Google Scholar] [CrossRef]
- Moon, J.; Lee, H.; Song, C.; Kang, S.; Lee, I. Relay-Assisted Proactive Eavesdropping With Cooperative Jamming and Spoofing. IEEE Trans. Wirel. Commun. 2018, 17, 6958–6971. [Google Scholar] [CrossRef]
- Yao, J.; Wu, T.; Zhang, Q.; Qin, J. Proactive Monitoring via Passive Reflection Using Intelligent Reflecting Surface. IEEE Commun. Lett. 2020, 24, 1909–1913. [Google Scholar] [CrossRef]
- Luo, Q.; Peng, Y.; Li, J.; Peng, X. RSSI-based localization through uncertain data mapping for wireless sensor networks. IEEE Sens. J. 2016, 16, 3155–3162. [Google Scholar] [CrossRef]
- Wang, T.; Ding, H.; Xiong, H.; Zheng, L. A compensated multi-anchors TOF-based localization algorithm for asynchronous wireless sensor networks. IEEE Access 2019, 7, 64162–64176. [Google Scholar] [CrossRef]
- Wang, T.; Xiong, H.; Ding, H.; Zheng, L. TDOA-based joint synchronization and localization algorithm for asynchronous wireless sensor networks. IEEE Trans. Commun. 2020, 68, 3107–3124. [Google Scholar] [CrossRef]
- Gui, L.; Xiao, F.; Zhou, Y.; Shu, F.; Val, T. Connectivity based DV-hop localization for Internet of Things. IEEE Trans. Veh. Technol. 2020, 69, 8949–8958. [Google Scholar] [CrossRef]
- Hartung, S.; Bochem, A.; Zdziarstek, A.; Hogrefe, D. Applied Sensor-Assisted Monte Carlo Localization for Mobile Wireless Sensor Networks. In Proceedings of the 2016 International Conference on Embedded Wireless Systems and Networks, Graz, Austria, 15–17 February 2016; pp. 181–192. [Google Scholar]
- Yousaf, M.Z.; Tahir, M.F.; Raza, A.; Khan, M.A.; Badshah, F. Intelligent Sensors for dc Fault Location Scheme Based on Optimized Intelligent Architecture for HVdc Systems. Sensors 2022, 22, 9936. [Google Scholar] [CrossRef]
- Feng, R.; Yuan, W.; Ge, L.; Ji, S. Nonintrusive Load Disaggregation for Residential Users Based on Alternating Optimization and Downsampling. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Feng, R.; Dai, M.; Wang, H. Distributed Beamforming in MISO SWIPT System. IEEE Trans. Veh. Technol. 2017, 66, 5440–5445. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, W.; Ding, G.; Wu, Q.; Wang, X. Topology Sensing of Non-Collaborative Wireless Networks with Conditional Granger Causality. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1501–1515. [Google Scholar] [CrossRef]
- Liu, Z.; Ding, G.; Wang, Z.; Zheng, S.; Sun, J.; Wu, Q. Cooperative Topology Sensing of Wireless Networks with Distributed Sensors. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 524–540. [Google Scholar] [CrossRef]
- Feng, R.; Cui, J. AINL: Network Topology Identification of Multiple Communication Modes via Active Intercepting and Node Locating. IEEE Access 2023, 11, 121399–121409. [Google Scholar] [CrossRef]
- Akaike, H. Canonical correlation analysis of time series and the use of an information criterion. In Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1976; Volume 126, pp. 27–96. [Google Scholar]





| channel | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| band | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| SNR | 114 | 99 | 90 | 79 | 123 | 129 | 178 | 30 | 172 | 10 |
| Transmitting Node | 1 | 2 | 3 | 3 | 3 | 4 |
| Receiving Node | 39 | 25 | 6 | 24 | 42 | 29 |
| Channel Number | 7279 | 5483 | 1456 | 3665 | 3027 | 7904 |
| Band Number | 5 | 5 | 7 | 6 | 3 | 3 |
| Methods | Accuracy | ||||
|---|---|---|---|---|---|
| 15 Nodes | 50 Nodes | 100 Nodes | 150 Nodes | 200 Nodes | |
| AIPI | 99.32% | 99.20% | 99.63% | 99.73% | 99.80% |
| AINL | 96.18% | 98.03% | 99.00% | 99.35% | 99.54% |
| Hawkess Process | 96.45% | 97.06% | 97.40% | 96.57% | 97.13% |
| Granger causality test | 95.53% | 95.73% | 95.72% | 95.51% | 95.69% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, P.; Feng, X.; Feng, R.; Cui, J. AIPI: Network Status Identification on Multi-Protocol Wireless Sensor Networks. Sensors 2025, 25, 1347. https://doi.org/10.3390/s25051347
Jiang P, Feng X, Feng R, Cui J. AIPI: Network Status Identification on Multi-Protocol Wireless Sensor Networks. Sensors. 2025; 25(5):1347. https://doi.org/10.3390/s25051347
Chicago/Turabian StyleJiang, Peng, Xinglin Feng, Renhai Feng, and Junpeng Cui. 2025. "AIPI: Network Status Identification on Multi-Protocol Wireless Sensor Networks" Sensors 25, no. 5: 1347. https://doi.org/10.3390/s25051347
APA StyleJiang, P., Feng, X., Feng, R., & Cui, J. (2025). AIPI: Network Status Identification on Multi-Protocol Wireless Sensor Networks. Sensors, 25(5), 1347. https://doi.org/10.3390/s25051347








