Quantitative Analysis of Phase Response Enhancement in Distributed Acoustic Sensing Systems Using Helical Fiber Winding Technology
Abstract
1. Introduction
- Quantitative phase response functions are also established to provide a more explicit link between wrapping geometry, wave incidence angles, and velocity components to predict amplitude behavior;
- Describing nonlinearity in order to improve the choice of parameters in DAS for the optimization of the decisions for media–velocity inversion;
- Offering empirical validation through active-source experiments that measure trade-offs, such as a 15–30% decrease in signal-to-noise ratio (SNR) for a 1–3-fold increase in amplitude gain.
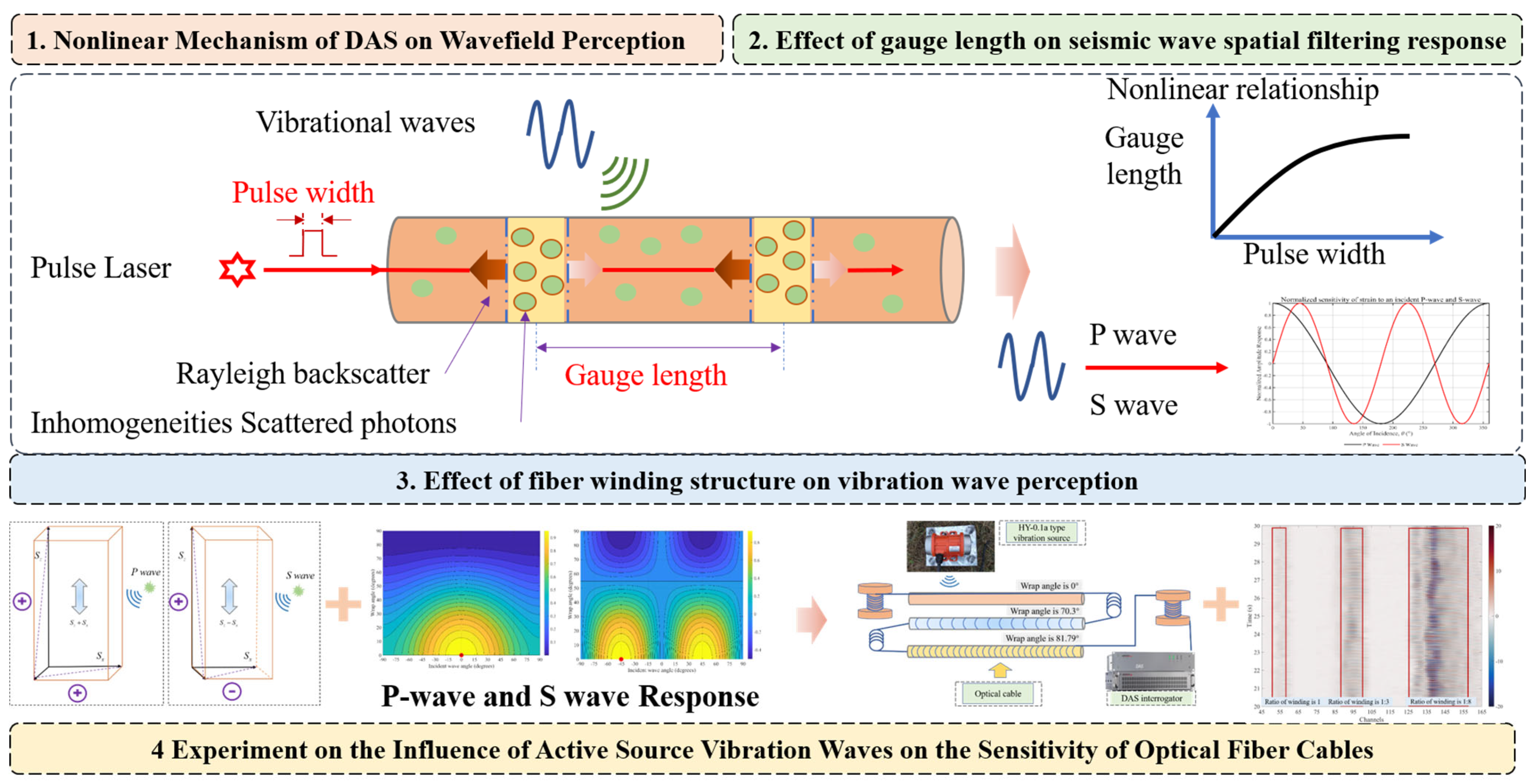
2. Nonlinear Mechanism of DAS on Wavefield Perception
2.1. Theory and Characteristics of Seismic Wave Propagation
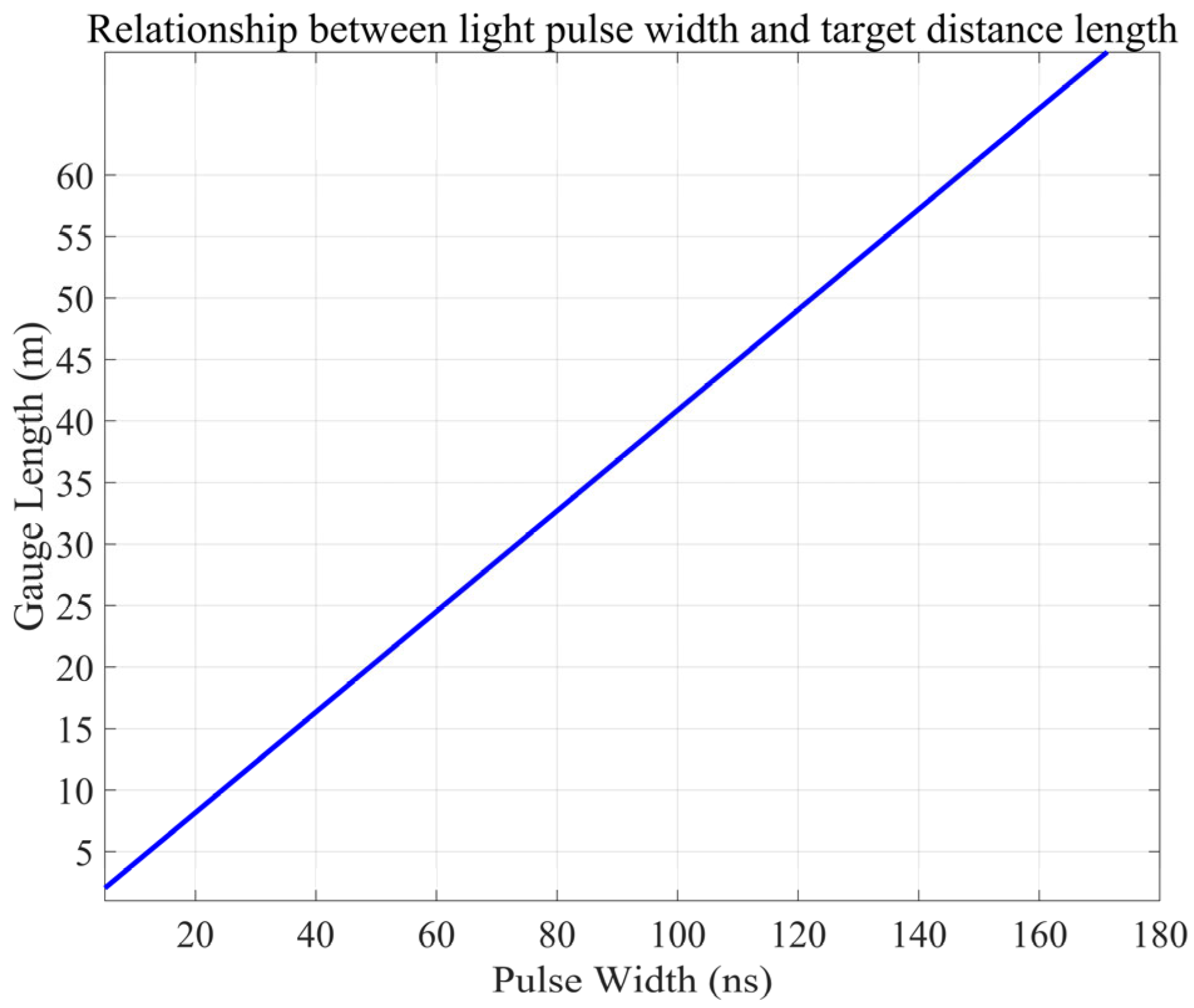
2.2. Nonlinear Relationship Between Gauge Length and Optical Pulse
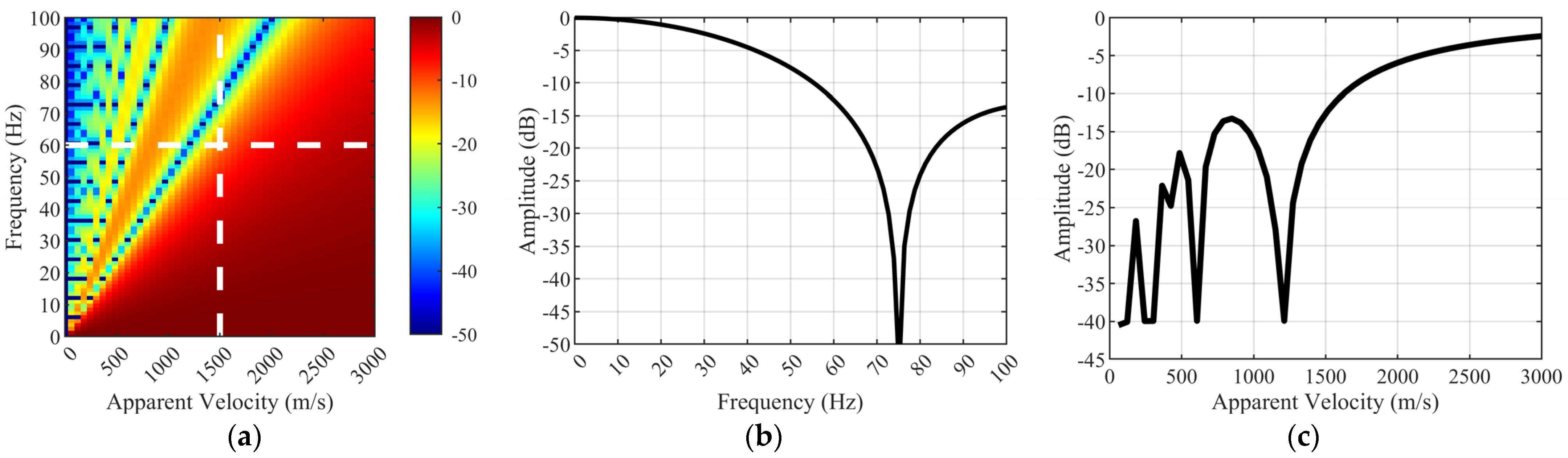
3. The Effect of Gauge Length on Seismic Wave Spatial Filtering Response
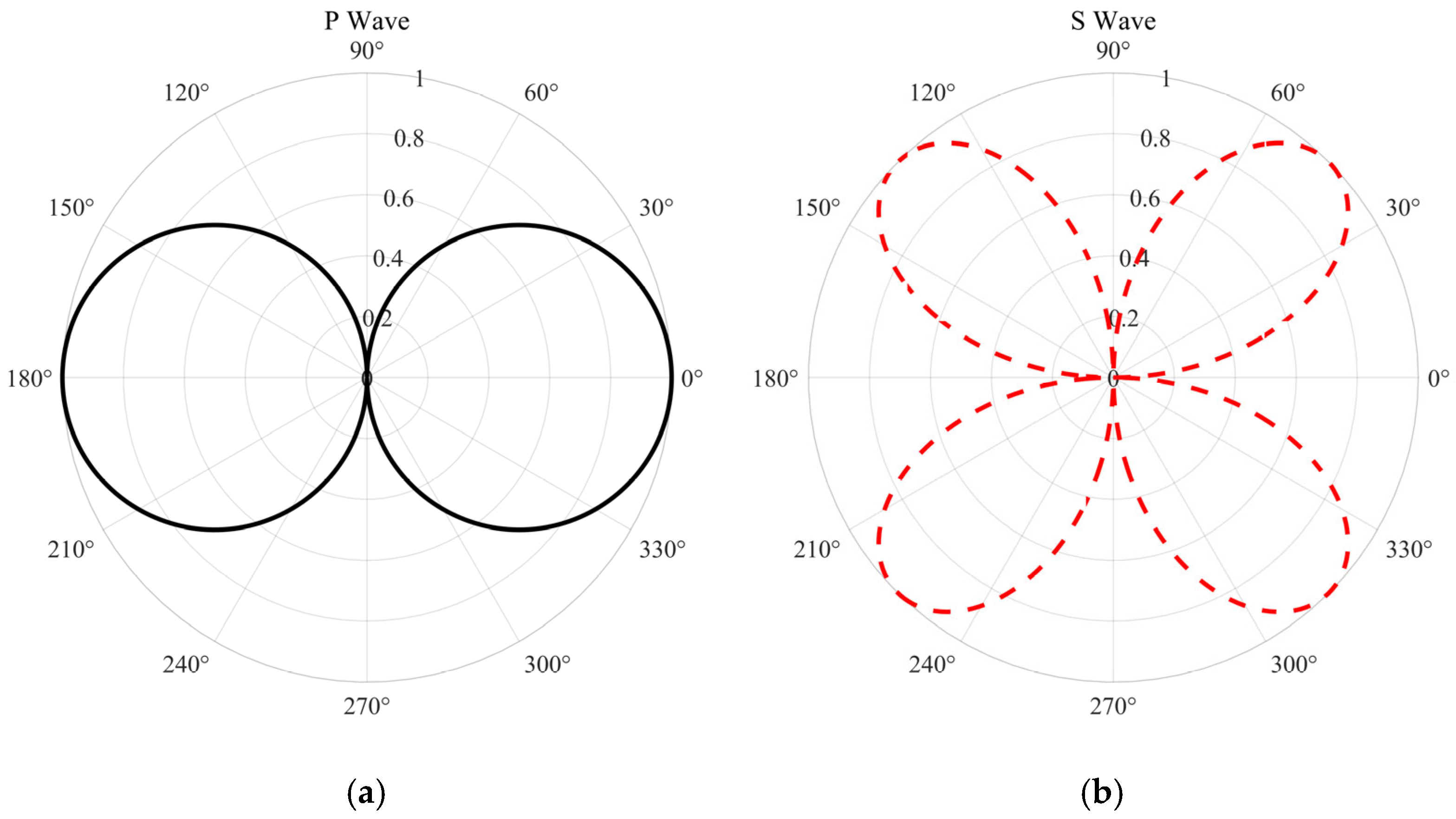
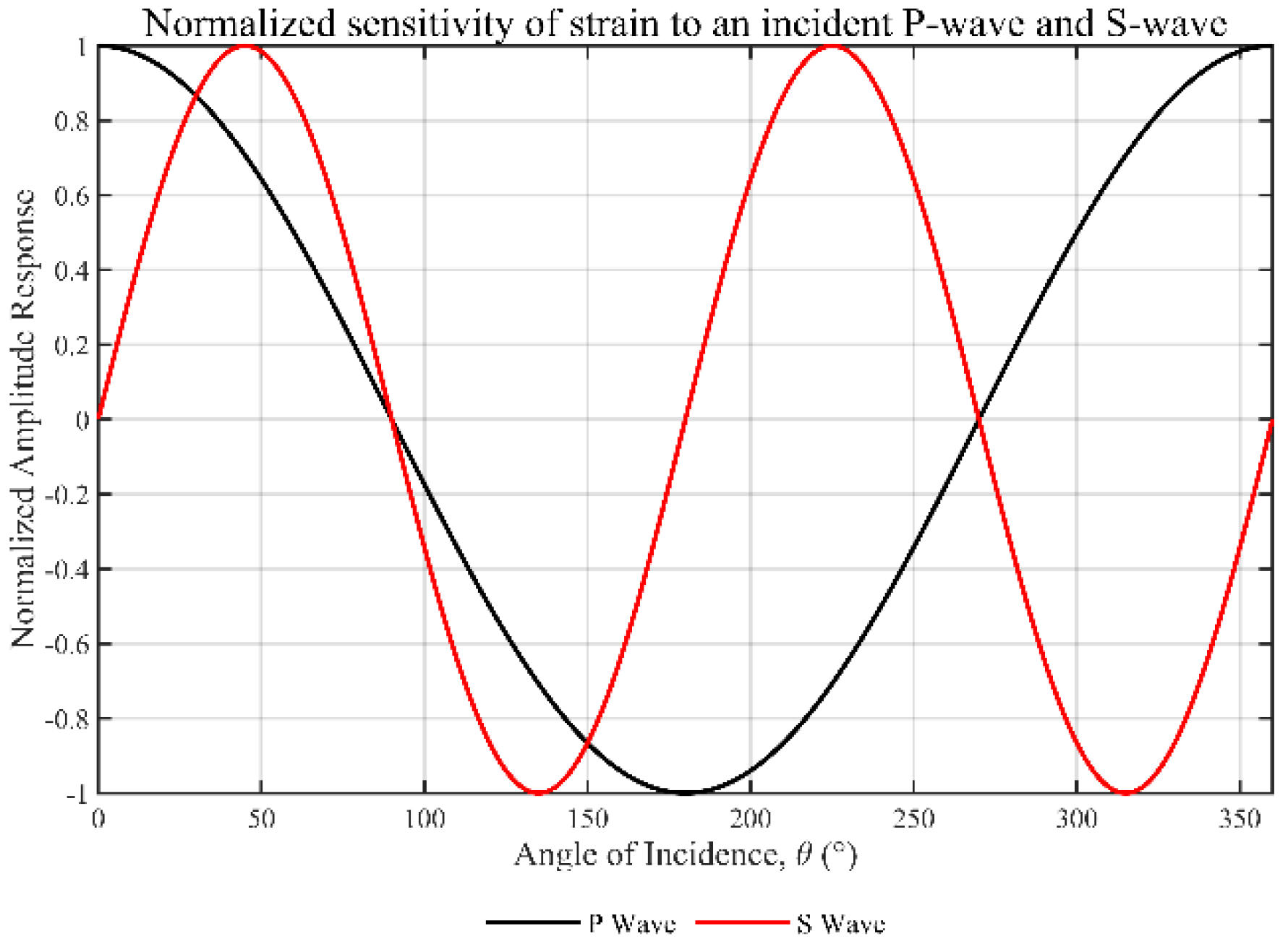
3.1. Response of a Straight Optical Fiber to Multi-Angle Vibration Waves
3.2. Spatial Filtering Mechanism and Wavefield Response of DAS Systems
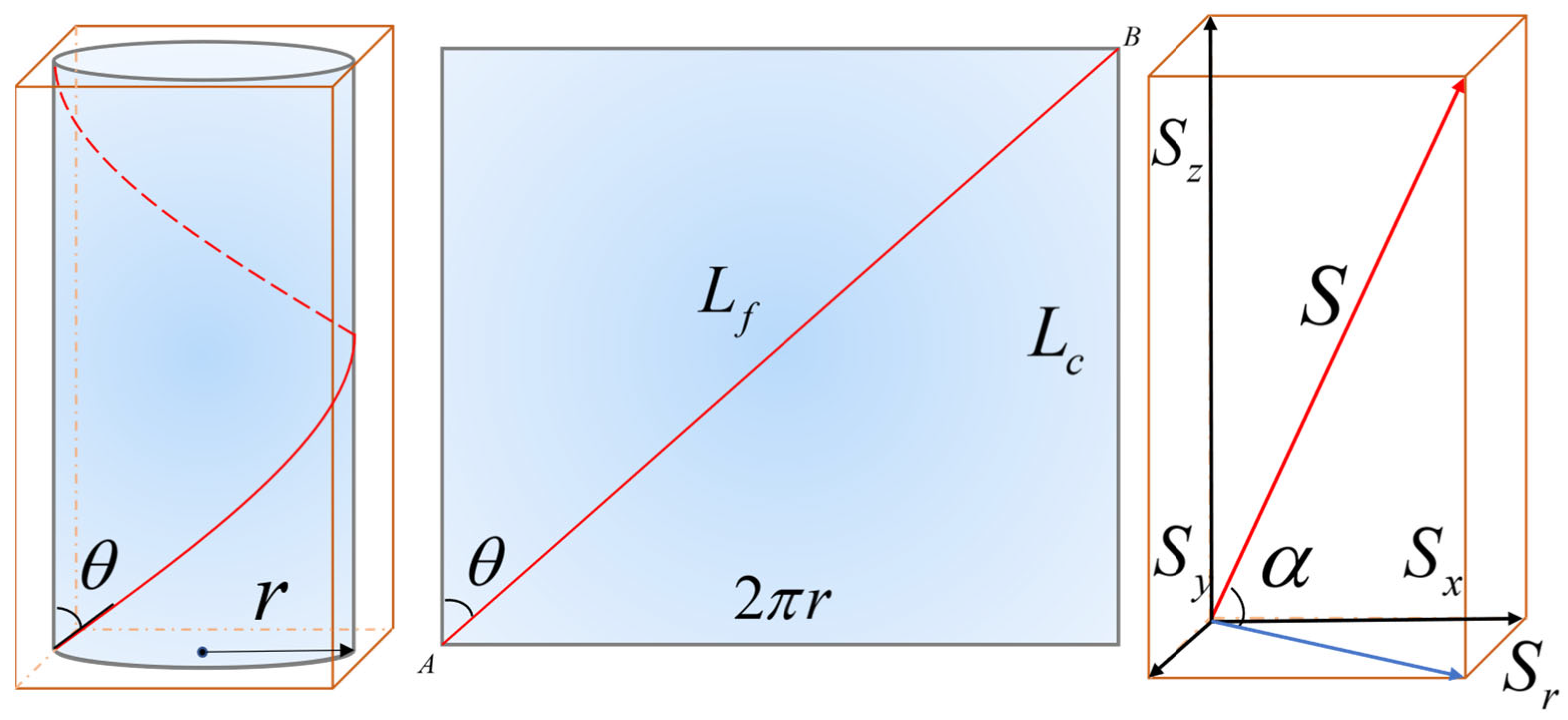
4. Impact of Fiber Winding Structure on Vibration Perception
4.1. The Effect of Fiber Winding Angle on the Increase in Marking Distance
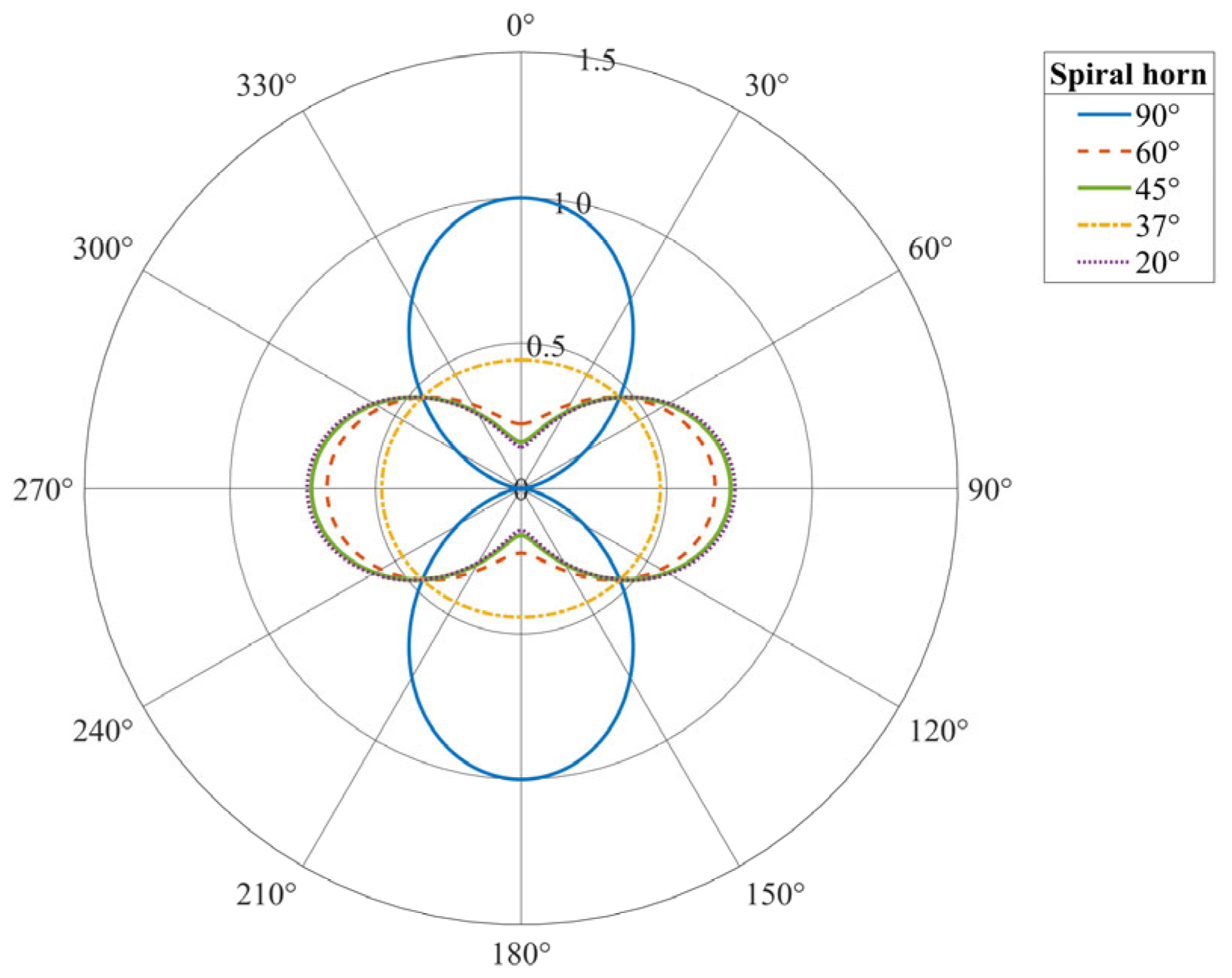
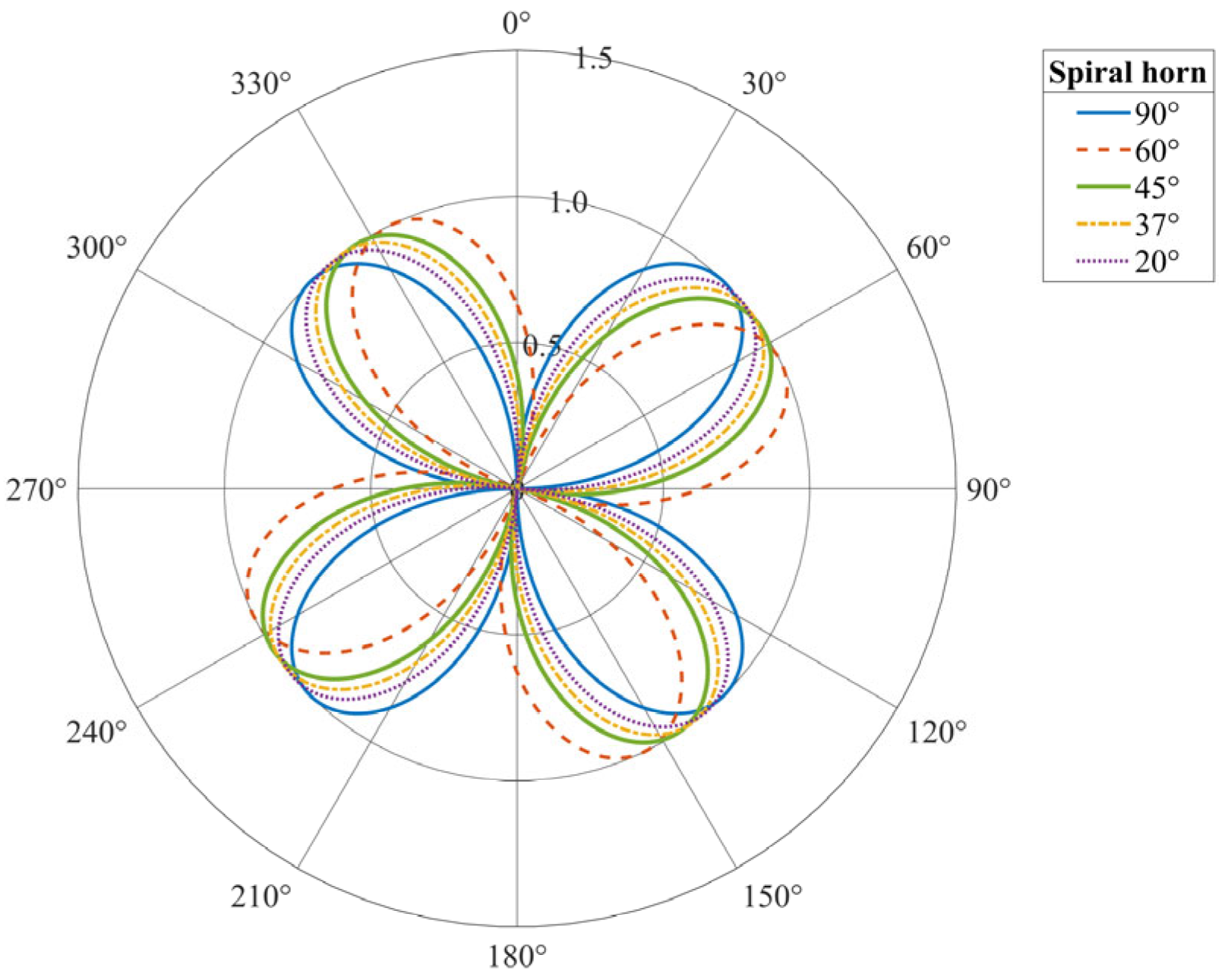
4.2. The Relationship Between Wrapping Angle and Incident Wave Phase Shift
4.3. Simulating Phase Change in Fiber Winding Under Vibration Waves
5. Experiment on the Influence of Active Source Vibration Waves on the Sensitivity of Optical Fiber Cables
5.1. Experimental Measurement and Deployment Plan
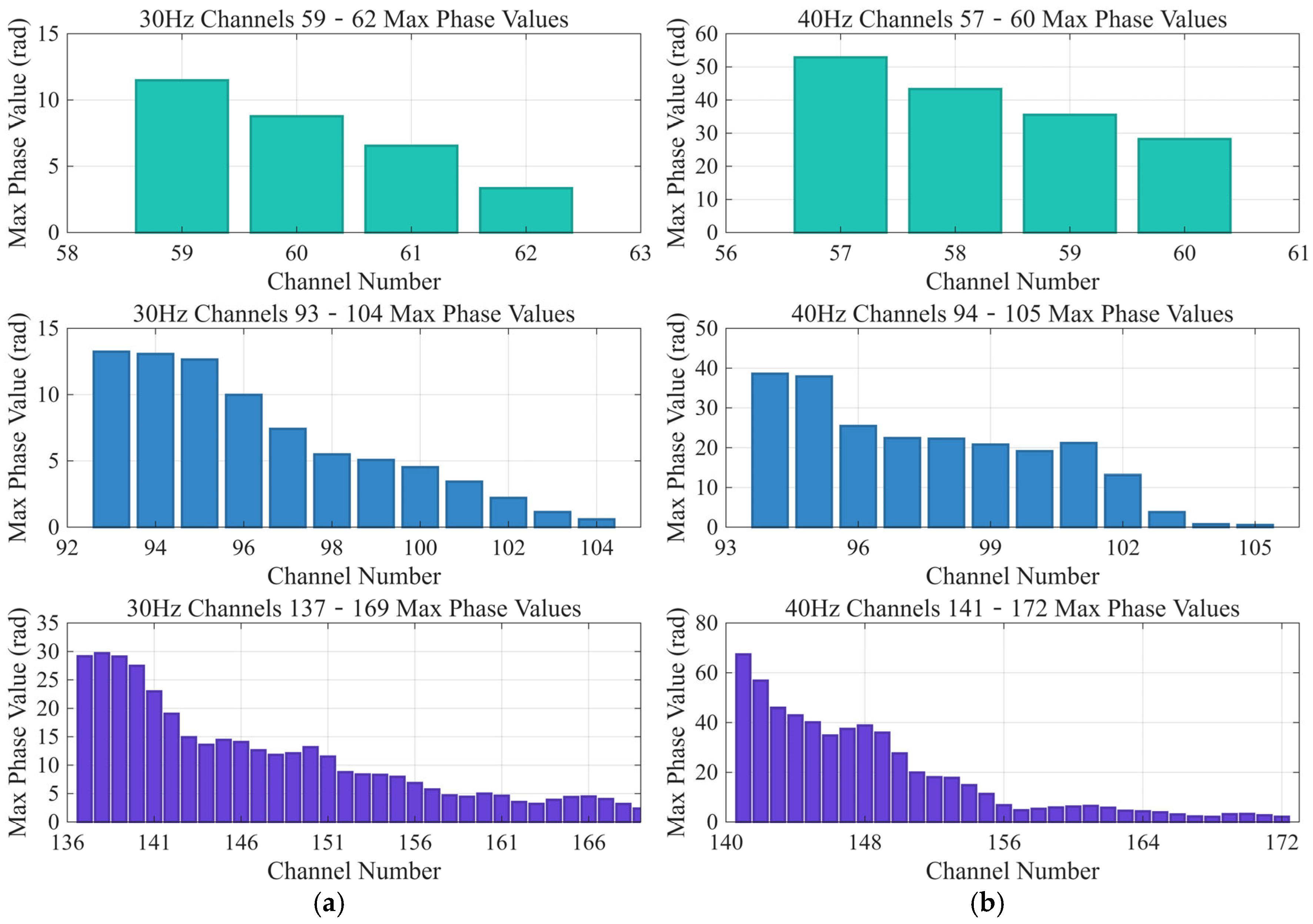
5.2. Experimental Results Analysis
- (1)
- Multichannel Power Spectral Density (PSD) Calculation: For channels with three different winding ratios (ratios of 1, 3, and 8), we calculated their average power spectral density using the Welch method (pwelch). To ensure high-precision spectral estimation, we set a window length of 1024 points, an overlap of 512 points, and an FFT size of 2048 points.
- (2)
- Multidimensional Visualization: We generated comparative charts, including overlaid PSD comparisons for the three ratios (0–70 Hz), subplot displays, detailed analysis of the four source frequencies, and peak power calculations.
- (3)
- Quantitative Analysis: Peak power (dB/Hz) at the four source locations, total power across the entire frequency band, power percentage within the 20–70 Hz range, and primary frequency components were automatically extracted and presented for each ratio. This offers a quantitative basis for assessing the frequency response characteristics of different winding ratios and the energy distribution under excitation from the four sources.
5.3. Practical Challenges
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Local angle in sensitivity decomposition. | |
| β | Helical winding angle |
| Incidence angle of the wave relative to the fiber axis | |
| Δϕ | Change in optical phase due to strain |
| ϕ-OTDR | Phase-sensitive optical time domain reflectometry |
| Axial strain along the fiber | |
| Effective strain after spatial averaging | |
| The actual axial strain component along the fiber direction | |
| θ | Helical winding angle of the fiber |
| First Lamé parameters for cable and geological formation | |
| Angular frequency of the wave | |
| Amplitude of the incident wave | |
| DAS | Distributed acoustic sensing |
| Sensitivity components | |
| Effective refractive index of the fiber mode | |
| GL | Gauge the length of the DAS system. |
| k | Wave number of light |
| Axial wavenumber component | |
| Actual length of helically wound fiber over one pitch | |
| Axial pitch length of the cable core | |
| n | Refractive index of the optical fiber |
| Shear moduli for cable and formation | |
| OTDR | Optical time domain reflectometry |
| Photoelastic coefficients of the fiber | |
| P-wave | Primary wave |
| S | Total sensitivity of the helically wound fiber |
| S-wave | Secondary wave |
| SH wave | Horizontally polarized Shear wave |
| SV wave | Vertically polarized Shear wave |
| SNR | Signal-to-noise ratio |
| Integration variable along the fiber axis |
References
- Ashry, I.; Mao, Y.; Wang, B.; Hveding, F.; Bukhamsin, A.Y.; Ng, T.K.; Ooi, B.S. A review of distributed fiber–optic sensing in the oil and gas industry. J. Light. Technol. 2022, 40, 1407–1431. [Google Scholar] [CrossRef]
- Pengchao, C. Advancements and future outlook of safety monitoring, inspection, and assessment technologies for oil and gas pipeline networks. J. Pipeline Sci. Eng. 2025, 100267, 100267. [Google Scholar] [CrossRef]
- Farghal, N.S.; Saunders, J.K.; Parker, G.A. The potential of using fiber optic distributed acoustic sensing (DAS) in earthquake early warning applications. Bull. Seismol. Soc. Am. 2022, 112, 1416–1435. [Google Scholar] [CrossRef]
- Shao, L.; Zhang, J.; Chen, X.; Xu, D.; Gu, H.; Mu, Q.; Yu, F.; Liu, S.; Shi, X.; Sun, J.; et al. Artificial intelligence-driven distributed acoustic sensing technology and engineering application. PhotoniX 2025, 6, 4. [Google Scholar] [CrossRef]
- Shang, Y.; Sun, M.; Wang, C.; Yang, J.; Du, Y.; Yi, J.; Zhao, W.; Wang, Y.; Zhao, Y.; Ni, J. Research progress in distributed acoustic sensing techniques. Sensors 2022, 22, 6060. [Google Scholar] [CrossRef] [PubMed]
- Dean, T.; Cuny, T.; Hartog, A.H. The effect of gauge length on axially incident P-waves measured using fibre optic distributed vibration sensing. Geophys. Prospect. 2017, 65, 184–193. [Google Scholar] [CrossRef]
- Alfataierge, E.; Aldawood, A.; Bakulin, A.; Stewart, R.R.; Merry, H. Influence of gauge length on DAS VSP data at the Houston Research Center Test Well. In SEG Technical Program Expanded Abstracts 2020; Society of Exploration Geophysicists: Houston, TX, USA, 2020; pp. 505–509. [Google Scholar] [CrossRef]
- Luckie, T.; Porritt, R. Performance of synthetic DAS as a function of array geometry. Seismica 2024, 3. [Google Scholar] [CrossRef]
- Muir, J.B.; Zhan, Z. Wavefield-based evaluation of DAS instrument response and array design. Geophys. J. Int. 2021, 229, 21–34. [Google Scholar] [CrossRef]
- Capdeville, Y.; Sladen, A. DAS sensitivity to heterogeneity scales much smaller than the minimum wavelength. Seismica 2024, 3. [Google Scholar] [CrossRef]
- Mellors, R.J.; Abbott, R.; Steedman, D.; Podrasky, D.; Pitarka, A. Modeling subsurface explosions recorded on a distributed fiber optic sensor. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022690. [Google Scholar] [CrossRef]
- Stepanov, K.V.; Zhirnov, A.A.; Koshelev, K.I.; Chernutsky, A.O.; Khan, R.I.; Pnev, A.B. Sensitivity improvement of phi-OTDR by fiber cable coils. Sensors 2021, 21, 7077. [Google Scholar] [CrossRef]
- Al Hasani, M.; Drijkoningen, G. Experiences with distributed acoustic sensing using both straight and helically wound fibers in surface-deployed cables—A case history in Groningen, the Netherlands. Geophysics 2023, 88, B369–B380. [Google Scholar] [CrossRef]
- Harmon, N.; Rychert, C.A.; Davis, J.; Brambilla, G.; Buffet, W.; Chichester, B.; Dai, Y.; Bogiatzis, P.; Snook, J.; van Putten, L.; et al. Surface deployment of DAS systems: Coupling strategies and comparisons to geophone data. Near Surf. Geophys. 2022, 20, 465–477. [Google Scholar] [CrossRef]
- Kuvshinov, B.N. Interaction of helically wound fibre-optic cables with plane seismic waves: Interaction of fibre-optic cables. Geophys. Prospect. 2016, 64, 671–688. [Google Scholar] [CrossRef]
- Eaid, M.; Keating, S.; Innanen, K. The Role of Fiber Gauge Lengths in Elastic FWI of Data from Coiled DAS Fibers. Available online: https://www.crewes.org/Documents/ResearchReports/2020/CRR202011.pdf (accessed on 26 November 2025).
- Hudson, T.; Stork, A.; Muir, J.; Fichtner, A. Unlocking DAS amplitude information through coherency coupling quantification. Seismica 2025, 4. [Google Scholar] [CrossRef]
- Wang, J.; Liu, B.; Zhu, J.; Duan, W. Application of distributed helically wound cable technology in ground seismic exploration. J. Seism. Explor. 2025, 34, 025300040. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, J.-D.; Huang, J.-P.; Qin, N.; Tian, K.; Yang, F.-L. Seismic simulation for distributed acoustic sensing data using a novel stress and strain-rate elastic wave equation. Pet. Sci. 2025, in press. [Google Scholar] [CrossRef]
- Adeniyi, B.A.; Latiff, A.H.A.; Adedeji, Z.O.; Arshad, A.R.M.; Asfha, D.T. Directional sensitivity of fibre optic cables for surface seismic reflection distributed acoustic sensing: A review and potential solutions for enhanced sensitivity. Geomech. Geophys. Geo Energy Geo Resour. 2025, 11, 60. [Google Scholar] [CrossRef]
- Strutz, D.; Kiers, T.; Curtis, A. Single and multi-objective optimization of distributed acoustic sensing cable layouts for geophysical applications. arXiv 2025, arXiv:2510.07531. [Google Scholar] [CrossRef]
- Foti, S.; Lai, C.G.; Rix, G.J.; Strobbia, C. Surface Wave Methods for Near-Surface Site Characterization, 2nd ed.; CRC Press: London, UK, 2014. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology, 2nd ed.; Corrected Printing; University Science Books: Mill Valley, CA, USA; New York, NY, USA, 2009. [Google Scholar]
- Duan, Y.; Liang, L.; Tong, X.; Luo, B.; Cheng, B. Application of pipeline leakage detection based on distributed optical fiber acoustic sensor system and convolutional neural network. J. Phys. D Appl. Phys. 2023, 57, 105102. [Google Scholar] [CrossRef]


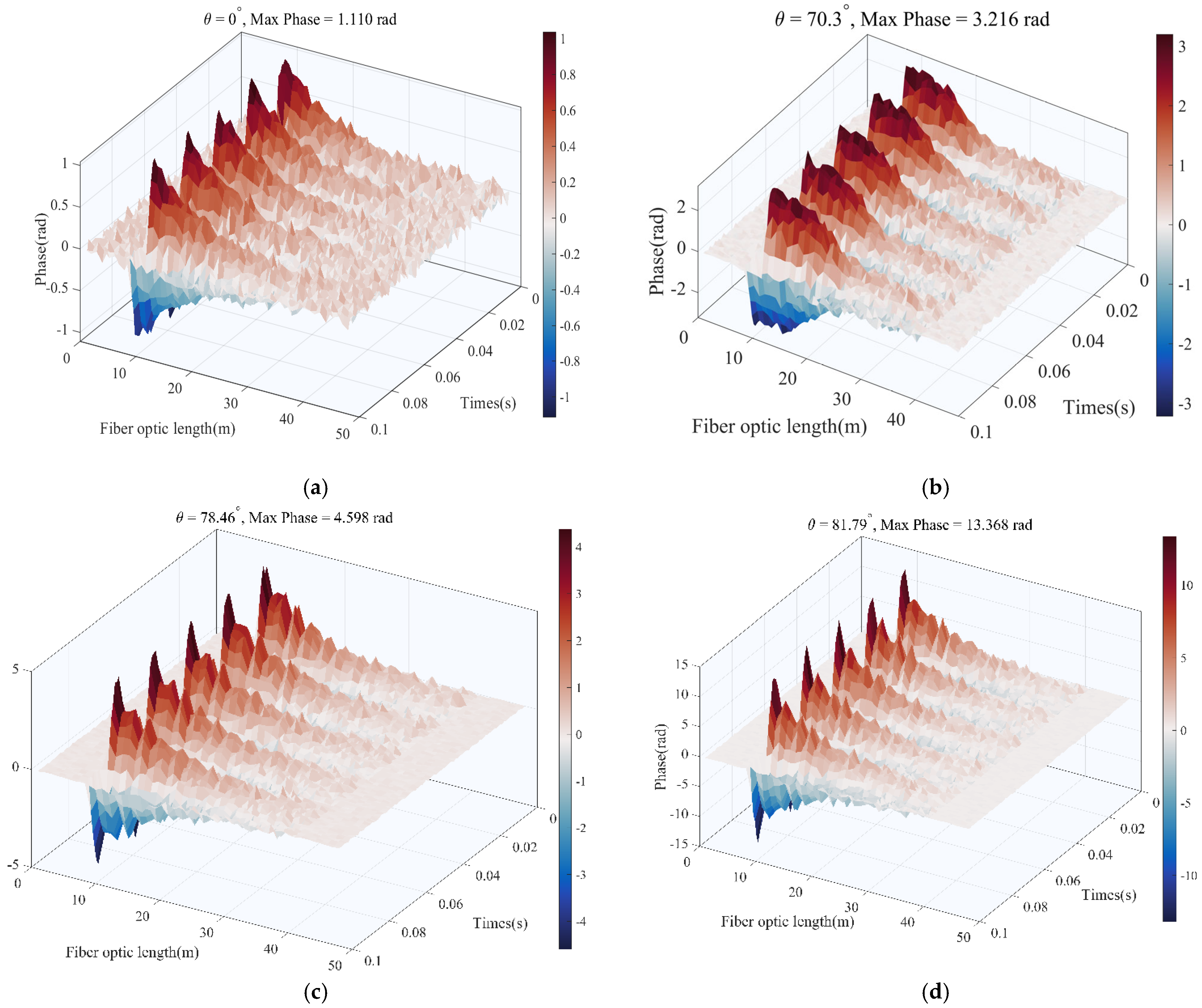
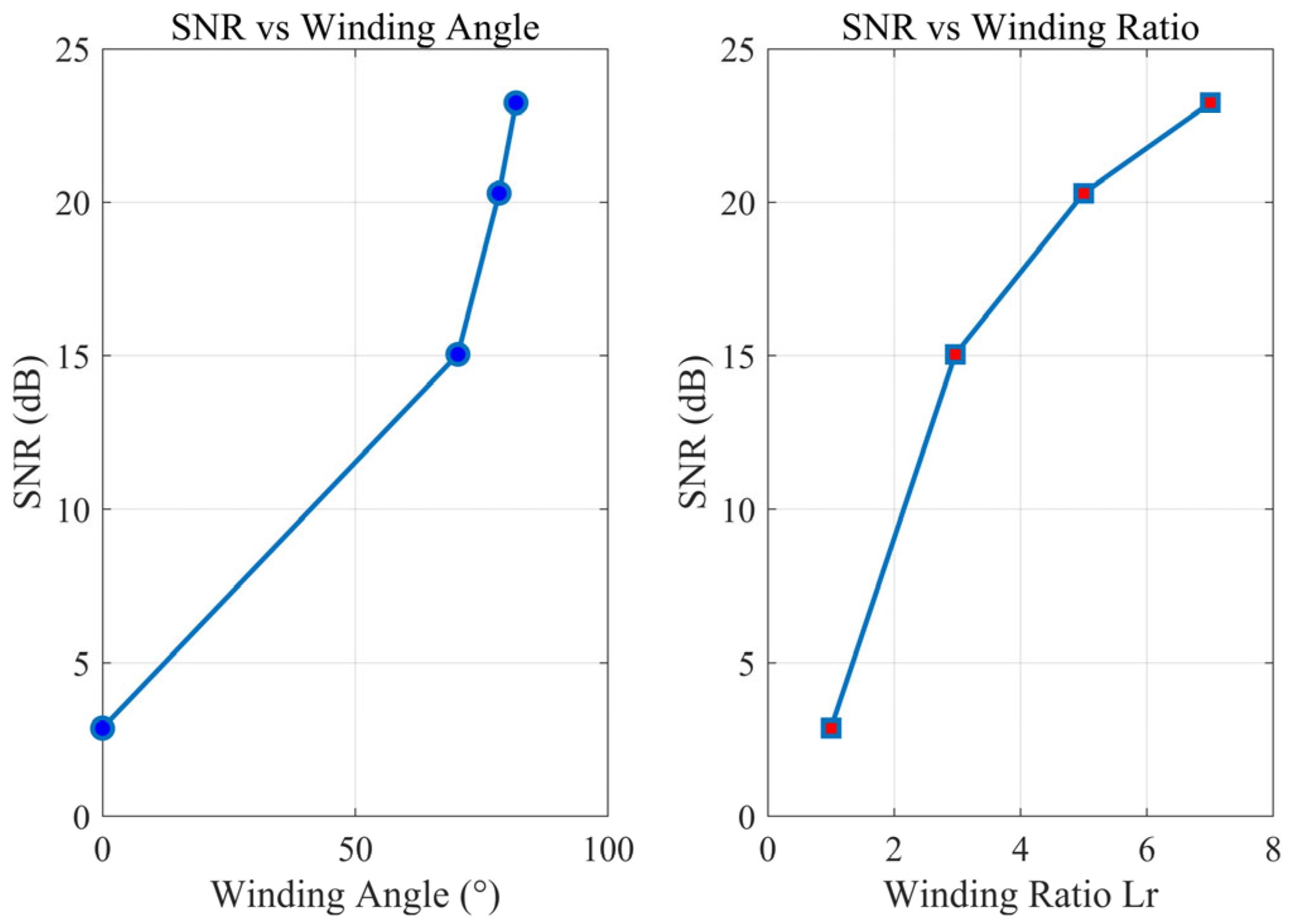

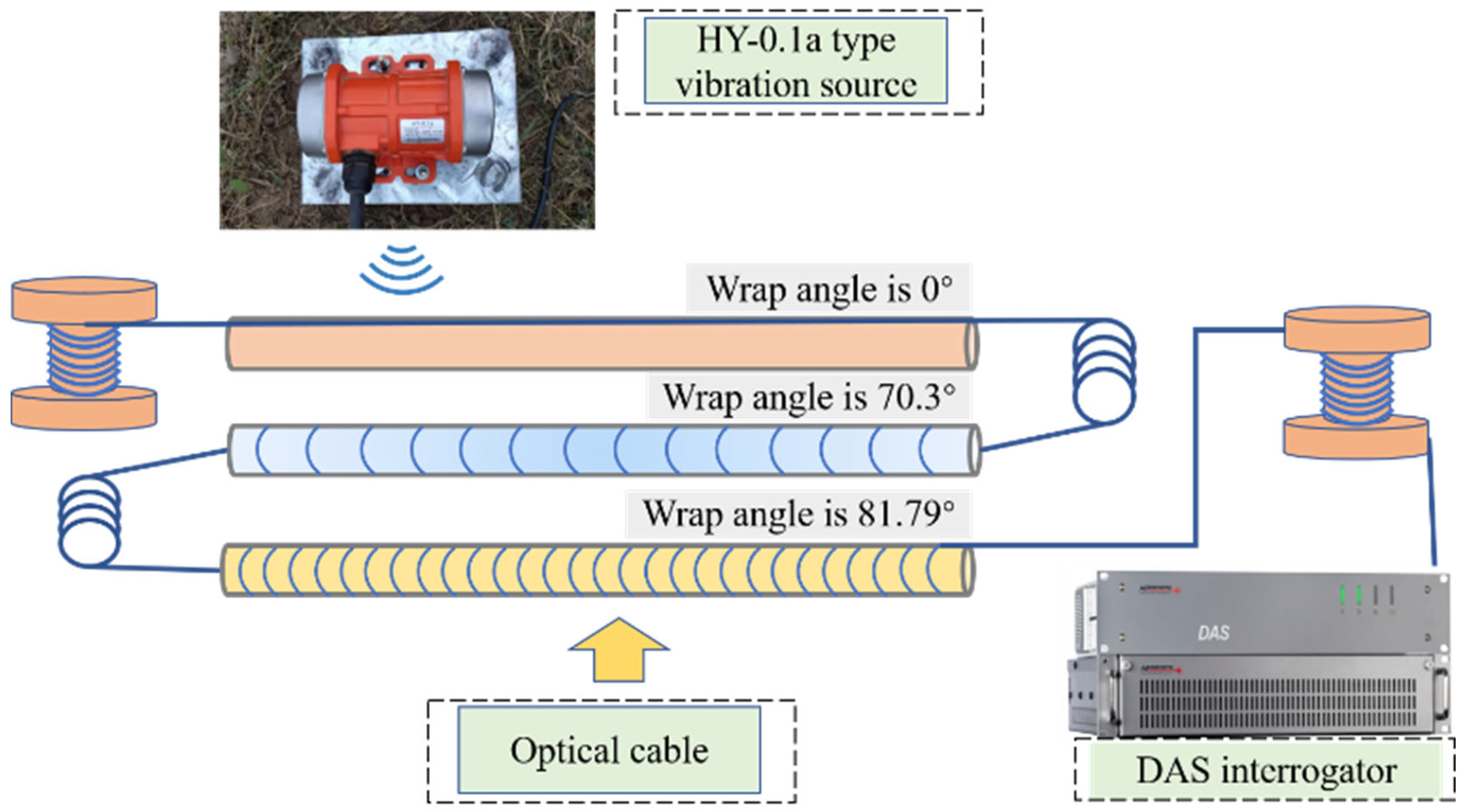

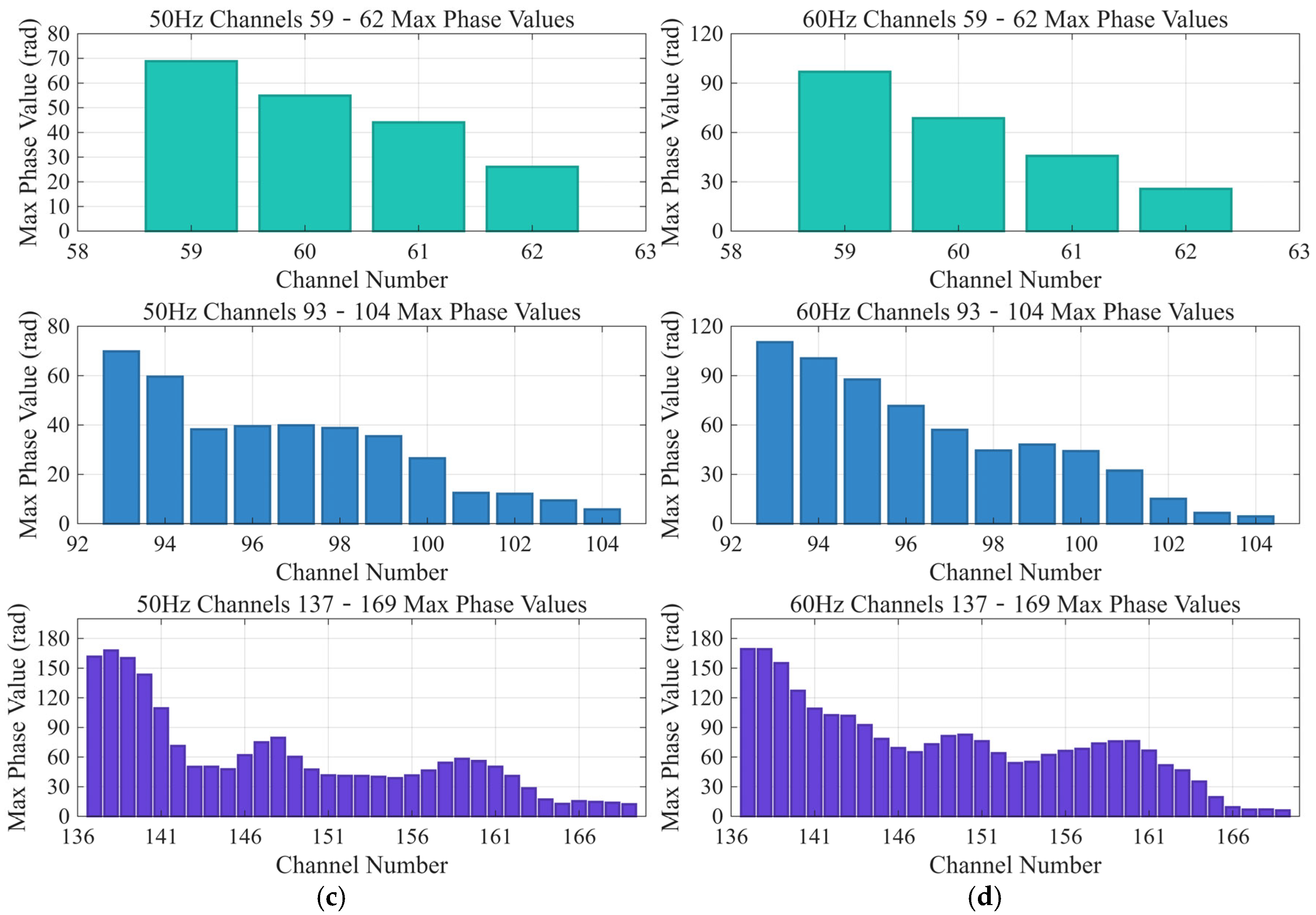
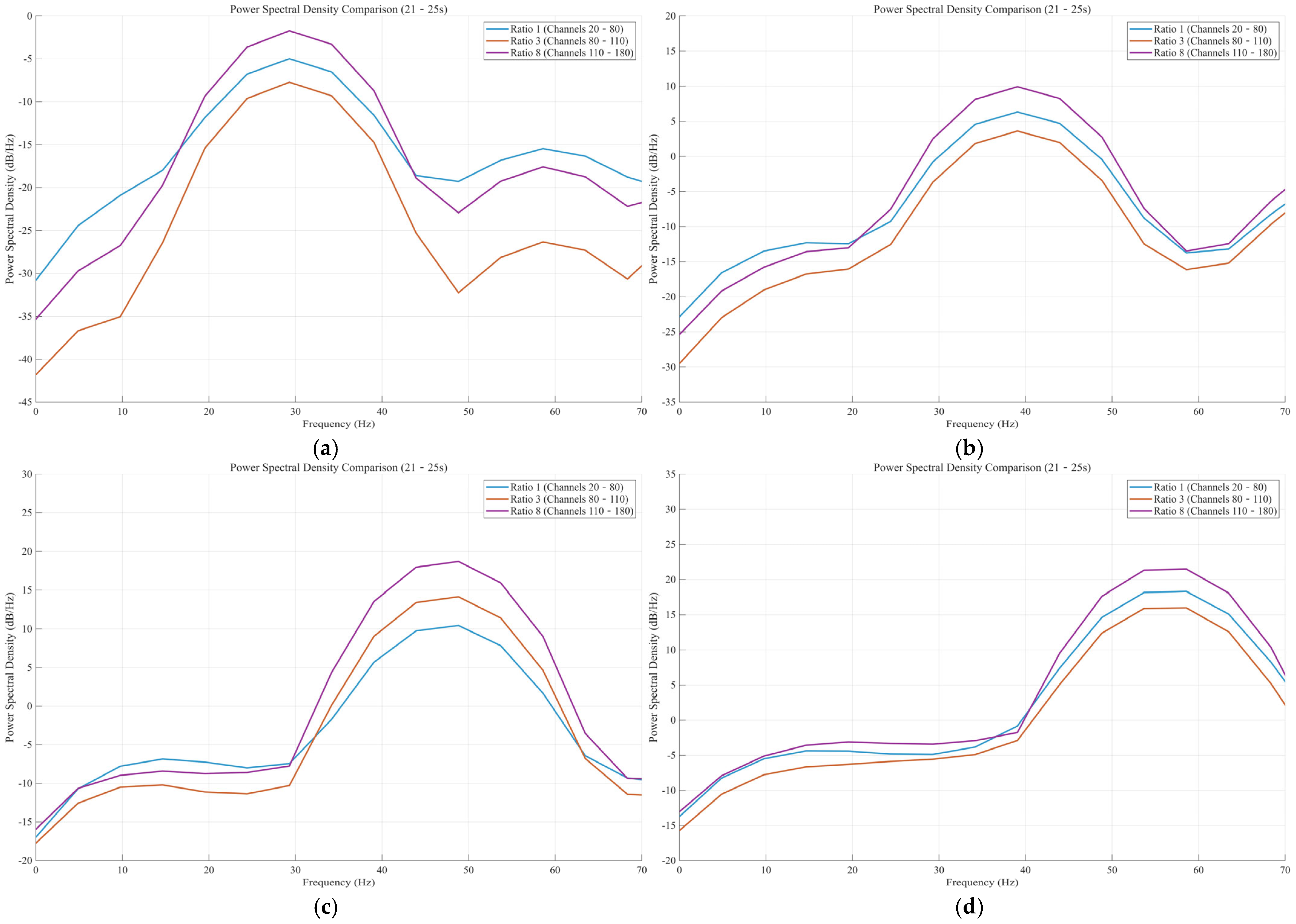

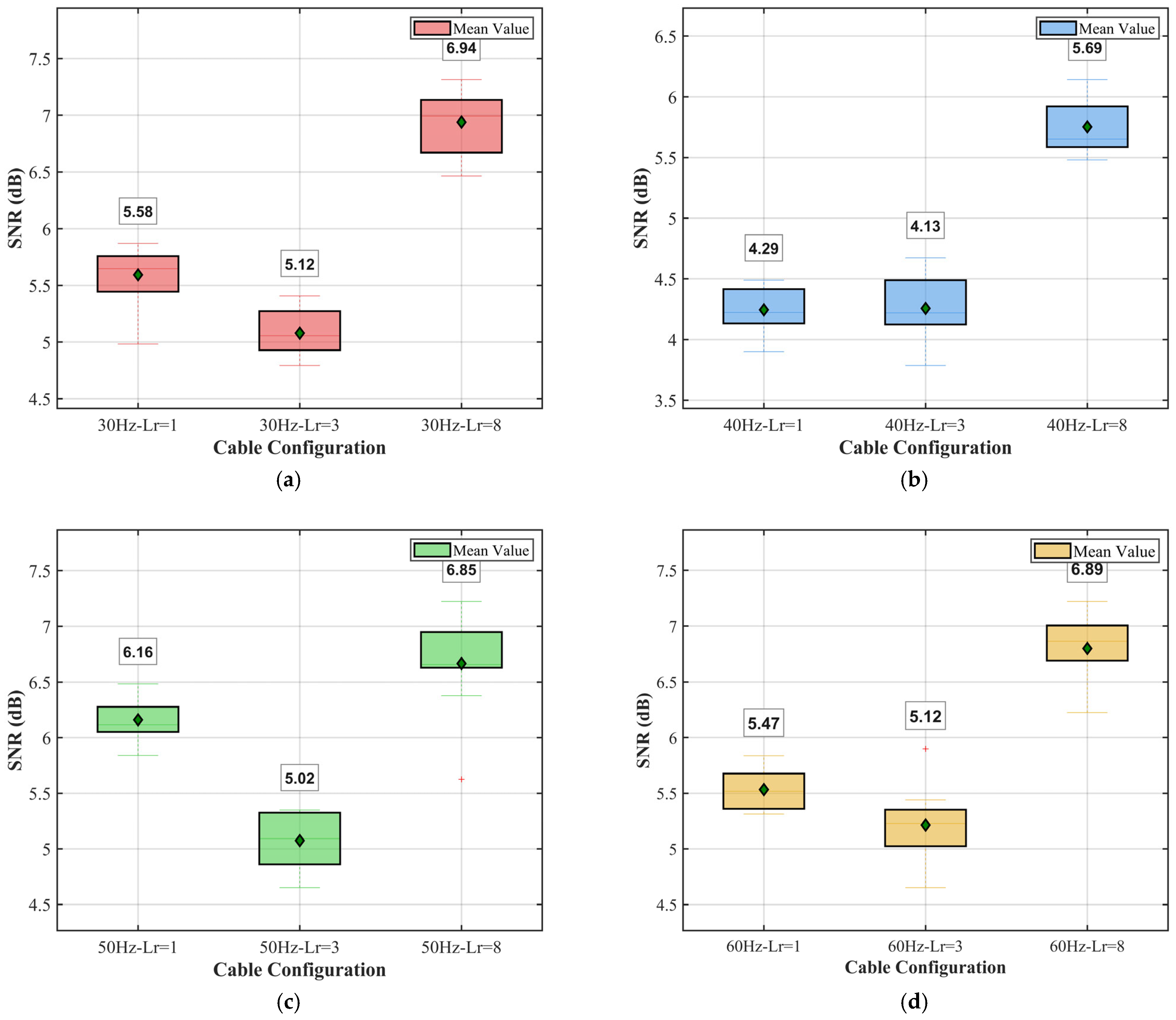
| Winding Angle | Winding Ratio | SNR(dB) | Maximum Phase Amplitude (rad) |
|---|---|---|---|
| 0° | 1 | 2.87 | 1.071 |
| 70.3° | 3 | 15.04 | 3.238 |
| 78.46° | 5 | 20.30 | 9.581 |
| 81.79° | 7 | 23.23 | 12.849 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Y.; Du, S.; Chen, T.; Guo, C.; Wu, S.; Liang, L. Quantitative Analysis of Phase Response Enhancement in Distributed Acoustic Sensing Systems Using Helical Fiber Winding Technology. Sensors 2025, 25, 7289. https://doi.org/10.3390/s25237289
Duan Y, Du S, Chen T, Guo C, Wu S, Liang L. Quantitative Analysis of Phase Response Enhancement in Distributed Acoustic Sensing Systems Using Helical Fiber Winding Technology. Sensors. 2025; 25(23):7289. https://doi.org/10.3390/s25237289
Chicago/Turabian StyleDuan, Yuxing, Shangming Du, Tianwei Chen, Can Guo, Song Wu, and Lei Liang. 2025. "Quantitative Analysis of Phase Response Enhancement in Distributed Acoustic Sensing Systems Using Helical Fiber Winding Technology" Sensors 25, no. 23: 7289. https://doi.org/10.3390/s25237289
APA StyleDuan, Y., Du, S., Chen, T., Guo, C., Wu, S., & Liang, L. (2025). Quantitative Analysis of Phase Response Enhancement in Distributed Acoustic Sensing Systems Using Helical Fiber Winding Technology. Sensors, 25(23), 7289. https://doi.org/10.3390/s25237289





