Low-Latency Marine-Based OTFS Echo Parameter Estimation Enabled by AI
Abstract
1. Introduction
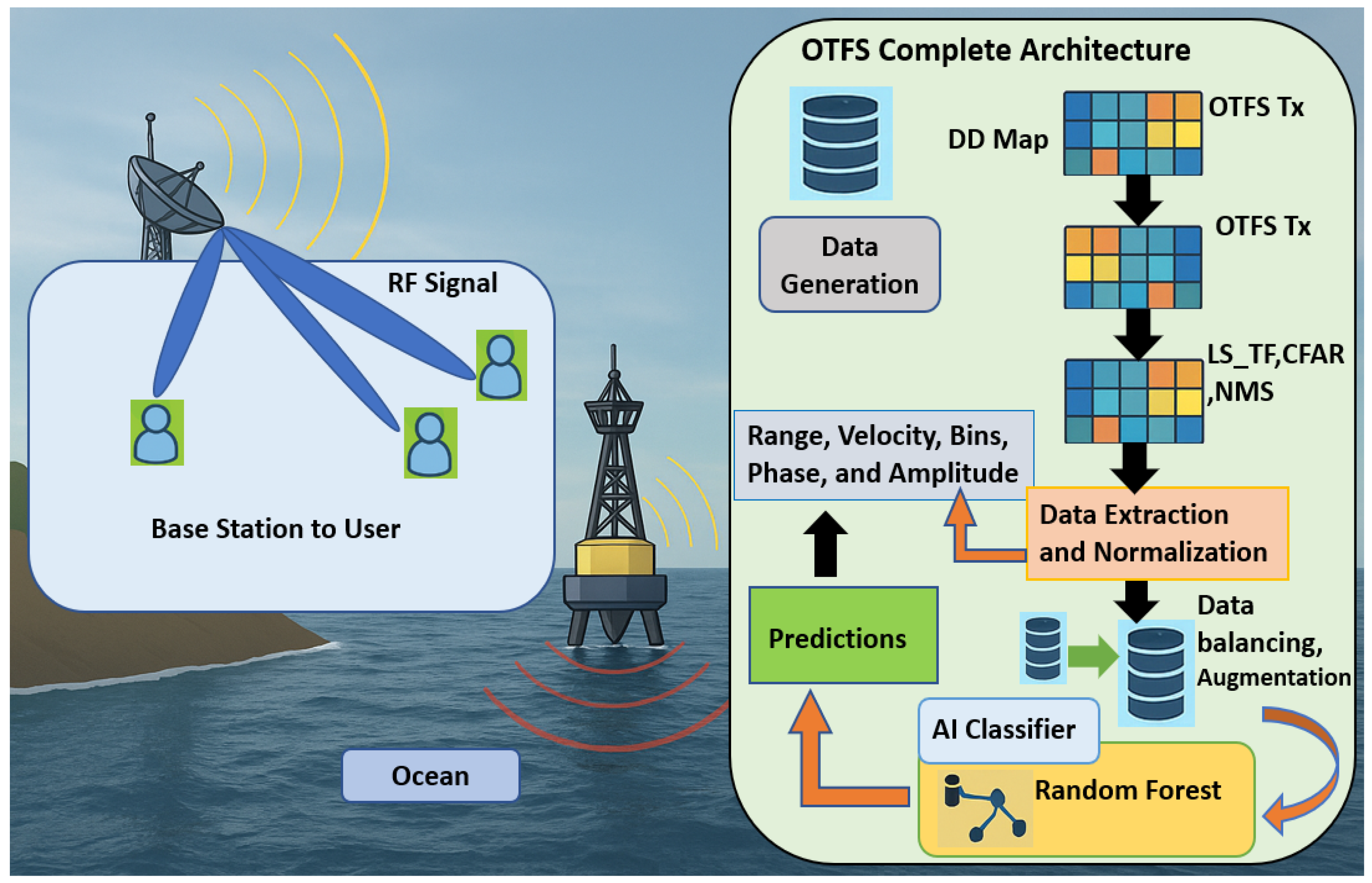
2. Marine OTFS Transmitter/Reception
2.1. Marine OTFS Transmitter
2.2. Marine OTFS Receiver
3. Parameter Extraction
4. Ai Implementation
4.1. Patch and Label Preparation
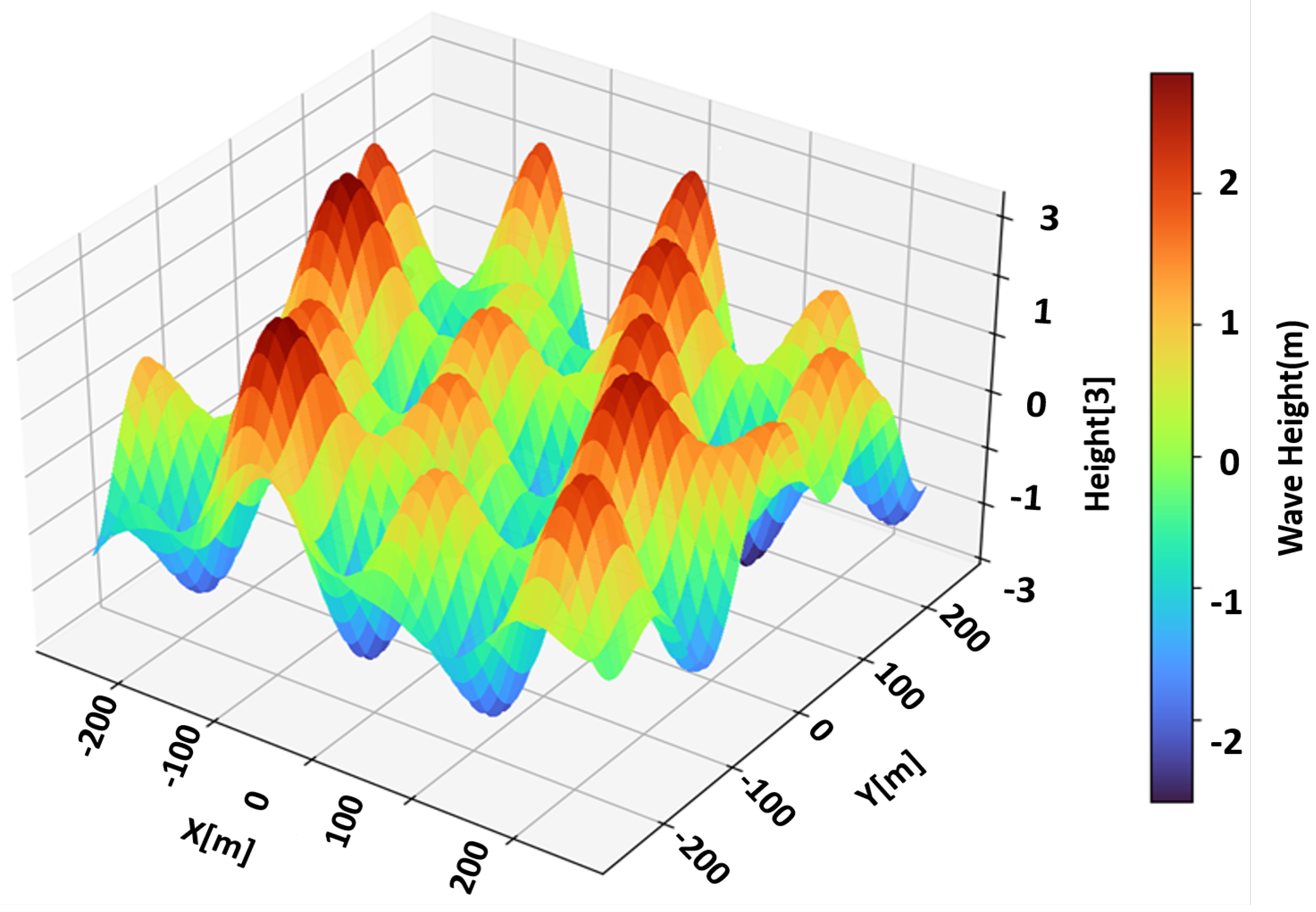
4.2. Dataset Generation and Scene Configuration
4.3. System Architecture
4.4. Balanced and Oversampling
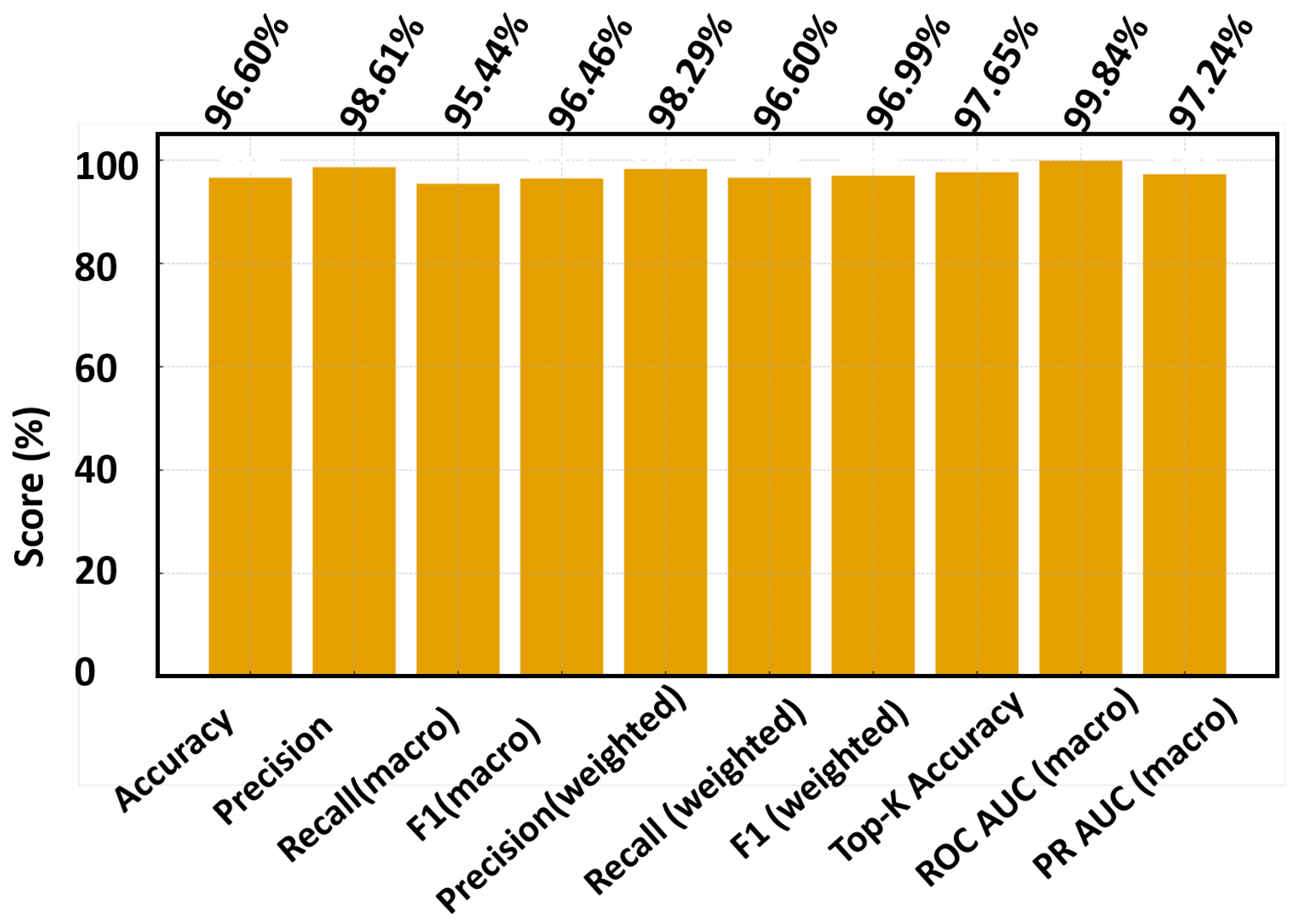
4.5. Fast Random-Forest Baseline
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.J.; Molisch, A.F.; Calderbank, R. Orthogonal time frequency space modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Bharatula, G.; Hadani, R.; Hanzo, L. Orthogonal time-frequency space modulation: A promising next-generation waveform. IEEE Wirel. Commun. 2021, 28, 136–144. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Li, S.; Yuan, J.; Ng, D.W.K. Integrated sensing and communication-assisted orthogonal time frequency space transmission for vehicular networks. IEEE J. Sel. Top. Signal Process. 2021, 15, 1515–1528. [Google Scholar] [CrossRef]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Orthogonal time frequency space (OTFS) modulation based radar system. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Li, S.; Yuan, W.; Liu, C.; Wei, Z.; Yuan, J.; Bai, B.; Ng, D.W.K. A novel ISAC transmission framework based on spatially-spread orthogonal time frequency space modulation. IEEE J. Sel. Areas Commun. 2020, 40, 1854–1872. [Google Scholar] [CrossRef]
- Gaudio, L.; Kobayashi, M.; Caire, G.; Colavolpe, G. On the effectiveness of OTFS for joint radar parameter estimation and communication. IEEE Trans. Wirel. Commun. 2020, 19, 5951–5965. [Google Scholar] [CrossRef]
- Hooli, K.; Juntti, M.; Latva-Aho, M. Inter-path interference suppression in WCDMA systems with low spreading factors. In Gateway to 21st Century Communications Village. VTC 1999-Fall. IEEE VTS 50th Vehicular Technology Conference (Cat. No. 99CH36324), Amsterdam, The Netherlands, 19–22 September 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 421–425. [Google Scholar]
- Ramachandran, M.K.; Chockalingam, A. MIMO-OTFS in high-Doppler fading channels: Signal detection and channel estimation. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 206–212. [Google Scholar]
- Raviteja, P.; Phan, K.T.; Hong, Y. Embedded pilot-aided channel estimation for OTFS in delay–Doppler channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, Z.; Guo, Q.; Wang, Z.; Sun, P. Message passing-based structured sparse signal recovery for estimation of OTFS channels with fractional Doppler shifts. IEEE Trans. Wirel. Commun. 2021, 20, 7773–7785. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Ng, D.W.K. Off-grid channel estimation with sparse Bayesian learning for OTFS systems. IEEE Trans. Wirel. Commun. 2022, 21, 7407–7426. [Google Scholar] [CrossRef]
- Khan, I.A.; Mohammed, S.K. Low complexity channel estimation for OTFS modulation with fractional delay and Doppler. arXiv 2021, arXiv:2111.06009. [Google Scholar] [CrossRef]
- Raviteja, P.; Hong, Y.; Viterbo, E.; Biglieri, E. Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS. IEEE Trans. Veh. Technol. 2018, 68, 957–961. [Google Scholar] [CrossRef]
- Thaj, T.; Viterbo, E.; Hong, Y. Orthogonal time sequency multiplexing modulation: Analysis and low-complexity receiver design. IEEE Trans. Wirel. Commun. 2021, 20, 7842–7855. [Google Scholar] [CrossRef]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference cancellation and iterative detection for orthogonal time frequency space modulation. IEEE Trans. Wirel. Commun. 2018, 17, 6501–6515. [Google Scholar] [CrossRef]
- Hong, Y.; Thaj, T.; Viterbo, E. Delay-Doppler Communications: Principles and Applications; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Wild, T.; Braun, V.; Viswanathan, H. Joint design of communication and sensing for beyond 5G and 6G systems. IEEE Access 2021, 9, 30845–30857. [Google Scholar] [CrossRef]
- Qi, Q.; Chen, X.; Khalili, A.; Zhong, C.; Zhang, Z.; Ng, D.W.K. Integrating sensing, computing, and communication in 6G wireless networks: Design and optimization. IEEE Trans. Commun. 2022, 70, 6212–6227. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Di, B.; Di Renzo, M.; Han, Z.; Poor, H.V.; Song, L. Holographic integrated sensing and communication. IEEE J. Sel. Areas Commun. 2022, 40, 2114–2130. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple Signal Classification (MUSIC); ESL Technical Memo TM 1098; ESL: Cologne, Germany, 1979. [Google Scholar]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 2002, 37, 984–995. [Google Scholar] [CrossRef]
- Sturm, C.; Wiesbeck, W. Waveform design and signal processing aspects for fusion of wireless communications and radar sensing. Proc. IEEE 2011, 99, 1236–1259. [Google Scholar] [CrossRef]
- Zeng, Y.; Ma, Y.; Sun, S. Joint radar-communication with cyclic prefixed single carrier waveforms. IEEE Trans. Veh. Technol. 2020, 69, 4069–4079. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, J.A.; Huang, X.; Guo, Y.J. Integrating low-complexity and flexible sensing into communication systems. IEEE J. Sel. Areas Commun. 2022, 40, 1873–1889. [Google Scholar] [CrossRef]
- Gong, Z.; Liu, S.; Li, L.; Huang, Y.; Yuan, J. Super-resolution delay-Doppler estimation for OTFS radar. In Proceedings of the 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 28 May–1 June 2023; pp. 921–924. [Google Scholar]
- Nie, G.; Zhang, J.; Zhang, Y.; Yu, L.; Zhang, Z.; Sun, Y.; Tian, L.; Wang, Q.; Xia, L. A predictive 6G network with environment sensing enhancement: From radio wave propagation perspective. China Commun. 2022, 19, 105–122. [Google Scholar] [CrossRef]
- Hussain, K.; Ali, E.M.; Hussain, W.; Raza, A.; Elkamchouchi, D.H. Robust OTFS-ISAC for Vehicular-to-Base Station End-to-End Sensing and Communication. Electronics 2025, 1, 4340. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Z.; Chen, X.; Feng, Z. Coherent compensation-based sensing for long-range targets in integrated sensing and communication system. IEEE Trans. Veh. Technol. 2025, 6, 9134–9148. [Google Scholar] [CrossRef]
- Sim, Y.; Heo, J.; Jung, Y.; Lee, S.; Jung, Y. Design of Reconfigurable Radar Signal Processor for Frequency Modulated Continuous Wave Radar. IEEE Sens. J. 2025, 25, 11601–11612. [Google Scholar] [CrossRef]
- Xia, X.; Fang, Z.; Xu, K.; Xie, W. An Ambiguity Function Assisted Active Sensing Scheme for OFDM Based ISAC Systems Toward Low-Altitude Airspace. IEEE Internet Things J. 2025, 12, 19471–19487. [Google Scholar] [CrossRef]
- Ni, Y.; Yuan, P.; Huang, Q.; Liu, F.; Wang, Z. An integrated sensing and communications system based on affine frequency division multiplexing. IEEE Trans. Wirel. Commun. 2025, 24, 3763–3779. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, G.; Ye, Q.; Huang, Y.; Hu, S. Low-complexity joint azimuth-range-velocity estimation for integrated sensing and communication with OFDM waveform. IEEE Trans. Wirel. Commun. 2025, 24, 7517–7529. [Google Scholar] [CrossRef]
- Peng, L.; Yin, M.; Zou, D.; Yang, N.; Xiao, Y.; Li, F. Photonics-assisted integrated sensing and communication with ranging resolution improvement by multiple signal classification. Opt. Express 2024, 32, 34796–34806. [Google Scholar] [CrossRef]
- Zegrar, S.E.; Haif, H.; Arslan, H. OTFS-based ISAC for super-resolution range-velocity profile. IEEE Trans. Commun. 2024, 72, 3934–3946. [Google Scholar] [CrossRef]
- Yu, Z.; Ren, H.; Pan, C.; Zhou, G.; Wang, R.; Liu, M.; Wang, J. Addressing the mutual interference in uplink ISAC receivers: A projection method. IEEE Wirel. Commun. Lett. 2024, 13, 3109–3113. [Google Scholar] [CrossRef]

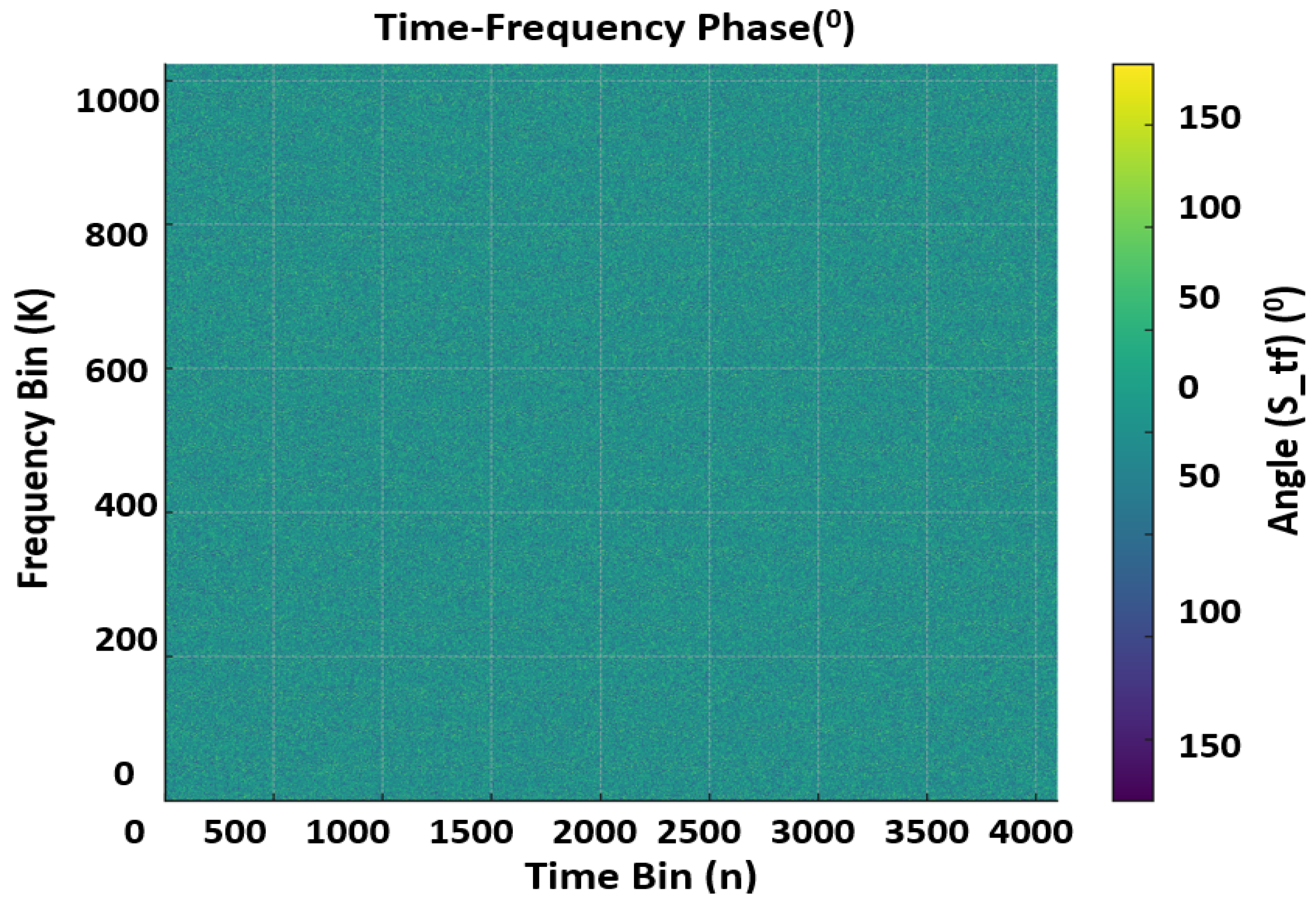
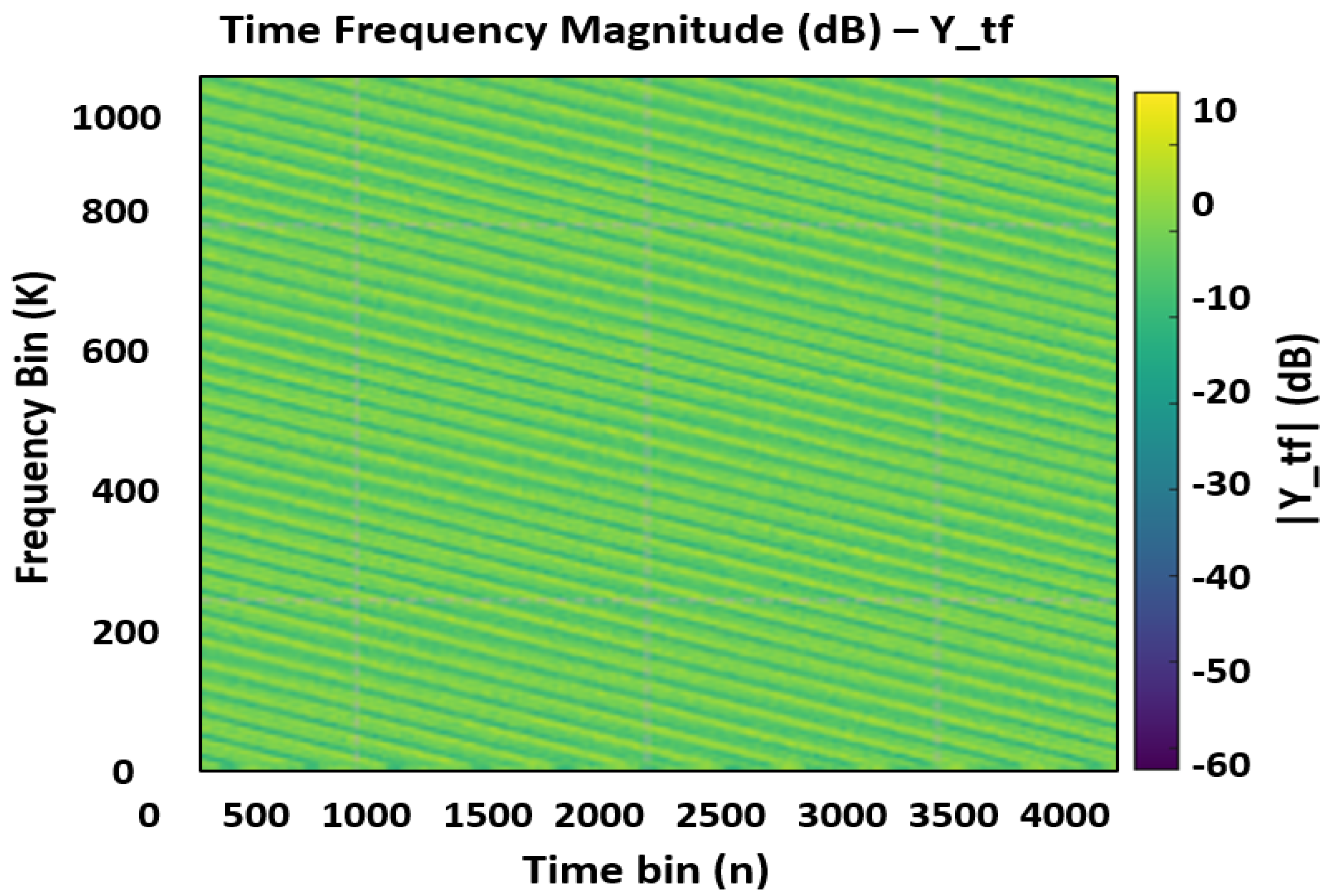
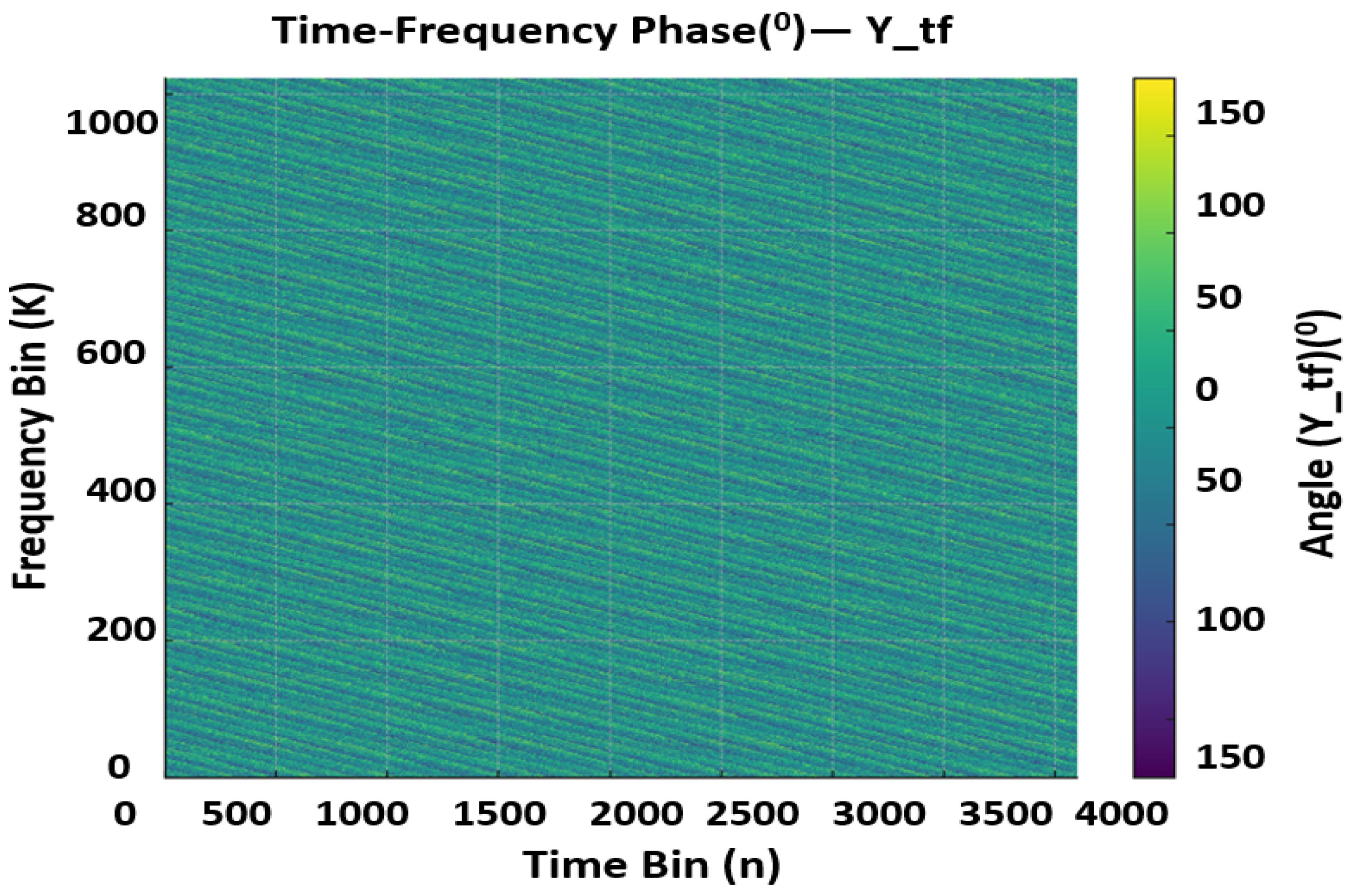
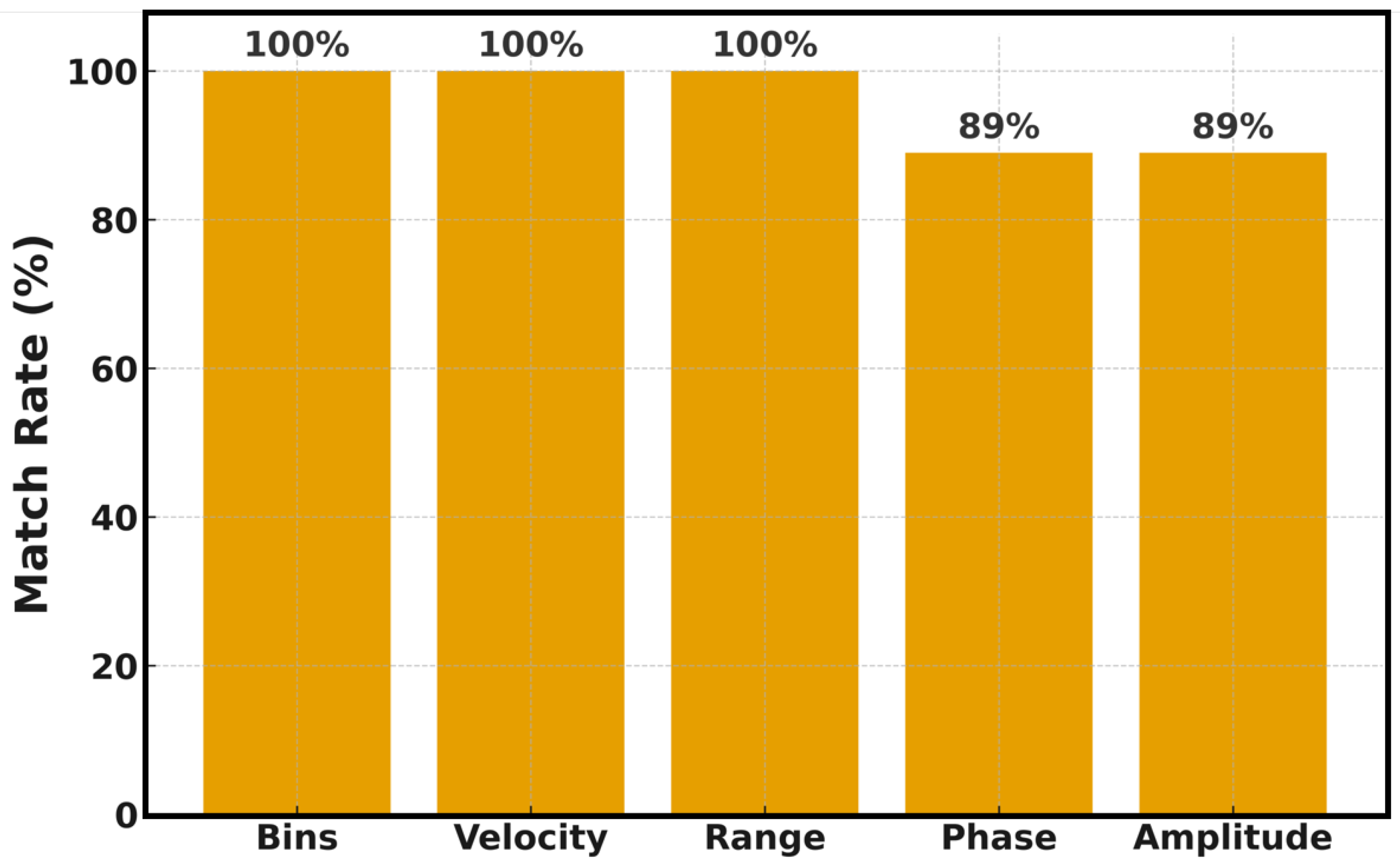
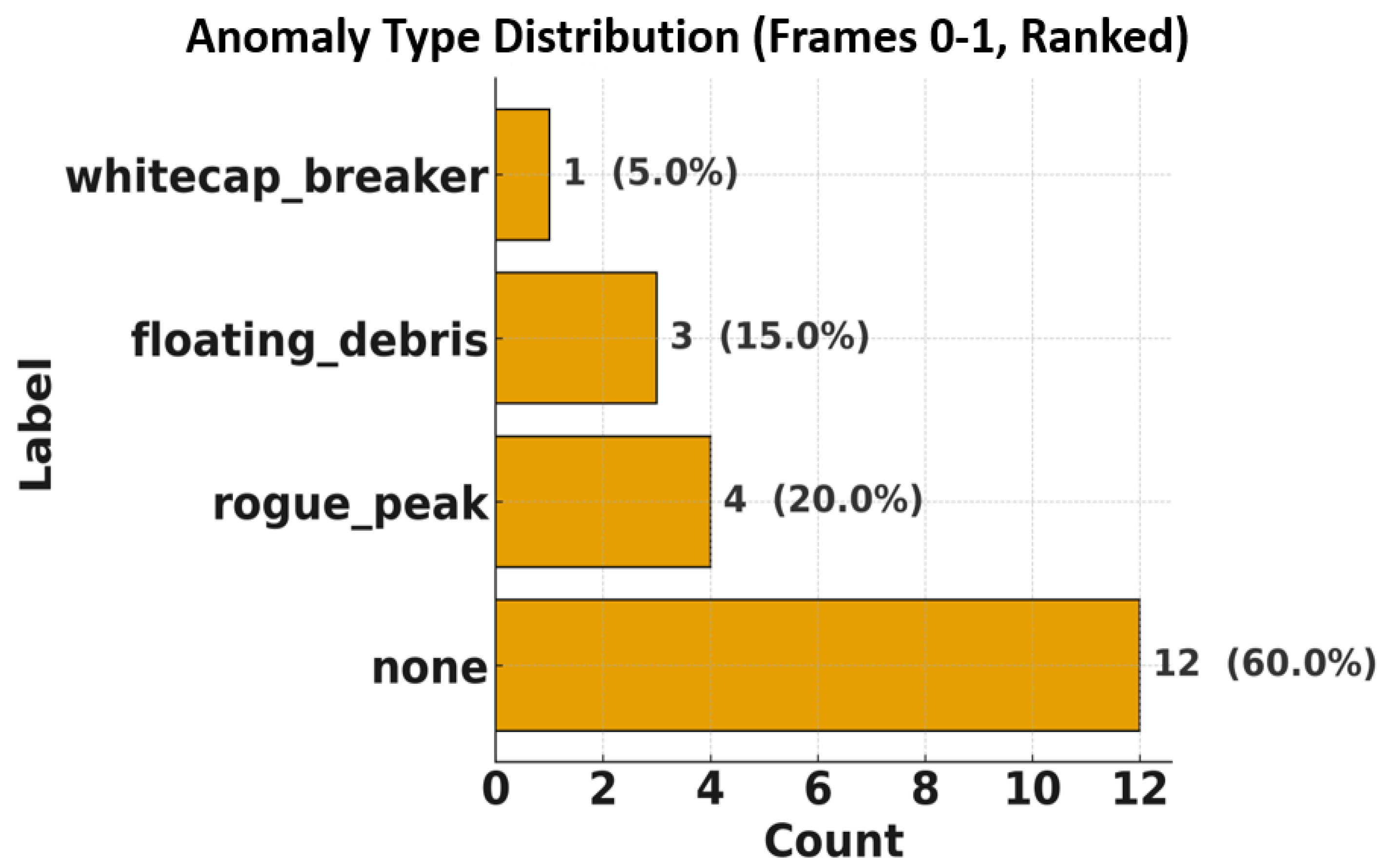
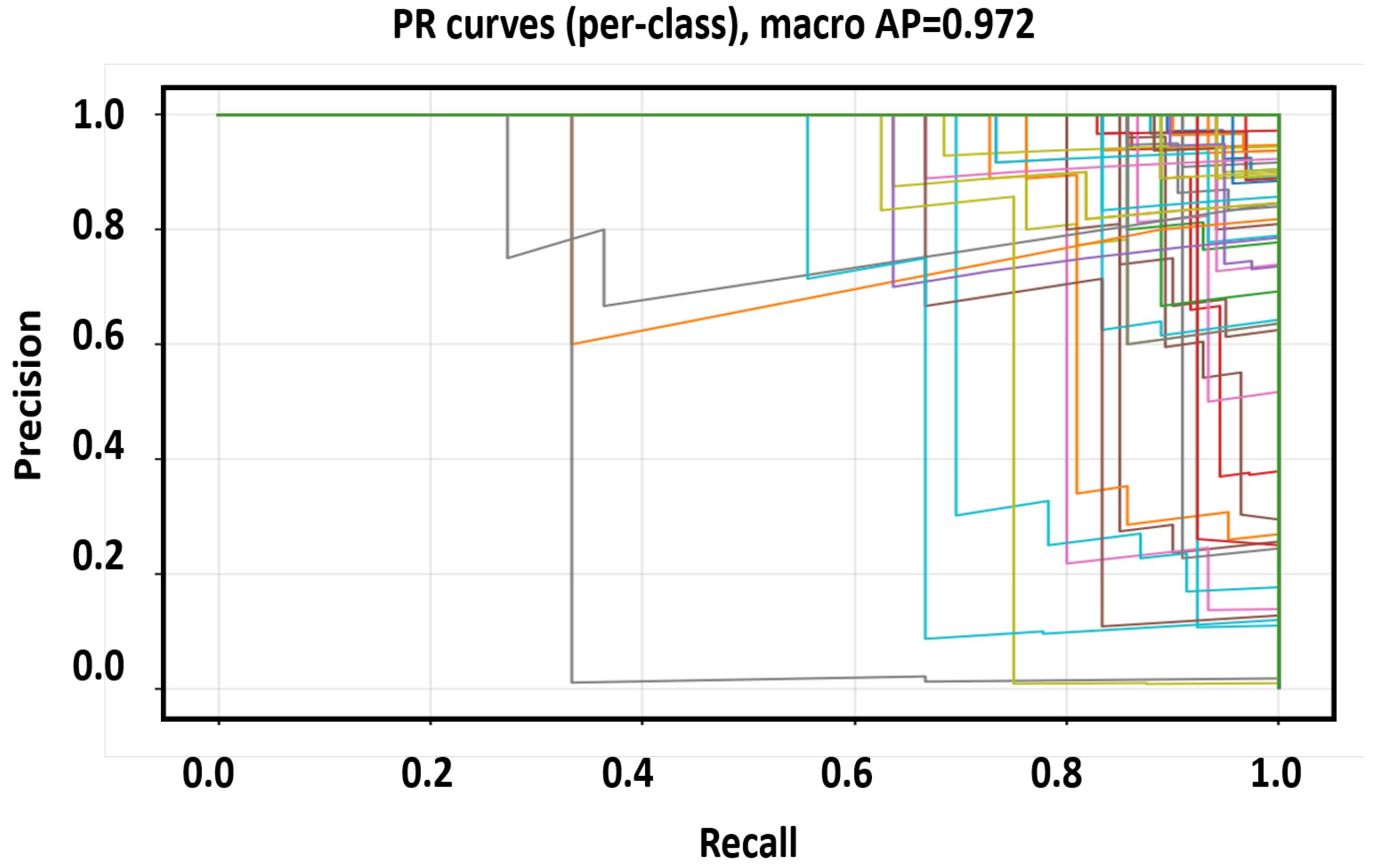
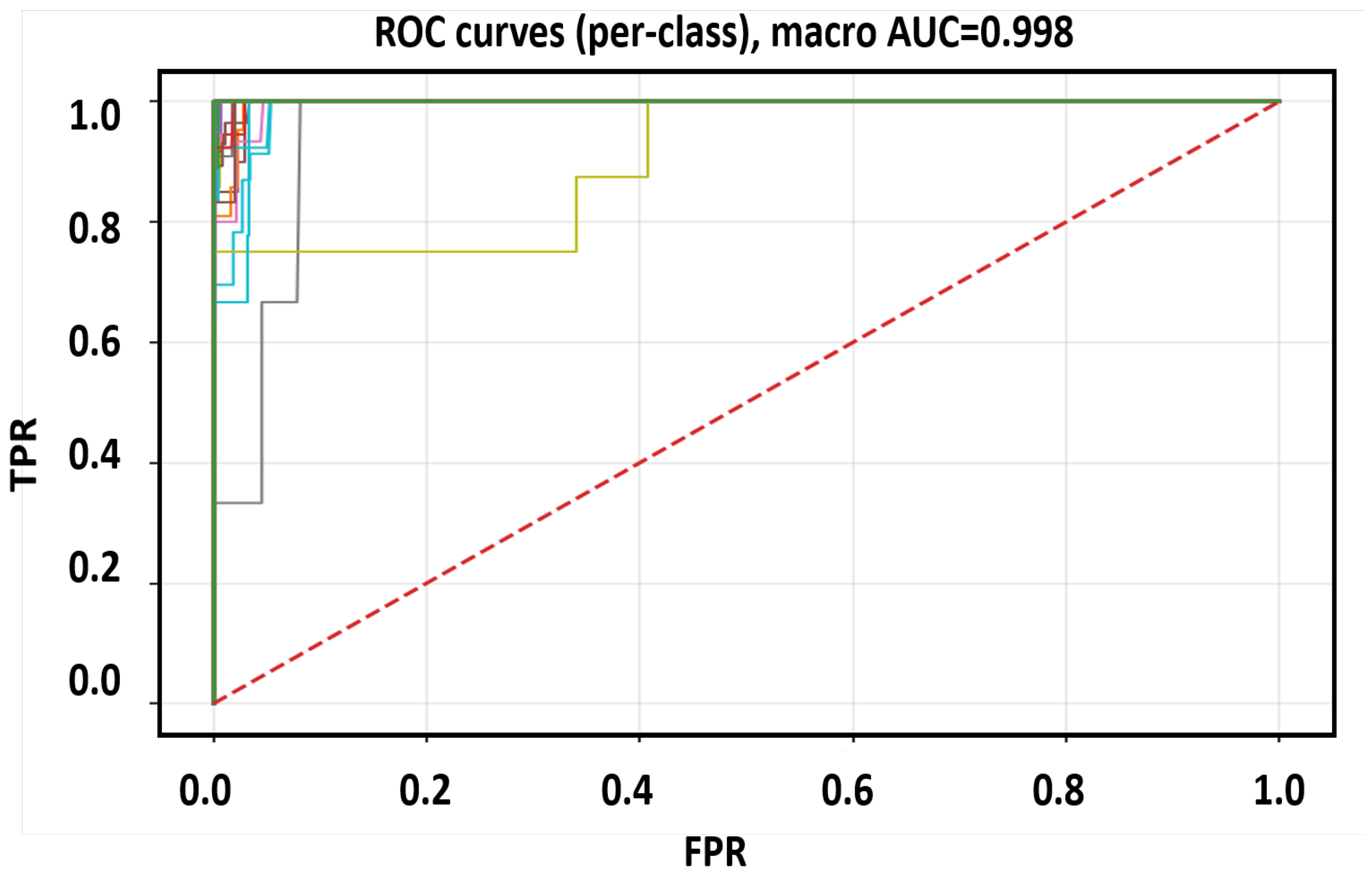
| Frame | [m] | [s] | [m/s] | Waves/Anoms | |
|---|---|---|---|---|---|
| 0 | 0.84 | 11.10 | 6.60 | 9.46 | 10/4 |
| 1 | 2.17 | 9.76 | 5.70 | 8.21 | 10/4 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 9 | 2.62 | 4.66 | 2.05 | 6.10 | 10/4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, K.; Yoo, J. Low-Latency Marine-Based OTFS Echo Parameter Estimation Enabled by AI. Sensors 2025, 25, 7104. https://doi.org/10.3390/s25237104
Hussain K, Yoo J. Low-Latency Marine-Based OTFS Echo Parameter Estimation Enabled by AI. Sensors. 2025; 25(23):7104. https://doi.org/10.3390/s25237104
Chicago/Turabian StyleHussain, Khurshid, and Jeseon Yoo. 2025. "Low-Latency Marine-Based OTFS Echo Parameter Estimation Enabled by AI" Sensors 25, no. 23: 7104. https://doi.org/10.3390/s25237104
APA StyleHussain, K., & Yoo, J. (2025). Low-Latency Marine-Based OTFS Echo Parameter Estimation Enabled by AI. Sensors, 25(23), 7104. https://doi.org/10.3390/s25237104








