Design and Evaluation of a Pneumatic-Actuated Active Balance Board for Sitting Postural Control
Abstract
1. Introduction
2. Materials and Methods
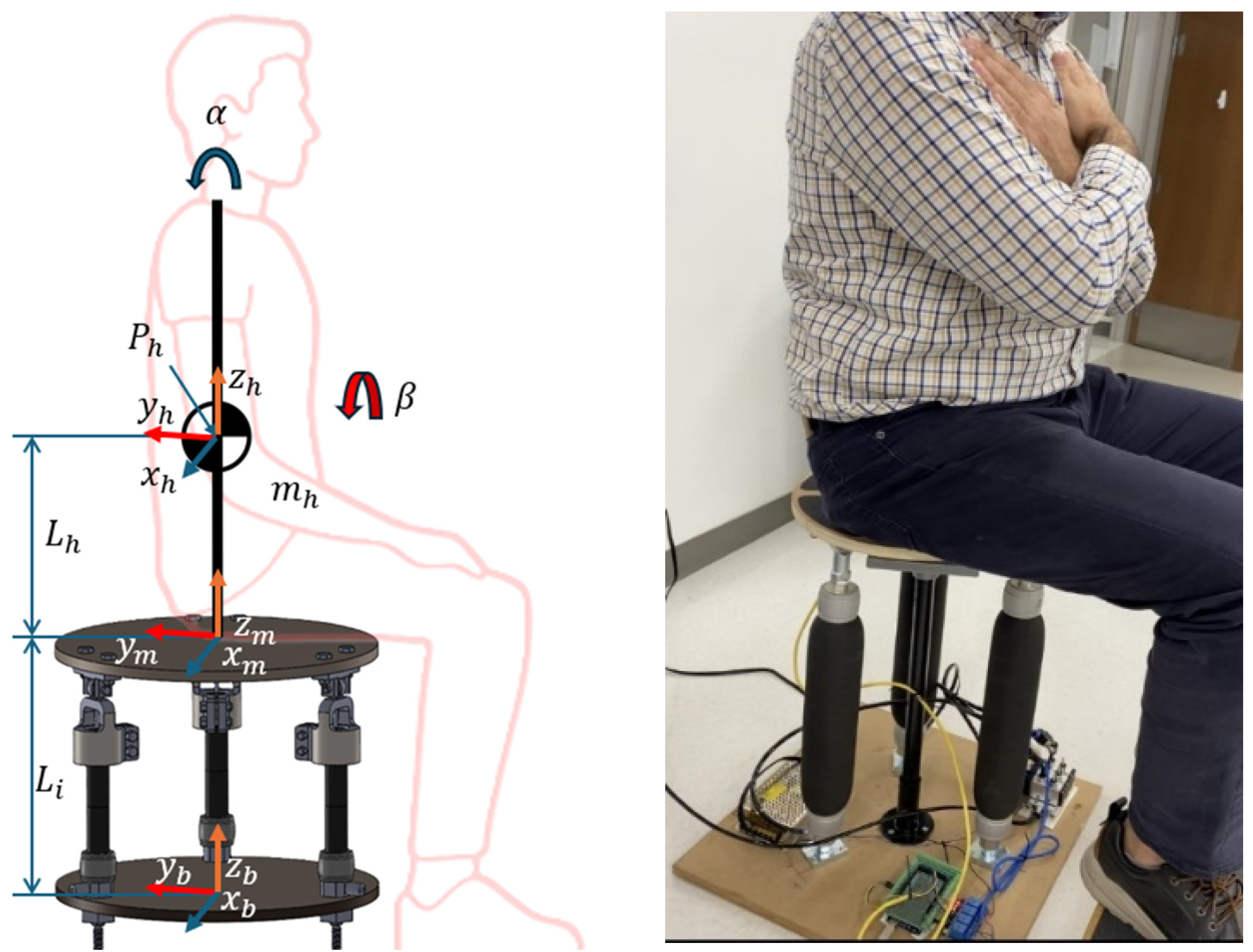
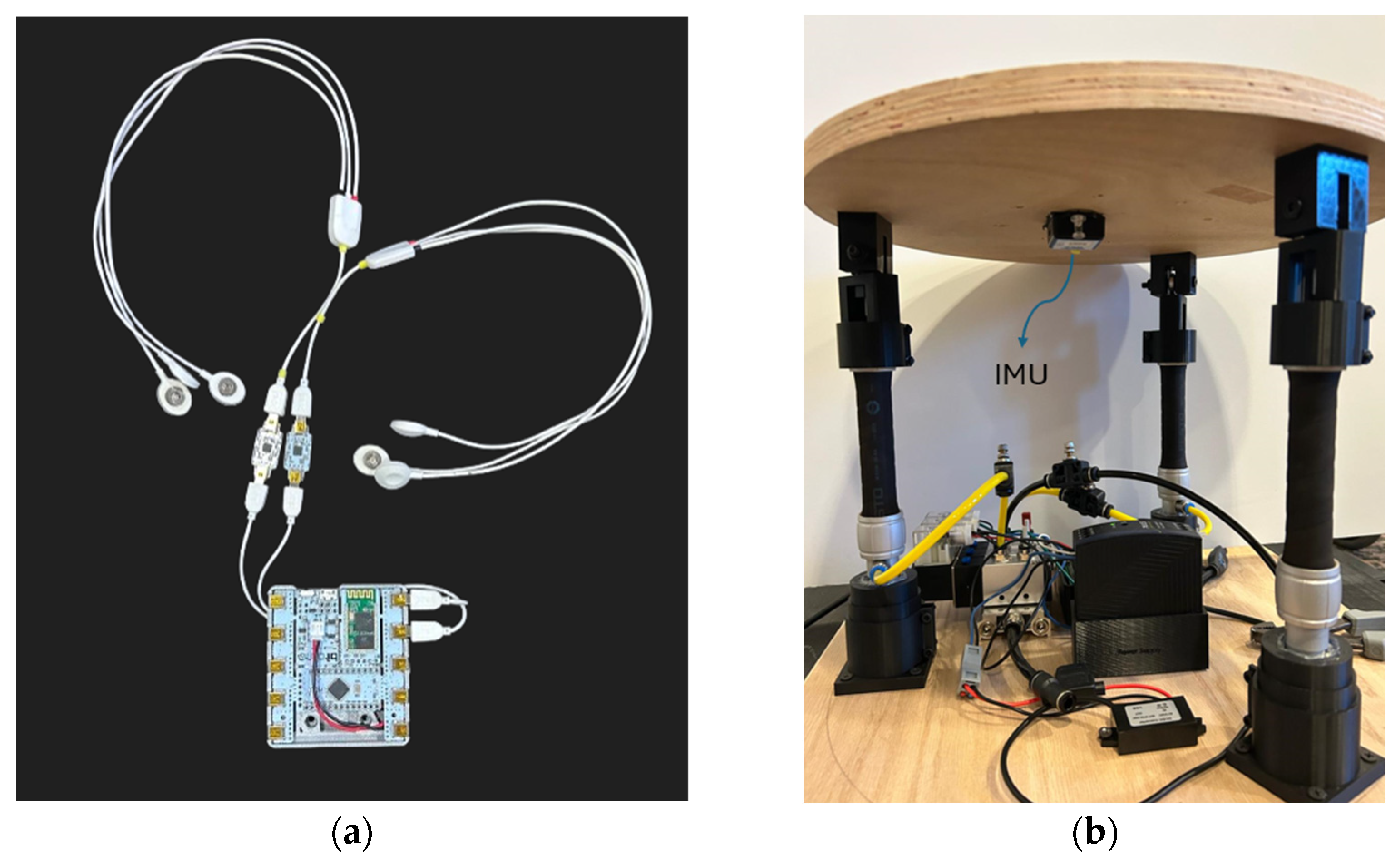
2.1. Experimental Protocol
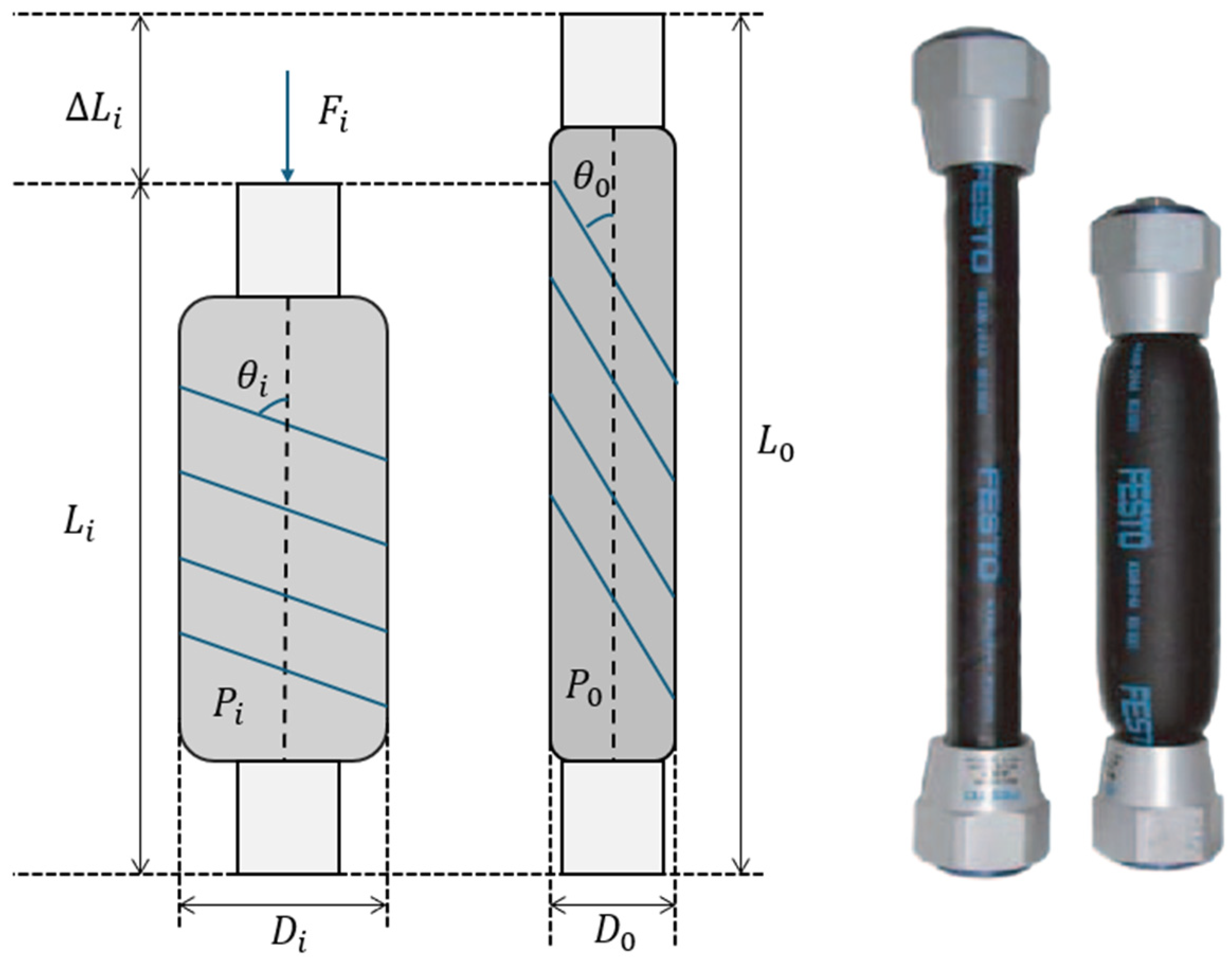
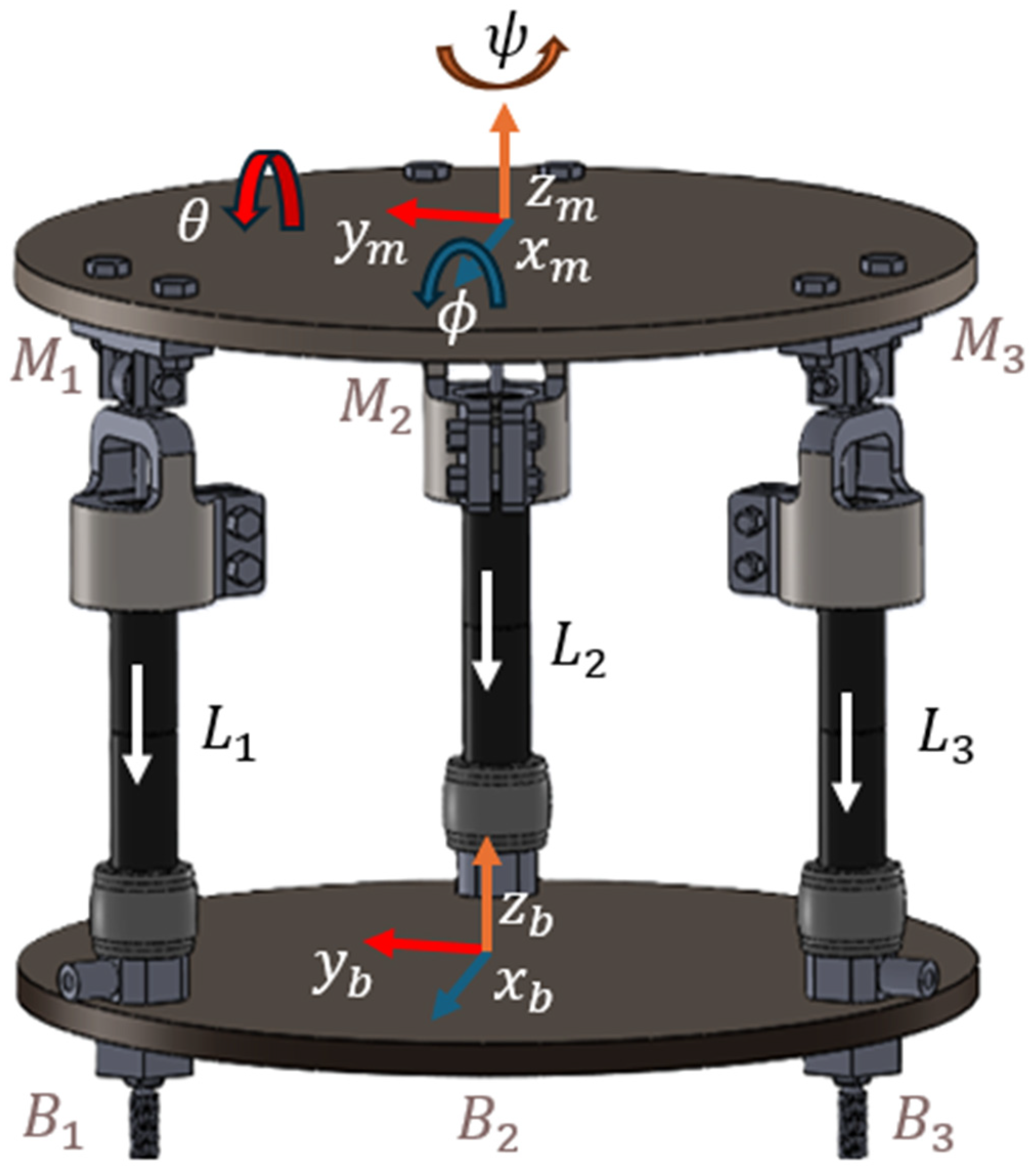
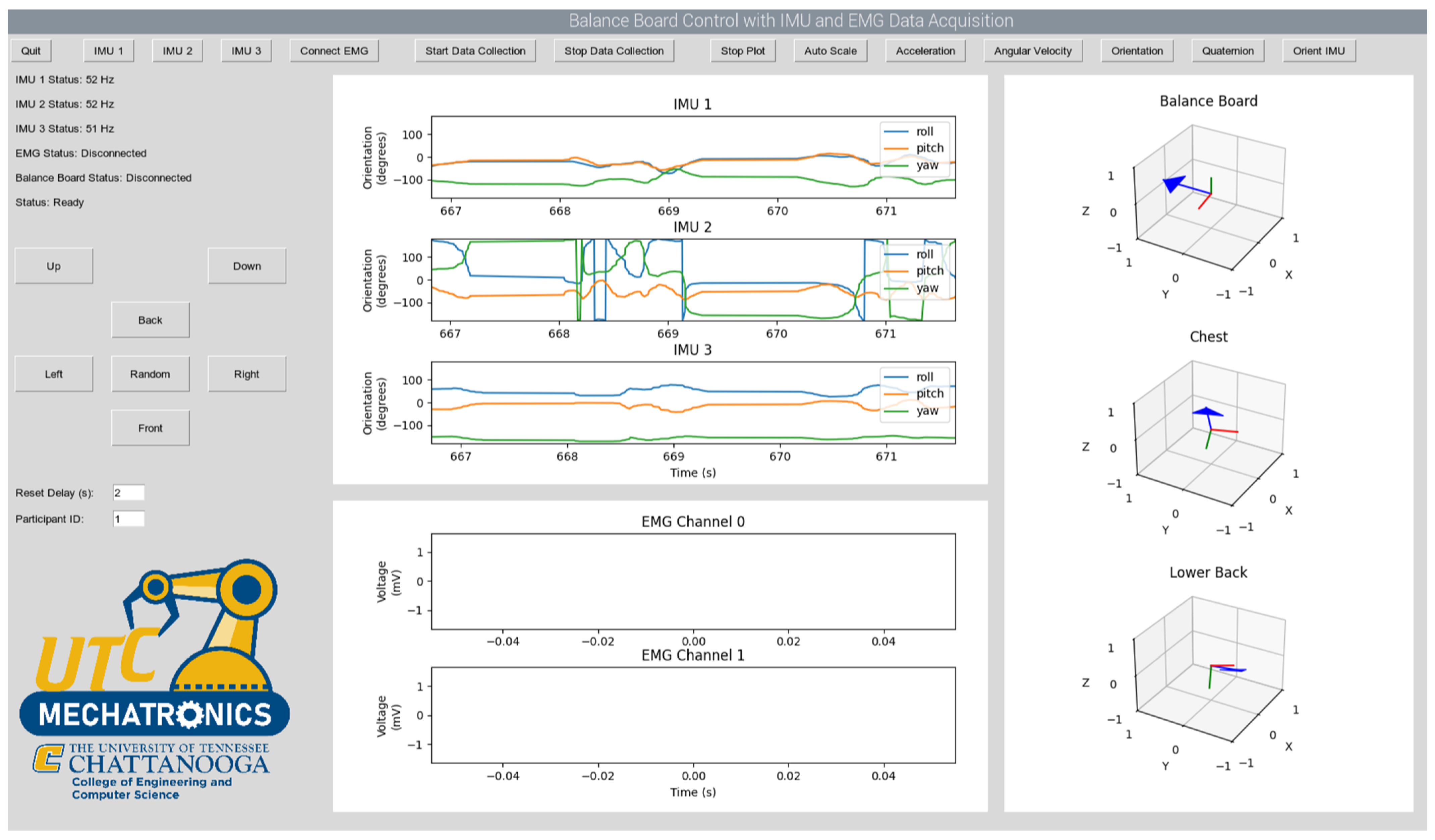
2.2. Pneumatic-Controlled Active Balance Board Design
3. Results
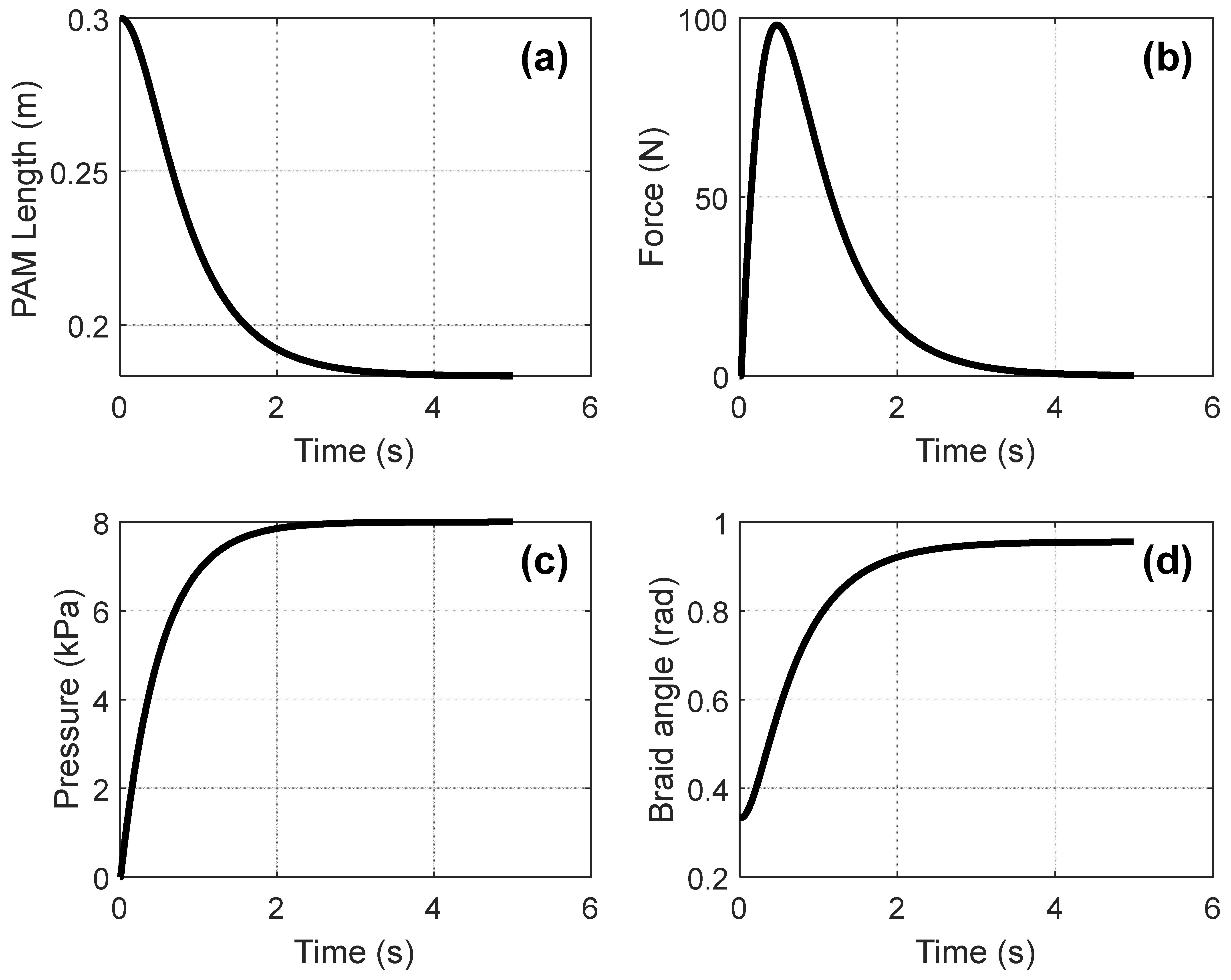
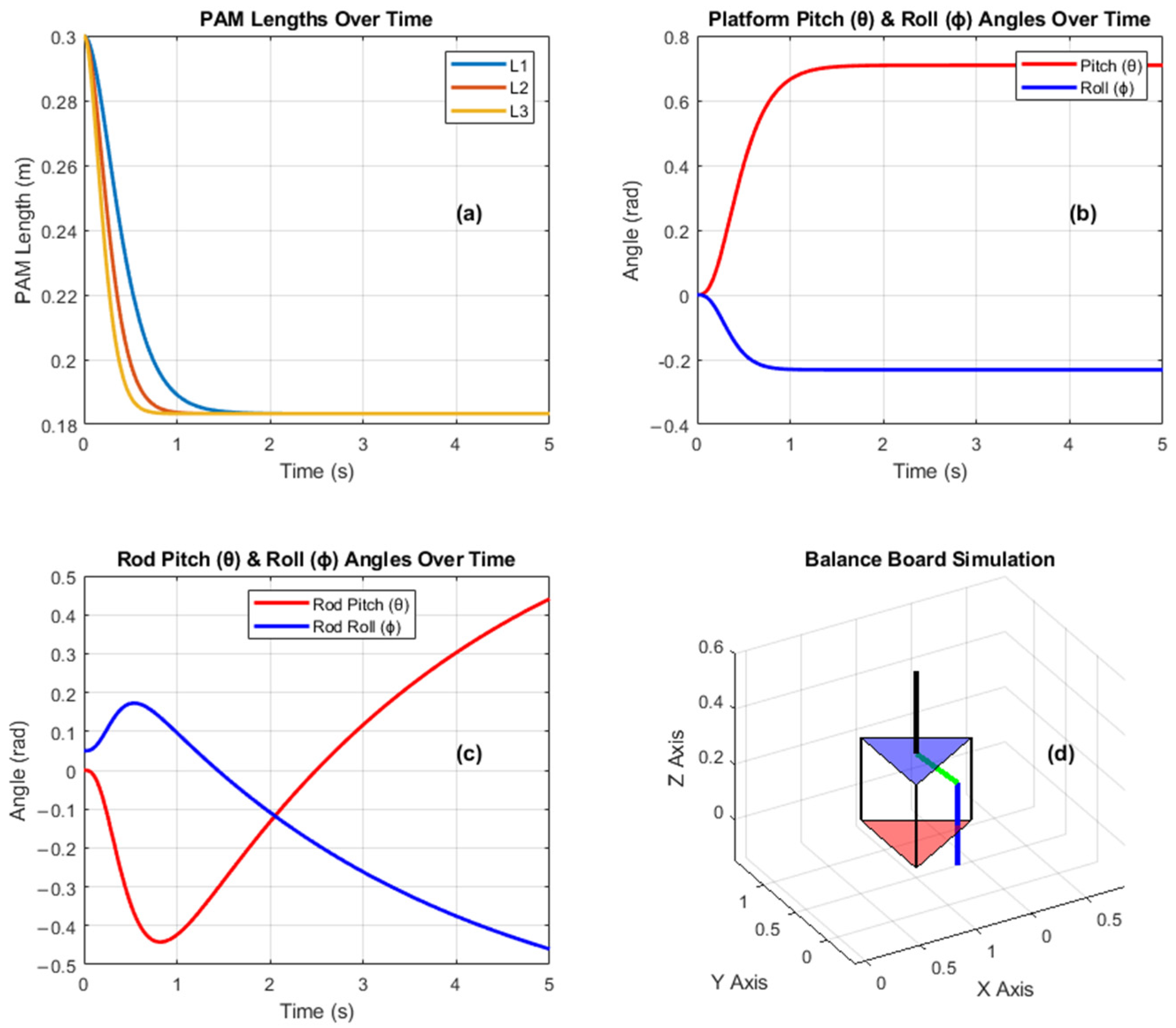
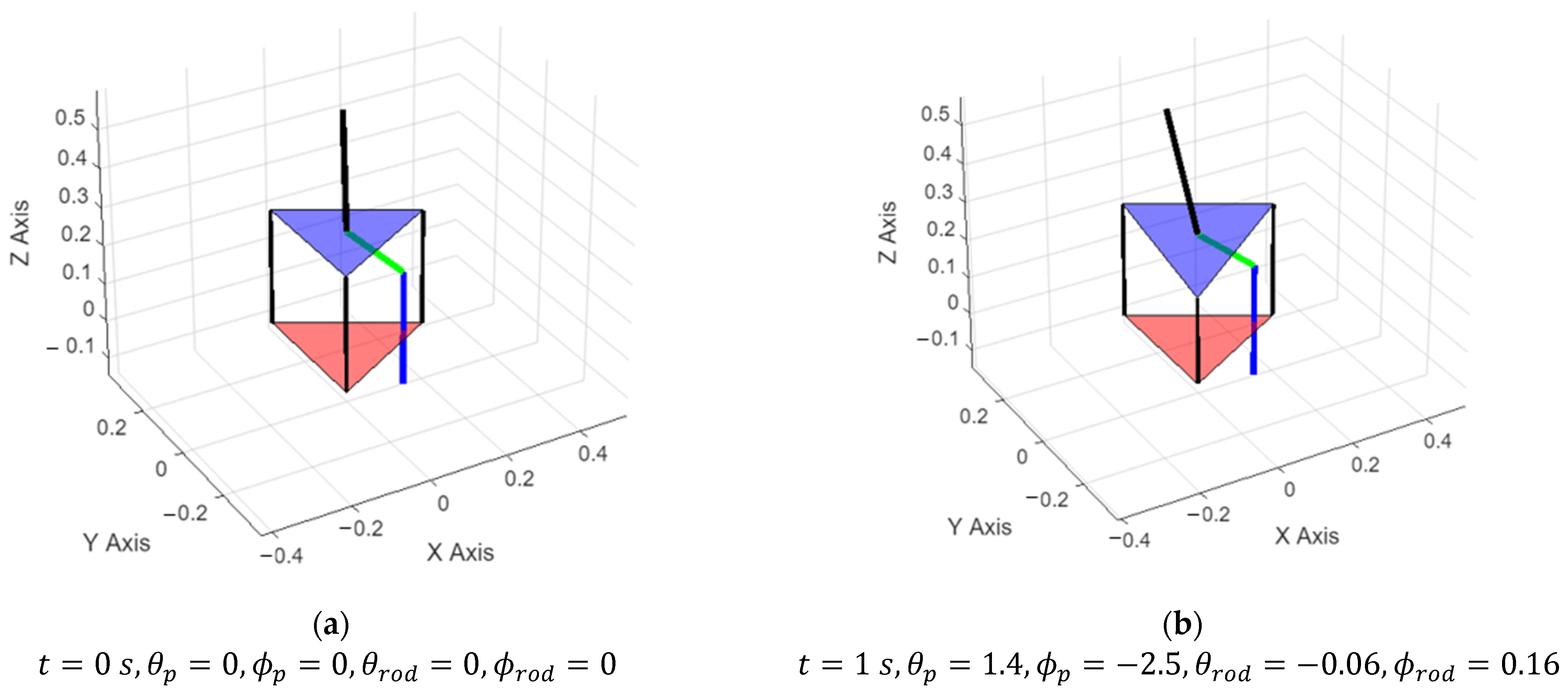
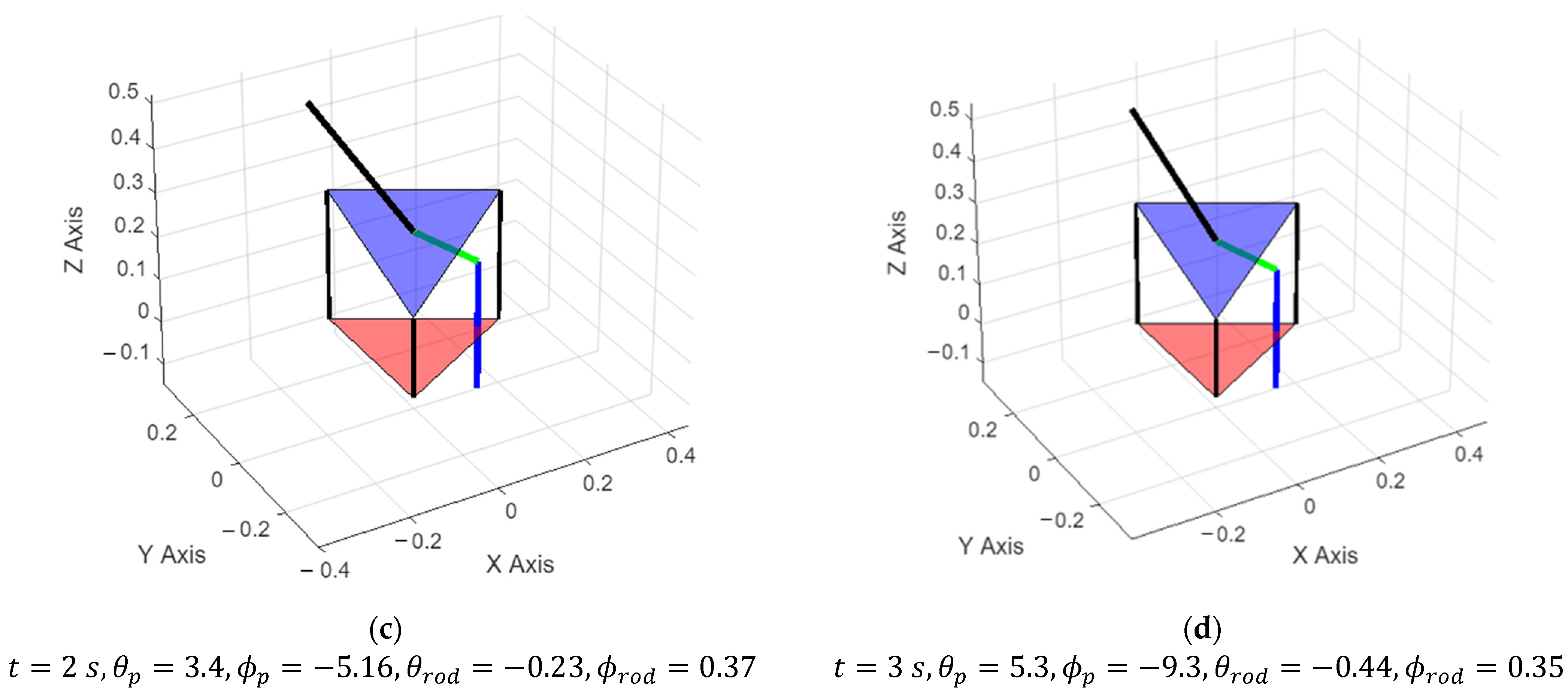
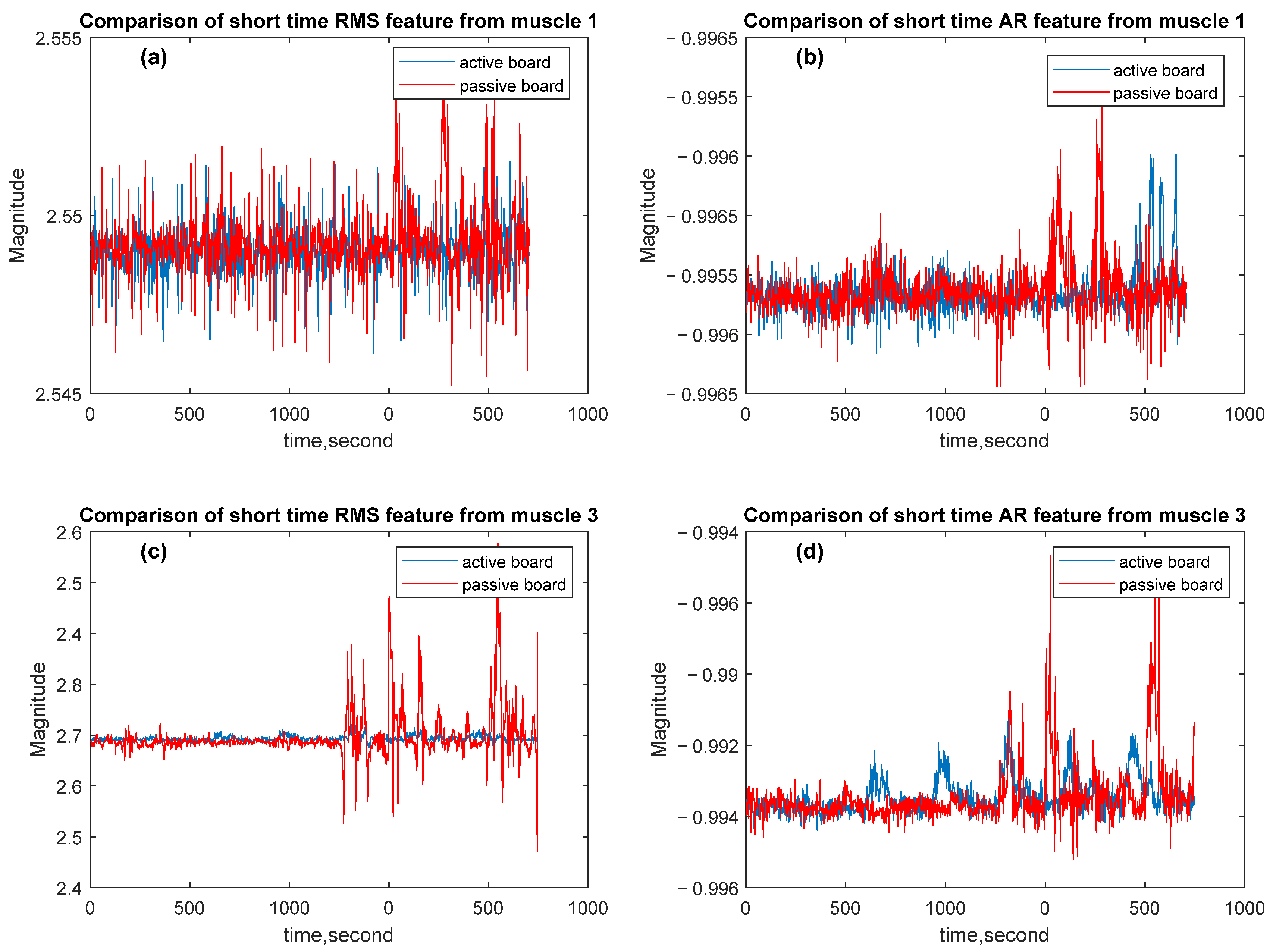
3.1. Simulation Results
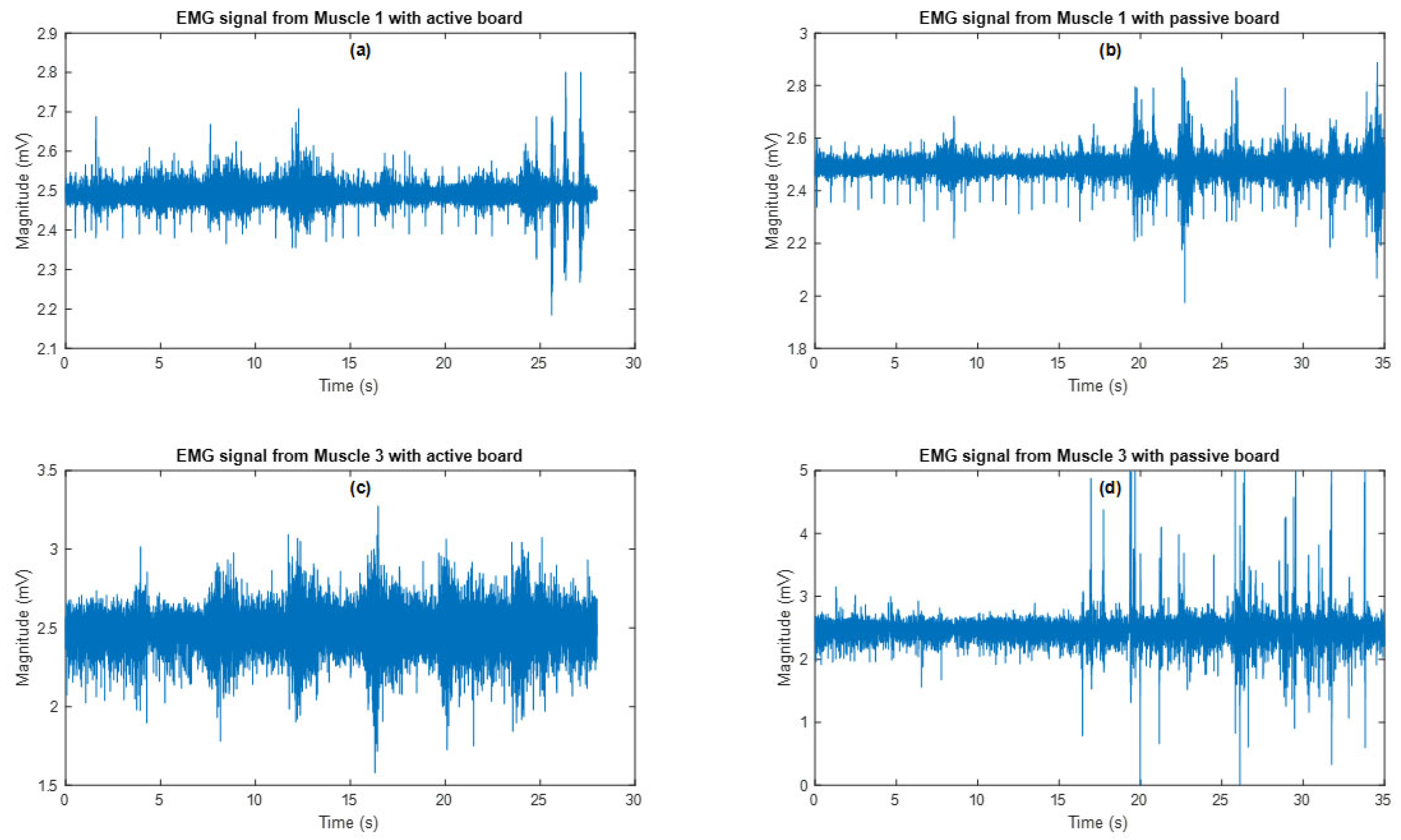
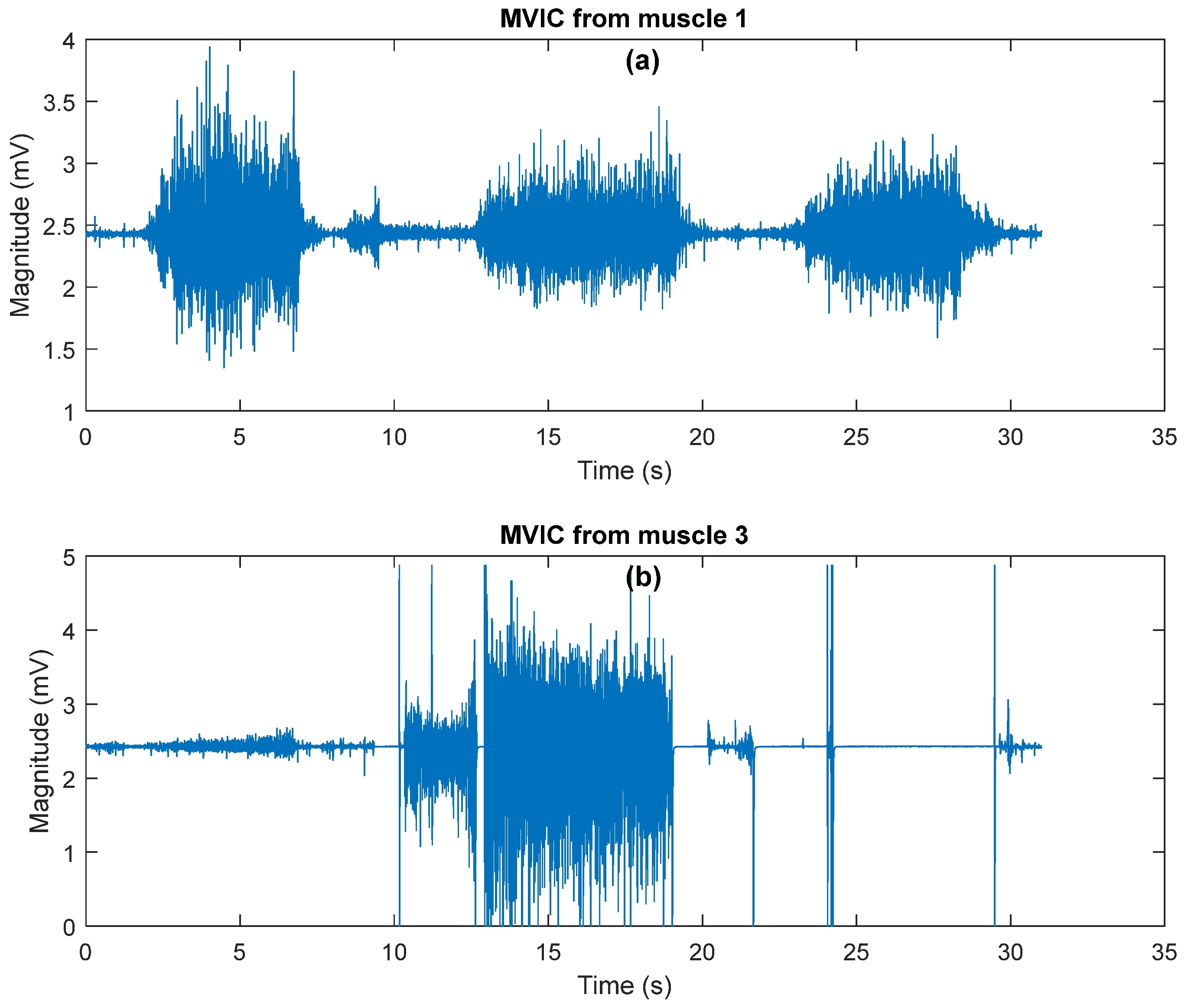
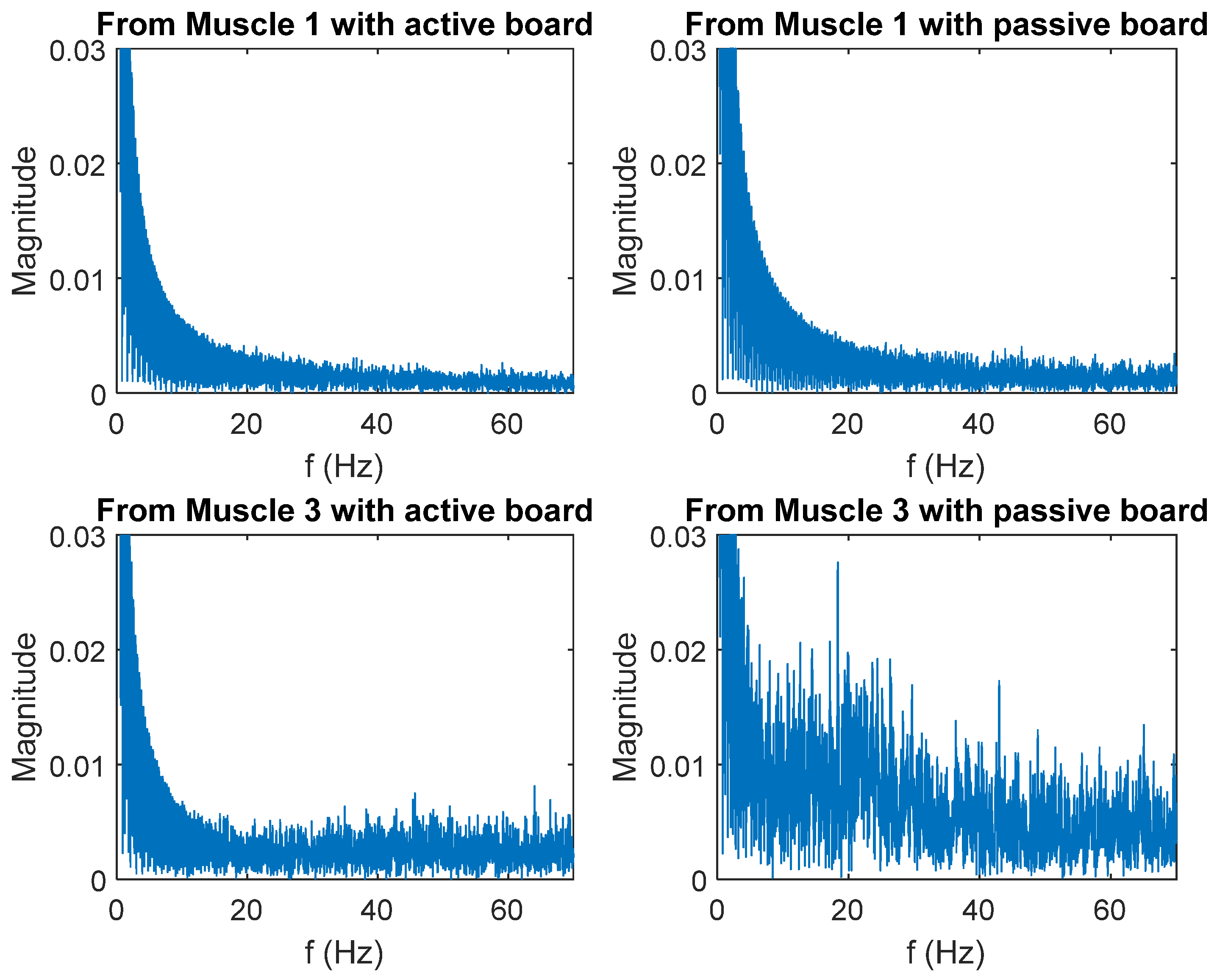
3.2. Evaluation Experiment Results
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| cLBP | Chronic Low Back Pain |
| PAM | Pneumatic Artificial Muscle |
| EMG | Electromyogram |
| IMU | Inertial Measurement Unit |
| RMS | Root Mean Square |
| FFT | Fast Fourier Transform |
| AR | Auto Regression |
| CoM | Center of Mass |
| PCB | Printed Circuit Board |
| GUI | Graphical User Interface |
| MVIC | Maximum Volitional Isometric |
| AUC | Area Under Curve |
References
- Wertheimer, G.; Mathieson, S.; Maher, C.G.; Lin, C.-W.C.; McLachlan, A.J.; Buchbinder, R.; Pearson, S.-A.; Underwood, M. The Prevalence of Opioid Analgesic Use in People with Chronic Noncancer Pain: Systematic Review and Meta-Analysis of Observational Studies; Oxford University Press: Oxford, UK, 2021. [Google Scholar] [CrossRef]
- Moses-Hampton, M.K.; Povieng, B.; Ghorayeb, J.H.; Zhang, Y.; Wu, H. Chronic low back pain comorbidity count and its impact on exacerbating opioid and non-opioid prescribing behavior. Pain Pract. 2023, 23, 252–263. [Google Scholar] [CrossRef] [PubMed]
- Deyo, R.A.; Dworkin, S.F.; Amtmann, D.; Andersson, G.; Borenstein, D.; Carragee, E.; Carrino, J.; Chou, R.; Cook, K.; Delitto, A.; et al. Report of the NIH task force on research standards for chronic low back pain. Phys. Ther. 2015, 95, e1–e18. [Google Scholar] [CrossRef]
- Gatchel, R.J.; Reuben, D.B.; Dagenais, S.; Turk, D.C.; Chou, R.; Hershey, A.D.; Hicks, G.E.; Licciardone, J.C.; Horn, S.D. Research Agenda for the Prevention of Pain and Its Impact: Report of the Work Group on the Prevention of Acute and Chronic Pain of the Federal Pain Research Strategy. J. Pain 2018, 19, 8372013851. [Google Scholar] [CrossRef] [PubMed]
- Christie, C.; Baker, C.; Cooper, R.; Kennedy, P.J.; Madras, B.; Bondi, P. The President’s Commission on Combating Drug Addiction and The Opioid Crisis Roster of Commissioners; US Government Printing Office: Washington, DC, USA, 2017.
- Koes, B.W.; Van Tulder, M.W.; Thomas, S. Diagnosis and Treatment of Low Back Pain; BMJ Publishing Group: London, UK, 2006. [Google Scholar] [CrossRef]
- Deyo, R.A.; Weinstein, J.N. Low Back Pain. N. Engl. J. Med. 2001, 344, 363–370. [Google Scholar] [CrossRef]
- Anderson, D.I.; Lohse, K.R.; Lopes, T.C.V.; Williams, A.M. Individual differences in motor skill learning: Past, present and future. Hum. Mov. Sci. 2021, 78, 102818. [Google Scholar] [CrossRef]
- Loeb, G.E. Learning to use muscles. J. Hum. Kinet. 2021, 76, 9–33. [Google Scholar] [CrossRef]
- Concha-Cisternas, Y.; Castro-Piñero, J.; Vásquez-Muñoz, M.; Molina-Márquez, I.; Vásquez-Gómez, J.; Guzmán-Muñoz, E. Effects of neuromuscular training on postural balance and physical performance in older women: Randomized controlled trial. J. Funct. Morphol. Kinesiol. 2024, 9, 195. [Google Scholar] [CrossRef] [PubMed]
- Antohe, B.A.; Panaet, E.A. The Effects of Proprioceptive Exercises on Postural Control in Handball Players with Chronic Ankle Instability—A Non-Randomized Control Trial. Sports 2024, 12, 304. [Google Scholar] [CrossRef]
- Zemková, E.; Kováčiková, Z. Sport-specific training induced adaptations in postural control and their relationship with athletic performance. Front. Hum. Neurosci. 2023, 16, 1007804. [Google Scholar] [CrossRef]
- Hao, Z.; Cheng, X.; Jiang, H.; Yang, J.; Li, Y.; Lo, W.L.A.; Yu, Q.; Wang, C. The associations between lumbar proprioception and postural control during and after calf vibration in people with and without chronic low back pain. Front. Bioeng. Biotechnol. 2024, 12, 1329437. [Google Scholar] [CrossRef]
- Ghai, S.; Nilson, F.; Gustavsson, J.; Ghai, I. Influence of compression garments on proprioception: A systematic review and meta-analysis. Ann. New York Acad. Sci. 2024, 1536, 60–81. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Tirosh, O.; Han, J.; Adams, R.; El-Ansary, D.; Pranata, A. Lower Limb Proprioception in Low Back Pain and Its Relationship with Voluntary Postural Control. J. Mot. Behav. 2024, 56, 760–771. [Google Scholar] [CrossRef]
- Nishi, Y.; Shigetoh, H.; Fujii, R.; Osumi, M.; Morioka, S. Changes in trunk variability and stability of gait in patients with chronic low back pain: Impact of laboratory versus daily-living environments. J. Pain Res. 2021, 14, 1675–1686. [Google Scholar] [CrossRef]
- Saein, A.M.; Kahrizi, S.; Boozari, S. Effects of unstable load and unstable surface ontrunk muscles activation and postural control in healthy subjects. J. Biomech. 2024, 173, 112257. [Google Scholar] [CrossRef]
- Alshehri, M.A.; Alzahrani, H.; Hoorn, W.V.D.; Klyne, D.M.; Vette, A.H.; Hendershot, B.D.; Roberts, B.W.R.; Larivière, C.; Barbado, D.; Vera-Garcia, F.J.; et al. Trunk Postural Control During Unstable Sitting Among Individuals with and Without Low Back Pain: A Systematic Review with an Individual Participant Data Meta-Analysis; Public Library of Science: San Francisco, CA, USA, 2024. [Google Scholar] [CrossRef]
- Ippersiel, P.; Teoli, A.; Wideman, T.H.; Preuss, R.A.; Robbins, S.M. The Relationship between Pain-Related Threat and Motor Behavior in Nonspecific Low Back Pain: A Systematic Review and Meta-Analysis. Phys. Ther. 2022, 102, pzab274. [Google Scholar] [CrossRef]
- Cruise, D.R.; Chagdes, J.R.; Liddy, J.J.; Rietdyk, S.; Haddad, J.M.; Zelaznik, H.N.; Raman, A. An active balance board system with real-time control of stiffness and time-delay to assess mechanisms of postural stability. J. Biomech. 2017, 60, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Allahverdi, F.; Korayem, M.H. Design of a new balance rehabilitation cable robot focused on patient with cerebral palsy. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 11. [Google Scholar] [CrossRef]
- Cinnera, A.M.; Ciancarelli, I.; Marrano, S.; Palagiano, M.; Federici, E.; Bisirri, A.; Iosa, M.; Paolucci, S.; Koch, G.; Morone, G. Sensor-Based Balance Training with Exergaming Feedback in Subjects with Chronic Stroke: A Pilot Randomized Controlled Trial. Brain Sci. 2024, 14, 917. [Google Scholar] [CrossRef] [PubMed]
- Fil-Balkan, A.; Salcı, Y.; Keklicek, H.; Armutlu, K.; Aksoy, S.; Kayıhan, H.; Elibol, B. Sensorimotor integration training in Parkinson’s disease. Neurosciences 2018, 23, 208–215. [Google Scholar] [CrossRef]
- Porwal, S.; Rizvi, M.R.; Sharma, A.; Ahmad, F.; Alshahrani, M.S.; Raizah, A.; Shaik, A.R.; Seyam, M.K.; Miraj, M.; Alkhamis, B.A.; et al. Enhancing Functional Ability in Chronic Nonspecific Lower Back Pain: The Impact of EMG-Guided Trunk Stabilization Exercises. Healthcare 2023, 11, 2153. [Google Scholar] [CrossRef]
- Khan, M.A.; Shaik, S.; Tariq, M.H.; Kamal, T. McKibben Pneumatic Artificial Muscle Robot Actuators—A Review. In Proceedings of the 2023 International Conference on Robotics and Automation in Industry, ICRAI 2023, Peshawar, Pakistan, 3–5 March 2023. [Google Scholar] [CrossRef]
- Krishnan, S.; Rani, A.M.A.; Kurappa, L.G.; Paramasivam, S. Fabrication of Parallel Mechanism Actuated by Pneumatic Artificial Muscle for Rehabilitation Therapy. In Lecture Notes in Electrical Engineering; Springer Science and Business Media Deutschland GmbH: Berlin/Heidelberg, Germany, 2022; pp. 355–363. [Google Scholar] [CrossRef]
- Andrievsky, B.; Kuznetsov, N.V.; Kudryashova, E.V.; Kuznetsova, O.A.; Zaitceva, I. Signal-parametric discrete-time adaptive controller for pneumatically actuated Stewart platform. Control. Eng. Pract. 2023, 138, 105616. [Google Scholar] [CrossRef]
- Ahern, D.K.; Follick, M.J.; Council, J.R.; Laser-Wolston, N.; Litchman, H. Comparison of lumbar paravertebral EMG patterns in chronic low back pain patients and non-patient controls. Pain 1988, 34, 153–160. [Google Scholar] [CrossRef]
- Kohler, J.M.; Flanagan, S.P.; Whiting, W.C. Muscle activation patterns while lifting stable and unstable loads on stable and unstable surfaces. J. Strength Cond. Res. 2010, 24, 313–321. [Google Scholar] [CrossRef] [PubMed]
- Stegeman, D.; Hermens, H. Standards for suface electromyography: The European project Surface EMG for non-invasive assessment of muscles (SENIAM). Ensch. Roessingh Res. Dev. 2007, 10, 8–12. [Google Scholar]
- Criswell, E. Cram’s Introduction to Surface Electromyography; Jones & Barlett Publishers: Burlington, MA, USA, 2010. [Google Scholar]
- Silfies, S.P.; Mehta, R.; Smith, S.S.; Karduna, A.R. Differences in Feedforward Trunk Muscle Activity in Subgroups of Patients with Mechanical Low Back Pain. Arch. Phys. Med. Rehabil. 2009, 90, 1159–1169. [Google Scholar] [CrossRef]
- Zhong, S.; Gai, Z.; Yang, Y.; Zhao, Y.; Qi, Y.; Peng, Y. A contraction length feedback method for the McKibben pneumatic artificial muscle. Sens. Actuators A Phys. 2022, 334, 113321. [Google Scholar] [CrossRef]
- Kalita, B.; Leonessa, A.; Dwivedy, S.K. A Review on the Development of Pneumatic Artificial Muscle Actuators: Force Model and Application. Actuators 2022, 11, 288. [Google Scholar] [CrossRef]
- Kanno, R.; Watanabe, S.; Shimizu, K.; Shintake, J. Self-Sensing McKibben Artificial Muscles Embedded with Dielectric Elastomer Sensor. IEEE Robot. Autom. Lett. 2021, 6, 6274–6280. [Google Scholar] [CrossRef]
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Jamil, B.; Oh, N.; Lee, J.G.; Lee, H.; Rodrigue, H. A Review and Comparison of Linear Pneumatic Artificial Muscles. Korean Soc. Precis. Eng. 2024, 11, 277–289. [Google Scholar] [CrossRef]
- Wang, S.; Pai, Y.C.; Bhatt, T. Neuromuscular mechanisms of motor adaptation to repeated gait-slip perturbations in older adults. Sci. Rep. 2022, 12, 19851. [Google Scholar] [CrossRef] [PubMed]
- Zech, A.; Hübscher, M.; Vogt, L.; Banzer, W.; Hänsel, F.; Pfeifer, K. Balance training for neuromuscular control and performance enhancement: A systematic review. J. Athl. Train. 2010, 45, 392–403. [Google Scholar] [CrossRef] [PubMed]
- Kaplanoglu, E. Athletic Balance Control Platform with Pneumatic Actuation. U.S. 29/884,368, 15 April 2025. [Google Scholar]
| Trial Name | Channel | Mean | RMS | Difference |
|---|---|---|---|---|
| MVIC | 1 | 509.7 | 509.9 | 0.2 |
| 2 | 509 | 509.1 | 0.1 | |
| Passive | 1 | 509.6 | 509.7 | 0.1 |
| 2 | 508.9 | 508.9 | 0 | |
| Active 1 | 1 | 509.6 | 509.8 | 0.2 |
| 2 | 508.6 | 508.6 | 0 | |
| Active 2 | 1 | 509.7 | 509.7 | 0 |
| 2 | 508.7 | 508.7 | 0 | |
| Active 3 | 1 | 509.7 | 509.7 | 0 |
| 2 | 508.7 | 508.7 | 0 | |
| Active 4 | 1 | 509.6 | 509.7 | 0.1 |
| 2 | 508.7 | 508.8 | 0.1 | |
| Active 5 | 1 | 509.7 | 509.7 | 0 |
| 2 | 508.7 | 508.8 | 0.1 |
| Active Board | Passive Board | |
|---|---|---|
| From Muscle 1 | 55.56 Hz | 64.85 Hz |
| From Muscle 3 | 106.58 Hz | 106.52 Hz |
| MPE of RMS Values | MPE of AR Vectors | |
|---|---|---|
| Muscle 1 | ||
| Muscle 3 |
| Peak % MVIC | AUC (%MVIC.s) | Active Time Ratio (> 10%MVIC) | Welch t-Test | p Value | ||||
|---|---|---|---|---|---|---|---|---|
| A | P | A | P | A | P | Between A and P | ||
| P1 | 24.60 | 5.92 | 37.11 | 55.96 | 0 | 0 | −9.90 | p < 0.0001 |
| P2 | 23.10 | 32 | 19.52 | 10.33 | 0 | 0 | 47.77 | p < 0.0001 |
| P3 | 54.26 | 24.41 | 33.01 | 38.62 | 0 | 0 | −5.4 | p < 0.0001 |
| P4 | 43.54 | 21.24 | 62.51 | 45.25 | 0 | 0 | 35.25 | p < 0.0001 |
| P5 | 53.50 | 10.57 | 25.32 | 31.88 | 0.0076 | 0.0077 | −16.46 | p < 0.0001 |
| P6 | 51.71 | 4.21 | 25.14 | 21.43 | 0.0072 | 0 | 11.54 | p < 0.0001 |
| P7 | 48.55 | 9.79 | 24.79 | 30.07 | 0 | 0 | −14.01 | p < 0.0001 |
| P8 | 55.82 | 20.07 | 24.34 | 30.00 | 0.0075 | 0.047 | −12.14 | p < 0.0001 |
| P9 | 55.33 | 27.54 | 38.99 | 76.79 | 0.0074 | 0.2169 | −56 | p < 0.0001 |
| P10 | 54.49 | 19.60 | 41.50 | 11.50 | 0.0072 | 0.0880 | −46 | p < 0.0001 |
| P11 | 62.63 | 22.86 | 66.20 | 47.80 | 0.0727 | 0.1210 | 31.44 | p < 0.0001 |
| P12 | 26.6 | 9.8 | 76.2 | 19.10 | 0 | 0 | 125.05 | p < 0.0001 |
| P13 | 54.07 | 19.36 | 45.05 | 62.71 | 0.0175 | 0.0976 | −37.39 | p < 0.0001 |
| P14 | 10.17 | 1.40 | 65.44 | 56.11 | 0 | 0 | 13.75 | p < 0.0001 |
| P15 | 15.25 | 7.54 | 45.40 | 62.52 | 0 | 0 | 42.51 | p < 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaplanoglu, E.; Jordon, M.; Bruce, J.; Akgun, G. Design and Evaluation of a Pneumatic-Actuated Active Balance Board for Sitting Postural Control. Sensors 2025, 25, 7101. https://doi.org/10.3390/s25237101
Kaplanoglu E, Jordon M, Bruce J, Akgun G. Design and Evaluation of a Pneumatic-Actuated Active Balance Board for Sitting Postural Control. Sensors. 2025; 25(23):7101. https://doi.org/10.3390/s25237101
Chicago/Turabian StyleKaplanoglu, Erkan, Max Jordon, Jeremy Bruce, and Gazi Akgun. 2025. "Design and Evaluation of a Pneumatic-Actuated Active Balance Board for Sitting Postural Control" Sensors 25, no. 23: 7101. https://doi.org/10.3390/s25237101
APA StyleKaplanoglu, E., Jordon, M., Bruce, J., & Akgun, G. (2025). Design and Evaluation of a Pneumatic-Actuated Active Balance Board for Sitting Postural Control. Sensors, 25(23), 7101. https://doi.org/10.3390/s25237101









