Multi-View Omnidirectional Vision and Structured Light for High-Precision Mapping and Reconstruction
Abstract
1. Introduction
2. Related Work
2.1. Virtual Simulation System
2.2. Multi-View Omnidirectional Vision Reconstruction
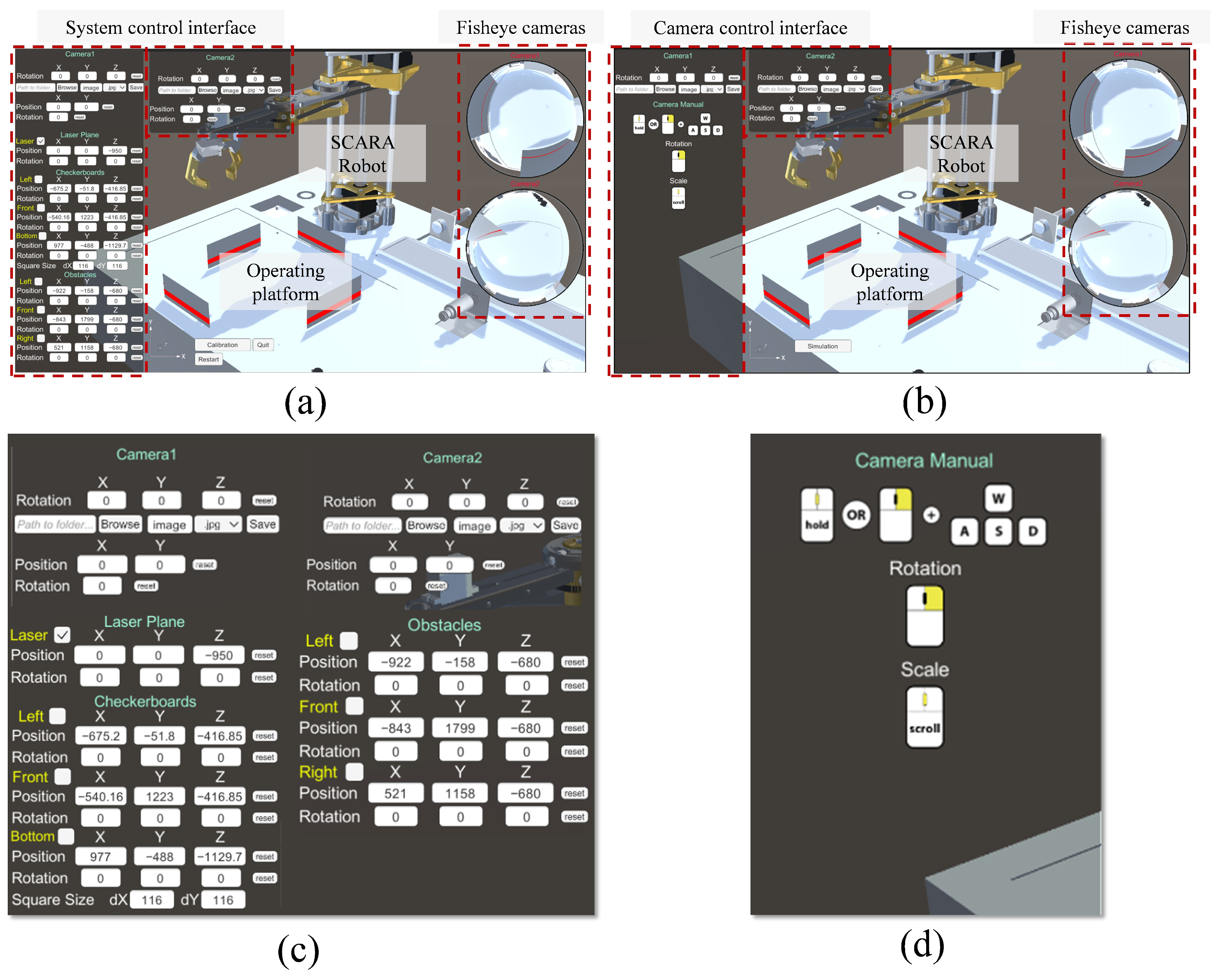
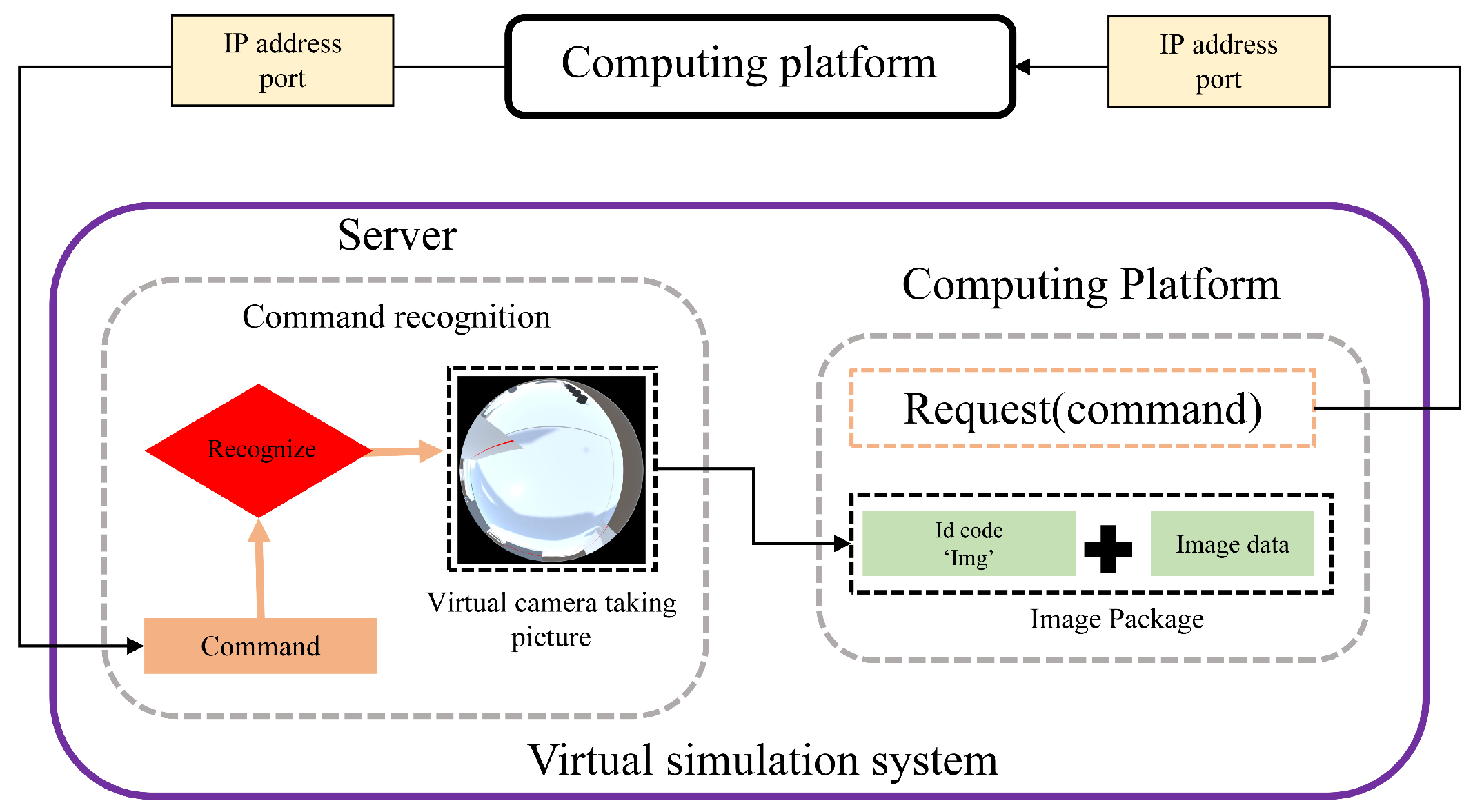
3. Virtual Simulation System
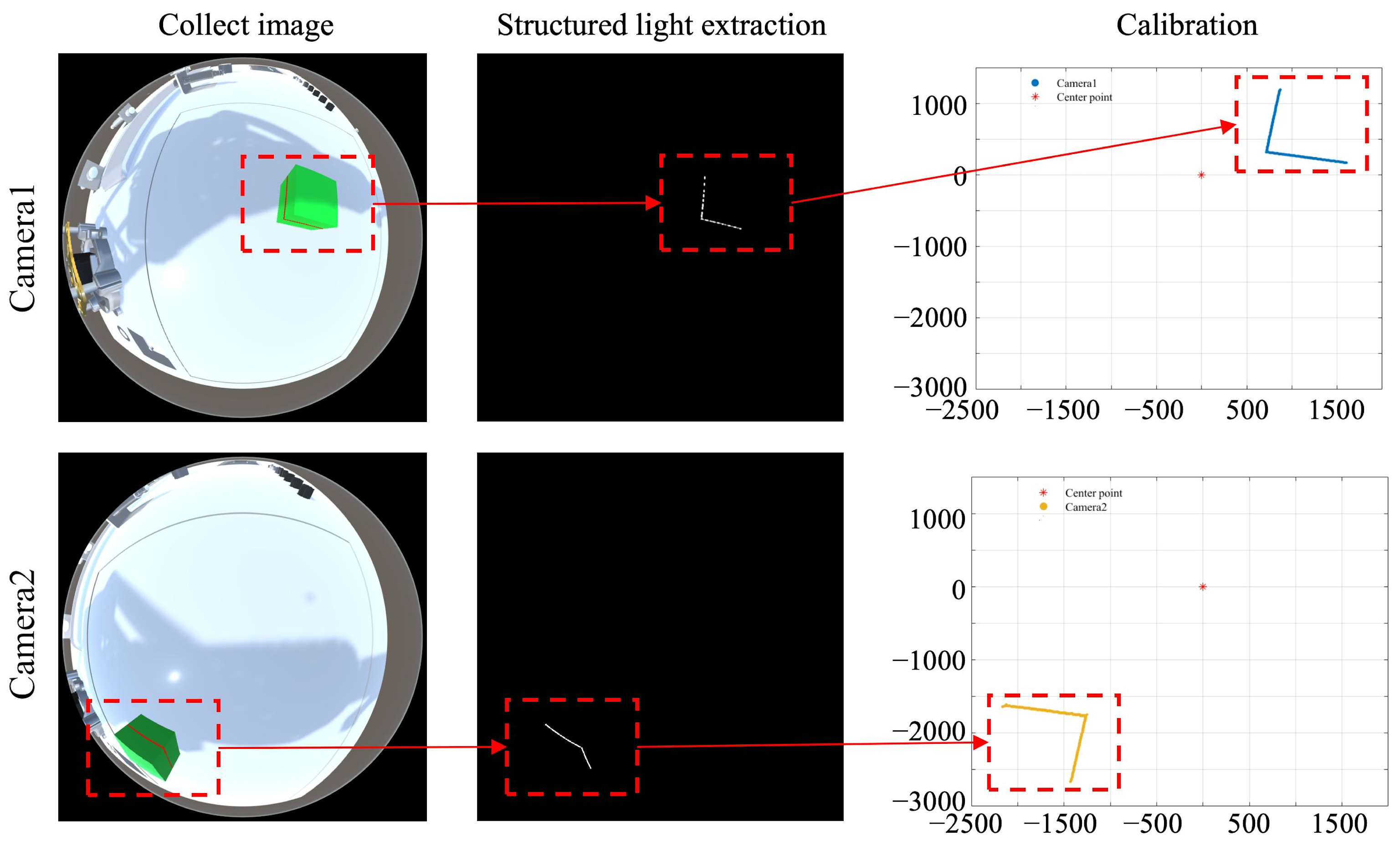
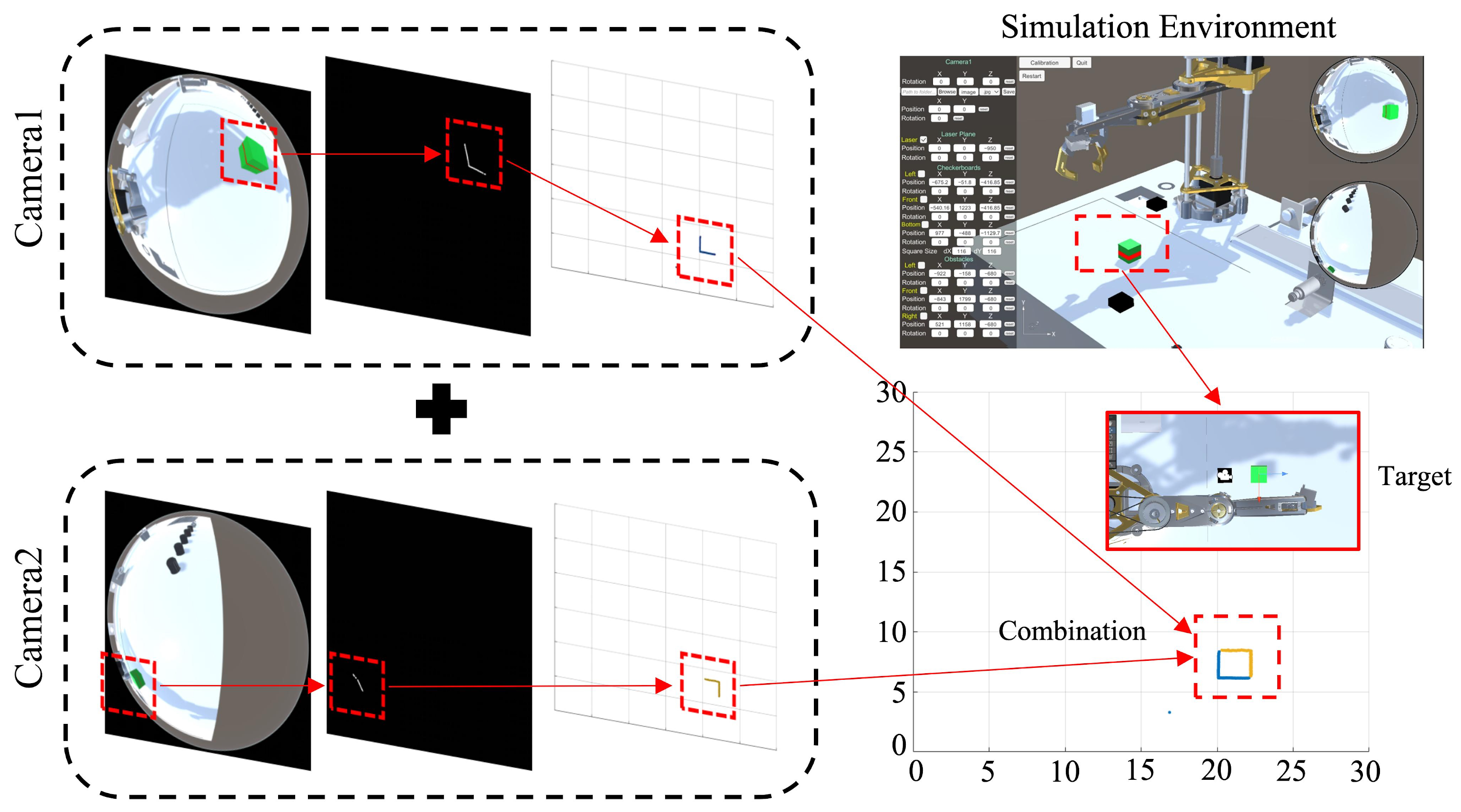
4. Reconstruction Method
5. Experimental Results and Analysis
5.1. Target Reconstruction Performance
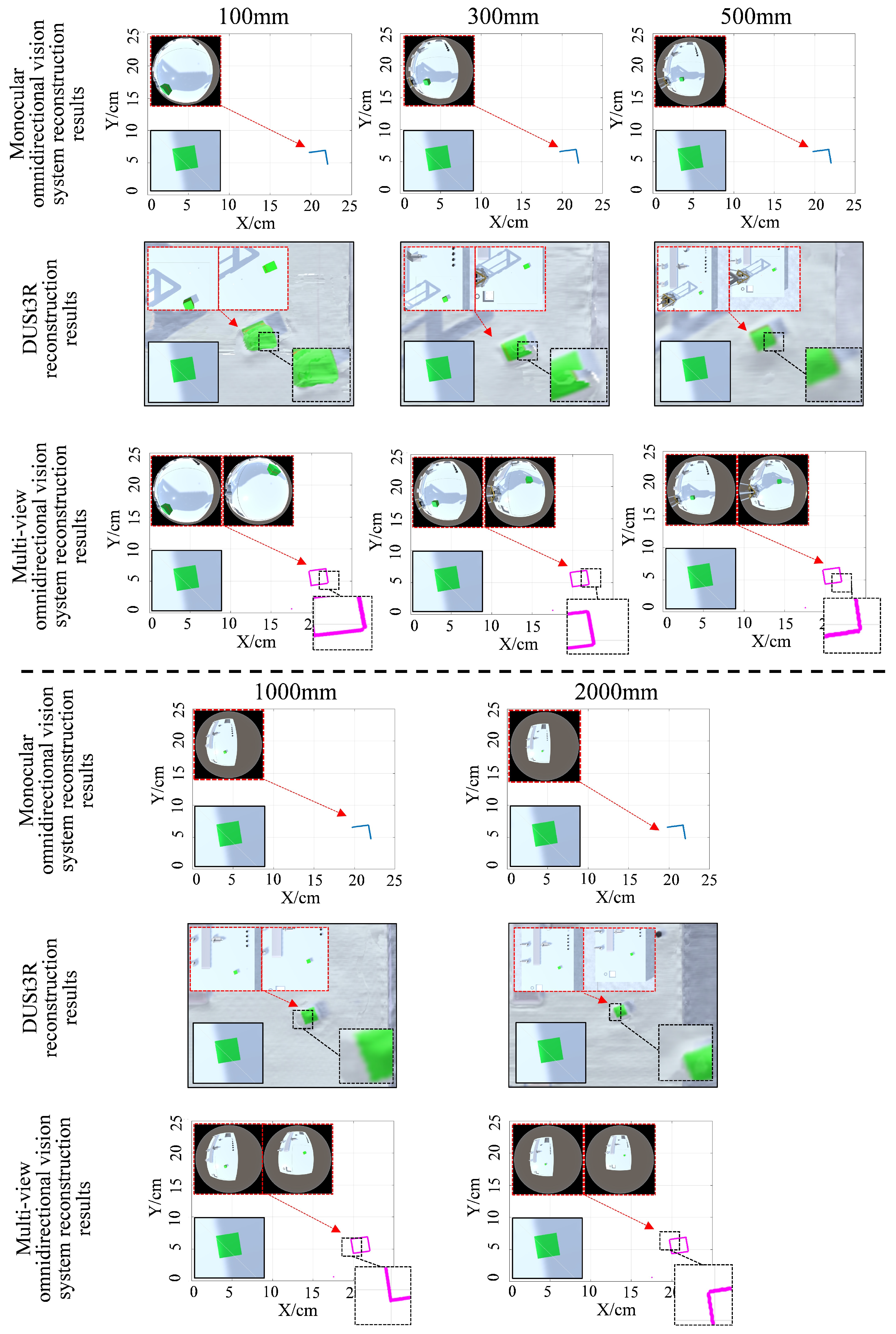
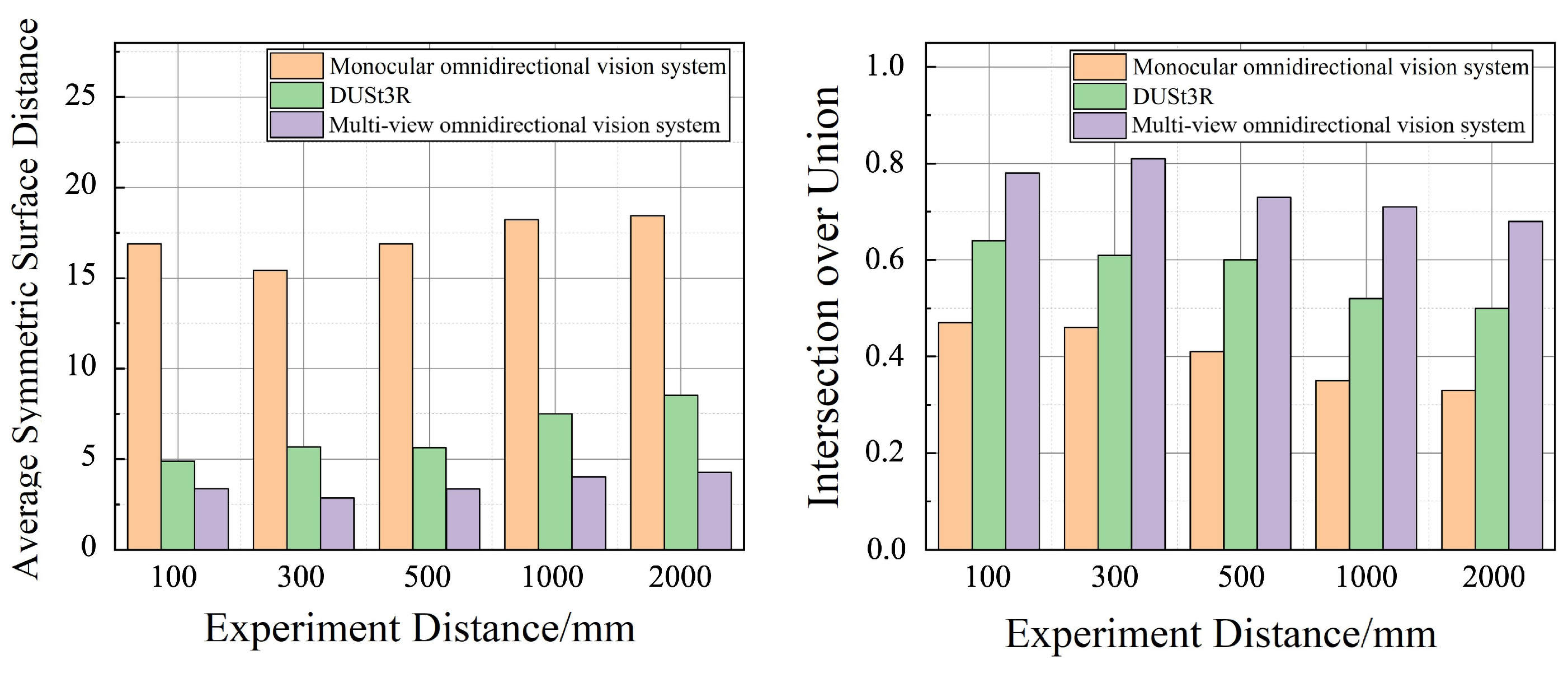
5.1.1. Target Reconstruction Performance at Different Distances
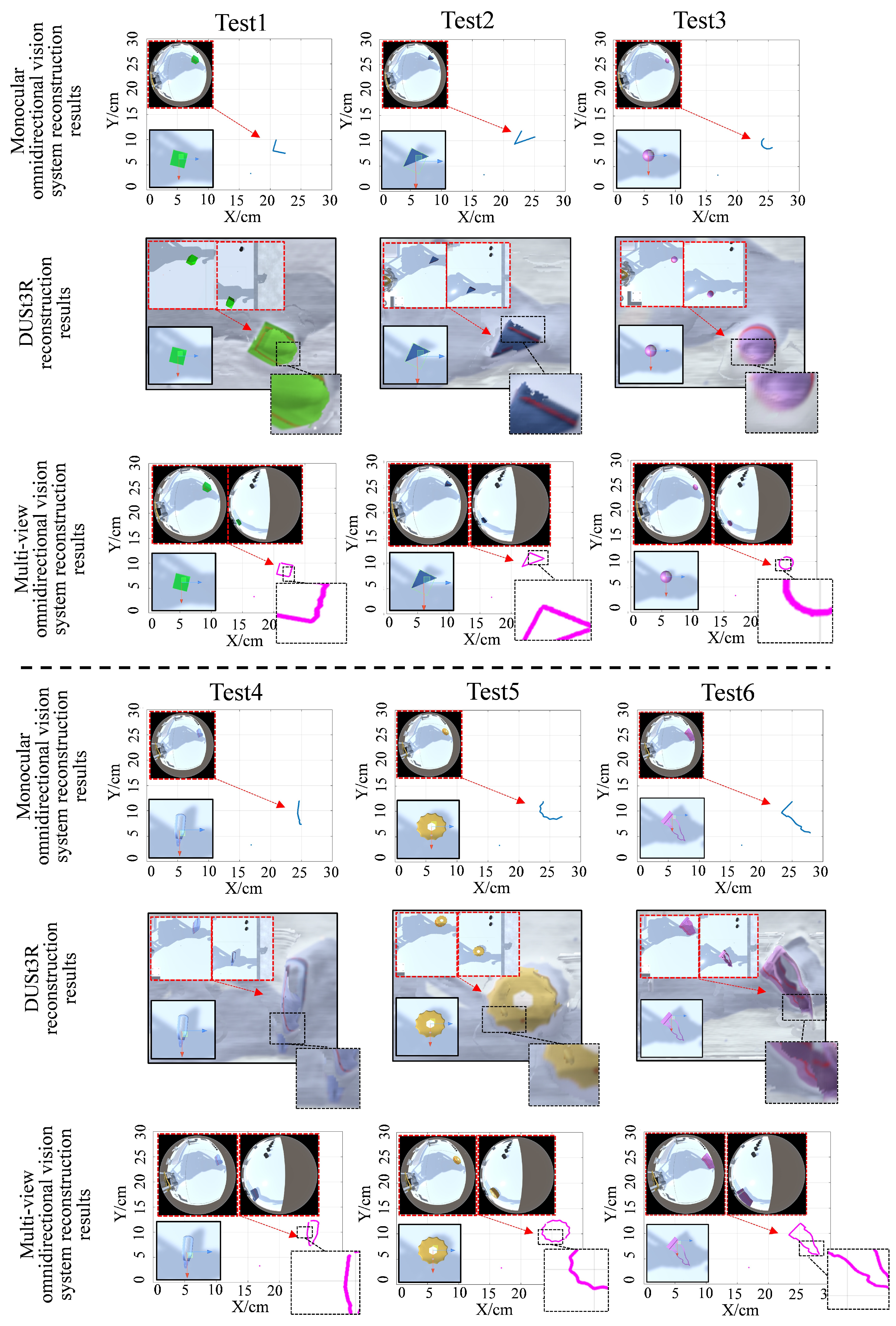
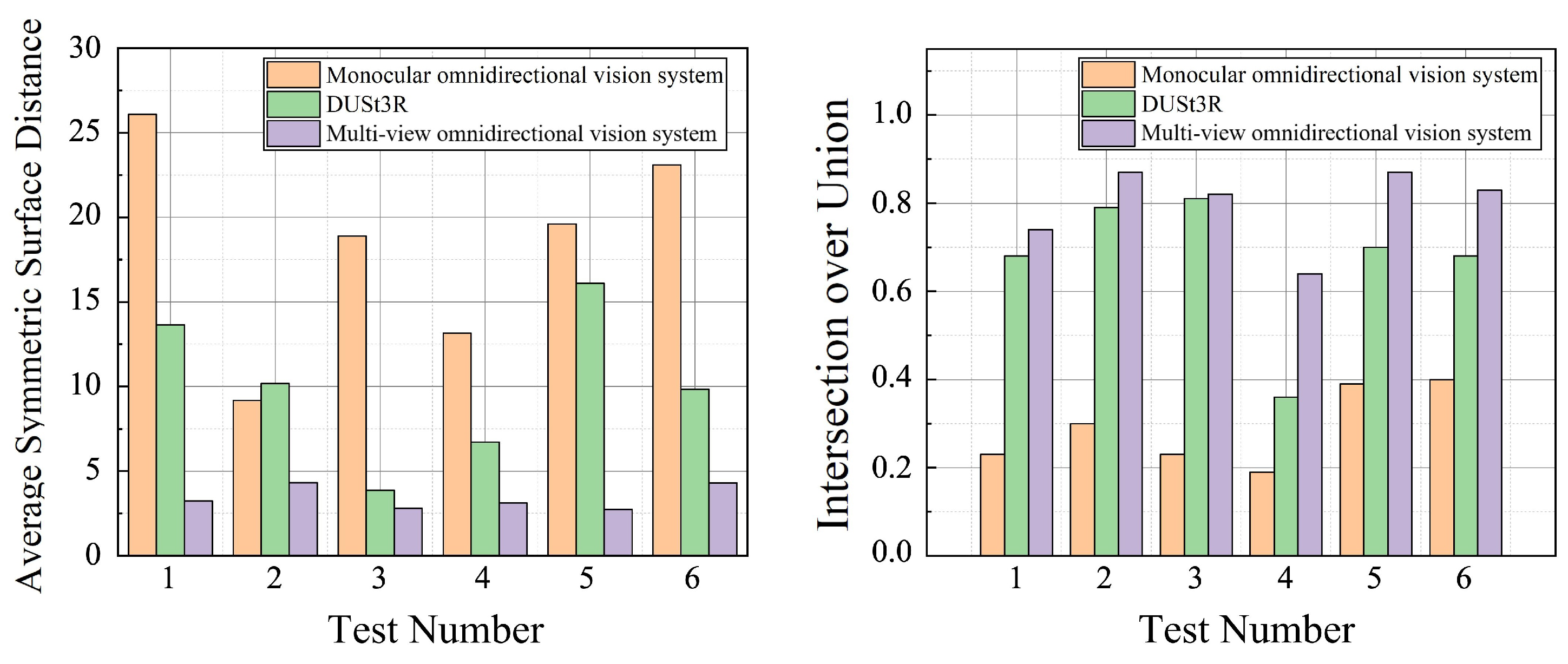
5.1.2. Reconstruction Performance for Objects with Different Shapes
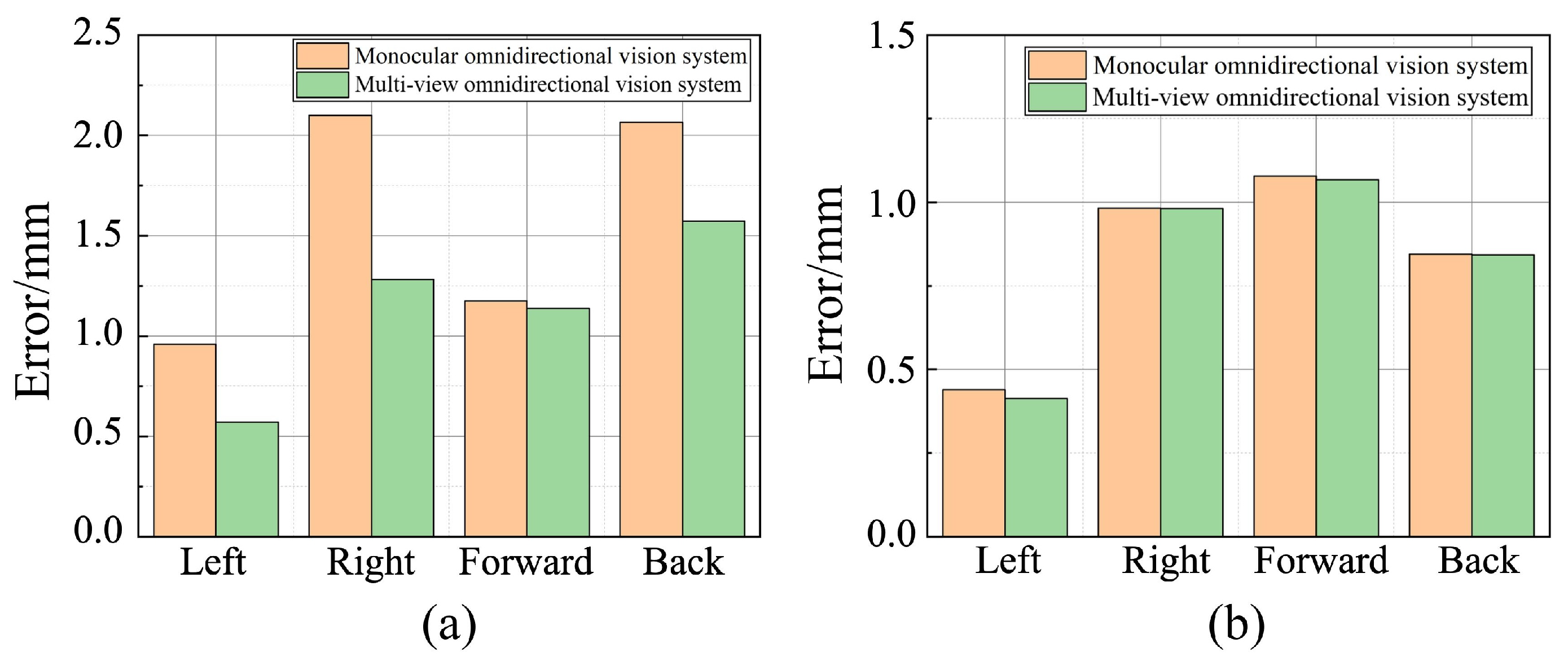
5.2. Distance Measurement Accuracy Experiments
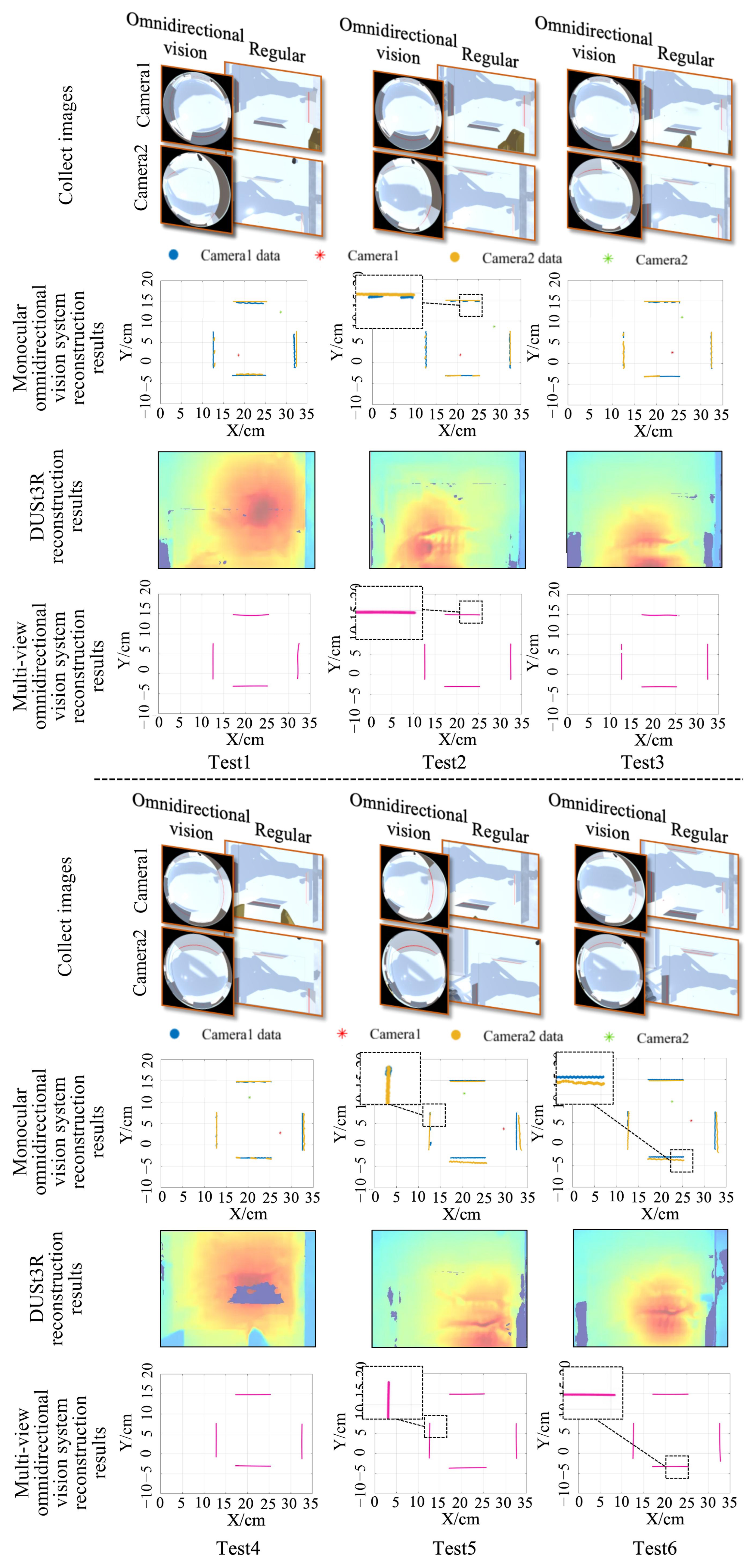
5.3. Real-World Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cebollada, S.; Payá, L.; Peidró, A.; Mayol, W.; Reinoso, O. Environment modeling and localization from datasets of omnidirectional scenes using machine learning techniques. Neural Comput. Appl. 2023, 35, 16487–16508. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, W.; Wang, Y.; Kong, L.; Xu, J.; Yang, J.; Song, Z. Omnidirectional optic fiber shape sensor for submarine landslide monitoring. Measurement 2025, 239, 115429. [Google Scholar] [CrossRef]
- Kawaharazuka, K.; Obinata, Y.; Kanazawa, N.; Tsukamoto, N.; Okada, K.; Inaba, M. Reflex-based open-vocabulary navigation without prior knowledge using omnidirectional camera and multiple vision-language models. Adv. Robot. 2024, 38, 1307–1317. [Google Scholar] [CrossRef]
- Patruno, C.; Renò, V.; Nitti, M.; Mosca, N.; di Summa, M.; Stella, E. Vision-based omnidirectional indoor robots for autonomous navigation and localization in manufacturing industry. Heliyon 2024, 10, e26042. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Liu, Y.; Zhang, P.; Chen, X.; Wang, D.; Lu, H. Safety-First Tracker: A Trajectory Planning Framework for Omnidirectional Robot Tracking. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 5416–5423. [Google Scholar]
- Xu, Y.; Liu, Y.; Li, H.; Wang, L.; Ai, J. A deep learning approach of intrusion detection and tracking with UAV-based 360 camera and 3-axis gimbal. Drones 2024, 8, 68. [Google Scholar] [CrossRef]
- del Blanco, C.R.; Carballeira, P.; Jaureguizar, F.; García, N. Robust people indoor localization with omnidirectional cameras using a grid of spatial-aware classifiers. Signal Process. Image Commun. 2021, 93, 116135. [Google Scholar] [CrossRef]
- Qian, Y.; Yang, M.; Dolan, J.M. Survey on fish-eye cameras and their applications in intelligent vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22755–22771. [Google Scholar] [CrossRef]
- Konrad, J.; Cokbas, M.; Tezcan, M.O.; Ishwar, P. Overhead fisheye cameras for indoor monitoring: Challenges and recent progress. Front. Imaging 2024, 3, 1387543. [Google Scholar] [CrossRef]
- Sharma, M.K.; Farhat, I.; Liu, C.F.; Sehad, N.; Hamidouche, W.; Debbah, M. Real-time immersive aerial video streaming: A comprehensive survey, benchmarking, and open challenges. IEEE Open J. Commun. Soc. 2024, 5, 5680–5705. [Google Scholar] [CrossRef]
- Kholodilin, I.; Li, Y.; Wang, Q.; Bourke, P.D. Calibration and three-dimensional reconstruction with a photorealistic simulator based on the omnidirectional vision system. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211059313. [Google Scholar] [CrossRef]
- Luo, X.; Cui, Z.; Su, F. Fe-det: An effective traffic object detection framework for fish-eye cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 7091–7099. [Google Scholar]
- Thomas, S. The Rise of Intelligent Surveillance: AI powered Behavioral Analysis in Home Security Cameras. J. Artif. Intell. Mach. Learn. Data Sci. 2025, 3, 2471–24675. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.R.; Eising, C.; Witt, C.; Yogamani, S.K. Surround-view fisheye camera perception for automated driving: Overview, survey & challenges. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3638–3659. [Google Scholar] [CrossRef]
- Guo, P.; Liu, C.; Hou, X.; Qian, X. Towards Better Distortion Feature Learning for Object Detection in Top-View Fisheye Cameras. IEEE Trans. Multimed. 2024. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, N.; Xu, X. Improved AO optimization algorithm for distortion parameter estimation of catadioptric omnidirectional lens. Chin. Opt. 2025, 18, 89–104. [Google Scholar] [CrossRef]
- Wong, C.C.; Weng, K.D.; Yu, B.Y.; Chou, Y.S. Implementation of a Small-Sized Mobile Robot with Road Detection, Sign Recognition, and Obstacle Avoidance. Appl. Sci. 2024, 14, 6836. [Google Scholar] [CrossRef]
- Meng, L.; Li, Y.; Wang, Q.L. A calibration method for mobile omnidirectional vision based on structured light. IEEE Sens. J. 2020, 21, 11451–11460. [Google Scholar] [CrossRef]
- Kholodilin, I.; Zhang, Z.; Guo, Q.; Grigorev, M. Calibration of the omnidirectional vision system for robotics sorting system. Sci. Rep. 2025, 15, 10256. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, C.; Chen, Z.; Wang, H.; Zhou, P.; Lin, B. A 360-degree panoramic stereo scanning measurement system based on a panoramic annular lens and omnidirectional ring structured light. Opt. Lasers Eng. 2024, 182, 108445. [Google Scholar] [CrossRef]
- Wu, T.; Tang, L.; Du, P.; Liu, N.; Zhou, Z.; Qi, X. Non-contact measurement method of beam vibration with laser stripe tracking based on tilt photography. Measurement 2022, 187, 110314. [Google Scholar] [CrossRef]
- Tan, Z.; Zhao, B.; Ji, Y.; Xu, X.; Kong, Z.; Liu, T.; Luo, M. A welding seam positioning method based on polarization 3D reconstruction and linear structured light imaging. Opt. Laser Technol. 2022, 151, 108046. [Google Scholar] [CrossRef]
- Chen, J.; Ping, S.; Liang, X.; Ma, X.; Pang, S.; He, Y. Line-Structured Light-Based Three-Dimensional Reconstruction Measurement System with an Improved Scanning-Direction Calibration Method. Remote Sens. 2025, 17, 2236. [Google Scholar] [CrossRef]
- Ye, T.; Wang, B.; Jiang, W.; Deng, X.; Tao, H.; Liu, J.; He, W. Research on deformation monitoring method for surrounding rock in roadway based on an omnidirectional structured light vision sensor system. Measurement 2025, 255, 117867. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, N. Catadioptric omnidirectional monocular visual distance measurement method integrating structured light. Opt. Precis. Eng. 2024, 32, 490–503. [Google Scholar] [CrossRef]
- Qi, Y.; Li, Y. Indoor key point reconstruction based on laser illumination and omnidirectional vision. J. Adv. Comput. Intell. Intell. Inform. 2020, 24, 864–871. [Google Scholar] [CrossRef]
- Tang, X.W.; Huang, Y.; Shi, Y.; Huang, X.L.; Shi, Q. 3D trajectory planning for real-time image acquisition in UAV-assisted VR. IEEE Trans. Wirel. Commun. 2023, 23, 16–30. [Google Scholar] [CrossRef]
- Tang, X.W.; Huang, Y.; Shi, Y.; Wu, Q. MUL-VR: Multi-UAV Collaborative Layered Visual Perception and Transmission for Virtual Reality. IEEE Trans. Wirel. Commun. 2025, 24, 2734–2749. [Google Scholar] [CrossRef]
- Farley, A.; Wang, J.; Marshall, J.A. How to pick a mobile robot simulator: A quantitative comparison of CoppeliaSim, Gazebo, MORSE and Webots with a focus on accuracy of motion. Simul. Model. Pract. Theory 2022, 120, 102629. [Google Scholar] [CrossRef]
- Sánchez, M.; Morales, J.; Martínez, J.L.; Fernández-Lozano, J.J.; García-Cerezo, A. Automatically annotated dataset of a ground mobile robot in natural environments via gazebo simulations. Sensors 2022, 22, 5599. [Google Scholar] [CrossRef]
- Károly, A.I.; Galambos, P. Automated dataset generation with blender for deep learning-based object segmentation. In Proceedings of the 2022 IEEE 20th Jubilee World Symposium on Applied Machine Intelligence and Informatics (SAMI), Poprad, Slovakia, 2–5 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 000329–000334. [Google Scholar]
- Yang, Z.; Chen, Y.; Wang, J.; Manivasagam, S.; Ma, W.C.; Yang, A.J.; Urtasun, R. Unisim: A neural closed-loop sensor simulator. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1389–1399. [Google Scholar]
- Zhang, Z.; Guo, Q.; Grigorev, M.A.; Kholodilin, I. Construction Method of a Digital-Twin Simulation System for SCARA Robots Based on Modular Communication. Sensors 2024, 24, 7183. [Google Scholar] [CrossRef]
- De Petrillo, M.; Beard, J.; Gu, Y.; Gross, J.N. Search planning of a uav/ugv team with localization uncertainty in a subterranean environment. IEEE Aerosp. Electron. Syst. Mag. 2021, 36, 6–16. [Google Scholar] [CrossRef]
- Feldotto, B.; Morin, F.O.; Knoll, A. The neurorobotics platform robot designer: Modeling morphologies for embodied learning experiments. Front. Neurorobotics 2022, 16, 856727. [Google Scholar] [CrossRef] [PubMed]
- Viecco, V.; González, D.; Vuelvas, J.; Cotrino, C.; Castiblanco, J.C. Development of a learning environment using the UniSim Design tool. In Proceedings of the 2023 IEEE 6th Colombian Conference on Automatic Control (CCAC), Popayan, Colombia, 17–20 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Lidon, M. Unity 3D; Marcombo: Barcelona, Spain, 2025. [Google Scholar]
- Haces-Garcia, A.; Zhu, W. Building an Accessible and Flexible Multi-User Robotic Simulation Framework with Unity-MATLAB Bridge. Computers 2024, 13, 282. [Google Scholar] [CrossRef]
- Platt, J.; Ricks, K. Comparative analysis of ros-unity3d and ros-gazebo for mobile ground robot simulation. J. Intell. Robot. Syst. 2022, 106, 80. [Google Scholar] [CrossRef]
- Seifert, E.; Seifert, S.; Vogt, H.; Drew, D.; Van Aardt, J.; Kunneke, A.; Seifert, T. Influence of drone altitude, image overlap, and optical sensor resolution on multi-view reconstruction of forest images. Remote Sens. 2019, 11, 1252. [Google Scholar] [CrossRef]
- Liu, A.; Li, Z.; Chen, Z.; Li, N.; Xu, Y.; Plummer, B.A. Panofree: Tuning-free holistic multi-view image generation with cross-view self-guidance. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2024; pp. 146–164. [Google Scholar]
- Li, Y.; Wang, J.; Chen, H.; Jiang, X.; Liu, Y. Object-aware view planning for autonomous 3-D model reconstruction of buildings using a mobile robot. IEEE Trans. Instrum. Meas. 2023, 72, 1–15. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, H.; Wang, H.; Wu, Q.; Qin, X.; Dong, K. Vision-based multi-view reconstruction for high-precision part positioning in industrial robot machining. Measurement 2025, 242, 116042. [Google Scholar] [CrossRef]
- Vulpi, F.; Marani, R.; Petitti, A.; Reina, G.; Milella, A. An RGB-D multi-view perspective for autonomous agricultural robots. Comput. Electron. Agric. 2022, 202, 107419. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, H.; Asano, Y.; Zheng, Y.; Sato, I. Multi-view 3D reconstruction of a texture-less smooth surface of unknown generic reflectance. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 16226–16235. [Google Scholar]
- Kim, J.; Eum, H.; Yun, K.; Shin, H.C.; Lee, G.; Seo, J. Calibration of a multiview display with a tilted parallax barrier for reduction of nonlinear extrinsic crosstalk. Appl. Opt. 2022, 61, 9112–9123. [Google Scholar] [CrossRef]
- Kholodilin, I.; Li, Y.; Wang, Q. Omnidirectional vision system with laser illumination in a flexible configuration and its calibration by one single snapshot. IEEE Trans. Instrum. Meas. 2020, 69, 9105–9118. [Google Scholar] [CrossRef]
- Shuzhe, W.; Vincent, L.; Yohann, C.; Boris, C.; Jerome, R. Dust3r: Geometric 3d vision made easy. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2024 (CVPR), Seattle, WA, USA, 17–21 June 2024; pp. 20697–20709. [Google Scholar]
- Mohammadi, R.; Shokatian, I.; Salehi, M.; Arabi, H.; Shiri, I.; Zaidi, H. Deep learning-based auto-segmentation of organs at risk in high-dose rate brachytherapy of cervical cancer. Radiother. Oncol. 2021, 159, 231–240. [Google Scholar] [CrossRef]
- Stuckner, J.; Harder, B.; Smith, T.M. Microstructure segmentation with deep learning encoders pre-trained on a large microscopy dataset. npj Comput. Mater. 2022, 8, 200. [Google Scholar] [CrossRef]



| Test 1/s | Test 2/s | Test 3/s | Test 4/s | Test 5/s | Test 6/s | Average/s | |
|---|---|---|---|---|---|---|---|
| Monocular omnidirectional vision system | 0.5519 | 0.6149 | 0.6147 | 0.9268 | 0.6817 | 0.9063 | 0.7161 |
| DUSt3R | 6.8 | 7.5 | 6.6 | 6.8 | 6.7 | 6.9 | 6.8833 |
| Multi-view omnidirectional vision system | 0.6666 | 0.6399 | 0.6971 | 0.9487 | 1.0550 | 0.9613 | 0.8281 |
| Parameters | Left /mm | Right /mm | Forward /mm | Back /mm | Camera-Laser Distance/mm |
|---|---|---|---|---|---|
| Value | 126.25 | 325.28 | 149.1 | −31.45 | 95 |
| Test Number | System | Camera Information | ||||
|---|---|---|---|---|---|---|
| x/mm | y/mm | Pitch/Degrees | Roll/Degrees | Yaw/Degrees | ||
| 1 | camera 1 | 186.56 | 18.61 | −3 | 1 | 5 |
| camera 2 | 287.08 | 123.10 | 1 | −2 | 2 | |
| 2 | camera 1 | 207.11 | 18.61 | 2 | −1 | 0 |
| camera 2 | 287.08 | 86.65 | 2 | 0 | −2 | |
| 3 | camera 1 | 235.70 | 26.39 | 1 | −1 | −3 |
| camera 2 | 258.04 | 110.95 | 2 | 0 | −2 | |
| 4 | camera 1 | 295.34 | 37.32 | 1 | −4 | 2 |
| camera 2 | 205.10 | 119.70 | 3 | 6 | 5 | |
| 5 | camera 1 | 270.33 | 54.57 | 0 | −4 | 2 |
| camera 2 | 226.77 | 98.80 | 3 | 4 | 6 | |
| System | Camera Information | ||||
|---|---|---|---|---|---|
| x/mm | y/mm | Pitch/Degrees | Roll/Degrees | Yaw/Degrees | |
| Camera 1 | 187.68 | 32.95 | 0 | 0 | 0 |
| Camera 2 | 255.81 | 102.45 | 0 | 0 | 0 |
| Test Number | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Distance of Camera 1/mm | 195 | 255 | 116 | 68 | 145 | 195 |
| Distance of Camera 2/mm | 95 | 145 | 235 | 285 | 205 | 165 |
| System | Camera Information | Camera–Laser Distance/mm | ||||
|---|---|---|---|---|---|---|
| x/mm | y/mm | Pitch/Degrees | Roll/Degrees | Yaw/Degrees | ||
| Camera 1 | 140 | 194 | 1 | 3 | 1 | 131 |
| Camera 2 | −122 | 100 | 4 | 2 | 2 | 131 |
| Test Number | 1 | 2 | 3 | 4 | 5 | 6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
x
/mm |
y
/mm |
x
/mm |
y
/mm |
x
/mm |
y
/mm |
x
/mm |
y
/mm |
x
/mm |
y
/mm |
x
/mm |
y
/mm | |
| Real | 161 | −8 | 129 | −47 | 208 | 36 | 167 | 43 | 172 | −23 | 147 | 28 |
| Single | 161.2 | −1.71 | 131.15 | −41 | 205.71 | 46.62 | 164.91 | 55.28 | 171.44 | −19.06 | 145.27 | 38.34 |
| Multi-view | 158.3 | −8.25 | 126.52 | −52.32 | 204.25 | 41.66 | 163.57 | 48.93 | 169.76 | −25.99 | 143.71 | 31.64 |
| Test 1/s | Test 2/s | Test 3/s | Test 4/s | Test 5/s | Test 6/s | Average/s | |
|---|---|---|---|---|---|---|---|
| Monocular omnidirectional vision system | 0.8315 | 0.9752 | 0.9547 | 0.9162 | 1.2774 | 0.8762 | 0.9719 |
| Multi-view omnidirectional vision system | 0.9916 | 1.0280 | 0.9861 | 0.9665 | 1.5773 | 0.9156 | 1.0775 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Grigorev, M.A.; Zhang, Z.; Kholodilin, I.; Li, B. Multi-View Omnidirectional Vision and Structured Light for High-Precision Mapping and Reconstruction. Sensors 2025, 25, 6485. https://doi.org/10.3390/s25206485
Guo Q, Grigorev MA, Zhang Z, Kholodilin I, Li B. Multi-View Omnidirectional Vision and Structured Light for High-Precision Mapping and Reconstruction. Sensors. 2025; 25(20):6485. https://doi.org/10.3390/s25206485
Chicago/Turabian StyleGuo, Qihui, Maksim A. Grigorev, Zihan Zhang, Ivan Kholodilin, and Bing Li. 2025. "Multi-View Omnidirectional Vision and Structured Light for High-Precision Mapping and Reconstruction" Sensors 25, no. 20: 6485. https://doi.org/10.3390/s25206485
APA StyleGuo, Q., Grigorev, M. A., Zhang, Z., Kholodilin, I., & Li, B. (2025). Multi-View Omnidirectional Vision and Structured Light for High-Precision Mapping and Reconstruction. Sensors, 25(20), 6485. https://doi.org/10.3390/s25206485








