Design Method of a Wide-Field, Dual-Slit, Low-Distortion, and High-Sensitivity Hyperspectral Imager
Abstract
1. Introduction
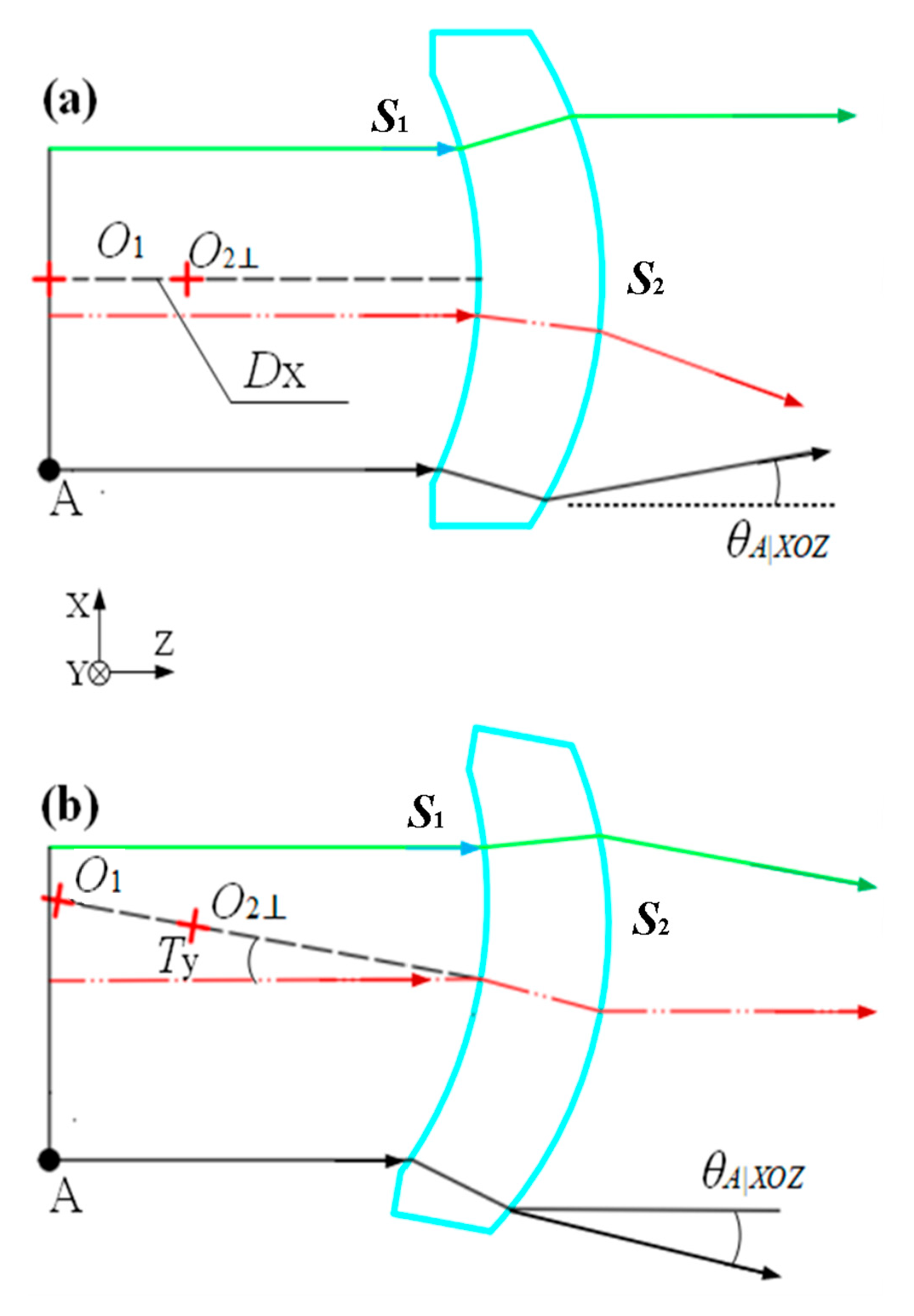
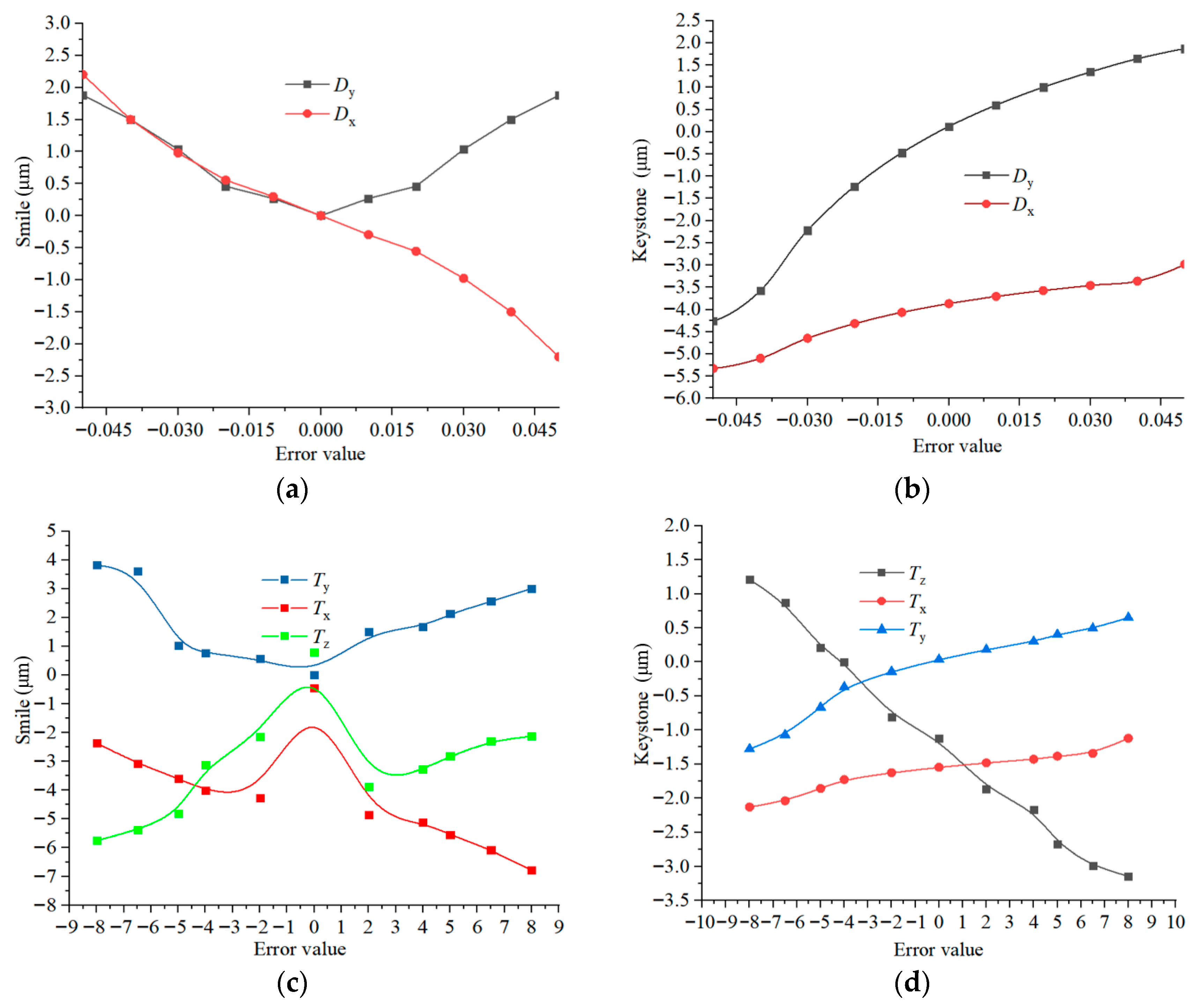
2. Impact of Processing and Assembly Errors on Spectral Performance
3. Spectroscopic System Design
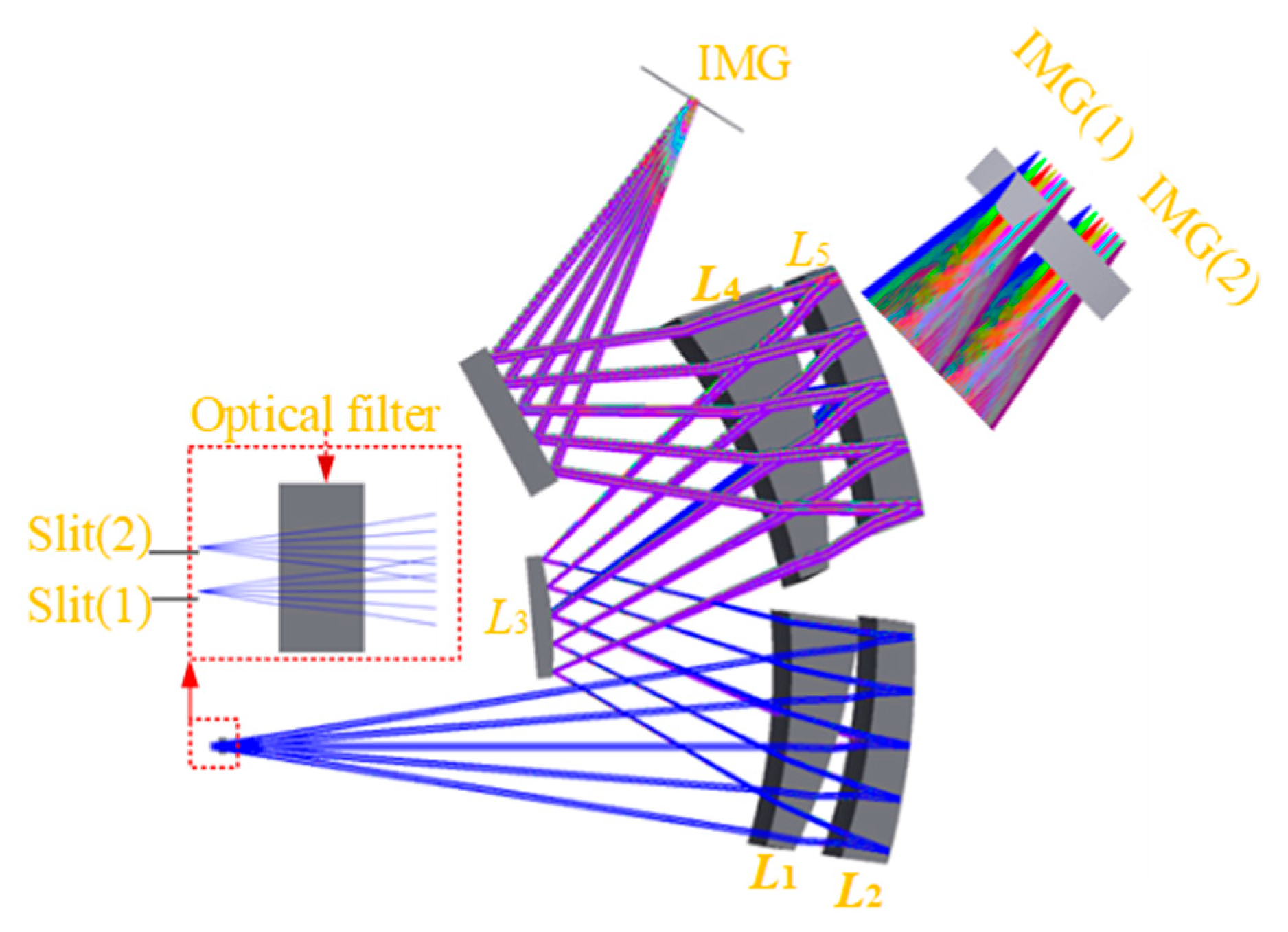
3.1. System Design
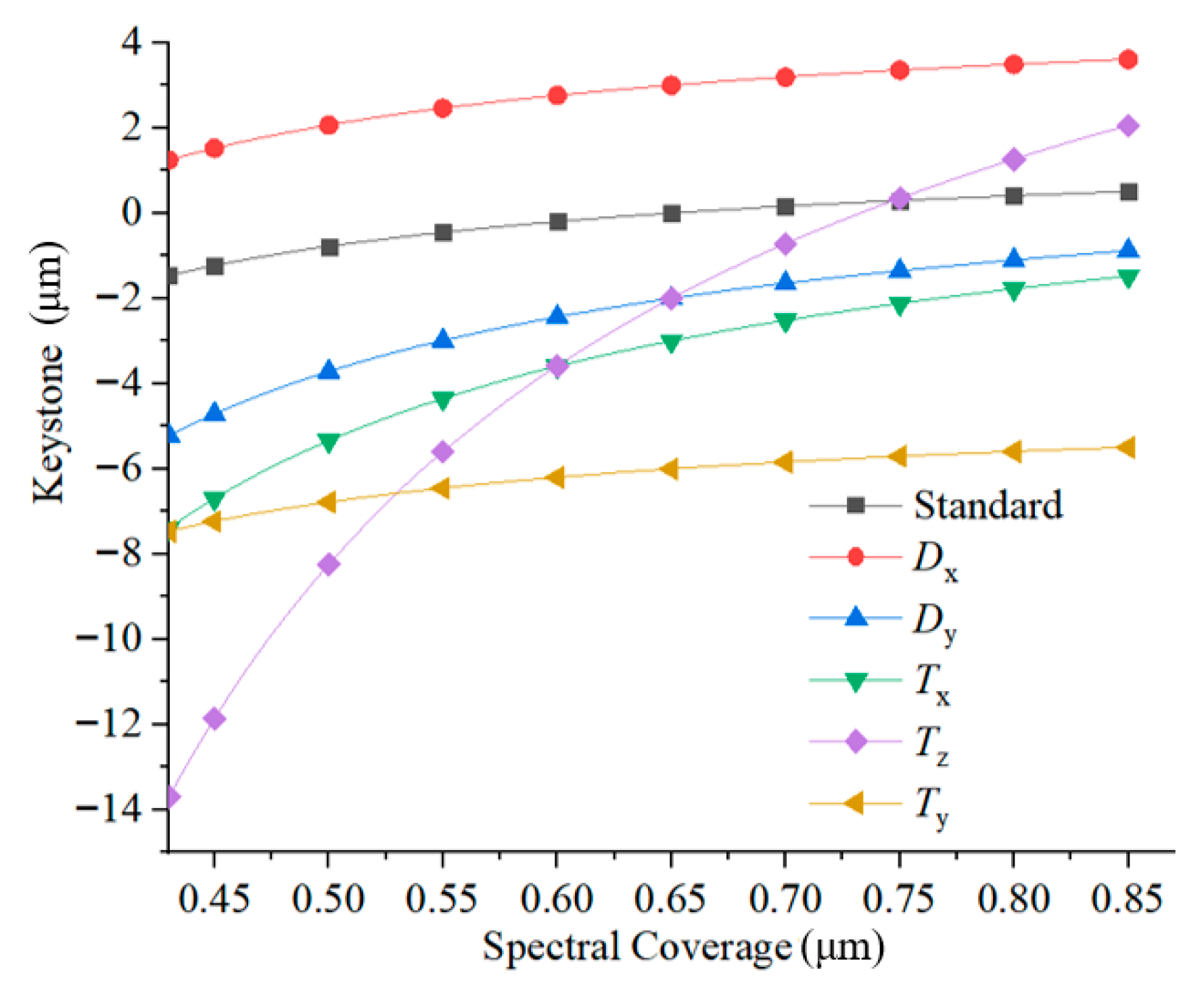
3.2. System Assembly Tolerance Analysis
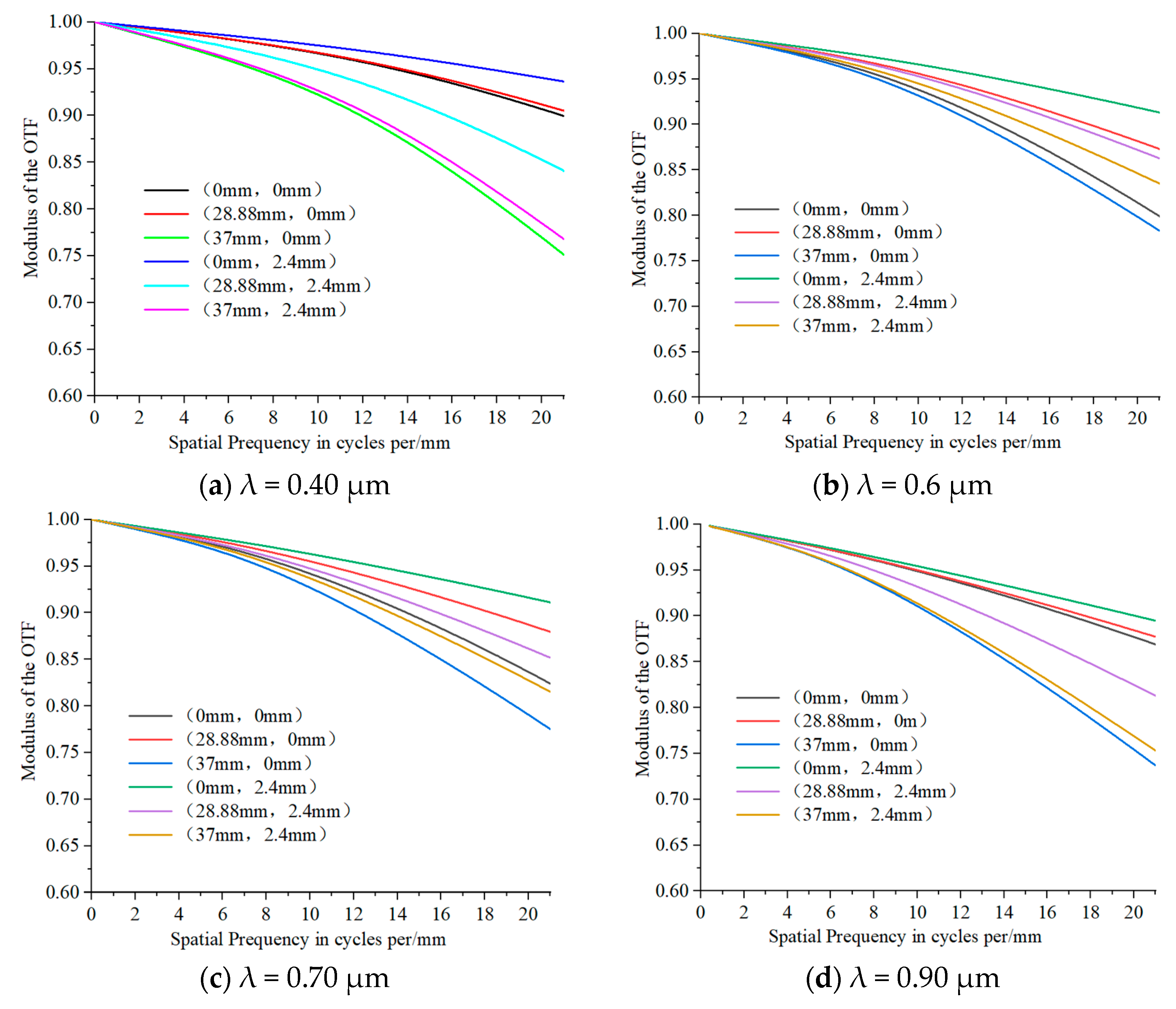
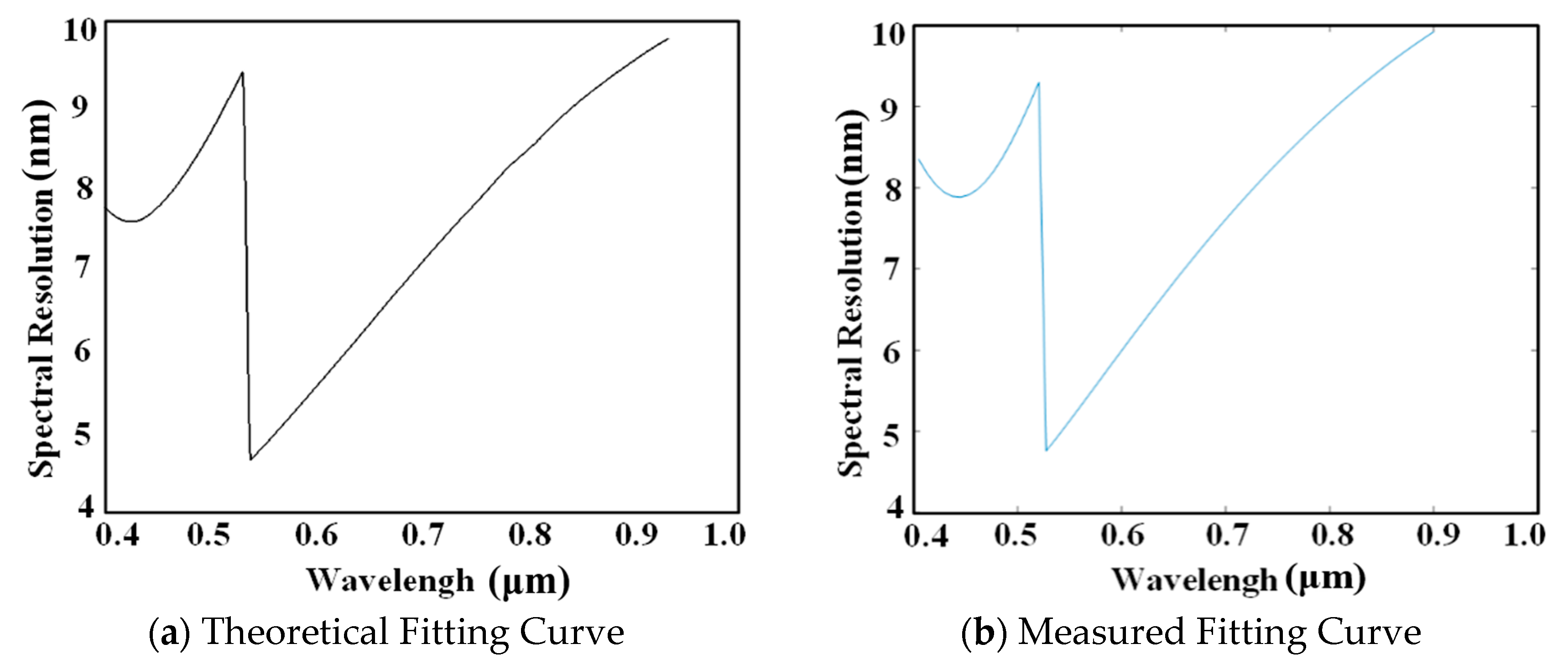
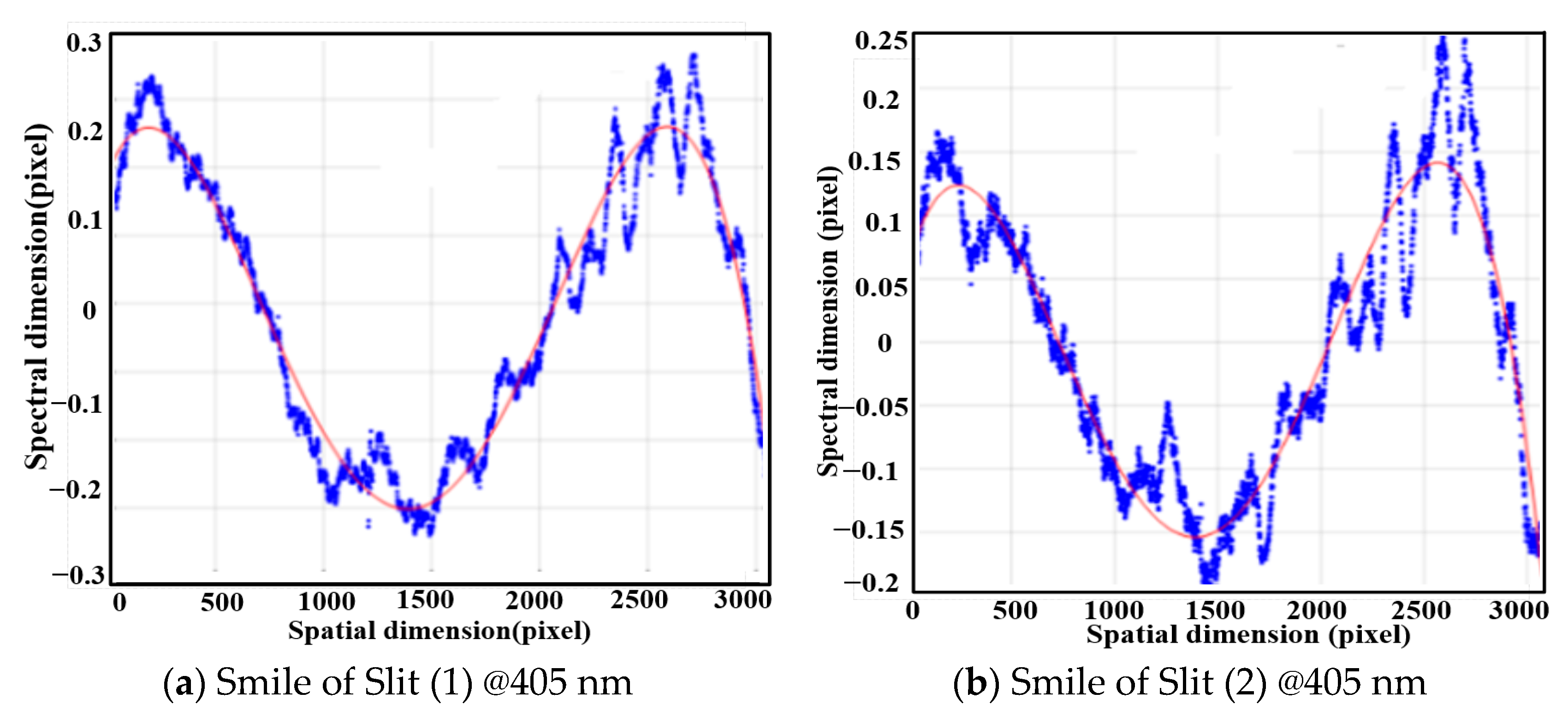
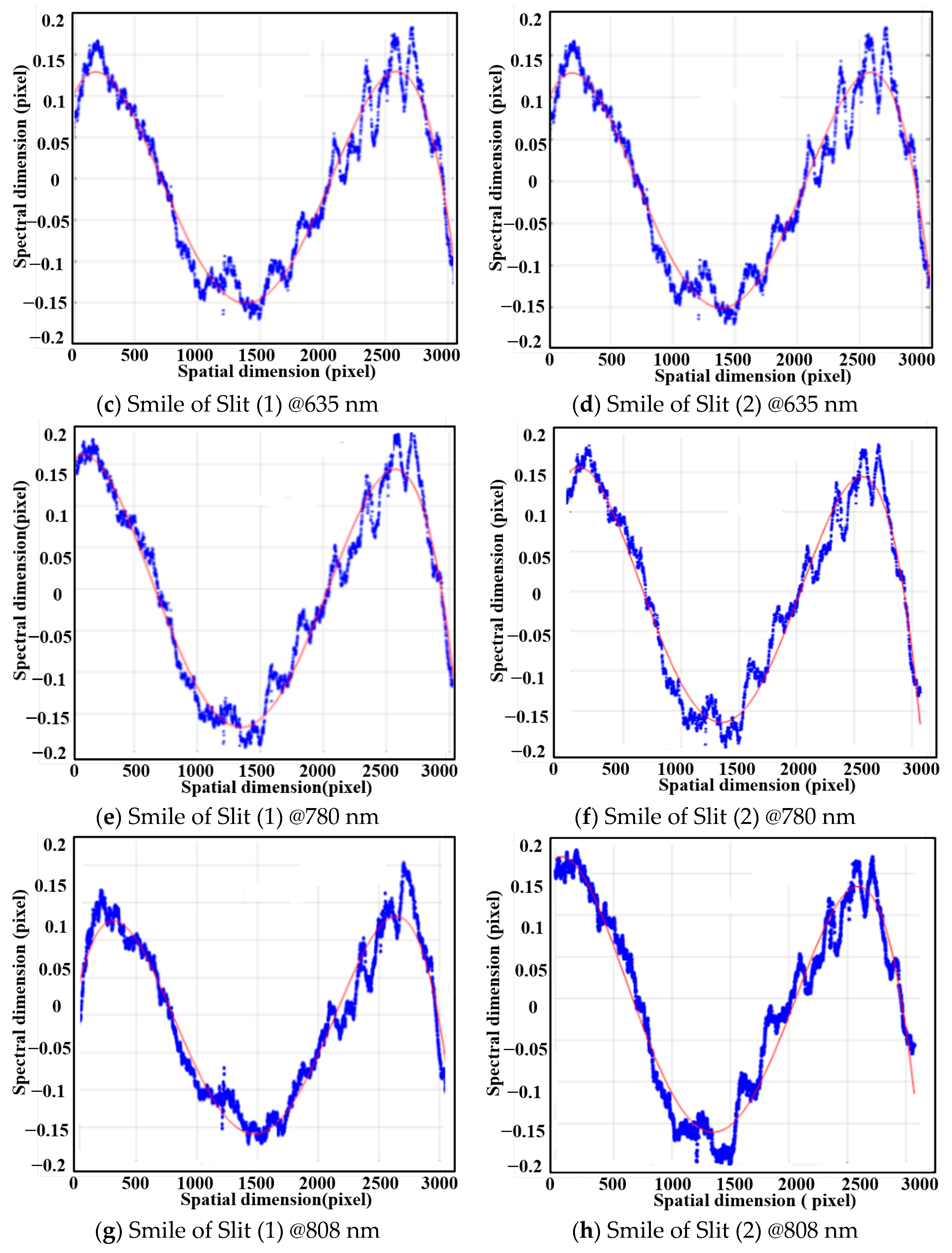
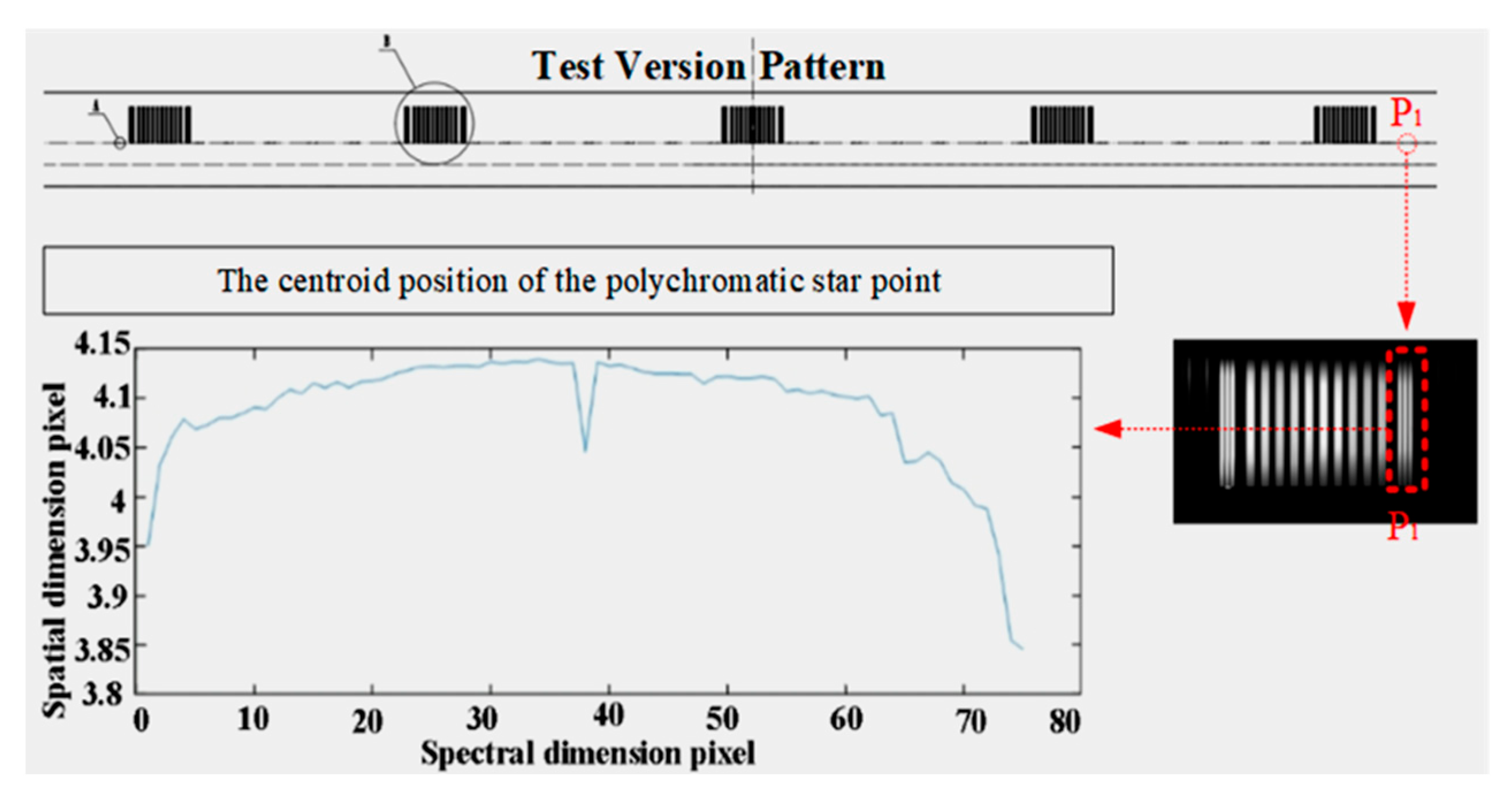
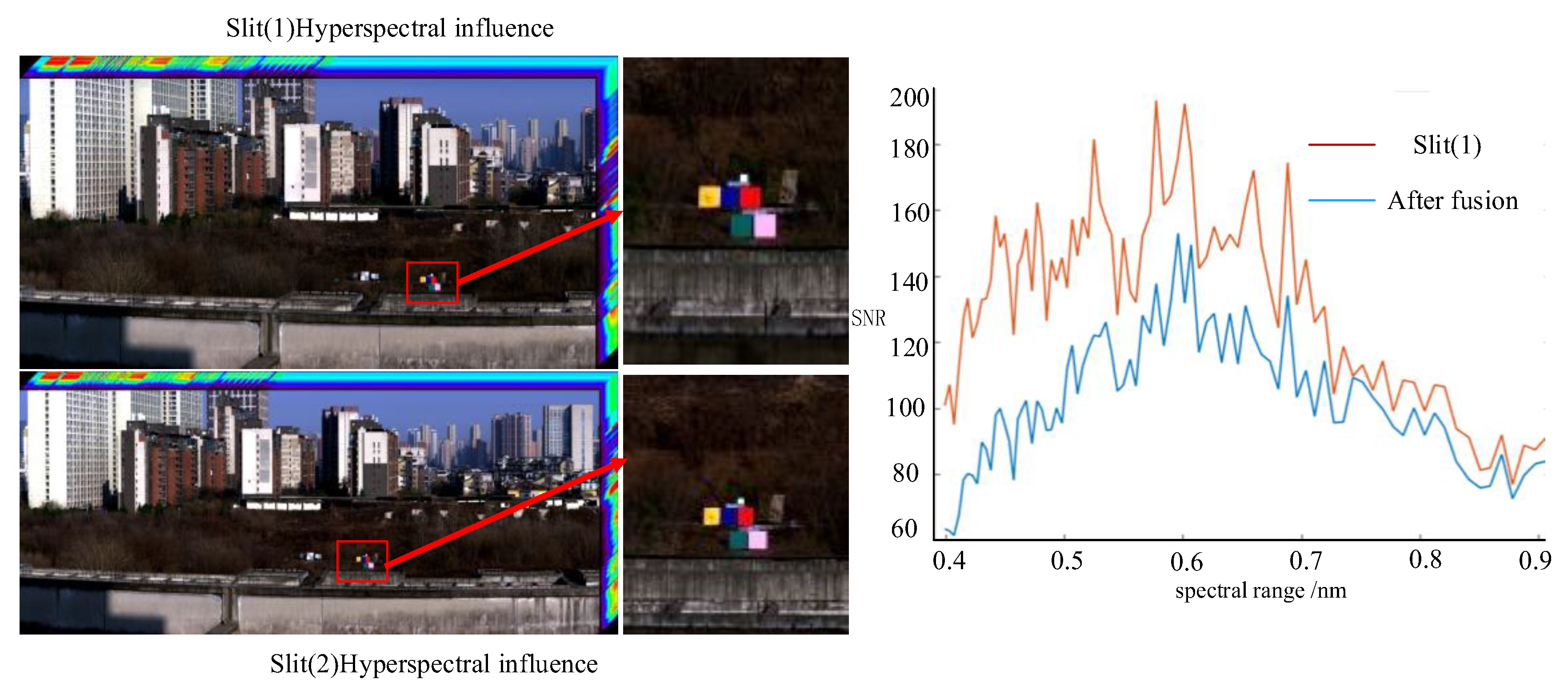
4. Performance Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hang, L.; Liao, N.; Li, H. High resolution ultraviolet imaging spectrometer for latent image analysis. Opt. Express 2016, 24, 6459–6468. [Google Scholar] [CrossRef] [PubMed]
- Sinitsa, L.N.; Serdyukov, V.I.; Emelyanov, N.M.; Marinina, A.; Perevalov, V. LED-based Fourier transform spectroscopy of 14N2 16O in the 9750-12050 cm−1 regions. J. Quant. Spectrosc. Radiat. Transf. 2024, 315, 108888. [Google Scholar] [CrossRef]
- Wu, T.; Li, G.; Yang, Z. Shortwave infrared imaging spectroscopy for analysis of ancient paintings. Appl. Spectrosc. 2017, 71, 977–987. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.C.; Tang, Y.G.; Han, P.; Pan, M.Z.; Zhang, J.N. Development of diagnostic imaging spectrometer for tumor on-line operation. Opt. Precis. Eng. 2013, 2, 3043–3049. [Google Scholar] [CrossRef]
- Bendor, E.; Chabrillat, S.; Demattê, J.A.M. Using imaging spectroscopy to study soil properties. Remote Sens. Environ. 2009, 113, S38–S55. [Google Scholar] [CrossRef]
- Sullenberger, R.M.; Milstein, A.B.; Rachlin, Y. Computational reconfigurable imaging spectrometer. Opt. Express 2017, 25, 31960–31969. [Google Scholar] [CrossRef] [PubMed]
- Hagen, N.; Kudenov, M.W. Review of snapshot spectral imaging technologies. Opt. Eng. 2013, 52, 090901. [Google Scholar] [CrossRef]
- Féry, C. A prism with curved faces, for spectrograph or spectroscope. Astrophys. J. Lett. 1911, 34, 79. [Google Scholar]
- Cutter, M.A.; Lobb, D.R.; Williams, T.L.; Renton, R.E. Integration and testing of the compact high-resolution imaging spectrometer (CHRIS). In Proceedings of the SPIE-The International Society for Optical Engineering 1999, Denver, CO, USA, 18–23 July 1999. [Google Scholar]
- Kim, D.H.; Yang, S.; Cheon, D.-I.; Lee, S.; Oh, H.-S. Combined estimation method for inertia properties of STSAT-3. J. Mech. Sci. Technol. 2010, 24, 1737–1741. [Google Scholar] [CrossRef]
- Kaiser, S.; Sang, B.; Schubert, J.; Hofer, S.; Stuffler, T. Compact prism spectrometer of pushbroom type for hyperspectral imaging. In Proceedings of the SPIE—The International Society for Optical Engineering 2008, Scotland, UK, 1 September 2008. [Google Scholar]
- Nie, Y.F.; Bin, X.; Zhou, J.S.; Huang, M. A Wide-Field Push-Broom Hyperspectral Imager Based on Curved Prism. Spectrosc. Spectr. Anal. 2012, 32, 1708–1711. [Google Scholar]
- Moore, L.B.; Bender, H.A.; Bradley, C.L.; Haag, J.M.; Zandbergen, S.; Green, R.O.; Mouroulis, P. Recent developments in tolerancing methods forimaging spectrometers. In Proceedings of the Optical System Alignment, Tolerancing, and Verification XIII, Online, 24 August–4 September 2020. [Google Scholar]
- Ku, H.; Kim, S.H.; Kong, H.J.; Lee, J.H. Optical design; performance, and tolerancing of an Offner imaging spectrograph. In Proceedings of the Optical System Alignment, Tolerancing, and Verification VI, San Diego, CA, USA, 12–16 August 2012. [Google Scholar]
- Feng, L.; Zhou, J.; Wei, L.; He, X.; Li, Y.; Jing, J.; Xiangli, B. Design of a compact wide-spectrum double-channel prism imaging spectrometer with freeform surface. Appl. Opt. 2018, 57, 9512–9522. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Zhou, J.; Li, Y.; Feng, L. Spectral curvature correction method based on inverse on inverse distance weighted interpolation. In Proceedings of the Image and Signal Processing for Remote Sensing XXII, Edinburgh, UK, 26–29 September 2016. [Google Scholar]
- Ji, Y.; Han, J.; Zhao, S.W.C. Ultra-compact dual band imaging spectrometer with freeform prisms. Appl. Opt. 2023, 62, 5991–5998. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Fang, X.; Li, T.; Wang, X.X.; Gu, G.C.; Li, H.S.; Lin, G.Y.; Li, B. Design method for eliminating spectral line tilt in a multiple sub-pupil ultra-spectral imager (MSPUI). Opt. Express 2024, 32, 17. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Lin, C.; Ji, Z.; Wu, H.; Li, C.; Du, B.; Zheng, Y. Design of a compact hyperspectral imagingspectrometer with freeform surface based on anastigmatism. Appl. Opt. 2020, 59, 1715–1725. [Google Scholar] [CrossRef] [PubMed]






| Parameters | Value |
|---|---|
| Wavelength | 0.4 μm~0.9 μm |
| Spectral Resolution | ≤10 nm |
| Width of Slit | 24 μm |
| Length of Slit | 73 mm |
| Pixel size | 24 μm |
| Image format | 3072 × 256 |
| Relative aperture | 0.15 |
| Spectral band | 68 |
| lateral magnification | 1:1 |
| Spectral lateral deviation | ≤3 nm |
| Spectral keystone | ≤0.3 pixel |
| Object’s telecentricity | ≤0.5° |
| Type | Curvature /mm | Prism Thickness /mm | Air Space /mm | Optical Material | Prism Wedge Angle/° | Off-Axis/mm | Tilt /° |
|---|---|---|---|---|---|---|---|
| L1 | −367.82 | 38 | 50.82 | H-K9L | 10.391 | 11.2 | 5.85 |
| −418.365 | |||||||
| L2 | −426.95 | 26.5 | 149.7 | H-TF8 | 2.256 | 5.1 | 8.98 |
| −449 | |||||||
| L3 | −218.02 | 40 | 127.5 | F_SILICA | - | 80 | −5.64 |
| L4 | −383.5 | 61.7 | 52 | H-K9L | 13.15 | 185.55 | −26.05 |
| −415.323 | |||||||
| L5 | −435.486 | 35.51 | 26 | H-TF8 | 4.213 | 209.5 | −16.83 |
| −460.724 |
| Type | ΔR/mm | Δd/mm | Δθy/° | RMS @632.8 nm |
|---|---|---|---|---|
| L1 | 0.047 | 0.03 | 10.4° | 1/45λ |
| L2 | 0.051 | 0.03 | 2.2° | 1/45λ |
| L3 | 0.02 | 0.1 | - | 1/70λ |
| L4 | 0.036 | 0.03 | 13.06° | 1/45λ |
| L5 | 0.041 | 0.03 | 3.91° | 1/45λ |
| Relative Positional Deviation | Notes | ||||||
|---|---|---|---|---|---|---|---|
| Type | Δx (mm) | Δy (mm) | Δz (mm) | Δθx (°) | Δθy (°) | Δθz (°) | |
| L1 | 0.03 | 0.03 | 0.03 | 15″ | 15″ | 15″ | |
| L2 | 0.03 | 0.03 | 0.03 | 15″ | 15″ | 15″ | Compensator |
| L3 | - | - | - | - | - | - | Reference |
| L4 | 0.03 | 0.03 | 0.03 | 10″ | 10″ | 15″ | |
| L5 | 0.03 | 0.03 | 0.03 | 10″ | 10″ | 15″ | Compensator |
| Type | Tilt Error | Eccentric Error | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔSmile (μm) | ΔKeystone (μm) | ΔSmile (μm) | ΔKeystone (μm) | |||||||
| θx | θy | θz | θx | θy | θz | Δx | Δy | Δx | Δy | |
| L1 | 0.115 | 0.126 | 0.415 | 0.02 | 0.05 | 0.08 | 0.045 | 0.04 | 0.024 | 0.003 |
| L2 | 0.821 | 0.002 | 0.13 | 0.041 | 0.00112 | 0.1 | 0.005 | 0.351 | 0.003 | 0.005 |
| L4 | 0.182 | 0.648 | 0.537 | 0.03 | 0.018 | 0.12 | 0.41 | 0.04 | 0.21 | 0.015 |
| L5 | 0.4798 | 0.33 | 0.145 | 0.042 | 0.121 | 0.27 | 0.012 | 0.017 | 0.142 | 0.021 |
| RSS | 1.412 | 0.3548 | 0.544958 | 0.256 | ||||||
| Type | Slit(1) MTF Average | Slit(2) MTF Average | ||||
|---|---|---|---|---|---|---|
| −1 h | 0 h | 1 h | −1 h | 0 h | 1 h | |
| 405 nm | 0.5279 | 0.5549 | 0.4467 | 0.521 | 0.505 | 0.489 |
| 635 nm | 0.541 | 0.5611 | 0.5112 | 0.571 | 0.552 | 0.478 |
| 780 nm | 0.504 | 0.545 | 0.481 | 0.578 | 0.567 | 0.459 |
| 808 nm | 0569 | 0.563 | 0.487 | 0.584 | 0.508 | 0.487 |
| Number | Wavelength /nm | Smile /pixel | Spectral Resolution/nm | Spectral Lateral Deviation/nm |
|---|---|---|---|---|
| 1 | 405 nm | 0.3669 | 3.7 nm | 1.36 nm |
| 2 | 635 nm | 0.2270 | 6.5 nm | 1.48 nm |
| 3 | 780 nm | 0.3286 | 8.7 nm | 2.86 nm |
| 4 | 808 nm | 0.1848 | 9.0 nm | 1.66 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, S.; Zhang, Z.; Feng, X.; Shen, Z.; Lu, X.; Gao, M. Design Method of a Wide-Field, Dual-Slit, Low-Distortion, and High-Sensitivity Hyperspectral Imager. Sensors 2025, 25, 6478. https://doi.org/10.3390/s25206478
Li X, Li S, Zhang Z, Feng X, Shen Z, Lu X, Gao M. Design Method of a Wide-Field, Dual-Slit, Low-Distortion, and High-Sensitivity Hyperspectral Imager. Sensors. 2025; 25(20):6478. https://doi.org/10.3390/s25206478
Chicago/Turabian StyleLi, Xijie, Siyuan Li, Zhinan Zhang, Xiangpeng Feng, Zhong Shen, Xin Lu, and Ming Gao. 2025. "Design Method of a Wide-Field, Dual-Slit, Low-Distortion, and High-Sensitivity Hyperspectral Imager" Sensors 25, no. 20: 6478. https://doi.org/10.3390/s25206478
APA StyleLi, X., Li, S., Zhang, Z., Feng, X., Shen, Z., Lu, X., & Gao, M. (2025). Design Method of a Wide-Field, Dual-Slit, Low-Distortion, and High-Sensitivity Hyperspectral Imager. Sensors, 25(20), 6478. https://doi.org/10.3390/s25206478





