Effect of Walking Speed on the Reliability of a Smartphone-Based Markerless Gait Analysis System
Abstract
Highlights
- OpenCap showed excellent agreement with MoCap for spatiotemporal gait parameters and continuous joint kinematics across different walking speeds.
- Discrete joint range of motion (especially at the hip and ankle) exhibited lower and speed-dependent reliability, although systematic biases remained small and clinically acceptable.
- OpenCap can be reliably applied for gait assessment and monitoring of spatiotemporal and continuous kinematic variables across various walking speeds.
- Clinicians should interpret range of motion outcomes with caution at higher speeds, as their accuracy decreases compared with marker-based measurements.
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
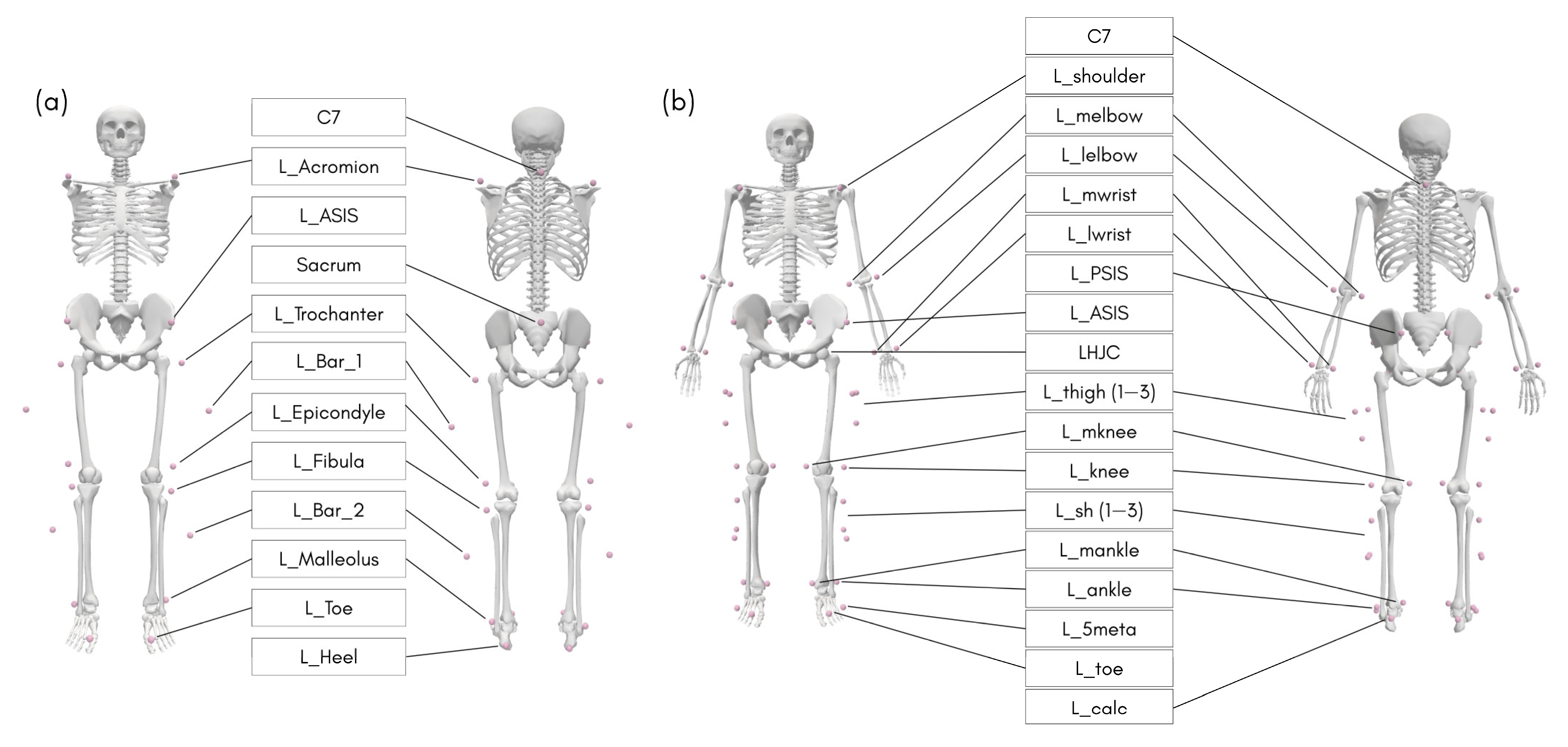
2.2. Experimental Setup
2.3. Recordings
2.3.1. MoCap
2.3.2. OpenCap
2.4. Raw Data Processing
2.5. Experimental Variables
2.5.1. Spatiotemporal
2.5.2. Joint Angles
2.6. Statistics
3. Results
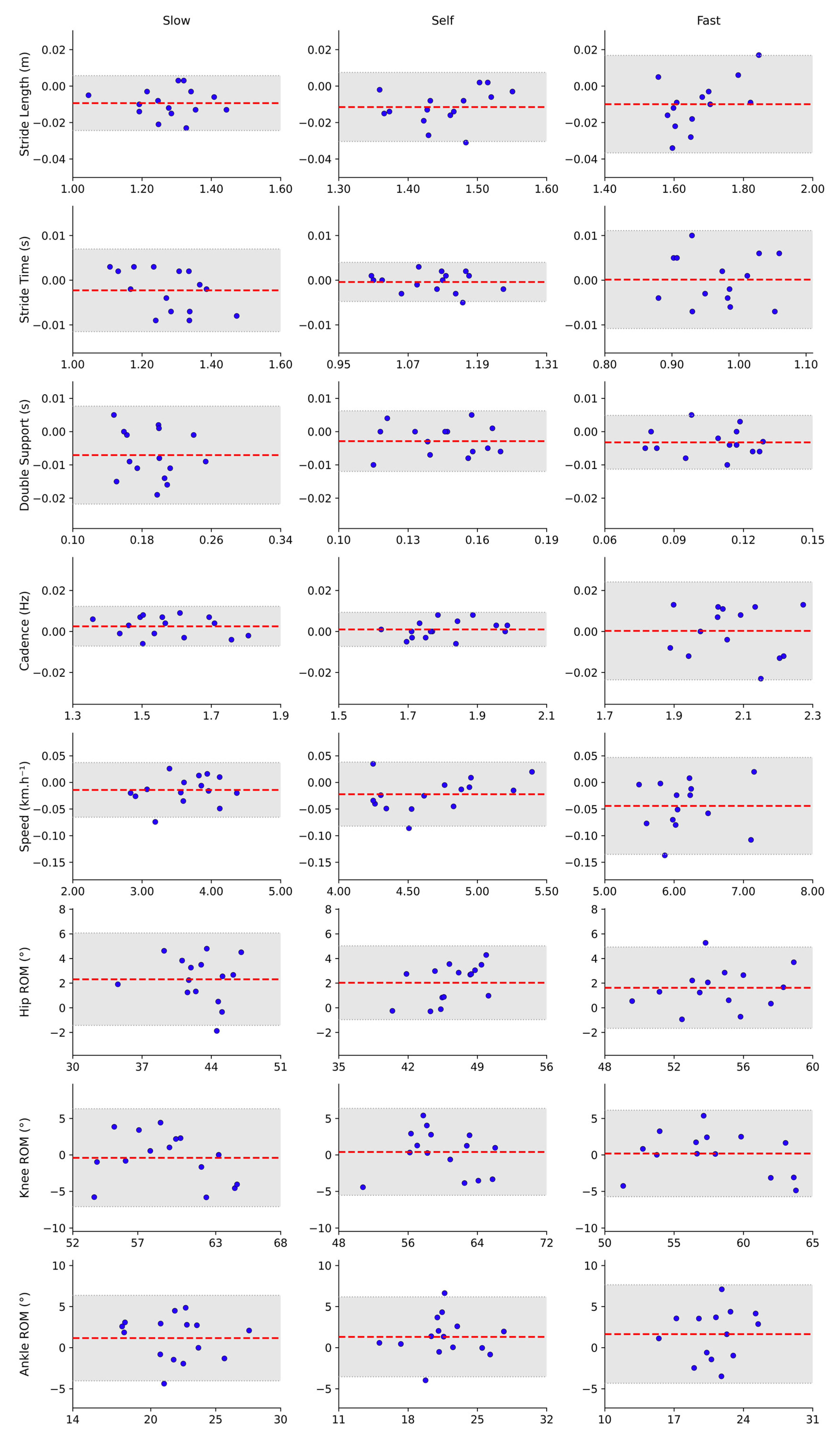
3.1. Agreement for Discrete Variables
3.1.1. Speed Condition Agreement
3.1.2. Speed vs. System Interaction and Effects
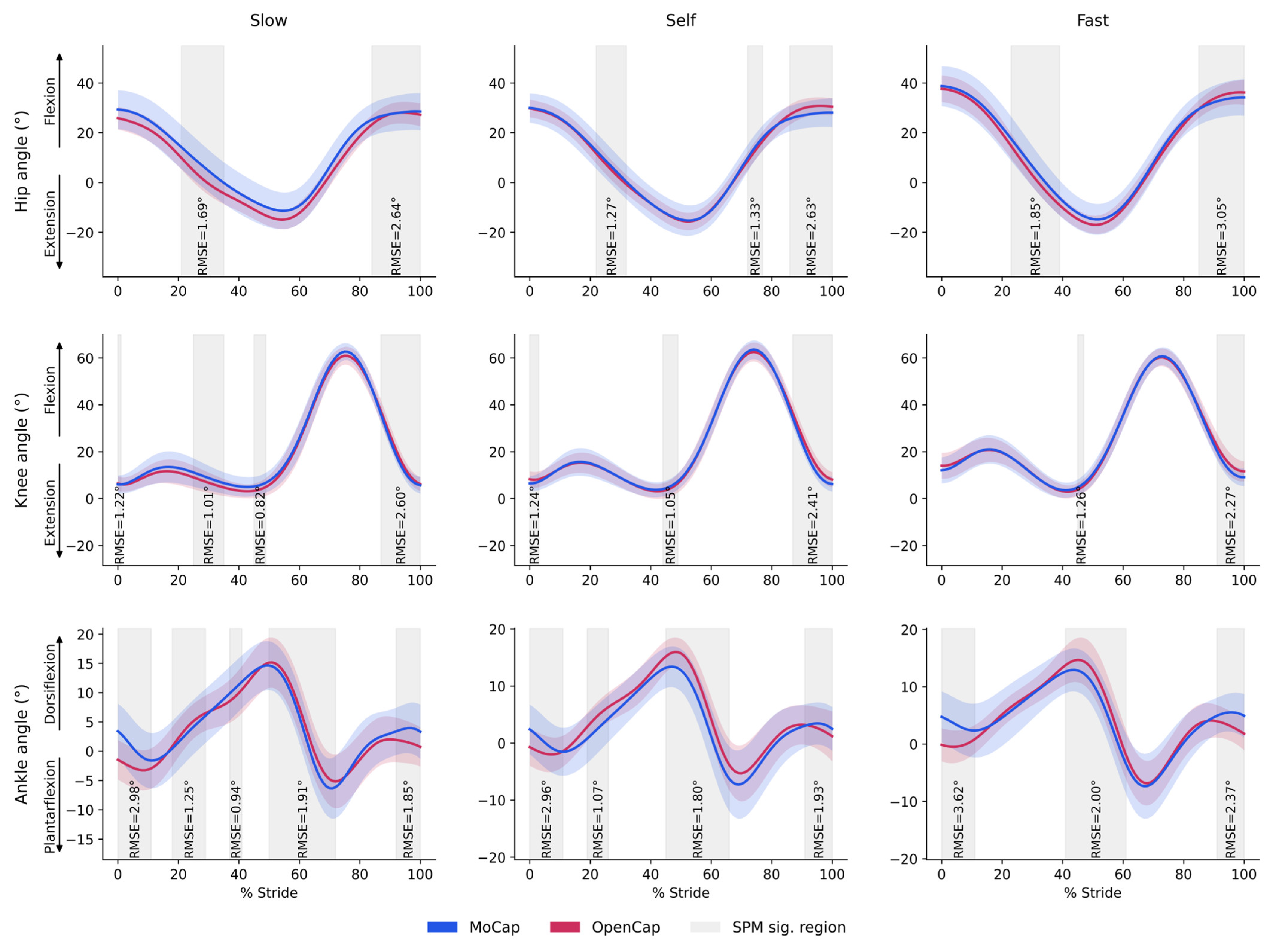
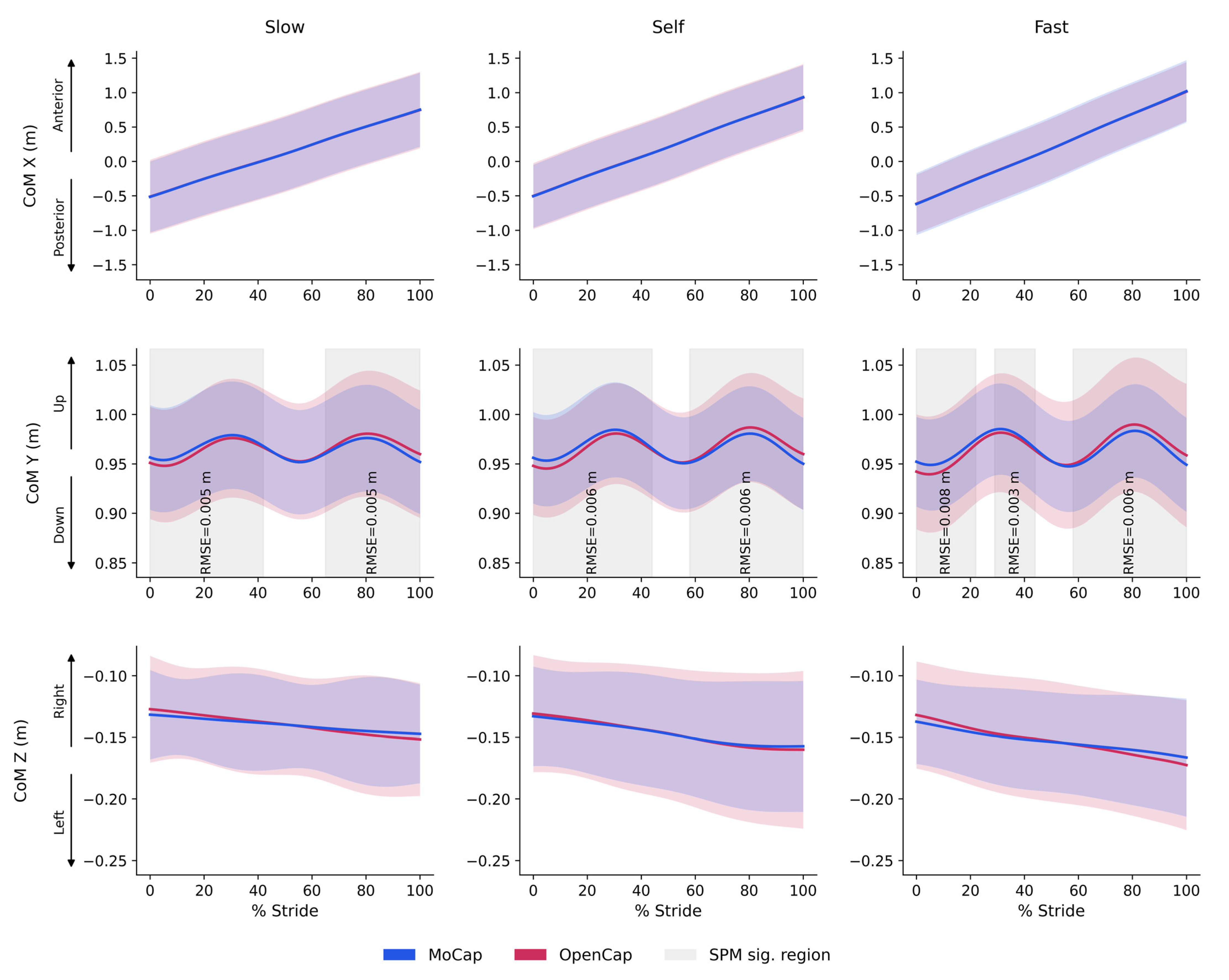
3.2. Agreement for Continuous Joint Angle Variables
Speed Condition Agreement
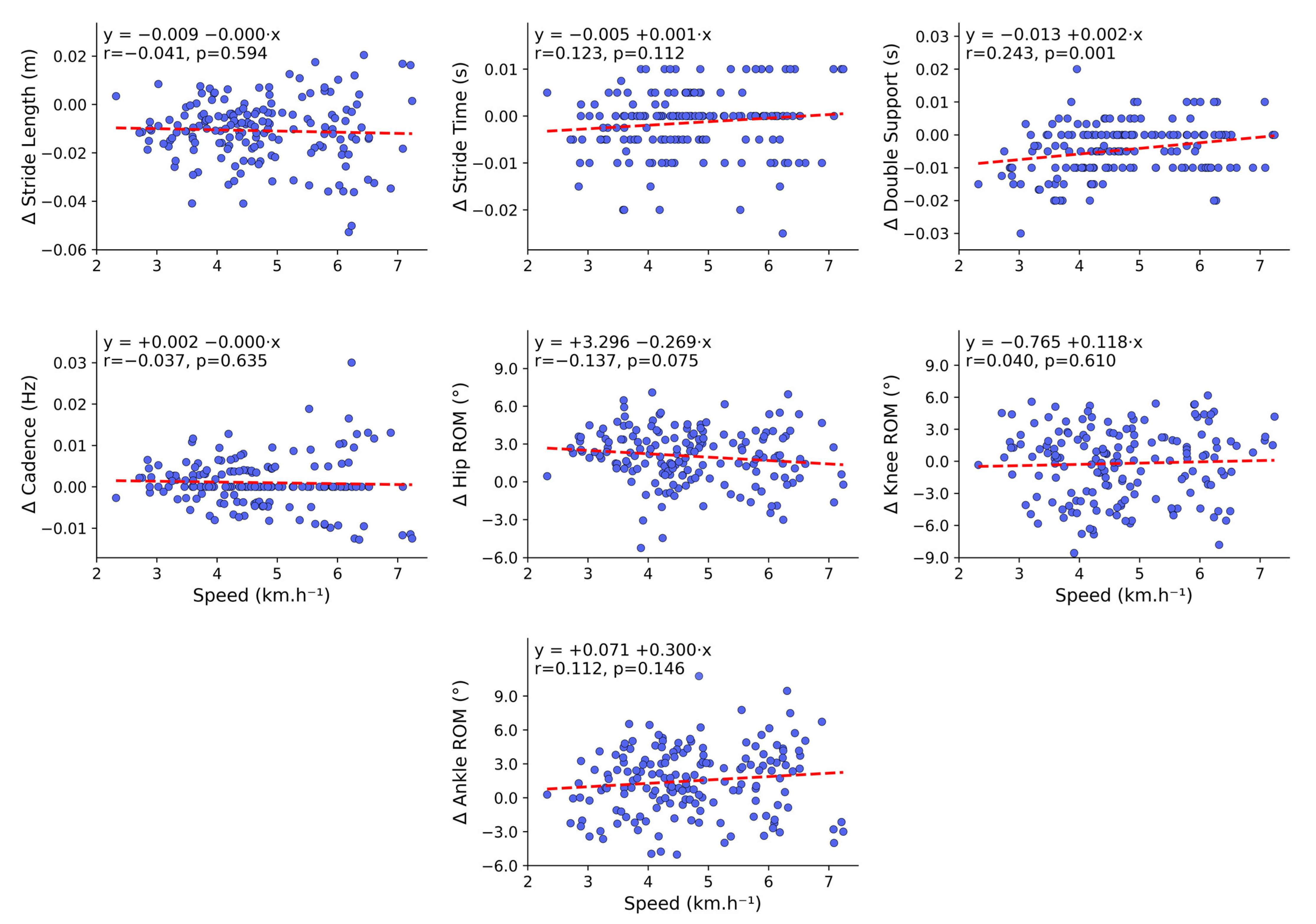
3.3. Relationship and Differences Between Walking Speeds and Between-System Error
4. Discussion
4.1. Agreement for Discrete Variables: Spatiotemporal Parameters
4.2. Agreement for Discrete Variables: Range of Motion Parameters
4.3. Agreement for Continuous Variables: Center of Mass Displacement
4.4. Agreement for Continuous Variables: Range of Motion Parameters
4.5. Relationship and Differences Between Walking Speeds and Between-System Error
4.6. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CoM | Center of Mass |
| G-G | Greenhouse–Geisser |
| ICC | Intraclass Correlation Coefficients |
| LoA | Limits of Agreement |
| MDC | Minimal Detectable Change |
| MoCap | Marker-based Motion Capture |
| .mot | Joint Angle Data |
| ROM | Range of Motion |
| RMSE | Root Mean Square Error |
| SPM | Statistical Parametric Mapping |
| TD | Touchdown |
| TO | Take-off |
| .trc | Three-dimensional Marker Position |
References
- Hausdorff, J.M. Gait Dynamics, Fractals and Falls: Finding Meaning in the Stride-to-Stride Fluctuations of Human Walking. Hum. Mov. Sci. 2007, 26, 555–589. [Google Scholar] [CrossRef]
- Gomeñuka, N.A.; Oliveira, H.B.; Silva, E.S.; Costa, R.R.; Kanitz, A.C.; Liedtke, G.V.; Schuch, F.B.; Peyré-Tartaruga, L.A. Effects of Nordic Walking Training on Quality of Life, Balance and Functional Mobility in Elderly: A Randomized Clinical Trial. PLoS ONE 2019, 14, e0211472. [Google Scholar] [CrossRef]
- Baker, R. Gait Analysis Methods in Rehabilitation. J. Neuroeng. Rehabil. 2006, 3, 4. [Google Scholar] [CrossRef]
- Monteiro, E.P.; Franzoni, L.T.; Cubillos, D.M.; de Oliveira Fagundes, A.; Carvalho, A.R.; Oliveira, H.B.; Pantoja, P.D.; Schuch, F.B.; Rieder, C.R.; Martinez, F.G.; et al. Effects of Nordic Walking Training on Functional Parameters in Parkinson’s Disease: A Randomized Controlled Clinical Trial. Scand. J. Med. Sci. Sports 2017, 27, 351–358. [Google Scholar] [CrossRef]
- Prasanth, H.; Caban, M.; Keller, U.; Courtine, G.; Ijspeert, A.; Vallery, H.; Von Zitzewitz, J. Wearable Sensor-Based Real-Time Gait Detection: A Systematic Review. Sensors 2021, 21, 2727. [Google Scholar] [CrossRef]
- Upadhyay, A.; Shukla, A.; Sharma, M.; Abraham, A. Simple yet Robust Markerless Motion Capture System Using Deep Learning. Eng. Appl. Artif. Intell. 2025, 160, 111905. [Google Scholar] [CrossRef]
- Uhlrich, S.D.; Falisse, A.; Kidziński, Ł.; Muccini, J.; Ko, M.; Chaudhari, A.S.; Hicks, J.L.; Delp, S.L. OpenCap: Human Movement Dynamics from Smartphone Videos. PLoS Comput. Biol. 2023, 19, e1011462. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xu, W.; Wu, Z.; Zhang, H.; Wang, B.; Zhou, Z.; Wang, C.; Li, K.; Nie, Y. Evaluation of a Smartphone-Based Markerless System to Measure Lower-Limb Kinematics in Patients with Knee Osteoarthritis. J. Biomech. 2025, 181, 112529. [Google Scholar] [CrossRef]
- Min, Y.-S.; Jung, T.-D.; Lee, Y.-S.; Kwon, Y.; Kim, H.J.; Kim, H.C.; Lee, J.C.; Park, E. Biomechanical Gait Analysis Using a Smartphone-Based Motion Capture System (Opencap) in Patients with Neurological Disorders. Bioengineering 2024, 11, 911. [Google Scholar] [CrossRef] [PubMed]
- Horsak, B.; Kainz, H.; Dumphart, B. Repeatability and Minimal Detectable Change Including Clothing Effects for Smartphone-Based 3D Markerless Motion Capture. J. Biomech. 2024, 175, 112281. [Google Scholar] [CrossRef] [PubMed]
- Martiš, P.; Košutzká, Z.; Kranzl, A. A Step Forward Understanding Directional Limitations in Markerless Smartphone-Based GAIT Analysis: A Pilot Study. Sensors 2024, 24, 3091. [Google Scholar] [CrossRef] [PubMed]
- Svetek, A.; Morgan, K.; Burland, J.; Glaviano, N.R. Validation of OpenCap on Lower Extremity Kinematics during Functional Tasks. J. Biomech. 2025, 183, 112602. [Google Scholar] [CrossRef]
- de Borba, E.F.; da Silva, E.S.; de Liz Alves, L.; Da Silva Neto, A.R.; Inda, A.R.; Ibrahim, B.M.; Ribas, L.R.; Correale, L.; Peyré-Tartaruga, L.A.; Tartaruga, M.P. Fatigue-Related Changes in Running Technique and Mechanical Variables After a Maximal Incremental Test in Recreational Runners. J. Appl. Biomech. 2024, 40, 424–431. [Google Scholar] [CrossRef]
- Jaén-Carrillo, D.; Ruiz-Alias, S.A.; Chicano-Gutiérrez, J.M.; Ruiz-Malagón, E.J.; Roche-Seruendo, L.E.; García-Pinillos, F. Test-Retest Reliability of the MotionMetrix Software for the Analysis of Walking and Running Gait Parameters. Sensors 2022, 22, 3201. [Google Scholar] [CrossRef]
- Moran, M.F.; Rogler, I.C.; Wager, J.C. Inter-Session Repeatability of Marker-Less Motion Capture of Treadmill Running Gait. Appl. Sci. 2023, 13, 1702. [Google Scholar] [CrossRef]
- Walker, J.; Thomas, A.; Lunn, D.E.; Nicholson, G.; Tucker, C.B. Concurrent Validity of Theia3D Markerless Motion Capture for Detecting Sagittal Kinematic Differences between Gait Speeds. J. Sports Sci. 2025, 43, 1560–1571. [Google Scholar] [CrossRef]
- Middleton, A.; Fritz, S.L.; Lusardi, M. Walking Speed: The Functional Vital Sign. J. Aging Phys. Act. 2015, 23, 314–322. [Google Scholar] [CrossRef] [PubMed]
- Bona, R.L.; Gomeñuka, N.A.; Storniolo, J.L.L.; Bonezi, A.; Biancardi, C.M. Self-Selected Walking Speed in Individuals with Transfemoral Amputation: Recovery, Economy and Rehabilitation Index. Eur. J. Physiother. 2020, 22, 133–140. [Google Scholar] [CrossRef]
- Peyré-Tartaruga, L.; Passos-Monteiro, E. A New Integrative Approach to Evaluate Pathological Gait: Locomotor Rehabilitation Index. Clin. Transl. Degener. Dis. 2016, 86–90. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, W.; Wang, L.; Zhou, H.; Chen, Z.; Zhang, Q.; Li, G. Smartphone Videos-Driven Musculoskeletal Multibody Dynamics Modelling Workflow to Estimate the Lower Limb Joint Contact Forces and Ground Reaction Forces. Med. Biol. Eng. Comput. 2024, 62, 3841–3853. [Google Scholar] [CrossRef]
- Davis III, R.B.; Ounpuu, S.; Tyburski, D.; Gage, J.R. A Gait Analysis Data Collection and Reduction Technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Lai, A.K.M.; Arnold, A.S.; Wakeling, J.M. Why Are Antagonist Muscles Co-Activated in My Simulation? A Musculoskeletal Model for Analysing Human Locomotor Tasks. Ann. Biomed. Eng. 2017, 45, 2762–2774. [Google Scholar] [CrossRef]
- Rajagopal, A.; Dembia, C.L.; DeMers, M.S.; Delp, D.D.; Hicks, J.L.; Delp, S.L. Full-Body Musculoskeletal Model for Muscle-Driven Simulation of Human Gait. IEEE Trans. Biomed. Eng. 2016, 63, 2068–2079. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 0470398183. [Google Scholar]
- Zeni, J.A., Jr.; Richards, J.G.; Higginson, J. Two Simple Methods for Determining Gait Events during Treadmill and Overground Walking Using Kinematic Data. Gait Posture 2008, 27, 710–714. [Google Scholar] [CrossRef]
- Mishra, P.; Pandey, C.M.; Singh, U.; Gupta, A.; Sahu, C.; Keshri, A. Descriptive Statistics and Normality Tests for Statistical Data. Ann. Card. Anaesth. 2019, 22, 67–72. [Google Scholar] [CrossRef] [PubMed]
- McGinley, J.L.; Baker, R.; Wolfe, R.; Morris, M.E. The Reliability of Three-Dimensional Kinematic Gait Measurements: A Systematic Review. Gait Posture 2009, 29, 360–369. [Google Scholar] [CrossRef]
- Turner, J.A.; Chaaban, C.R.; Padua, D.A. Validation of OpenCap: A Low-Cost Markerless Motion Capture System for Lower-Extremity Kinematics during Return-to-Sport Tasks. J. Biomech. 2024, 171, 112200. [Google Scholar] [CrossRef] [PubMed]
- Horsak, B.; Eichmann, A.; Lauer, K.; Prock, K.; Krondorfer, P.; Siragy, T.; Dumphart, B. Concurrent Validity of Smartphone-Based Markerless Motion Capturing to Quantify Lower-Limb Joint Kinematics in Healthy and Pathological Gait. J. Biomech. 2023, 159, 111801. [Google Scholar] [CrossRef] [PubMed]
- Lima, Y.L.; Collings, T.; Hall, M.; Bourne, M.N.; Diamond, L.E. Validity and Reliability of Trunk and Lower-Limb Kinematics during Squatting, Hopping, Jumping and Side-Stepping Using OpenCap Markerless Motion Capture Application. J. Sports Sci. 2024, 42, 1847–1858. [Google Scholar] [CrossRef]
- Falisse, A.; Uhlrich, S.D.; Chaudhari, A.S.; Hicks, J.L.; Delp, S.L. Marker Data Enhancement for Markerless Motion Capture. IEEE Trans. Biomed. Eng. 2025, 72, 2013–2022. [Google Scholar] [CrossRef]
- Daynes, E.; Barker, R.E.; Jones, A.V.; Walsh, J.A.; Nolan, C.M.; Man, W.D.C.; Singh, S.J.; Greening, N.J.; Houchen-Wolloff, L.; Evans, R.A. Determining the Minimum Important Differences for Field Walking Tests in Adults with Long–Term Conditions: A Systematic Review and Meta-Analysis. Eur. Respir. Rev. 2025, 34, 240198. [Google Scholar] [CrossRef]
- Bohannon, R.W.; Glenney, S.S. Minimal Clinically Important Difference for Change in Comfortable Gait Speed of Adults with Pathology: A Systematic Review. J. Eval. Clin. Pract. 2014, 20, 295–300. [Google Scholar] [CrossRef]
- Guzik, A.; Drużbicki, M.; Perenc, L.; Wolan-Nieroda, A.; Turolla, A.; Kiper, P. Establishing the Minimal Clinically Important Differences for Sagittal Hip Range of Motion in Chronic Stroke Patients. Front. Neurol. 2021, 12, 700190. [Google Scholar] [CrossRef]
- Guzik, A.; Drużbicki, M.; Wolan-Nieroda, A.; Turolla, A.; Kiper, P. Estimating Minimal Clinically Important Differences for Knee Range of Motion after Stroke. J. Clin. Med. 2020, 9, 3305. [Google Scholar] [CrossRef] [PubMed]
- Oonk, G.A.; Kempe, M.; Lemmink, K.A.P.M.; Buurke, T.J.W. Examining the Concurrent Validity of Markerless Motion Capture in Dual-Athlete Team Sports Movements. J. Sports Sci. 2025, 45, 1–12. [Google Scholar] [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef] [PubMed]
- Mentiplay, B.F.; Perraton, L.G.; Bower, K.J.; Pua, Y.H.; McGaw, R.; Heywood, S.; Clark, R.A. Gait Assessment Using the Microsoft Xbox One Kinect: Concurrent Validity and Inter-Day Reliability of Spatiotemporal and Kinematic Variables. J. Biomech. 2015, 48, 2166–2170. [Google Scholar] [CrossRef] [PubMed]
- Scataglini, S.; Abts, E.; Van Bocxlaer, C.; Van den Bussche, M.; Meletani, S.; Truijen, S. Accuracy, Validity, and Reliability of Markerless Camera-Based 3D Motion Capture Systems versus Marker-Based 3D Motion Capture Systems in Gait Analysis: A Systematic Review and Meta-Analysis. Sensors 2024, 24, 3686. [Google Scholar] [CrossRef]
- Cerfoglio, S.; Ferraris, C.; Vismara, L.; Amprimo, G.; Priano, L.; Bigoni, M.; Galli, M.; Mauro, A.; Cimolin, V. Estimation of Gait Parameters in Healthy and Hemiplegic Individuals Using Azure Kinect: A Comparative Study with the Optoelectronic System. Front. Bioeng. Biotechnol. 2024, 12, 1449680. [Google Scholar] [CrossRef]
- Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. Effects of Walking Speed on Gait Biomechanics in Healthy Participants: A Systematic Review and Meta-Analysis. Syst. Rev. 2019, 8, 153. [Google Scholar] [CrossRef]
- Bohannon, R.W. Comfortable and Maximum Walking Speed of Adults Aged 20–79 Years: Reference Values and Determinants. Age Ageing 1997, 26, 15–19. [Google Scholar] [CrossRef] [PubMed]

| Variable | Speed | MoCap Mean ± SD | OpenCap Mean ± SD | Bias (95% LoA) | ICC (2,1) | r | MDC |
|---|---|---|---|---|---|---|---|
| Stride Length (m) | Slow | 1.286 ± 0.103 | 1.276 ± 0.102 | −0.009 (−0.024, 0.006) | 0.993 | 0.997 | 0.015 |
| Self | 1.450 ± 0.062 | 1.439 ± 0.065 | −0.012 (−0.030, 0.008) | 0.969 | 0.988 | 0.019 | |
| Fast | 1.664 ± 0.082 | 1.652 ± 0.086 | −0.010 (−0.037, 0.017) | 0.984 | 0.992 | 0.027 | |
| Stride Time (s) | Slow | 1.285 ± 0.113 | 1.283 ± 0.111 | −0.002 (−0.012, 0.007) | 0.999 | 0.999 | 0.009 |
| Self | 1.116 ± 0.069 | 1.116 ± 0.068 | 0.000 (−0.005, 0.004) | 0.999 | 0.999 | 0.004 | |
| Fast | 0.977 ± 0.056 | 0.976 ± 0.058 | 0.000 (−0.011, 0.011) | 0.995 | 0.995 | 0.011 | |
| Double Support (s) | Slow | 0.197 ± 0.036 | 0.190 ± 0.034 | −0.007 (−0.022, 0.008) | 0.950 | 0.973 | 0.015 |
| Self | 0.149 ± 0.020 | 0.146 ± 0.018 | −0.003 (−0.012, 0.006) | 0.957 | 0.967 | 0.009 | |
| Fast | 0.111 ± 0.019 | 0.107 ± 0.020 | −0.003 (−0.011, 0.005) | 0.959 | 0.973 | 0.008 | |
| Cadence (Hz) | Slow | 1.565 ± 0.137 | 1.568 ± 0.136 | 0.003 (−0.007, 0.012) | 0.999 | 0.999 | 0.010 |
| Self | 1.796 ± 0.112 | 1.797 ± 0.113 | 0.001 (−0.007, 0.009) | 0.999 | 0.999 | 0.008 | |
| Fast | 2.052 ± 0.118 | 2.055 ± 0.120 | 0.000 (−0.024, 0.024) | 0.995 | 0.995 | 0.024 | |
| Walking Speed (km.h−1) | Slow | 3.614 ± 0.501 | 3.599 ± 0.505 | −0.014 (−0.066, 0.037) | 0.998 | 0.998 | 0.051 |
| Self | 4.640 ± 0.373 | 4.616 ± 0.382 | −0.022 (−0.082, 0.038) | 0.995 | 0.997 | 0.060 | |
| Fast | 6.106 ± 0.478 | 6.059 ± 0.481 | −0.044 (−0.135, 0.047) | 0.992 | 0.995 | 0.091 | |
| Hip ROM (°) | Slow | 41.875 ± 3.290 | 44.158 ± 3.183 | 2.318 (−1.427, 6.063) | 0.665 | 0.829 | 3.745 |
| Self | 45.456 ± 2.684 | 47.544 ± 3.155 | 2.031 (−0.960, 5.021) | 0.709 | 0.898 | 2.990 | |
| Fast | 53.845 ± 3.093 | 55.505 ± 3.431 | 1.629 (−1.669, 4.926) | 0.706 | 0.823 | 3.298 | |
| Knee ROM (°) | Slow | 59.461 ± 4.594 | 59.079 ± 3.713 | −0.389 (−7.010, 6.32) | 0.647 | 0.650 | 6.711 |
| Self | 60.408 ± 4.804 | 60.155 ± 4.846 | 0.412 (−5.549, 6.372) | 0.776 | 0.770 | 5.960 | |
| Fast | 57.890 ± 4.742 | 57.939 ± 4.533 | 0.191 (−5.738, 6.120) | 0.775 | 0.774 | 5.929 | |
| Ankle ROM (°) | Slow | 21.712 ± 3.203 | 22.821 ± 3.116 | 1.164 (−4.038, 6.366) | 0.591 | 0.622 | 5.202 |
| Self | 21.004 ± 3.715 | 22.589 ± 3.815 | 1.313 (−3.550, 6.175) | 0.700 | 0.739 | 4.862 | |
| Fast | 20.590 ± 3.006 | 22.408 ± 3.508 | 1.651 (−4.341, 7.643) | 0.482 | 0.538 | 5.992 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Borba, E.F.; Storniolo, J.L.; Cerfoglio, S.; Capodaglio, P.; Cimolin, V.; Peyré-Tartaruga, L.A.; Tartaruga, M.P.; Cavallari, P. Effect of Walking Speed on the Reliability of a Smartphone-Based Markerless Gait Analysis System. Sensors 2025, 25, 6474. https://doi.org/10.3390/s25206474
de Borba EF, Storniolo JL, Cerfoglio S, Capodaglio P, Cimolin V, Peyré-Tartaruga LA, Tartaruga MP, Cavallari P. Effect of Walking Speed on the Reliability of a Smartphone-Based Markerless Gait Analysis System. Sensors. 2025; 25(20):6474. https://doi.org/10.3390/s25206474
Chicago/Turabian Stylede Borba, Edilson Fernando, Jorge L. Storniolo, Serena Cerfoglio, Paolo Capodaglio, Veronica Cimolin, Leonardo A. Peyré-Tartaruga, Marcus P. Tartaruga, and Paolo Cavallari. 2025. "Effect of Walking Speed on the Reliability of a Smartphone-Based Markerless Gait Analysis System" Sensors 25, no. 20: 6474. https://doi.org/10.3390/s25206474
APA Stylede Borba, E. F., Storniolo, J. L., Cerfoglio, S., Capodaglio, P., Cimolin, V., Peyré-Tartaruga, L. A., Tartaruga, M. P., & Cavallari, P. (2025). Effect of Walking Speed on the Reliability of a Smartphone-Based Markerless Gait Analysis System. Sensors, 25(20), 6474. https://doi.org/10.3390/s25206474











