ON-NSW: Accelerating High-Dimensional Vector Search on Edge Devices with GPU-Optimized NSW
Abstract
1. Introduction
- We propose a GPU-centric NSW design that removes the upper hierarchy of HNSW and executes the entire bottom-layer search on the GPU for on-device ANN tasks.
- We design ON-NSW, which exploits the NVIDIA Jetson device’s unified architecture by enabling zero-copy access to pinned memory and maximizes efficiency during search by leveraging GPU shared memory.
- We implement parallel neighbor exploration that leverages GPU cores to concurrently fetch neighbors and compute distances for efficient search.
2. Background
2.1. Approximate Nearest Neighbor Search (ANNS)
2.2. Hierarchical Navigable Small World (HNSW)
| Algorithm 1: Search algorithm of HNSW [18] |
 |
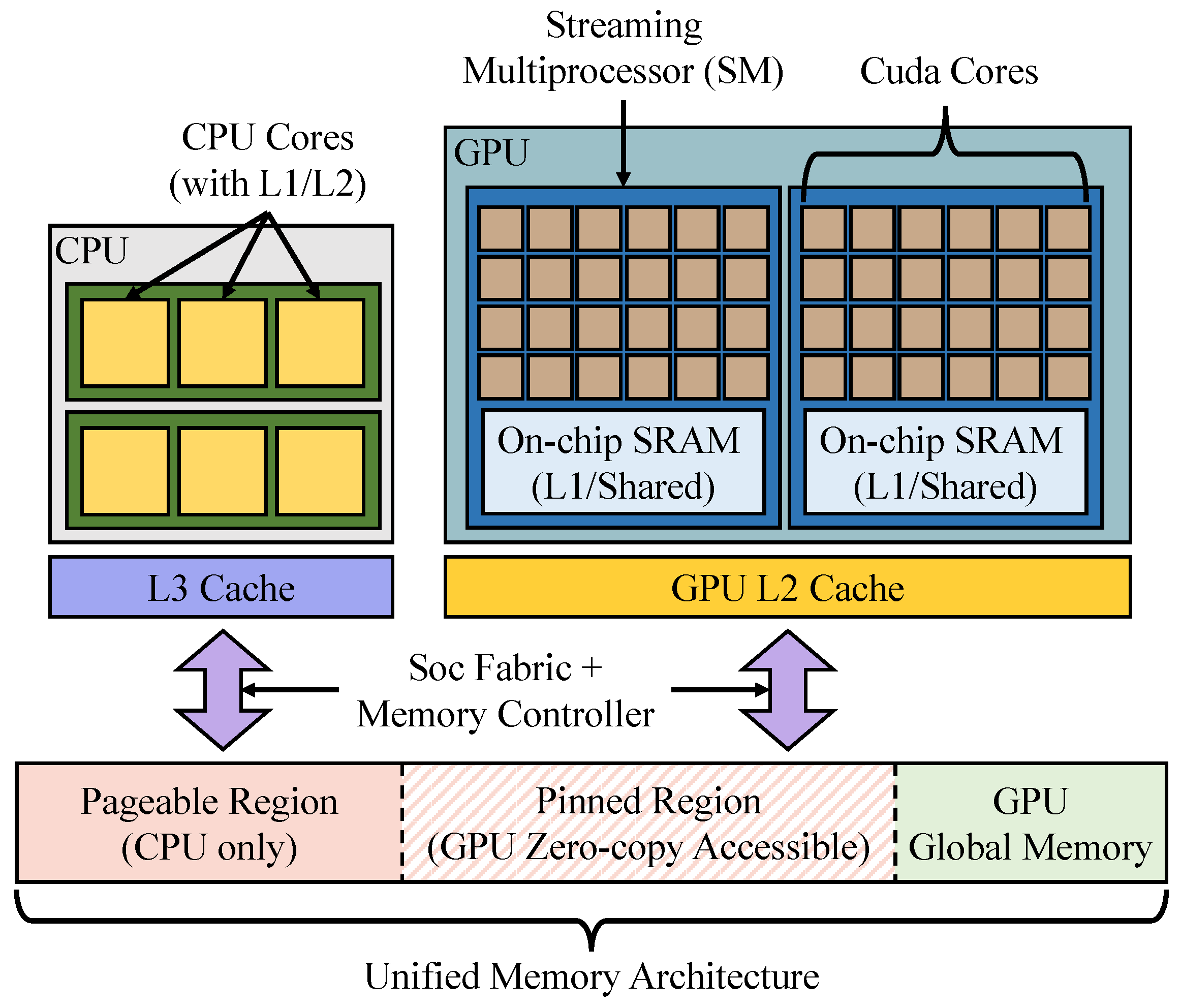
2.3. GPU Structure on NVIDIA Jetson Device
3. Design
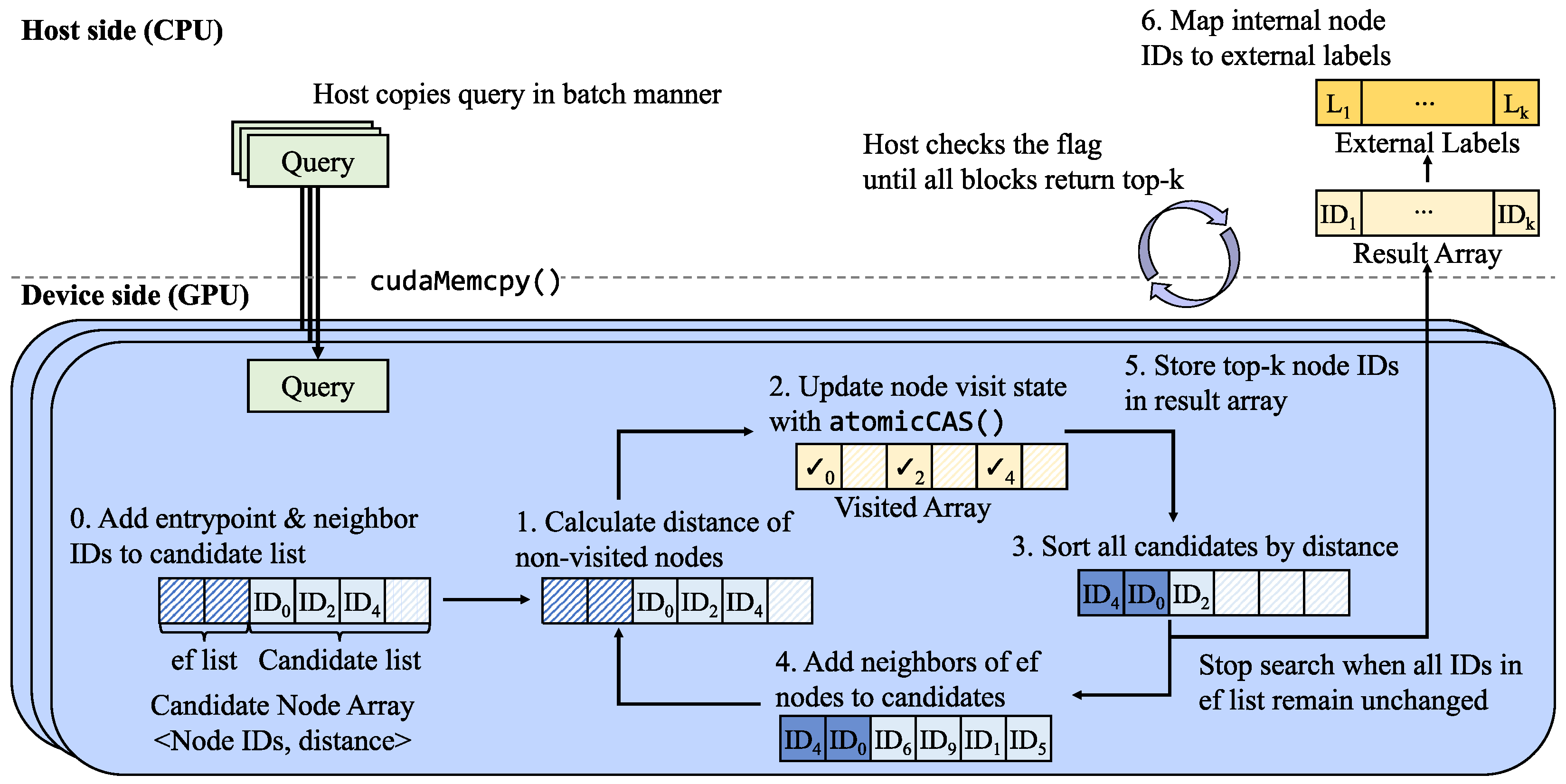
3.1. Design Overview
| Algorithm 2: Search algorithm of ON-NSW |
 |
3.2. Flat Graph Structure for GPU Parallelism
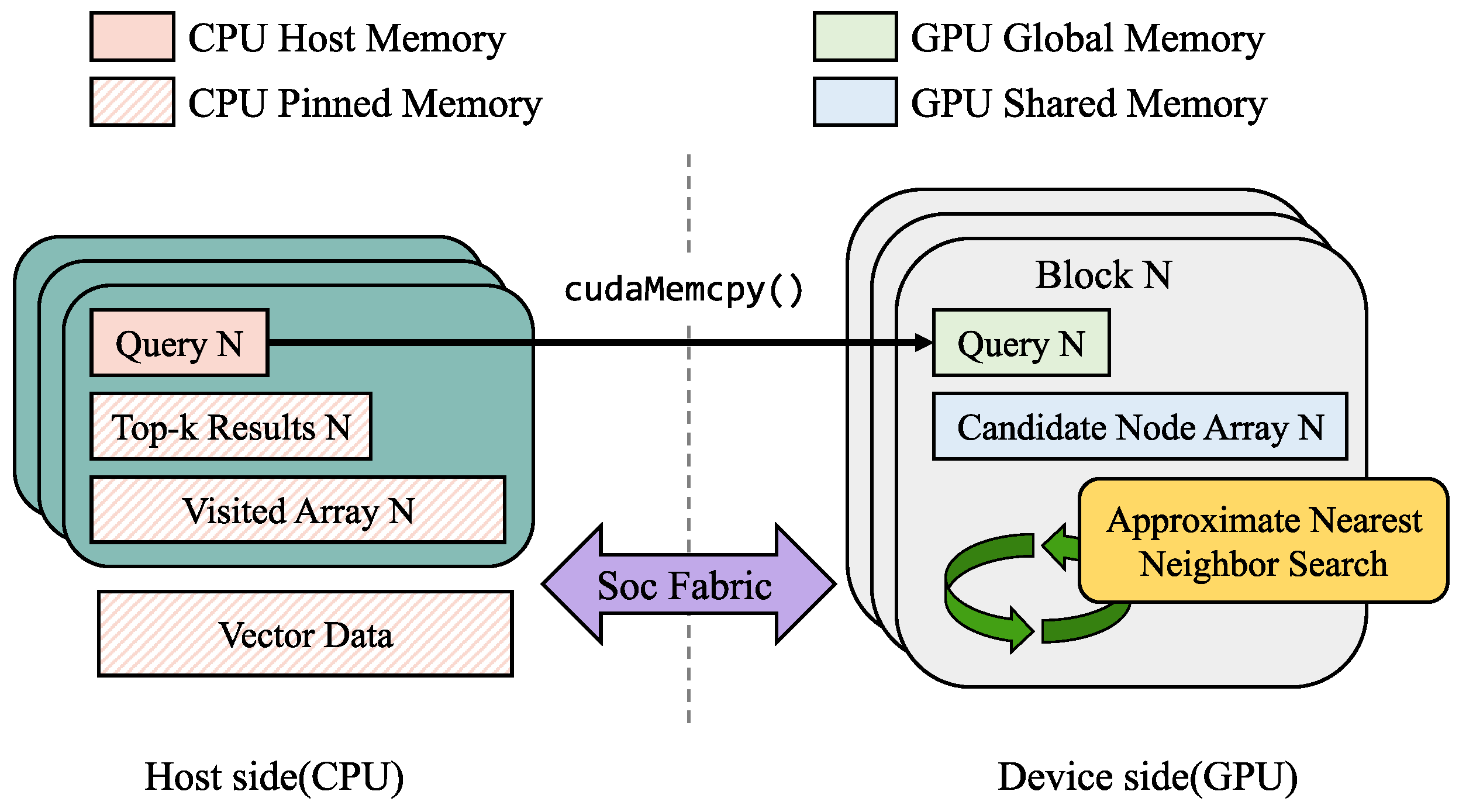
3.3. Optimizing Data Placement in a Unified Memory Architecture
- Vector Data. ON-NSW stores vector data in pinned memory, which is accessible to both the CPU and GPU. The GPU can directly access pinned memory through the SoC fabric using DMA, enabling zero-copy data transfer between the host and GPU. However, because pinned pages are locked in physical memory, they cannot take advantage of CPU-side caching policies and may therefore incur higher latency for CPU access compared to pageable memory.
- Visited Array. During the search process, the visit state of each node is tracked using a visited array. The visited state indicates that the distance to a node has already been calculated, thereby preventing redundant distance calculations for the same node. Since this array must have the same size as the number of data points in the dataset, it is too large to fit in GPU shared memory and is therefore placed in pinned memory.
- Top-k Results. As the top-k results found by the GPU must be accessible by both CPU and GPU, ON-NSW stores the top-k result array in pinned memory. This placement allows CPU and GPU to share the results without incurring additional copy overhead.
- Query Vector. Query vector is used solely during the GPU search process. ON-NSW copies it into GPU global memory and utilizes it within the GPU kernel. To reduce the overhead of cudaMemcpy() calls, ON-NSW processes queries in batches.
- Candidate Array. The candidate array stores the IDs and distances of nodes whose similarities to the query vector have been calculated. After each iteration, the array is sorted by distance, and the top-ef nodes are retained for further neighbor expansion in the next step. If the top-ef entries remain unchanged after sorting, the search is considered converged and terminates. Therefore, the candidate array is essential for managing neighbor expansion and determining the termination condition during the GPU-based search.
3.4. Parallel Neighbor Exploration at Warp Level
3.5. Optimizations
- Flag-based synchronization. As introduced earlier, ON-NSW uses a synchronization flag to coordinate the completion of GPU blocks. Launching a CUDA kernel typically requires the CPU to wait for completion by invoking cudaDeviceSynchronize(), but we observed that this synchronization method introduces significant overhead. To mitigate this cost, ON-NSW employs a flag-based lightweight synchronization mechanism. Each GPU block updates the flag variable using atomicAdd once it completes its search. The CPU then checks the flag through spin-wait loop until all blocks have finished. This method reduces synchronization overhead and improves overall performance.
- Vectorization. During the search operation, the most time-consuming operation is distance calculation, particularly for high-dimensional vectors. To optimize this process, ON-NSW vectorizes the floating-point values into float4 type, enabling 128-bit memory loads. This approach ensures coalesced memory access and improves GPU memory bandwidth utilization.
- Prefetching. To hide the high latency of pinned memory, ON-NSW loads multiple nodes at once during the warp-based distance calculation. This prefetching allows memory access latency to overlap with calculation, leading to enhanced search efficiency.
- Multithreading for Mapping. After the search, ON-NSW employs multithreading on CPU to map internal node IDs to external labels in parallel, thereby reducing the execution time.
4. Evaluation
4.1. Experimental Environment
- System Configuration. We conduct experiments on an NVIDIA Jetson Orin Nano (NVIDIA Corporation, Santa Clara, CA, USA), equipped with two sockets of Arm Cortex-A78AE v8.2 64-bit processors (Arm Ltd., Cambridge, UK), with each socket containing three cores. The system has 8 GB of memory, and the SoC integrates a GPU based on the Ampere architecture. The GPU consists of 8 Streaming Multiprocessors (SMs) and 1024 CUDA cores, with a maximum clock frequency of 625 MHz. Each warp is organized into 32 threads, and a single GPU block can support up to 1024 threads with 48 KB of shared memory. In addition, the GPU global memory is shared with the system DRAM.
- Dataset. We use 4 real-world datasets: three high-dimensional and one low-dimensional vector-embedding dataset. For the high-dimensional datasets, we use OpenAI [31,32] text embeddings with 1536 and 3072 dimensions as well as the GIST [33] dataset with 960 dimensions. For the low-dimensional case, we use the SIFT [33] dataset with 128 dimensions. All datasets consist of 4-byte floating-point values. We build graph index structures with 50,000 vectors, randomly selected from each original dataset.
- Baseline. For comparison, we use the original HNSW implementation provided by hnswlib [36] and execute it on the NVIDIA Jetson device. We set the index-building parameters to M = 16 and efConstruction = 100 for both the original HNSW and ON-NSW. Since layer 0 maintains twice as many neighbors, the value of M for layer 0 is set to 32 in both implementations. Following the original HNSW design, layer 0 is configured to have twice as many maximum neighbors as the upper layers. Because layer 0 contains all vector data, maintaining a larger number of connections helps preserve local connectivity among nearby nodes and improves search efficiency. We use the L2 (Euclidean) distance as the similarity metric. In addition, we modified the original distance computation function of HNSW, which was optimized for x86_64 SIMD instructions, to instead use ARM_NEON instructions.
4.2. Graph Search Quality
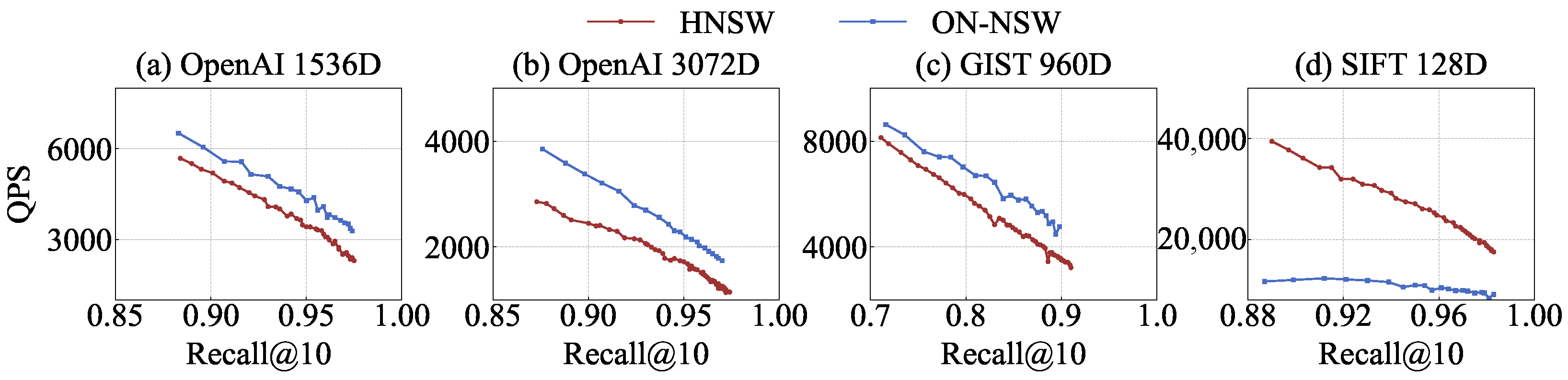
- Total Execution Time. ON-NSW consistently outperforms the original HNSW on high-dimensional datasets across all Recall@10 levels. For example, at Recall@10 values of 0.974 and 0.971 on the OpenAI 1536D and 3072D datasets, respectively, ON-NSW reduces the total execution time by about 27% compared to HNSW (0.305 s vs. 0.417 s). A similar trend is observed on the GIST dataset, where at a Recall@10 of 0.900, ON-NSW completes in 0.210 s while HNSW requires 0.280 s. In contrast, on the relatively low-dimensional SIFT dataset, at a Recall@10 of 0.981, HNSW remains faster (0.054 s vs. 0.103 s).
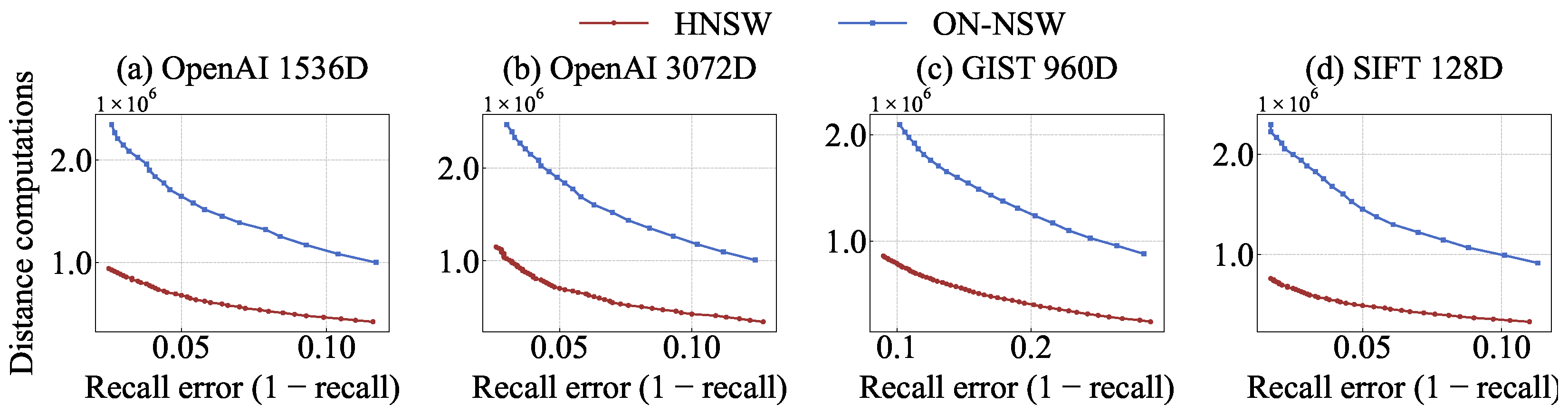
- Distance Calculation Comparison. As shown in Figure 5a–d, ON-NSW performs up to 3.5× more distance computations than the original HNSW at the same recall level. This occurs because ON-NSW exploits GPU parallelism to compute distances for a larger number of vector data within each hop. Although the total number of computations increases, ON-NSW reaches vectors closer to the query more quickly by fully utilizing GPU parallelism.
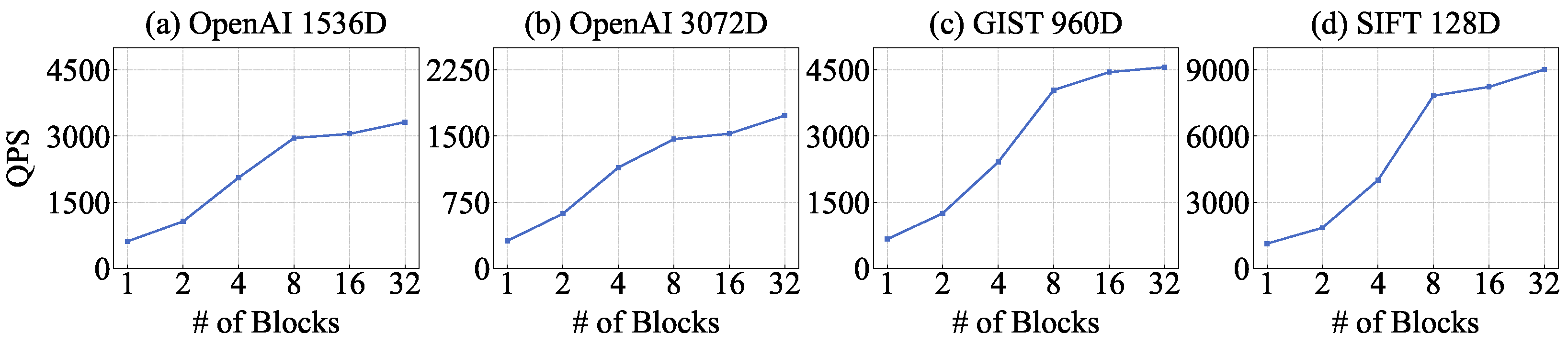
4.3. Throughput over Varying Number of GPU Blocks
4.4. Performance Breakdown
4.5. Energy Efficiency
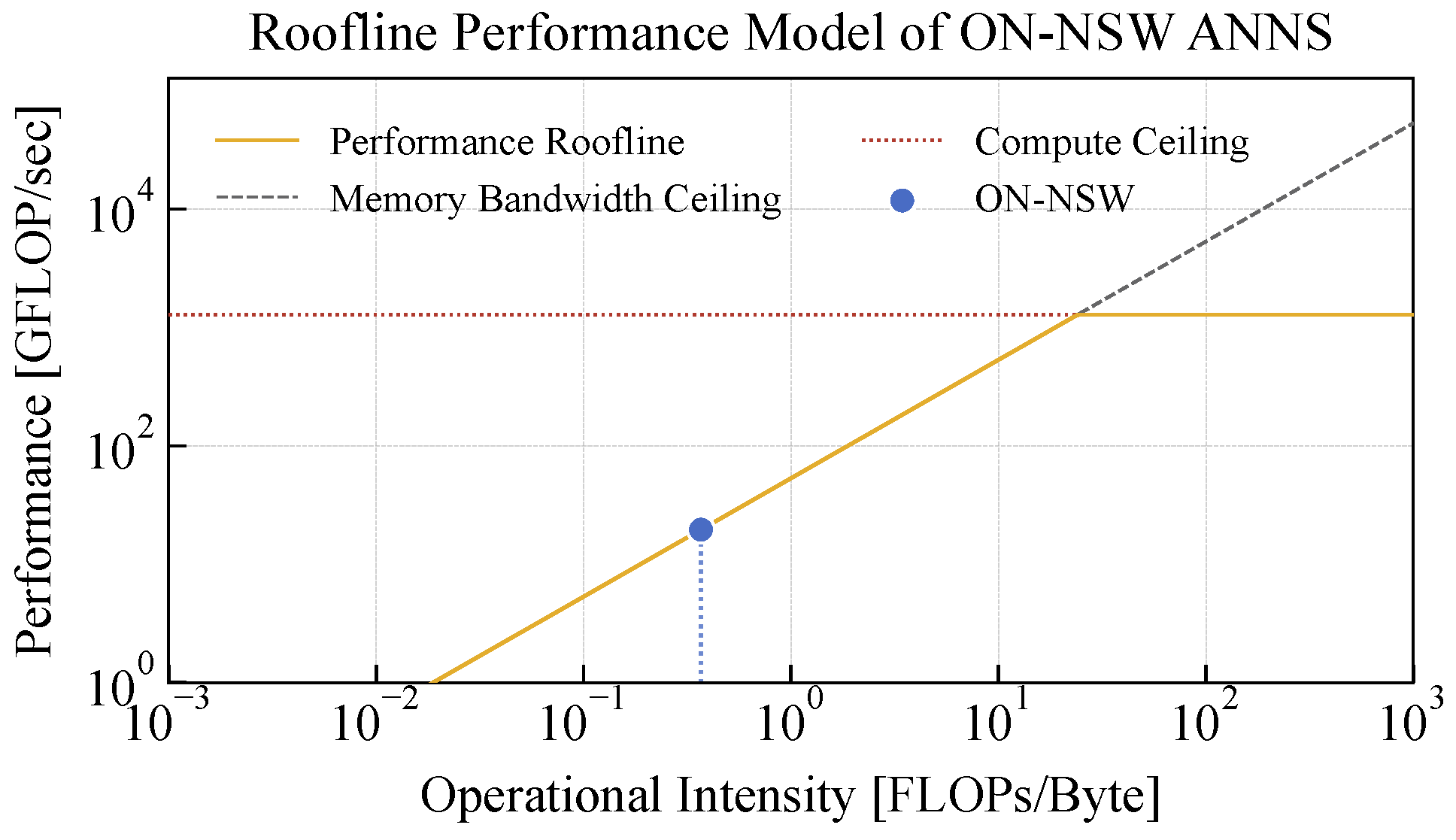
4.6. GPU Utilization on an Edge Device
5. Related Works
5.1. GPU-Accelerated ANN Search
5.2. HNSW Variants
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hasan, R.T. Internet of things and big data analytic: A state of the art review. J. Appl. Sci. Technol. Trends 2022, 3, 93–100. [Google Scholar] [CrossRef]
- Varalakshmi, K.; Kumar, J. Optimized predictive maintenance for streaming data in industrial IoT networks using deep reinforcement learning and ensemble techniques. Sci. Rep. 2025, 15, 27201. [Google Scholar] [CrossRef] [PubMed]
- Elkateb, S.; Métwalli, A.; Shendy, A.; Abu-Elanien, A.E. Machine learning and IoT–Based predictive maintenance approach for industrial applications. Alex. Eng. J. 2024, 88, 298–309. [Google Scholar] [CrossRef]
- Chatterjee, A.; Ahmed, B.S. IoT anomaly detection methods and applications: A survey. Internet Things 2022, 19, 100568. [Google Scholar] [CrossRef]
- Jaramillo-Alcazar, A.; Govea, J.; Villegas-Ch, W. Anomaly detection in a smart industrial machinery plant using IoT and machine learning. Sensors 2023, 23, 8286. [Google Scholar] [CrossRef]
- Rahman, M.A.; Shahrior, M.F.; Iqbal, K.; Abushaiba, A. Enabling Intelligent Industrial Automation: A Review of Machine Learning Applications with Digital Twin and Edge AI Integration. Automation 2025, 6, 37. [Google Scholar] [CrossRef]
- Dritsas, E.; Trigka, M. A survey on the applications of cloud computing in the industrial internet of things. BIg Data Cogn. Comput. 2025, 9, 44. [Google Scholar] [CrossRef]
- Somu, N.; Dasappa, N.S. An edge-cloud IIoT framework for predictive maintenance in manufacturing systems. Adv. Eng. Inform. 2025, 65, 103388. [Google Scholar] [CrossRef]
- Shi, Y.; Yi, C.; Chen, B.; Yang, C.; Zhu, K.; Cai, J. Joint online optimization of data sampling rate and preprocessing mode for edge–cloud collaboration-enabled industrial IoT. IEEE Internet Things J. 2022, 9, 16402–16417. [Google Scholar] [CrossRef]
- Alabadi, M.; Habbal, A.; Wei, X. Industrial internet of things: Requirements, architecture, challenges, and future research directions. IEEE Access 2022, 10, 66374–66400. [Google Scholar] [CrossRef]
- Bourechak, A.; Zedadra, O.; Kouahla, M.N.; Guerrieri, A.; Seridi, H.; Fortino, G. At the confluence of artificial intelligence and edge computing in iot-based applications: A review and new perspectives. Sensors 2023, 23, 1639. [Google Scholar] [CrossRef]
- Kumari, M.; Singh, M.P.; Singh, A.K. A latency sensitive and agile IIoT architecture with optimized edge node selection and task scheduling. Digit. Commun. Netw. 2025, in press. [Google Scholar] [CrossRef]
- Hidayat, R.; Utama, D.N. Performance Prediction Model for Predictive Maintenance Based on K-Nearest Neighbor Method for Air Navigation Equipment Facilities. J. Comput. Sci. 2025, 21, 800–809. [Google Scholar] [CrossRef]
- Nizan, O.; Tal, A. k-NNN: Nearest neighbors of neighbors for anomaly detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 1–6 January 2024; pp. 1005–1014. [Google Scholar]
- Dobson, M.; Shen, Z.; Blelloch, G.E.; Dhulipala, L.; Gu, Y.; Simhadri, H.V.; Sun, Y. Scaling graph-based anns algorithms to billion-size datasets: A comparative analysis. arXiv 2023, arXiv:2305.04359. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Malkov, Y.; Ponomarenko, A.; Logvinov, A.; Krylov, V. Approximate nearest neighbor algorithm based on navigable small world graphs. Inf. Syst. 2014, 45, 61–68. [Google Scholar] [CrossRef]
- Malkov, Y.A.; Yashunin, D.A. Efficient and Robust Approximate Nearest Neighbor Search Using Hierarchical Navigable Small World Graphs. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 824–836. [Google Scholar] [CrossRef] [PubMed]
- Shuvo, M.M.H.; Islam, S.K.; Cheng, J.; Morshed, B.I. Efficient acceleration of deep learning inference on resource-constrained edge devices: A review. Proc. IEEE 2022, 111, 42–91. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, F.; Li, C.; Cao, L.; Chen, Z.; Zhai, J.; Du, X. HARMONY: A Scalable Distributed Vector Database for High-Throughput Approximate Nearest Neighbor Search. Proc. ACM Manag. Data 2025, 3, 249. [Google Scholar] [CrossRef]
- Wang, M.; Xu, X.; Yue, Q.; Wang, Y. A comprehensive survey and experimental comparison of graph-based approximate nearest neighbor search. arXiv 2021, arXiv:2101.12631. [Google Scholar] [CrossRef]
- Huang, Q.; Tung, A.K.H. Lightweight-Yet-Efficient: Revitalizing Ball-Tree for Point-to-Hyperplane Nearest Neighbor Search. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering (ICDE), Anaheim, CA, USA, 3–7 April 2023. [Google Scholar]
- Indyk, P.; Motwani, R. Approximate nearest neighbors: Towards removing the curse of dimensionality. In Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, Dallas, TX, USA, 24–26 May 1998; pp. 604–613. [Google Scholar]
- Lv, Q.; Josephson, W.; Wang, Z.; Charikar, M.; Li, K. Multi-probe LSH: Efficient indexing for high-dimensional similarity search. In Proceedings of the 33rd International Conference on Very Large Data Bases, Vienna, Austria, 23–27 September 2007; pp. 950–961. [Google Scholar]
- Nguyen, H.; Nguyen, N.H.; Nguyen, N.L.B.; Thudumu, S.; Du, H.; Vasa, R.; Mouzakis, K. Dual-Branch HNSW Approach with Skip Bridges and LID-Driven Optimization. arXiv 2025, arXiv:2501.13992. [Google Scholar]
- Wang, M.; Xu, W.; Yi, X.; Wu, S.; Peng, Z.; Ke, X.; Gao, Y.; Xu, X.; Guo, R.; Xie, C. Starling: An i/o-efficient disk-resident graph index framework for high-dimensional vector similarity search on data segment. Proc. ACM Manag. Data 2024, 2, 14. [Google Scholar] [CrossRef]
- Agarwal, P.; SK, M.I.; Pancha, N.; Hazra, K.S.; Xu, J.; Rosenberg, C. OmniSearchSage: Multi-Task Multi-Entity Embeddings for Pinterest Search. In Proceedings of the 33rd International World Wide Web Conference (WWW), Singapore, 13–17 May 2024; pp. 121–130. [Google Scholar]
- Voyager Library. Available online: https://github.com/spotify/voyager (accessed on 8 September 2025).
- NVIDIA Corporation. Jetson Orin Nano Developer Kit Getting Started—NVIDIA Developer. 2024. Available online: https://developer.nvidia.com/embedded/learn/get-started-jetson-orin-nano-devkit (accessed on 26 March 2024).
- Chakraborty, A.; Tavernier, W.; Kourtis, A.; Pickavet, M.; Oikonomakis, A.; Colle, D. Profiling Concurrent Vision Inference Workloads on NVIDIA Jetson–Extended. arXiv 2025, arXiv:2508.08430. [Google Scholar]
- VectorDBBench. Available online: https://github.com/zilliztech/VectorDBBench (accessed on 10 September 2025).
- Qdrant. dbpedia-entities-openai3-text-embedding-3-large-3072-1M. Hugging Face Dataset, Apache-2.0 License. 2024. Available online: https://huggingface.co/datasets/Qdrant/dbpedia-entities-openai3-text-embedding-3-large-3072-1M (accessed on 10 September 2025).
- Jégou, H.; Douze, M.; Schmid, C. Product Quantization for Nearest Neighbor Search. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 117–128. [Google Scholar] [CrossRef]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the 31st Conference and Workshop on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 6629–6640. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the 28th Conference and Workshop on Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Hnswlib Library. Available online: https://github.com/nmslib/hnswlib (accessed on 21 August 2025).
- NVIDIA Corporation. NVIDIA Jetson Orin Nano Series Data Sheet. 2023. Available online: https://www.mouser.com/pdfDocs/Jetson_Orin_Nano_Series_DS-11105-001_v11.pdf (accessed on 21 August 2025).
- Zhao, W.; Tan, S.; Li, P. SONG: Approximate Nearest Neighbor Search on GPU. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 1033–1044. [Google Scholar] [CrossRef]
- Ootomo, H.; Naruse, A.; Nolet, C.; Wang, R.; Feher, T.; Wang, Y. CAGRA: Highly Parallel Graph Construction and Approximate Nearest Neighbor Search for GPUs. In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering (ICDE), Utrecht, The Netherlands, 13–16 May 2024; pp. 4236–4247. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.; Deng, Y.; Tang, B. ParaGraph: Accelerating Graph Indexing through GPU-CPU Parallel Processing for Efficient Cross-modal ANNS. In Proceedings of the 21st International Workshop on Data Management on New Hardware, DaMoN ’25, Berlin, Germany, 22–27 June 2025. [Google Scholar] [CrossRef]
- Li, Z.; Ke, X.; Zhu, Y.; Yu, B.; Zheng, B.; Gao, Y. Scalable Graph Indexing using GPUs for Approximate Nearest Neighbor Search. arXiv 2025, arXiv:2508.08744. [Google Scholar] [CrossRef]
- Douze, M.; Guzhva, A.; Deng, C.; Johnson, J.; Szilvasy, G.; Mazaré, P.E.; Lomeli, M.; Hosseini, L.; Jégou, H. The Faiss library. arXiv 2024, arXiv:2401.08281. [Google Scholar] [CrossRef]
- Ganbarov, A.; Yuan, J.; Le-Tuan, A.; Hauswirth, M.; Le-Phuoc, D. Experimental comparison of graph-based approximate nearest neighbor search algorithms on edge devices. arXiv 2024, arXiv:2411.14006. [Google Scholar] [CrossRef]
- Jin, H.; Lee, J.; Piao, S.; Seo, S.; Kwon, S.; Park, S. Efficient Approximate Nearest Neighbor Search via Data-Adaptive Parameter Adjustment in Hierarchical Navigable Small Graphs. In Proceedings of the 2025 Design, Automation & Test in Europe Conference (DATE), Lyon, France, 31 March–2 April 2025; pp. 1–7. [Google Scholar] [CrossRef]
- Liu, Y.; Fang, F.; Qian, C. Efficient Vector Search on Disaggregated Memory with d-HNSW. In Proceedings of the 17th ACM Workshop on Hot Topics in Storage and File Systems, HotStorage ’25, Boston, MA, USA, 10–11 July 2025; pp. 1–8. [Google Scholar] [CrossRef]
- Jiang, M.; Yang, Z.; Zhang, F.; Hou, G.; Shi, J.; Zhou, W.; Li, F.; Wang, S. DIGRA: A Dynamic Graph Indexing for Approximate Nearest Neighbor Search with Range Filter. Proc. ACM Manag. Data 2025, 3, 148. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, T.; Lee, H.; Na, Y.; Kim, W.-H. ON-NSW: Accelerating High-Dimensional Vector Search on Edge Devices with GPU-Optimized NSW. Sensors 2025, 25, 6461. https://doi.org/10.3390/s25206461
Park T, Lee H, Na Y, Kim W-H. ON-NSW: Accelerating High-Dimensional Vector Search on Edge Devices with GPU-Optimized NSW. Sensors. 2025; 25(20):6461. https://doi.org/10.3390/s25206461
Chicago/Turabian StylePark, Taeyoon, Haena Lee, Yedam Na, and Wook-Hee Kim. 2025. "ON-NSW: Accelerating High-Dimensional Vector Search on Edge Devices with GPU-Optimized NSW" Sensors 25, no. 20: 6461. https://doi.org/10.3390/s25206461
APA StylePark, T., Lee, H., Na, Y., & Kim, W.-H. (2025). ON-NSW: Accelerating High-Dimensional Vector Search on Edge Devices with GPU-Optimized NSW. Sensors, 25(20), 6461. https://doi.org/10.3390/s25206461




