Deep Relevance Hashing for Remote Sensing Image Retrieval
Abstract
1. Introduction
- We propose a global hashing learning model (GHLM) to explore image features from different perspectives. The GHLM incorporates a weighted similarity loss to evaluate the differences between easy and difficult image pairs, thereby improving the discriminative capacity of the generated hash codes.
- We design a local hashing reranking model (LHRM) to refine the initial retrieval results. The LHRM predicts relevance scores to reduce confusion among images with identical Hamming distances, further enhancing retrieval precision and robustness.
- We conduct extensive experiments on three benchmark datasets. The results demonstrate that the proposed method consistently outperforms other competitive approaches.
2. Related Work
2.1. Hash Function Learning
2.2. Hashing for Remote Sensing Image Retrieval
3. Proposed Method
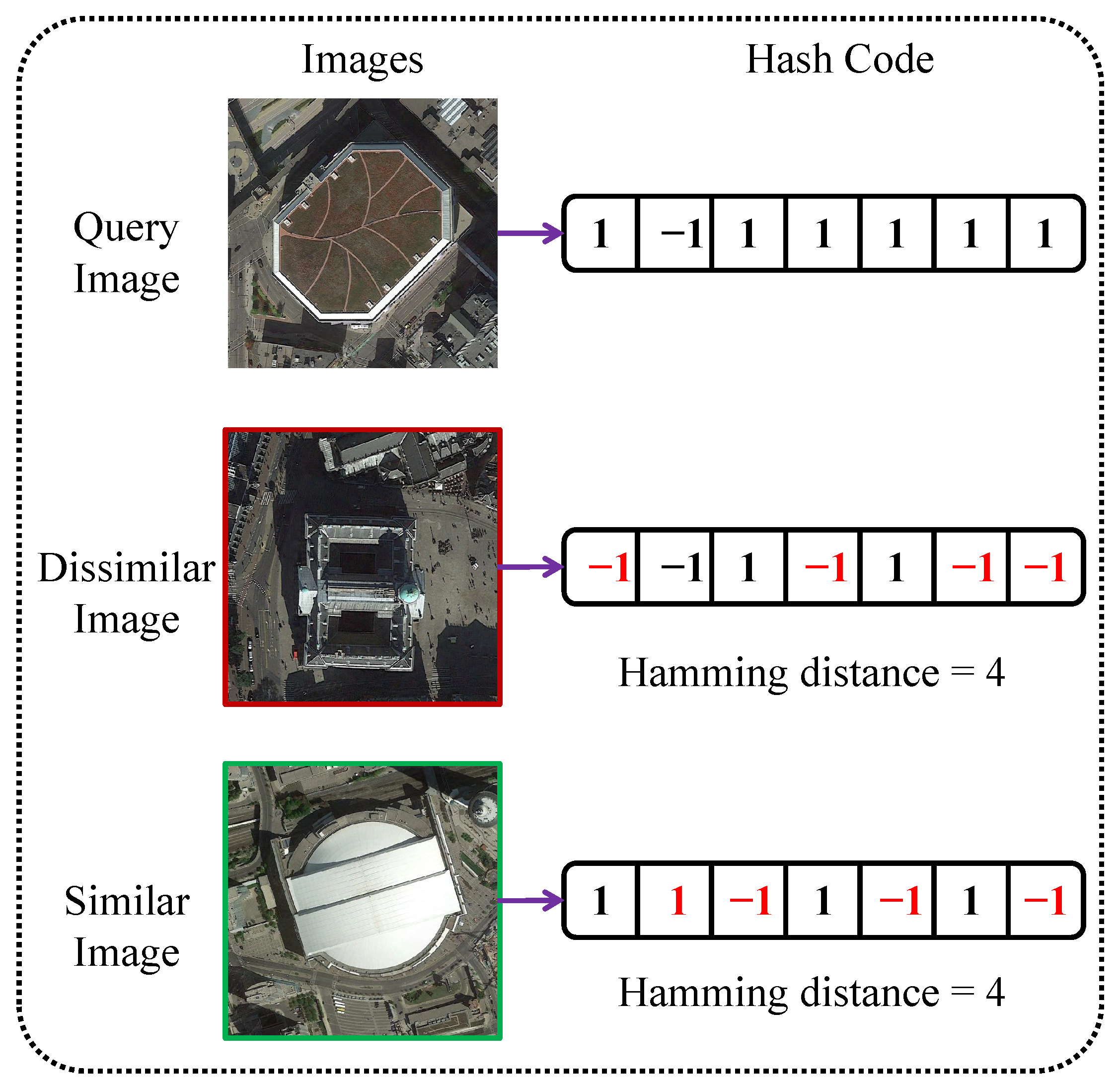
3.1. Problem Definition
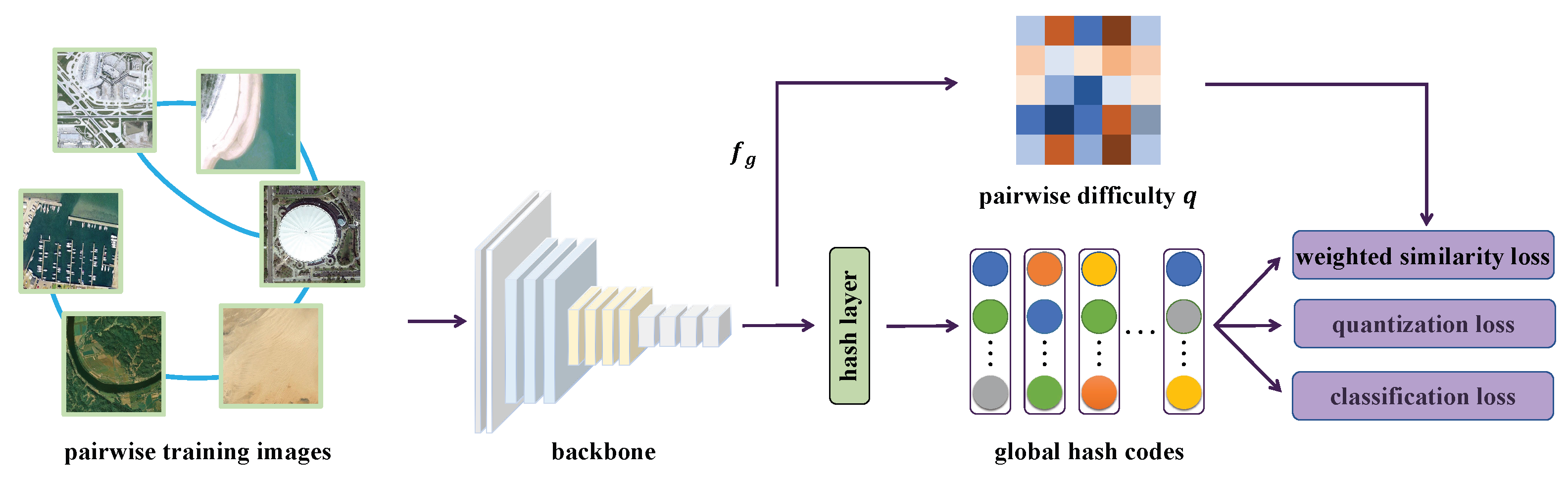
3.2. Global Hash Learning Model
3.2.1. Network Structure
3.2.2. Loss Function
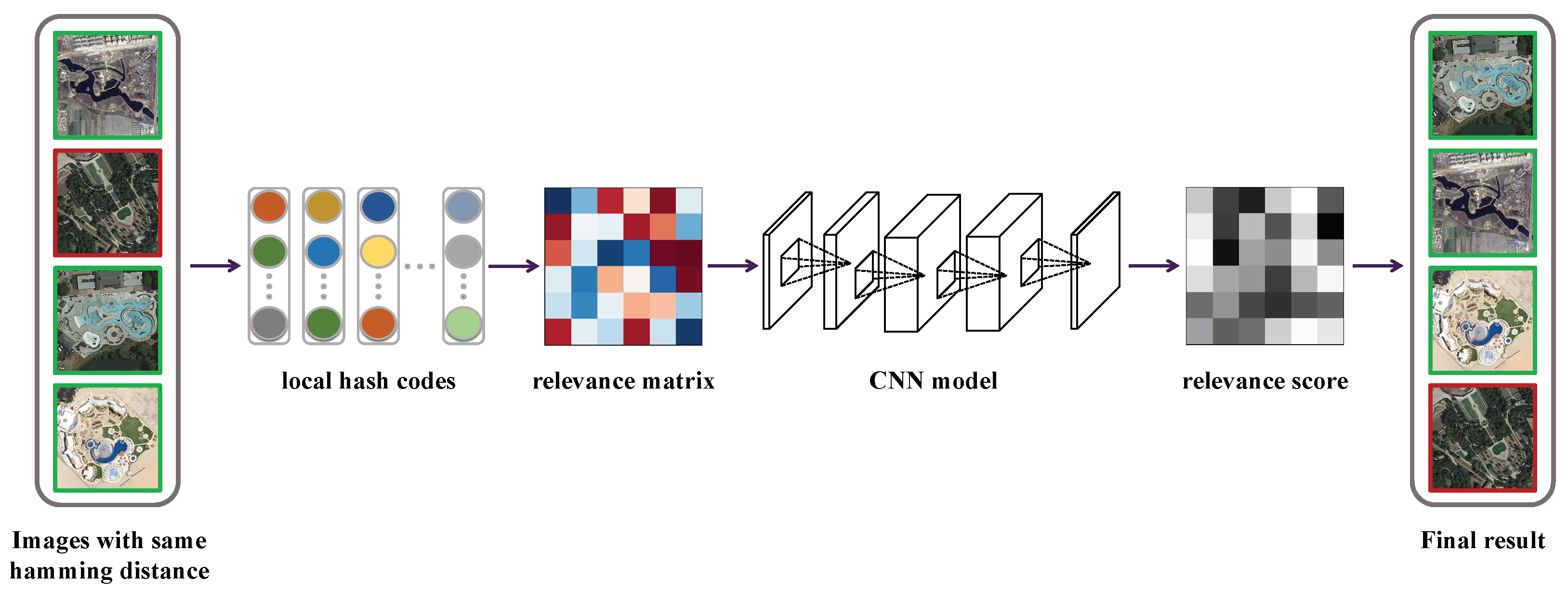
3.3. Local Hash Re-Ranking Model
3.3.1. Training Stage
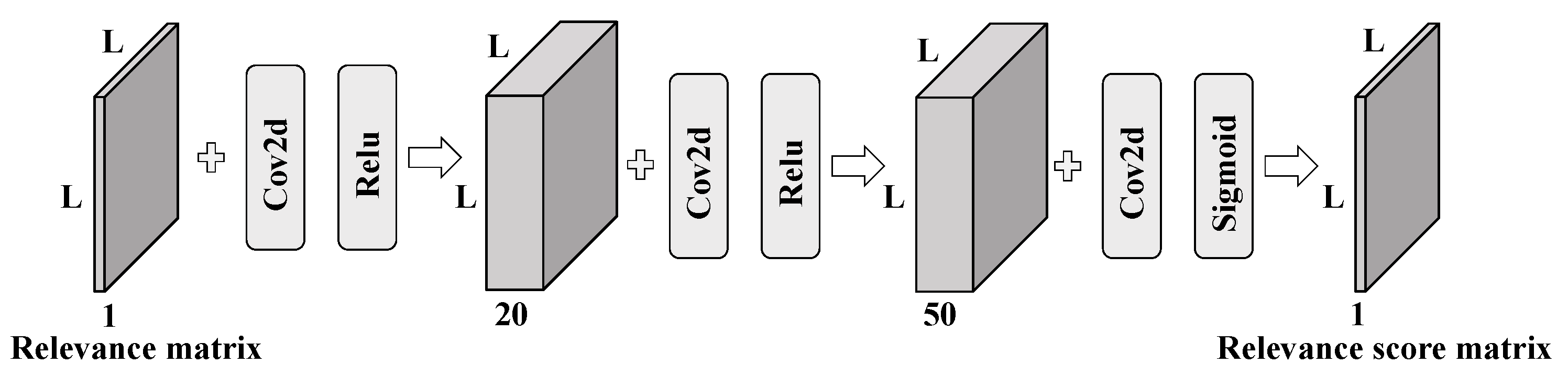
3.3.2. Re-Ranking Process
4. Experiment
4.1. Dataset
4.1.1. WHU-RS
4.1.2. UCMD
4.1.3. AID
4.2. Experimental Settings
4.3. Evaluation Metrics
4.3.1. Mean Average Precision (MAP)
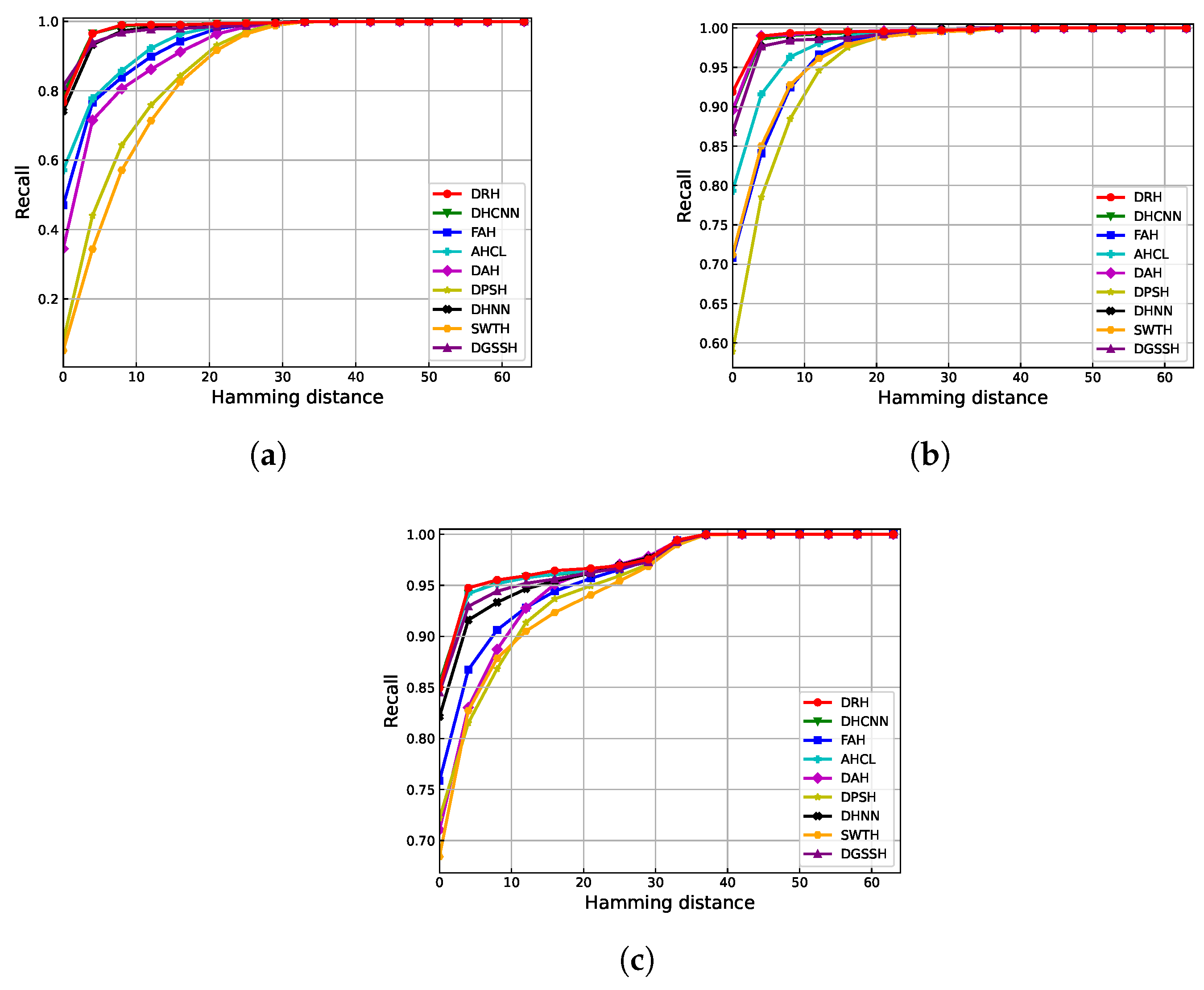
4.3.2. Recall
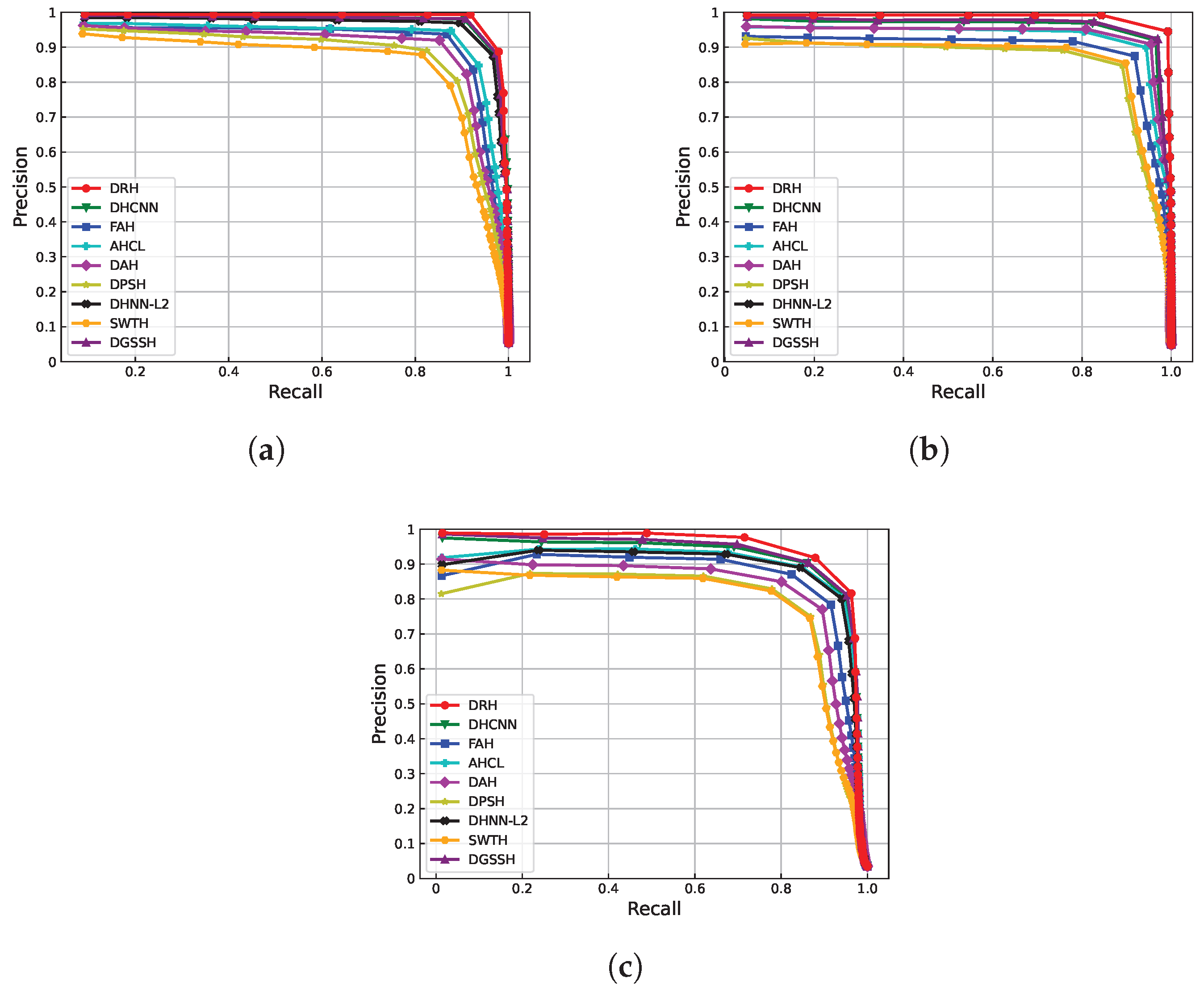
4.3.3. Precision–Recall
4.4. Retrieval Result
4.5. Ablation Study
- DRH-B: Includes only the backbone, hash layer, and classification layer, without any weighting applied to the pairwise similarity loss and without LHRM.
- DRH-R: Adds LHRM to DRH-B, which refines the retrieval results by re-ranking based on local feature analysis.
- DRH-W: Integrates the weighted pairwise similarity loss into DRH-B, allowing the model to focus more on difficult image pairs during training.
- Impact of LHRM: The inclusion of LHRM in DRH-R refines the retrieval process by incorporating local feature re-ranking. This improvement leads to a notable increase in retrieval performance, with MAP increases of 2.12% (16 bit), 1.86% (32 bit), and 1.37% (64 bit).
- Effect of Weighted Pairwise Similarity Loss: In DRH-B, all image pairs contribute equally to training. However, DRH-W introduces weighting to the pairwise similarity loss, allowing the network to focus on more challenging image pairs. This results in a more discriminative model and yields MAP improvements of 3.22% (16 bit), 3.33% (32 bit), and 3.59% (64 bit) over DRH-B.
- Combined Impact of Both Components: Both the weighted pairwise similarity loss and LHRM contribute positively to the MAP improvement. The combination of these two components results in the best retrieval performance, surpassing the performance of each component individually.
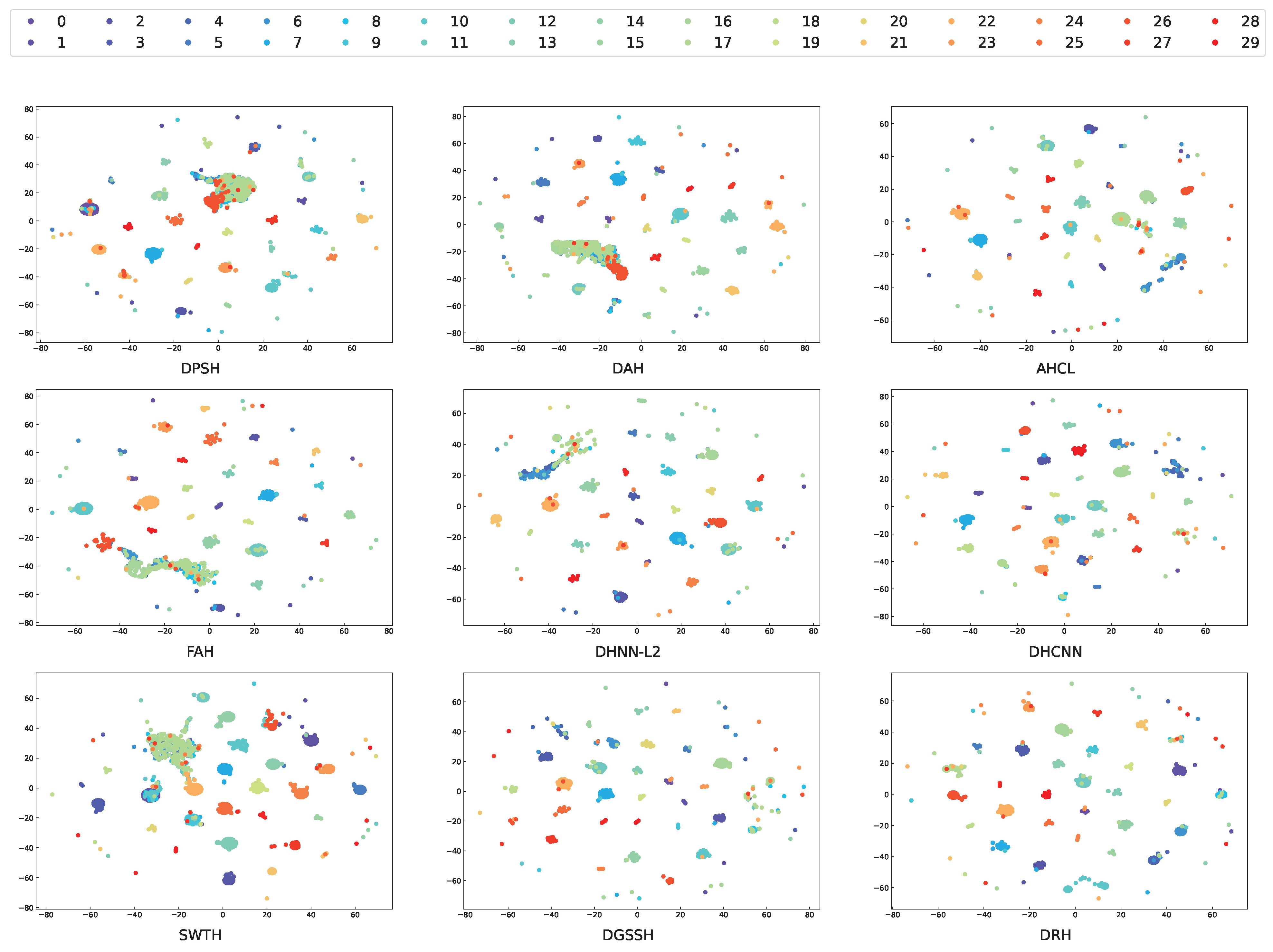
4.6. Visualization of Hash Codes and Retrieval Examples
4.7. Hyperparameter Analysis
4.8. Retrieval Efficiency Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, W.; Guan, H.; Li, Z.; Shao, Z.; Delavar, M.R. Remote Sensing Image Retrieval in the Past Decade: Achievements, Challenges, and Future Directions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1447–1473. [Google Scholar] [CrossRef]
- Li, Y.; Ma, J.; Zhang, Y. Image retrieval from remote sensing big data: A survey. Inf. Fusion 2021, 67, 94–115. [Google Scholar] [CrossRef]
- Scott, G.J.; Klaric, M.N.; Davis, C.H.; Shyu, C.R. Entropy-Balanced Bitmap Tree for Shape-Based Object Retrieval From Large-Scale Satellite Imagery Databases. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1603–1616. [Google Scholar] [CrossRef]
- Vharkate, M.N.; Musande, V.B. Retrieval of Remote Sensing Images Using Fused Color and Texture Features with K-Means Clustering. In Proceedings of the 2018 Fourth International Conference on Computing Communication Control and Automation (ICCUBEA), Pune, India, 16–18 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Singha, M.; Hemachandran, K. Content based image retrieval using color and texture. Signal Image Process. 2012, 3, 39. [Google Scholar] [CrossRef]
- Aptoula, E. Remote sensing image retrieval with global morphological texture descriptors. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3023–3034. [Google Scholar] [CrossRef]
- Li, J.; Cai, Y.; Gong, X.; Jiang, J.; Lu, Y.; Meng, X.; Zhang, L. Semantic Retrieval of Remote Sensing Images Based on the Bag-of-Words Association Mapping Method. Sensors 2023, 23, 5807. [Google Scholar] [CrossRef]
- Imbriaco, R.; Sebastian, C.; Bondarev, E.; de With, P.H. Aggregated deep local features for remote sensing image retrieval. Remote Sens. 2019, 11, 493. [Google Scholar] [CrossRef]
- Boureau, Y.L.; Bach, F.; LeCun, Y.; Ponce, J. Learning mid-level features for recognition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2559–2566. [Google Scholar] [CrossRef]
- Tong, X.Y.; Xia, G.S.; Hu, F.; Zhong, Y.; Datcu, M.; Zhang, L. Exploiting deep features for remote sensing image retrieval: A systematic investigation. IEEE Trans. Big Data 2019, 6, 507–521. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, X.; Zhu, H.; Ma, J. Large-Scale Remote Sensing Image Retrieval by Deep Hashing Neural Networks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 950–965. [Google Scholar] [CrossRef]
- Li, P.; Han, L.; Tao, X.; Zhang, X.; Grecos, C.; Plaza, A.; Ren, P. Hashing Nets for Hashing: A Quantized Deep Learning to Hash Framework for Remote Sensing Image Retrieval. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7331–7345. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, X.; Lu, X. Remote Sensing Image Retrieval by Deep Attention Hashing with Distance-Adaptive Ranking. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 4301–4311. [Google Scholar] [CrossRef]
- Song, W.; Gao, Z.; Dian, R.; Ghamisi, P.; Zhang, Y.; Benediktsson, J.A. Asymmetric Hash Code Learning for Remote Sensing Image Retrieval. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5617514. [Google Scholar] [CrossRef]
- Liu, P.; Liu, Z.; Shan, X.; Zhou, Q. Deep Hash Remote-Sensing Image Retrieval Assisted by Semantic Cues. Remote Sens. 2022, 14, 6358. [Google Scholar] [CrossRef]
- Weiss, Y.; Torralba, A.; Fergus, R. Spectral hashing. Adv. Neural Inf. Process. Syst. 2008, 21. Available online: https://proceedings.neurips.cc/paper_files/paper/2008/file/d58072be2820e8682c0a27c0518e805e-Paper.pdf (accessed on 24 May 2025).
- Gong, Y.; Lazebnik, S. Iterative quantization: A procrustean approach to learning binary codes. In Proceedings of the CVPR 2011, Providence, RI, USA, 20–25 June 2011; pp. 817–824. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Kumar, S.; Chang, S.F. Hashing with graphs. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 1–8. [Google Scholar]
- Wang, J.; Kumar, S.; Chang, S.F. Semi-Supervised Hashing for Large-Scale Search. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2393–2406. [Google Scholar] [CrossRef]
- Wang, D.; Gao, X.; Wang, X. Semi-supervised constraints preserving hashing. Neurocomputing 2015, 167, 230–242. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, Y. SSDH: Semi-Supervised Deep Hashing for Large Scale Image Retrieval. IEEE Trans. Circuits Syst. Video Technol. 2016, 29, 212–225. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, L.; Li, W.J. Semi-Supervised Deep Hashing with a Bipartite Graph. In Proceedings of the International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Liu, W.; Wang, J.; Ji, R.; Jiang, Y.G.; Chang, S.F. Supervised hashing with kernels. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2074–2081. [Google Scholar] [CrossRef]
- Shen, F.; Shen, C.; Liu, W.; Shen, H.T. Supervised Discrete Hashing. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 37–45. [Google Scholar] [CrossRef]
- Kang, W.C.; Li, W.J.; Zhou, Z.H. Column Sampling Based Discrete Supervised Hashing. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar] [CrossRef]
- Cao, Y.; Long, M.; Liu, B.; Wang, J. Deep Cauchy Hashing for Hamming Space Retrieval. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1229–1237. [Google Scholar] [CrossRef]
- Peng, L.; Qian, J.; Wang, C.; Liu, B.; Dong, Y. Swin transformer-based supervised hashing. Appl. Intell. 2023, 53, 17548–17560. [Google Scholar] [CrossRef]
- Chaudhuri, B.; Demir, B.; Bruzzone, L.; Chaudhuri, S. Region-Based Retrieval of Remote Sensing Images Using an Unsupervised Graph-Theoretic Approach. IEEE Geosci. Remote Sens. Lett. 2016, 13, 987–991. [Google Scholar] [CrossRef]
- Demir, B.; Bruzzone, L. Hashing-Based Scalable Remote Sensing Image Search and Retrieval in Large Archives. IEEE Trans. Geosci. Remote Sens. 2016, 54, 892–904. [Google Scholar] [CrossRef]
- Reato, T.; Demir, B.; Bruzzone, L. An Unsupervised Multicode Hashing Method for Accurate and Scalable Remote Sensing Image Retrieval. IEEE Geosci. Remote Sens. Lett. 2019, 16, 276–280. [Google Scholar] [CrossRef]
- Fernandez-Beltran, R.; Demir, B.; Pla, F.; Plaza, A. Unsupervised Remote Sensing Image Retrieval Using Probabilistic Latent Semantic Hashing. IEEE Geosci. Remote Sens. Lett. 2021, 18, 256–260. [Google Scholar] [CrossRef]
- Tang, X.; Liu, C.; Ma, J.; Zhang, X.; Liu, F.; Jiao, L. Large-Scale Remote Sensing Image Retrieval Based on Semi-Supervised Adversarial Hashing. Remote Sens. 2019, 11, 2055. [Google Scholar] [CrossRef]
- Han, L.; Li, P.; Bai, X.; Grecos, C.; Zhang, X.; Ren, P. Cohesion Intensive Deep Hashing for Remote Sensing Image Retrieval. Remote Sens. 2020, 12, 101. [Google Scholar] [CrossRef]
- Shan, X.; Liu, P.; Gou, G.; Zhou, Q.; Wang, Z. Deep Hash Remote Sensing Image Retrieval with Hard Probability Sampling. Remote Sens. 2020, 12, 2789. [Google Scholar] [CrossRef]
- Roy, S.; Sangineto, E.; Demir, B.; Sebe, N. Metric-Learning-Based Deep Hashing Network for Content-Based Retrieval of Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2021, 18, 226–230. [Google Scholar] [CrossRef]
- Shan, X.; Liu, P.; Wang, Y.; Zhou, Q.; Wang, Z. Deep Hashing Using Proxy Loss on Remote Sensing Image Retrieval. Remote Sens. 2021, 13, 2924. [Google Scholar] [CrossRef]
- Zhao, D.; Chen, Y.; Xiong, S. Multiscale Context Deep Hashing for Remote Sensing Image Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 7163–7172. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, Q.; Hou, J.; Dai, J.; Huang, L.; Zhang, W. Deep global semantic structure-preserving hashing via corrective triplet loss for remote sensing image retrieval. Expert Syst. Appl. 2024, 238, 122105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Lu, X. Deep discrete hashing with pairwise correlation learning. Neurocomputing 2020, 385, 111–121. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, W.; Tian, Q.; Yang, M.; Li, H. Assessing Image Retrieval Quality at the First Glance. IEEE Trans. Image Process. 2018, 27, 6124–6134. [Google Scholar] [CrossRef]
- Ouyang, J.; Zhou, W.; Wang, M.; Tian, Q.; Li, H. Collaborative Image Relevance Learning for Visual Re-Ranking. IEEE Trans. Multimed. 2021, 23, 3646–3656. [Google Scholar] [CrossRef]
- Xia, G.S.; Yang, W.; Delon, J.; Gousseau, Y.; Sun, H.; Maître, H. Structural High-resolution Satellite Image Indexing. In Proceedings of the ISPRS TC VII Symposium—100 Years ISPRS, Vienna, Austria, 5–7 July 2010; Wagner, W., Székely, B., Eds.; Volume XXXVIII, pp. 298–303. [Google Scholar]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar] [CrossRef]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A Benchmark Data Set for Performance Evaluation of Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Li, W.J.; Wang, S.; Kang, W.C. Feature Learning Based Deep Supervised Hashing with Pairwise Labels. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI), New York, NY, USA, 9–15 July 2016; pp. 1711–1717. [Google Scholar]
- Liu, C.; Ma, J.; Tang, X.; Liu, F.; Zhang, X.; Jiao, L. Deep Hash Learning for Remote Sensing Image Retrieval. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3420–3443. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Benediktsson, J.A. Deep Hashing Learning for Visual and Semantic Retrieval of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9661–9672. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Wang, C.; Cao, R.; Wang, R. Learning discriminative topological structure information representation for 2D shape and social network classification via persistent homology. Knowl.-Based Syst. 2025, 311, 113125. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, G.; Ji, C. Combining Hilbert Feature Sequence and Lie Group Metric Space for Few-Shot Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5620415. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, G.; Wei, J. MMML: Multimanifold Metric Learning for Few-Shot Remote-Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5618714. [Google Scholar] [CrossRef]








| Methods | WHU-RS | UCMD | AID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 16 Bit | 32 Bit | 64 Bit | 16 Bit | 32 Bit | 64 Bit | 16 Bit | 32 Bit | 64 Bit | |
| DHNNs-L2 [11] | 94.25 | 96.34 | 97.76 | 92.29 | 94.72 | 95.03 | 83.31 | 86.19 | 93.15 |
| DPSH [47] | 86.67 | 90.87 | 92.37 | 82.24 | 91.26 | 92.97 | 81.96 | 84.22 | 87.68 |
| FAH [48] | 91.78 | 95.19 | 96.74 | 91.23 | 94.88 | 95.14 | 84.51 | 91.51 | 93.33 |
| DAH [13] | 94.15 | 95.99 | 96.32 | 86.79 | 96.27 | 96.57 | 81.01 | 86.37 | 87.58 |
| AHCL [14] | 93.47 | 94.62 | 97.32 | 94.39 | 95.23 | 95.66 | 86.67 | 91.71 | 94.07 |
| DHCNN [49] | 96.27 | 97.92 | 98.31 | 95.70 | 95.64 | 96.34 | 87.54 | 92.22 | 95.85 |
| SWTH [27] | 86.67 | 87.87 | 90.37 | 82.71 | 84.05 | 87.52 | 78.91 | 86.73 | 87.15 |
| DGSSH [38] | 96.66 | 96.62 | 97.64 | 96.32 | 97.13 | 98.47 | 87.17 | 93.31 | 95.61 |
| DRH | 97.14 | 98.46 | 98.73 | 97.73 | 97.94 | 98.72 | 88.35 | 94.68 | 96.21 |
| Method | AID | UCMD | WHURS-19 |
|---|---|---|---|
| DRH | 0.9338 | 0.9401 | 0.8934 |
| DHCNN | 0.9068 | 0.9122 | 0.8851 |
| FAH | 0.8563 | 0.8513 | 0.8330 |
| AHCL | 0.8894 | 0.8861 | 0.8445 |
| DAH | 0.8212 | 0.8936 | 0.8152 |
| DPSH | 0.7845 | 0.8177 | 0.7950 |
| DHNN-L2 | 0.8832 | 0.9301 | 0.8758 |
| SWTH | 0.7787 | 0.8259 | 0.7718 |
| DGSSH | 0.9171 | 0.9184 | 0.8852 |
| Methods | Weighted Loss | Reranking | WHU-RS | UCMD | AID | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 16 Bit | 32 Bit | 64 Bit | 16 Bit | 32 Bit | 64 Bit | 16 Bit | 32 Bit | 64 Bit | |||
| DRH-B | x | x | 92.08 | 96.14 | 96.52 | 94.43 | 94.43 | 95.02 | 85.11 | 92.62 | 93.02 |
| DRH-R | x | ✓ | 92.52 | 96.85 | 96.91 | 96.55 | 96.29 | 96.39 | 86.23 | 92.88 | 94.17 |
| DRH-W | ✓ | x | 96.77 | 98.43 | 98.59 | 97.65 | 97.76 | 98.61 | 88.21 | 93.41 | 95.33 |
| DRH | ✓ | ✓ | 97.14 | 98.46 | 98.73 | 97.73 | 97.94 | 98.72 | 88.35 | 94.68 | 96.21 |
| Backbone | mAP (%) | Retrieval Time (s) |
|---|---|---|
| AlexNet [50] | 84.72 | 12.37 |
| ResNet50 [51] | 88.33 | 12.45 |
| VGG11 [39] | 92.25 | 12.43 |
| Swin–Transformer [52] | 92.41 | 13.56 |
| Methods | Similar | Dissimilar | ||
|---|---|---|---|---|
| Pair 1 | Pair 2 | Pair 1 | Pair 2 | |
| AHCL [14] | 32 | 31 | 32 | 31 |
| DAH [13] | 32 | 34 | 18 | 31 |
| DHNN-L2 [11] | 33 | 32 | 31 | 26 |
| DHCNN [49] | 31 | 30 | 34 | 26 |
| FAH [48] | 32 | 35 | 32 | 31 |
| DPSH [47] | 34 | 33 | 14 | 30 |
| SWTH [27] | 35 | 34 | 16 | 25 |
| DGSSH [38] | 30 | 29 | 35 | 33 |
| DRH | 29 | 28 | 37 | 35 |
| Methods | Training Time | Retrieval Time | ||||
|---|---|---|---|---|---|---|
| 16 Bit | 32 Bit | 64 Bit | 16 Bit | 32 Bit | 64 Bit | |
| DPSH [47] | 1221.41 | 1231.21 | 1240.89 | 11.41 | 11.82 | 12.16 |
| AHCL [14] | 946.31 | 965.37 | 986.82 | 11.10 | 11.25 | 11.42 |
| DAH [13] | 1234.91 | 1236.32 | 1284.45 | 12.55 | 12.63 | 12.88 |
| SWTH [27] | 1336.31 | 1346.24 | 1334.61 | 13.22 | 13.44 | 13.42 |
| DGSSH [38] | 975.51 | 971.52 | 1019.86 | 13.17 | 13.38 | 13.46 |
| DRH | 1398.36 | 1403.14 | 1404.23 | 13.23 | 13.27 | 13.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Chen, X.; Zhu, G. Deep Relevance Hashing for Remote Sensing Image Retrieval. Sensors 2025, 25, 6379. https://doi.org/10.3390/s25206379
Liu X, Chen X, Zhu G. Deep Relevance Hashing for Remote Sensing Image Retrieval. Sensors. 2025; 25(20):6379. https://doi.org/10.3390/s25206379
Chicago/Turabian StyleLiu, Xiaojie, Xiliang Chen, and Guobin Zhu. 2025. "Deep Relevance Hashing for Remote Sensing Image Retrieval" Sensors 25, no. 20: 6379. https://doi.org/10.3390/s25206379
APA StyleLiu, X., Chen, X., & Zhu, G. (2025). Deep Relevance Hashing for Remote Sensing Image Retrieval. Sensors, 25(20), 6379. https://doi.org/10.3390/s25206379






