Burg-Aided 2D MIMO Array Extrapolation for Improved Spatial Resolution
Abstract
1. Introduction
2. MIMO Antenna
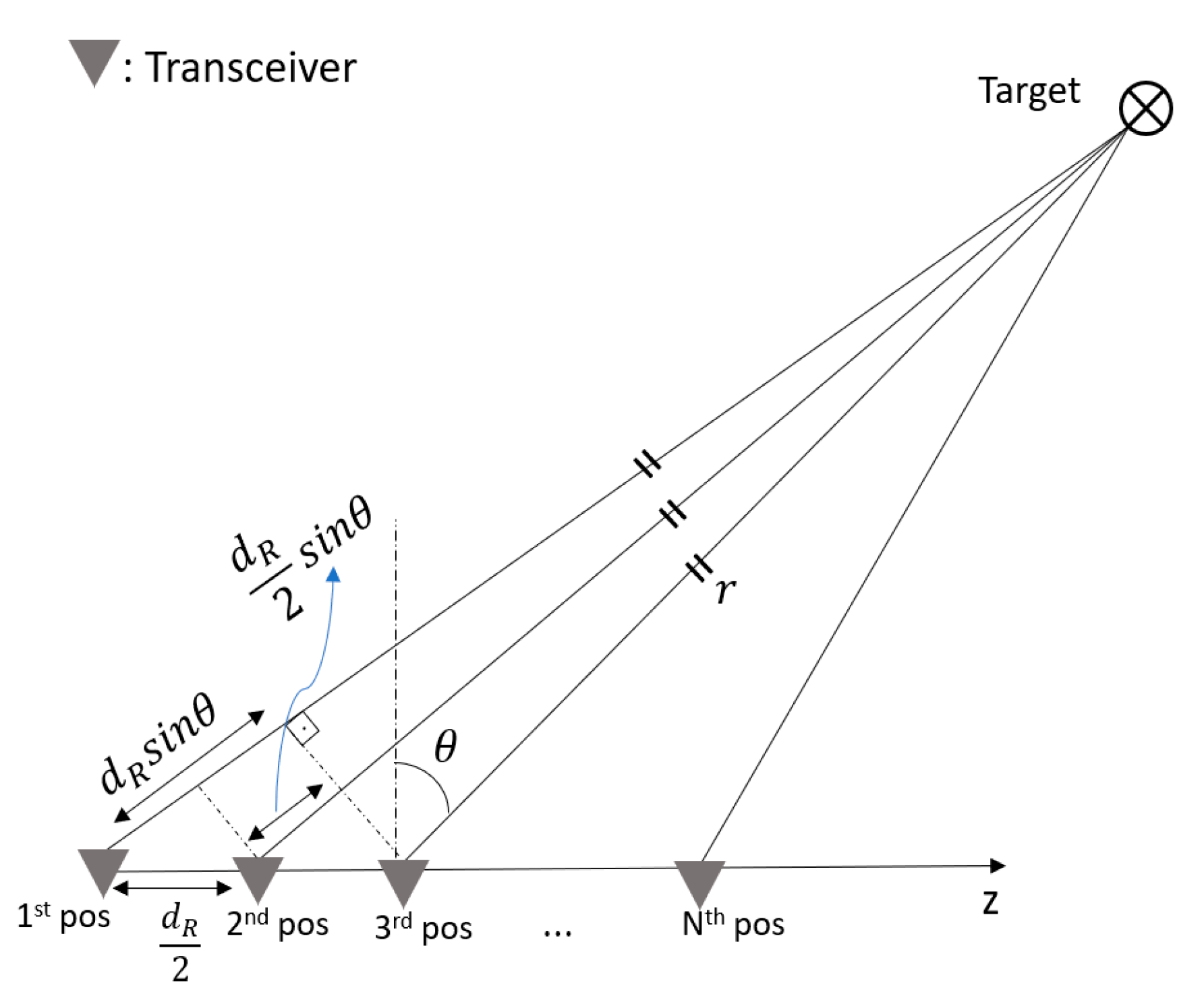
2.1. 1D MIMO
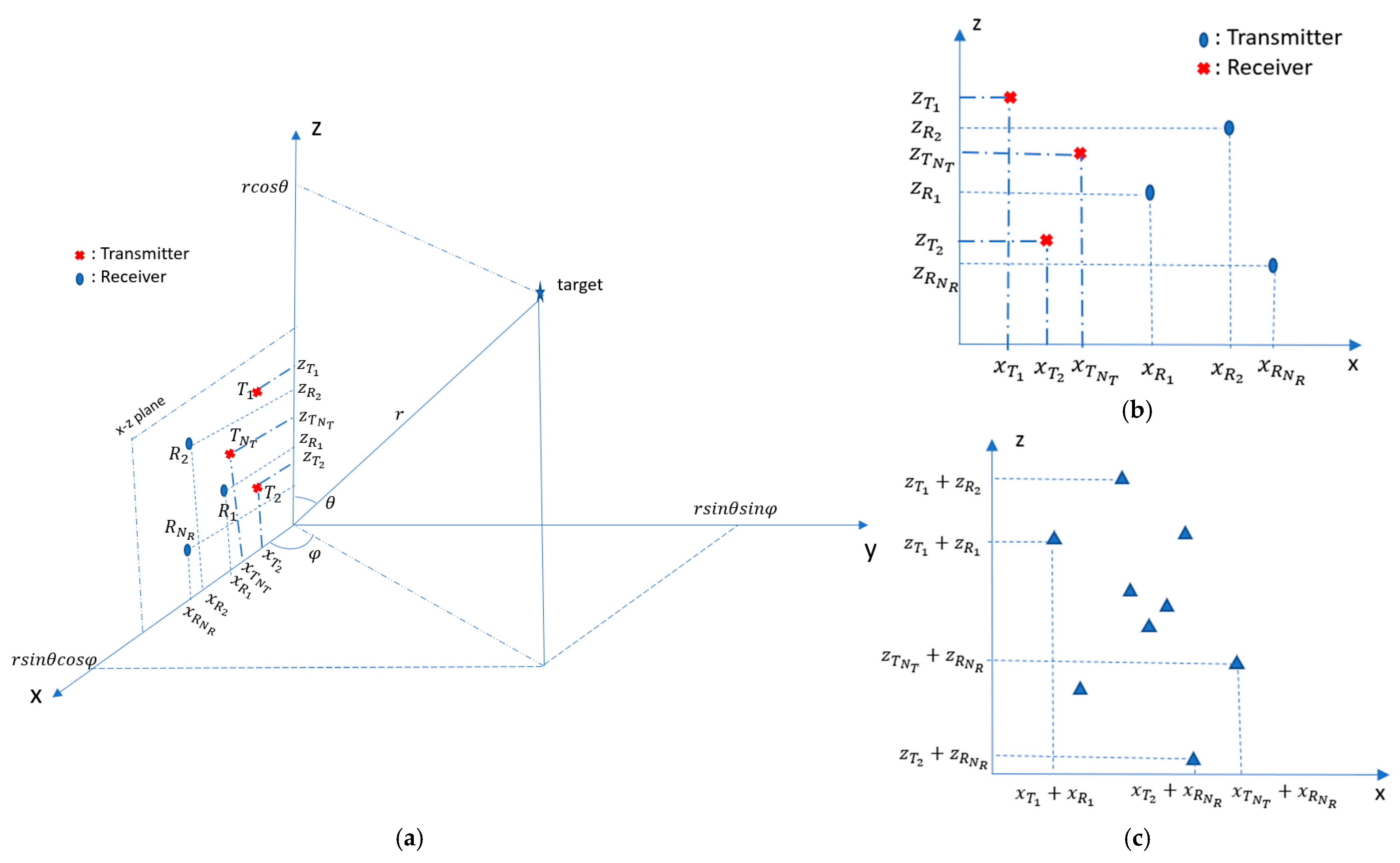
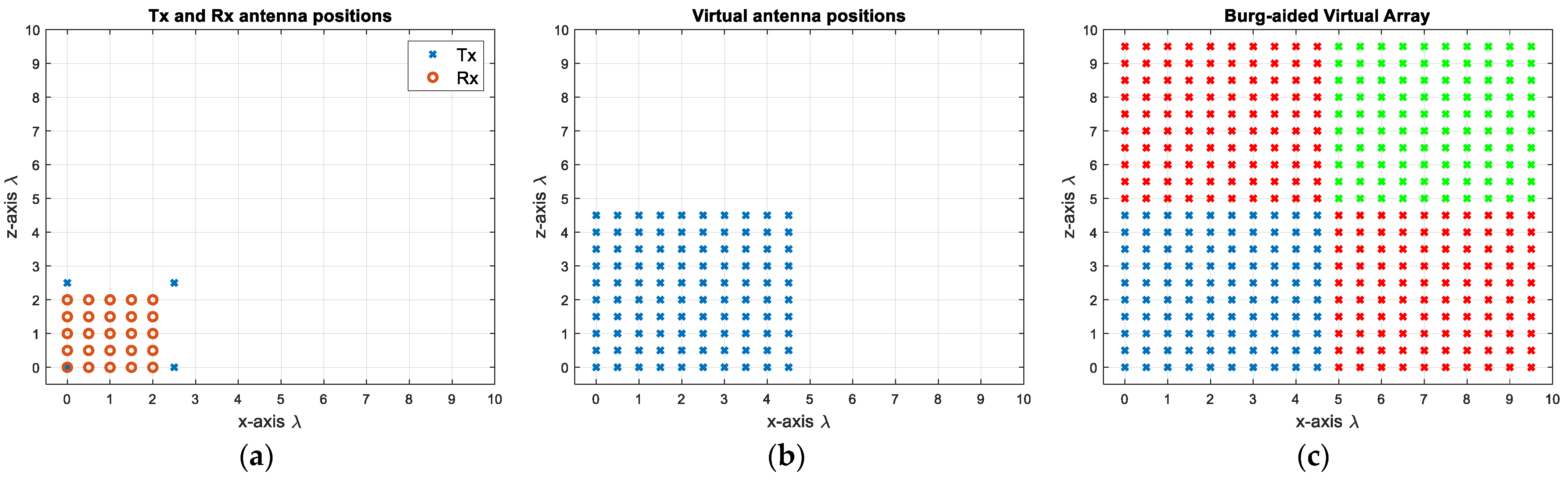
2.2. 2D MIMO
3. The Burg Algorithm
- 1.
- At the first iteration (), the initial forward and backward prediction error vectors ( and ) are assumed to be equal to :
- 2.
- The first element is then removed from , and the last element is removed from in each iteration so that
- 3.
- At each next iteration , the reflection coefficient () is calculated as
- 4.
- The updated prediction vectors are calculated as
- 5.
- The updated FIR coefficients are calculated as
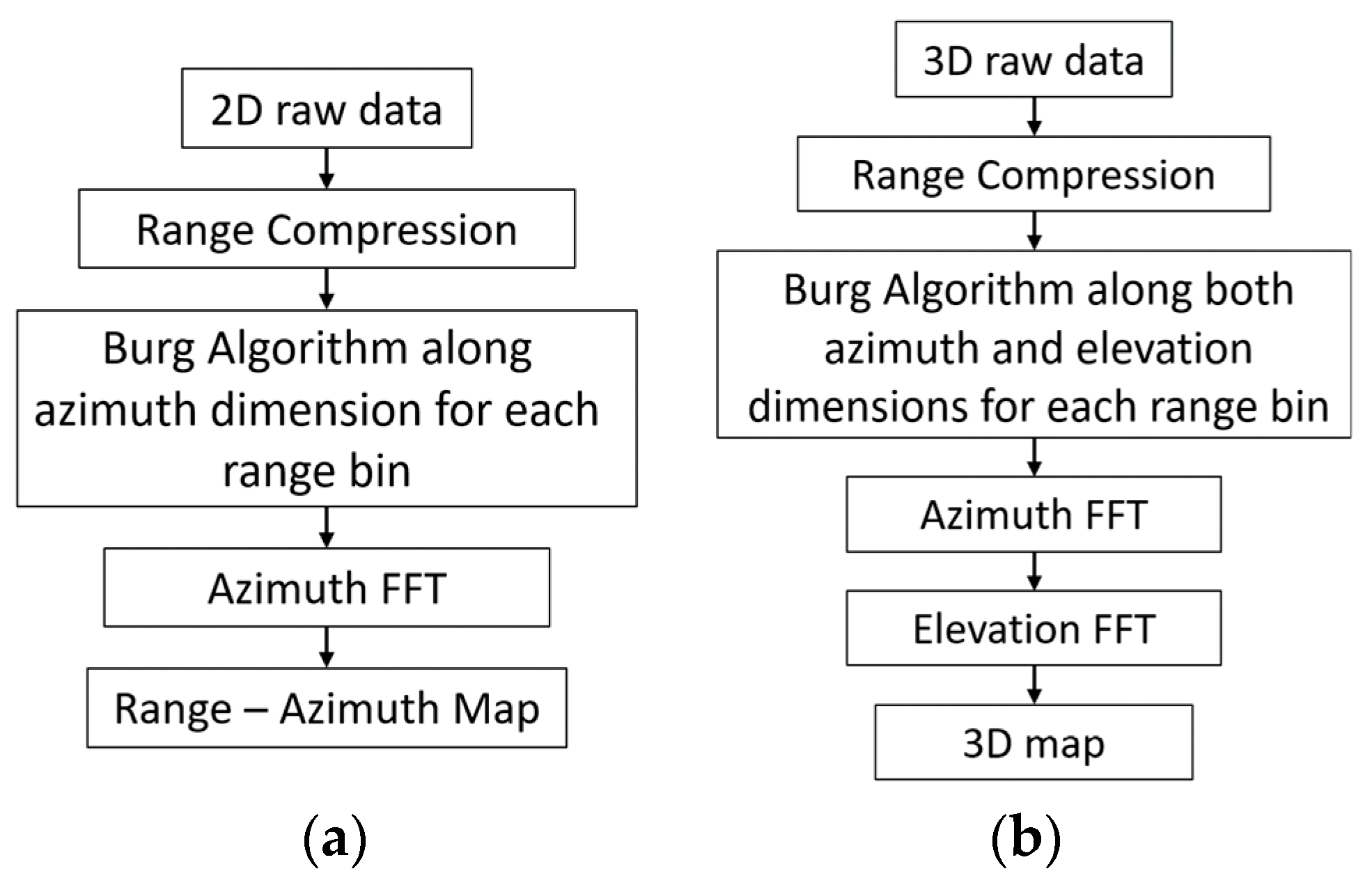
4. Burg-Aided MIMO
- for range compression.
- for extrapolation along the azimuth and the azimuth FFT.
- for range compression.
- for extrapolation along the azimuth and the azimuth FFT.
- for extrapolation along elevation and the elevation FFT.
5. Simulation Results
5.1. Burg-Aided 1D MIMO
5.1.1. Estimation of Missing Data (Interpolation)
5.1.2. Estimation of Forward Data (Extrapolation)
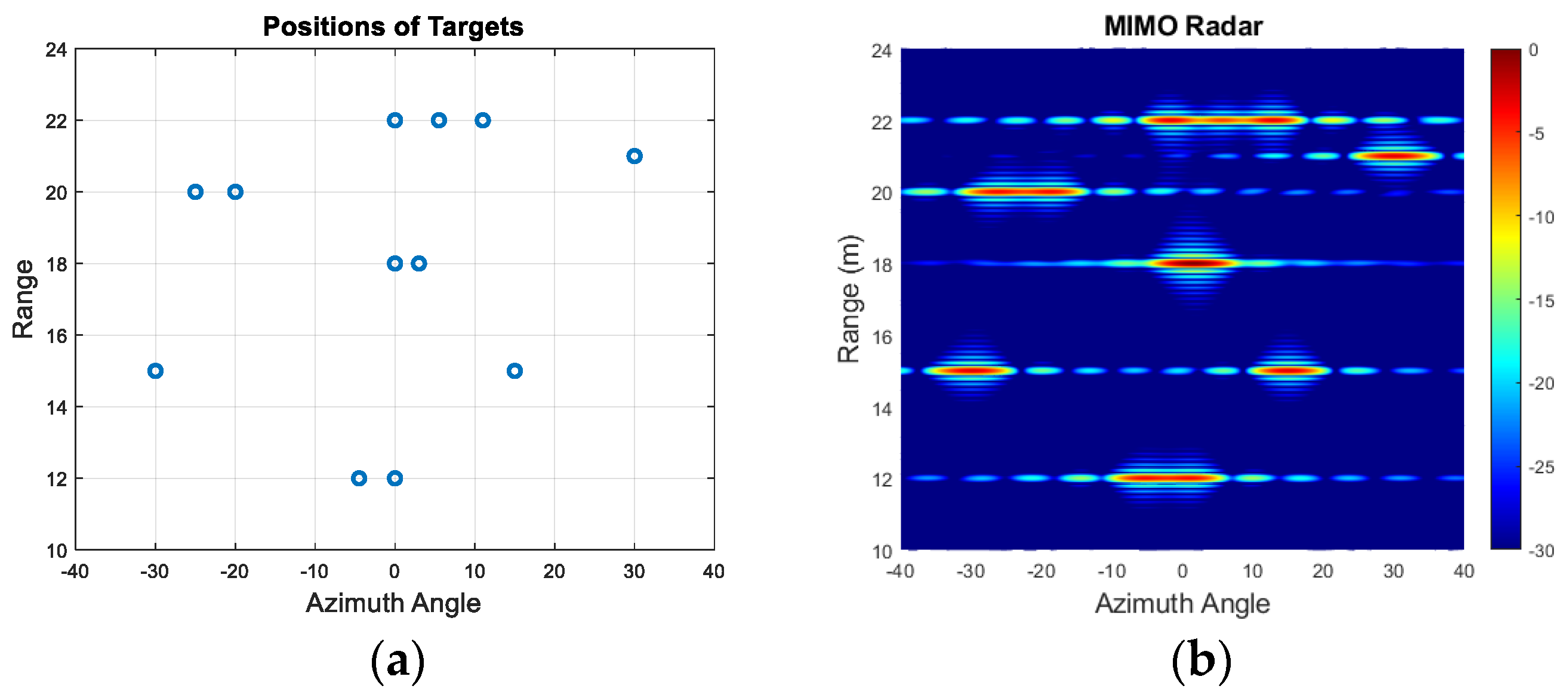
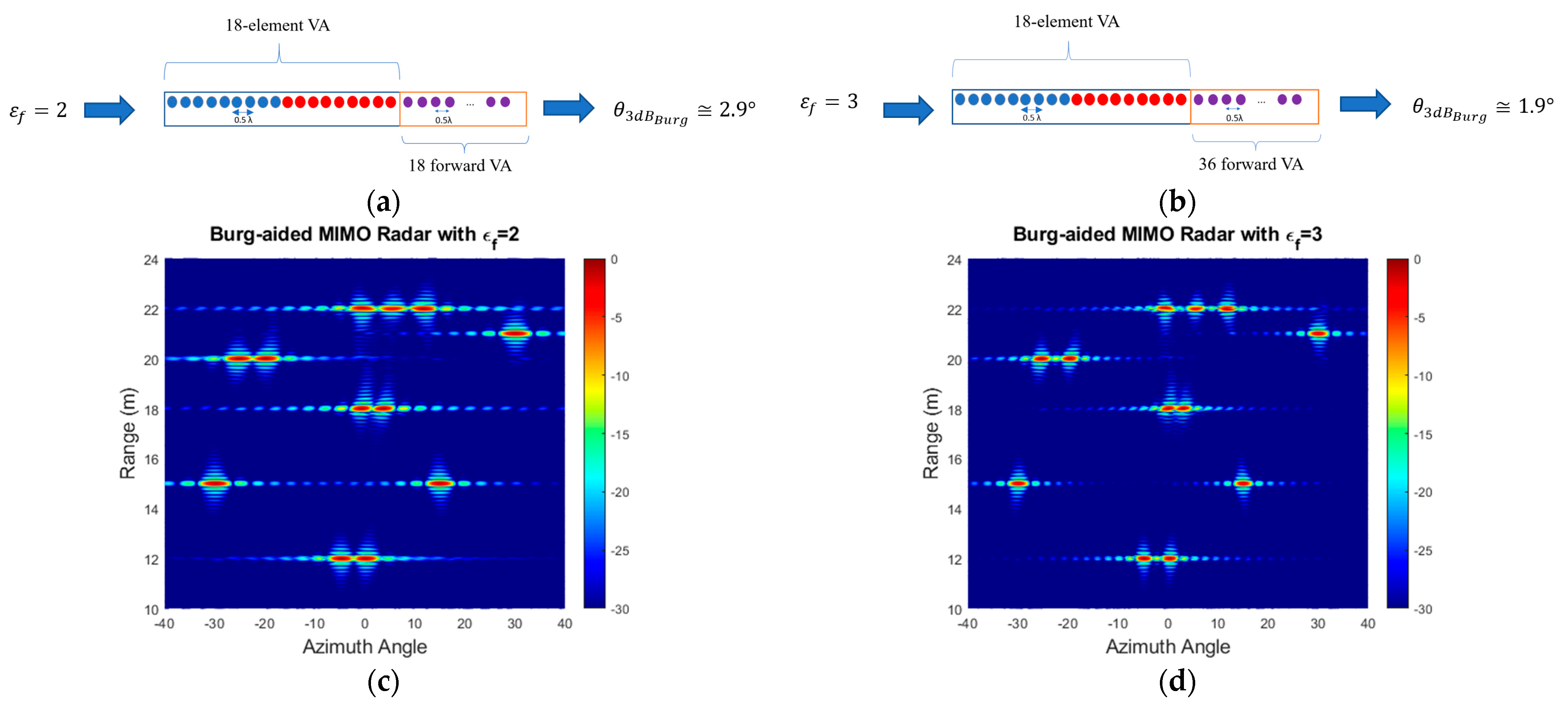
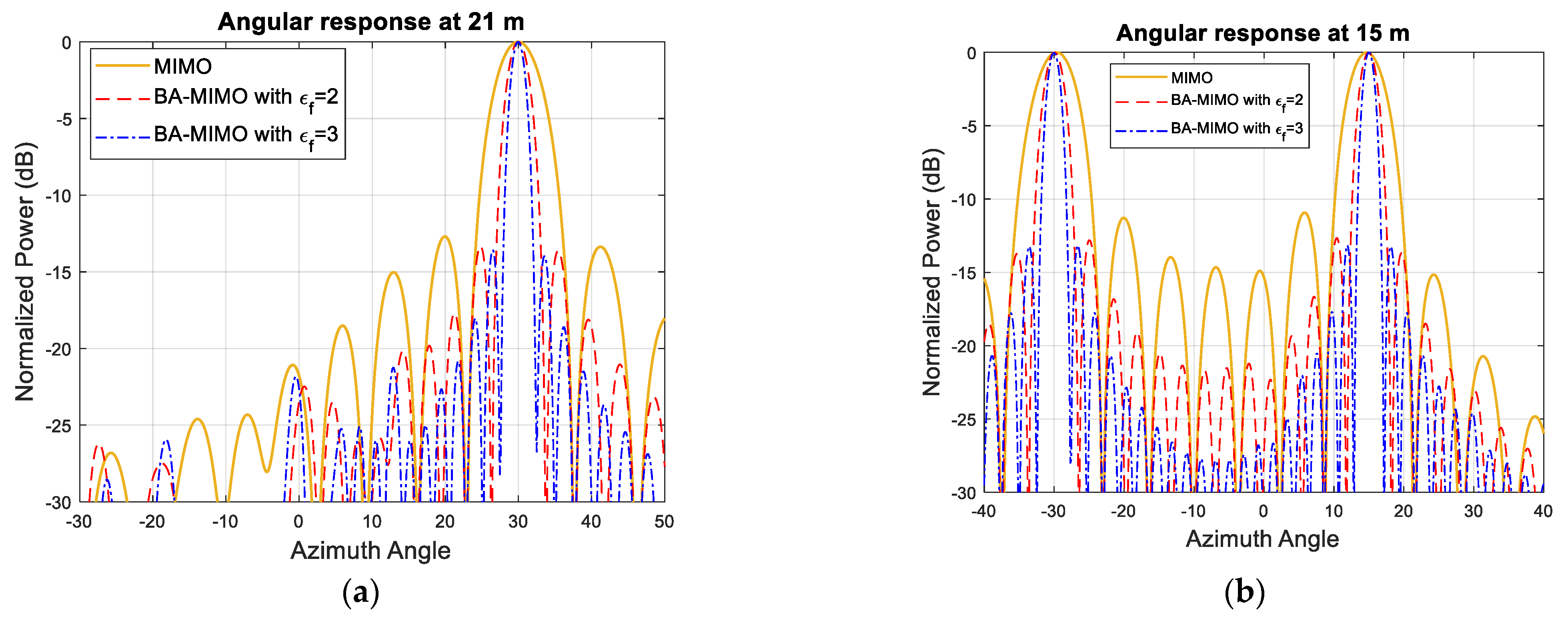
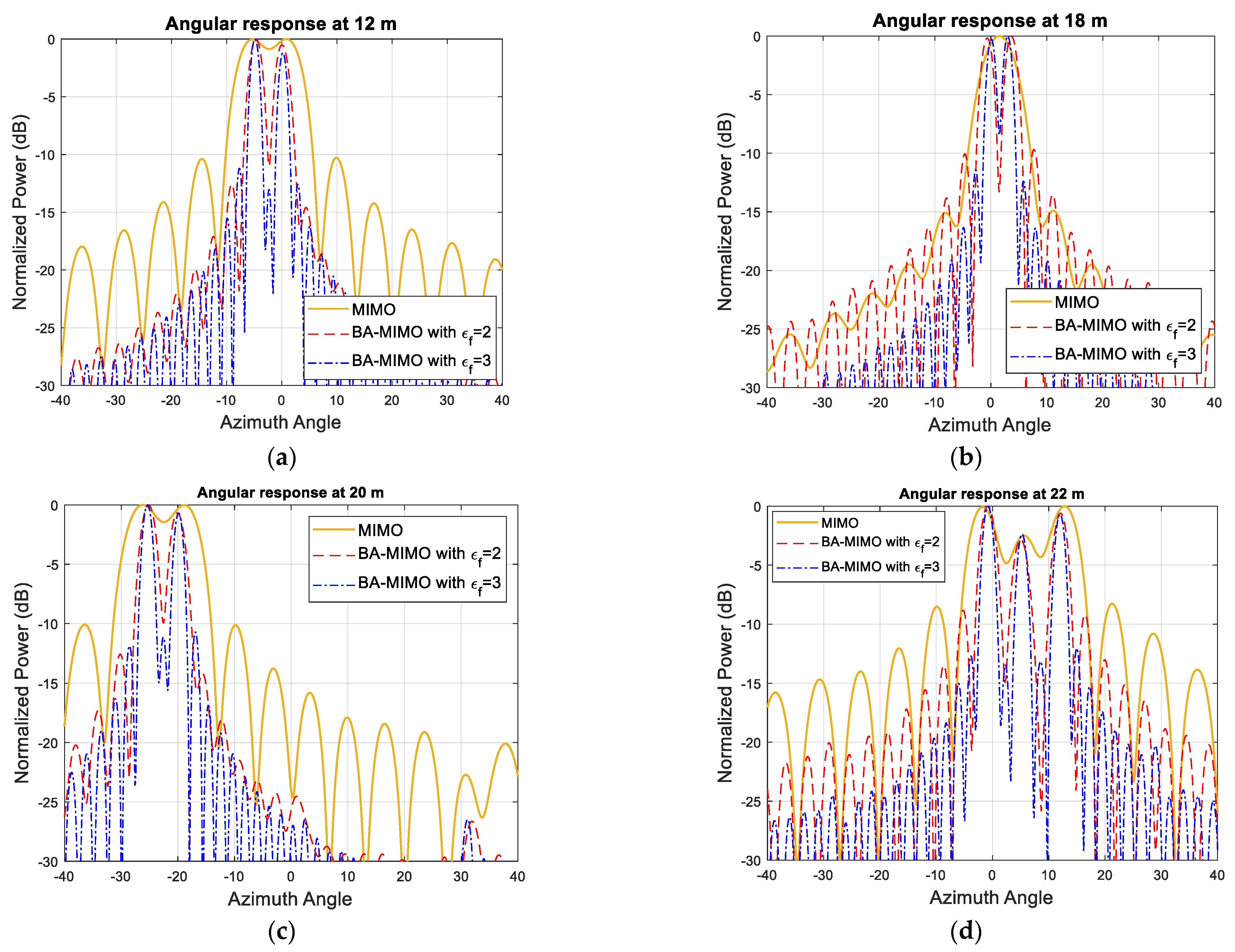
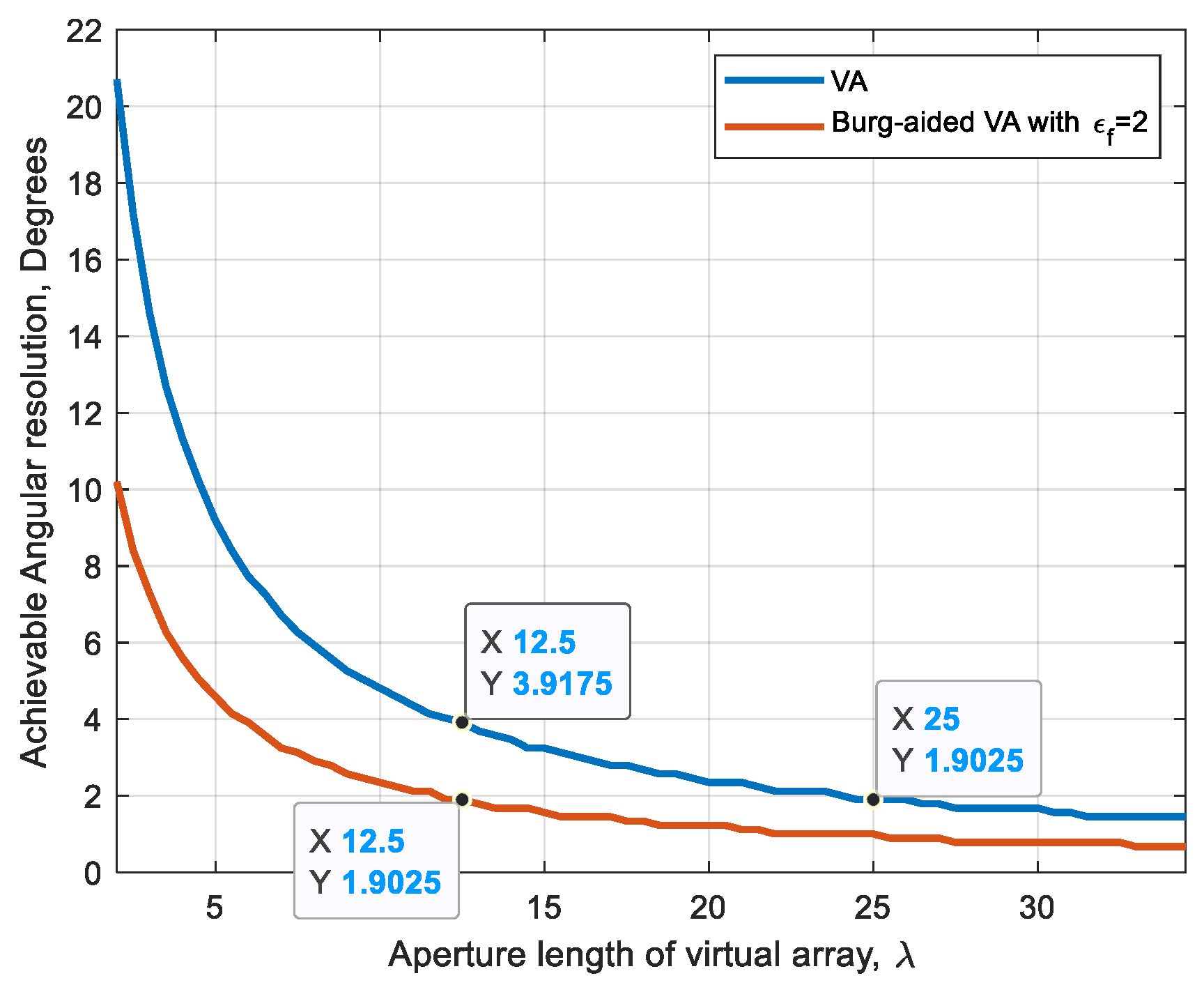
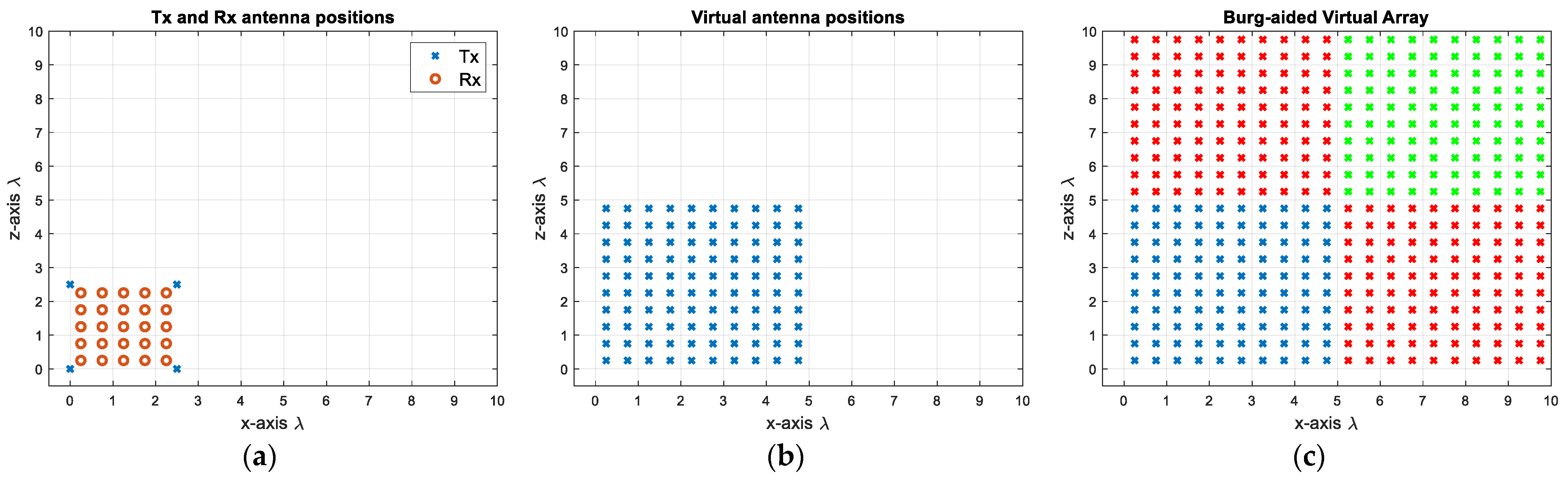
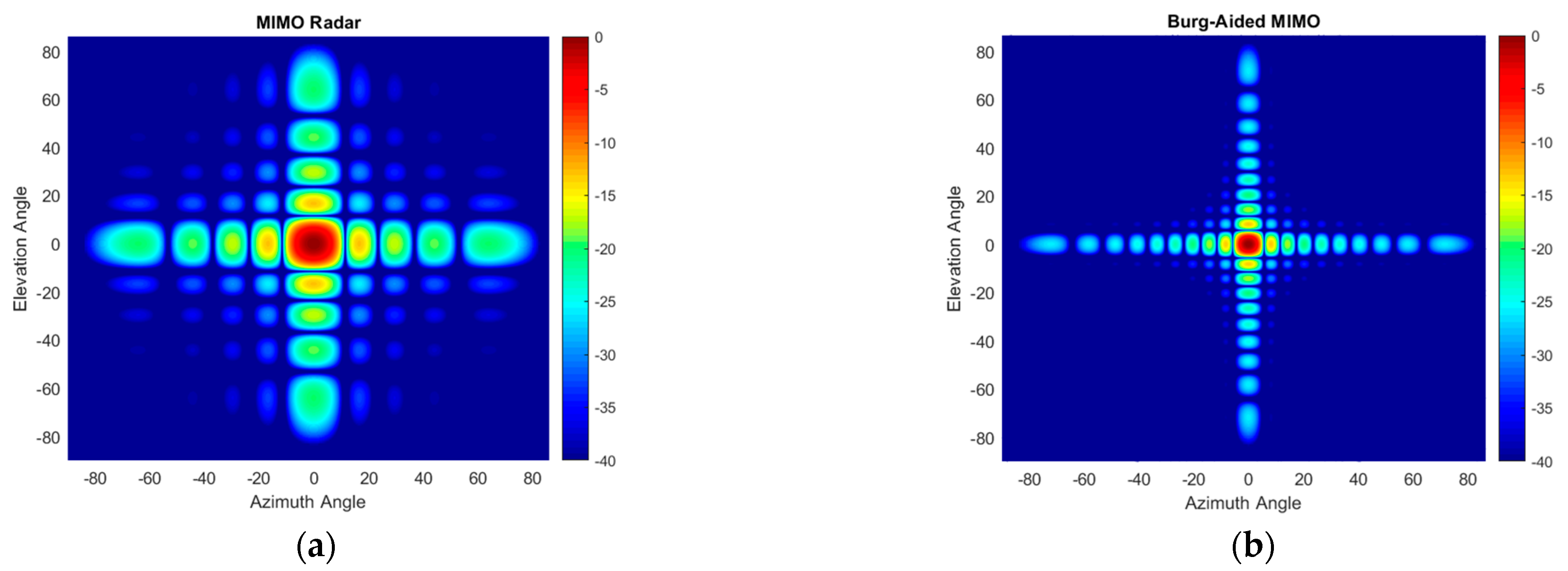
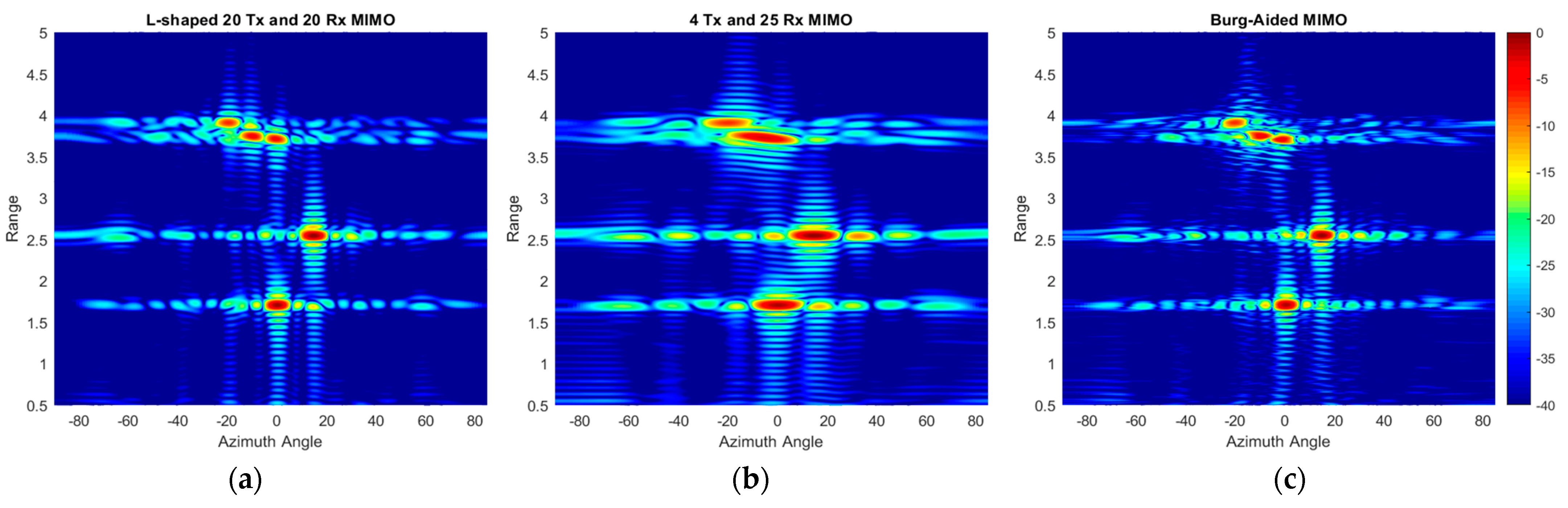
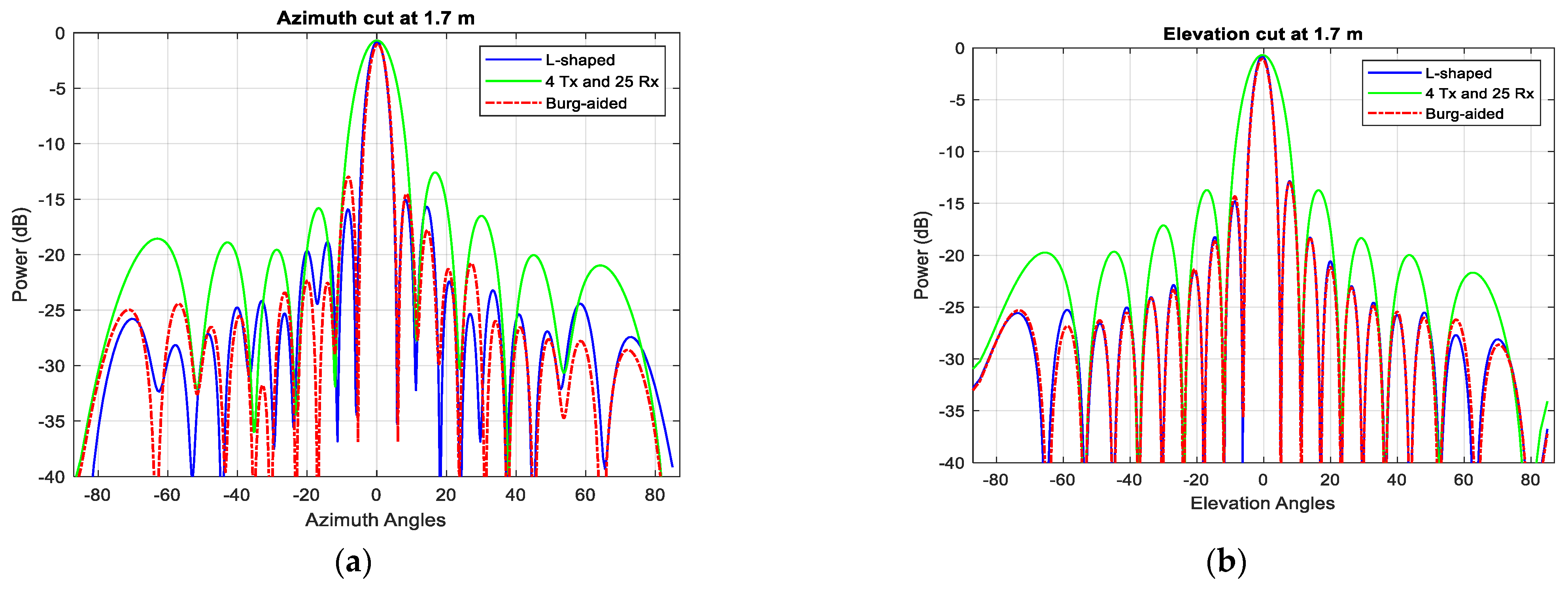
5.2. Burg-Aided 2D MIMO
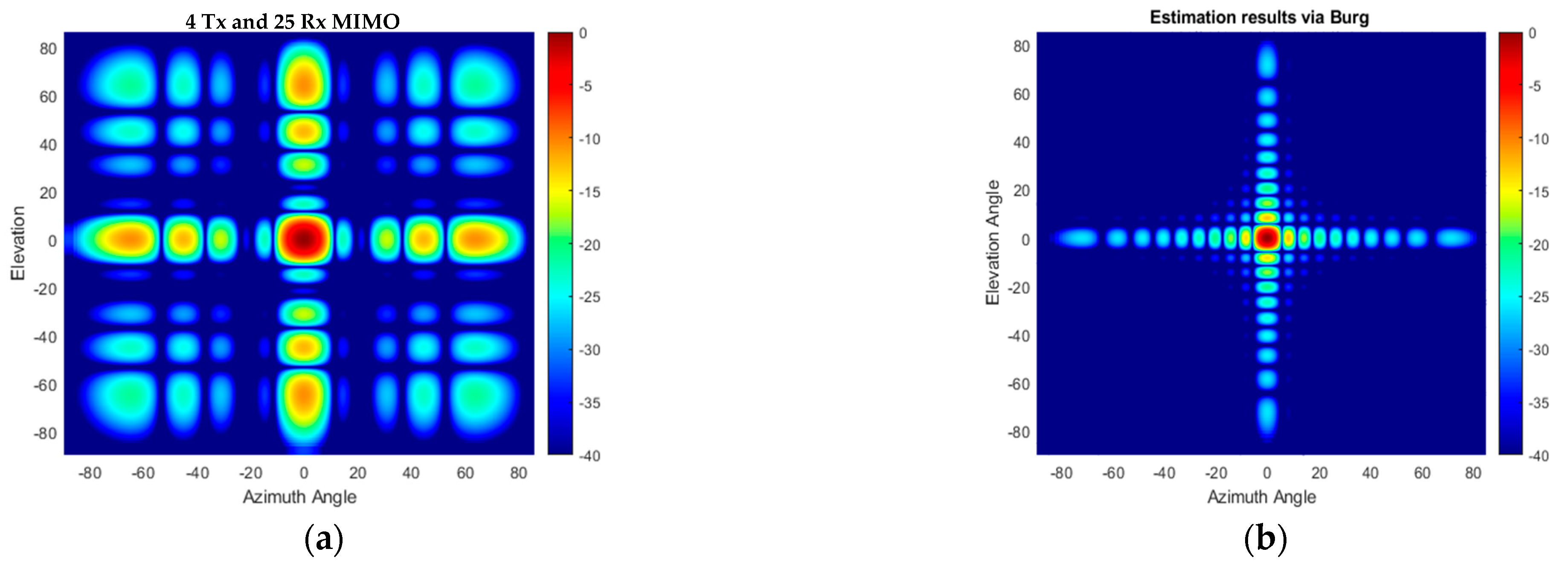
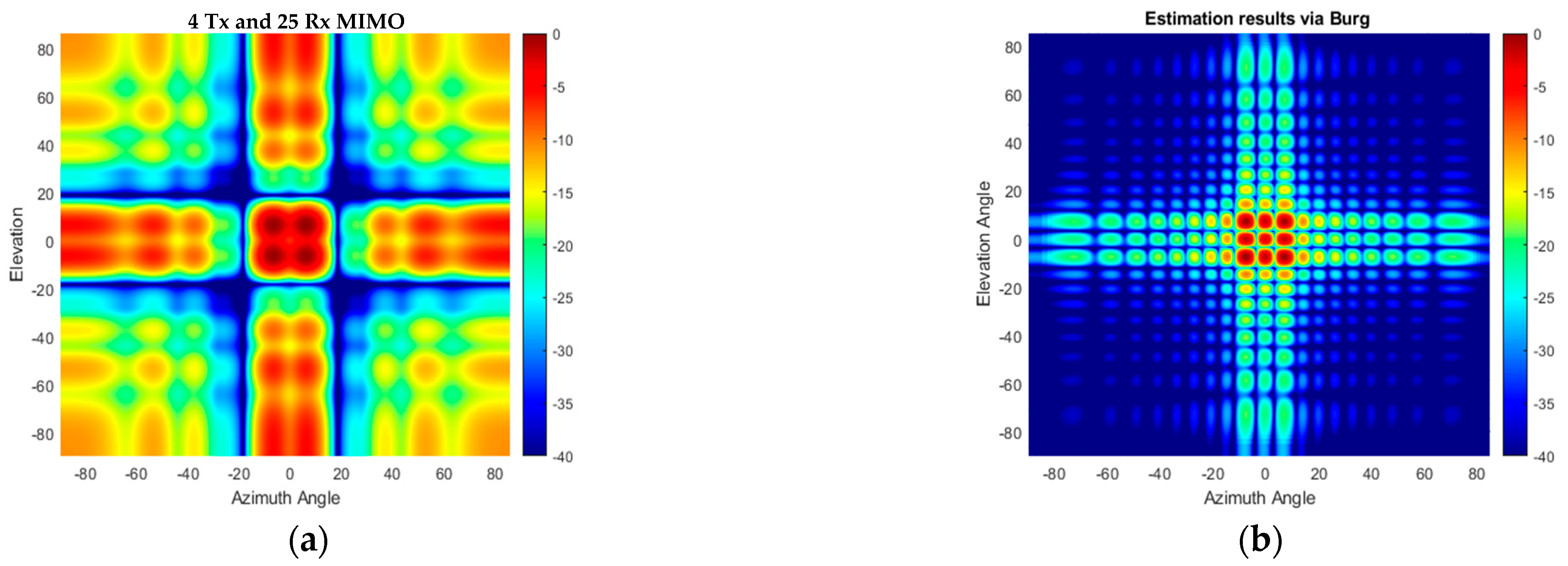
6. Experimental Setup and Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Melvin, W.L.; Scheer, J.A. Volume II, Advanced Techniques. In Principles of Modern Radar; SciTech Pub.: Raleigh, NC, USA, 2013; pp. 119–145. [Google Scholar]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Yanik, M.E.; Wang, D.; Torlak, M. Development and Demonstration of MIMO-SAR mmWave Imaging Testbeds. IEEE Access 2020, 8, 126019–126038. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar Signal Processing; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chen, C.-Y.; Vaidyanathan, P.P. Minimum redundancy MIMO radars. In Proceedings of the 2008 IEEE International Symposium on Circuits and Systems (ISCAS), Seattle, WA, USA, 18–21 May 2008; pp. 45–48. [Google Scholar] [CrossRef]
- Unz, H. Linear Arrays with arbitrarily distributed elements. IEEE Trans. Antennas Propag. 1960, 8, 222–223. [Google Scholar] [CrossRef]
- Haupt, R.L.; Menozzi, J.J.; McCormack, C.J. Thinned arrays using genetic algorithms. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Ann Arbor, MI, USA, 28 June–2 July 1993; Volume 2, pp. 712–715. [Google Scholar] [CrossRef]
- Kurup, D.G.; Himdi, M.; Rydberg, A. Synthesis of uniform amplitude unequally spaced antenna arrays using the differential evolution algorithm. IEEE Trans. Antennas Propag. 2003, 51, 2210–2217. [Google Scholar] [CrossRef]
- Robinson, J.; Rahmat-Samii, Y. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Rajo-Iglesias, E. Ant Colony Optimization in Thinned Array Synthesis with Minimum Sidelobe Level. IEEE Antennas Wirel. Propag. Lett. 2006, 5, 349–352. [Google Scholar] [CrossRef]
- Bekar, M.; Baker, C.J.; Gashinova, M. Sparse 2D MIMO Antenna Designs using Simulated Annealing. In Proceedings of the 2023 20th European Radar Conference (EuRAD), Berlin, Germany, 20–22 September 2023; pp. 371–374. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Hua, Y.; Sarkar, T.K. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 814–824. [Google Scholar] [CrossRef]
- Cho, H.-W.; Kim, W.; Choi, S.; Eo, M.; Khang, S.; Kim, J. Guided Generative Adversarial Network for Super Resolution of Imaging Radar. In Proceedings of the 2020 17th European Radar Conference (EuRAD), Utrecht, Netherlands, 10–15 January 2021; pp. 144–147. [Google Scholar] [CrossRef]
- Roldan, I.; Fioranelli, F.; Yarovoy, A. Self-Supervised Learning for Enhancing Angular Resolution in Automotive MIMO Radars. IEEE Trans. Veh. Technol. 2023, 72, 11505–11514. [Google Scholar] [CrossRef]
- Gupta, I.J.; Beals, M.J.; Moghaddar, A. Data extrapolation for high resolution radar imaging. IEEE Trans. Antennas Propag. 1994, 42, 1540–1545. [Google Scholar] [CrossRef]
- Chen, H.; Li, M.; Wang, Z.; Lu, Y.; Cao, R.; Zhang, P.; Zuo, L.; Zang, P. Cross-Range Resolution Enhancement for DBS Imaging in a Scan Mode Using Aperture-Extrapolated Sparse Representation. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 1459–1463. [Google Scholar] [CrossRef]
- Andres, M.; Menzel, W.; Bloecher, H.-L.; Dickmann, J. Detection of slow moving targets using automotive radar sensors. In Proceedings of the 7th German Microwave Conference, Ilmenau, Germany, 12–14 March 2012; pp. 1–4. [Google Scholar]
- Cho, B.L.; Sun, S.-G. Cross-range resolution improvement in forward-looking imaging radar using autoregressive model-based data extrapolation. IET Radar Sonar Navig. 2015, 9, 933–941. [Google Scholar] [CrossRef]
- de Hoon, M.J.L.; van der Hagen, T.H.J.J.; Schoonewelle, H.; van Dam, H. Why Yule-Walker should not be used for autoregressive modelling. Ann. Nucl. Energy 1996, 23, 1219–1228. [Google Scholar] [CrossRef]
- Rezek, I.A.; Roberts, S.J. Parametric model order estimation: A brief review. In Proceedings of the IEE Colloquium on Model Based Digital Signal Processing Techniques in the Analysis of Biomedical Signals (Digest No. 1997/009), London, UK, 16 April 1997; pp. 3/1–3/6. [Google Scholar] [CrossRef]
- Salzman, J.; Akamine, D.; Lefevre, R.; Kirk, J.C. Interrupted synthetic aperture radar (SAR). IEEE Aerosp. Electron. Syst. Mag. 2002, 17, 33–39. [Google Scholar] [CrossRef]
- Chen, H.; Li, M.; Zhang, P.; Liu, G.; Jia, L.; Wu, Y. Resolution enhancement for Doppler beam sharpening imaging. IET Radar Sonar Navig. 2015, 9, 843–851. [Google Scholar] [CrossRef]
- Hott, M.; Mietzner, J.; Lutz, S.; Bockmair, M.; Hoeher, P.A. Joint Super-Resolution and Array Interpolation for MIMO Radar Virtual Arrays. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 126–129. [Google Scholar] [CrossRef]
- Bekar, M.; Baker, C.; Gashinova, M. Enhanced Angular Resolution in Automotive Radar Imagery Using Burg-Aided MIMO-DBS Approach. In Proceedings of the 2023 20th European Radar Conference (EuRAD), Berlin, Germany, 20–22 September 2023; pp. 315–318. [Google Scholar] [CrossRef]
- Bekar, M.; Baker, C.J.; Gashinova, M. Reconstructed 2D MIMO Using Burg Algorithm. In Proceedings of the 2023 20th European Radar Conference (EuRAD), Berlin, Germany, 20–22 September 2023; pp. 375–378. [Google Scholar] [CrossRef]
- Shakibi, B.; Honarvar, F.; Moles, M.D.C.; Caldwell, J.; Sinclair, A.N. Resolution enhancement of ultrasonic defect signals for crack sizing. NDT E Int. 2012, 52, 37–50. [Google Scholar] [CrossRef]
- Ning, J.; Wang, R.; Deng, Y.; Li, N.; Song, H.; Fei, W. AET-IAA: A Novel Approach to Enhance Azimuth Resolution for ScanSAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2017, 10, 5674–5685. [Google Scholar] [CrossRef]
- Li, N.; Wang, R.; Deng, Y.; Chen, J.; Zhang, Z.; Liu, Y.; Xu, Z.; Zhao, F. Improved Full-Aperture ScanSAR Imaging Algorithm Based on Aperture Interpolation. IEEE Geosci. Remote. Sens. Lett. 2015, 12, 1101–1105. [Google Scholar] [CrossRef]
- Moore, T.G.; Zuerndorfer, B.W.; Burt, E.C. Enhanced imagery using spectral-estimation-based techniques. Linc. Lab. J. 1997, 10, 171–186. [Google Scholar]
- Wang, H.; Su, Y. Narrowband MIMO radar imaging with two orthogonal linear T/R arrays. In Proceedings of the 2008 9th International Conference on Signal Processing, Beijing, China, 26–29 October 2008; pp. 2513–2516. [Google Scholar] [CrossRef]
- Harter, M.; Mahler, T.; Schipper, T.; Ziroff, A.; Zwick, T. 2-D antenna array geometries for MIMO radar imaging by Digital Beamforming. In Proceedings of the 2013 European Microwave Conference, Nuremberg, Germany, 6–10 October 2013; pp. 1695–1698. [Google Scholar]
- Cetinkaya, H.; Kueppers, S.; Herschel, R.; Pohl, N. Comparison of near and far field focusing patterns for two-dimensional sparse MIMO arrays. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Ganis, A.; Navarro, E.M.; Schoenlinner, B.; Prechtel, U.; Meusling, A.; Heller, C.; Spreng, T.; Mietzner, J.; Krimmer, C.; Haeberle, B.; et al. A Portable 3-D Imaging FMCW MIMO Radar Demonstrator with a 24 × 24 Antenna Array for Medium-Range Applications. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 298–312. [Google Scholar] [CrossRef]
- Vos, K. A fast implementation of Burg’s method. Signal Process. 2013, 10, 2–4. [Google Scholar]
- Bekar, A.; Gilliam, C.; Antoniou, M. Passive SAR Range Resolution Enhancement Using Multiple DVB-T Channels. IEEE Trans. Geosci. Remote. Sens. 2025, 63, 1–13. [Google Scholar] [CrossRef]
- Wu, P.-R. A criterion for radar resolution enhancement with Burg algorithm. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 897–915. [Google Scholar] [CrossRef]
- Silicon Radar. Available online: https://siliconradar.com/ (accessed on 16 November 2023).
- Daniel, L.; Gashinova, M. Sub-THz Radar Imagery for Automotive Application. In Proceedings of the 2022 19th European Radar Conference (EuRAD), Milan, Italy, 28–30 September 2022; pp. 261–264. [Google Scholar] [CrossRef]
- Haderer, A. MIMO-77-TX4RX8 Frontend (User Manual); Inras GmbH: Linz, Austria, 2015. [Google Scholar]
- Available online: https://www.standa.lt/products/catalog/motorised_positioners?item=60 (accessed on 22 August 2023).








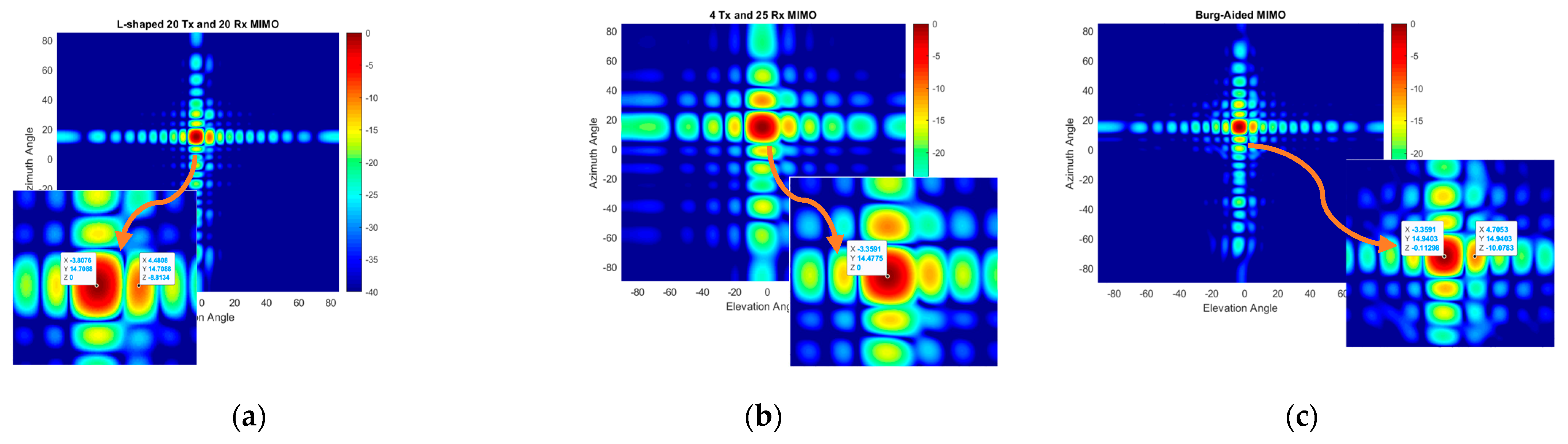
| L-Shaped 20 Tx and 20 Rx MIMO | Burg-Aided MIMO | Changes | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Target | Range | Power (PL) | Azimuth (AzL) | Elevation (ElL) | Power (PB) | Azimuth (AzB) | Elevation (ElB) | ΔP = PL − PB | ΔAz = AzL − AzB | ΔEl = ElL − ElB |
| Target I | 1.7 m | −0.81 dB | 0° | −0.448° | −1.063 dB | 0° | −0.448° | 0.253 dB | 0° | 0° |
| Target II | 2.5 m | 0 dB | 14.709° | −3.808° | −0.113 dB | 14.940° | −3.359° | 0.113 dB | −0.231° | −0.449° |
| Target III | 2.5 m | −8.813 dB | 14.709° | 4.481° | −10.078 dB | 14.940° | 4.705° | 1.265 dB | −0.231° | −0.224° |
| Target IV | 3.711 m | −4.90 dB | −0.671° | 2.911° | −4.078 dB | −0.895° | 2.911° | −0.822 dB | 0.224° | 0° |
| Target V | 3.743 m | −4.630 dB | −9.897° | 3.359° | −4.052 dB | −9.670° | 3.135° | −0.578 dB | −0.227° | 0.224° |
| Target VI | 3.903 m | −6.808 dB | −19.867° | 2.687° | −7.047 dB | −20.106° | 2.686° | 0.029 dB | 0.239° | 0.01° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekar, M.; Bekar, A.; Pirkani, A.; Baker, C.J.; Gashinova, M. Burg-Aided 2D MIMO Array Extrapolation for Improved Spatial Resolution. Sensors 2025, 25, 6310. https://doi.org/10.3390/s25206310
Bekar M, Bekar A, Pirkani A, Baker CJ, Gashinova M. Burg-Aided 2D MIMO Array Extrapolation for Improved Spatial Resolution. Sensors. 2025; 25(20):6310. https://doi.org/10.3390/s25206310
Chicago/Turabian StyleBekar, Muge, Ali Bekar, Anum Pirkani, Christopher John Baker, and Marina Gashinova. 2025. "Burg-Aided 2D MIMO Array Extrapolation for Improved Spatial Resolution" Sensors 25, no. 20: 6310. https://doi.org/10.3390/s25206310
APA StyleBekar, M., Bekar, A., Pirkani, A., Baker, C. J., & Gashinova, M. (2025). Burg-Aided 2D MIMO Array Extrapolation for Improved Spatial Resolution. Sensors, 25(20), 6310. https://doi.org/10.3390/s25206310






