Experimentally Validated Modelling of a Base-Excited Piezoelectric Vibration Energy Harvester Connected to a Full Wave Rectified Load
Abstract
1. Introduction
- (a)
- Mechanical nonlinearities of geometric or design type—these can be geometric nonlinearities arising from the beam not being sufficiently stiff, resulting in large amplitude deformation even at moderate excitation, or intentionally designed nonlinearities (via modification of the geometry or the addition of nonlinear force sources) to alter the frequency response, e.g., enabling broadband energy harvesting by using magnetic forces to create bistable Duffing oscillators [22,23,24] or enabling frequency-up conversion (from a low ambient excitation frequency to a higher resonant frequency of the harvester) through a magnetic “plucking force” [25].
- (b)
- (c)
- Electrical circuit nonlinearities—these arise from the aforementioned need to include rectifiers and regulators for AC-DC rectification, which is a nonlinear process [19,21]. Moreover, such nonlinear circuit elements present the opportunity for optimal power generation [20], voltage multipliers [28], active or switching interface circuits to reduce charge losses [28,29,30,31,32], and voltage inversion [33].
- FBR for each piezo resonator (with the FBR circuits interconnected in series or in parallel);
- Storage capacitor;
- DC/DC converter to provide the optimal load impedance and regulate the output voltage (to the battery);
- The battery, which ultimately stores the charge and supplies the power to the application requiring it.
- Simulation of a base-excited vibration energy harvester connected to a full-wave rectified load, combining the analytical modal transformation of the Euler–Bernoulli model of a piezoelectric beam with the Shockley diode model (SDM) and considering the effect of the acquisition procedure on the response voltages.
2. Theoretical Analysis
- is the mass per unit length, and the length of the beam;
- is the natural frequency corresponding to ;
- is the damping ratio of the rth free vibration mode of the electrically uncoupled and undamped cantilever bimorph with a fixed base;
- is the modal electrical coupling term, which, for the present case of electrodes extending from to is given by
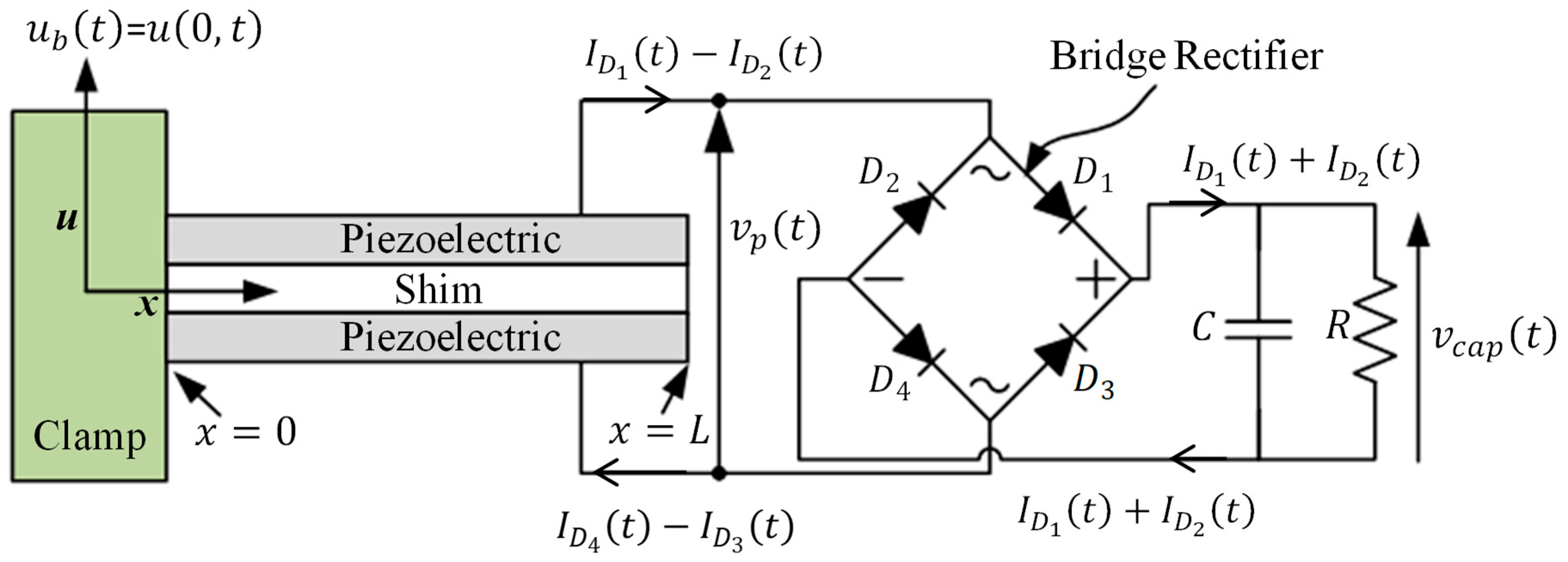
- is the saturation current (or reverse bias current) of the diode;
- is the instantaneous voltage across diode no. , ;
- is the emission factor (also known as the ideality factor, typically between 1 and 2);
- is the thermal voltage, defined as
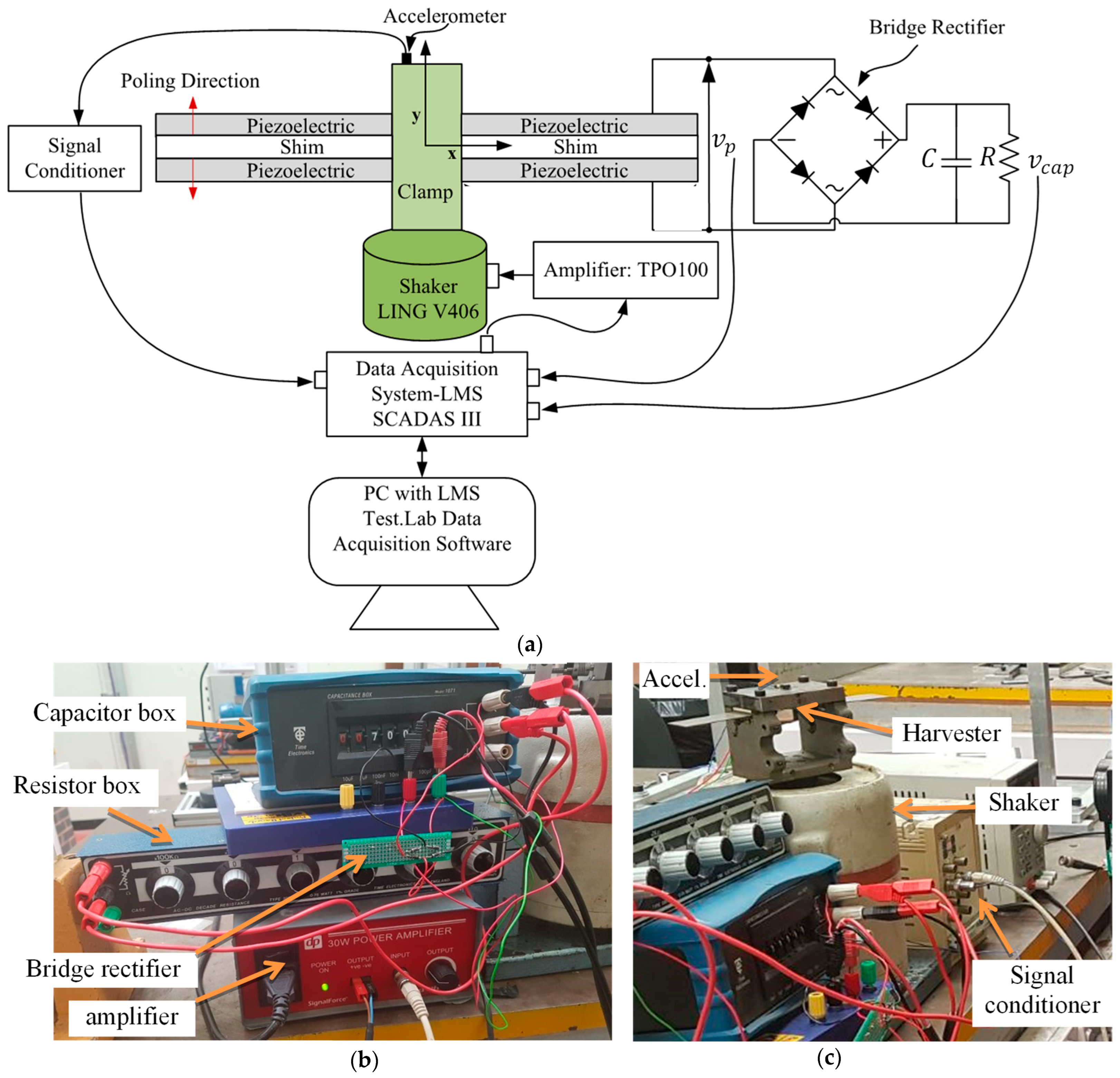
3. Experimental Setup and Procedure
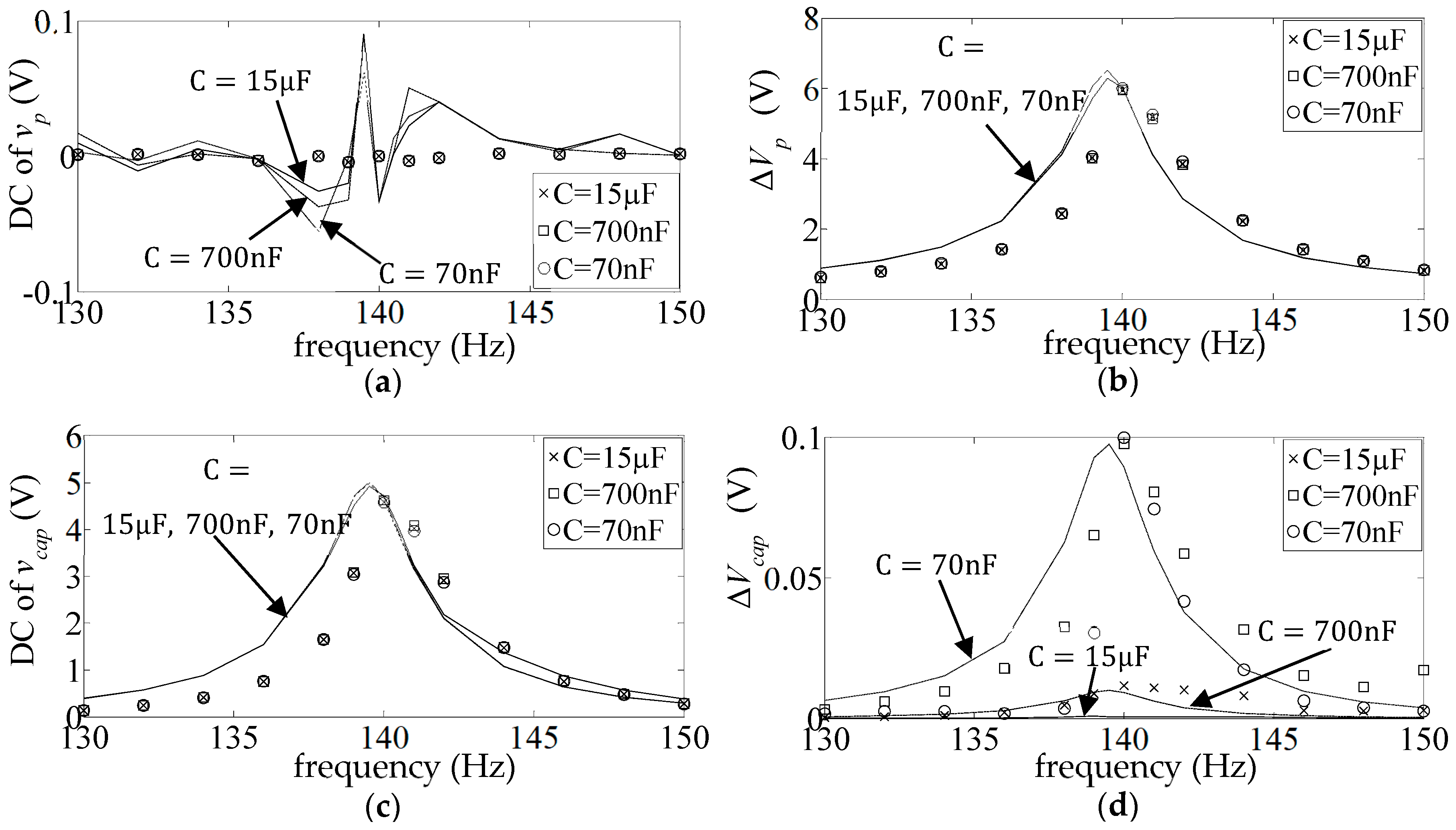
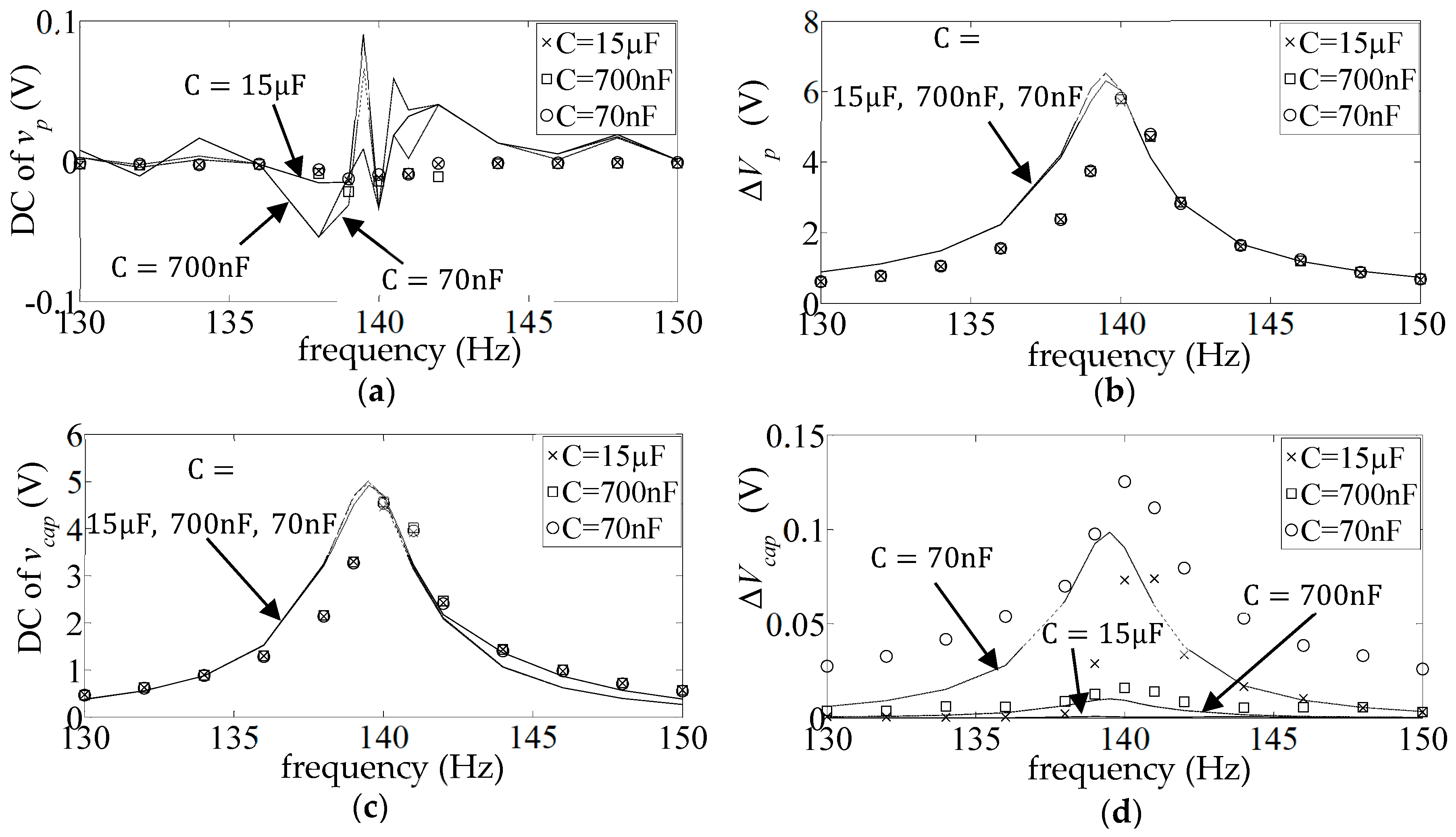
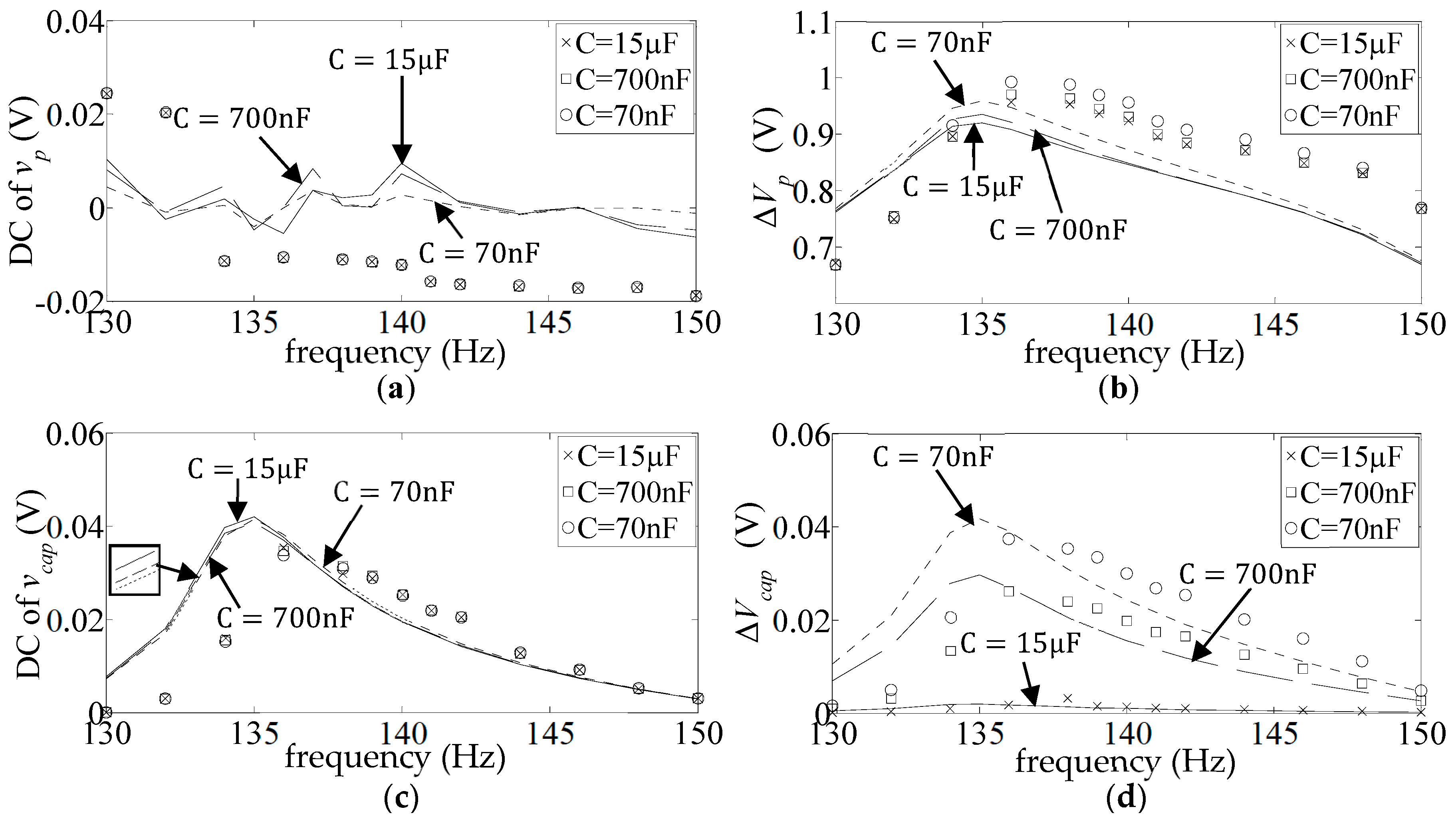
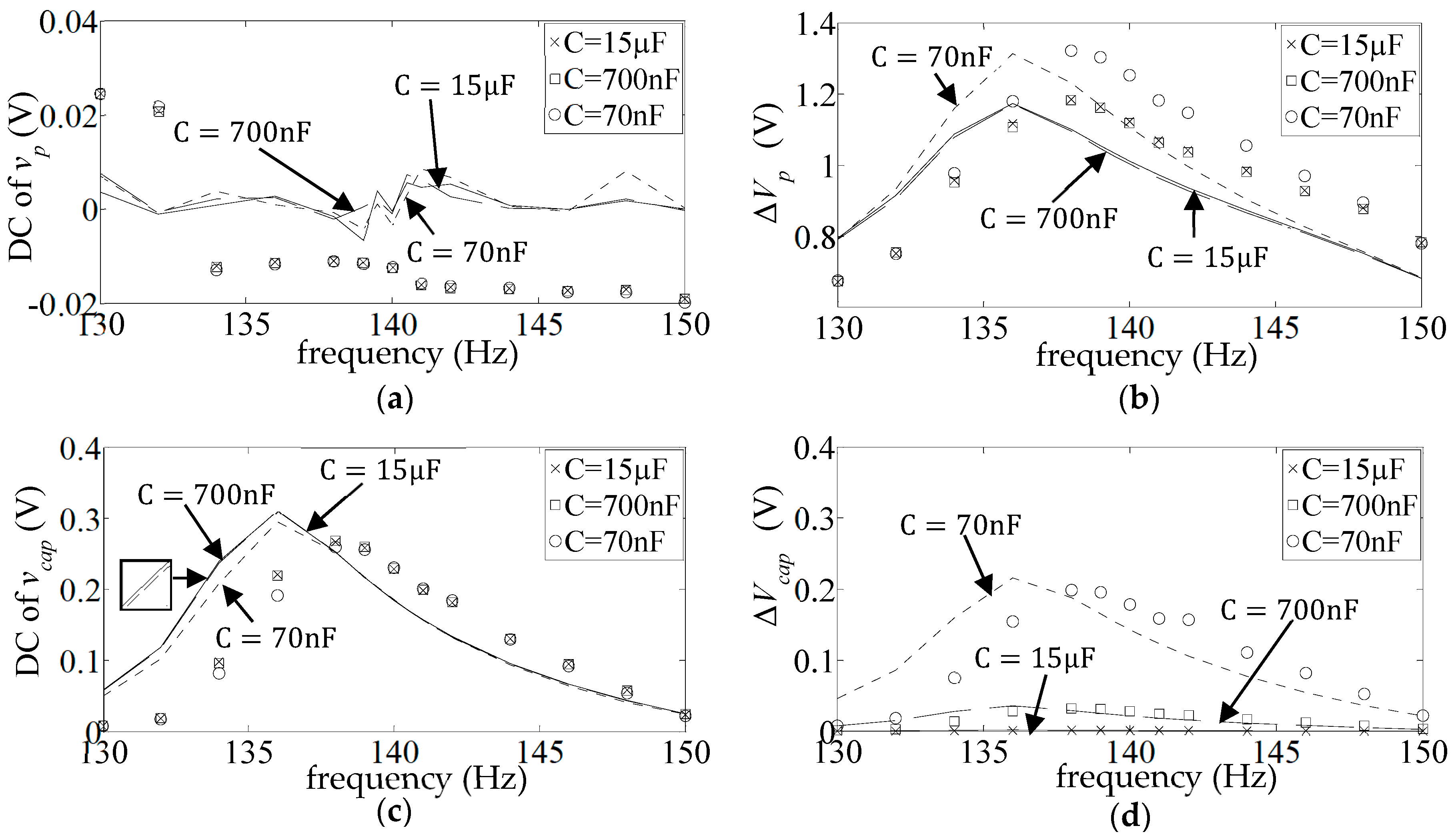
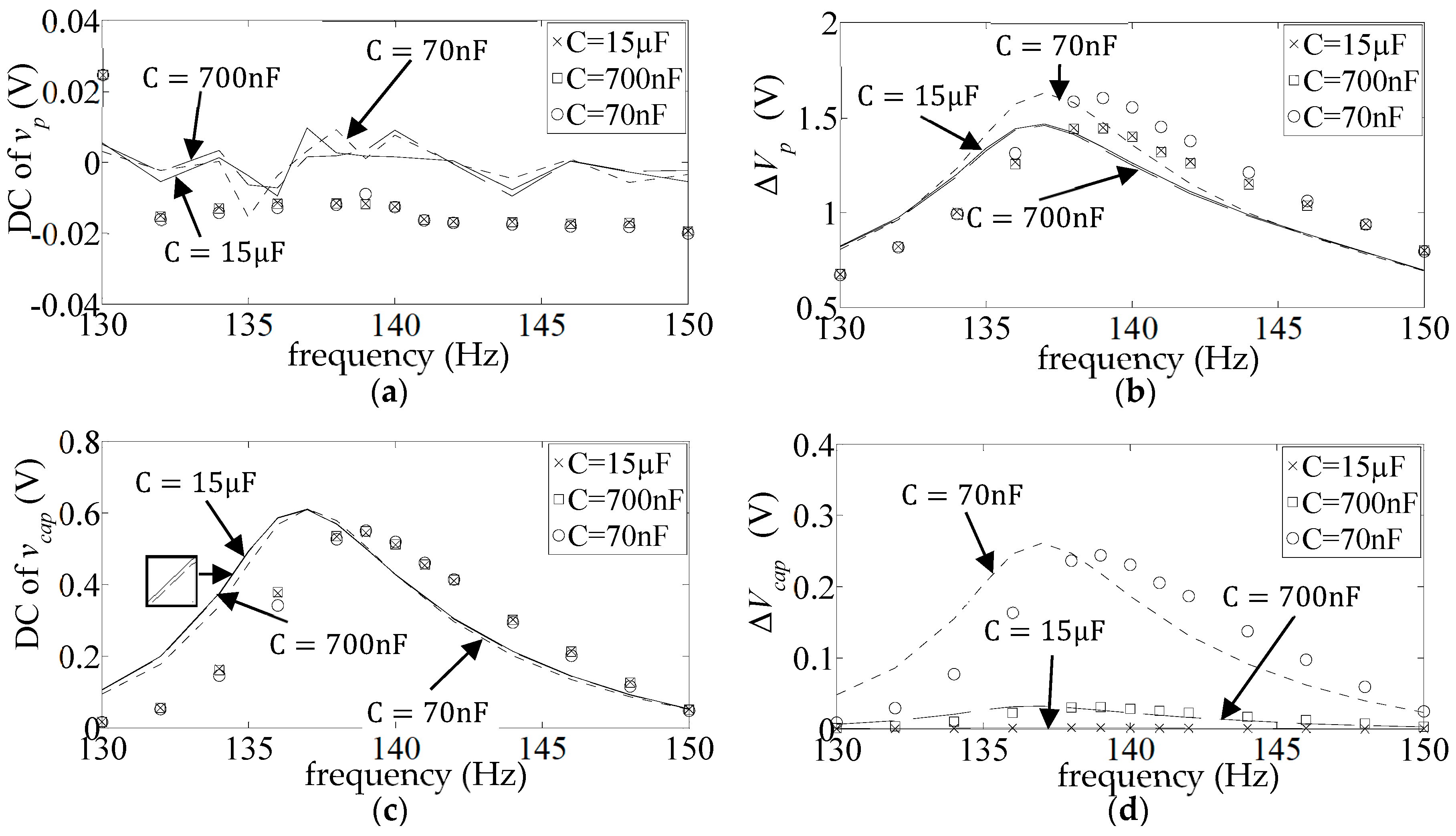
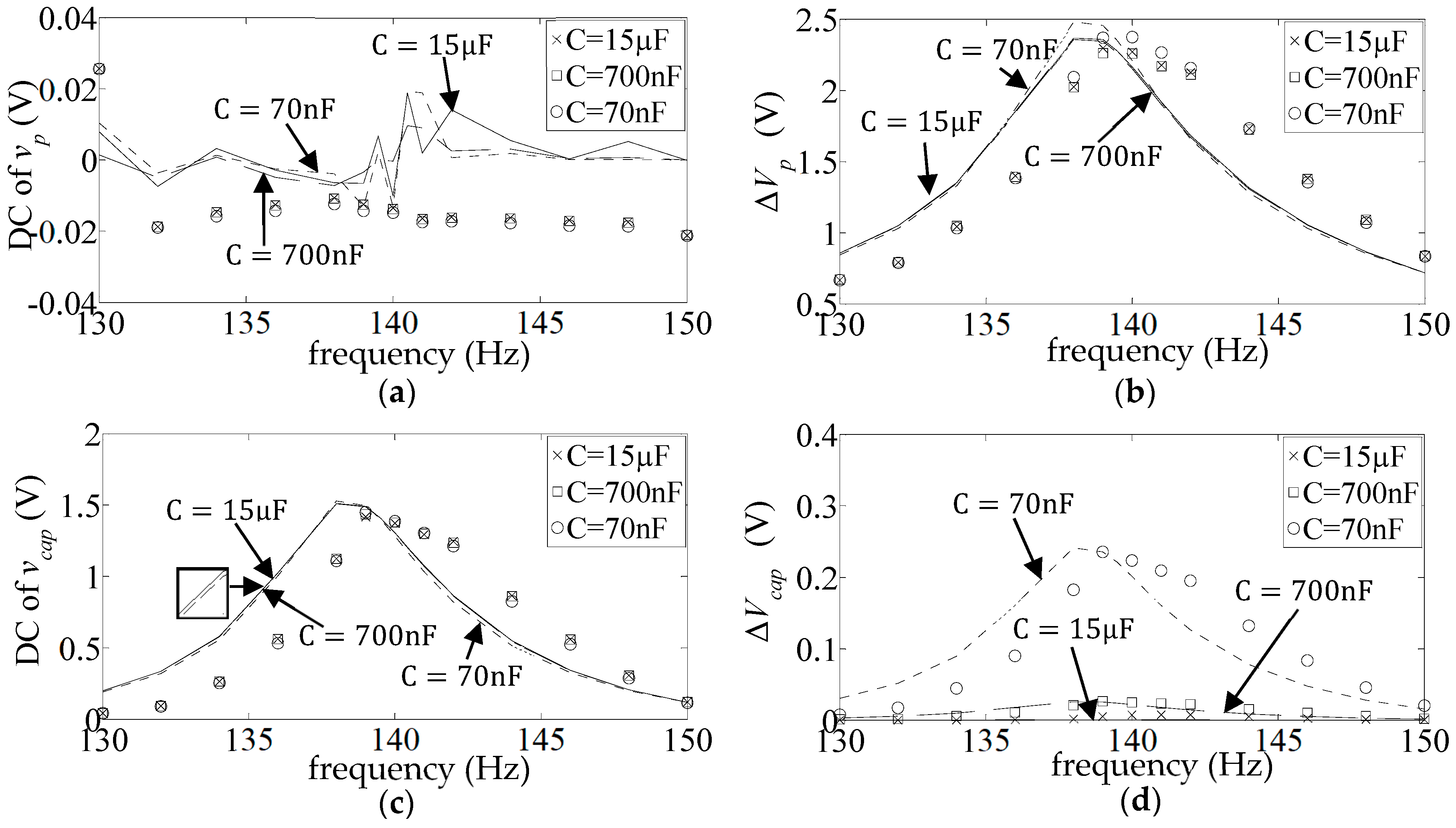
- ‘DC’ FR plots of the mean value divided by the amplitude of the base acceleration:
- ‘AC’ FR plots of the amplitude of the fluctuating part, divided by the amplitude of the base acceleration:
4. Presentation of Results and Discussion
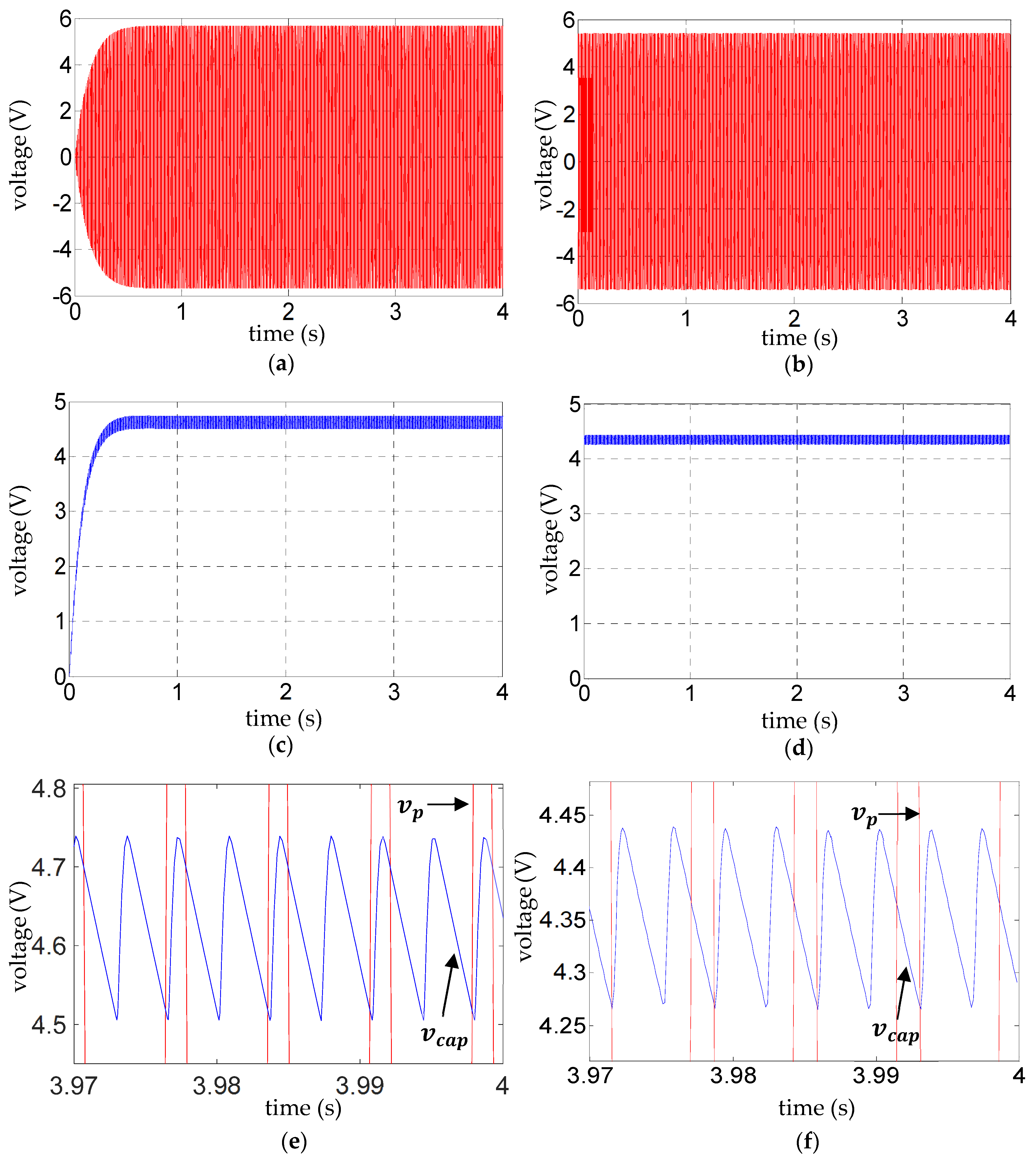
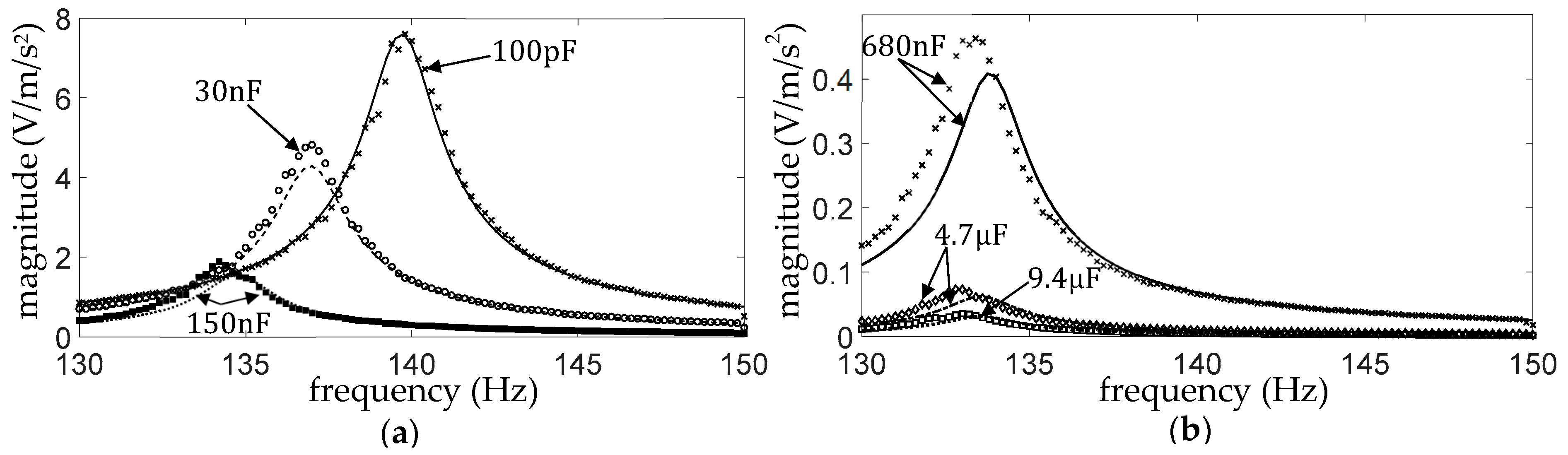
4.1. External Load Comprising Storage Capacitor Only ()
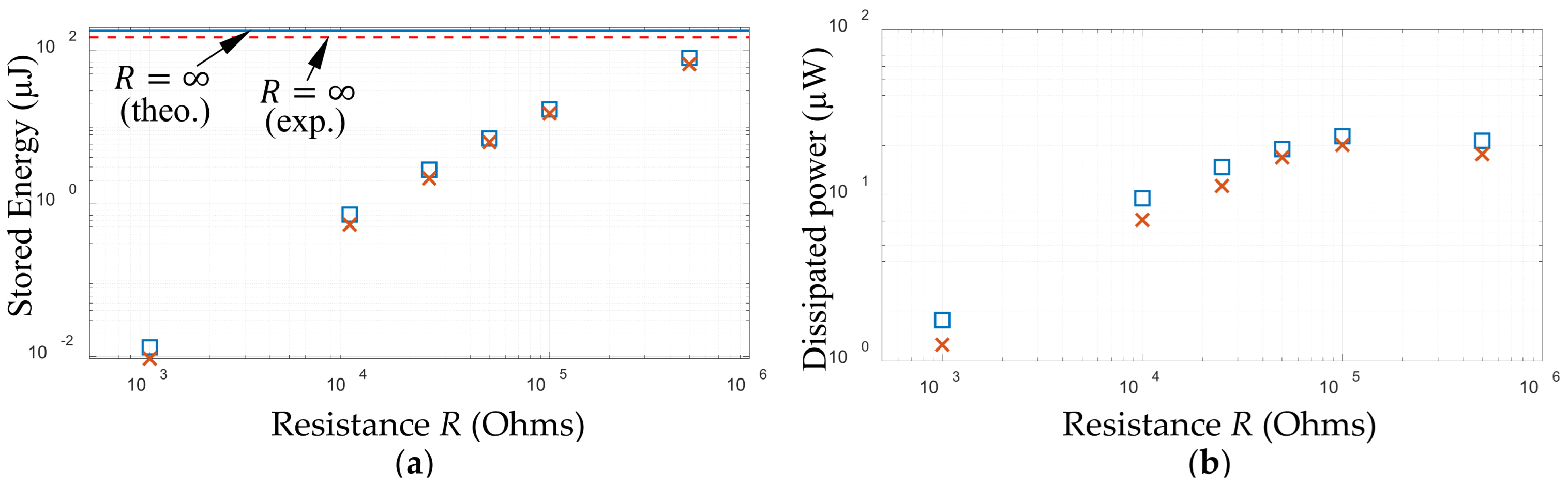
4.2. External Load Comprising Storage Capacitor and a Parallel Resistor
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC, DC | Alternating current, direct current |
| AMAM | Analytical modal analysis method |
| DSM | Dynamic stiffness method |
| DAQ | Data acquisition |
| FBR | Full-bridge rectification |
| FR | Frequency response |
| SDM | Shockley diode model |
| SPICE | Simulation program with integrated circuit emphasis |
References
- Landaluce, H.; Arjona, L.; Perallos, A.; Falcone, F.; Angulo, I.; Muralter, F. A review of IoT sensing applications and challenges using RFID and wireless sensor networks. Sensors 2020, 20, 2495. [Google Scholar] [CrossRef]
- Çiftci, B.; Chamanian, S.; Ulusan, H.; Yigit, A.H.; Koyuncuoğlu, A.; Muhtaroğlu, A.; Külah, H. Low-cost fully autonomous piezoelectric energy harvesting interface circuit with up to 6.14 x power capacity gain. In Proceedings of the IEEE 2019 Custom Integrated Circuits Conference (CICC), Austin, TX, USA, 14–17 April 2019. [Google Scholar]
- Lumentut, M.; Howard, I. Analytical modeling of self-powered electromechanical piezoelectric bimorph beams with multidirectional excitation. Int. J. Smart Nano Mater. 2011, 2, 134–175. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. On mechanical modeling of cantilevered piezoelectric vibration energy harvesters. J. Intell. Mater. Syst. Struct. 2008, 19, 1311–1325. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Lu, F.; Lee, H.P.; Lim, S.P. Modelling and analysis of micro piezoelectric power generators for micro-electromechanical-systems applications. Smart Mater. Struct. 2004, 13, 57–63. [Google Scholar]
- Chen, S.-N.; Wang, G.-J.; Chien, M.-C. Analytical modeling of piezoelectric vibration-induced micro power generator. Mechatronics 2006, 16, 379–387. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. ASME J. Vib. Acoust. 2008, 130, 041002. [Google Scholar]
- Rafique, S.; Bonello, P. Experimental validation of a distributed parameter piezoelectric bimorph cantilever energy harvester. Smart Mater. Struct. 2010, 19, 094008. [Google Scholar] [CrossRef]
- Bonello, P.; Rafique, S. Modeling and analysis of piezoelectric energy harvesting beams using the dynamic stiffness and modal analysis methods. ASME J. Vib. Acoust. 2011, 133, 011009. [Google Scholar]
- Dalzell, P.; Bonello, P. Analysis of an energy harvesting piezoelectric beam with energy storage circuit. Smart Mater. Struct. 2012, 21, 105029. [Google Scholar] [CrossRef]
- Renno, J.M.; Daqaq, M.F.; Inman, D.J. On the optimal energy harvesting from a vibration source. J. Sound Vib. 2009, 320, 386–405. [Google Scholar] [CrossRef]
- Dietl, J.; Wickenheiser, A.; Garcia, E. A Timoshenko beam model for cantilevered piezoelectric energy harvesters. Smart Mater. Struct. 2010, 19, 055018. [Google Scholar] [CrossRef]
- Banerjee, S.; Roy, S. A Timoshenko like model for piezoelectric energy harvester with shear mode. Compos. Struct. 2018, 204, 677–688. [Google Scholar] [CrossRef]
- Szarka, G.D.; Stark, B.H.; Burrow, S.G. Review of power conditioning for kinetic energy harvesting systems. IEEE Trans. Power Electron. 2012, 27, 803–815. [Google Scholar] [CrossRef]
- Brusa, E.; Carrera, A.; Delprete, A. A review of piezoelectric energy harvesting: Materials, design, and readout circuits. Actuators 2023, 12, 457. [Google Scholar] [CrossRef]
- Al Ghazi, A.; Ouslimani, A.; Kasbari, A.-E. Advances in interface circuits for self-powered piezoelectric energy harvesting systems: A comprehensive review. Sensors 2025, 25, 4029. [Google Scholar] [CrossRef]
- Rupp, C.J.; Dunn, M.L.; Maute, K. Analysis of piezoelectric energy harvesting systems with non-linear circuits using the harmonic balance method. J. Intell. Mater. Syst. Struct. 2010, 21, 1383–1396. [Google Scholar] [CrossRef]
- Shu, Y.C.; Lien, Y.C. Analysis of power output for piezoelectric energy harvesting systems. Smart Mater. Struct. 2006, 15, 1499–1512. [Google Scholar] [CrossRef]
- Leadenham, S.; Erturk, A. Mechanically and electrically nonlinear non-ideal piezoelectric energy harvesting framework with experimental validations. Nonlinear Dyn. 2020, 99, 625–641. [Google Scholar]
- Arrieta, A.F.; Hagedorn, P.; Erturk, A.; Inman, D.J. A piezoelectric bistable plate for nonlinear broadband energy harvesting. Appl. Phys. Lett. 2010, 97, 104102. [Google Scholar] [CrossRef]
- Daqaq, M.F. Response of uni-modal duffing-type harvesters to random forced excitations. J. Sound Vib. 2010, 329, 3621–3631. [Google Scholar] [CrossRef]
- Leadenham, S.; Erturk, A. Nonlinear m-shaped broadband piezoelectric energy harvester for very low base accelerations: Primary and secondary resonances. Smart Mater. Struct. 2015, 24, 055021. [Google Scholar] [CrossRef]
- Rosso, M.; Kohtanen, E.; Corigliano, A.; Ardito, R.; Erturk, A. Nonlinear phenomena in magnetic plucking of pezoelectric vibration energy harvesters. Sens. Actuators A Phys. 2023, 362, 114667. [Google Scholar] [CrossRef]
- Stanton, S.C.; Erturk, A.; Mann, B.P.; Inman, D.J. Nonlinear piezoelectricity in electroelastic energy harvesters: Modeling and experimental identification. J. Appl. Phys. 2010, 108, 074903. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Effects of nonlinear piezoelectric coupling on energy harvesters under direct excitation. Nonlinear Dyn. 2011, 67, 1221–1232. [Google Scholar] [CrossRef]
- Le, T.; Han, J.; von Jouanne, A.; Mayaram, K.; Fiez, T.S. Piezoelectric power generation interface circuits. In Proceedings of the IEEE 2003 Custom Integrated Circuits Conference (CICC), San Jose, CA, USA, 21–24 September 2003. [Google Scholar]
- Ramadass, Y.K.; Chandrakasan, A.P. An efficient piezoelectric energy harvesting interface circuit using a bias-flip rectifier and shared inductor. IEEE J. Solid-State Circuits 2010, 45, 189–204. [Google Scholar] [CrossRef]
- Shu, Y.C.; Lien, Y.C.; Wu, W.J. An improved analysis of SSHI interface in piezoelectric energy harvesting. Smart Mater. Struct. 2007, 16, 2253–2264. [Google Scholar] [CrossRef]
- Lallart, M.; Guyomar, D. An Optimized Self-powered Switching Circuit for Non-linear Energy Harvesting with Low Voltage Output. Smart Mater. Struct. 2008, 17, 035030. [Google Scholar] [CrossRef]
- Costanzo, L.; Lo Schiavo, A. Analytical study of piezoelectric harvesters with SECE and SSHI under variable excitation. IEEE Trans. Indust. Appl. 2022, 58, 2280–2290. [Google Scholar] [CrossRef]
- Guyomar, D.; Badel, A.; Lefeuvre, E.; Richard, C. Toward energy harvesting using active materials and conversion improvement by nonlinear processing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 584–595. [Google Scholar] [PubMed]
- Clementino, M.A.; Reginatto, R.; da Silva, S. Modeling of piezoelectric energy harvesting considering the dependence of the rectifier circuit. J. Braz. Soc. Mech. Sci. Eng. 2014, 36, 283–292. [Google Scholar] [CrossRef]
- Dai, Q.; Harne, R.L. Charging power optimization for nonlinear vibration energy harvesting systems subjected to arbitrary, persistent base excitations. Smart Mater. Struct. 2017, 27, 015011. [Google Scholar] [CrossRef]
- Dai, Q.; Harne, R.L. Investigation of direct current power delivery from nonlinear vibration energy harvesters under combined harmonic and stochastic excitations. J. Intell. Mater. Syst. Struct. 2018, 29, 514–529. [Google Scholar] [CrossRef]
- Hegendörfer, A.; Steinmann, P.; Mergheim, J. Nonlinear finite element system simulation of piezoelectric vibration-based energy harvesters. J. Intell. Mater. Syst. Struct. 2022, 33, 1292–1307. [Google Scholar]
- Febbo, M.; Machado, S.P.; Olivo, A.; Ortiz, M.; Pereyra, N. Modelling of a piezoelectric beam with a full bridge rectifier under arbitrary excitation: Experimental validation. Energy Harvest. Syst. 2023, 10, 311–324. [Google Scholar] [CrossRef]
- Askari, M.; Ghandchi Tehrani, M.; Brusa, E.; Carrera, A.; Delprete, C. Design, fabrication and evaluation of a Quad-Finger multimodal vibration energy harvester utilizing MFC generators. Mech. of Adv. Mat. Struct. 2025, 1537–6494. [Google Scholar] [CrossRef]
- Liu, S.; Chen, S.; Gao, W.; Zhang, J.; Xu, D.; Chen, F.; Lu, Z.; Yu, X. A High-Efficiency Piezoelectric Energy Harvesting and Management Circuit Based on Full-Bridge Rectification. J. Low Power Electron. Appl. 2024, 14, 49. [Google Scholar] [CrossRef]
- Mendes dos Santos, L.; Santos, F.L.; Scinocca, F. Characterization of a vibration energy harvesting system for piezoelectric materials. Rev. Cad. Pedagog. Stud. Publicacoes Ltda. 2025, 22, 1–27. [Google Scholar]
- Liu, Y.; Liang, J. Equivalent Impedance Analysis and Compensation of Full-Wave Bridge Rectifier under High-Frequency Operation with Extended Impedance Method. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Republic of Korea, 22–28 May 2021. [Google Scholar]
- Standard.dio. Available online: https://ltwiki.org/index.php?title=Standard.dio (accessed on 14 July 2025).
- Onsemi. Available online: https://www.onsemi.com/download/models/sp3/1n4007.rev0.sp3 (accessed on 14 July 2025).
- diodes_schottky-diodes.txt. Available online: https://github.com/peteut/spice-models/blob/master/diodes/diodes/diodes_schottky-diodes.txt (accessed on 14 July 2025).
- Massobrio, G.; Antognetti, P. Semiconductor Device Modeling with SPICE, 2nd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The Matlab ODE suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- 1N4001 Thru 1N4007 General Purpose Plastic Rectifier. Available online: https://global.oup.com/us/companion.websites/fdscontent/uscompanion/us/pdf/microcircuits/students/diode/1n4004-general.pdf (accessed on 9 September 2025).








| Property | Value | Units |
|---|---|---|
| Length, | 58 | mm |
| Width, | 25 | mm |
| Thickness of the piezoelectric layer, | 0.267 | mm |
| Thickness of the shim layer, | 0.3 | mm |
| Young’s Modulus (piezoelectric layer) | 66 | GPa |
| Young’s Modulus (shim layer) | 72 | GPa |
| Density (piezoelectric layer) | 7800 | kg/m3 |
| Density (shim layer) | 2700 | kg/m3 |
| Piezoelectric coefficient, | pm/V | |
| Permittivity at constant strain, | F/m | |
| Damping ratio of first mode, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonello, P.; Alalwan, M. Experimentally Validated Modelling of a Base-Excited Piezoelectric Vibration Energy Harvester Connected to a Full Wave Rectified Load. Sensors 2025, 25, 6305. https://doi.org/10.3390/s25206305
Bonello P, Alalwan M. Experimentally Validated Modelling of a Base-Excited Piezoelectric Vibration Energy Harvester Connected to a Full Wave Rectified Load. Sensors. 2025; 25(20):6305. https://doi.org/10.3390/s25206305
Chicago/Turabian StyleBonello, Philip, and Maher Alalwan. 2025. "Experimentally Validated Modelling of a Base-Excited Piezoelectric Vibration Energy Harvester Connected to a Full Wave Rectified Load" Sensors 25, no. 20: 6305. https://doi.org/10.3390/s25206305
APA StyleBonello, P., & Alalwan, M. (2025). Experimentally Validated Modelling of a Base-Excited Piezoelectric Vibration Energy Harvester Connected to a Full Wave Rectified Load. Sensors, 25(20), 6305. https://doi.org/10.3390/s25206305







