Fringe-Based Structured-Light 3D Reconstruction: Principles, Projection Technologies, and Deep Learning Integration
Abstract
1. Introduction
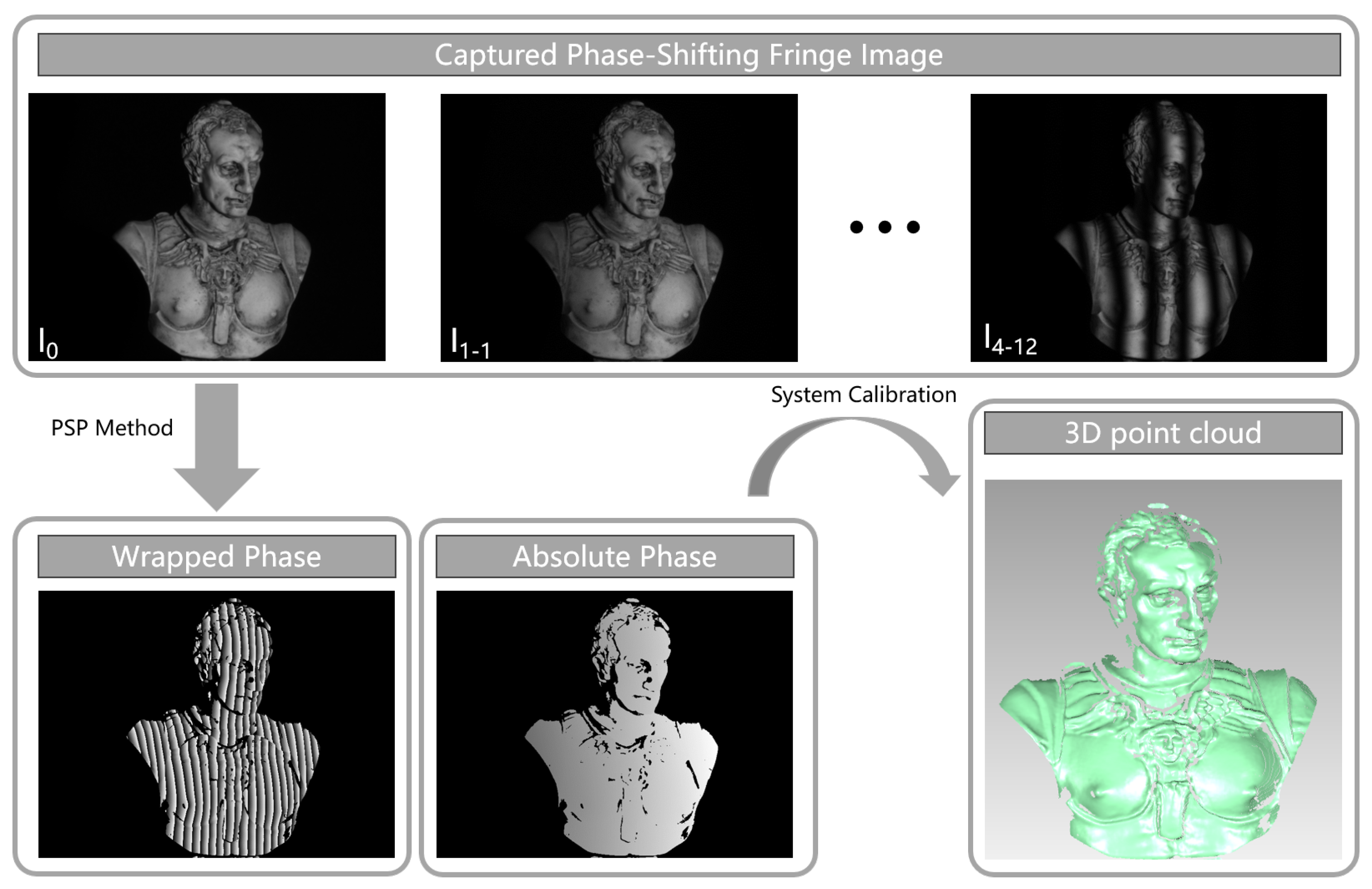
2. Fringe-Structured-Light 3D Reconstruction Approach
2.1. Wrapped-Phase Extraction
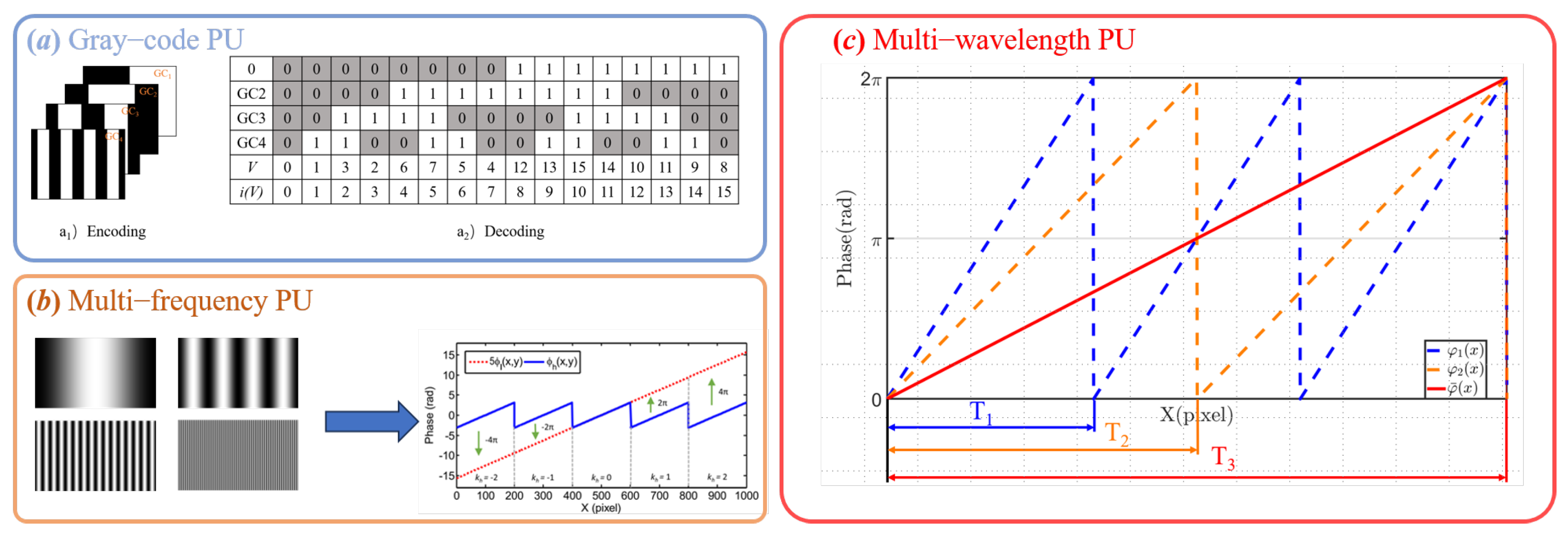
2.2. Phase Unwrapping Algorithms
2.2.1. Temporal-Phase Unwrapping
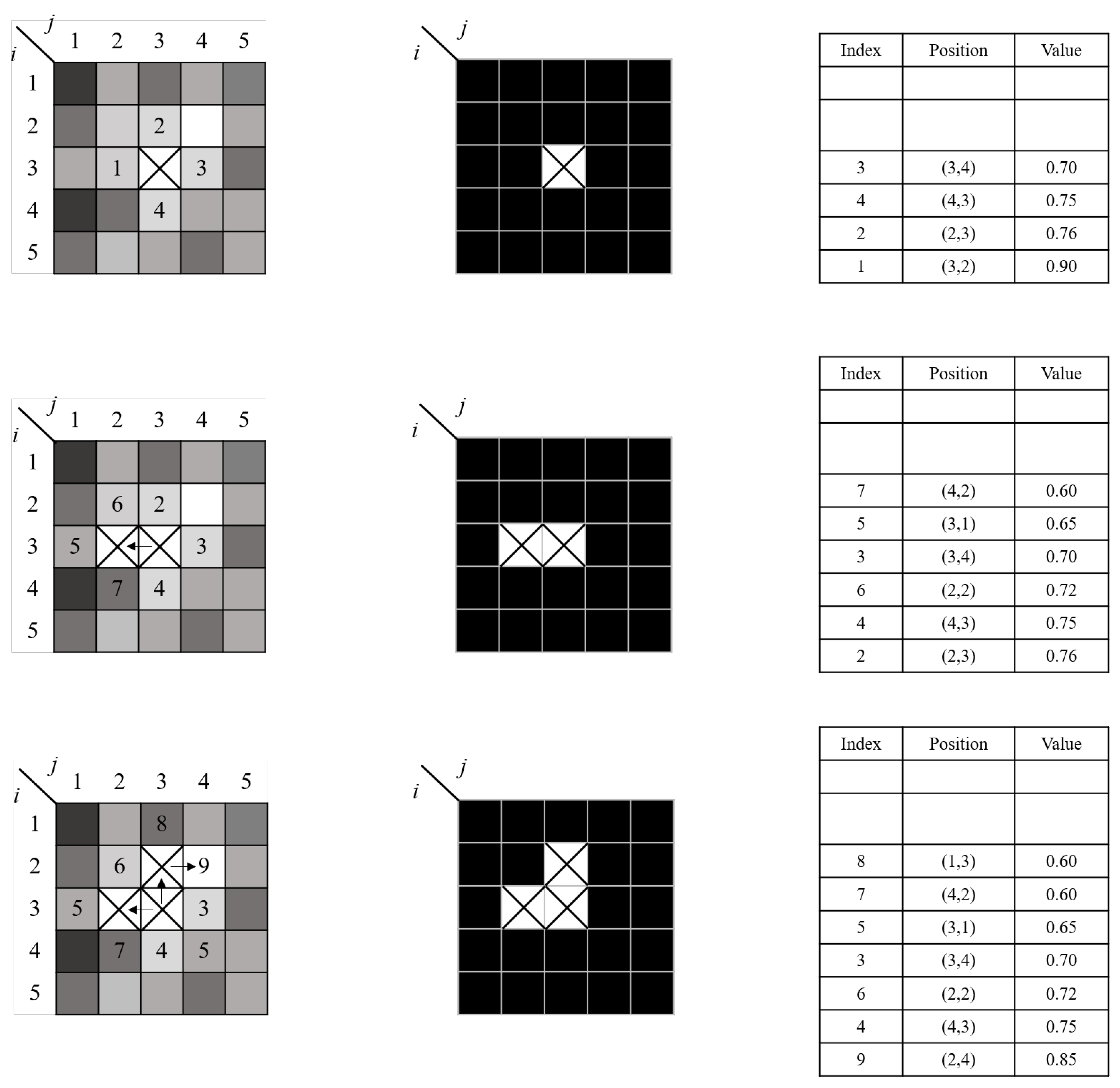
2.2.2. Spatial-Phase Unwrapping
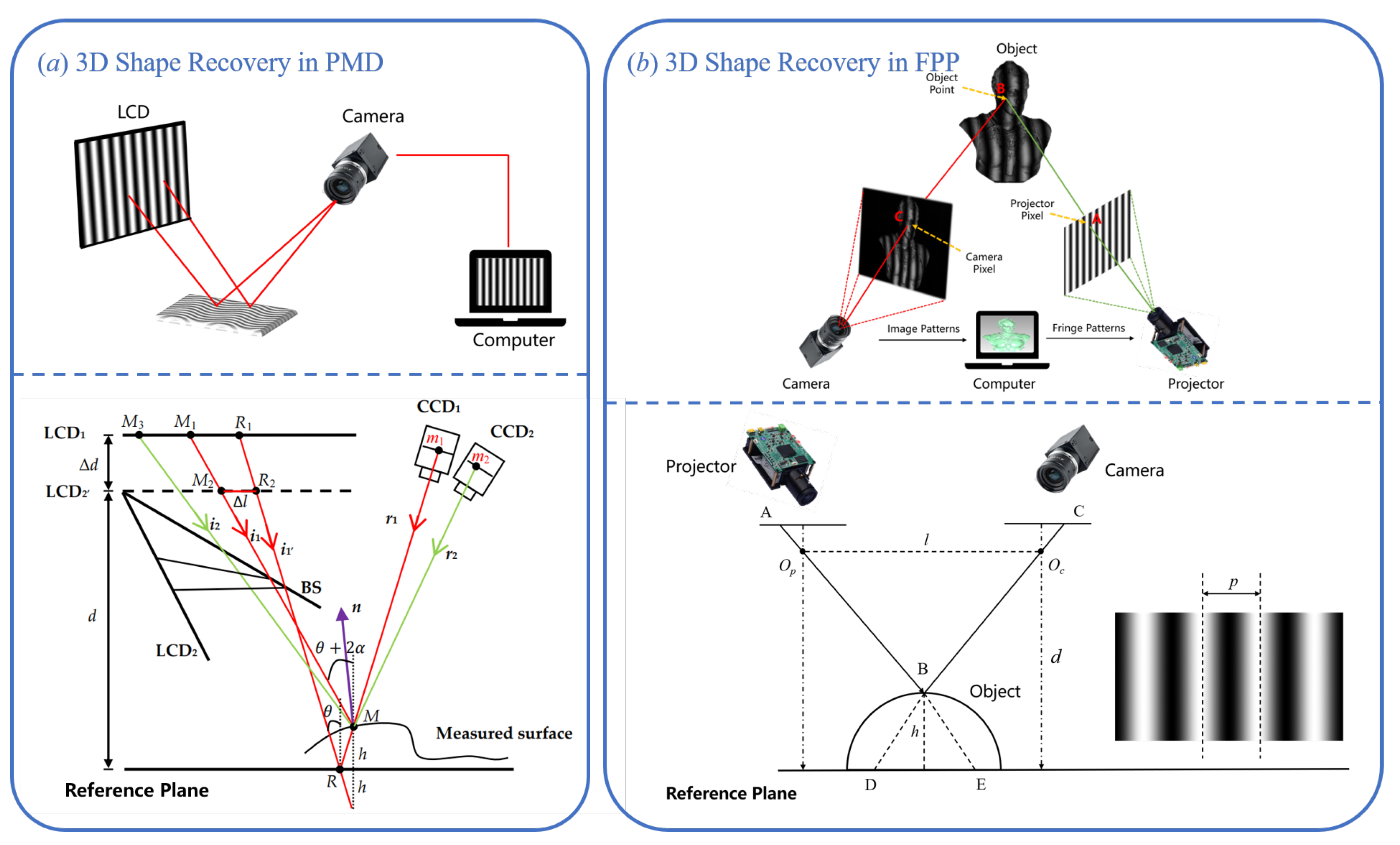
2.3. 3D Shape Reconstruction from Phase
2.3.1. 3D Shape Recovery in PMD
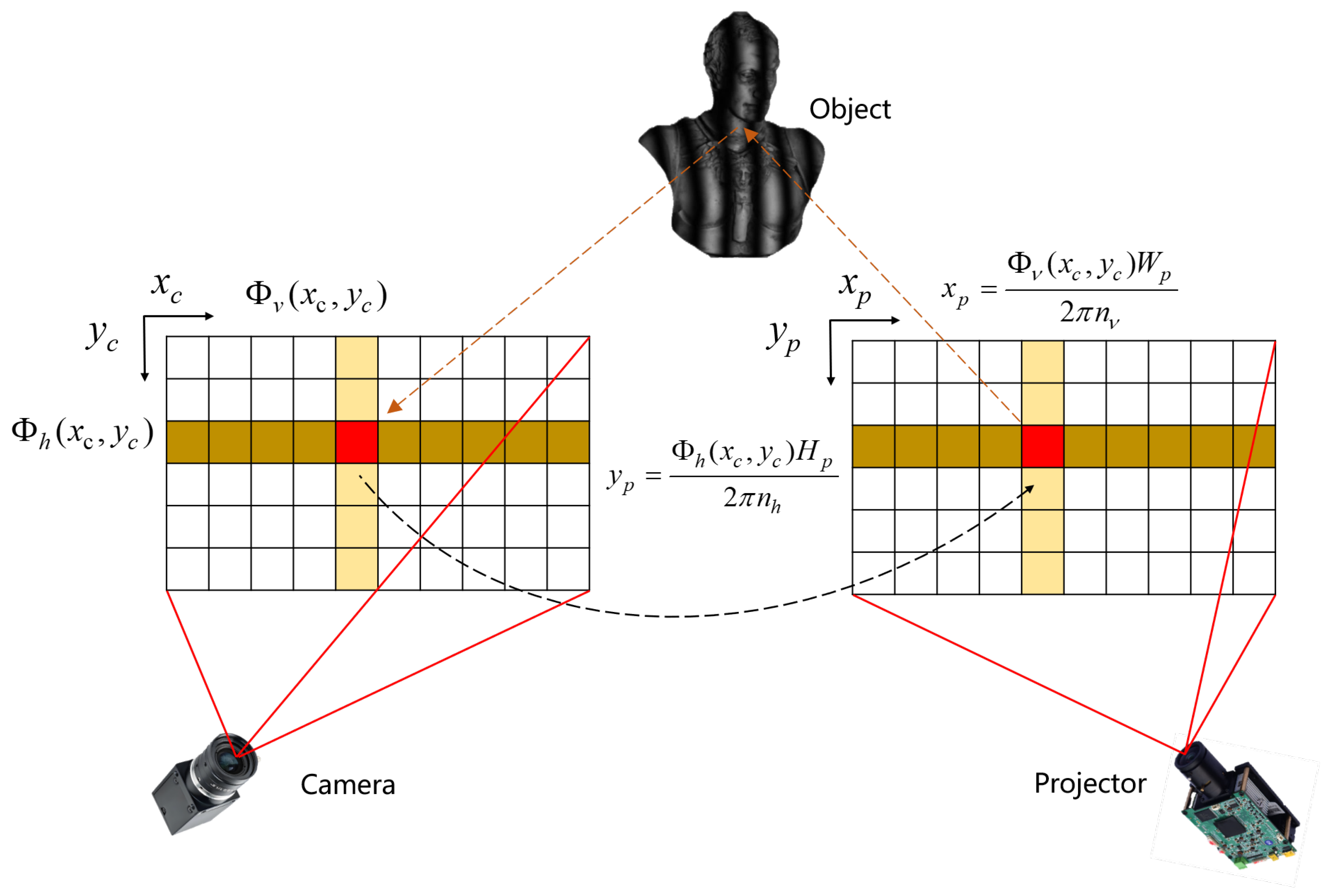
2.3.2. 3D Shape Recovery in FPP
3. Evolution and Advances of PMD Systems
3.1. Single-Screen and Single-Camera Systems
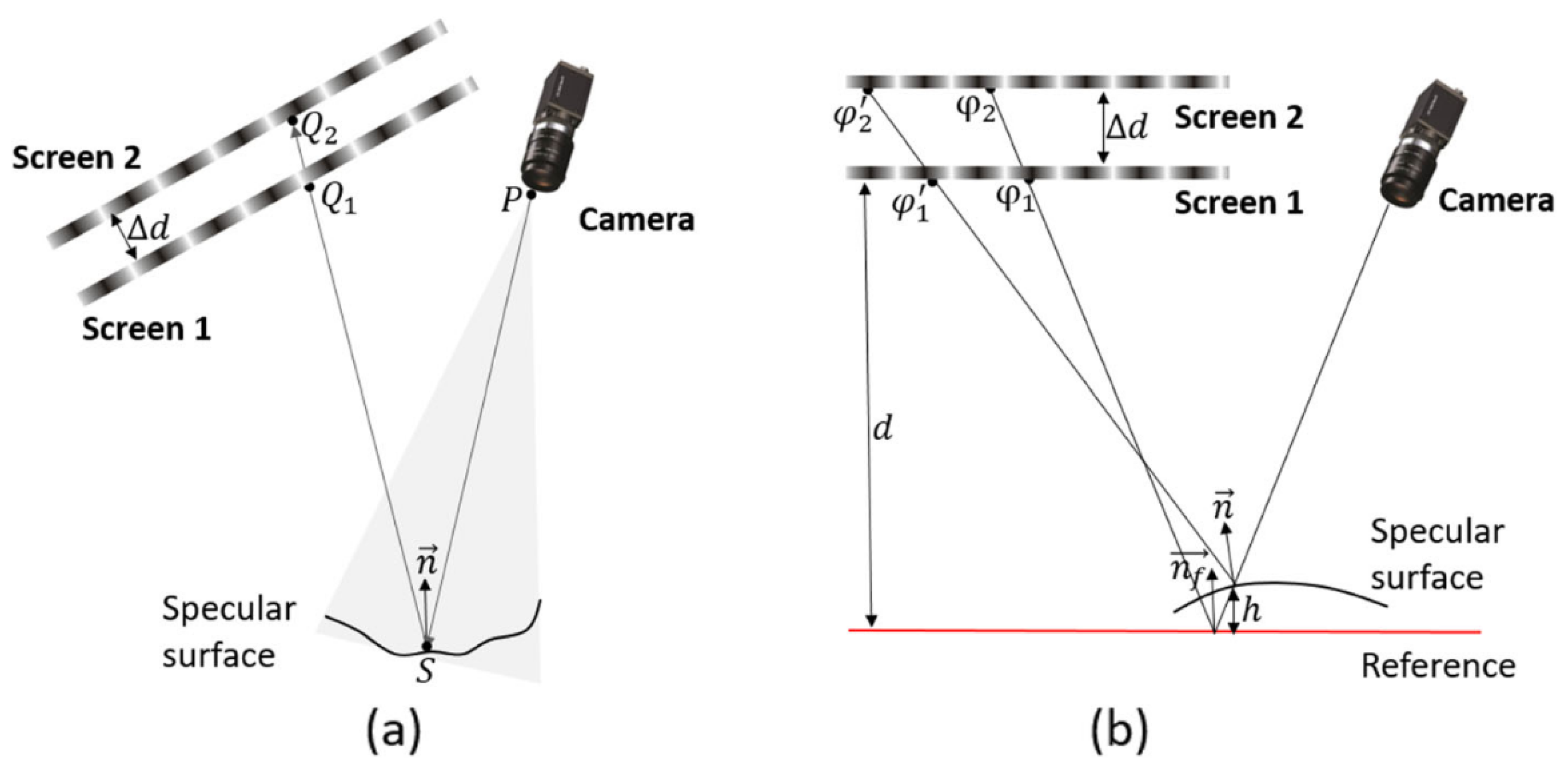
3.2. Multi-Screen Direct PMD
3.3. Multi-Camera Stereo PMD
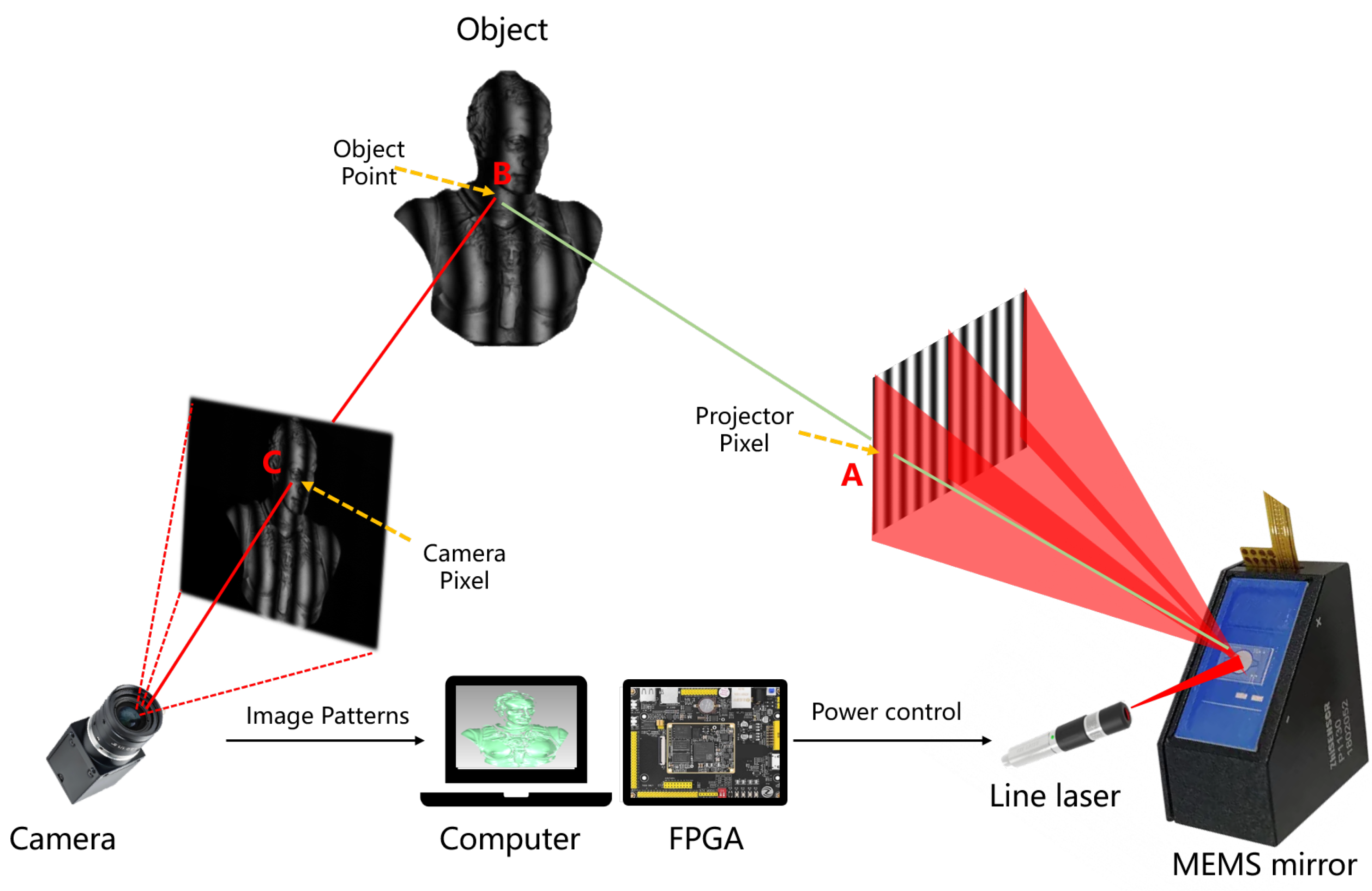
4. Evolution and Advances of FPP Systems
4.1. Comparison of Mainstream Fringe Projection Technologies
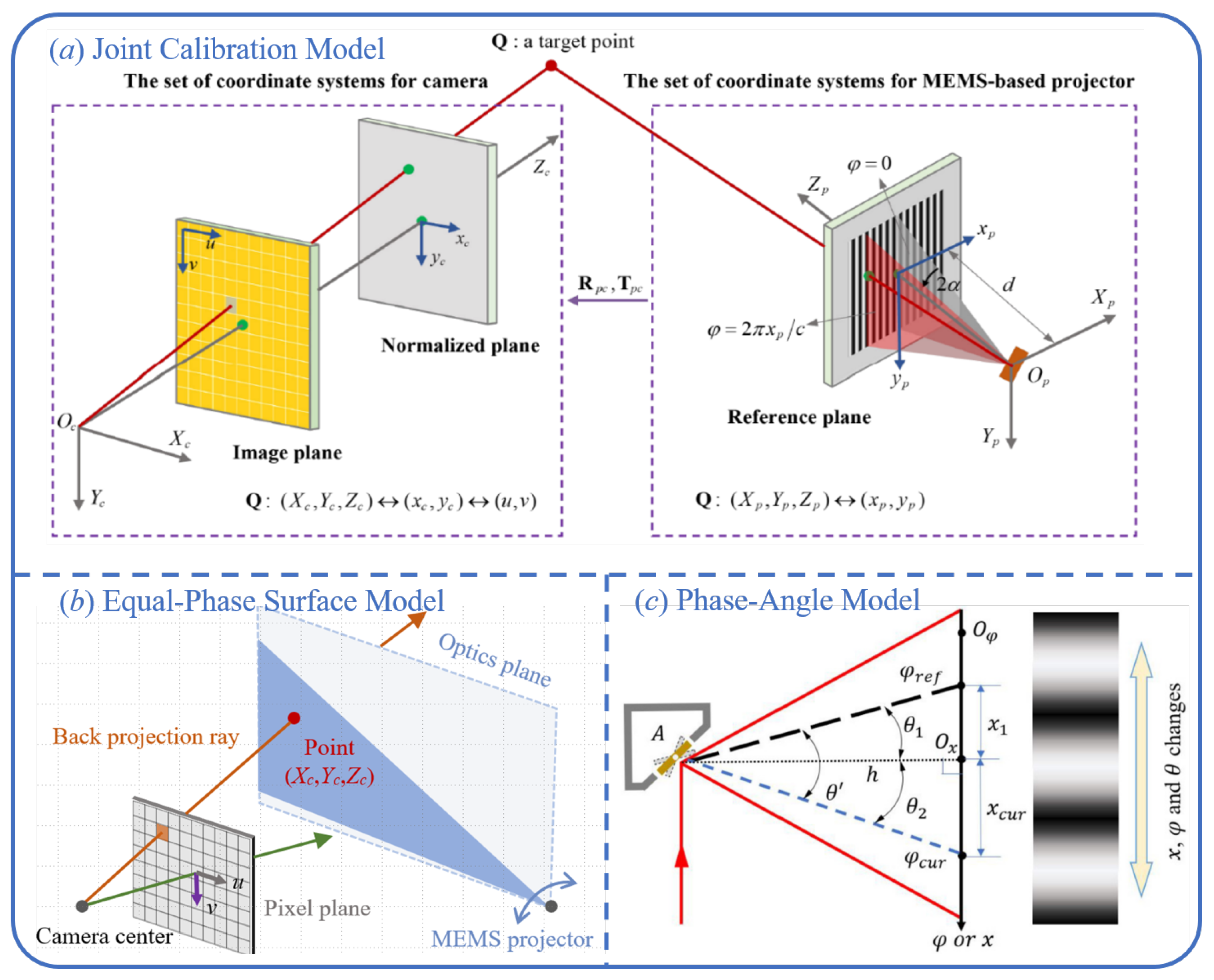
4.2. System Calibration Strategies for MEMS-Based Structured-Light Systems
4.2.1. Joint Calibration Model
4.2.2. Equal-Phase Surface Model
4.2.3. Phase-Angle Model
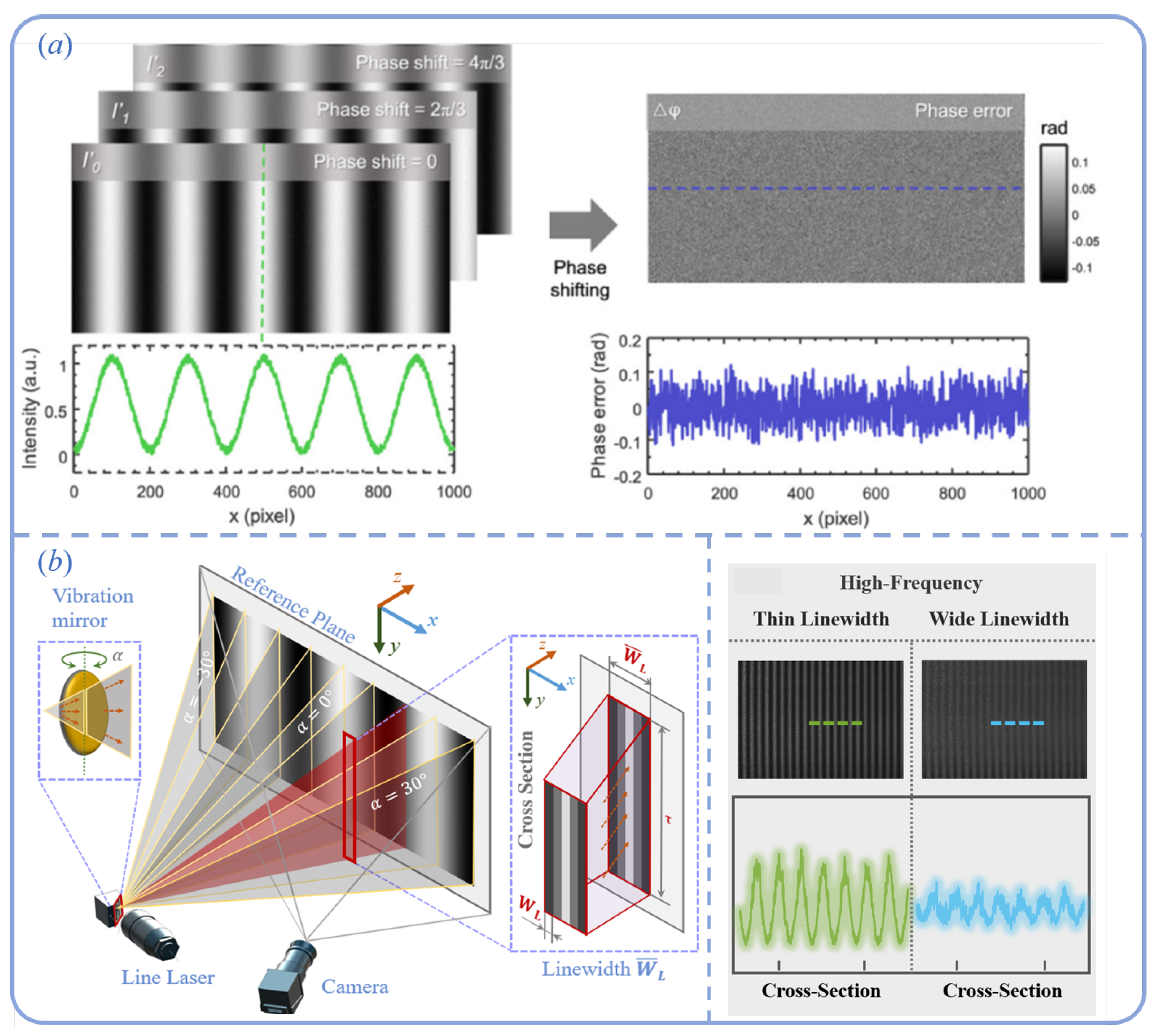
4.3. Analysis of Systematic and Random Errors
4.3.1. Random Errors
4.3.2. Impact of Line Laser Intensity Fluctuations
4.3.3. High-Order Harmonics
5. Application of Deep Learning in Fringe-Structured Light
5.1. Learning Paradigm for Deep Learning-Driven FPP
5.2. Deep Learning Framework Design and Advancements
5.2.1. Network Architecture Innovations
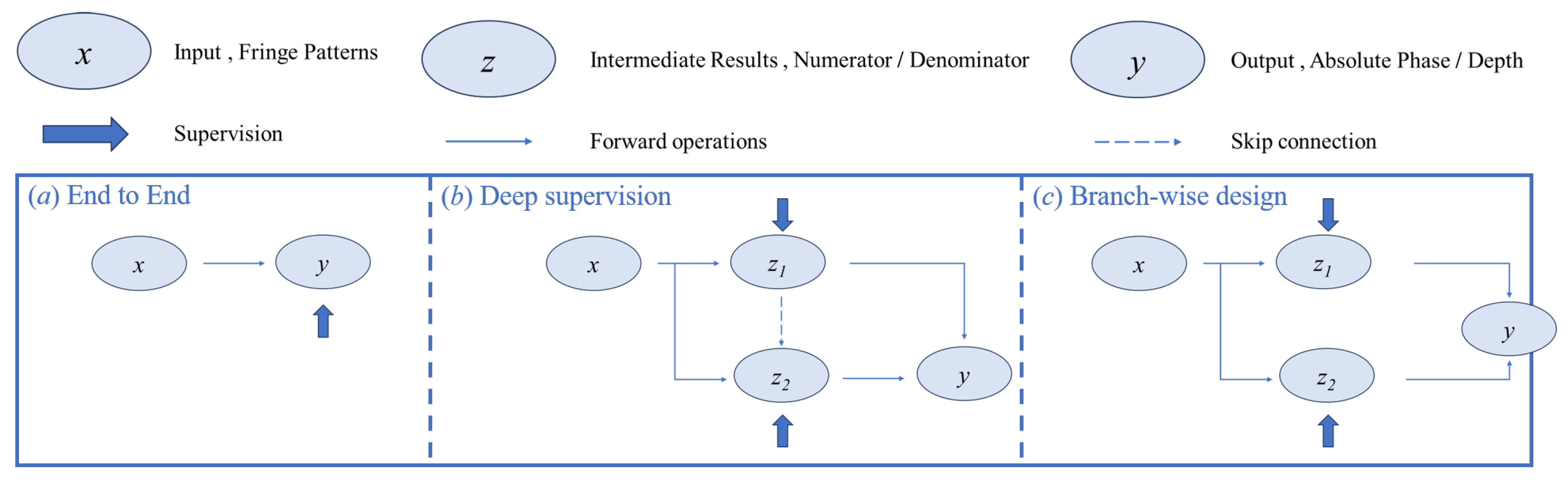
5.2.2. Supervision Strategies
5.2.3. Input Design
5.3. Evaluation Metrics
6. Challenges and Perspectives
6.1. HDR Issues
6.2. Extended Depth of Field
6.3. High-Speed Deployment and Real-Time Reconstruction
6.4. Transferability, Generalization, and Interpretability of Deep Learning Methods
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FPP | Fringe Projection Profilometry |
| PMD | Phase Measuring Deflectometry |
| DLP | Digital Light Processing |
| TPU | Temporal-Phase Unwrapping |
| SPU | Spatial-Phase Unwrapping |
| LCD | Liquid-Crystal Display |
| DMD | Digital Micromirror Device |
| MEMS | Micro-Electro-Mechanical Systems |
| CMM | Coordinate Measuring Machines |
| SOTA | State-of-the-Art |
| CNNs | Convolutional Neural Networks |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| RMSE | Root Mean Square Error |
| PSNR | Peak Signal-to-Noise Ratio |
| SSIM | Structural Similarity Index Measure |
| HDR | High Dynamic Range |
| SNR | Signal-to-Noise Ratios |
| DOF | Depth of Field |
| PSF | Point Spread Function |
References
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A state of the art in structured light patterns for surface profilometry. Pattern Recognit. 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Van der Jeught, S.; Dirckx, J.J. Real-time structured light profilometry: A review. Opt. Lasers Eng. 2016, 87, 18–31. [Google Scholar] [CrossRef]
- Lv, S.; Kemao, Q. Modeling the measurement precision of fringe projection profilometry. Light. Sci. Appl. 2023, 12, 257. [Google Scholar] [CrossRef]
- Zhou, Q.; Qiao, X.; Ni, K.; Li, X.; Wang, X. Depth detection in interactive projection system based on one-shot black-and-white stripe pattern. Opt. Express 2017, 25, 5341–5351. [Google Scholar] [CrossRef]
- Han, M.; Xing, Y.; Wang, X.; Li, X. Projection superimposition for the generation of high-resolution digital grating. Opt. Lett. 2024, 49, 4473–4476. [Google Scholar] [CrossRef] [PubMed]
- Juarez-Salazar, R.; Esquivel-Hernandez, S.; Diaz-Ramirez, V.H. Optical Fringe Projection: A Straightforward Approach to 3D Metrology. Metrology 2025, 5, 47. [Google Scholar] [CrossRef]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.; Lu, X.; Knapp, W.; Weckenmann, A.; Estler, W.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Li, X.; Shimizu, Y.; Ito, T.; Cai, Y.; Ito, S.; Gao, W. Measurement of six-degree-of-freedom planar motions by using a multiprobe surface encoder. Opt. Eng. 2014, 53, 122405. [Google Scholar] [CrossRef]
- Wu, J.; Hong, Y.; Shin, D.W.; Sato, R.; Quan, L.; Matsukuma, H.; Gao, W. On-machine calibration of pitch deviations of a linear scale grating by using a differential angle sensor. Int. J. Autom. Technol. 2024, 18, 4–10. [Google Scholar] [CrossRef]
- Gao, W.; Kim, S.; Bosse, H.; Minoshima, K. Dimensional metrology based on ultrashort pulse laser and optical frequency comb. CIRP Ann. 2025, 74, 993–1018. [Google Scholar] [CrossRef]
- Ding, D.; Ding, W.; Huang, R.; Fu, Y.; Xu, F. Research progress of laser triangulation on-machine measurement technology for complex surface: A review. Measurement 2023, 216, 113001. [Google Scholar] [CrossRef]
- Chen, R.; Li, Y.; Xue, G.; Tao, Y.; Li, X. Laser triangulation measurement system with Scheimpflug calibration based on the Monte Carlo optimization strategy. Opt. Express 2022, 30, 25290–25307. [Google Scholar] [CrossRef]
- Boesl, U. Time-of-flight mass spectrometry: Introduction to the basics. Mass Spectrom. Rev. 2017, 36, 86–109. [Google Scholar] [CrossRef]
- Hansard, M.; Lee, S.; Choi, O.; Horaud, R.P. Time-of-Flight Cameras: Principles, Methods and Applications; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Ma, R.; Li, C.; Xing, Y.; Wang, S.; Ma, R.; Feng, F.; Qian, X.; Wang, X.; Li, X. Defect focused Harris3D & boundary fine-tuning optimized region growing: Lithium battery pole piece defect segmentation. Measurement 2025, 242, 116147. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Q.; Li, X.; Chen, R.; Ni, K. An improved low-noise processing methodology combined with PCL for industry inspection based on laser line scanner. Sensors 2019, 19, 3398. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Li, X.; Wang, X.; Li, J.; Xue, G.; Zhou, Q.; Ni, K. A planar pattern based calibration method for high precision structured laser triangulation measurement. In Proceedings of the Optical Metrology and Inspection for Industrial Applications VI, Hangzhou, China, 20–23 October 2019; SPIE: Washington, DC, USA, 2019; Volume 11189, pp. 212–218. [Google Scholar] [CrossRef]
- Han, M.; Wang, X.; Li, X. Fast and accurate fringe projection based on a MEMS micro-vibration mirror. In Proceedings of the Optical Metrology and Inspection for Industrial Applications XI, Nantong, China, 12–14 October 2024; SPIE: Washington, DC, USA, 2024; Volume 13241, pp. 12–19. [Google Scholar] [CrossRef]
- Almaraz-Cabral, C.C.; Gonzalez-Barbosa, J.J.; Villa, J.; Hurtado-Ramos, J.B.; Ornelas-Rodriguez, F.J.; Cordova-Esparza, D.M. Fringe projection profilometry for panoramic 3D reconstruction. Opt. Lasers Eng. 2016, 78, 106–112. [Google Scholar] [CrossRef]
- Nguyen, H.; Liang, J.; Wang, Y.; Wang, Z. Accuracy assessment of fringe projection profilometry and digital image correlation techniques for three-dimensional shape measurements. J. Phys. Photonics 2021, 3, 014004. [Google Scholar] [CrossRef]
- Muyshondt, P.G.; Van der Jeught, S.; Dirckx, J.J. A calibrated 3D dual-barrel otoendoscope based on fringe-projection profilometry. Opt. Lasers Eng. 2022, 149, 106795. [Google Scholar] [CrossRef]
- Stavroulakis, P.; Leach, R.K. Invited review article: Review of post-process optical form metrology for industrial-grade metal additive manufactured parts. Rev. Sci. Instrum. 2016, 87, 041101. [Google Scholar] [CrossRef]
- Forbes, A.; De Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Gibelli, D.; Dolci, C.; Cappella, A.; Sforza, C. Reliability of optical devices for three-dimensional facial anatomy description: A systematic review and meta-analysis. Int. J. Oral Maxillofac. Surg. 2020, 49, 1092–1106. [Google Scholar] [CrossRef]
- Antonacci, D.; Caponio, V.C.A.; Troiano, G.; Pompeo, M.G.; Gianfreda, F.; Canullo, L. Facial scanning technologies in the era of digital workflow: A systematic review and network meta-analysis. J. Prosthodont. Res. 2022, 67, 321–336. [Google Scholar] [CrossRef] [PubMed]
- Zong, Y.; Duan, M.; Yu, C.; Li, J. Robust phase unwrapping algorithm for noisy and segmented phase measurements. Opt. Express 2021, 29, 24466–24485. [Google Scholar] [CrossRef] [PubMed]
- Rosell-Polo, J.R.; Cheein, F.A.; Gregorio, E.; Andújar, D.; Puigdomènech, L.; Masip, J.; Escolà, A. Advances in structured light sensors applications in precision agriculture and livestock farming. Adv. Agron. 2015, 133, 71–112. [Google Scholar] [CrossRef]
- Burke, J.; Pak, A.; Höfer, S.; Ziebarth, M.; Roschani, M.; Beyerer, J. Deflectometry for specular surfaces: An overview. Adv. Opt. Technol. 2023, 12, 1237687. [Google Scholar] [CrossRef]
- Rolland, J.P.; Davies, M.A.; Suleski, T.J.; Evans, C.; Bauer, A.; Lambropoulos, J.C.; Falaggis, K. Freeform optics for imaging. Optica 2021, 8, 161–176. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Wu, J.; Chen, X.; Wang, Y. Spatial binary coding method for stripe-wise phase unwrapping. Appl. Opt. 2020, 59, 4279–4285. [Google Scholar] [CrossRef]
- Yang, S.P.; Seo, Y.H.; Kim, J.B.; Kim, H.; Jeong, K.H. Optical MEMS devices for compact 3D surface imaging cameras. Micro Nano Syst. Lett. 2019, 7, 8. [Google Scholar] [CrossRef]
- Han, M.; Lei, F.; Shi, W.; Lu, S.; Li, X. Uniaxial MEMS-based 3D reconstruction using pixel refinement. Opt. Express 2022, 31, 536–554. [Google Scholar] [CrossRef]
- Möller, T.; Kraft, H.; Frey, J.; Albrecht, M.; Lange, R. Robust 3D Measurement with PMD Sensors; Range Imaging Day, Zürich, Switzerland; Springer Business Media: New York, NY, USA, 2005; Volume 7, p. 8. [Google Scholar]
- Xu, Y.; Gao, F.; Jiang, X. A brief review of the technological advancements of phase measuring deflectometry. PhotoniX 2020, 1, 14. [Google Scholar] [CrossRef]
- He, X.; Kemao, Q. A comparative study on temporal phase unwrapping methods in high-speed fringe projection profilometry. Opt. Lasers Eng. 2021, 142, 106613. [Google Scholar] [CrossRef]
- Lv, S.; Tang, D.; Zhang, X.; Yang, D.; Deng, W.; Kemao, Q. Fringe projection profilometry method with high efficiency, precision, and convenience: Theoretical analysis and development. Opt. Express 2022, 30, 33515–33537. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Z.; Fu, S.; Zhao, H.; Ni, Y.; Gao, N.; Meng, Z.; Yang, Z.; Zhang, G.; Yin, W. Recent progress of full-field three-dimensional shape measurement based on phase information. Nanomanuf. Metrol. 2024, 7, 9. [Google Scholar] [CrossRef]
- Kulkarni, R.; Rastogi, P. Fringe denoising algorithms: A review. Opt. Lasers Eng. 2020, 135, 106190. [Google Scholar] [CrossRef]
- Liu, H.; Yan, N.; Shao, B.; Yuan, S.; Zhang, X. Deep learning in fringe projection: A review. Neurocomputing 2024, 581, 127493. [Google Scholar] [CrossRef]
- Burnes, S.; Villa, J.; Moreno, G.; de la Rosa, I.; Alaniz, D.; González, E. Temporal fringe projection profilometry: Modified fringe-frequency range for error reduction. Opt. Lasers Eng. 2022, 149, 106788. [Google Scholar] [CrossRef]
- Lei, F.; Ma, R.; Li, X. Use of phase-angle model for full-field 3d reconstruction under efficient local calibration. Sensors 2024, 24, 2581. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.; Park, Y.H. Highly accurate three-dimensional measurement of large structures using multiple stereo vision with improved two-step calibration algorithm. Measurement 2024, 234, 114886. [Google Scholar] [CrossRef]
- Zhou, W.; Jia, Y.; Fan, L.; Fan, G.; Lu, F. A MEMS-based real-time structured light 3-D measuring architecture on FPGA. J. Real-Time Image Process. 2024, 21, 98. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Qian, X.; Wang, X.; Gui, W.; Gao, W.; Liang, X.; Li, X. HDRSL Net for Accurate High Dynamic Range Imaging-based Structured Light 3D Reconstruction. IEEE Trans. Image Process. 2025, 34, 5486–5499. [Google Scholar] [CrossRef]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Opt. 1984, 23, 3105–3108. [Google Scholar] [CrossRef]
- Su, X.Y.; Von Bally, G.; Vukicevic, D. Phase-stepping grating profilometry: Utilization of intensity modulation analysis in complex objects evaluation. Opt. Commun. 1993, 98, 141–150. [Google Scholar] [CrossRef]
- Ishikawa, K.; Yatabe, K.; Ikeda, Y.; Oikawa, Y.; Onuma, T.; Niwa, H.; Yoshii, M. Interferometric imaging of acoustical phenomena using high-speed polarization camera and 4-step parallel phase-shifting technique. In Proceedings of the Selected Papers from the 31st International Congress on High-Speed Imaging and Photonics, Osaka, Japan, 7–10 November 2017; SPIE: Washington, DC, USA, 2017; Volume 10328, pp. 93–99. [Google Scholar] [CrossRef]
- Jaganathan, K.; Eldar, Y.C.; Hassibi, B. Phase retrieval: An overview of recent developments. In Optical Compressive Imaging; CRC Press: Boca Raton, FL, USA, 2016; pp. 279–312. [Google Scholar] [CrossRef]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Lasers Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Zhang, Z.; Jing, Z.; Wang, Z.; Kuang, D. Comparison of Fourier transform, windowed Fourier transform, and wavelet transform methods for phase calculation at discontinuities in fringe projection profilometry. Opt. Lasers Eng. 2012, 50, 1152–1160. [Google Scholar] [CrossRef]
- Balasubramaniam, B.; Li, J.; Liu, L.; Li, B. 3d imaging with fringe projection for food and agricultural applications—A tutorial. Electronics 2023, 12, 859. [Google Scholar] [CrossRef]
- Saldner, H.O.; Huntley, J.M. Temporal phase unwrapping: Application to surface profiling of discontinuous objects. Appl. Opt. 1997, 36, 2770–2775. [Google Scholar] [CrossRef]
- Sansoni, G.; Carocci, M.; Rodella, R. Three-dimensional vision based on a combination of gray-code and phase-shift light projection: Analysis and compensation of the systematic errors. Appl. Opt. 1999, 38, 6565–6573. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Zhang, Y. Absolute phase-measurement technique based on number theory in multifrequency grating projection profilometry. Appl. Opt. 2001, 40, 492–500. [Google Scholar] [CrossRef]
- Hung, K.M.; Yamada, T. Phase unwrapping by regions using least-squares approach. Opt. Eng. 1998, 37, 2965–2970. [Google Scholar] [CrossRef]
- Zebker, H.A.; Lu, Y. Phase unwrapping algorithms for radar interferometry: Residue-cut, least-squares, and synthesis algorithms. J. Opt. Soc. Am. A 1998, 15, 586–598. [Google Scholar] [CrossRef]
- McKilliam, R.G.; Quinn, B.G.; Clarkson, I.V.L.; Moran, B.; Vellambi, B.N. Polynomial phase estimation by least squares phase unwrapping. IEEE Trans. Signal Process. 2014, 62, 1962–1975. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Robledo-Sanchez, C.; Guerrero-Sanchez, F. Phase-unwrapping algorithm by a rounding-least-squares approach. Opt. Eng. 2014, 53, 024102. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Jia, D.; Zhang, M.; Ji, X.; Li, Y.; Wu, Y. Experimental Study on the Reconstruction of a Light Field through a Four-Step Phase-Shift Method and Multiple Improvement Iterations of the Least Squares Method for Phase Unwrapping. Photonics 2024, 11, 716. [Google Scholar] [CrossRef]
- Asundi, A.; Wensen, Z. Fast phase-unwrapping algorithm based on a gray-scale mask and flood fill. Appl. Opt. 1998, 37, 5416–5420. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Chen, W. Reliability-guided phase unwrapping algorithm: A review. Opt. Lasers Eng. 2004, 42, 245–261. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Huntley, J. Noise-immune phase unwrapping algorithm. Appl. Opt. 1989, 28, 3268–3270. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.; Da, F. A novel algorithm for branch cut phase unwrapping. Opt. Lasers Eng. 2011, 49, 609–617. [Google Scholar] [CrossRef]
- Gdeisat, M.A.; Burton, D.R.; Lilley, F.; Arevalillo-Herráez, M.; Ammous, M.M. Aiding phase unwrapping by increasing the number of residues in two-dimensional wrapped-phase distributions. Appl. Opt. 2015, 54, 10073–10078. [Google Scholar] [CrossRef]
- Du, G.; Wang, M.; Zhou, C.; Si, S.; Li, H.; Lei, Z.; Li, Y. A simple spatial domain algorithm to increase the residues of wrapped phase maps. J. Mod. Opt. 2017, 64, 231–237. [Google Scholar] [CrossRef]
- Cheng, N.J.; Su, W.H. Phase-shifting projected fringe profilometry using binary-encoded patterns. Photonics 2021, 8, 362. [Google Scholar] [CrossRef]
- Xie, X.; Tian, X.; Shou, Z.; Zeng, Q.; Wang, G.; Huang, Q.; Qin, M.; Gao, X. Deep learning phase-unwrapping method based on adaptive noise evaluation. Appl. Opt. 2022, 61, 6861–6870. [Google Scholar] [CrossRef]
- Yu, J.; Da, F. Absolute phase unwrapping for objects with large depth range. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Yue, M.; Wang, J.; Zhang, J.; Zhang, Y.; Tang, Y.; Feng, X. Color crosstalk correction for synchronous measurement of full-field temperature and deformation. Opt. Lasers Eng. 2022, 150, 106878. [Google Scholar] [CrossRef]
- Li, Z.; Gao, N.; Meng, Z.; Zhang, Z.; Gao, F.; Jiang, X. Aided imaging phase measuring deflectometry based on concave focusing mirror. Photonics 2023, 10, 519. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Zhang, Z.; Gao, F.; Jiang, X. 3D measurement of structured specular surfaces using stereo direct phase measurement deflectometry. Machines 2021, 9, 170. [Google Scholar] [CrossRef]
- Ri, S.; Takimoto, T.; Xia, P.; Wang, Q.; Tsuda, H.; Ogihara, S. Accurate phase analysis of interferometric fringes by the spatiotemporal phase-shifting method. J. Opt. 2020, 22, 105703. [Google Scholar] [CrossRef]
- Feng, S.; Zuo, C.; Zhang, L.; Tao, T.; Hu, Y.; Yin, W.; Qian, J.; Chen, Q. Calibration of fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2021, 143, 106622. [Google Scholar] [CrossRef]
- Zhang, S.; Yau, S.T. High-resolution, real-time 3D absolute coordinate measurement based on a phase-shifting method. Opt. Express 2006, 14, 2644–2649. [Google Scholar] [CrossRef]
- Zhou, W.S.; Su, X.Y. A direct mapping algorithm for phase-measuring profilometry. J. Mod. Opt. 1994, 41, 89–94. [Google Scholar] [CrossRef]
- Huang, L.; Chua, P.S.; Asundi, A. Least-squares calibration method for fringe projection profilometry considering camera lens distortion. Appl. Opt. 2010, 49, 1539–1548. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, H.; Zhang, S.; Guo, T.; Towers, C.E.; Towers, D.P. Simple calibration of a phase-based 3D imaging system based on uneven fringe projection. Opt. Lett. 2011, 36, 627–629. [Google Scholar] [CrossRef] [PubMed]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 1983, 22, 3977–3982. [Google Scholar] [CrossRef]
- Jia, P.; Kofman, J.; English, C. Comparison of linear and nonlinear calibration methods for phase-measuring profilometry. Opt. Eng. 2007, 46, 043601. [Google Scholar] [CrossRef]
- Guo, H.; He, H.; Yu, Y.; Chen, M. Least-squares calibration method for fringe projection profilometry. Opt. Eng. 2005, 44, 033603. [Google Scholar] [CrossRef]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. Available online: https://api.semanticscholar.org/CorpusID:1150626 (accessed on 3 October 2025). [CrossRef]
- Kafri, O.; Glatt, I. Moiré deflectometry: A ray deflection approach to optical testing. Opt. Eng. 1985, 24, 944–960. [Google Scholar] [CrossRef]
- Servin, M.; Rodriguez-Vera, R.; Carpio, M.; Morales, A. Automatic fringe detection algorithm used for moiré deflectometry. Appl. Opt. 1990, 29, 3266–3270. [Google Scholar] [CrossRef]
- Wang, B.; Luo, X.; Pfeifer, T.; Mischo, H. Moire deflectometry based on Fourier-transform analysis. Measurement 1999, 25, 249–253. [Google Scholar] [CrossRef]
- Legarda-Saenz, R. Robust wavefront estimation using multiple directional derivatives in moiré deflectometry. Opt. Lasers Eng. 2007, 45, 915–921. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, S.W. Precision profile measurement of aspheric surfaces by improved Ronchi test. Opt. Eng. 1999, 38, 1041–1047. [Google Scholar] [CrossRef]
- Butel, G.P.; Smith, G.A.; Burge, J.H. Binary pattern deflectometry. Appl. Opt. 2014, 53, 923–930. [Google Scholar] [CrossRef]
- Schulz, M.; Ehret, G.; Fitzenreiter, A. Scanning deflectometric form measurement avoiding path-dependent angle measurement errors. J. Eur. Opt. Soc. Rapid Publ. 2010, 5, 10026. Available online: https://api.semanticscholar.org/CorpusID:54037587 (accessed on 1 October 2025). [CrossRef]
- Hao, Q.; Zhu, Q.; Wang, Y. Deflectometer with synthetically generated reference circle for aspheric surface testing. Opt. Laser Technol. 2005, 37, 375–380. [Google Scholar] [CrossRef]
- van Amstel, W.D.; Baumer, S.M.; Horijon, J.L. Optical figure testing by scanning deflectometry. In Proceedings of the Optical Manufacturing and Testing III, Berlin, Germany, 26–28 May 1999; SPIE: Washington, DC, USA, 1999; Volume 3782, pp. 320–327. [Google Scholar] [CrossRef]
- Miks, A.; Novak, J.; Novak, P. Method for reconstruction of shape of specular surfaces using scanning beam deflectometry. Opt. Lasers Eng. 2013, 51, 867–872. [Google Scholar] [CrossRef]
- Huang, L.; Idir, M.; Zuo, C.; Asundi, A. Review of phase measuring deflectometry. Opt. Lasers Eng. 2018, 107, 247–257. [Google Scholar] [CrossRef]
- Häusler, G.; Richter, C.; Leitz, K.H.; Knauer, M.C. Microdeflectometry—A novel tool to acquire three-dimensional microtopography with nanometer height resolution. Opt. Lett. 2008, 33, 396–398. [Google Scholar] [CrossRef]
- Liu, Y.; Lehtonen, P.; Su, X. High-accuracy measurement for small scale specular objects based on PMD with illuminated film. Opt. Laser Technol. 2012, 44, 459–462. [Google Scholar] [CrossRef]
- Huang, L.; Ng, C.S.; Asundi, A.K. Dynamic three-dimensional sensing for specular surface with monoscopic fringe reflectometry. Opt. Express 2011, 19, 12809–12814. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Sandner, M.; Gesierich, A.; Burke, J. Absolute optical surface measurement with deflectometry. In Proceedings of the Interferometry XVI: Applications, San Diego, CA, USA, 13–15 August 2012; SPIE: Washington, DC, USA, 2012; Volume 8494, pp. 129–135. [Google Scholar] [CrossRef]
- Bothe, T.; Li, W.; von Kopylow, C.; Juptner, W.P. High-resolution 3D shape measurement on specular surfaces by fringe reflection. In Proceedings of the Optical Metrology in Production Engineering, Strasbourg, France, 26–30 April 2004; SPIE: Washington, DC, USA, 2004; Volume 5457, pp. 411–422. Available online: https://ui.adsabs.harvard.edu/link_gateway/2004SPIE.5457..411B/doi:10.1117/12.545987 (accessed on 1 October 2025).
- Su, P.; Parks, R.; Angel, R.; Wang, L.; Burge, J. A new test for optical surfaces. Spie Newsroom 2011, 20. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Niu, Z.; Wang, W.; Zhu, Y.; Xu, M. Self-calibration of in situ monoscopic deflectometric measurement in precision optical manufacturing. Opt. Express 2019, 27, 7523–7536. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Zhang, X.; Niu, Z.; Wang, W.; Xu, M. Extra-detection-free monoscopic deflectometry for the in situ measurement of freeform specular surfaces. Opt. Lett. 2019, 44, 4271–4274. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Su, X.; Liu, Y.; Jing, H. 3D shape measurement of the aspheric mirror by advanced phase measuring deflectometry. Opt. Express 2008, 16, 15090–15096. [Google Scholar] [CrossRef] [PubMed]
- Petz, M.; Tutsch, R. Measurement of optically effective surfaces by imaging of gratings. In Proceedings of the Optical Measurement Systems for Industrial Inspection III, Munich, Germany, 23–26 June 2003; SPIE: Washington, DC, USA, 2003; Volume 5144, pp. 288–294. [Google Scholar] [CrossRef]
- Guo, H.; Feng, P.; Tao, T. Specular surface measurement by using least squares light tracking technique. Opt. Lasers Eng. 2010, 48, 166–171. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Xiao, Y.; Zhang, X.; Tu, D. Phase measurement deflectometry with refraction model and its calibration. Opt. Express 2018, 26, 33510–33522. [Google Scholar] [CrossRef]
- Ren, H.; Gao, F.; Jiang, X. Iterative optimization calibration method for stereo deflectometry. Opt. Express 2015, 23, 22060–22068. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, F.; Zhang, Z.; Jiang, X. A holistic calibration method with iterative distortion compensation for stereo deflectometry. Opt. Lasers Eng. 2018, 106, 111–118. [Google Scholar] [CrossRef]
- Han, M.; Zhang, C.; Zhang, Z.; Li, X. Review of MEMS vibration-mirror-based 3D reconstruction of structured light. Opt. Precis. Eng. 2025, 33, 1065–1090. [Google Scholar] [CrossRef]
- Yang, T.; Gu, F. Overview of modulation techniques for spatially structured-light 3D imaging. Opt. Laser Technol. 2024, 169, 110037. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, X. Research progress of dynamic three-dimensional shape measurement. Laser Optoelectron. Prog. 2013, 50, 4–17. [Google Scholar] [CrossRef]
- Zhang, Z. Review of single-shot 3D shape measurement by phase calculation-based fringe projection techniques. Opt. Lasers Eng. 2012, 50, 1097–1106. [Google Scholar] [CrossRef]
- Yang, D.; Qiao, D.; Xia, C. Curved light surface model for calibration of a structured light 3D modeling system based on striped patterns. Opt. Express 2020, 28, 33240–33253. [Google Scholar] [CrossRef]
- Yang, S.; Yang, T.; Wu, G.; Wu, Y.; Liu, F. Flexible and fast calibration method for uni-directional multi-line structured light system. Opt. Lasers Eng. 2023, 164, 107525. [Google Scholar] [CrossRef]
- Zhang, S. Flexible and high-accuracy method for uni-directional structured light system calibration. Opt. Lasers Eng. 2021, 143, 106637. [Google Scholar] [CrossRef]
- Yang, Y.; Miao, Y.; Liu, X.; Pedrini, G.; Tang, Q.; Osten, W.; Peng, X. Intrinsic parameter-free calibration of FPP using a ray phase mapping model. Opt. Lett. 2022, 47, 3564–3567. [Google Scholar] [CrossRef] [PubMed]
- Lei, F.; Han, M.; Jiang, H.; Wang, X.; Li, X. A phase-angle inspired calibration strategy based on MEMS projector for 3D reconstruction with markedly reduced calibration images and parameters. Opt. Lasers Eng. 2024, 176, 108078. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z.; Zhang, Q. Phase Error Compensation Technique Based on Phase-Shifting Fringe Analysis: A Review. Laser Optoelectron. Prog. 2024, 61, 0211008. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, X.; Jiang, H.; He, D.; Peng, X.; Huang, S.; Zhang, Z. Flexible phase error compensation based on Hilbert transform in phase shifting profilometry. Opt. Express 2015, 23, 25171–25181. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, J.; Zhang, D.; Chen, X.; Wang, Y. Nonlinear correction for fringe projection profilometry with shifted-phase histogram equalization. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, L.; Li, W.; Xia, H.; Deng, H.; Zhang, J. Black-box phase error compensation for digital phase-shifting profilometry. IEEE Trans. Instrum. Meas. 2017, 66, 2755–2761. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Zhu, H.; Rao, Y.; Wang, Y. Nonlinear high-order harmonics correction for phase measuring profilometry. Opt. Laser Technol. 2024, 170, 110248. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y. Triple N-step phase shift algorithm for phase error compensation in fringe projection profilometry. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Zhang, S. Comparative study on passive and active projector nonlinear gamma calibration. Appl. Opt. 2015, 54, 3834–3841. [Google Scholar] [CrossRef]
- Han, M.; Jiang, H.; Lei, F.; Xing, Y.; Wang, X.; Li, X. Modeling window smoothing effect hidden in fringe projection profilometry. Measurement 2025, 242, 115852. [Google Scholar] [CrossRef]
- Li, J.; Hassebrook, L.G.; Guan, C. Optimized two-frequency phase-measuring-profilometry light-sensor temporal-noise sensitivity. J. Opt. Soc. Am. A 2003, 20, 106–115. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Yan, K.; Yu, Y.; Huang, C.; Sui, L.; Qian, K.; Asundi, A. Fringe pattern denoising based on deep learning. Opt. Commun. 2019, 437, 148–152. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, H.; Bai, L.; Zheng, D.; Han, J. Accurate fringe projection profilometry using instable projection light source. Opt. Commun. 2022, 507, 127643. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; He, J.; Ji, F. Phase shift extraction and wavefront retrieval from interferograms with background and contrast fluctuations. J. Opt. 2015, 17, 025704. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, R.; Guo, H. Correction of illumination fluctuations in phase-shifting technique by use of fringe histograms. Appl. Opt. 2015, 55, 184–197. [Google Scholar] [CrossRef]
- Chen, C.; Wan, Y.; Cao, Y. Instability of projection light source and real-time phase error correction method for phase-shifting profilometry. Opt. Express 2018, 26, 4258–4270. [Google Scholar] [CrossRef]
- Zheng, Z.; Gao, J.; Mo, J.; Zhang, L.; Zhang, Q. A fast self-correction method for nonlinear sinusoidal fringe images in 3-D measurement. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, W.; Lu, L.; Zhang, Q. Generalized phase unwrapping method that avoids jump errors for fringe projection profilometry. Opt. Express 2021, 29, 27181–27192. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.S.; Hu, Q.J.; Chiang, F.P. Double three-step phase-shifting algorithm. Appl. Opt. 2002, 41, 4503–4509. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yau, S.T. Generic nonsinusoidal phase error correction for three-dimensional shape measurement using a digital video projector. Appl. Opt. 2006, 46, 36–43. [Google Scholar] [CrossRef]
- Pan, B.; Kemao, Q.; Huang, L.; Asundi, A. Phase error analysis and compensation for nonsinusoidal waveforms in phase-shifting digital fringe projection profilometry. Opt. Lett. 2009, 34, 416–418. [Google Scholar] [CrossRef]
- Song, H.; Kong, L. Mask information-based gamma correction in fringe projection profilometry. Opt. Express 2023, 31, 19478–19490. [Google Scholar] [CrossRef]
- Han, M.; Shi, W.; Lu, S.; Lei, F.; Li, Y.; Wang, X.; Li, X. Internal–External Layered Phase Shifting for Phase Retrieval. IEEE Trans. Instrum. Meas. 2023, 73, 1–13. [Google Scholar] [CrossRef]
- Li, K.; Zhang, Z.; Lin, J.; Sato, R.; Matsukuma, H.; Gao, W. Angle measurement based on second harmonic generation using artificial neural network. Nanomanuf. Metrol. 2023, 6, 28. [Google Scholar] [CrossRef]
- Sato, R.; Li, X.; Fischer, A.; Chen, L.C.; Chen, C.; Shimomura, R.; Gao, W. Signal processing and artificial intelligence for dual-detection confocal probes. Int. J. Precis. Eng. Manuf. 2024, 25, 199–223. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.; Leach, R.; Cheung, C.; Savio, E.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. CIRP Ann. 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Wang, S.; Luo, L.; Li, X. Design and parameter optimization of zero position code considering diffraction based on deep learning generative adversarial networks. Nanomanuf. Metrol. 2024, 7, 2. [Google Scholar] [CrossRef]
- Li, C.; Pan, X.; Zhu, P.; Zhu, S.; Liao, C.; Tian, H.; Qian, X.; Li, X.; Wang, X.; Li, X. Style Adaptation module: Enhancing detector robustness to inter-manufacturer variability in surface defect detection. Comput. Ind. 2024, 157, 104084. [Google Scholar] [CrossRef]
- Li, C.; Yan, H.; Qian, X.; Zhu, S.; Zhu, P.; Liao, C.; Tian, H.; Li, X.; Wang, X.; Li, X. A domain adaptation YOLOv5 model for industrial defect inspection. Measurement 2023, 213, 112725. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, C.; Liang, X.; Han, Z.; Li, Y.; Yang, C.; Gui, W.; Gao, W.; Wang, X.; Li, X. Attention Mono-depth: Attention-enhanced transformer for monocular depth estimation of volatile kiln burden surface. IEEE Trans. Circuits Syst. Video Technol. 2024, 35, 1686–1699. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Liang, X.; Huang, H.; Qian, X.; Feng, F.; Zhang, C.; Wang, X.; Gui, W.; Li, X. Global phase accuracy enhancement of structured light system calibration and 3D reconstruction by overcoming inevitable unsatisfactory intensity modulation. Measurement 2024, 236, 114952. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Zhang, C.; Han, M.; Lei, F.; Liang, X.; Wang, X.; Gui, W.; Li, X. Deep learning-driven one-shot dual-view 3-D reconstruction for dual-projector system. IEEE Trans. Instrum. Meas. 2023, 73, 1–14. [Google Scholar] [CrossRef]
- Caggiano, A.; Zhang, J.; Alfieri, V.; Caiazzo, F.; Gao, R.; Teti, R. Machine learning-based image processing for on-line defect recognition in additive manufacturing. CIRP Ann. 2019, 68, 451–454. [Google Scholar] [CrossRef]
- Wang, H.; He, X.; Zhang, C.; Liang, X.; Zhu, P.; Wang, X.; Gui, W.; Li, X.; Qian, X. Accelerating surface defect detection using normal data with an attention-guided feature distillation reconstruction network. Measurement 2025, 246, 116702. [Google Scholar] [CrossRef]
- Nguyen, H.; Novak, E.; Wang, Z. Accurate 3D reconstruction via fringe-to-phase network. Measurement 2022, 190, 110663. [Google Scholar] [CrossRef]
- Qiao, G.; Huang, Y.; Song, Y.; Yue, H.; Liu, Y. A single-shot phase retrieval method for phase measuring deflectometry based on deep learning. Opt. Commun. 2020, 476, 126303. [Google Scholar] [CrossRef]
- Fan, L.; Wu, Z.; Wang, J.; Wei, C.; Yue, H.; Liu, Y. Deep learning-based Phase Measuring Deflectometry for single-shot 3D shape measurement and defect detection of specular objects. Opt. Express 2022, 30, 26504–26518. [Google Scholar] [CrossRef]
- Fan, X.; Ma, T.; Li, C.; Li, Y.; Liu, S.; Chen, H. A deep learning-based approach to solve the height-slope ambiguity in phase measuring deflectometry. Meas. Sci. Technol. 2023, 34, 095007. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Ghim, Y.S.; Rhee, H.G. DYnet++: A deep learning based single-shot phase-measuring deflectometry for the 3-D measurement of complex free-form surfaces. IEEE Trans. Ind. Electron. 2023, 71, 2112–2121. [Google Scholar] [CrossRef]
- Ghim, Y.S.; Rhee, H.G. Deep learning-based phase measuring deflectometry for one-shot measurement and inspection of specular free-form surfaces. In Proceedings of the Interferometry and Structured Light 2024, San Diego, CA, USA, 21–22 August 2024; SPIE: Washington, DC, USA, 2024; Volume 13135, pp. 4–7. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Li, X.; Liang, X.; Li, Z.; Chen, W.; Wang, H.; Zhang, C.; Wang, X.; Gui, W. Single-frame structured light depth map reconstruction with absolute phase-aided supervision. In Proceedings of the Optoelectronic Imaging and Multimedia Technology XI, Nantong, China, 13–15 October 2024; SPIE: Washington, DC, USA, 2024; Volume 13239, pp. 172–177. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Li, X.; Li, Z.; Chen, W.; Zhang, C.; Liang, X. An end-to-end structured light depth prediction approach using Mamba networks. In Proceedings of the Optoelectronic Imaging and Multimedia Technology XI, Nantong, China, 13–15 October 2024; SPIE: Washington, DC, USA, 2024; Volume 13239, pp. 178–183. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Ma, R.; Wang, S.; Li, Z.; Zhang, C.; Chen, M.; Wang, X.; Gui, W.; Liang, X. X+ 1+ 1: A fast three-frequency heterodyne absolute phase measurement method integrating modified Fourier transform. In Proceedings of the Optical Metrology and Inspection for Industrial Applications XI, Nantong, China, 12–14 October 2024; SPIE: Washington, DC, USA, 2024; Volume 13241, pp. 27–34. [Google Scholar] [CrossRef]
- Su, X.; Zhang, Q. Dynamic 3-D shape measurement method: A review. Opt. Lasers Eng. 2010, 48, 191–204. [Google Scholar] [CrossRef]
- Nguyen, H.; Wang, Y.; Wang, Z. Single-shot 3D shape reconstruction using structured light and deep convolutional neural networks. Sensors 2020, 20, 3718. [Google Scholar] [CrossRef]
- Wang, F.; Wang, C.; Guan, Q. Single-shot fringe projection profilometry based on deep learning and computer graphics. Opt. Express 2021, 29, 8024–8040. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, P.; Zhu, J. Deep learning-based end-to-end 3D depth recovery from a single-frame fringe pattern with the MSUNet++ network. Opt. Express 2023, 31, 33287–33298. [Google Scholar] [CrossRef]
- Zhu, X.; Han, Z.; Zhang, Z.; Song, L.; Wang, H.; Guo, Q. PCTNet: Depth estimation from single structured light image with a parallel CNN-transformer network. Meas. Sci. Technol. 2023, 34, 085402. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Chen, W.; Zhang, C.; Chen, M.; Wang, X.; Gui, W.; Liang, X. DSAS-S2APNet: A dual-stage auxiliary supervision network for single-frame to absolute phase prediction. In Proceedings of the Optical Metrology and Inspection for Industrial Applications XI, Nantong, China, 12–14 October 2024; SPIE: Washington, DC, USA, 2024; Volume 13241, pp. 255–260. [Google Scholar] [CrossRef]
- Cai, Y.; Guo, M.; Wang, C.; Lu, X.; Zeng, X.; Sun, Y.; Ai, Y.; Xu, S.; Li, J. Ttfdnet: Precise depth estimation from single-frame fringe patterns. Sensors 2024, 24, 4733. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Wang, X.; Huang, G.; Yang, W.; Zhang, K.; Gu, X.; Tran, S.N.; Garg, S.; Alty, J.; Bai, Q. A comprehensive review on deep supervision: Theories and applications. arXiv 2022, arXiv:2207.02376. [Google Scholar] [CrossRef]
- Liu, X.; Xu, X.; Rao, A.; Gan, C.; Yi, L. Autogpart: Intermediate supervision search for generalizable 3d part segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11624–11634. [Google Scholar] [CrossRef]
- Li, C.; Zia, M.Z.; Tran, Q.H.; Yu, X.; Hager, G.D.; Chandraker, M. Deep supervision with intermediate concepts. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1828–1843. [Google Scholar] [CrossRef]
- Nguyen, H.; Ly, K.L.; Tran, T.; Wang, Y.; Wang, Z. hNet: Single-shot 3D shape reconstruction using structured light and h-shaped global guidance network. Results Opt. 2021, 4, 100104. [Google Scholar] [CrossRef]
- Zhu, X.; Zhao, H.; Song, L.; Wang, H.; Guo, Q. Triple-output phase unwrapping network with a physical prior in fringe projection profilometry. Appl. Opt. 2023, 62, 7910–7916. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.H.; Ly, K.L.; Lam, V.K.; Wang, Z. Generalized fringe-to-phase framework for single-shot 3D reconstruction integrating structured light with deep learning. Sensors 2023, 23, 4209. [Google Scholar] [CrossRef]
- Qian, J.; Feng, S.; Li, Y.; Tao, T.; Han, J.; Chen, Q.; Zuo, C. Single-shot absolute 3D shape measurement with deep-learning-based color fringe projection profilometry. Opt. Lett. 2020, 45, 1842–1845. [Google Scholar] [CrossRef]
- Li, Y.; Qian, J.; Feng, S.; Chen, Q.; Zuo, C. Composite fringe projection deep learning profilometry for single-shot absolute 3D shape measurement. Opt. Express 2022, 30, 3424–3442. [Google Scholar] [CrossRef]
- Jiang, Y.; Qin, J.; Liu, Y.; Yang, M.; Cao, Y. Deep-Learning-Based Single-Shot Fringe Projection Profilometry Using Spatial Composite Pattern. IEEE Trans. Instrum. Meas. 2024, 73, 1–14. [Google Scholar] [CrossRef]
- Zhu, X.; Lan, T.; Zhao, Y.; Wang, H.; Song, L. End-to-end color fringe depth estimation based on a three-branch U-net network. Appl. Opt. 2024, 63, 7465–7474. [Google Scholar] [CrossRef]
- Shen, S.; Lu, R.; Wan, D.; Yin, J.; He, P. Real-Time 3-D Measurement With Dual-Frequency Fringes by Deep Learning. IEEE Sens. J. 2024, 24, 16576–16586. [Google Scholar] [CrossRef]
- Yin, W.; Che, Y.; Li, X.; Li, M.; Hu, Y.; Feng, S.; Lam, E.Y.; Chen, Q.; Zuo, C. Physics-informed deep learning for fringe pattern analysis. Opto-Electron. Adv. 2024, 7, 230034-1. [Google Scholar] [CrossRef]
- Nawaz, M.; Uvaliyev, A.; Bibi, K.; Wei, H.; Abaxi, S.M.D.; Masood, A.; Shi, P.; Ho, H.P.; Yuan, W. Unraveling the complexity of Optical Coherence Tomography image segmentation using machine and deep learning techniques: A review. Comput. Med. Imaging Graph. 2023, 108, 102269. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Liu, C.; Lu, S.; Qian, X.; Wang, X.; Zou, Y.; Li, X. An efficient exposure fusion method for 3D measurement with high-reflective objects. In Proceedings of the Optoelectronic Imaging and Multimedia Technology XI, Nantong, China, 13–15 October 2024; SPIE: Washington, DC, USA, 2024; Volume 13239, pp. 348–356. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Ma, R.; Zhang, C.; Liang, X.; Li, X. Correction of grating patterns for high dynamic range 3D measurement based on deep learning. In Proceedings of the Optoelectronic Imaging and Multimedia Technology XI, Nantong, China, 13–15 October 2024; SPIE: Washington, DC, USA, 2024; Volume 13239, pp. 317–325. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Z.; Huang, Z.; Li, Y.; Zhang, C.; Qian, X.; Wang, X.; Gui, W.; Liang, X.; Li, X. A High-Accuracy and Reliable End-to-End Phase Calculation Network and Its Demonstration in High Dynamic Range 3D Reconstruction. Nanomanuf. Metrol. 2025, 8, 5. [Google Scholar] [CrossRef]
- Li, Y.; Chen, W.; Li, Z.; Zhang, C.; Wang, X.; Gui, W.; Gao, W.; Liang, X.; Li, X. SL3D-BF: A Real-World Structured Light 3D Dataset with Background-to-Foreground Enhancement. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 9850–9864. [Google Scholar] [CrossRef]
- Zhang, S.; Yau, S.T. High dynamic range scanning technique. Opt. Eng. 2009, 48, 033604. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Q.; Zuo, C.; Feng, S. High-speed high dynamic range 3D shape measurement based on deep learning. Opt. Lasers Eng. 2020, 134, 106245. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Zhang, Z.; Zuo, C.; Zhang, Y.; Zheng, D.; Han, J. Dynamic 3-D measurement based on fringe-to-fringe transformation using deep learning. Opt. Express 2020, 28, 9405–9418. [Google Scholar] [CrossRef]
- Yao, P.; Gai, S.; Chen, Y.; Chen, W.; Da, F. A multi-code 3D measurement technique based on deep learning. Opt. Lasers Eng. 2021, 143, 106623. [Google Scholar] [CrossRef]
- Yao, P.; Gai, S.; Da, F. Coding-Net: A multi-purpose neural network for Fringe Projection Profilometry. Opt. Commun. 2021, 489, 126887. [Google Scholar] [CrossRef]
- Song, X.; Wang, L. Y-ffc net for 3d reconstruction of highly reflective surfaces. IEEE Trans. Ind. Inform. 2024, 20, 13966–13974. [Google Scholar] [CrossRef]
- Liu, X.; Chen, W.; Madhusudanan, H.; Ge, J.; Ru, C.; Sun, Y. Optical measurement of highly reflective surfaces from a single exposure. IEEE Trans. Ind. Inform. 2020, 17, 1882–1891. [Google Scholar] [CrossRef]
- Nayar, S.K.; Krishnan, G.; Grossberg, M.D.; Raskar, R. Fast separation of direct and global components of a scene using high frequency illumination. In ACM SIGGRAPH 2006 Papers; Association for Computing Machinery: New York, NY, USA, 2006; pp. 935–944. [Google Scholar] [CrossRef]
- Drouin, M.A.; Godin, G. Deconvolution-based structured light system with geometrically plausible regularization. In Proceedings of the 2008 Congress on Image and Signal Processing, Sanya, China, 27–30 May 2008; Volume 3, pp. 557–564. [Google Scholar] [CrossRef]
- Drouin, M.A.; Godin, G.; Blais, F. Efficient representation of the variant PSF of structured light system. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 1693–1696. [Google Scholar] [CrossRef]
- Chen, T.; Lensch, H.P.; Fuchs, C.; Seidel, H.P. Polarization and phase-shifting for 3D scanning of translucent objects. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Chen, T.; Seidel, H.P.; Lensch, H.P. Modulated phase-shifting for 3D scanning. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Gupta, M.; Nayar, S.K. Micro phase shifting. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 813–820. Available online: https://api.semanticscholar.org/CorpusID:14927216 (accessed on 3 October 2025).
- Couture, V.; Martin, N.; Roy, S. Unstructured light scanning to overcome interreflections. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 1895–1902. [Google Scholar] [CrossRef]
- Moreno, D.; Son, K.; Taubin, G. Embedded phase shifting: Robust phase shifting with embedded signals. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2301–2309. [Google Scholar] [CrossRef]
- Zuo, C.; Tao, T.; Feng, S.; Huang, L.; Asundi, A.; Chen, Q. Micro Fourier transform profilometry (μFTP): 3D shape measurement at 10,000 frames per second. Opt. Lasers Eng. 2018, 102, 70–91. [Google Scholar] [CrossRef]
- Zhang, S.; Van Der Weide, D.; Oliver, J. Superfast phase-shifting method for 3-D shape measurement. Opt. Express 2010, 18, 9684–9689. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, S. Ultrafast 3-D shape measurement with an off-the-shelf DLP projector. Opt. Express 2010, 18, 19743–19754. [Google Scholar] [CrossRef] [PubMed]
- Lei, S.; Zhang, S. Flexible 3-D shape measurement using projector defocusing. Opt. Lett. 2009, 34, 3080–3082. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Feng, S.; Feng, F.; Gu, G.; Sui, X. Optimized pulse width modulation pattern strategy for three-dimensional profilometry with projector defocusing. Appl. Opt. 2012, 51, 4477–4490. [Google Scholar] [CrossRef] [PubMed]
- Heist, S.; Lutzke, P.; Schmidt, I.; Dietrich, P.; Kühmstedt, P.; Tünnermann, A.; Notni, G. High-speed three-dimensional shape measurement using GOBO projection. Opt. Lasers Eng. 2016, 87, 90–96. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Qian, J.; Feng, S.; Chen, Q.; Zuo, C. Single-shot super-resolved fringe projection profilometry (SSSR-FPP): 100,000 frames-per-second 3D imaging with deep learning. Light. Sci. Appl. 2025, 14, 70. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, C.; Qi, X.; Li, H. UHRNet: A deep learning-based method for accurate 3D reconstruction from a single fringe-pattern. J. Mod. Opt. 2023, 70, 707–722. [Google Scholar] [CrossRef]
- Li, Y.; Shen, J.; Wu, Z.; Wang, Y.; Zhang, Q. Real-time 3d imaging based on roi fringe projection and a lightweight phase-estimation network. Adv. Imaging 2024, 1, 021004. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Zheng, Y.; Chao, Q.; An, Y.; Hirsh, S.; Fix, A. Fringe projection-based single-shot 3d eye tracking using deep learning and computer graphics. In Proceedings of the Optical Architectures for Displays and Sensing in Augmented, Virtual, and Mixed Reality (AR, VR, MR) IV, San Diego, CA, USA, 20–24 August 2023; SPIE: Washington, DC, USA, 2023; Volume 12449, pp. 265–275. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Y.; Wan, Y.; Luo, L.; Peng, J. Single-shot multi-frequency 3D shape measurement for discontinuous surface object based on deep learning. Micromachines 2023, 14, 328. [Google Scholar] [CrossRef] [PubMed]







| Author | Year | FPP | PMD | MEMS | Deep Learning | Description |
|---|---|---|---|---|---|---|
| Tobias Möller et al. [33] | 2005 | × | ✓ | × | × | Early review of PMD-range imaging |
| Xu et al. [34] | 2020 | × | ✓ | × | × | PMD for 3D specular-surface measurement |
| Lv et al. [36] | 2020 | ✓ | × | × | × | FPP measurement theory |
| Kulkarni et al. [38] | 2020 | ✓ | × | ✓ | × | Fringe denoising algorithms |
| He et al. [35] | 2021 | ✓ | × | × | × | Temporal-phase unwrapping methods |
| Liu et al. [39] | 2024 | ✓ | × | × | ✓ | Deep learning in fringe projection |
| Bai et al. [37] | 2024 | ✓ | ✓ | × | ✓ | Three-dimensional shape measurement |
| Our article | 2025 | ✓ | ✓ | ✓ | ✓ | First comprehensive review systematically summarizing FPP, PMD, MEMS, and deep learning integration |
| Parameter | Interference | Physical Grating | LCD | DLP | MEMS |
|---|---|---|---|---|---|
| Accuracy | mm | mm | mm | mm | mm |
| Speed | ∼50 fps | ∼100 fps | ∼50 fps | ∼120 fps | >1000 fps |
| Resolution | <1 K | <1 K | ∼1 K | ∼1 K | >4 K |
| Programmable | No | No | Yes | Yes | Yes |
| Power Consumption | ∼100 W | ∼300 W | ∼40 W | ∼50 W | ∼5 W |
| Cost | > | > | ∼ | ∼ | ∼ |
| Optical Efficiency | Medium | Low | Medium | Low | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, H.; Li, Y.; Li, Z.; Gui, W.; Wang, X.; Zhang, C.; Liang, X.; Li, X. Fringe-Based Structured-Light 3D Reconstruction: Principles, Projection Technologies, and Deep Learning Integration. Sensors 2025, 25, 6296. https://doi.org/10.3390/s25206296
Zhang Z, Wang H, Li Y, Li Z, Gui W, Wang X, Zhang C, Liang X, Li X. Fringe-Based Structured-Light 3D Reconstruction: Principles, Projection Technologies, and Deep Learning Integration. Sensors. 2025; 25(20):6296. https://doi.org/10.3390/s25206296
Chicago/Turabian StyleZhang, Zhongyuan, Hao Wang, Yiming Li, Zinan Li, Weihua Gui, Xiaohao Wang, Chaobo Zhang, Xiaojun Liang, and Xinghui Li. 2025. "Fringe-Based Structured-Light 3D Reconstruction: Principles, Projection Technologies, and Deep Learning Integration" Sensors 25, no. 20: 6296. https://doi.org/10.3390/s25206296
APA StyleZhang, Z., Wang, H., Li, Y., Li, Z., Gui, W., Wang, X., Zhang, C., Liang, X., & Li, X. (2025). Fringe-Based Structured-Light 3D Reconstruction: Principles, Projection Technologies, and Deep Learning Integration. Sensors, 25(20), 6296. https://doi.org/10.3390/s25206296






