Assessing Obstructive Sleep Apnea Severity During Wakefulness via Tracheal Breathing Sound Analysis
Abstract
Highlights
- This study demonstrates a significant correlation between tracheal breathing sounds (TBS) recorded during wakefulness, anthropometric features, and the apnea–hypopnea index (AHI).
- A machine learning model trained on these features can form the basis of classifications of OSA severity in standard clinics.
- Categories (Non-, Mild-, Moderate-, and Severe-OSA) are formed without the need for sleep-based recordings.
- The proposed method enables the rapid, low-cost, and accessible estimation of OSA severity using brief, wakefulness-based TBS and basic anthropometric data.
- This approach can serve as a reliable screening and triage tool in clinical settings, helping reduce perioperative risks by informing earlier intervention and referral for full diagnosis.
Abstract
1. Introduction
2. Literature Review of Tracheal Breathing Sounds Analysis
3. Materials and Methods
3.1. Tracheal Breathing Sounds Dataset
3.1.1. Splitting Dataset for Training and Testing
3.1.2. Splitting Dataset for K-Fold
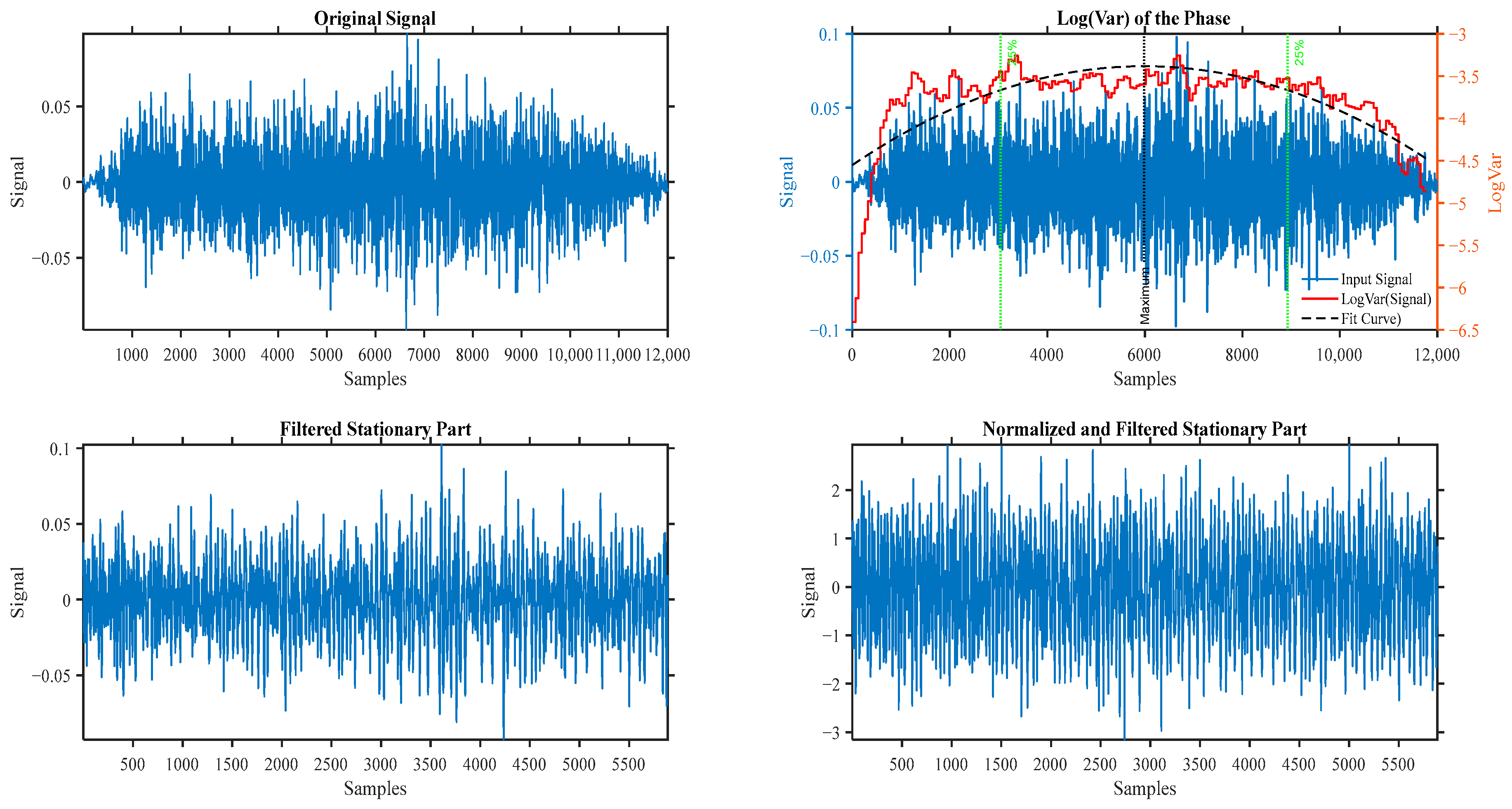
3.2. Tracheal Breathing Pre-Processing
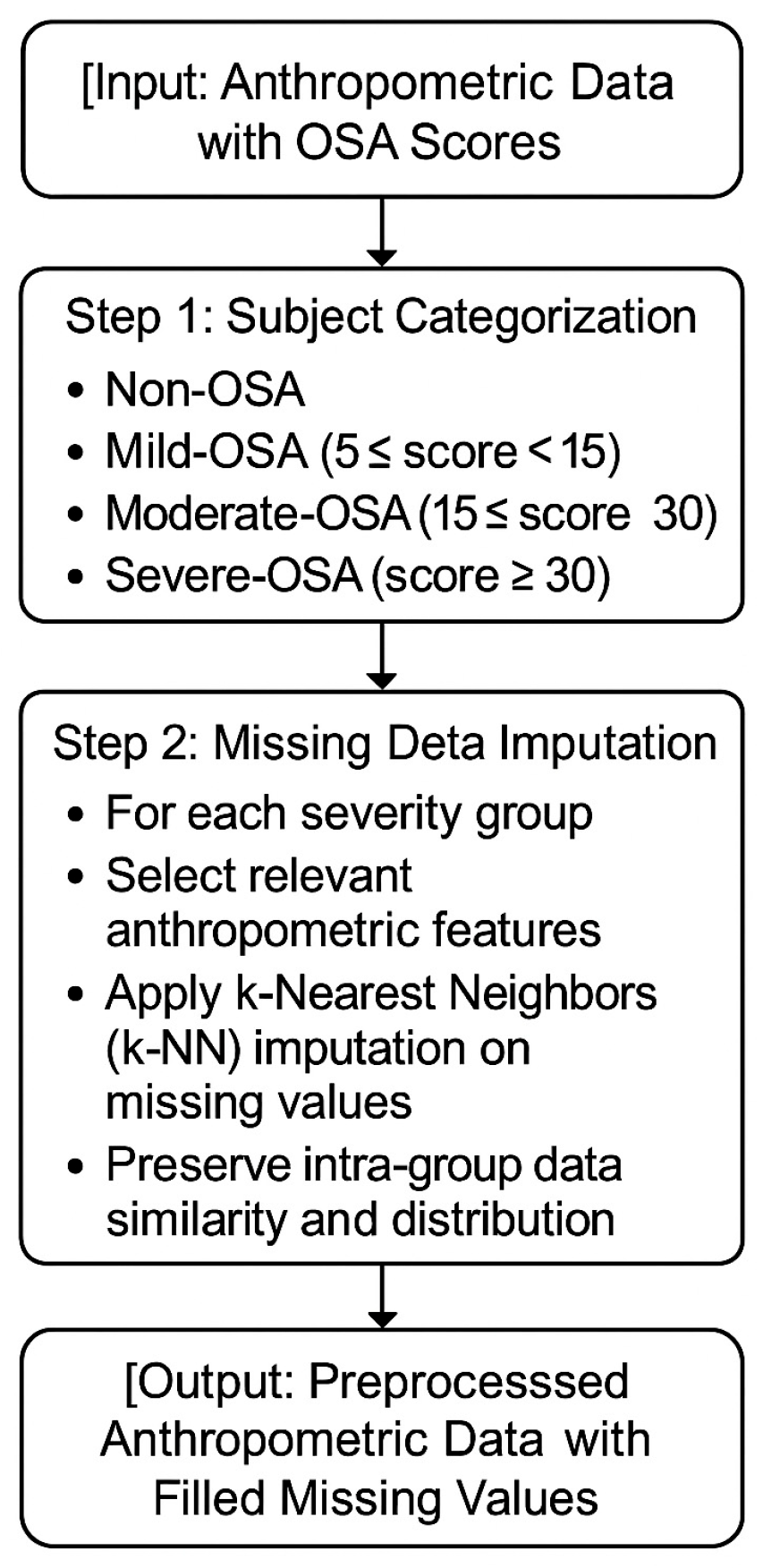
3.3. Anthropometric Missing Value Imputation
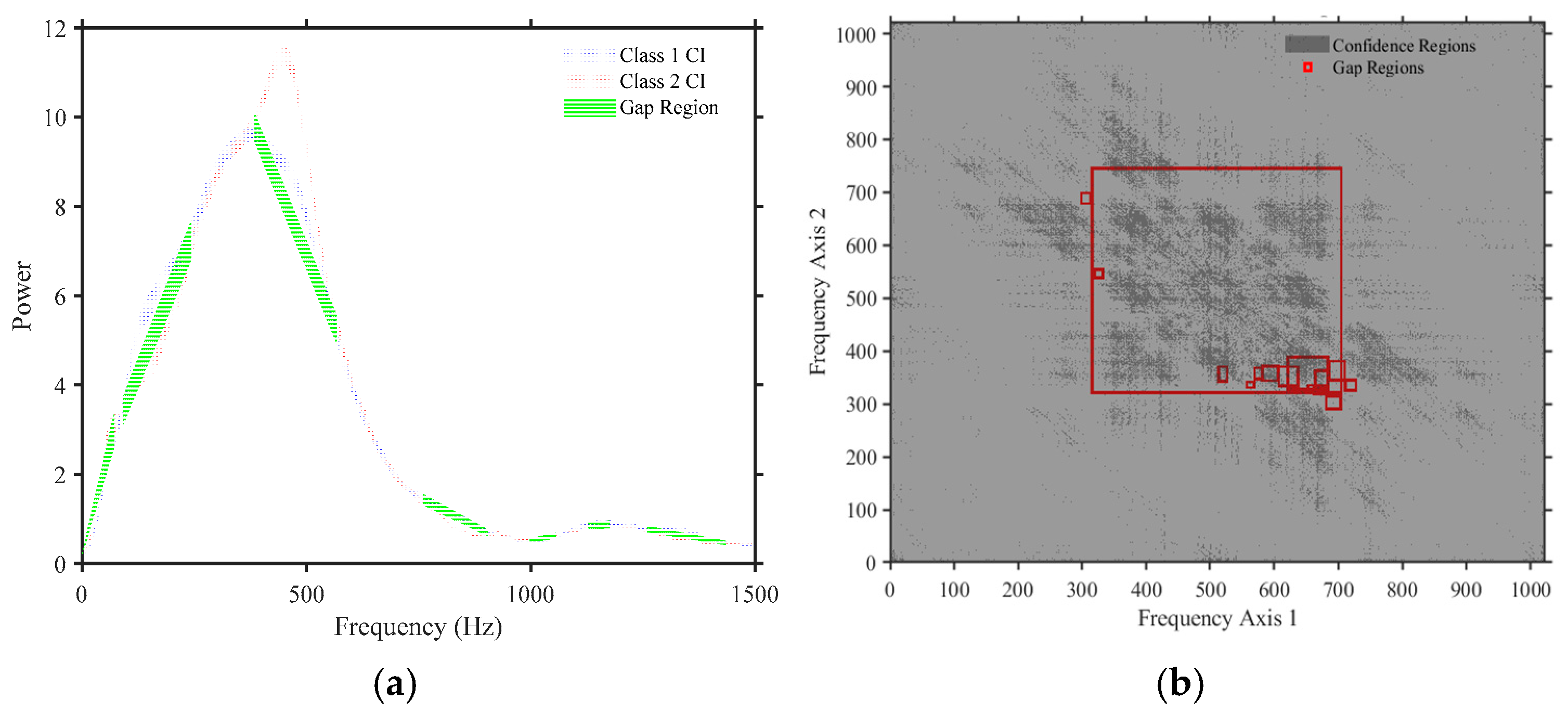
3.4. Feature Extractions
3.5. Automatic Feature Normalization
3.6. Selecting Best Features
3.7. Experiments Models Training
- Non-OSA vs. Mild-OSA;
- Non-OSA vs. Moderate-OSA;
- Non-OSA vs. Severe-OSA;
- Mild-OSA vs. Moderate-OSA;
- Mild-OSA vs. Severe-OSA;
- Moderate-OSA vs. Severe-OSA.
3.7.1. Classifier Configuration and Hyperparameter Optimization
- Traditional models: Decision Trees, Naïve Bayes, and Logistic Regression (L1 and L2 regularized).
- Distance- and projection-based models: k-Nearest Neighbors (kNN), Linear Discriminant Analysis (LDA), and Quadratic Discriminant Analysis (QDA).
- Margin-based models: Support Vector Machines (SVMs) with linear, radial basis function (RBF) and polynomial kernels.
- Ensemble methods: Random Forests, Bagged Trees, Gradient Boosting Machines (GBM), RUSBoost, and Subspace kNN.
- Neural networks: Both shallow and deep architectures.
3.7.2. Bootstrap Aggregation with OOB Validation
- 1.
- A resample was generated with replacement , where is the number of training instances.
- 2.
- Classifier was trained on using optimized .
- 3.
- OOB samples were retained for validation.
- OOB Accuracy: Overall correct classification rate.
- OOB Sensitivity: True positive rate, capturing the ability to detect positive cases.
- OOB Specificity: True negative rate, reflecting the ability to identify negative cases correctly.
3.7.3. Class Imbalance Mitigation
3.7.4. Robust Model Selection via Repeated Trials
3.7.5. Final Model Selection
3.8. Model Evaluation
3.8.1. Evaluation Protocol
- (a)
- Out-of-Bag (OOB) Validation
- (b)
- Independent Test Evaluation
3.8.2. Performance Metrics
4. Results
4.1. Feature Selection Results
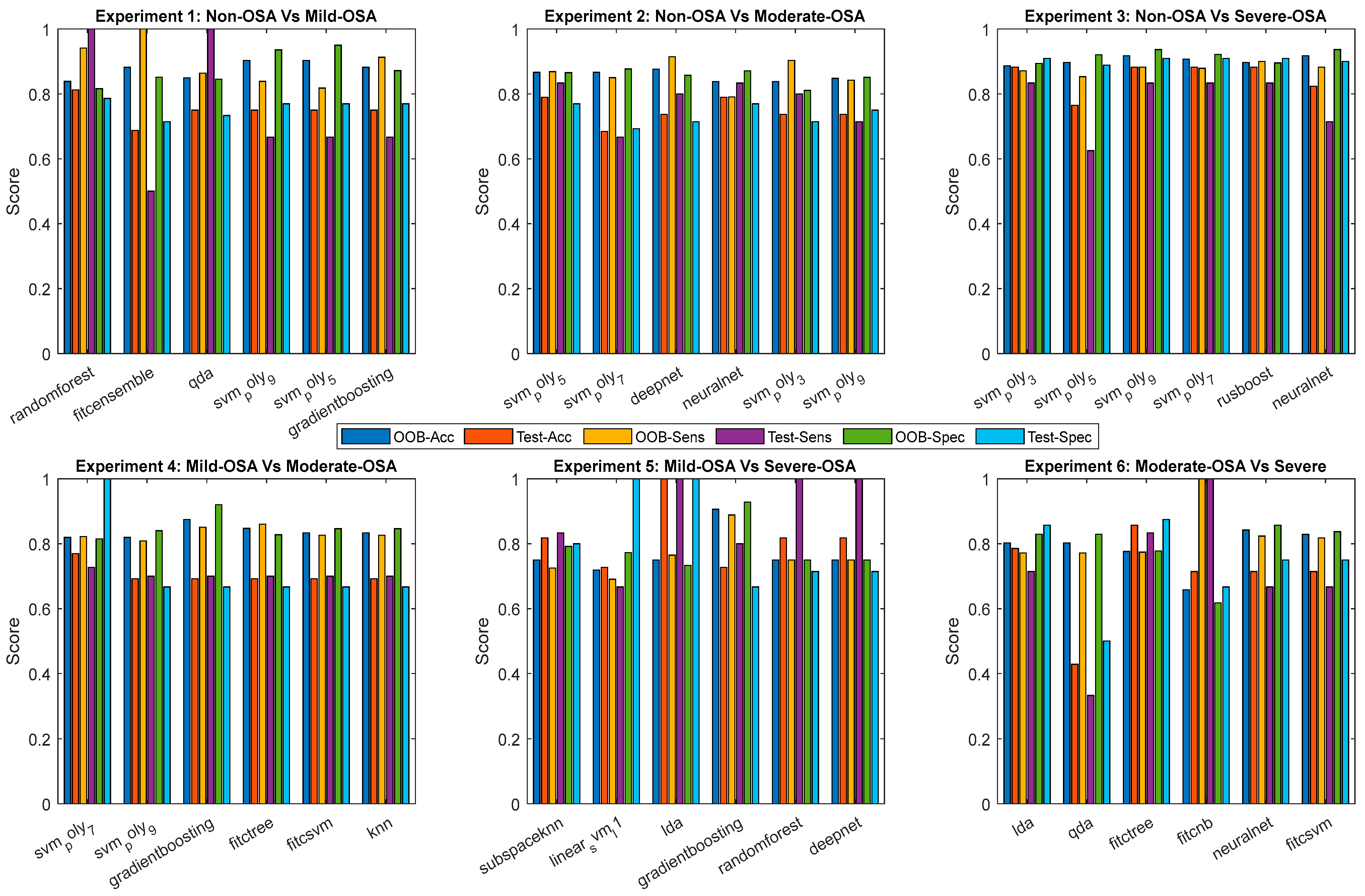
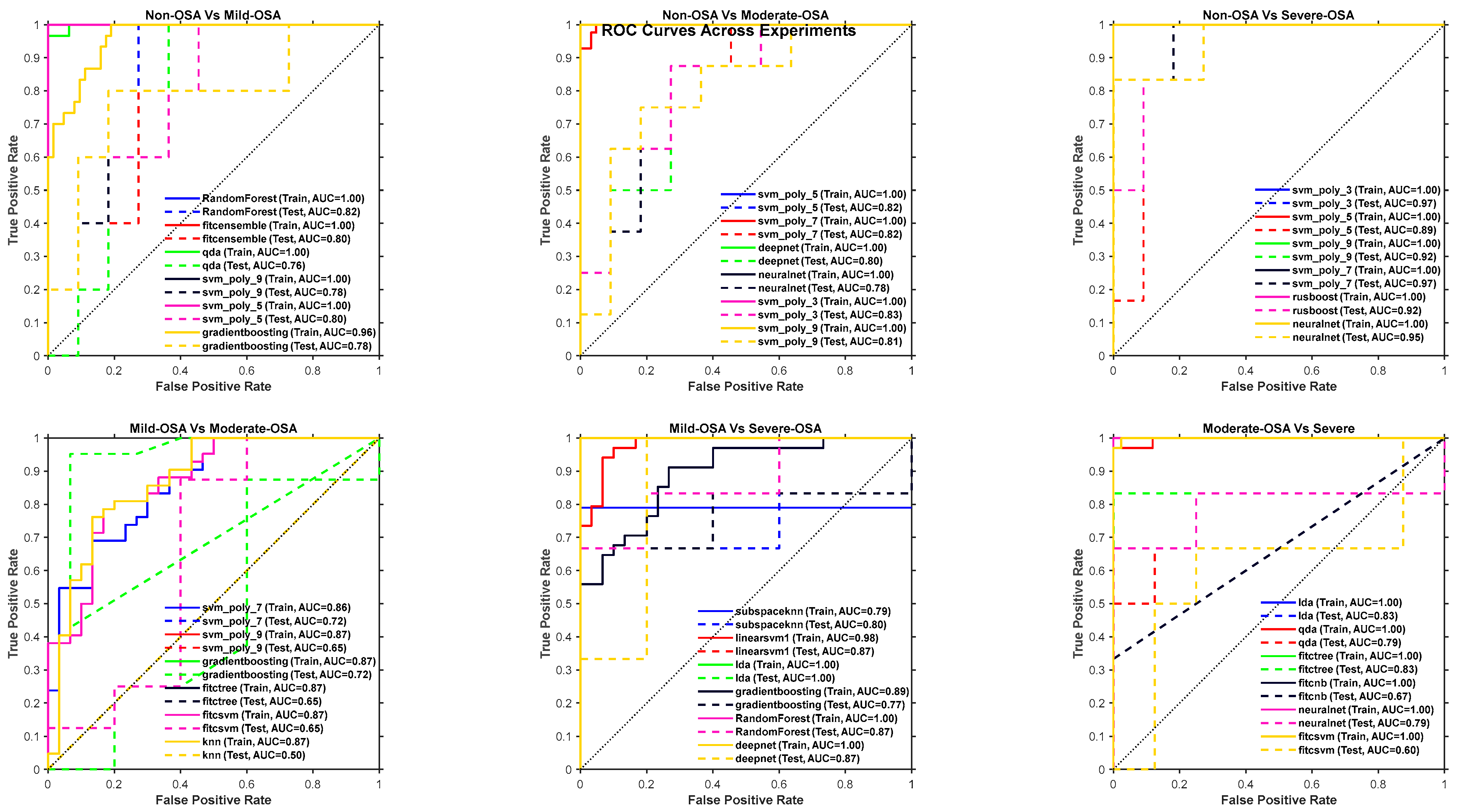
4.2. Experiments Models Results
4.2.1. Training and Testing Results
4.2.2. K-Fold Results
5. Discussion
6. Limitations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHI | Apnea–Hypopnea Index |
| BMI | Body Mass Index |
| CQT | Constant-Q Transform |
| DFA | Detrended Fluctuation Analysis |
| ECOC | Error-Correcting Output Codes |
| GBM | Gradient Boosting Machine |
| kNN | k-Nearest Neighbors |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LDA | Linear Discriminant Analysis |
| LR | Logistic Regression |
| MFCC | Mel-Frequency Cepstral Coefficients |
| MPS | Mallampati Score |
| NC | Neck Circumference |
| OOB | Out-of-Bag |
| OSA | Obstructive Sleep Apnea |
| PSG | Polysomnography |
| RF | Random Forest |
| RFE | Recursive Feature Elimination |
| RQA | Recurrence Quantification Analysis |
| SHAP | SHapley Additive exPlanations |
| SVM | Support Vector Machine |
| TBS | Tracheal Breathing Sounds |
| TQWT | Tunable Q-Factor Wavelet Transform |
| VMD | Variational Mode Decomposition |
Appendix A. Anthropometric Missing Value Imputation
Appendix B. Automatic Feature Normalization
- Min–Max Scaling: Rescales data to the [0, 1] range [54] using
- Z-Score Normalization: Standardizes features to a zero mean and unit variance [54]:
- Mean-Range Scaling: Centers by the mean and scales by the range [54]:
- Robust Scaling: Centers by the median and scales by the interquartile range (IQR) [54]:

Appendix C. Selecting Best Features
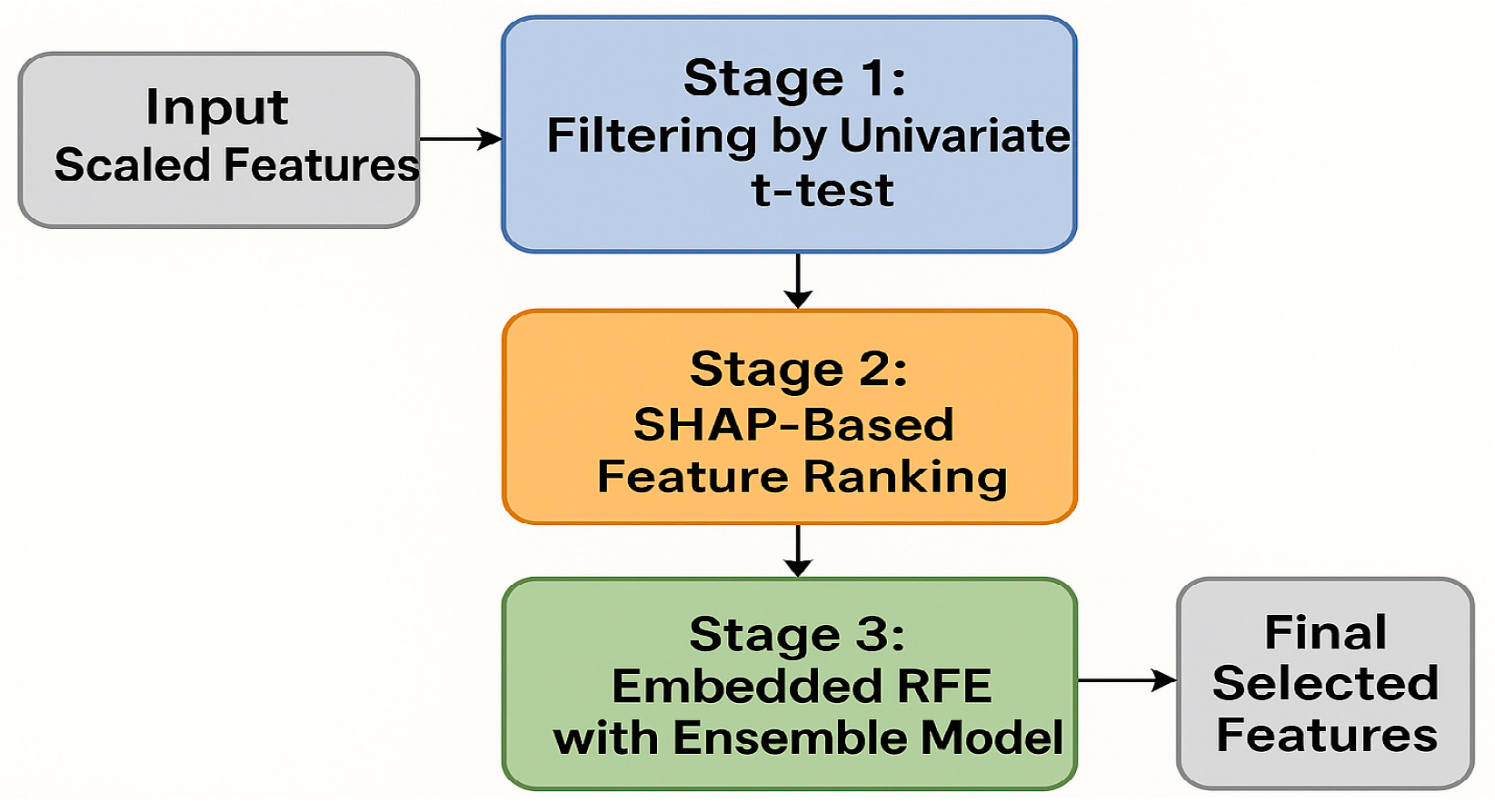
Appendix C.1. Stage 1: Filtering by Univariate t-Test
Appendix C.2. Stage 2: SHAP-Based Feature Ranking
- The classifier was trained and evaluated.
- SHAP values were computed for each feature.
- The top N/2 features with the highest mean absolute SHAP value were stored.

Appendix C.3. Stage 3: Embedded Recursive Feature Elimination (RFE) with Ensemble Model
Appendix D
| Power Spectrum Features | Bi-Spectrum Features | Wavelet | Wavelet | MFCC | TP | CDF |
|---|---|---|---|---|---|---|
| MeanPower | Hf2 2 | Wavelet Approx Mean L1 | Wavelet Approx Mean L4 | MFCC Mean C1 | TP Histogram 1 | CDFMean |
| StandardDeviation | En F Bi D 3 | Wavelet Approx Std L1 | Wavelet Approx Std L4 | MFCC Std C1 | TP Histogram 2 | CDFStd |
| Maximum | Mean Bi D F 3 | Wavelet Approx Skewness L1 | Wavelet Approx Skewness L4 | MFCC Skewness C1 | TP Histogram 3 | Lyapunov |
| Slope | WCOB D Fx 3 | Wavelet Approx Kurtosis L1 | Wavelet Approx Kurtosis L4 | MFCC Kurtosis C1 | TP Entropy | LyapunovExponentMean |
| SCBWCenter | WCOB D Fy 3 | Wavelet Approx Entropy L1 | Wavelet Approx Entropy L4 | MFCC Median C1 | TP Energy | LyapunovExponentStd |
| SCBWBandwidth | Hf1 3 | Wavelet Approx Log Energy L1 | Wavelet Approx Log Energy L4 | MFCC Range C1 | TP Skewness | LyapunovExponentMax |
| SpectralSkewness | Hf2 3 | Wavelet Approx Max To Min Ratio L1 | Wavelet Approx Max To Min Ratio L4 | MFCC Entropy C1 | TP Kurtosis | LyapunovExponentMin |
| SpectralKurtosis | Total Energy | Wavelet Approx Spectral Centroid L1 | Wavelet Approx Spectral Centroid L4 | MFCC Mean Abs Diff C1 | TP Max Prob | Recurrence |
| PeakFrequency | Normalized Energy | Wavelet Approx Spectral Bandwidth L1 | Wavelet Approx Spectral Bandwidth L4 | Spectral Centroid C1 | TP Ratio1 | RecurrenceDeterminism |
| SpectralEnergy | Max Abs Bi | Wavelet Detail Mean L1 | Wavelet Detail Mean L4 | Spectral Bandwidth C1 | TP Ratio2 | Amplitude Modulation |
| SpectralEntropy | Mean Abs Bi | Wavelet Detail Std L1 | Wavelet Detail Std L4 | MFCC Mean C2 | EP | AmplitudeModulationMean |
| ZeroCrossingRate | Entropy Skewness | Wavelet Detail Skewness L1 | Wavelet Detail Skewness L4 | MFCC Std C2 | EP Energy | AmplitudeModulationStd |
| RMS | Entropy Kurtosis | Wavelet Detail Kurtosis L1 | Wavelet Detail Kurtosis L4 | MFCC Skewness C2 | EP Mean Energy | AmplitudeModulationMax |
| SpectralFlatness | Symmetry Metric | Wavelet Detail Entropy L1 | Wavelet Detail Entropy L4 | MFCC Kurtosis C2 | EP Max Energy | AmplitudeModulationMin |
| FM2MFreq1 | Asymmetry Ratio | Wavelet Detail Log Energy L1 | Wavelet Detail Log Energy L4 | MFCC Median C2 | EP Min Energy | AmplitudeModulationMedian |
| FM2MFreq2 | Sym Mean | Wavelet Detail Max To Min Ratio L1 | Wavelet Detail Max To Min Ratio L4 | MFCC Range C2 | EP Std Energy | Miscellaneous |
| FreqSkewness1 | Sym Max | WaveletApproxSkewnessL3 | Wavelet Detail Spectral Centroid L4 | MFCC Entropy C2 | AVP | DFA_ScalingExponent |
| FreqSkewness2 | Sym Std | WaveletApproxKurtosisL3 | Wavelet Detail Spectral Bandwidth L4 | MFCC Mean Abs Diff C2 | AVP Histogram 1 | |
| SpectralCrest | Sym Var | WaveletApproxEntropyL3 | TQWT | Spectral Centroid C2 | AVP Histogram 2 | |
| BandPower | Mean Value | WaveletApproxLogEnergyL3 | TQWT | Spectral Bandwidth C2 | AVP Mean | |
| Bi-Spectrum Features | Std Value | Wavelet Approx Entropy L2 | SpectralEntropy | MFCC Mean C3 | AVP Std | |
| En T Bi | Skewness Value | Wavelet Approx Log Energy L2 | BandPowerLow | MFCC Std C3 | AVP Max | |
| En T Bi D | Kurtosis Value | Wavelet Approx Max To Min Ratio L2 | BandPowerMid | MFCC Skewness C3 | AVP Min | |
| En F Bi | Range Value | Wavelet Approx Spectral Centroid L2 | BandPowerHigh | MFCC Kurtosis C3 | AVP Entropy | |
| En F Bi D | Energy Value | Wavelet Approx Spectral Bandwidth L2 | CQT | MFCC Median C3 | AVP Energy | |
| Mean Bi T F | Median Value | Wavelet Detail Mean L2 | CQT Mean Power | MFCC Range C3 | DIR | |
| Mean Bi D F | IQR Value | Wavelet Detail Std L2 | CQT Std Power | MFCC Entropy C3 | DIR Histogram 1 | |
| Mean Bi T F G | Coef Variation | Wavelet Detail Skewness L2 | CQT Skewness Power | MFCC Mean Abs Diff C3 | DIR Histogram 2 | |
| Mean Bi D F G | Region Area | Wavelet Detail Kurtosis L2 | CQT Kurtosis Power | Spectral Centroid C3 | DIR Histogram 3 | |
| Mean Bi T F H | Bounding Box Area | Wavelet Detail Entropy L2 | CQT Total Energy | Spectral Bandwidth C3 | MAG Mean | |
| Mean Bi D F H | Aspect Ratio | Wavelet Detail Log Energy L2 | CQT Temporal Centroid | MFCC Mean C4 | MAG Std | |
| WCOB Tx | Centroid X | Wavelet Detail Max To Min Ratio L2 | CQT Temporal Spread | MFCC Std C4 | MAG Max | |
| WCOB Ty | Centroid Y | Wavelet Detail Spectral Centroid L2 | CQT Spectral Centroid | MFCC Skewness C4 | MAG Min | |
| WCOB Dx | Perimeter | Wavelet Detail Spectral Bandwidth L2 | CQT Spectral Bandwidth | MFCC Kurtosis C4 | DIR Entropy | |
| WCOB Dy | Compactness | Wavelet Approx Mean L3 | CQT Spectral Flatness | MFCC Median C4 | DIR Energy | |
| WCOB T Fx | Bounding Box Diagonal | Wavelet Approx Std L3 | CQT Time Entropy | MFCC Range C4 | Noise Metrics | |
| WCOB T Fy | Peak Value | Wavelet Approx Skewness L3 | CQT Freq Entropy | MFCC Entropy C4 | NoiseToHarmonicRatio | |
| WCOB D Fx | Frequency Centroid X | Wavelet Approx Kurtosis L3 | CQT Gabor Energy Std | MFCC Mean Abs Diff C4 | Shimmer | |
| WCOB D Fy | Frequency Centroid Y | Wavelet Approx Entropy L3 | CQT Gabor Mean Mean | Spectral Centroid C4 | Jitter | |
| H1 | Frequency Bandwidth X | Wavelet Approx Log Energy L3 | CQT Gabor Std Mean | Spectral Bandwidth C4 | PBP | |
| H2 | Frequency Bandwidth Y | Wavelet Approx Max To Min Ratio L3 | CQT Gabor Skewness Mean | MFCC Mean C5 | PBP Mean | |
| En F Bi D 1 | Spectral Flux | Wavelet Approx Spectral Centroid L3 | CQT Gabor Kurtosis Mean | MFCC Std C5 | PBP Variance | |
| Mean Bi D F 1 | Entropy Value | Wavelet Approx Spectral Bandwidth L3 | CQT Freq Shifts Mean | MFCC Skewness C5 | PBP Skewness | |
| WCOB D Fx 1 | Texture Contrast | Wavelet Detail Mean L3 | CQT Freq Shifts Std | MFCC Kurtosis C5 | PBP Kurtosis | |
| WCOB D Fy 1 | Texture Correlation | Wavelet Detail Std L3 | CQT Freq Shifts Dynamic Range | MFCC Median C5 | PBP Entropy | |
| Hf1 1 | Texture Energy | Wavelet Detail Skewness L3 | CQT Freq Intervals Mean | MFCC Range C5 | LBP | |
| Hf2 1 | Texture Homogeneity | Wavelet Detail Kurtosis L3 | CQT Freq Intervals Std | MFCC Entropy C5 | LBP Mean | |
| En F Bi D 2 | Fractal Dimension | Wavelet Detail Entropy L3 | CQT Bandwidth Mean | MFCC Mean Abs Diff C5 | LBP Variance | |
| Mean Bi D F 2 | Connected Components | Wavelet Detail Log Energy L3 | CQT Bandwidth Std | Spectral Centroid C5 | LBP Skewness | |
| WCOB D Fx 2 | Euler Number | Wavelet Detail Max To Min Ratio L3 | CQT Bandwidth Dynamic Range | Spectral Bandwidth C5 | LBP Kurtosis | |
| WCOB D Fy 2 | Num Holes | Wavelet Detail Spectral Centroid L3 | LBP Entropy |
| Feature Number | Non-OSA vs. Mild-OSA | Non-OSA vs. Moderate-OSA | Non-OSA vs. Severe-OSA | Mild-OSA vs. Moderate-OSA | Mild-OSA vs. Severe-OSA | Moderate-OSA vs. Severe-OSA |
|---|---|---|---|---|---|---|
| 1 | MouthExpiration_Gap_163-296_SpectralEntropy | Average_Gap_45-329_SpectralSkewness | NoseInspiration_Gap_816-885_SpectralKurtosis | NoseExpiration_Gap_299-707_MeanPower | MouthExpiration_Gap_367-515_SCBW_Bandwidth | NoseExpiration_Gap_384-567_SpectralCrest |
| 2 | MouthExpiration_Gap_163-296_SpectralCrest | NoseInspiration_Gap_321-577_SpectralSkewness | NoseInspiration_Gap_816-885_FreqSkewness1 | Mouth Expiration_BBox_229_712_22_26_iqrValue | Average_Average_BBoxes_EnFBiD_2 | Average_BBox_584_362_21_35_numHoles |
| 3 | MouthExpiration_Gap_1375-1499_SpectralCrest | Average_BBox_548_370_24_29_entropyValue | NoseExpiration_Gap_986-1325_SCBW_Bandwidth | Mouth_Inspiration_FNMidFlow_MFCCMean_C1 | Nose Expiration_BBox_787_244_15_15_rangeValue | Mouth_Inspiration_FNMidFlow_WaveletApproxEntropyL2 |
| 4 | NoseInspiration_Gap_1066-1424_SCBW_Bandwidth | Mouth Inspiration_BBox_203_786_12_11_rangeValue | Average_BBox_527_294_11_18_textureEnergy | Nose_Expiration_FNMidFlow_WaveletApproxSkewnessL3 | Average_Gap_73-307_SpectralCrest | Nose_Expiration_FNMidFlow_PeakCount |
| 5 | Mouth_Inspiration_FNMidFlow_MFCCMean_C1 | Mouth_Expiration_FNMidFlow_WaveletApproxSpectralBandwidthL1 | Average_BBox_526_336_15_18_centroidY | Mouth_Inspiration_FN_MFCCMean_C1 | Nose Inspiration_BBox_766_223_15_15_medianValue | Mouth_Inspiration_FN_MFCCMean_C2 |
| 6 | Mouth_Inspiration_FNMidFlow_MFCCMedian_C5 | Mouth_Expiration_FNMidFlow_WaveletDetailEntropyL3 | Nose Inspiration_BBox_0_0_22_23_aspectRatio | Mouth_Inspiration_FN_MFCCStd_C1 | Nose Inspiration_BBox_220_207_581_615_peakValue | MouthExpiration_Gap_282-460_SCBW_Bandwidth |
| 7 | Nose_Expiration_FNMidFlow_WaveletApproxMeanL3 | Mouth Inspiration_BBox_229_756_15_17_iqrValue | Mouth Inspiration_BBox_0_934_73_89_eulerNumber | Mouth_Inspiration_FN_SpectralCentroid_C1 | Nose Inspiration_BBox_766_223_15_15_frequencyCentroidY | MouthInspiration_Gap_79-281_RMS |
| 8 | NoseExpiration_Gap_534-1003_BandPower | Nose Inspiration_BBox_533_433_14_13_coefVariation | Mouth Inspiration_BBox_74_955_16_16_meanValue | Mouth_Inspiration_FN_SpectralBandwidth_C1 | Nose Inspiration_BBox_989_487_34_58_peakValue | NoseInspiration_Gap_327-532_MeanPower |
| 9 | NoseExpiration_Gap_1029-1329_SpectralSkewness | Nose Expiration_BBox_515_348_11_29_entropyValue | Mouth Inspiration_BBox_74_955_16_16_stdValue | Mouth_Inspiration_FN_MFCCKurtosis_C2 | Nose Inspiration_BBox_989_487_34_58_frequencyCentroidY | NoseInspiration_Gap_327-532_SCBW_Bandwidth |
| 10 | Mouth Inspiration_BBox_10_480_22_39_numHoles | Average_FNMidFlow_DIR_Histogram_2 | Mouth Expiration_Average_BBoxes_totalEnergy | Mouth_Expiration_FN_WaveletDetailSpectralCentroidL2 | Nose Inspiration_BBox_989_487_34_58_spectralFlux | NoseInspiration_Gap_327-532_SpectralEnergy |
| 11 | Mouth Expiration_BBox_30_0_11_13_frequencyCentroidX | Average_FNMidFlow_AVP_Histogram_2 | Mouth Expiration_Average_BBoxes_normalizedEnergy | Mouth_Expiration_FN_CQTBandwidthDynamicRange | Nose Inspiration_BBox_989_487_34_58_connectedComponents | NoseInspiration_Gap_327-532_BandPower |
| 12 | Mouth Expiration_BBox_504_333_51_42_kurtosisValue | Mouth_Inspiration_FNMidFlow_ZeroCrossing1 | Mouth Expiration_Average_BBoxes_stdAbsBi | Mouth_Expiration_FN_MFCCStd_C1 | Nose Inspiration_BBox_989_487_34_58_eulerNumber | Mouth Inspiration_BBox_290_464_45_80_regionArea |
| 13 | Mouth Expiration_BBox_504_333_51_42_boundingBoxArea | Mouth_Inspiration_FNMidFlow_WaveletDetailSpectralBandwidthL1 | Mouth Expiration_Average_BBoxes_symStd | Mouth_Expiration_FN_SpectralCentroid_C1 | Nose Inspiration_BBox_226_683_94_101_iqrValue | Nose Inspiration_BBox_367_371_287_304_iqrValue |
| 14 | Mouth Expiration_BBox_504_333_51_42_boundingBoxDiagonal | Mouth_Inspiration_FNMidFlow_WaveletDetailSpectralBandwidthL4 | Mouth Expiration_BBox_588_259_169_356_perimeter | Mouth_Expiration_FN_MFCCSkewness_C2 | Nose Inspiration_BBox_226_683_94_101_frequencyCentroidX | Nose Inspiration_BBox_367_371_287_304_textureHomogeneity |
| 15 | Mouth Expiration_BBox_977_478_46_82_numHoles | Mouth_Inspiration_FNMidFlow_MFCCMean_C2 | Mouth Expiration_BBox_266_279_435_530_centroidY | Mouth_Expiration_FN_MFCCKurtosis_C2 | Nose Inspiration_BBox_241_721_42_42_boundingBoxArea | Nose Inspiration_BBox_367_371_287_304_numHoles |
| 16 | Mouth Expiration_BBox_0_975_48_48_aspectRatio | Mouth_Inspiration_FNMidFlow_MFCCKurtosis_C5 | Mouth Expiration_BBox_774_364_23_29_perimeter | Mouth_Expiration_FN_MFCCKurtosis_C3 | Nose Inspiration_BBox_241_721_42_42_frequencyCentroidY | Nose Expiration_BBox_315_321_390_424_textureContrast |
| 17 | Mouth Expiration_BBox_0_975_48_48_textureContrast | Mouth_Inspiration_FNMidFlow_PBP_Skewness | Mouth Expiration_BBox_300_553_19_16_centroidX | Nose_Inspiration_FN_ZeroCrossing2 | Nose Inspiration_BBox_243_745_14_14_textureEnergy | Nose Expiration_BBox_582_344_24_27_aspectRatio |
| 18 | Nose Inspiration_BBox_0_959_64_64_boundingBoxDiagonal | Mouth_Inspiration_FNMidFlow_TP_Histogram_1 | Nose Inspiration_Average_BBoxes_EnFBiD_1 | Nose_Inspiration_FN_WaveletApproxSkewnessL1 | Nose Inspiration_BBox_243_745_14_14_eulerNumber | Nose Expiration_BBox_582_344_24_27_perimeter |
| 19 | Nose Inspiration_BBox_0_959_64_64_textureEnergy | Mouth_Inspiration_FNMidFlow_TP_MaxProb | Nose Inspiration_Average_BBoxes_MeanBiDF_1 | Nose_Inspiration_FN_WaveletApproxSpectralCentroidL2 | Nose Inspiration_BBox_223_765_15_16_stdValue | Average_FNMidFlow_WaveletDetailMaxToMinRatioL3 |
| 20 | Average_FNMidFlow_WaveletApproxMaxToMinRatioL1 | Mouth_Inspiration_FNMidFlow_EP_MaxEnergy | Nose Inspiration_Average_BBoxes_WCOBDFx_1 | Nose_Inspiration_FN_WaveletDetailKurtosisL3 | Nose Inspiration_BBox_223_765_15_16_entropyValue | Average_FNMidFlow_WaveletDetailKurtosisL4 |
| 21 | Nose_Inspiration_FNMidFlow_HurstExponent | Mouth_Expiration_FNMidFlow_WaveletApproxKurtosisL1 | Nose Inspiration_Average_BBoxes_WCOBDFy_1 | Nose_Inspiration_FN_CQTStdPower | Nose Inspiration_BBox_202_787_14_17_entropyValue | Mouth_Inspiration_FNMidFlow_LyapunovExponentMean |
| 22 | Nose_Expiration_FN_KatzFD | Mouth_Expiration_FNMidFlow_WaveletApproxSkewnessL2 | Nose Inspiration_Average_BBoxes_Hf1_1 | Nose_Inspiration_FN_CQTSkewnessPower | Nose Inspiration_BBox_202_787_14_17_textureContrast | Mouth_Inspiration_FNMidFlow_BandPowerHigh |
| 23 | MouthInspiration_Gap_1217-1499_PeakFrequency | Mouth_Expiration_FNMidFlow_PBP_Kurtosis | Nose Inspiration_Average_BBoxes_Hf2_1 | Nose_Inspiration_FN_CQTTemporalCentroid | Nose Inspiration_BBox_202_787_14_17_textureEnergy | Nose_Inspiration_FNMidFlow_WaveletApproxEntropyL1 |
| 24 | Mouth Expiration_BBox_504_333_51_42_centroidY | Mouth_Expiration_FNMidFlow_PBP_Entropy | Nose Inspiration_Average_BBoxes_reserved1 | Nose_Inspiration_FN_CQTSpectralCentroid | Nose Inspiration_BBox_0_989_39_34_stdValue | Nose_Inspiration_FNMidFlow_WaveletApproxEntropyL2 |
| 25 | Mouth Expiration_BBox_504_333_51_42_peakValue | MouthInspiration_Gap_0-18_FM2MFreq1 | Nose Inspiration_Average_BBoxes_EnFBiD_2 | Nose_Inspiration_FN_CQTBandwidthDynamicRange | Nose Expiration_BBox_0_0_39_44_connectedComponents | Nose_Inspiration_FNMidFlow_WaveletDetailSpectralCentroidL3 |
| 26 | Mouth Expiration_BBox_977_478_46_82_textureCorrelation | MouthInspiration_Gap_64-362_MeanPower | Nose Inspiration_Average_BBoxes_MeanBiDF_2 | Nose_Inspiration_FN_MFCCSkewness_C1 | Nose Expiration_BBox_465_0_66_46_medianValue | Nose_Expiration_FNMidFlow_WaveletApproxSkewnessL2 |
| 27 | Nose Inspiration_BBox_0_0_38_38_rangeValue | MouthInspiration_Gap_64-362_RMS | Nose Inspiration_Average_BBoxes_WCOBDFx_2 | Nose_Inspiration_FN_MFCCKurtosis_C1 | Nose Expiration_BBox_465_0_66_46_iqrValue | Average_FN_AVP_Mean |
| 28 | Nose Inspiration_BBox_477_0_55_39_stdValue | MouthInspiration_Gap_64-362_FM2MFreq1 | Nose Inspiration_Average_BBoxes_WCOBDFy_2 | Nose_Inspiration_FN_SpectralBandwidth_C1 | Nose Expiration_BBox_465_0_66_46_textureCorrelation | Mouth_Inspiration_FN_KatzFD |
| 29 | Nose Expiration_BBox_0_981_41_42_fractalDimension | MouthInspiration_Gap_64-362_BandPower | Nose Inspiration_Average_BBoxes_Hf1_2 | Nose_Inspiration_FN_MFCCKurtosis_C2 | Nose Expiration_BBox_465_0_66_46_textureEnergy | Mouth_Inspiration_FN_LyapunovExponentMax |
| 30 | Nose Expiration_BBox_495_986_47_37_stdValue | MouthInspiration_Gap_378-565_StandardDeviation | Nose Inspiration_Average_BBoxes_Hf2_2 | Nose_Inspiration_FN_TP_Skewness | Nose Expiration_BBox_465_0_66_46_fractalDimension | Mouth_Expiration_FN_MFCCMedian_C3 |
| 31 | Mouth_Expiration_FNMidFlow_MFCCMedian_C1 | MouthInspiration_Gap_378-565_FM2MFreq1 | Nose Inspiration_Average_BBoxes_reserved2 | Nose_Expiration_FN_WaveletDetailSkewnessL2 | Nose Expiration_BBox_465_0_66_46_connectedComponents | Nose_Inspiration_FN_WaveletDetailEntropyL3 |
| 32 | Mouth_Expiration_FNMidFlow_PBP_Kurtosis | MouthInspiration_Gap_584-810_FM2MFreq1 | Nose Inspiration_Average_BBoxes_bisEntropy | Nose_Expiration_FN_CQTMeanPower | Nose Expiration_BBox_873_128_24_23_centroidY | Nose_Inspiration_FN_CQTGaborEnergyMean |
| 33 | Mouth_Expiration_FNMidFlow_TP_Histogram_1 | MouthInspiration_Gap_837-1499_FM2MFreq1 | Nose Inspiration_BBox_140_140_733_744_spectralFlux | Nose_Expiration_FN_CQTSkewnessPower | Nose Expiration_BBox_873_128_24_23_compactness | Nose_Inspiration_FN_MFCCMedian_C3 |
| 34 | Mouth_Expiration_FNMidFlow_TP_MaxProb | MouthExpiration_Gap_0-353_StandardDeviation | Nose Inspiration_BBox_140_140_733_744_connectedComponents | Nose_Expiration_FN_CQTSpectralDynamicsStd | Nose Expiration_BBox_841_162_21_21_energyValue | Average_Gap_306-496_Maximum |
| 35 | Mouth_Expiration_FNMidFlow_TP_Ratio1 | MouthExpiration_Gap_815-1435_StandardDeviation | Nose Inspiration_BBox_782_151_70_73_skewnessValue | Mouth_Inspiration_FNMidFlow_ZeroCrossing1 | Nose Expiration_BBox_787_244_15_15_frequencyCentroidX | Average_Gap_1282-1359_SCBW_Bandwidth |
References
- Rizzo, D.; Baltzan, M.; Sirpal, S.; Dosman, J.; Kaminska, M.; Chung, F. Prevalence and Regional Distribution of Obstructive Sleep Apnea in Canada: Analysis from the Canadian Longitudinal Study on Aging. Can. J. Public Health 2024, 115, 970–979. [Google Scholar] [CrossRef]
- Lechat, B.; Naik, G.; Reynolds, A.; Aishah, A.; Scott, H.; Loffler, K.A.; Vakulin, A.; Escourrou, P.; McEvoy, R.D.; Adams, R.J.; et al. Multinight Prevalence, Variability, and Diagnostic Misclassification of Obstructive Sleep Apnea. Am. J. Respir. Crit. Care Med. 2022, 205, 563–569. [Google Scholar] [CrossRef]
- Singh, M.; Liao, P.; Kobah, S.; Wijeysundera, D.N.; Shapiro, C.; Chung, F. Proportion of Surgical Patients with Undiagnosed Obstructive Sleep Apnoea. Br. J. Anaesth. 2013, 110, 629–636. [Google Scholar] [CrossRef] [PubMed]
- Espiritu, J.R.D. Health Consequences of Obstructive Sleep Apnea. In Management of Obstructive Sleep Apnea; Springer International Publishing: Cham, Switzerland, 2021; pp. 23–43. [Google Scholar]
- American Academy of Sleep Medicine. Hidden Health Crisis Costing America Billions: Underdiagnosing and Undertreating Obstructive Sleep Apnea Draining Healthcare System, 1st ed.; Frost & Sullivan: Darien, IL, USA, 2016. [Google Scholar]
- The Harvard Medical School Division of Sleep Medicine. The Price of Fatigue: The Surprising Economic Costs of Unmanaged Sleep Apnea; Harvard Medical School Division of Sleep Medicine Boston: Boston, MA, USA, 2010. [Google Scholar]
- Colten, H.R.; Altevogt, B.M. Sleep Disorders and Sleep Deprivation; National Academies Press: Washington, DC, USA, 2006; ISBN 978-0-309-10111-0. [Google Scholar]
- American Academy of Sleep Medicine. International Classification of Sleep Disorders: Diagnostic & Coding Manual, 2nd ed.; American Academy of Sleep Medicine: Westchester, IL, USA, 2005; ISBN 0965722023. [Google Scholar]
- Noda, A.; Yasuma, F.; Miyata, S.; Iwamoto, K.; Yasuda, Y.; Ozaki, N. Sleep Fragmentation and Risk of Automobile Accidents in Patients with Obstructive Sleep Apnea—Sleep Fragmentation and Automobile Accidents in OSA. Health 2019, 11, 171–181. [Google Scholar] [CrossRef]
- Young, T.; Finn, L.; Peppard, P.E.; Szklo-Coxe, M.; Austin, D.; Nieto, F.J.; Stubbs, R.; Hla, K.M. Sleep Disordered Breathing and Mortality: Eighteen-Year Follow-up of the Wisconsin Sleep Cohort. Sleep 2008, 31, 1071. [Google Scholar] [CrossRef]
- Yoshihisa, A.; Takeishi, Y. Sleep Disordered Breathing and Cardiovascular Diseases. J. Atheroscler. Thromb. 2019, 26, 315–327. [Google Scholar] [CrossRef]
- Berry, R.B.; Brooks, R.; Gamaldo, C.E.; Harding, S.M.; Marcus, C.; Vaughn, B.V. The AASM Manual for the Scoring of Sleep and Associated Events, Rules, Terminology and Technical Specifications; American Academy of Sleep Medicine: Darien, IL, USA, 2012; Volume 176. [Google Scholar]
- Kushida, C.A.; Littner, M.R.; Morgenthaler, T.; Alessi, C.A.; Bailey, D.; Coleman, J.; Friedman, L.; Hirshkowitz, M.; Kapen, S.; Kramer, M.; et al. Practice Parameters for the Indications for Polysomnography and Related Procedures: An Update for 2005. Sleep 2005, 28, 499–523. [Google Scholar] [CrossRef] [PubMed]
- Bradley, T.D.; Floras, J.S. Sleep Apnea: Implications in Cardiovascular and Cerebrovascular Disease, 2nd ed.; Bradley, T.D., Floras, J.S., Eds.; CRC Press: Boca Raton, FL, USA, 2013; ISBN 978-0-429-11867-8. [Google Scholar]
- Butt, M.; Dwivedi, G.; Khair, O.; Lip, G.Y.H. Obstructive Sleep Apnea and Cardiovascular Disease. Int. J. Cardiol. 2010, 139, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Pivetta, B.; Nagappa, M.; Saripella, A.; Islam, S.; Englesakis, M.; Chung, F. Validation of the STOP-Bang Questionnaire for Screening of Obstructive Sleep Apnea in the General Population and Commercial Drivers: A Systematic Review and Meta-Analysis. Sleep Breath. 2021, 25, 1741–1751. [Google Scholar] [CrossRef] [PubMed]
- Mazzotti, D.R.; Keenan, B.T.; Thorarinsdottir, E.H.; Gislason, T.; Pack, A.I.; Pack, A.I.; Schwab, R.; Maislin, G.; Keenan, B.T.; Jafari, N.; et al. Is the Epworth Sleepiness Scale Sufficient to Identify the Excessively Sleepy Subtype of OSA? Chest 2022, 161, 557–561. [Google Scholar] [CrossRef]
- Yadollahi, A.; Moussavi, Z. Acoustic Obstructive Sleep Apnea Detection. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 7110–7113. [Google Scholar]
- Elwali, A.; Moussavi, Z. A Novel Decision Making Procedure during Wakefulness for Screening Obstructive Sleep Apnea Using Anthropometric Information and Tracheal Breathing Sounds. Sci. Rep. 2019, 9, 11467. [Google Scholar] [CrossRef] [PubMed]
- Elwali, A.; Moussavi, Z. Obstructive Sleep Apnea Screening and Airway Structure Characterization During Wakefulness Using Tracheal Breathing Sounds. Ann. Biomed. Eng. 2017, 45, 839–850. [Google Scholar] [CrossRef]
- Montazeri, A.; Giannouli, E.; Moussavi, Z. Assessment of Obstructive Sleep Apnea and Its Severity during Wakefulness. Ann. Biomed. Eng. 2012, 40, 916–924. [Google Scholar] [CrossRef]
- Hajipour, F.; Jozani, M.J.; Moussavi, Z. A Comparison of Regularized Logistic Regression and Random Forest Machine Learning Models for Daytime Diagnosis of Obstructive Sleep Apnea. Med. Biol. Eng. Comput. 2020, 58, 2517–2529. [Google Scholar] [CrossRef] [PubMed]
- Hajipour, F.; Jozani, M.J.; Elwali, A.; Moussavi, Z. Regularized Logistic Regression for Obstructive Sleep Apnea Screening during Wakefulness Using Daytime Tracheal Breathing Sounds and Anthropometric Information. Med. Biol. Eng. Comput. 2019, 57, 2641–2655. [Google Scholar] [CrossRef]
- Simply, R.M.; Dafna, E.; Zigel, Y. Diagnosis of Obstructive Sleep Apnea Using Speech Signals From Awake Subjects. IEEE J. Sel. Top. Signal Process. 2020, 14, 251–260. [Google Scholar] [CrossRef]
- Sola-Soler, J.; Fiz, J.A.; Torres, A.; Jane, R. Identification of Obstructive Sleep Apnea Patients from Tracheal Breath Sound Analysis during Wakefulness in Polysomnographic Studies. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4232–4235. [Google Scholar]
- Alqudah, A.M.; Elwali, A.; Kupiak, B.; Hajipour, F.; Jacobson, N.; Moussavi, Z. Obstructive Sleep Apnea Detection during Wakefulness: A Comprehensive Methodological Review. Med. Biol. Eng. Comput. 2024, 62, 1277–1311. [Google Scholar] [CrossRef]
- Tregear, S.; Reston, J.; Schoelles, K.; Phillips, B. Obstructive Sleep Apnea and Risk of Motor Vehicle Crash: Systematic Review and Meta-Analysis. J. Clin. Sleep. Med. 2009, 5, 573. [Google Scholar] [CrossRef] [PubMed]
- Hajipour, F.; Moussavi, Z. Spectral and Higher Order Statistical Characteristics of Expiratory Tracheal Breathing Sounds During Wakefulness and Sleep in People with Different Levels of Obstructive Sleep Apnea. J. Med. Biol. Eng. 2019, 39, 244–250. [Google Scholar] [CrossRef]
- Elwali, A.; Moussavi, Z. Predicting Polysomnography Parameters from Anthropometric Features and Breathing Sounds Recorded during Wakefulness. Diagnostics 2021, 11, 905. [Google Scholar] [CrossRef] [PubMed]
- Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing Value Estimation Methods for DNA Microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef] [PubMed]
- Batista, G.E.A.P.A.; Monard, M.C. An Analysis of Four Missing Data Treatment Methods for Supervised Learning. Appl. Artif. Intell. 2003, 17, 519–533. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: Boca Raton, FL, USA, 1994; ISBN 9780429246593. [Google Scholar]
- Rangayyan, R.M.; Reddy, N.P. Biomedical Signal Analysis: A Case-Study Approach; Pergamon Press: New York, NY, USA, 2002; Volume 30. [Google Scholar]
- Mendel, J.M. Tutorial on Higher-Order Statistics (Spectra) in Signal Processing and System Theory: Theoretical Results and Some Applications. Proc. IEEE 1991, 79, 278–305. [Google Scholar] [CrossRef]
- Astfalck, L.C.; Sykulski, A.M.; Cripps, E.J. Debiasing Welch’s Method for Spectral Density Estimation. Biometrika 2023, 111, 1313–1329. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, D.; Kuang, Y.; Mo, X. A Bicoherence-Based Nonlinearity Measurement Method for Identifying the Quadratic Phase Coupling of Nonlinear Systems. Int. J. Non Linear Mech. 2021, 131, 103–109. [Google Scholar]
- Dlask, M.; Kukal, J. Hurst Exponent Estimation from Short Time Series. Signal Image Video Process. 2019, 13, 263–269. [Google Scholar] [CrossRef]
- Farrús, M.; Hernando, J.; Ejarque, P. Jitter and Shimmer Measurements for Speaker Recognition. In Proceedings of the Interspeech 2007, Antwerp, Belgium, 27–31 August 2007; ISCA: Singapore, 2007; pp. 778–781. [Google Scholar]
- Jotz, G.P.; Cervantes, O.; Abrahão, M.; Settanni, F.A.P.; de Angelis, E.C. Noise-to-Harmonics Ratio as an Acoustic Measure of Voice Disorders in Boys. J. Voice 2002, 16, 28–31. [Google Scholar] [CrossRef]
- Gosala, B.; Kapgate, P.D.; Jain, P.; Chaurasia, R.N.; Gupta, M. Wavelet transforms for feature engineering in EEG data processing: An application on Schizophrenia. Biomed. Signal Process. Control. 2023, 85, 104811. [Google Scholar] [CrossRef]
- Abdul, Z.K.; Al-Talabani, A.K. Mel Frequency Cepstral Coefficient and Its Applications: A Review. IEEE Access 2022, 10, 122136–122158. [Google Scholar] [CrossRef]
- Wang, J.-C.; Wang, J.-F.; Weng, Y.-S. Chip design of MFCC extraction for speech recognition. Integration 2002, 32, 111–131. [Google Scholar] [CrossRef]
- Kohlrausch, A. Binaural Masking Experiments Using Noise Maskers with Frequency-Dependent Interaural Phase Differences. II: Influence of Frequency and Interaural-Phase Uncertainty. J. Acoust. Soc. Am. 1990, 88, 1749–1756. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets. Phys. D 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Zhao, K.; Wen, H.; Guo, Y.; Scano, A.; Zhang, Z. Feasibility of Recurrence Quantification Analysis (RQA) in Quantifying Dynamical Coordination among Muscles. Biomed. Signal Process. Control 2023, 79, 104042. [Google Scholar] [CrossRef]
- Borowska, M. Entropy-Based Algorithms in the Analysis of Biomedical Signals. In Studies in Logic, Grammar and Rhetoric; University of Bialystok: Bialystok, Poland, 2015; Volume 43, pp. 21–32. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Divya, S.; Suresh, L.P.; John, A. Image Feature Generation Using Binary Patterns—LBP, SLBP and GBP. In ICT Analysis and Applications; Springer: Singapore, 2022; pp. 233–239. [Google Scholar]
- Selesnick, I.W. Wavelet Transform with Tunable Q-Factor. IEEE Trans. Signal Process. 2011, 59, 3560–3575. [Google Scholar] [CrossRef]
- Márton, L.F.; Brassai, S.T.; Bakó, L.; Losonczi, L. Detrended fluctuation analysis of EEG signals. Procedia Technol. 2014, 12, 125–132. [Google Scholar] [CrossRef]
- Vergara, J.R.; Estévez, P.A. A Review of Feature Selection Methods Based on Mutual Information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, H. Feature Selection Based on Mutual Information with Correlation Coefficient. Appl. Intell. 2022, 52, 1169–1180. [Google Scholar] [CrossRef]
- Liu, S.; Motani, M. Improving Mutual Information Based Feature Selection by Boosting Unique Relevance. arXiv 2022, arXiv:2212.06143. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Feature Wise Normalization: An Effective Way of Normalizing Data. Pattern Recognit. 2022, 122, 108307. [Google Scholar] [CrossRef]
- Haury, A.-C.; Gestraud, P.; Vert, J.-P. The Influence of Feature Selection Methods on Accuracy, Stability and Interpretability of Molecular Signatures. PLoS ONE 2011, 6, e28210. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, H.; Liu, R.; Lv, W.; Wang, D. t-Test Feature Selection Approach Based on Term Frequency for Text Categorization. Pattern Recognit. Lett. 2014, 45, 1–10. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Wang, H.; Liang, Q.; Hancock, J.T. Feature Selection Strategies: A Comparative Analysis of SHAP-Value and Importance-Based Methods. J. Big Data 2024, 11, 44. [Google Scholar] [CrossRef]
- Seiffert, C.; Khoshgoftaar, T.M.; Van Hulse, J.; Napolitano, A. RUSBoost: A Hybrid Approach to Alleviating Class Imbalance. IEEE Trans. Syst. Man Cybern. Part. A Syst. Hum. 2010, 40, 185–197. [Google Scholar] [CrossRef]
- Mounce, S.R.; Ellis, K.; Edwards, J.M.; Speight, V.L.; Jakomis, N.; Boxall, J.B. Ensemble Decision Tree Models Using RUSBoost for Estimating Risk of Iron Failure in Drinking Water Distribution Systems. Water Resour. Manag. 2017, 31, 925–942. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked Generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Wang, M.; Qian, Y.; Yang, Y.; Chen, H.; Rao, W.-F. Improved Stacking Ensemble Learning Based on Feature Selection to Accurately Predict Warfarin Dose. Front. Cardiovasc. Med. 2024, 10, 1320938. [Google Scholar] [CrossRef] [PubMed]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef] [PubMed]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Pereira, F., Burges, C.J., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; Volume 25. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Büchlmann, P.; Yu, B. Analyzing Bagging. Ann. Stat. 2002, 30, 927–961. [Google Scholar] [CrossRef]
- Kwon, Y.; Zou, J. Data-OOB: Out-of-Bag Estimate as a Simple and Efficient Data Value. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; Krause, A., Brunskill, E., Cho, K., Engelhardt, B., Sabato, S., Scarlett, J., Eds.; PMLR: Cambridge, MA, USA, 2023; Volume 202, pp. 18135–18152. [Google Scholar]
- Klevak, E.; Lin, S.; Martin, A.; Linda, O.; Ringger, E. Out-Of-Bag Anomaly Detection. arXiv 2020, arXiv:2009.09358. [Google Scholar] [CrossRef]
- Japkowicz, N.; Stephen, S. The Class Imbalance Problem: A Systematic Study. Intell. Data Anal. 2002, 6, 429–449. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Varma, S.; Simon, R. Bias in Error Estimation When Using Cross-Validation for Model Selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. On Over-Fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence—Volume 2; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; pp. 1137–1143. [Google Scholar]
- Dietterich, T.G. Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms. Neural Comput. 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [PubMed]
- Alqudah, A.M.; Moussavi, Z. A Review of Deep Learning for Biomedical Signals: Current Applications, Advancements, Future Prospects, Interpretation, and Challenges. Comput. Mater. Contin. 2025, 83, 3753–3841. [Google Scholar] [CrossRef]
- Finkelstein, Y.; Wolf, L.; Nachmani, A.; Lipowezky, U.; Rub, M.; Shemer, S.; Berger, G. Velopharyngeal Anatomy in Patients With Obstructive Sleep Apnea Versus Normal Subjects. J. Oral Maxillofac. Surg. 2014, 72, 1350–1372. [Google Scholar] [CrossRef] [PubMed]
- Goldshtein, E.; Tarasiuk, A.; Zigel, Y. Automatic Detection of Obstructive Sleep Apnea Using Speech Signals. IEEE Trans. Biomed. Eng. 2011, 58, 1373–1382. [Google Scholar] [CrossRef] [PubMed]
- Qi, F.; Li, C.; Wang, S.; Zhang, H.; Wang, J.; Lu, G. Contact-Free Detection of Obstructive Sleep Apnea Based on Wavelet Information Entropy Spectrum Using Bio-Radar. Entropy 2016, 18, 306. [Google Scholar] [CrossRef]
- Shams, E.; Karimi, D.; Moussavi, Z. Bispectral Analysis of Tracheal Breath Sounds for Obstructive Sleep Apnea. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 37–40. [Google Scholar]
- Gramegna, A.; Giudici, P. Shapley Feature Selection. FinTech 2022, 1, 72–80. [Google Scholar] [CrossRef]



| Group | Num. of Subjects | AHI | AGE | Sex | BMI | MPS | NC |
|---|---|---|---|---|---|---|---|
| Non-OSA | 74 | 1.2 ± 1.3 | 46.8 ± 12.9 | 29 M, 45 F | 30.6 ± 6.2 | 41 (1), 19 (2), 6 (3), 8 (4) | 38.8 ± 4.0 |
| Mild | 35 | 8.7 ± 2.6 | 52.3 ± 11.6 | 21 M, 14 F | 34.3 ± 8.4 | 18 (1), 6 (2), 9 (3), 1 (4) | 42.1 ± 6.5 |
| Moderate | 50 | 21.5 ± 4.2 | 54.7 ± 11.3 | 36 M, 14 F | 33.8 ± 6.4 | 17 (1), 17 (2), 8 (3), 8 (4) | 43.1 ± 3.4 |
| Severe | 40 | 69.5 ± 33.3 | 48.9 ± 11.1 | 30 M, 10 F | 39.7 ± 8.7 | 5 (1), 13 (2), 14 (3), 8 (4) | 45.3 ± 3.6 |
| Group | Num. of Subjects | AHI | AGE | Sex | BMI | MPS | NC |
|---|---|---|---|---|---|---|---|
| Non-OSA | 63 | 1.2 ± 1.2 | 46.8 ± 13.5 | 24 M, 39 F | 30.6 ± 6.6 | 36 (1), 17 (2), 5 (3), 5 (4) | 39.0 ± 3.5 |
| Mild | 30 | 8.8 ± 2.6 | 50.9 ± 10.4 | 17 M, 13 F | 34.1 ± 8.2 | 14 (1), 7 (2), 8 (3), 0 (4) | 41.5 ± 7.0 |
| Moderate | 42 | 22.0 ± 4.3 | 53.7 ± 10.3 | 31 M, 11 F | 33.7 ± 6.8 | 11 (1), 15 (2), 8 (3), 8 (4) | 433 ± 3.3 |
| Severe | 34 | 68.5 ± 32.5 | 50.9 ± 11.1 | 24 M, 10 F | 39.9 ± 9.3 | 4 (1), 11 (2), 13 (3), 6 (4) | 45. ± 3.4 |
| Group | Num. of Subjects | AHI | AGE | Sex | BMI | MPS | NC |
|---|---|---|---|---|---|---|---|
| Non-OSA | 11 | 0.9 ± 1.0 | 45.4 ± 10.7 | 6 M, 5 F | 30.6 ± 3.8 | 6 (1), 3 (2), 1 (3), 1 (4) | 40.1 ± 4.5 |
| Mild | 5 | 6.7 ± 1.7 | 52.4 ± 12.6 | 3 M, 2 F | 30.3 ± 10.2 | 3 (1), 1 (2), 1 (3), 0 (4) | 41.9 ± 1.5 |
| Moderate | 8 | 20.7 ± 4.5 | 58.5 ± 7.3 | 4 M, 4 F | 33.7 ± 6.2 | 4 (1), 3 (2), 1 (3), 0 (4) | 41.5 ± 4.0 |
| Severe | 6 | 80.0 ± 35.1 | 46.4 ± 11.3 | 4 M, 2 F | 44.4 ± 6.2 | 1 (1), 2 (2), 1 (3), 2 (4) | 44.0 ± 3.7 |
| Group | Folds | Num. of Subjects | AHI | AGE | Sex | BMI | MPS | NC |
|---|---|---|---|---|---|---|---|---|
| Non-OSA | 1 | 23 | 0.6 ± 0.8 | 44.9 ± 12.1 | 10 M, 13 F | 29.2 ± 4.7 | 12 (1), 7 (2), 1 (3), 3 (4) | 38.0 ± 4.7 |
| 2 | 27 | 1.1 ± 1.3 | 45.7 ± 12.1 | 10 M, 17 F | 32.3 ± 7.6 | 12 (1), 9 (2), 4 (3), 2 (4) | 39.2 ± 4.3 | |
| 3 | 24 | 1.8 ± 1.3 | 50.0 ± 14.3 | 9 M, 15 F | 30.0 ± 5.8 | 17 (1), 3 (2), 1 (3), 3 (4) | 39.0 ± 2.9 | |
| Mild | 1 | 16 | 8.7 ± 2.4 | 50.9 ± 12.5 | 10 M, 6 F | 36.6 ± 9.9 | 7 (1), 1 (2), 7 (3), 1 (4) | 43.5 ± 5.3 |
| 2 | 10 | 8.6 ± 2.2 | 51.3 ± 11.6 | 5 M, 5 F | 31.8 ± 8.4 | 6 (1), 1 (2), 2 (3), 1 (4) | 38.5 ± 8.8 | |
| 3 | 9 | 8.8 ± 3.5 | 56.0 ± 10.3 | 6 M, 3 F | 33.0 ± 4.2 | 5 (1), 4 (2) | 43.4 ± 2.7 | |
| Moderate | 1 | 16 | 19.9 ± 2.9 | 56.3 ± 10.8 | 10 M, 6 F | 34.6 ± 7.8 | 4 (1), 6 (2), 2 (3), 4 (4) | 42.3 ± 4.0 |
| 2 | 18 | 22.8 ± 4.5 | 53.6 ± 9.7 | 13 M, 5 F | 31.8 ± 5.7 | 8 (1), 5 (2), 3 (3), 2 (4) | 42.7 ± 3.8 | |
| 3 | 16 | 21.6 ± 4.7 | 54.5 ± 13.9 | 13 M, 3 F | 35.2 ± 5.2 | 5 (1), 6 (2), 3 (3), 2 (4) | 43.6 ± 2.8 | |
| Severe | 1 | 14 | 72.9 ± 35.0 | 45.5 ± 10.5 | 11 M, 3 F | 39.1 ± 10.1 | 2 (1), 3 (2), 5 (3), 4 (4) | 44.3 ± 4.2 |
| 2 | 16 | 66.6 ± 29.6 | 50.2 ± 11.0 | 13 M, 3 F | 40.1 ± 8.5 | 1 (1), 6 (2), 5 (3), 4 (4) | 46.6 ± 3.2 | |
| 3 | 10 | 69.6 ± 39.1 | 51.9 ± 12.2 | 6 M, 4 F | 40.2 ± 7.5 | 2 (1), 4 (2), 4 (3) | 43.8 ± 3.5 |
| Experiment | Classifier | OOB Accuracy | OOB Sensitivity | OOB Specificity |
|---|---|---|---|---|
| 1 | Random Forests | 83.9 | 94.1 | 81.6 |
| 2 | SVM Poly 5 | 86.7 | 86.8 | 86.6 |
| 3 | SVM Poly 3 | 88.7 | 87.1 | 89.4 |
| 4 | SVM Poly 7 | 81.9 | 82.2 | 81.5 |
| 5 | Subspace KNN | 75.0 | 72.5 | 79.2 |
| 6 | LDA | 80.3 | 77.1 | 82.9 |
| Experiment | Classifier | Test Accuracy | Test Sensitivity | Test Specificity |
|---|---|---|---|---|
| 1 | Random Forests | 81.2 | 100 | 78.6 |
| 2 | SVM Poly 5 | 78.9 | 83.3 | 76.9 |
| 3 | SVM Poly 3 | 88.2 | 83.3 | 90.9 |
| 4 | SVM Poly 7 | 76.9 | 72.7 | 100 |
| 5 | Subspace KNN | 81.8 | 83.3 | 80.0 |
| 6 | LDA | 78.6 | 71.4 | 85.7 |
| Experiment | Fold | Classifier | OOB Accuracy | OOB Sensitivity | OOB Specificity |
|---|---|---|---|---|---|
| 1 | 1 | Logistic | 85.7 | 79.9 | 94.0 |
| 2 | Decision Trees | 86.1 | 79.7 | 95.7 | |
| 3 | Deep Neural Net | 85.5 | 72.8 | 94.0 | |
| 2 | 1 | Random Forest | 84.7 | 92.2 | 73.5 |
| 2 | SVM RBF | 84.8 | 89.4 | 78.1 | |
| 3 | Shallow Neural Net | 88.1 | 92.0 | 82.4 | |
| 3 | 1 | SVM Poly 9 | 83.1 | 77.1 | 92.2 |
| 2 | SVM Poly 3 | 98.6 | 97.9 | 100.0 | |
| 3 | Gradient Boosting | 93.8 | 94.0 | 93.3 | |
| 4 | 1 | Ensemble Model | 81.1 | 88.2 | 70.5 |
| 2 | RUSBoost | 91.2 | 88.0 | 93.8 | |
| 3 | Logistic | 83.3 | 76.9 | 88.2 | |
| 5 | 1 | Decision Trees | 80.0 | 78.9 | 80.8 |
| 2 | Deep Neural Net | 85.7 | 88.0 | 83.3 | |
| 3 | Random Forest | 82.1 | 84.6 | 80.0 | |
| 6 | 1 | SVM RBF | 78.3 | 82.4 | 73.1 |
| 2 | Shallow Neural Net | 81.1 | 83.8 | 77.1 | |
| 3 | SVM Poly 9 | 82.8 | 85.3 | 80.0 |
| Experiment | Fold | Classifier | Test Accuracy | Test Sensitivity | Test Specificity |
|---|---|---|---|---|---|
| 1 | 1 | Logistic | 82.1 | 84.6 | 78.3 |
| 2 | Decision Trees | 77.1 | 77.0 | 77.2 | |
| 3 | Deep Neural Net | 77.8 | 79.6 | 75.0 | |
| 2 | 1 | Random Forest | 82.1 | 87.0 | 75.0 |
| 2 | SVM RBF | 77.8 | 81.5 | 72.2 | |
| 3 | Shallow Neural Net | 84.6 | 88.2 | 79.2 | |
| 3 | 1 | SVM Poly 9 | 81.9 | 85.7 | 79.4 |
| 2 | SVM Poly 3 | 72.1 | 70.4 | 75.0 | |
| 3 | Gradient Boosting | 73.5 | 75.0 | 70.0 | |
| 4 | 1 | Ensemble Model | 76.4 | 78.6 | 75.0 |
| 2 | RUSBoost | 87.4 | 81.8 | 91.2 | |
| 3 | Logistic | 73.5 | 70.7 | 77.8 | |
| 5 | 1 | Decision Trees | 76.7 | 75.1 | 79.0 |
| 2 | Deep Neural Net | 84.6 | 90.0 | 81.3 | |
| 3 | Random Forest | 73.7 | 71.2 | 71.2 | |
| 6 | 1 | SVM RBF | 72.7 | 71.4 | 74.7 |
| 2 | Shallow Neural Net | 73.5 | 74.4 | 72.2 | |
| 3 | SVM Poly 9 | 71.9 | 72.2 | 71.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqudah, A.M.; Moussavi, Z. Assessing Obstructive Sleep Apnea Severity During Wakefulness via Tracheal Breathing Sound Analysis. Sensors 2025, 25, 6280. https://doi.org/10.3390/s25206280
Alqudah AM, Moussavi Z. Assessing Obstructive Sleep Apnea Severity During Wakefulness via Tracheal Breathing Sound Analysis. Sensors. 2025; 25(20):6280. https://doi.org/10.3390/s25206280
Chicago/Turabian StyleAlqudah, Ali Mohammad, and Zahra Moussavi. 2025. "Assessing Obstructive Sleep Apnea Severity During Wakefulness via Tracheal Breathing Sound Analysis" Sensors 25, no. 20: 6280. https://doi.org/10.3390/s25206280
APA StyleAlqudah, A. M., & Moussavi, Z. (2025). Assessing Obstructive Sleep Apnea Severity During Wakefulness via Tracheal Breathing Sound Analysis. Sensors, 25(20), 6280. https://doi.org/10.3390/s25206280







