Distributed Phased-Array Radar Mainlobe Interference Suppression and Cooperative Localization Based on CEEMDAN–WOBSS
Abstract
1. Introduction
- (1)
- To address the failure of traditional empirical mode decomposition (EMD) due to the nonstationary nature of PA radar-received signals, we propose a noise-adaptive complete ensemble empirical mode decomposition method combined with an improved wavelet-based signal preprocessing approach, thereby enabling modal decomposition for PA radar echoes.
- (2)
- For low-SNR scenarios, we introduce a CEEMDAN combined with wavelet-optimized maximum-SNR blind source separation (CEEMDAN–WOBSS) joint processing method, which enhances the separation performance of PA radar-received signals and strengthens interference suppression capabilities under low SNRs.
- (3)
- In order to address the cooperative localization problem in distributed radar networks under low-SNR conditions, a signal–data dual-domain cooperative antijamming and localization (SDCAL) framework is constructed to integrate signal-level interference suppression with data-level collaborative positioning, thereby achieving accurate target spatial localization.
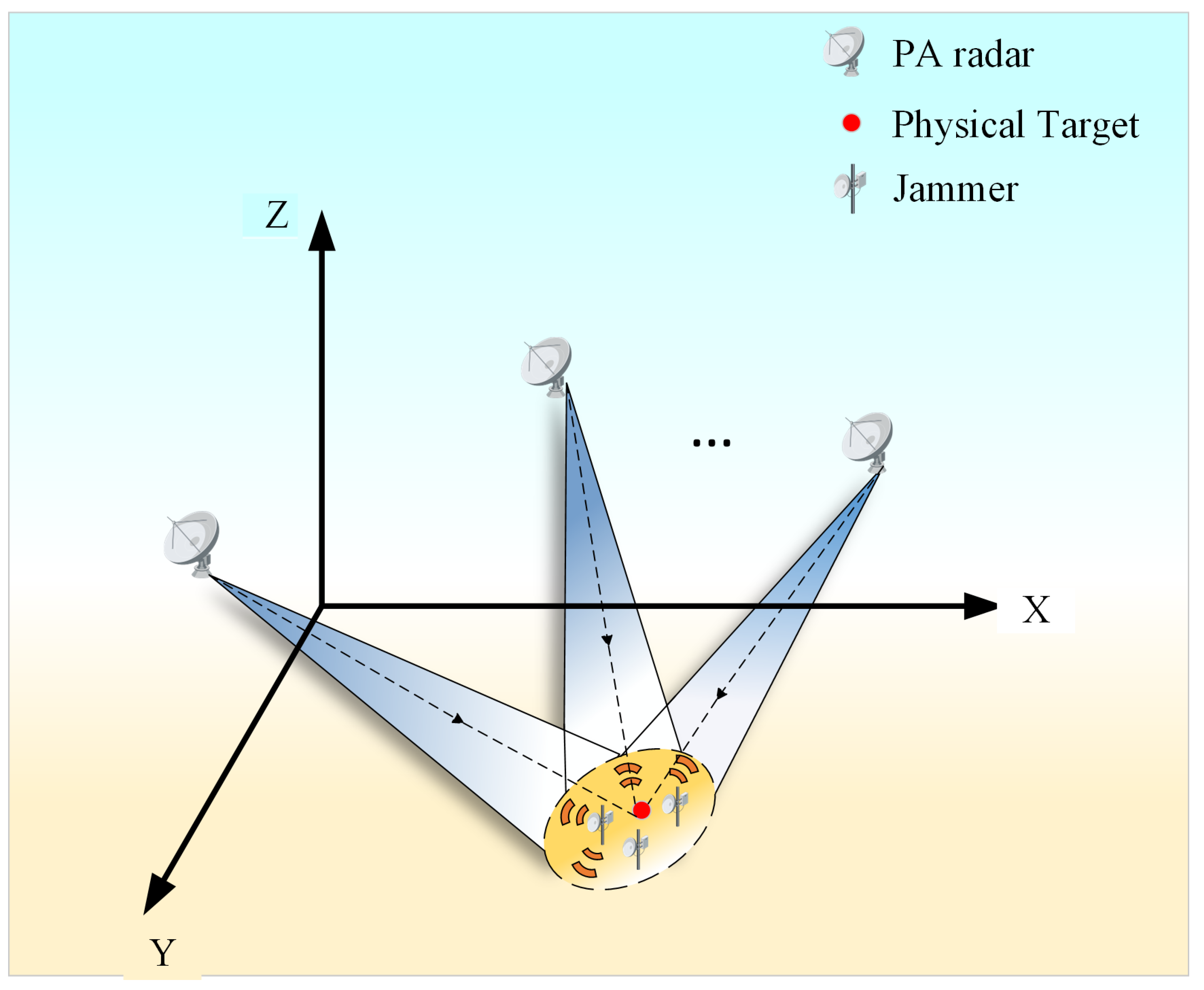
2. Radar Signal Model
3. Signal-Domain Antijamming for Distributed Radar
3.1. Algorithm Flow
- Perform mean-subtraction processing on the PA radar reception signals from each node in the distributed radar system to eliminate DC components, followed by pre-whitening processing to decorrelate the components of the reception signals.
- Apply joint CEEMDAN-WOBSS processing to the echo signals received by the PA radar, then calculate the separation matrix based on the maximum signal-to-noise ratio criterion and perform blind source separation on the whitened signals.
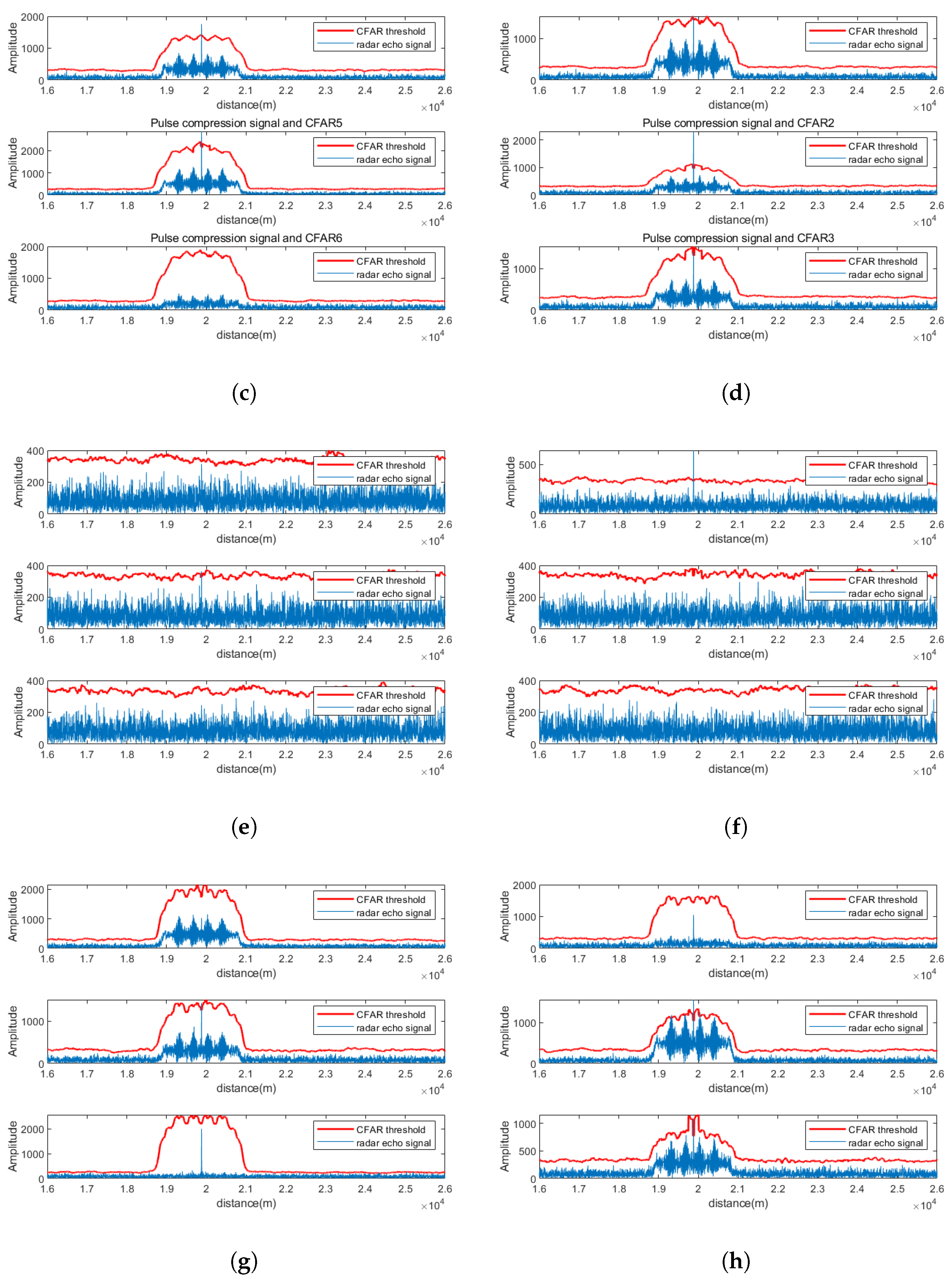
- CFAR detection is performed on all channel signals after pulse compression, and the detected signal channels are superimposed to obtain the radial distance of the target. Finally, the spatial position of the target is jointly calculated using the radial distances of the target from two or three PA radars in the distributed radar network.
3.2. PA Radar-Received Signal Preprocessing
- is the received-signal matrix, , and D denotes the number of fast-time samples;
- is the source-signal matrix containing all target-echo and jammer signals impinging on the S array elements;
- is the mixing matrix for the mth radar;
- is the complex Gaussian white-noise matrix with zero mean and covariance .
3.3. Signal Separation and Interference Suppression
4. Target Detection and Cooperative Localization
4.1. Cooperative Localization
4.2. Downgrade Strategy
| Algorithm 1: Signal–data cooperative antijamming and localization (SDCAL) |
 |
5. Simulation Results
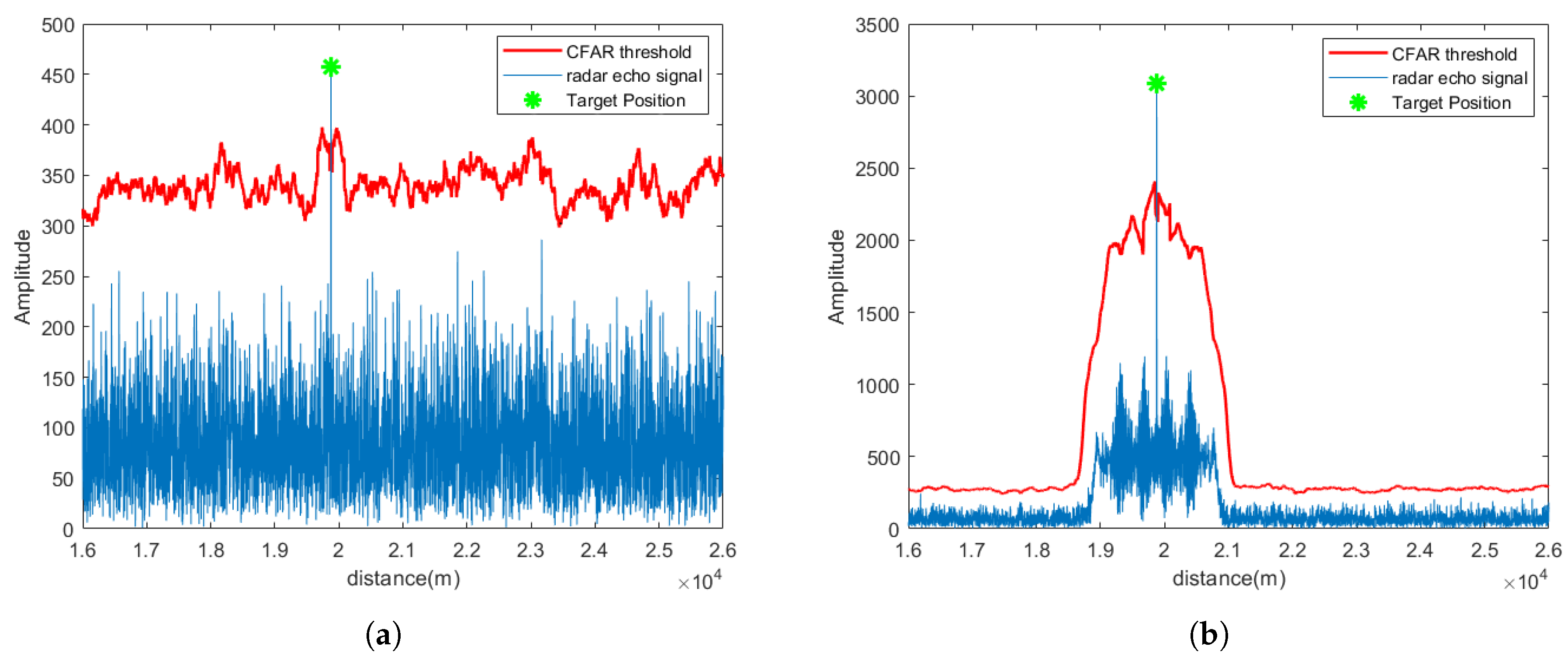
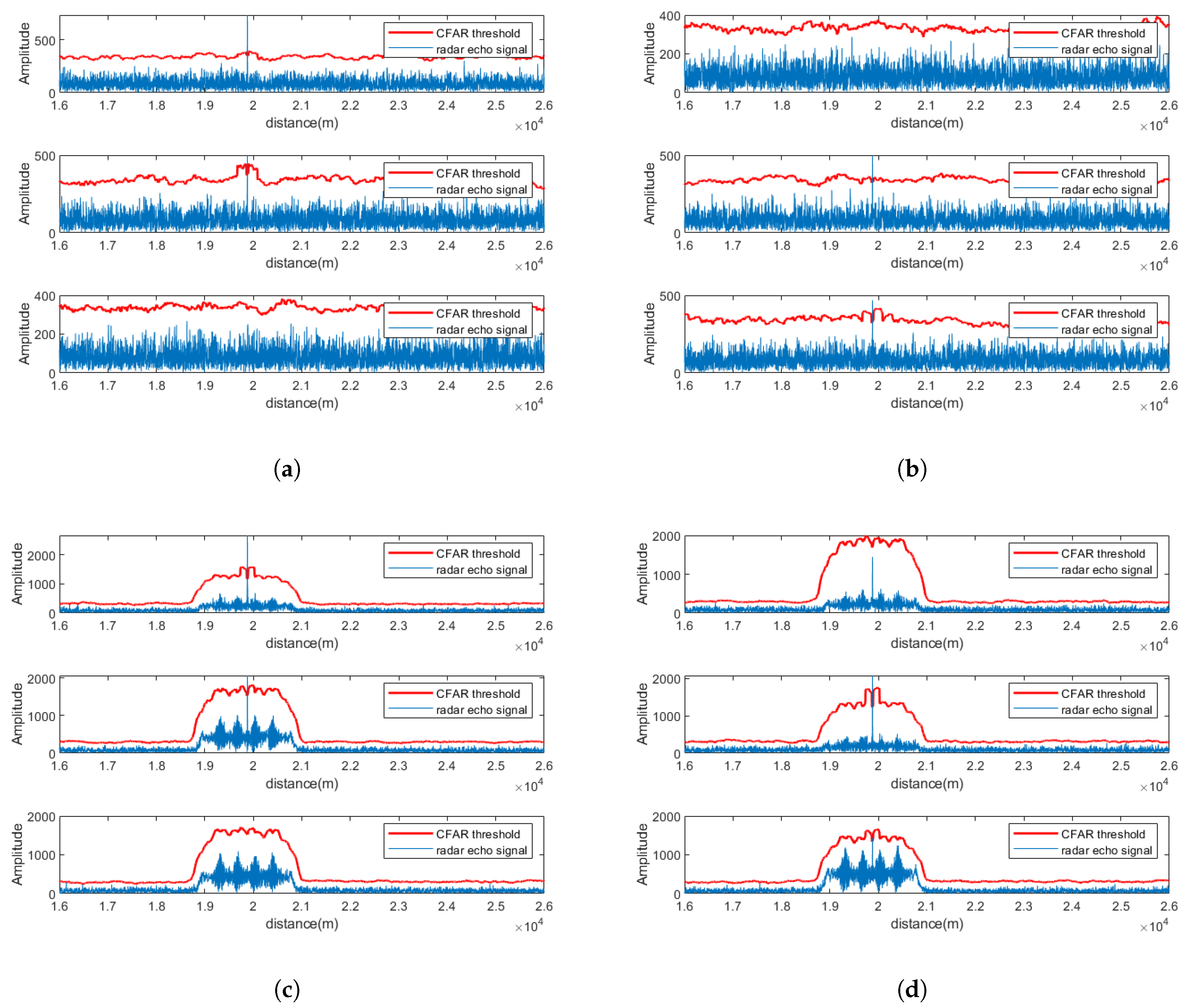
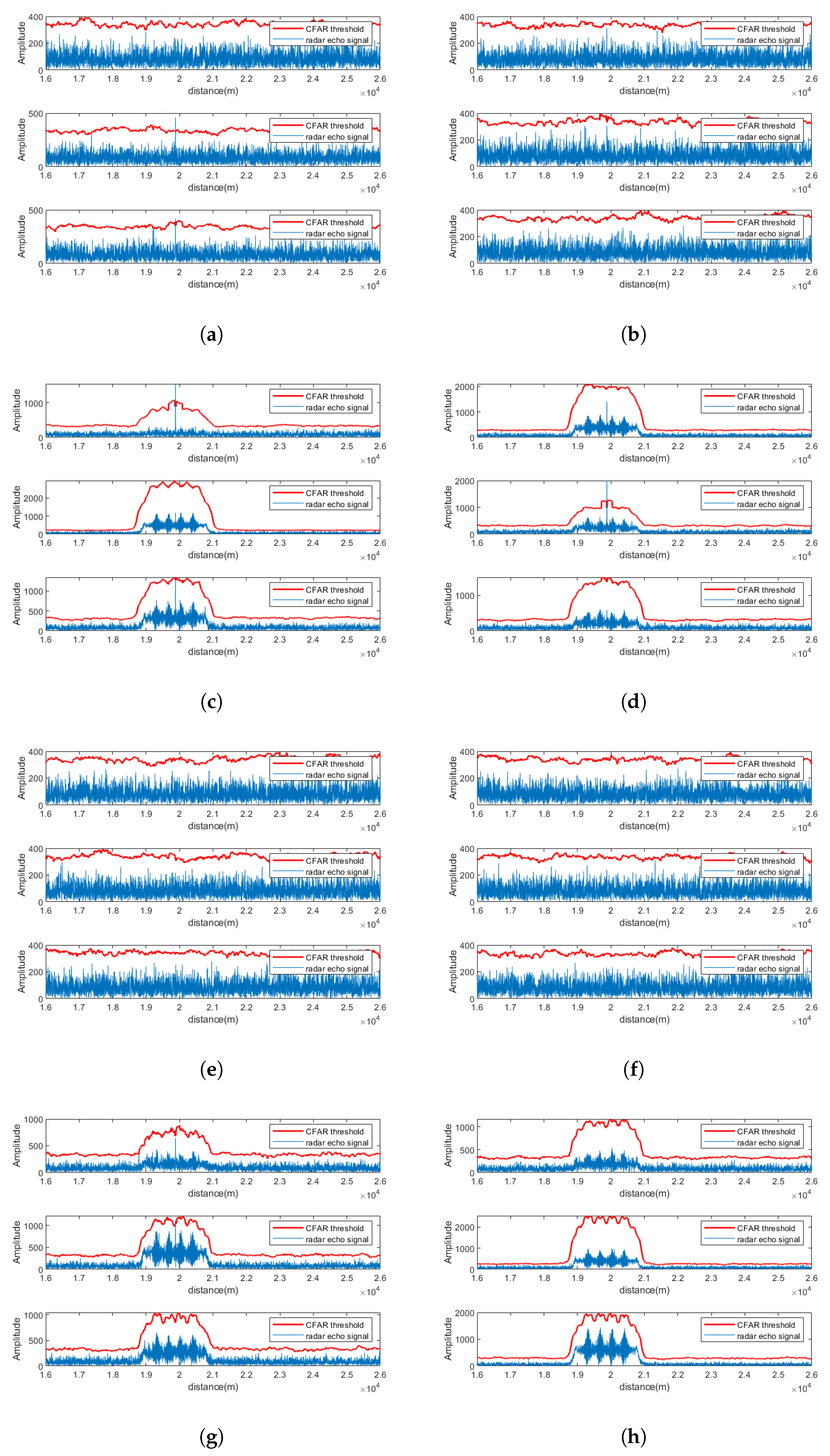
5.1. Signal Separation Performance at SNR = −5 dB
5.2. Signal Separation Performance at SNR = 0 dB
5.3. Signal Separation Performance at SNR = 5 dB
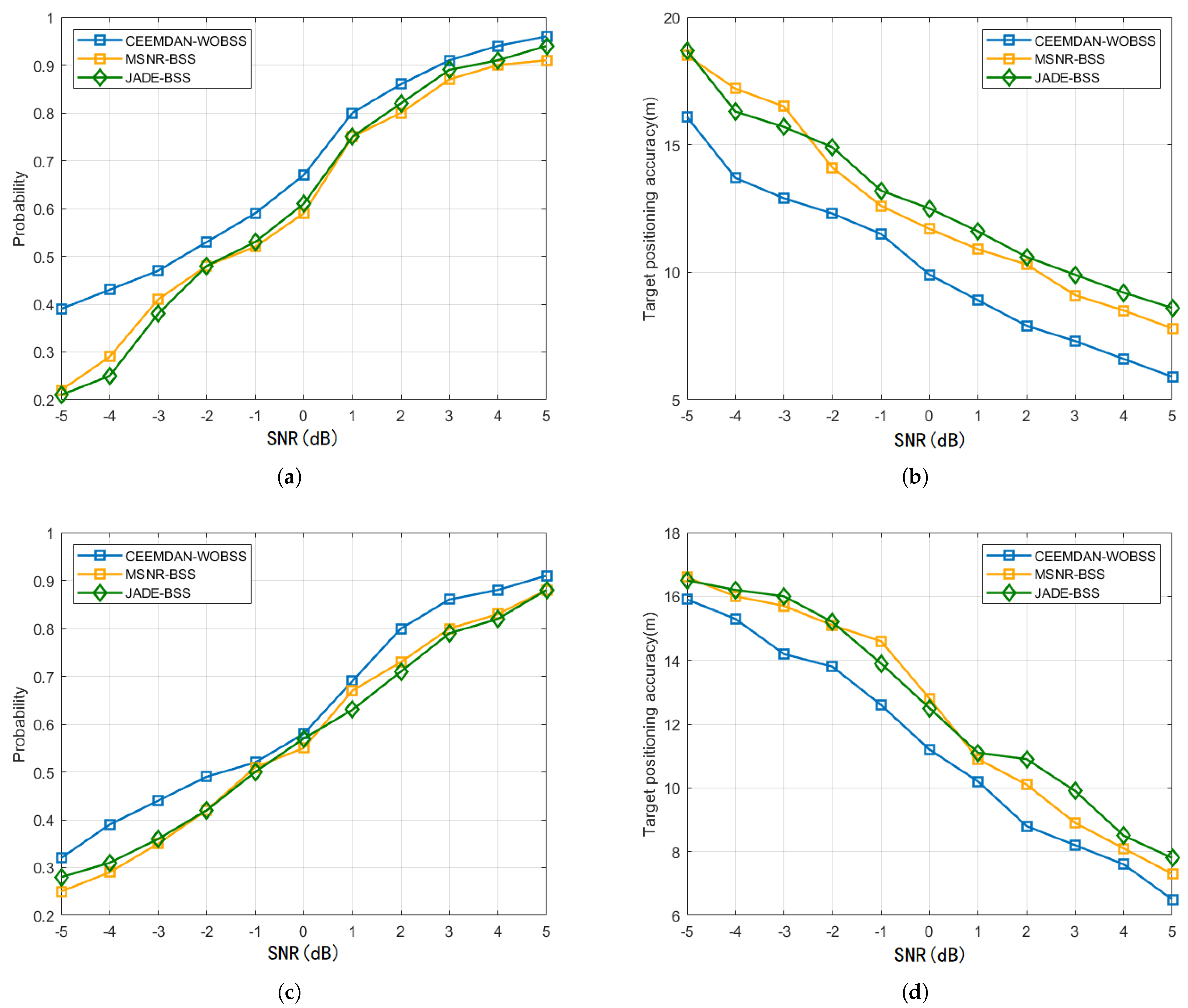
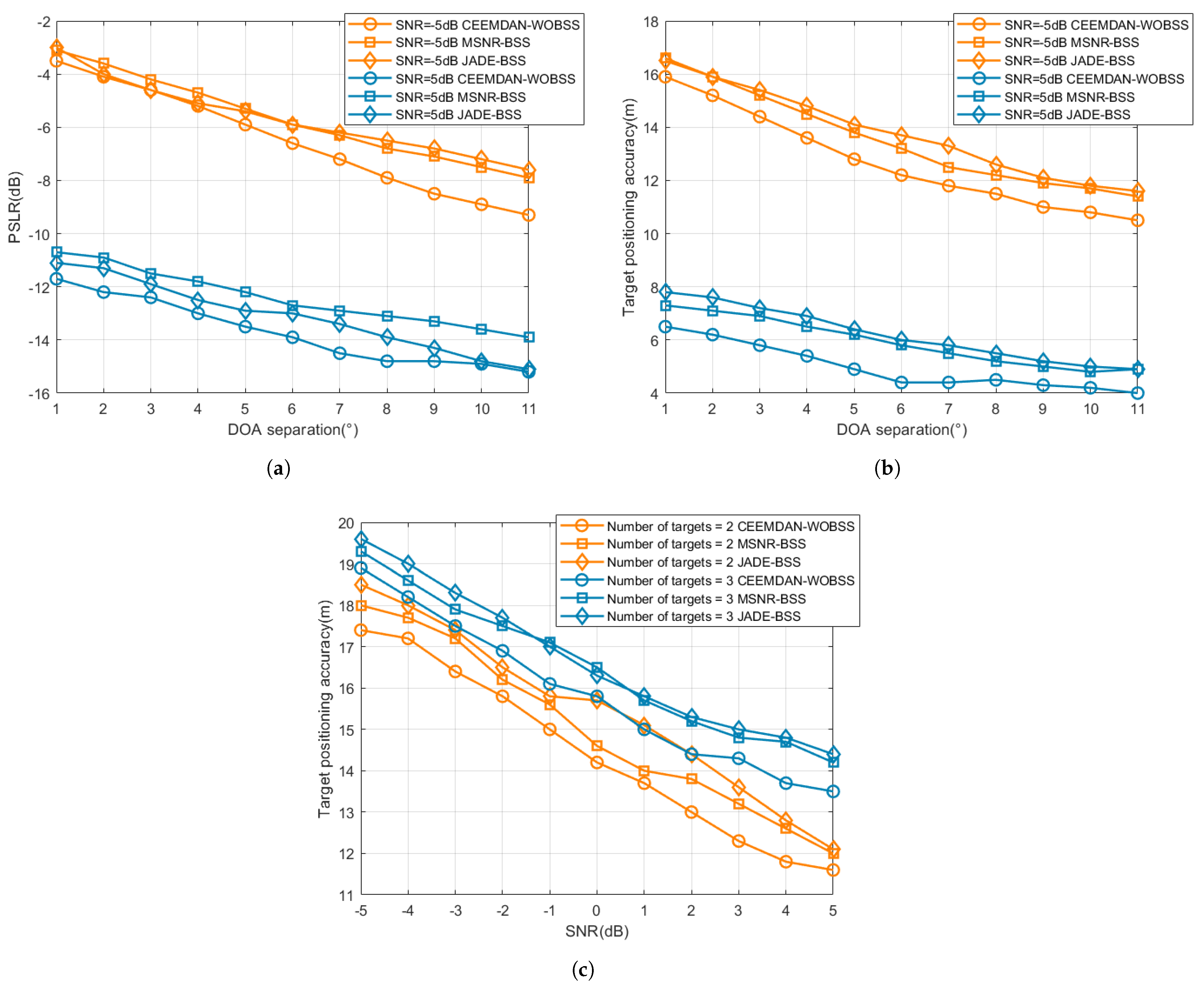
5.4. Quantitative Evaluation of Effectiveness
- Peak side-lobe ratio (PSLR): The PSLR is defined aswhere SLP is the peak amplitude of the side lobe and MLP is that of the main lobe. The average PSLR across N Monte Carlo trials is given bywhere denotes the expectation operator.
- Target Detection Probability, defined aswhere is the number of successful detections and is the total number of Monte Carlo simulations.
- Localization Accuracy, measured by the 3D Euclidean distance between the estimated and true target positions:The average localization error over N simulations is then calculated as
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, A.; Yuan, Z.; Longdon, S.N.; Bore, J.-C.; Bin, T. A study of ECCM techniques and their performance. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 19–22 September 2015; pp. 1–6. [Google Scholar]
- Luo, M.; Hao, Z.; Zhu, Y. Intelligent ECCM Technology via Cognition and Agility for the Airborne Radar. J. Eng. 2019, 2019, 6656–6659. [Google Scholar] [CrossRef]
- Han, B.; Qu, X.; Yang, X.; Li, W.; Zhang, Z. DRFM-Based Repeater Jamming Reconstruction and Cancellation Method with Accurate Edge Detection. Remote Sens. 2023, 15, 1759. [Google Scholar] [CrossRef]
- Chen, X.; Shu, T.; Yu, K.-B.; He, J.; Yu, W. Joint adaptive beamforming techniques for distributed array radars in multiple mainlobe and sidelobe jamming. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 248–252. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Y.; Ma, H.; Peng, X.; Yan, J. Optimized masking for MIMO radar signals. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3433–3451. [Google Scholar] [CrossRef]
- Liao, Y.; Tang, H.; Wang, W.; Xing, M. A low sidelobe deceptive jamming suppression beamforming method with a frequency diverse array. IEEE Trans. Antennas Propag. 2022, 70, 4884–4889. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, J.; Su, R.; Li, C. A Multi-machine Jamming Method for Side-lobe Cancellation. J. Phys. Conf. Ser. 2023, 2478, 122076. [Google Scholar] [CrossRef]
- Liu, X.; Sun, C.; Yang, Y.; Zhuo, J. Low sidelobe range profile synthesis for sonar imaging using stepped-frequency pulse. IEEE Geosci. Remote Sens. Lett. 2017, 14, 218–221. [Google Scholar] [CrossRef]
- Dong, S.; Quan, Y.; Fang, W.; Wang, H. Anti-intermittent sampling jamming method based on frequency agile radar and K-means. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 1140–1144. [Google Scholar]
- Greco, M.; Gini, F.; Farina, A. Radar detection and classification of jamming signals belonging to a cone class. IEEE Trans. Signal Process. 2008, 56, 1984–1993. [Google Scholar] [CrossRef]
- Dai, H.; Wang, X.; Li, Y.; Liu, Y.; Xiao, S. Main-lobe jamming suppression method of using spatial polarization characteristics of antennas. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2167–2179. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, D.; Zhang, G. New antivelocity deception jamming technique using pulses with adaptive initial phases. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1290–1300. [Google Scholar] [CrossRef]
- Wang, B.; Cui, G.; Zhang, S.; Sheng, B.; Kong, L.; Ran, D. Deceptive Jamming Suppression Based on Coherent Cancelling in Multistatic Radar System. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–5. [Google Scholar]
- Liu, J.; Zhang, L.; Zhao, S.; Liu, N.; Yu, H. Antideception jamming method for active/passive radar based on distributed frameworks. J. Xidian Univ. 2018, 45, 1–6. [Google Scholar]
- Wang, G.; Ji, Z. Multi-range-false-target jamming for radar network based on multiple discriminations. Syst. Eng. Electron. 2017, 39, 40–48. [Google Scholar]
- Liu, J.; Gong, M.; Nie, Z.; Li, H.; Liu, J.; Zhao, S. Subset Selection Strategies Based on Target Positioning Characteristics for Anti-Jamming Technology. Remote Sens. 2022, 14, 6230. [Google Scholar] [CrossRef]
- Li, D.; Yao, S.; Liao, Y.; Yan, J.; Fu, Y. Frequency offset deception velocity-based method for discriminating between physical targets and active false targets. Signal Process. 2025, 234, 109977. [Google Scholar] [CrossRef]
- Yang, Y.; Da, K.; Zhu, Y.; Xiang, S. Consensus based target tracking against deception jamming in distributed radar networks. IET Radar Sonar Navig. 2023, 17, 683–700. [Google Scholar] [CrossRef]
- Li, Q.; Guo, Y.; Zhang, P.; Xu, H.; Zhang, L.; Chen, Z.; Huang, Y. Deception Velocity-Based Method to Discriminate Physical Targets and Active False Targets in a Multistatic Radar System. Remote Sens. 2024, 16, 382. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Zhang, M.; Li, H.; Zhao, S. An Anti-jamming Method in Multistatic Radar System Based on Convolutional Neural Network. IET Signal Process. 2022, 16, 220–231. [Google Scholar] [CrossRef]
- Yu, H.; Liu, N.; Zhang, L.; Li, Q.; Zhao, S. An interference suppression method for multistatic radar based on noise subspace projection. IEEE Sens. J. 2020, 20, 8797–8805. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhou, Y.; Liu, N.; Liu, J. Discrimination of active false targets in multistatic radar using spatial scattering properties. IET Radar Sonar Navig. 2016, 10, 817–826. [Google Scholar] [CrossRef]
- Sun, M.; Ding, C.; Zhang, S.; Lu, J.; Shao, P. Recognition of Deception Jamming Based on Statistical Correlation Difference in a Multistatic Radar System. J. Electron. Inf. Technol. 2020, 42, 2992–2998. [Google Scholar]
- Kong, Y.; Wang, X.; Wu, C.; Yu, X.; Cui, G. Active deception jamming recognition in the presence of extended target. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, J.; Zhang, L.; Li, S. Polarimetric multiple-radar frameworks with distributed antennas for discriminating between radar targets and deception jamming. Digit. Signal Process. 2019, 90, 46–53. [Google Scholar] [CrossRef]
- Li, C.; Zhu, L.; Xie, A.; Luo, Z. Weak signal blind source separation in passive radar system with strong interference. In Proceedings of the MILCOM IEEE Military Communications Conference, Tampa, FL, USA, 26–28 October 2015; pp. 501–505. [Google Scholar]
- Wang, W.; Zhang, J.; Liu, X.; Li, L. Radar anti-main-lobe-jamming based on blind source separation algorithm of JADE. Fire Control Command. Control 2015, 40, 104–108. [Google Scholar]
- Zhou, C.; Wang, C.; Gong, J.; Tan, M.; Li, X.; Bao, L. Hybrid polarization anti-SMSP jamming based on jamming reconstruction and blind source separation. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 1841–1848. [Google Scholar]
- Liu, Y.; Yu, L.; Wei, Y. Mainlobe multiple false targets deceptive jamming suppression via joint transmit-receive design. Digit. Signal Process. 2025, 164, 105289. [Google Scholar] [CrossRef]
- Lei, Z.; Qu, Q.; Chen, H.; Zhang, Z.; Dou, G.; Wang, Y. Mainlobe jamming suppression with space–time multichannel via blind source separation. IEEE Sens. J. 2023, 23, 17042–17053. [Google Scholar] [CrossRef]
- Yan, Z.; Ge, M.; Cui, G.; Yu, X.; Hu, R. DOA estimation with subarrays via blind source separation algorithm. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021; pp. 1–6. [Google Scholar]
- Liu, Z.; Liang, W.; Fu, N.; Qiao, L.; Zhang, J. Main lobe deceptive jamming suppression based on blind source separation and energy detection for monopulse radar. IET Radar Sonar Navig. 2024, 18, 2170–2181. [Google Scholar] [CrossRef]
- Ge, M.; Cui, G.; Yu, X.; Kong, L. Main lobe jamming suppression via blind source separation sparse signal recovery with subarray configuration. J. Syst. Eng. Electron. 2020, 14, 431–438. [Google Scholar] [CrossRef]
- Ge, M.; Cui, G.; Kong, L.; Huang, D. Jamming suppression based on blind source separation in distributed radars. J. Signal Process. 2017, 33, 1562–1570. [Google Scholar]
- Han, X.; He, H.; Zhang, Q.; Yang, L.; He, Y. Main-lobe jamming suppression method for phased array netted radar based on MSNR-BSS. IEEE Sens. J. 2022, 22, 22972–22984. [Google Scholar] [CrossRef]
- Gao, X.; Quan, Y.; Li, Y.; Zhu, S.; Xing, M. Main-lobe deceptive jamming suppression with FDAMIMO radar based on BSS. Syst. Eng. Electron. 2020, 42, 1926–1934. [Google Scholar]
- Borga, M. Learning Multidimensional Signal Processing. Ph.D. Thesis, Linkoping University, Linkoping, Sweden, 1998. [Google Scholar]







| Radar Serial Number | Position Coordinates (m) |
|---|---|
| PA Radar 1 | 8000, 22,000, 15,000 |
| PA Radar 2 | 10,000, 20,000, 15,000 |
| PA Radar 3 | 8000, 24,000, 15,000 |
| Target location | 15,000, 35,000, 0 |
| Interference location | 15,500, 35,600, 0 |
| Signal Parameter | Parameter Value |
|---|---|
| Bandwidth/B | 20 MHz |
| Carrier Frequency/Fc | 16 GHz |
| Pulse Repetition Frequency/PRF | 8 MHz |
| Sampling Frequency/Fs | 80 MHz |
| Number of Sampling Points | 4096 |
| Pulse Width/Tp | 25 s |
| CEEMDAN decomposition level | 10 |
| Wavelet basis | sym8 |
| Wavelet decomposition level | 6 |
| balancing parameter | 2 |
| CFAR type | CA-CFAR |
| CFAR false alarm probability | |
| Number of reference units | 50 |
| Number of protection units | 5 |
| Radar Number | Actual Distance (m) | Estimated Distance (NAM) (m) | Estimated Distance (SMSP) (m) |
|---|---|---|---|
| PA Radar 1 | 21,048 | 21,050.1 | 21,049.9 |
| PA Radar 2 | 21,794 | 21,796.4 | 21,796.1 |
| PA Radar 3 | 19,875 | 19,877.5 | 198,877.4 |
| Positioning Method | SNR = −5 dB (m) | SNR = 0 dB (m) | SNR = 5 dB (m) |
|---|---|---|---|
| Single-site radar | 18.6 | 12.3 | 7.6 |
| Multi-site radar | 16.1 | 9.8 | 5.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; He, H.; Li, R.; Wu, Y.; Zhang, X.; You, Y. Distributed Phased-Array Radar Mainlobe Interference Suppression and Cooperative Localization Based on CEEMDAN–WOBSS. Sensors 2025, 25, 6277. https://doi.org/10.3390/s25206277
Liu X, He H, Li R, Wu Y, Zhang X, You Y. Distributed Phased-Array Radar Mainlobe Interference Suppression and Cooperative Localization Based on CEEMDAN–WOBSS. Sensors. 2025; 25(20):6277. https://doi.org/10.3390/s25206277
Chicago/Turabian StyleLiu, Xiang, Huafeng He, Ruike Li, Yubin Wu, Xin Zhang, and Yongquan You. 2025. "Distributed Phased-Array Radar Mainlobe Interference Suppression and Cooperative Localization Based on CEEMDAN–WOBSS" Sensors 25, no. 20: 6277. https://doi.org/10.3390/s25206277
APA StyleLiu, X., He, H., Li, R., Wu, Y., Zhang, X., & You, Y. (2025). Distributed Phased-Array Radar Mainlobe Interference Suppression and Cooperative Localization Based on CEEMDAN–WOBSS. Sensors, 25(20), 6277. https://doi.org/10.3390/s25206277






