Interplay of the Mass Transport and Reaction Kinetics for Lateral Flow Immunoassay Integrated on Lab-on-Disc
Abstract
Highlights
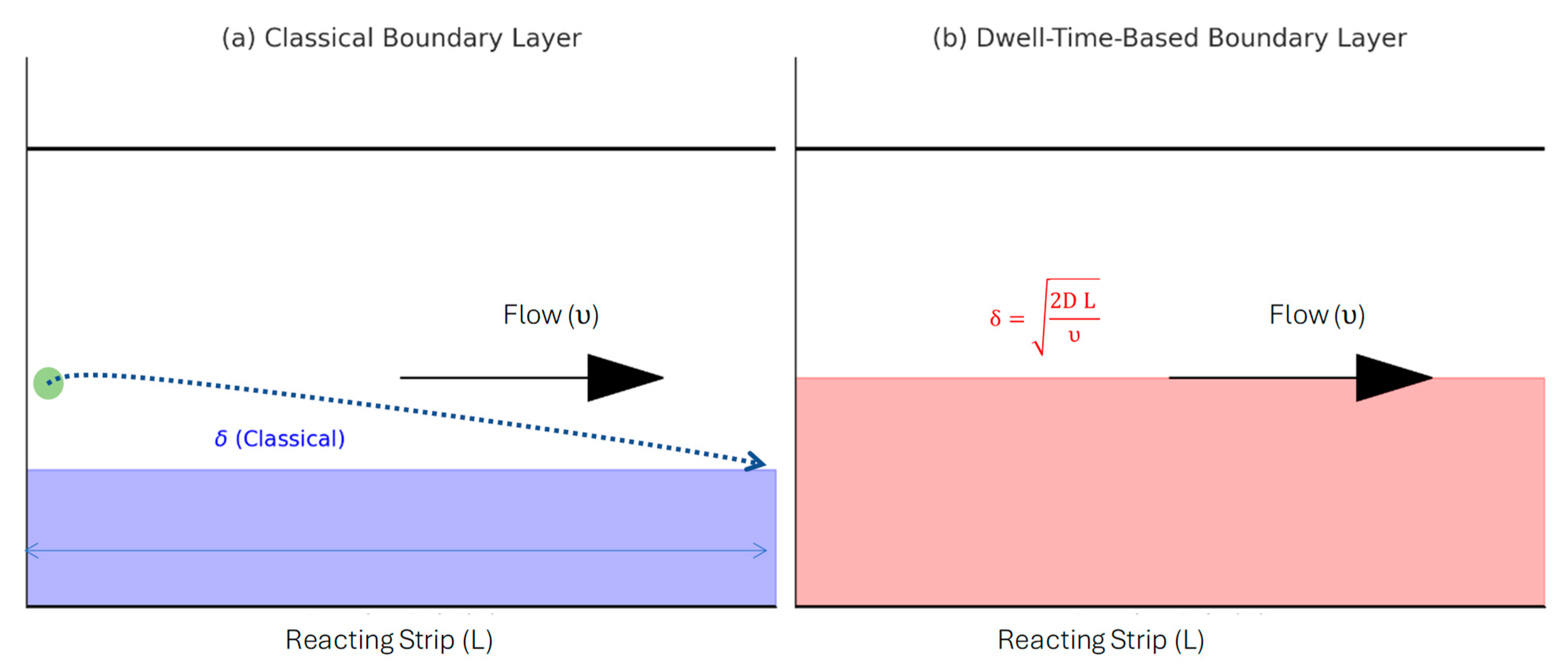
- Introduced a new Transport Reaction Constant (TRc) that extends the traditional Damköhler number by incorporating film thickness, enabling better prediction of surface-based assay performance.
- Demonstrated that integrating lateral flow assays (LFAs) with a centrifugal Lab-on-Disc (LFA-CD) improves sensitivity by both increasing analyte dwell time at the test line and allowing for the increase of sample volume.
- TRc provides a generalizable design parameter for optimizing LFA and other surface-reaction assays under flow, complementing existing dimensionless numbers like Da.
- The use of LFA-CD platforms facilitates the increase in test sensitivity and lowering the limit of detection.
- The presented approach provides a scalable, low-cost pathway to prototype next-generation diagnostic devices whose microfluidic geometry and fluidic controls can be optimized based on the analytes’ reaction kinetics.
Abstract
1. Introduction
2. Materials and Methods
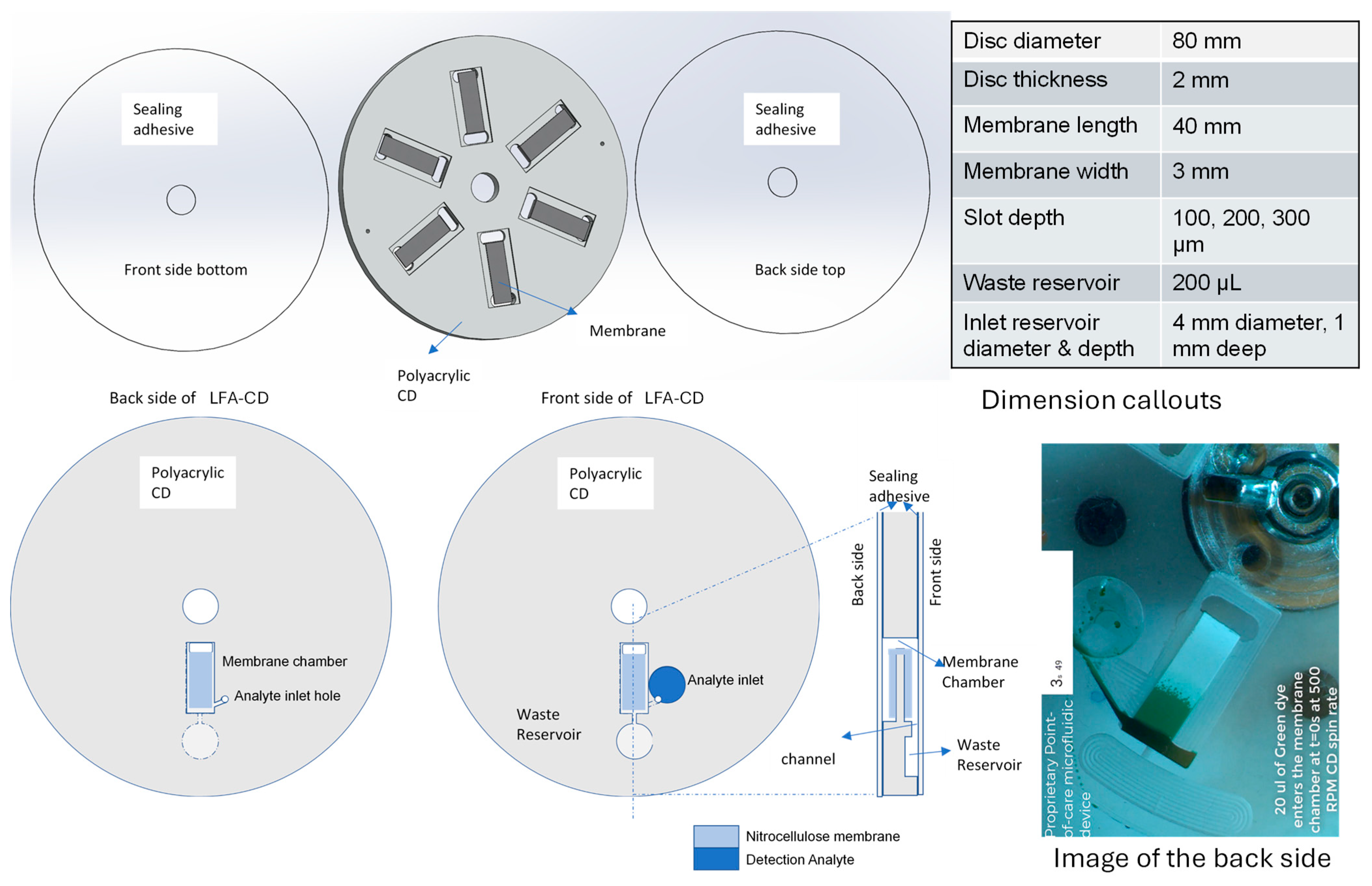
2.1. Fabrication of the LFA-CD
- CAD Design and CNC Milling: The disc was designed in SolidWorks and machined from 3 mm-thick polyacrylic (PMMA) sheets using a Tormach 440 PCNC Mill (Tormach Inc., Waunakee, WI, USA). The features included
- A 3.2 mm-wide membrane chamber (depth varied: 100–300 µm);
- Circular inlet well (~1 mm deep);
- Waste reservoir;
- Through-hole for membrane bending.
- Membrane Preparation: Hi-Flow Plus HF120 (Millipore Sigma, Burlington, MA, USA) (3 mm × 40 mm) were cut using a Silhouette Cameo 4 (Silhouette America, Lindon, UT, USA); detection lines dispensed using BioDot AD3050 (BioDot Inc., Irvine, CA, USA).
- Membrane Integration: NC membranes were affixed to the chamber using double-sided lateral-flow adhesive from Adhesives Research #90445Q (distributed by Parafix Tapes & Conversions Ltd., Lancing, UK).
- Sealing: Single-sided 3M 9795R single-sided tape (3M Company, Saint Paul, MN, USA). was used to seal the top and bottom surfaces of the fluidic disc.
- Inlet Channel Connection: A via hole was machined to connect the inlet well to the start of the NC strip, allowing sample introduction.
- Final Assembly and Venting: A pressure roller Akiro Manual Roller B07YDNKSH6 (Amazon USA) was used to ensure uniform sealing. Vent holes were added to inlet and outlet chambers for pressure equalization.
2.2. Experimental Setup
2.3. Lateral Flow CD Design and Operation
- Pipetting 20 μL of analyte (Streptavidin coated Polystyrene particles with Europium) into the analyte inlet reservoir.
- Spinning the disc at 500, 1000, 1500 or signal enhancement specified rpm (see Section 5.2) for 2 min.
- Stopping the disc.
- Spinning the disc at 5000 rpm in order to squeeze out the fluid from the section of NC membrane bent to the back side of the CD. Draining the section of NC strip restores the ability of the NC membrane to pull up more liquid samples.
- Adding more volume of analyte via analyte inlet reservoir and proceeding from step 2 on. It is possible to go through steps 2–5 multiple times until the NC membrane is soaked through and no further capillary action is possible. Three of these cycles were performed and additional two sample volumes of 20 μL each (for the total 60 μL of sample) were processed.
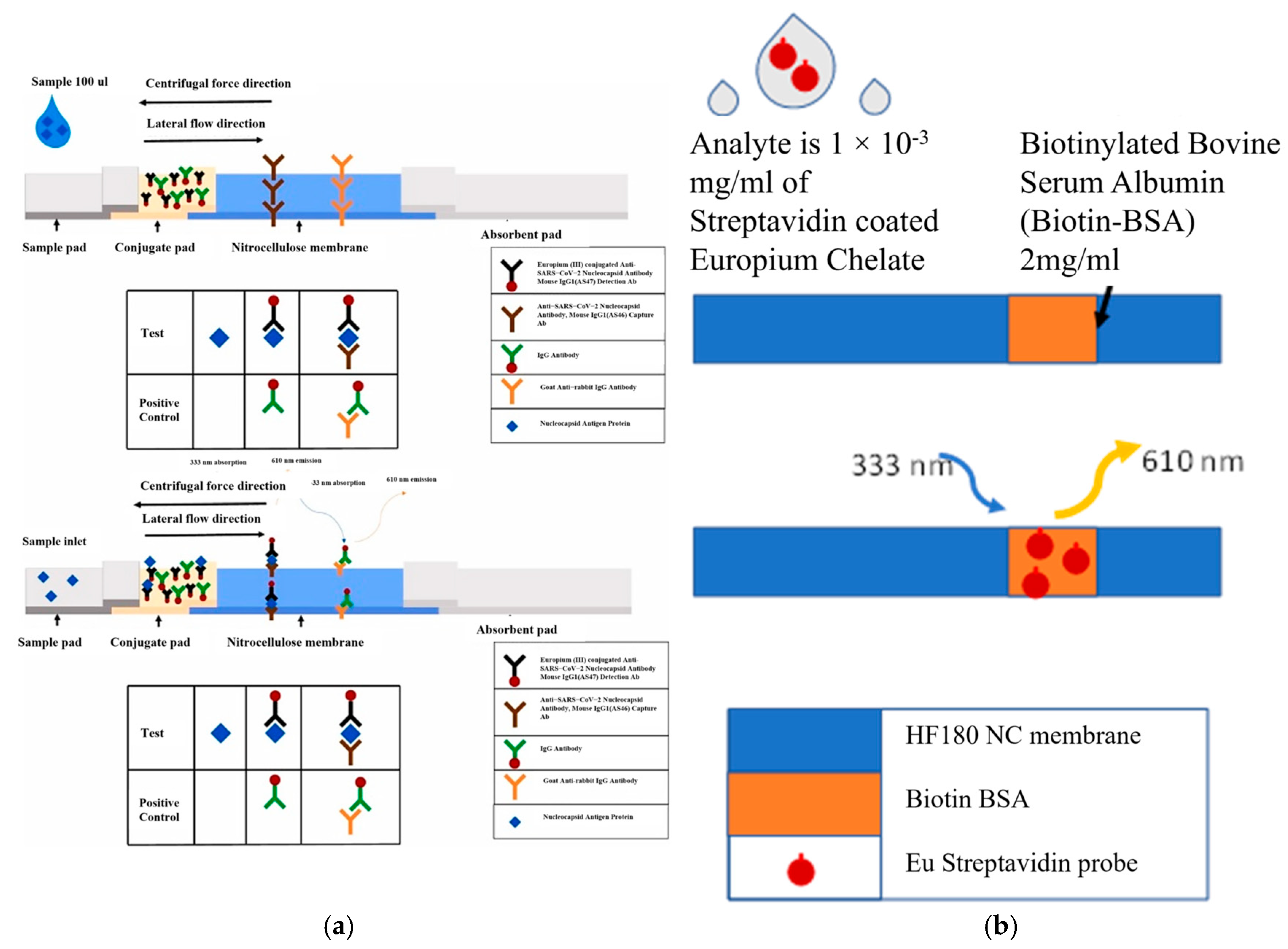
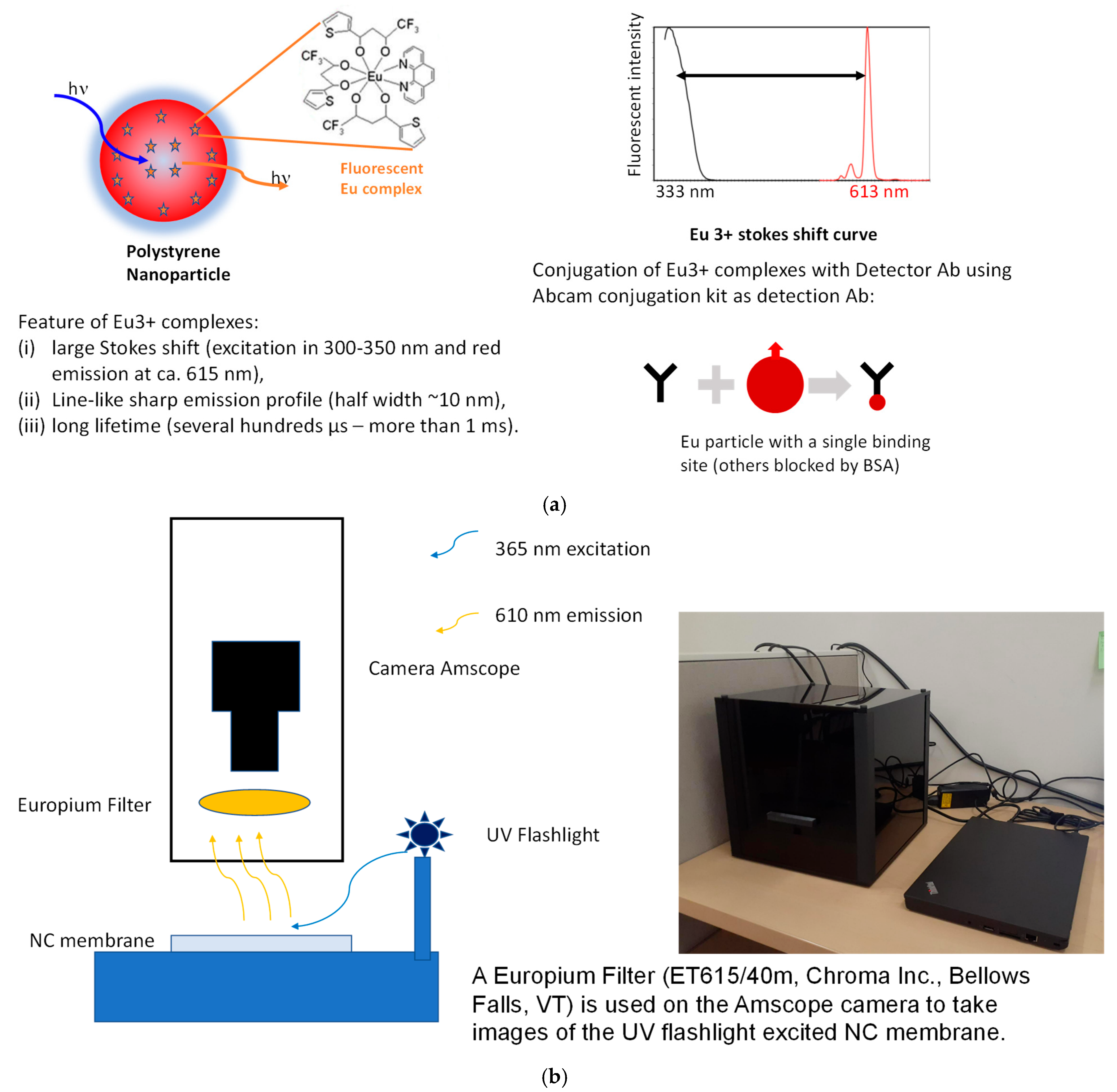
2.4. Fluorescent Probes and Detection Method
- Biotin–streptavidin: Kd = 10−15 M (Fastest Reacting)
- Eotaxin: Kd = 7.1 × 10−11 M (Moderate Reaction)
- CD79b: Kd = 3.9 × 10−9 M (Slowest Reacting)
Antibody–Europium Conjugation and Quality Control
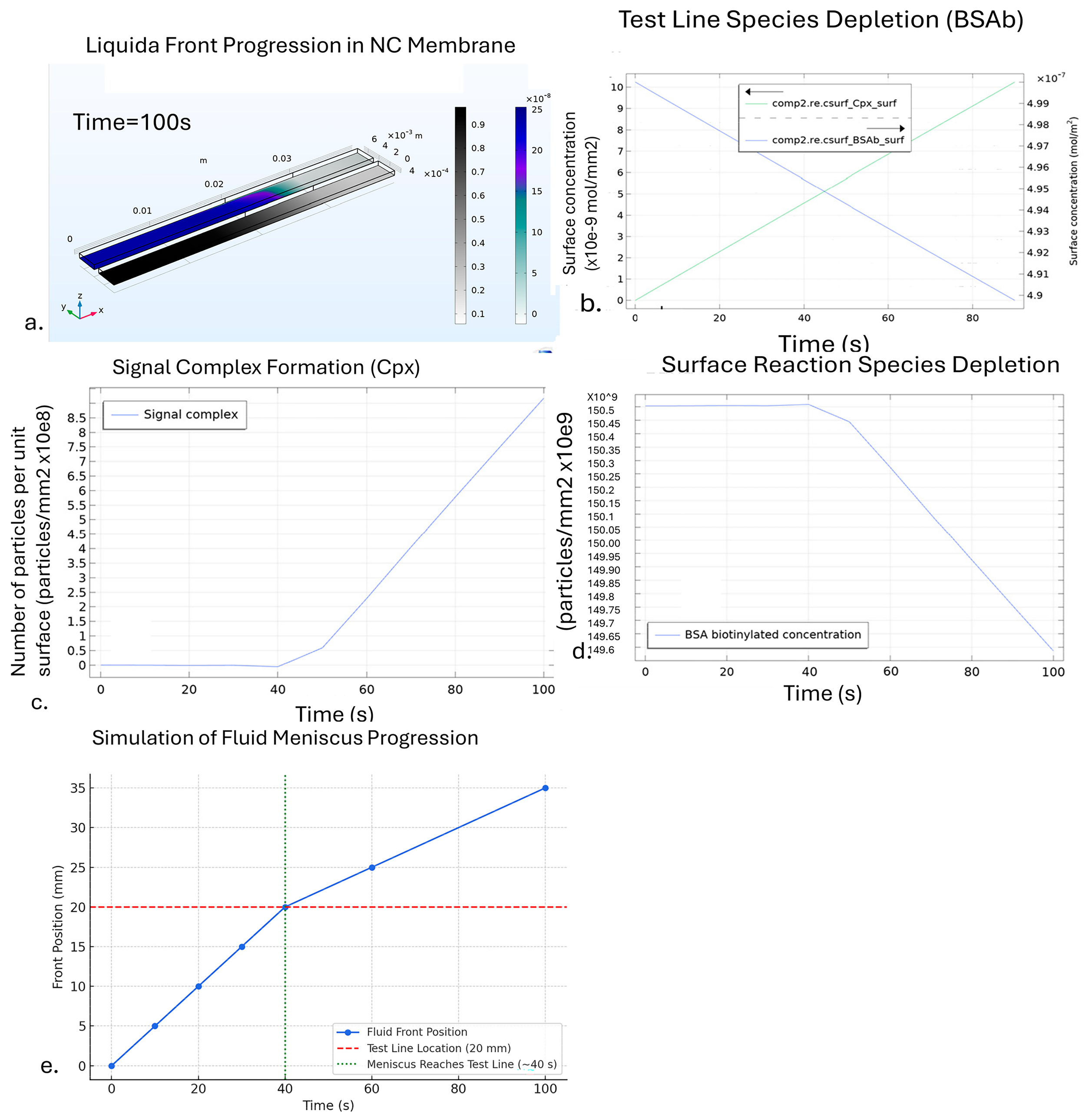
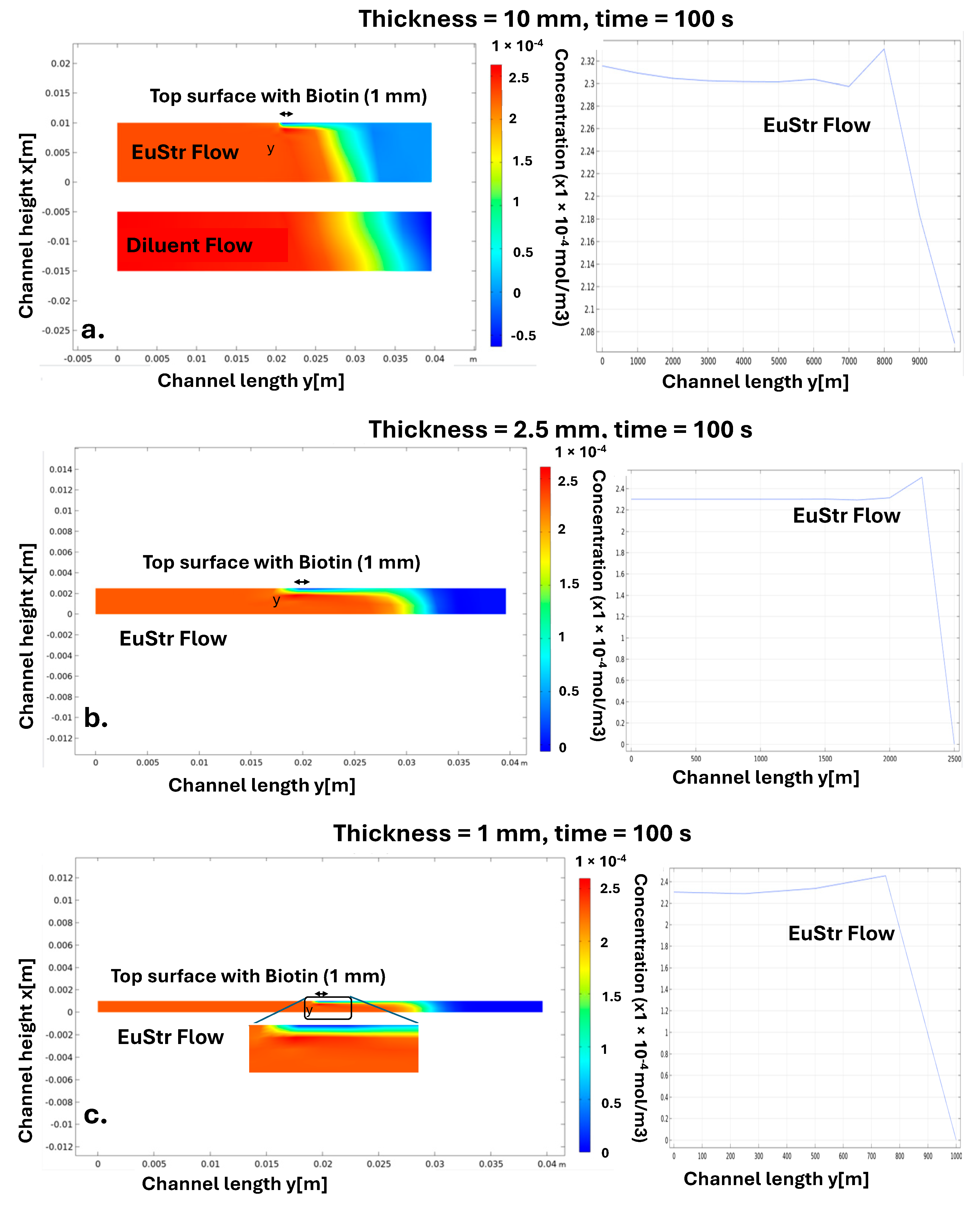
3. COMSOL Simulation
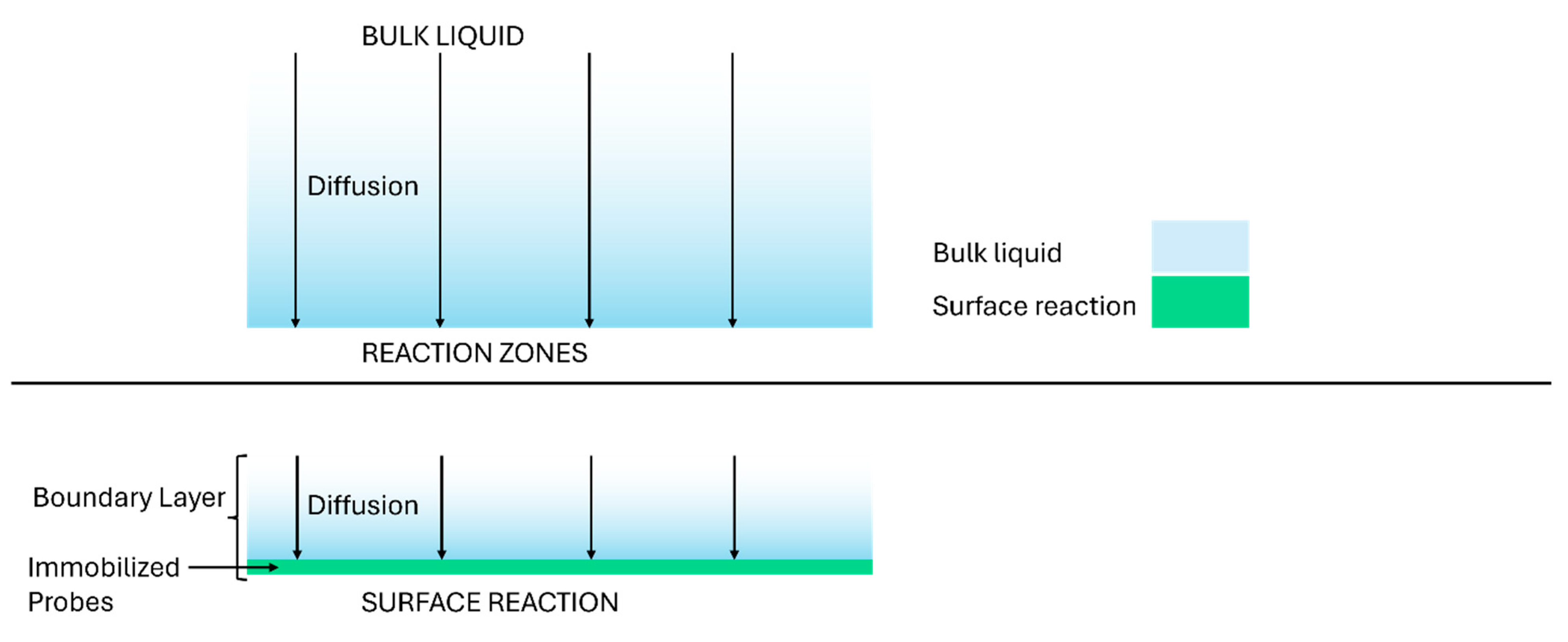
4. Mass Transport-Reaction Kinetics Analysis
TRc Model Assumption and Limitations
5. Results and Discussion
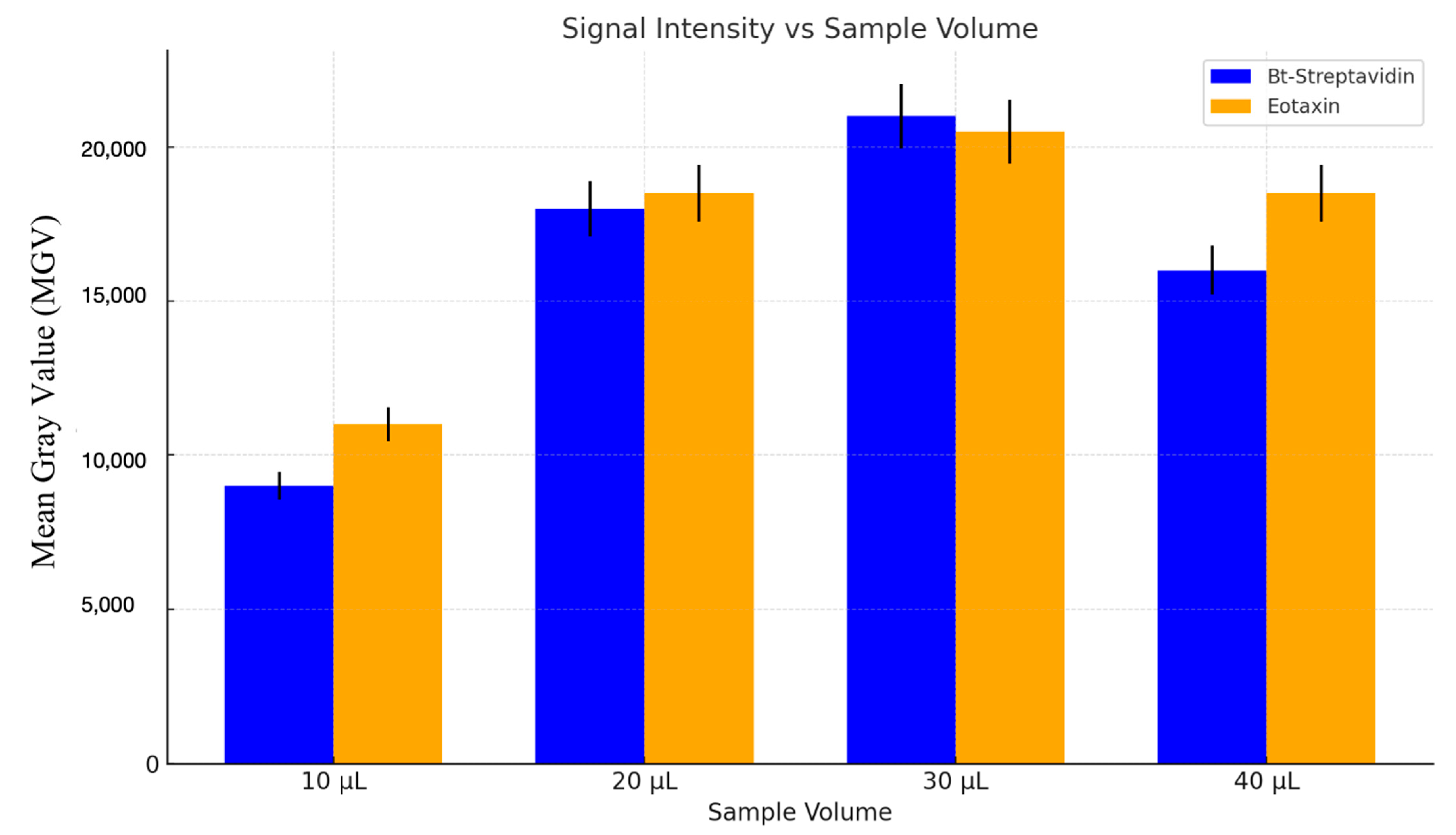
5.1. Sample Volume Influence on the Detection Signal Strength
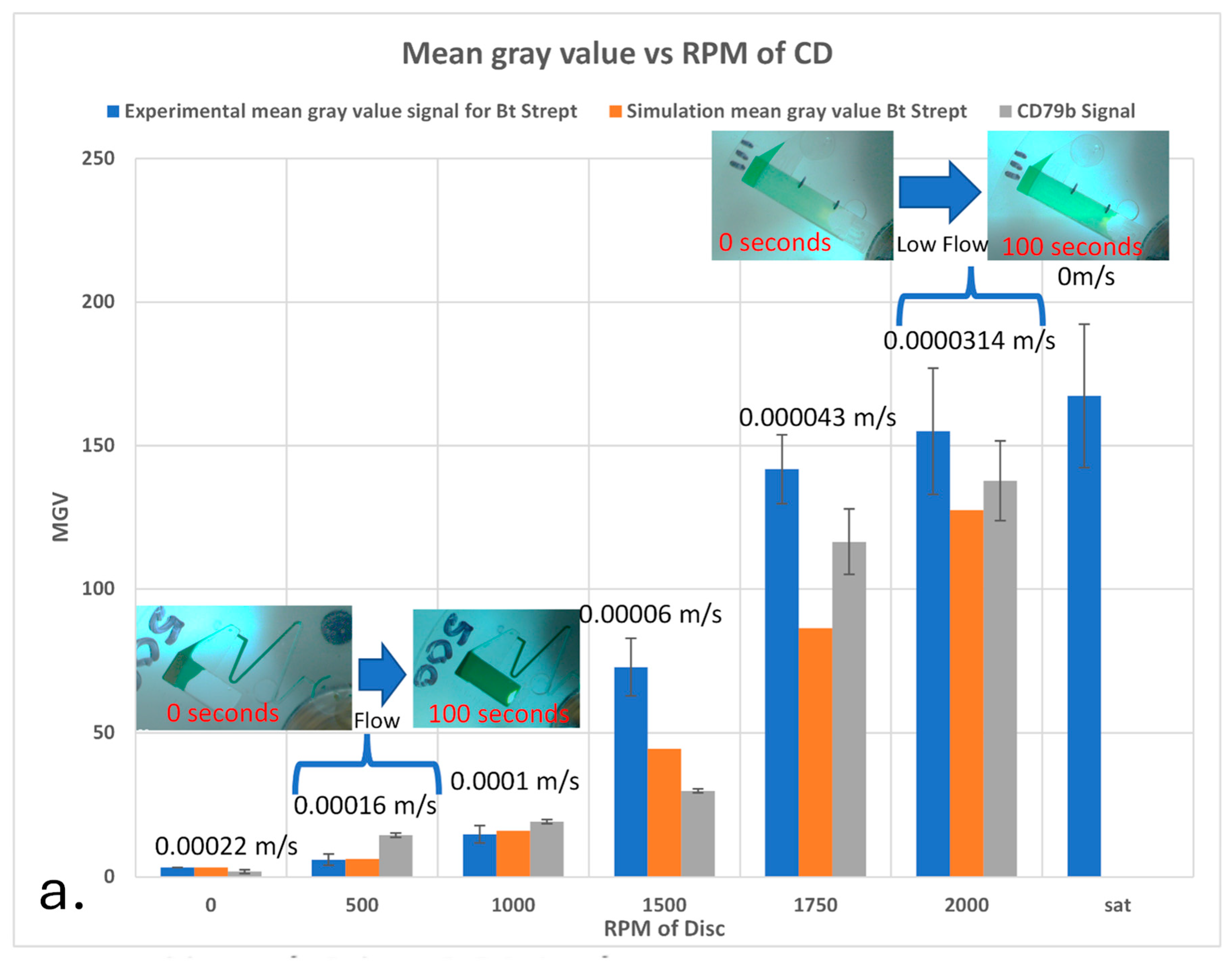
5.2. CD Spin Speed Influence on the Detection Signal Strength
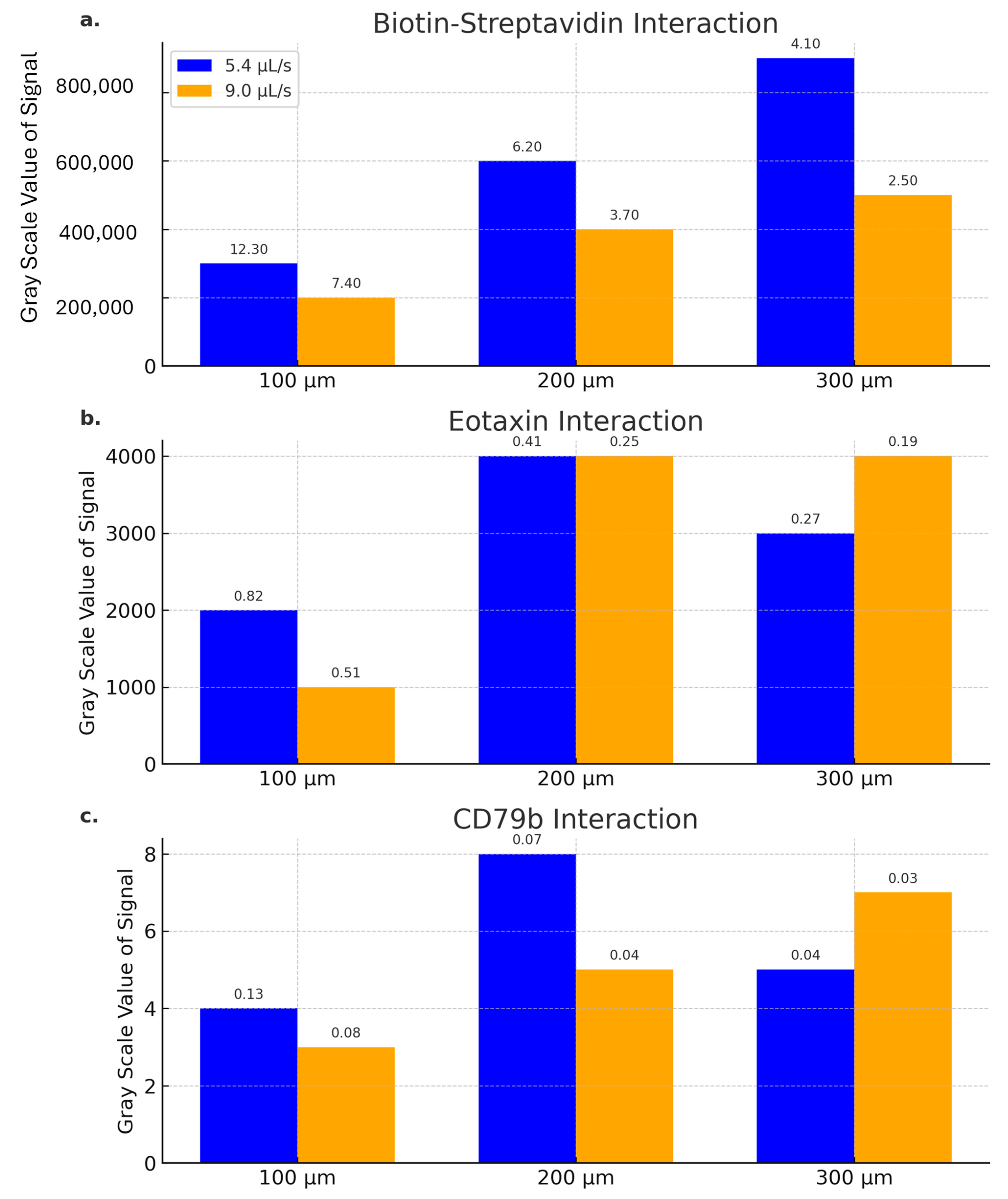
5.3. Speed of Reaction Kinetics of Various Analytes and the Height of Microfluidic Channel Influence on the Detection Signal Strength
- TRc > 1: Reaction rate dominates over mass transport.
- 0.1 < TRc < 1: Reaction and transport effects are balanced.
- TRc < 0.1: Mass transport limits reactant access to the active surface [58].
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Bhushan, P.; Krishna, V.; Bhattacharya, S. Tapered Lateral Flow Immunoassay Based Point-of-Care Diagnostic Device for Ultrasensitive Colorimetric Detection of Dengue NS1. Biomicrofluidics 2018, 12, 034104. [Google Scholar] [CrossRef]
- Rani, A.; Ravindran, V.B.; Surapaneni, A.; Mantri, N.; Ball, A.S. Review: Trends in Point-of-Care Diagnosis for Escherichia coli O157:H7 in Food and Water. Int. J. Food Microbiol. 2021, 349, 109233. [Google Scholar] [CrossRef]
- Markandan, K.; Tiong, Y.W.; Sankaran, R.; Subramanian, S.; Markandan, U.D.; Chaudhary, V.; Numan, A.; Khalid, M.; Walvekar, R. Emergence of Infectious Diseases and Role of Advanced Nanomaterials in Point-of-Care Diagnostics: A Review. Biotechnol. Genet. Eng. Rev 2024, 40, 3438–3526. [Google Scholar] [CrossRef]
- Li, F.; You, M.; Li, S.; Hu, J.; Liu, C.; Gong, Y.; Yang, H.; Xu, F. Paper-Based Point-of-Care Immunoassays: Recent Advances and Emerging Trends. Biotechnol. Adv. 2020, 39, 107442. [Google Scholar] [CrossRef]
- Hansen, S.; Abd El Wahed, A. Point-of-Care or Point-of-Need Diagnostic Tests: Time to Change Outbreak Investigation and Pathogen Detection. Trop. Med. Infect. Dis. 2020, 5, 151. [Google Scholar] [CrossRef]
- Shu, T.; Hunter, H.; Zhou, Z.; Sun, Y.; Cheng, X.; Ma, J.; Su, L.; Zhang, X.; Serpe, M.J. Portable Point-of-Care Diagnostic Devices: An Updated Review. Anal. Methods 2021, 13, 5418–5435. [Google Scholar] [CrossRef] [PubMed]
- Yadav, S.; Sadique, M.A.; Ranjan, P.; Kumar, N.; Singhal, A.; Srivastava, A.K.; Khan, R. SERS Based Lateral Flow Immunoassay for Point-of-Care Detection of SARS-CoV-2 in Clinical Samples. ACS Appl. Bio Mater. 2021, 4, 2974–2995. [Google Scholar] [CrossRef]
- Koczula, K.M.; Gallotta, A. Lateral Flow Assays. Essays Biochem. 2016, 60, 111–120. [Google Scholar] [CrossRef]
- Lateral Flow Immunoassay (LFIA) Based Rapid Test Market Scope and overview, Outlook to 2022: Emerging Trends, Highlights and Challenges Forecast 2031. MarketWatch. Available online: https://www.marketwatch.com/press-release/lateral-flow-immunoassay-lfia-based-rapid-test-market-scope-and-overview-outlook-to-2022-emerging-trends-highlights-and-challenges-forecast-2031-2022-01-11 (accessed on 24 March 2022).
- Rosen, S. Market Trends in Lateral Flow Immunoassays. In Lateral Flow Immunoassay; Wong, R., Tse, H., Eds.; Humana Press: Totowa, NJ, USA, 2009; pp. 1–15. [Google Scholar] [CrossRef]
- O’Farrell, B. Evolution in Lateral Flow–Based Immunoassay Systems. In Lateral Flow Immunoassay; Humana Press: Totowa, NJ, USA, 2008; pp. 1–33. [Google Scholar] [CrossRef]
- Serrano, M.M.; Rodríguez, D.N.; Palop, N.T.; Arenas, R.O.; Córdoba, M.M.; Mochón, M.D.O.; Cardona, C.G. Comparison of Commercial Lateral Flow Immunoassays and ELISA for SARS-CoV-2 Antibody Detection. J. Clin. Virol. 2020, 129, 104529. [Google Scholar] [CrossRef] [PubMed]
- de Puig, H.; Bosch, I.; Gehrke, L.; Hamad-Schifferli, K. Challenges of the Nano–Bio Interface in Lateral Flow and Dipstick Immunoassays. Trends Biotechnol. 2017, 35, 1169–1180. [Google Scholar] [CrossRef] [PubMed]
- Shirshahi, V.; Liu, G. Enhancing the Analytical Performance of Paper Lateral Flow Assays: From Chemistry to Engineering. TrAC Trends Anal. Chem. 2021, 136, 116200. [Google Scholar] [CrossRef]
- Wang, W.; Stafford, J.W.; Banik, D.; Keller, M.D. Customization and Testing of a Mobile Reader App for an Open-Access SARS-CoV-2 Antigen Lateral Flow Assay. In Optics and Biophotonics in Low-Resource Settings VIII; SPIE: Bellingham, WA, USA, 2022; Volume 11950, pp. 69–76. [Google Scholar] [CrossRef]
- Sun, Y.; Qin, P.; He, J.; Li, W.; Shi, Y.; Xu, J.; Wu, Q.; Chen, Q.; Li, W.; Wang, X.; et al. Rapid and Simultaneous Visual Screening of SARS-CoV-2 and Influenza Virufses with Customized Isothermal Amplification Integrated Lateral Flow Strip. Biosens. Bioelectron. 2022, 197, 113771. [Google Scholar] [CrossRef]
- Zhan, L.; Granade, T.; Liu, Y.; Wei, X.; Youngpairoj, A.; Sullivan, V.; Johnson, J.; Bischof, J. Development and Optimization of Thermal Contrast Amplification Lateral Flow Immunoassays for Ultrasensitive HIV P24 Protein Detection. Microsyst. Nanoeng. 2020, 6, 54. [Google Scholar] [CrossRef]
- Grant, B.D.; Anderson, C.E.; Williford, J.R.; Alonzo, L.F.; Glukhova, V.A.; Boyle, D.S.; Weigl, B.H.; Nichols, K.P. SARS-CoV-2 Coronavirus Nucleocapsid Antigen-Detecting Half-Strip Lateral Flow Assay Toward the Development of Point of Care Tests Using Commercially Available Reagents. Anal. Chem. 2020, 92, 11305–11309. [Google Scholar] [CrossRef] [PubMed]
- Qian, S.; Bau, H.H. Analysis of Lateral Flow Biodetectors: Competitive Format. Anal. Biochem. 2004, 326, 211–224. [Google Scholar] [CrossRef] [PubMed]
- Pratt, G.W.; Fan, A.; Melakeberhan, B.; Klapperich, C.M. A Competitive Lateral Flow Assay for the Detection of Tenofovir. Anal. Chim. Acta 2018, 1017, 34–40. [Google Scholar] [CrossRef]
- Liu, C.; Jia, Q.; Yang, C.; Qiao, R.; Jing, L.; Wang, L.; Xu, C.; Gao, M. Lateral Flow Immunochromatographic Assay for Sensitive Pesticide Detection by Using Fe3O4 Nanoparticle Aggregates as Color Reagents. Anal. Chem. 2011, 83, 6778–6784. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, Y.; Wang, J.; Tang, Z.; Pounds, J.G.; Lin, Y. Rapid and Sensitive Detection of Protein Biomarker Using a Portable Fluorescence Biosensor Based on Quantum Dots and a Lateral Flow Test Strip. Anal. Chem. 2010, 82, 7008–7014. [Google Scholar] [CrossRef]
- Recent Research Trends in Fluorescent Reporters-Based Lateral Flow Immunoassay for Protein Biomarkers Specific to Acute Myocardial Infarction—Supianto—2022—Bulletin of the Korean Chemical Society—Wiley Online Library. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/bkcs.12430?casa_token=RXb1Q5nMYy8AAAAA:-fPBuMKzI9TlzW2P5e6SSPK099R-vhvlvvuWBLbjnfSZ5YybMa0SySsNRbIAnespGibfKudNdmIcgNA (accessed on 11 September 2023).
- Parolo, C.; de la Escosura-Muñiz, A.; Merkoçi, A. Enhanced Lateral Flow Immunoassay Using Gold Nanoparticles Loaded with Enzymes. Biosens. Bioelectron. 2013, 40, 412–416. [Google Scholar] [CrossRef]
- Khlebtsov, B.N.; Tumskiy, R.S.; Burov, A.M.; Pylaev, T.E.; Khlebtsov, N.G. Quantifying the Numbers of Gold Nanoparticles in the Test Zone of Lateral Flow Immunoassay Strips. ACS Appl. Nano Mater. 2019, 2, 5020–5028. [Google Scholar] [CrossRef]
- Fan, R.; Zhang, W.; Jin, Y.; Zhao, R.; Yang, C.; Chen, Q.; He, L.; Chen, Y. Lateral Flow Immunoassay for 5-Hydroxyflunixin Based on near-Infrared Fluorescence Molecule as an Alternative Label to Gold Nanoparticles. Microchim. Acta 2020, 187, 368. [Google Scholar] [CrossRef]
- Beloglazova, N.V.; Sobolev, A.M.; Tessier, M.D.; Hens, Z.; Goryacheva, I.Y.; De Saeger, S. Fluorescently Labelled Multiplex Lateral Flow Immunoassay Based on Cadmium-Free Quantum Dots. Methods 2017, 116, 141–148. [Google Scholar] [CrossRef]
- Mohd Hanafiah, K.; Arifin, N.; Bustami, Y.; Noordin, R.; Garcia, M.; Anderson, D. Development of Multiplexed Infectious Disease Lateral Flow Assays: Challenges and Opportunities. Diagnostics 2017, 7, 51. [Google Scholar] [CrossRef]
- Anfossi, L.; Di Nardo, F.; Cavalera, S.; Giovannoli, C.; Baggiani, C. Multiplex Lateral Flow Immunoassay: An Overview of Strategies towards High-Throughput Point-of-Need Testing. Biosensors 2019, 9, 2. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, K.; Zheng, W.; Cheng, Y.; Li, T.; Cao, B.; Jin, Q.; Cui, D. Rapid Developments in Lateral Flow Immunoassay for Nucleic Acid Detection. Analyst 2021, 146, 1514–1528. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Liu, Y.; Wu, Y.; Xia, X.; Liao, Y.; Li, Q. Fluorescent Probe-Based Lateral Flow Assay for Multiplex Nucleic Acid Detection. Anal. Chem. 2014, 86, 5611–5614. [Google Scholar] [CrossRef] [PubMed]
- Peshin, S.; Golden, J.; Gan, B.; Mast, C.; Kulinsky, L. Controlling the Advancement of the Liquid Front of the Nitrocellulose Membrane Assay under the Influence of the Centrifugal Force on the Lab-on-a-Disc Platform. Sens. Actuators B Chem. 2023, 386, 133735. [Google Scholar] [CrossRef]
- Wiederoder, M.S.; Smith, S.; Madzivhandila, P.; Mager, D.; Moodley, K.; DeVoe, D.L.; Land, K.J. Novel Functionalities of Hybrid Paper-Polymer Centrifugal Devices for Assay Performance Enhancement. Biomicrofluidics 2017, 11, 054101. [Google Scholar] [CrossRef]
- Kainz, D.M.; Früh, S.M.; Hutzenlaub, T.; Zengerle, R.; Paust, N. Flow Control for Lateral Flow Strips with Centrifugal Microfluidics. Lab Chip 2019, 19, 2718–2727. [Google Scholar] [CrossRef]
- Shen, M.; Li, N.; Lu, Y.; Cheng, J.; Xu, Y. An Enhanced Centrifugation-Assisted Lateral Flow Immunoassay for the Point-of-Care Detection of Protein Biomarkers. Lab Chip 2020, 20, 2626–2634. [Google Scholar] [CrossRef]
- Shen, M.; Chen, Y.; Zhu, Y.; Zhao, M.; Xu, Y. Enhancing the Sensitivity of Lateral Flow Immunoassay by Centrifugation-Assisted Flow Control. Anal. Chem. 2019, 91, 4814–4820. [Google Scholar] [CrossRef]
- Madou, M.; Zoval, J.; Jia, G.; Kido, H.; Kim, J.; Kim, N. Lab on a CD. Annu. Rev. Biomed. Eng. 2006, 8, 601–628. [Google Scholar] [CrossRef]
- Mark, D.; Haeberle, S.; Roth, G.; von Stetten, F.; Zengerle, R. Microfluidic Lab-on-a-Chip Platforms: Requirements, Characteristics and Applications. Chem. Soc. Rev. 2010, 39, 1153–1182. [Google Scholar] [CrossRef] [PubMed]
- Kainz, D.M.; Breiner, B.J.; Früh, S.M.; Hutzenlaub, T.; Zengerle, R.; Paust, N. Eliminating Viscosity Bias in Lateral Flow Tests. Microsyst. Nanoeng. 2021, 7, 72. [Google Scholar] [CrossRef]
- Xia, G.; Wang, J.; Liu, Z.; Bai, L.; Ma, L. Effect of Sample Volume on the Sensitivity of Lateral Flow Assays through Computational Modeling. Anal. Biochem. 2021, 619, 114130. [Google Scholar] [CrossRef] [PubMed]
- Ragavendar, M.S.; Anmol, C.M. A Mathematical Model to Predict the Optimal Test Line Location and Sample Volume for Lateral Flow Immunoassays. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2012, 2012, 2408–2411. [Google Scholar] [CrossRef] [PubMed]
- EMD Millipore. Rapid Lateral Flow Test Strips: Considerations for Product Development; EMD Millipore Corp.: Billerica, MA, USA, 2013; Volume 29, pp. 702–707. [Google Scholar]
- Zhan, L.; Guo, S.; Song, F.; Gong, Y.; Xu, F.; Boulware, D.R.; McAlpine, M.C.; Chan, W.C.W.; Bischof, J.C. The Role of Nanoparticle Design in Determining Analytical Performance of Lateral Flow Immunoassays. Nano Lett. 2017, 17, 7207–7212. [Google Scholar] [CrossRef]
- Austin, D.; Maciolek, D.; Davis, B.; Wallace, S. Damköhler Number Design Method to Avoid Clogging of Subsurface Flow Constructed Wetlands by Heterotrophic Biofilms. Water Sci. Technol. 2007, 56, 7–14. [Google Scholar] [CrossRef]
- Nalumachu, R.; Anandita, A.; Rath, D. Computational Modelling of a Competitive Immunoassay in Lateral Flow Diagnostic Devices. Sens. Diagn. 2023, 2, 687–698. [Google Scholar] [CrossRef]
- Kainz, D.M.; Breiner, B.J.; Klebes, A.; Borst, N.; Zengerle, R.; von Stetten, F.; Hutzenlaub, T.; Paust, N.; Früh, S.M. Centrifugal Microfluidic Lateral Flow Assay Enables High Sensitivity Interleukin-6 Detection and Ultrafast Readout of Elevated Analyte Levels. Anal. Chem. 2025, 97, 8984–8991. [Google Scholar] [CrossRef]
- Peshin, S.; George, D.; Shiri, R.; Kulinsky, L.; Madou, M. Capillary Flow-Driven and Magnetically Actuated Multi-Use Wax Valves for Controlled Sealing and Releasing of Fluids on Centrifugal Microfluidic Platforms. Micromachines 2022, 13, 303. [Google Scholar] [CrossRef] [PubMed]
- Vlcnovska, M.; Stossova, A.; Kuchynka, M.; Dillingerova, V.; Polanska, H.; Masarik, M.; Hrstka, R.; Adam, V.; Kanicky, V.; Vaculovic, T.; et al. Comparison of Metal Nanoparticles (Au, Ag, Eu, Cd) Used for Immunoanalysis Using LA-ICP-MS Detection. Molecules 2021, 26, 630. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhou, X.; Wang, J.; Fang, D. A Red-Emitting Europium(III) Complex as a Luminescent Probe with Large Stokes Shift for the Sequential Determination of Cu2+ and Biothiols in Real Samples. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 282, 121663. [Google Scholar] [CrossRef]
- An Introduction to the Physics of Rapid Detection Tests. COMSOL. Available online: https://www.comsol.com/blogs/an-introduction-to-the-physics-of-rapid-detection-tests/ (accessed on 25 September 2025).
- Snyder, L.R.; Kirkland, J.J.; Dolan, J.W. Introduction to Modern Liquid Chromatography; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Peshin, S.; George, D.; Shiri, R.; Madou, M. Reusable Capillary Flow-Based Wax Switch Valve for Centrifugal Microfluidics. In Electrochemical Society Meeting Abstracts 239; MA2021-01; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2021; p. 1611. [Google Scholar] [CrossRef]
- McWhorter, D.B. 6.1 Effective Molecular Diffusion Coefficient. In Flux Equations for Gas Diffusion in Porous Media; The Groundwater Project: Guelph, ON, Canada, 2021; Available online: https://gw-project.org/books/flux-equations-for-gas-diffusion-in-porous-media (accessed on 5 October 2025).
- Samant, K.D.; Ng, K.M. Effect of kinetics and mass transfer on design of extractive reaction processes. AIChE J. 1998, 44, 2212–2228. [Google Scholar] [CrossRef]
- Fogler, H.S.; Fogler, S.H. Elements of Chemical Reaction Engineering; Pearson Educación: Madrid, Spain, 1999. [Google Scholar]
- Gasperino, D.; Baughman, T.; Hsieh, H.V.; Bell, D.; Weigl, B.H. Improving Lateral Flow Assay Performance Using Computational Modeling. Annu. Rev. Anal. Chem. 2018, 11, 219–244. [Google Scholar] [CrossRef]
- Zhang, X.; Huk, D.J.; Wang, Q.; Lincoln, J.; Zhao, Y. A Microfluidic Shear Device That Accommodates Parallel High and Low Stress Zones within the Same Culturing Chamber. Biomicrofluidics 2014, 8, 054106. [Google Scholar] [CrossRef]
- Kašpar, O.; Koyuncu, A.H.; Hubatová-Vacková, A.; Balouch, M.; Tokárová, V. Influence of Channel Height on Mixing Efficiency and Synthesis of Iron Oxide Nanoparticles Using Droplet-Based Microfluidics. RSC Adv. 2020, 10, 15179–15189. [Google Scholar] [CrossRef]




| Name | Value | Description |
|---|---|---|
| L0 | 39.6 mm | Paper strip height |
| W0 | 2.96 mm | Paper strip width |
| th | 0.63 mm | Paper strip thickness |
| gamma | 0.0723 N/m | Surface tension |
| theta | 50 deg | Contact angle |
| Rc | 13.5 × 10−6 m | Pore radius/HF090 membrane |
| pec | 44,492 N/m2 | Entry capillary pressure |
| lp | 2 | Pore size distribution index |
| por | 0.8 | Porosity |
| K | 3.58 × 10−12 m2 | Permeability |
| rho_air | 1 kg/m3 | Air density |
| rho_water | 1000 kg/m3 | Water density |
| mu_air | 1.76 × 10−5 Pa·s | Air viscosity |
| mu_water | 0.001 Pa·s | Water viscosity |
| omega | 100 rad/s | Angular acceleration |
| Rout | 5 cm | Strip outer-end location on disc |
| Rin | Rout-L0 | Strip inner-end location on disc |
| k1 | 13.5 × 108 m3/s·mol | Kon |
| c0 | 2.3 × 10−4 mol/m3 | Inlet antibody concentration |
| c0ads | 5 × 10−7 mol/m2 | Adsorbed species surface concentration, conjugate pad |
| D1 | 3 × 10−11 m2/s | viscosity |
| k2 | k1/10 | Koff |
| N_a | 6.022 × 1023 mol−1 | Avogadro’s number |
| d_pa | 1.3 × 10−5 m | Particle diameter |
| Damköhler (Da) | Péclet (Pe) | Sherwood (Sh) | Transport–Reaction (TRc) | |
|---|---|---|---|---|
| What does each merit number represent? | Reaction rate vs. advective transport | Convective vs. diffusive transport | Mass transfer coefficient vs. diffusion | Effective surface reaction efficiency under constrained film thickness |
| Does it explicitly include the liquid film height? | ✗ | ✗ | ✗ | ✓ |
| Surface vs. bulk assay applicability | ✗ Bulk reactions with limited applicability for surface reactions | ✗ Bulk transport | ✗ Mass flux at interface, no reaction kinetics | ✓ Applicable for surface-based reactions |
| Does it include the dwell time over active surface? | ✓ Indirectly via flow rate | ✗ | ✓ Indirectly, via convective mass transfer coefficient | ✓ (tres = L/u) |
| Can it be used as a guideline for surface assay optimization? | ✗ | ✗ | ✗ | ✓ Consideration of three TRc regimes (>1, 0.1–1, <0.1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peshin, S.; Gavin, A.; Rie, N.; Jain, A.; Felgner, P.; Madou, M.J.; Kulinsky, L. Interplay of the Mass Transport and Reaction Kinetics for Lateral Flow Immunoassay Integrated on Lab-on-Disc. Sensors 2025, 25, 6271. https://doi.org/10.3390/s25206271
Peshin S, Gavin A, Rie N, Jain A, Felgner P, Madou MJ, Kulinsky L. Interplay of the Mass Transport and Reaction Kinetics for Lateral Flow Immunoassay Integrated on Lab-on-Disc. Sensors. 2025; 25(20):6271. https://doi.org/10.3390/s25206271
Chicago/Turabian StylePeshin, Snehan, Anthony Gavin, Nakajima Rie, Aarti Jain, Philip Felgner, Marc J. Madou, and Lawrence Kulinsky. 2025. "Interplay of the Mass Transport and Reaction Kinetics for Lateral Flow Immunoassay Integrated on Lab-on-Disc" Sensors 25, no. 20: 6271. https://doi.org/10.3390/s25206271
APA StylePeshin, S., Gavin, A., Rie, N., Jain, A., Felgner, P., Madou, M. J., & Kulinsky, L. (2025). Interplay of the Mass Transport and Reaction Kinetics for Lateral Flow Immunoassay Integrated on Lab-on-Disc. Sensors, 25(20), 6271. https://doi.org/10.3390/s25206271









