Abstract
To date, visual analysis is mainly used to evaluate images of dehydrated films (facies) of biological fluids—microscopy at various magnifications, illumination with white or polarized light, as well as using a dark field. At the same time, important information on the architectonics of optically anisotropic supramolecular networks of facies is unknown (inaccessible). In our work, a model of optical anisotropy of the architectonics of supramolecular networks of blood facies is proposed. Algorithms and a methodology for a new multifunctional method of polarization-interference visualization of the Jones matrix and digital layer-by-layer phase reconstruction of optical anisotropy maps (theziograms) have been developed. As a result, statistically significant markers of oncological changes in the polycrystalline architectonics of supramolecular networks of blood facies samples from healthy donors and patients with papillary thyroid cancer at different stages of the oncological process have been determined and physically analyzed. A comparative study of the diagnostic efficiency of Jones matrix theziography (JT) and Mueller matrix diffusion tomography (MDT) of blood facies samples was conducted within the framework of evidence-based medicine. The main advantages of the Jones matrix method are shown: its multifunctionality (complex detection of birefringence and dichroism), high accuracy of early (stage 1: JM—90.4% and MDT—78.8%) and current (stage 2: JM—96.2% and MDT—88.5%) cancer diagnostics and an excellent level (JM—94.2% and MDT—84.6%) of differentiation of papillary thyroid cancer stages.
1. Introduction
One of the most important systems for ensuring the vital activity of the body is a set of biological fluids involved in metabolic processes. In biological liquid (BL), there are high-speed changes in the molecular composition and the nature of the interaction of various components in physiological, extreme, and pathological conditions [1,2,3].
A BL drop lying on a horizontal plane is a convenient model of a self-organizing system for the study of physical–chemical processes whose properties are determined by the composition of dissolved substances in a liquid, external dehydration conditions, and the substrate material. As a result of dehydration of the BL drop, a dry film is formed—a “facia”—the structure of which carries information about the composition and relationships of substances dissolved in BL. By studying such a system at the macroscopic level of its self-organization, the researcher receives information about the behavior of the system at the molecular level [4,5]. To date, visual analysis—microscopy at various magnifications, illumination with white or polarized light, as well as using a dark field—has been mainly used to evaluate images of facies of biological fluids [6,7,8].
The existing microscopic methods for processing the geometric structure of BL images contain only general algorithms, the result of which does not depend on the specifics of the processed images. At the same time, no less important information about the architectonics of supramolecular self-organized networks of BL molecular crystals, and their optical anisotropic properties, which can be extracted by polarization introscopy, turns out to be unknown (inaccessible). The first steps toward polarimetry of the crystalline structure of biological fluid facies were made at the end of the last century [9,10]. This direction was subsequently developed using laser polarimetry techniques; the methods of 2D polarization mapping of microscopic images of facies of blood plasma, blood, urine, and other BL have been developed and experimentally tested using various algorithms (statistical, correlation, wavelet, and Fourier analysis) of data processing [11,12,13,14,15,16,17,18,19,20]. As a result, the first objective criteria (markers) were found, which provided the possibility of differential diagnosis of various pathologies in urology, gynecology, and oncology. However, the sensitivity and progress of these methods were limited by the lack of algorithms for obtaining theziograms of polycrystalline networks of volumetrically inhomogeneous facies of biological fluids.
A new stage in this area of biomedical diagnostics was the successful integration of polarization and interference techniques for mapping laser speckle fields—optical coherence tomography (OCT) [21,22,23,24,25,26,27,28,29]. This technique makes it possible to obtain layer-by-layer coordinate distributions of Jones and Mueller matrix elements, as well as anisotropy maps from small depths (up to 2 ) of biological tissues. As a result, it was possible to accurately diagnose fibrosis and determine tumor areas with low fibrosis [29]. However, the sensitivity of such systems is limited by the distorting effect of a high level of depolarized laser speckle background on the contrast of polarization images of layers of such tissues. In addition, OCT systems are expensive, have insignificant (8 –10 ) resolution, and do not provide differentiation of benign and malignant tumors, which is important at the early stages of cancer diagnostics. At the same time, the OCT technique has demonstrated new possibilities for three-dimensional polarimetric biomedical diagnostics of pathological changes in biological tissues.
Nevertheless, the results obtained using the OCT technique still remain somewhat empirical. At the moment, there is no systematic information on the capabilities of this method for tissue samples with different optical thickness and depolarizing capacity, morphological structure, and various types of pathology (cancer of various organs and its stages).
From a physical point of view, the solution to this problem consists of establishing criteria for an unambiguous determination of the biological significance of OCT data. The basis for such a solution may be the development and experimental testing of a new laser polarization-interference technology that will expand the functionality of OCT and increase its sensitivity by minimizing the influence of diffuse depolarized background.
The main advantage of the indicated polarization-interference methods is the possibility of selecting components of speckles scattered with different multiplicity by means of layer-by-layer phase scanning of the algorithmically reconstructed object field of complex amplitudes. As a result, conditions are achieved for selecting a single scattered amplitude-phase component, which is unambiguously related to the parameters of the optically anisotropic architectonics of the biological layer.
At present, a small number of publications are known that are aimed at the implementation and diagnostic use of the polarization-interference layer-by-layer visualization techniques of biological preparations of polycrystalline architectonics [30,31,32,33,34,35]. This makes it possible to obtain information on the layer-by-layer statistical structure of tissue biological samples optically anisotropic architectonics, which is inaccessible to traditional 2D matrix polarimetry [9,10,11,12,13,14,15,16,17,18] and OCT techniques [21,22,23,24,25,26,27,28,29]. As a result, the diagnostics and differentiation sensitivity and accuracy of various pathological and necrotic changes in such objects increase. In particular, the high accuracy of benign and malignant tumor differentiation [30,31,32], as well as the possibility of determining the necrotic and traumatic changes in age in the internal organ’s tissues optically anisotropic structure have been demonstrated [33,34,35].
Another important vector of polarization-interference methods development is the study of the biological fluids dehydrated films (facies) polycrystalline architectonics volumetric structure. Such objects are more easily accessible and do not require traumatic biopsy surgery.
In the “pioneering” polarization-interference studies [36] of blood films’ optical anisotropy layered maps the possibility of diagnosing late middle (3 + 3) and low-differentiation prostate cancer (4 + 4; 5 + 3 on the Gleason scale) with high accuracy (90%) was demonstrated. However, the sensitivity of this method was insufficient for diagnosing and differentiating earlier stages of cancer. This circumstance is associated with the following analytical and physical factors:
- The Mueller matrix technique has been developed and is analytically adequate for measuring the coordinate distributions of the magnitude of polarization-filtered intensity arrays of scattered object fields of biological preparations [36,37,38,39,40,41,42,43,44].
- The specified vector parametric approach does not provide the possibility of implementing a direct Fourier reconstruction of layer-by-layer distributions of complex amplitudes of the scattered laser field.
Based on the above, it can be concluded that the 3D technique of Mueller matrix tomography of the polycrystalline structure of biological preparations using laser probing requires further development, both in terms of sensitivity, as well as in analytical and instrumental aspects.
Our work uses a different methodology that is more adapted to polarization-inhomogeneous laser fields. Its main differences are:
- Adequate analytical Jones matrix formalism for the direct description of the processes of formation of polarization structure of amplitude-phase coherent object fields of polycrystalline blood films.
- Application of digital Fourier reconstruction and layer-by-layer phase scanning of Jones matrix images of complex amplitudes with subsequent reconstruction of distributions of linear and circular birefringence-dichroism of blood film samples.
Based on the above, it can be assumed that the proposed polarization-interference Jones matrix sensor of changes in optical anisotropy of blood film samples will provide greater accuracy and sensitivity in early cancer diagnostics. Therefore, we took advantage of these advantages in order to determine the criteria for differential diagnostics of earlier stages of cancer using stage 1 papillary thyroid cancer as an example.
The relevance of this task is due to the fact that traditional digital microscopy techniques [45] aimed at studying thyroid nodule biopsy with subsequent obtaining of intensity distribution histograms have become an addition to histological methods. On this basis, the possibility of differential diagnosis of thyroid nodules as benign (follicular adenoma) or malignant (papillary carcinoma) was demonstrated.
New objective quantitative technologies with high spatial resolution have become a qualitative development of digital histology [46]. First of all, these include polarization-sensitive second harmonic generation (PSHG) microscopy methods [47,48]. These techniques have demonstrated the ability to differentiate cancerous or diseased tissues by analyzing circular dichroism and modulating laser polarization states [49].
However, at this point in time, there is no systematic quantitative information on the effect of light scattering on the accuracy of differential diagnostics within representative samples of histological biopsy specimens of thyroid tissue.
The question of the possibility of using the PSHG technique in studying the relationships between the optically anisotropic architecture of blood films and pathological conditions of the thyroid gland remains open.
The goal of our work is development of algorithms and experimental testing of a new multifunctional method of polarization-interference visualization of the Jones matrix and digital layer-by-layer phase reconstruction of optical anisotropy maps (theziograms) of supramolecular networks of dehydrated blood films (phases) by determining statistically significant markers characterizing the reconstructed layer-by-layer theziograms of birefringence and dichroism for early diagnosis (stage 1) and differentiation of stages (stage 1 and stage 2) of papillary thyroid cancer.
2. Basic Equations and Theoretical Remarks
This part of the article is devoted to the theoretical substantiation of the multifunctional method of Jones matrix theziography of optically anisotropic polycrystalline architectonics of dehydrated blood films. Analytical interrelations between linear and circular birefringence and dichroism of supramolecular networks and matrix elements, the value of which is determined by the orthogonal components of complex amplitudes of the object field of blood facies, are determined. This ensured the development of principles for layer-by-layer reconstruction of the parameters of optical anisotropy of the polycrystalline structure of biological films.
According to traditional concepts [50,51,52,53], single scattering approximations by a polycrystalline film of any biological fluid can be represented as a sequence of partial layers with six different optical anisotropy types: linear and circular birefringence () and dichroism (). These , , , and —“linear dichroism—birefringence”; and —“circular dichroism—birefringence” of the biological layer of the optically anisotropic component for linearly ( and ) and circularly right—() and left—() polarized orthes.
The mechanisms of linear birefringence and dichroism (structural anisotropy ) are inherent in the dendrite polycrystalline networks, which are formed by needle-like crystals [9,10,11].
Molecular complexes of spherulite crystals have optical activity () and circular dichroism () [12,13,14,15,16].
An analytical form of the generalized Jones matrix of a polycrystalline medium with complex anisotropy was found in [40,41]
here —generalized anisotropy vector
where
from (2), (3) we obtain an explicit form of the vector modulus
here
The algorithm for calculating the elements of the generalized Jones matrix (Equation (1)) includes the irradiation of a polycrystalline BF sample by linearly polarized beams with azimuths (Jones vector ) and (Jones vector )
Based on (1)–(8), theoretical relationships between the parameters of linear and circular birefringence-dichroism and optically anisotropic BF layer Jones matrix elements are established
Birefringence
Dichroism
As a result, we obtain the following expressions for the BF polycrystalline structure Jones matrix theziography
Birefringence
Dichroism
In what follows, expressions (13)–(14) will be called Jones matrix theziogram
Note that the theziograms (15) of the BF are obtained in the single scattering approximation and, therefore, they unambiguously display the optical properties of their polycrystalline structure. However, for most real BF, such an approximation is not performed or is difficult to achieve. As a result, the set of theziograms (15) displays integrally averaged information about the optical anisotropy maps of the facies under study.
In our work, we will consider the possibility of overcoming this problem. It is based on the principles of Mueller polarization-interference reconstruction and phase scanning biological layers object complex amplitude field technique [28,29,30,31,32,33,34,35].
As we have already noted, the peculiarity of our method in the implementation of the technique of phase scanning of laser object fields of polycrystalline blood films is the application of the Jones matrix formalism (relations (1)–(9)) for the reconstruction of optical anisotropy theziograms (relations (10)–(15)).
The main experimental toolkit of this approach is the sequential implementation of:
- complex interference registration and polarization filtering of the object field of blood facies;
- digital Fourier reconstruction of the amplitude-phase structure of the object field;
- step-by-step phase scanning of distributions of complex amplitudes;
- algorithmic reconstruction of Jones matrix theziograms of “birefringence-dichroism” in a set of phase planes.
The methodological implementation of this polarization-interference technique is illustrated in the following section of the article.
3. Three-Dimensional Jones Matrix Scanning Method
- Two states of linear polarization are sequentially formed in the “irradiating” () and “reference” () parallel laser beams— and .
- For each of the polarization states ( and ), two partial interference patterns are recorded through the polarizer–analyzer with the transmission plane orientation at angles .
- For each partial interference distribution, we perform a two-dimensional discrete Fourier transform [10,12]:Digital Fourier transforms (16) for determining the set of Jones matrix theziograms can be rewritten in the following formwhere complex amplitude orthogonal components for different orientations *—denotes the complex conjugation operation; they are the spatial frequencies and are the quantity of pixels of the CCD camera.
- The digital Fourier transforms (relations (16)–(18)) results are used to obtain complex amplitude distributions according to the following algorithms:
- Using stepwise () phase () reconstructed complex amplitudes (relations (19), (20)) scanning and using algorithms (13), (14) we obtain Jones matrix theziograms for differently scattered components of the BF object field.
- The resulting set of BF Jones matrix theziograms was analyzed in a statistical approach using the following algorithms to calculate the mean (), variance (), skewness (), and kurtosis () [9,10,11,12,13,14,15,28,29,30,31,32,33,34,35]where —CCD pixels quantity.
The presented analytical relations (16)–(21) constituted the algorithmic basis of the methodology of multifunctional Jones matrix theziography of polycrystalline blood films.
The results of its experimental implementation are presented in the next section of the article.
4. Experimental Results and Discussion
This study was conducted in accordance with the principles of the Declaration of Helsinki, and in compliance with the International Conference on Harmonization Good Clinical Practice, and local regulatory requirements. Ethical approval was obtained from the Ethics Committee (protocol №7, 16 May 2024) of the Bukovinian State Medical University (Chernivtsi, Ukraine), and written informed consent was obtained from all subjects prior to study initiation.
The fundamental aspect of the research is considered, which is related to the fact that in the process of dehydration and molecular self-assembly, various architectonics and optical anisotropy of polycrystalline networks of various constituent BF are formed [54,55,56]. The obtained data on the polarization manifestations of the optical properties of such networks can be used to determine the totality of physical and quantitative relationships between the topology of optical anisotropy maps and the specifics of the biological crystal’s ensembles spatial-angular structure. For this purpose, polarization-interference mapping, analytical reconstruction, statistical processing, and physical analysis of integral and layered Jones matrix theziograms of linear and circular birefringence and dichroism of healthy donors BF were carried out.
4.1. Objects of Investigations
In our work, we will consider BF, which consists of two main parts:
- blood plasma;
- shaped elements.
Blood plasma. It is a liquid of a complex structure, a heterogeneous colloidal polymer solution. Traditionally, the molecular components (monomers of albumin (~60%), globulin (~40%), fibrinogen, hemoglobin) of blood plasma are effectively studied by biochemical methods. However, there are currently insufficient effective research methods to study supramolecular optically anisotropic (dimers, trimers, and monomers) protein structures () of blood plasma [54,55,56].
Three zones of different thickness are distinguished in the structure of the blood plasma surface:
- edge (polycrystalline albumin layer with linear birefringence and dichroism, ;
- transitional (outer and inner layers of optically isotropic cubic crystals of the Na–Cl salt, intermediate globulin layer with circular birefringence and dichroism, ~25 μm–30 μm);
- the central (outer layer of cubic crystals of salt Na–Cl, ~).
Such an image of plasma binding possesses mainly a dendritic supramolecular polycrystalline network with structural anisotropy (“”) and insignificant optical activity (“”). In the future, such a network will be called dendritic.
The shaped elements are erythrocytes, platelets, and leukocytes with circular birefringence and dichroism. As a result, a spherulite polycrystalline network is formed (“”).
Experimental samples of blood facies were provided by the Department of Surgery № 1 of the Bukovinian State Medical University (as example—Figure 1).
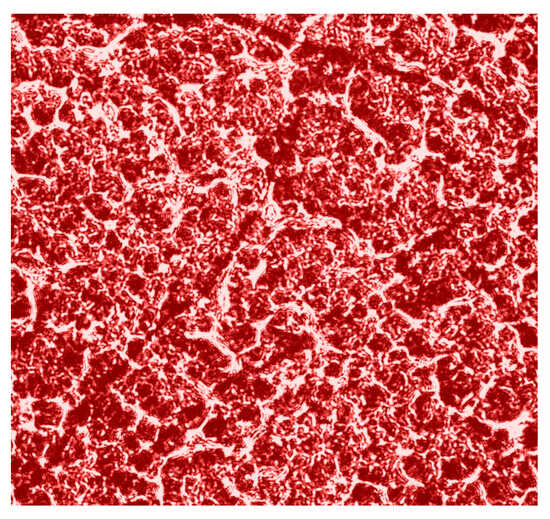
Figure 1.
Microscopic image (×4) of the polycrystalline structure of blood facies.
BF samples were obtained by applying a liquid drop to a glass substrate at room temperature () and drying for 24 h. We reduced the volume of a liquid drop to 0.035–0.004 . As a result of blood dehydration, blood facies were formed with an average height of up to 60 μm and a diameter of up to 3–4 .
The extinction coefficient () of BF layers was measured according to the standard photometry attenuation illuminating beam intensity method [57] using an integral light-scattering sphere [58]. The measurement of the BF sample’s integral depolarization degree () was carried out in the standard Mueller matrix polarimeter scheme [12,13,14,15,16].
Optical-geometric parameters of samples BF are presented in Table 1.

Table 1.
BF samples optical parameters.
The number of samples to ensure statistical significance (representativeness) of the blood facies group was determined by the cross-validation method [59]. The standard deviation of the statistical moments , which characterize the distribution of the Jones matrix theziograms parameter values, was determined. The specified number () of samples provided the level . This standard deviation corresponds to a confidence interval of , which demonstrates the statistical reliability of the 3D Jones matrix mapping method.
In order to study the volumetric optically anisotropic polycrystalline structure of blood facies samples, the polarization-interference method of mapping laser object fields was used. For the purpose of experimental implementation of theoretical algorithms of laser layer-by-layer Jones matrix theziography (relationships (1)–(20)) of supramolecular networks of blood facies samples (Table 1), a Mach-Zehnder interferometer platform was used, a photograph and a brief description of the laboratory implementation of which are presented in the next part of the article.
4.2. The Experimental Setup
Photograph and optical scheme of the tabletop experimental setup of the Mach-Zehnder polarization interferometry scheme is shown in Figure 2 [28,29,30,31,32,33,34,35].

Figure 2.
Optical scheme for BF polarization-interference mapping: 1—He–Ne laser; 2—collimator—“O”; 3, 11—beam splitters—“BS”; 4, 5—mirrors—“M”; 6, 9, and 13—polarizer’s “P”; 7, 10—quarter wave plates—“QP”; 8—object; 12—polarization objective—“O”; 14—digital camera—“CCD”; 15—personal computer—“PC”.
The parallel beam of He–Ne () laser 1 formed by spatial-frequency filter 2, with 50% of beam splitter 3 is divided into “object” and “reference” ones. The “object” beam is guided by rotating mirror 5 through polarizing filters 6–7 toward BF sample 8. The polarization-inhomogeneous image of BF 8 is then projected onto digital camera 14 plane using the strain-free objective 12.
The “reference” beam is directed by mirror 4 through the polarization filter 9–10 into the BF 8 polarization-inhomogeneous image plane. As a result, an interference pattern is formed, the coordinate intensity distribution of which is recorded by digital camera 14 through polarizer 13. Before carrying out the measurements of BF, the experimental device passed metrological certification with the model objects (“clean air”, “linear polarizer”, “phase plates 0”.25” λ”, “0”.5” λ”) introduction. As 50 measurements result for each object, the optical anisotropy errors were determined .
The next part of the article is devoted to the analysis of group experimental measurements of polarization-filtered interference distributions of image intensity of blood facies samples with the subsequent algorithmic restoration of a set of layered Jones matrix theziograms of optically anisotropic architectonics of supramolecular networks.
4.3. Jones Matrix Theziography of Phase Anisotropy of Polycrystalline Blood Films
The series of fragments in Figure 3 show the experimental results of the polarization-interference Jones matrix theziography method (relationships (7)–(20)) of linear and circular birefringence of BF:
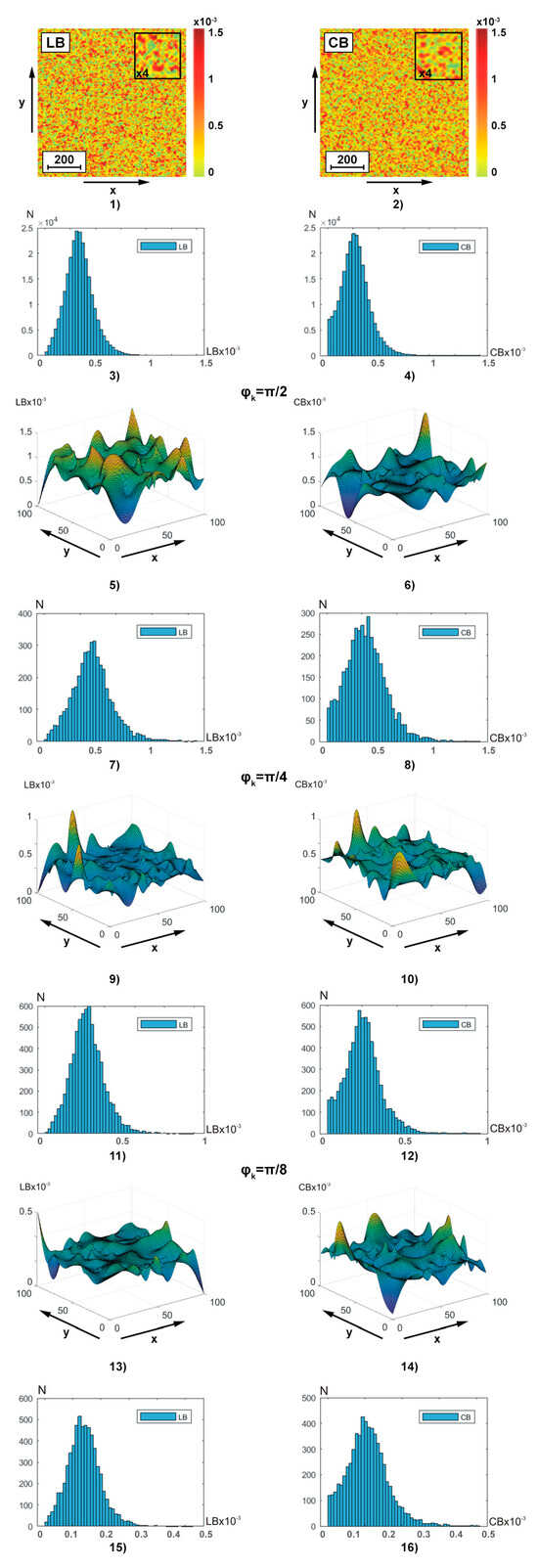
Figure 3.
Two-dimensional distributions and histograms of integral ((1)–(4)) and layer-by-layer () ((5)–(16)) linear ((1), (3), (5), (7), (9), (11), (13), and (15)) and circular ((2), (4), (6), (8), (10), (12), (14), and (16)) birefringence BF theziograms. Explanation in the text.
- coordinate distributions ( and ) of integral theziograms and —fragments (1) and (2);
- histograms of probability distributions of and integral values of linear and circular birefringence of polycrystalline architectonics—fragments (3) and (4);
- coordinate distributions () of reconstructed (ratios (13), (14), (17), (19), and (20)) layer-by-layer theziograms (fragments (5), (9), and (13)) and (fragments (6), (10), and (14) in different phase sections (, fragments (5) and (6)), , (fragments (9) and (10)), , fragments (13) and (14));
- histograms and of layer-by-layer distributions of linear and circular birefringence values of polycrystalline architectonics in different phase planes in different phase sections (, fragments (7) and (8)), , fragments (11) and (12)), , fragments (15) and (16)).
Integral theziograms were obtained by polarization-interference mapping (Figure 2) of the coordinate distributions of the elements of the Jones matrix of the blood facies (relations (7), (8), (10), (11), and (16)) with subsequent analytical reconstruction (relation (13), (14), (17), (19), and (20)) of the and maps.
Reconstruction (relation (17) and (19)) of the layered theziograms in different phase planes () of the object field of complex amplitudes (relation (16)) was carried out by step-by-step phase scanning (relations (19) and (20)) and sequential algorithmic calculations (relation (13)). The analysis of the theziograms of linear and circular birefringence confirmed the adequacy of the proposed model representations (relationships (1)–(15)) about the optical anisotropy of the BF polycrystalline architectonics.
Comparison of coordinate (Figure 3, fragments (1), (2), (5), (6), (9), (10), (13), and (14))) and probabilistic (Figure 3, fragments (3), (4), (7), (8), (11), (12), (15), and (16))) distributions of phase anisotropy parameters ( and ) of BF revealed:
- individual structure of algorithmically reconstructed integral and layer-by-layer theziograms of linear and circular birefringence of optically anisotropic architectonics—fragments (1), (3) and (2), and (4);
- dependence of the average level and the magnitude of the range of change in fluctuations of random values of phase anisotropy parameters on the magnitude of the phase parameter in the reconstructed object field of complex amplitudes—fragments (5), (7), (9), (11), (13), and (15) and (6), (8), (10), (12), (14), and (16);
- the tendency to decrease the magnitude of fluctuations of random values of linear and circular birefringence in the phase planes ) of the field of complex amplitudes with smaller values of the scanning parameter (relationships (19) and (20))—fragments (5), (9), and (13) and (6), (10), and (14).
The discovered features of the Jones transformation of matrix reconstructed theziograms can be associated with the influence on the calculated value of the birefringence parameter of different multiplicities () of light scattering in the considered phase planes ()) of the BF object field.
For integral theziograms and the scattering factor of laser radiation in the volume of polycrystalline blood facies is maximal. Each local () act of interactions of laser radiation with an optically anisotropic domain of polycrystalline architectonics corresponds to “true” values of the set of elements of the Jones matrix (Equations (7) and (8)). Applying algorithm (10) to them, it is possible to reconstruct the theziograms of the real 3D polycrystalline structure of the blood facies. This “ideal” situation is distorted (multiplied) by multiple () acts of interaction—scattering. As a result, the Jones algorithms for reconstructing phase anisotropy theziograms (Equation (10)) recreate coordinate distributions with significantly greater values of linear and circular birefringence. As the value of the phase scanning parameter decreases (), components with a lower multiplicity () of light scattering are extracted from the object field of complex amplitudes. This enables Jones matrix reconstruction of the BF phase anisotropy theziograms are closer to real ones.
Finally, starting from a certain level of the phase scanning parameter , the most informative component with a minimum (mainly single ) multiplicity of light scattering in the volume of the blood facies is “extracted” from the object field. In this situation, the maximum sensitivity of the reconstructed theziograms to pathological changes in the BF optically anisotropic architectonics is realized. The considered scenario of layer-by-layer polarization-interference Jones matrix reconstruction of phase anisotropy parameters quantitatively characterizes the results of statistical analysis (ratios (21)) of the distributions of and —Table 2.

Table 2.
First–fourth-order statistical moments that characterize the and theziograms.
The following has been established:
- individual and different Gaussian () statistics of holographically reproduced BF theziograms and ;
- the third and fourth orders of statistical moments were the most sensitive to changes in the topographic structure of BF phase anisotropy theziograms;
- twofold range of phase change (for different conditions of light scattering in the BF volume) of and values.
The results obtained may be related to the following physical considerations, which are based on the model analysis ((1)–(20)) of the BF optical-anisotropic properties.
We have already noted that the biochemical structure of blood can be conditionally represented in the form of a “two-component mixture”—plasma and shaped elements.
The magnitude of linear birefringence is mainly determined by the degree of needle crystals optical axes spatial orientation () of the marginal albumin layer, which can be quite large— [9,10,57,58,59]. As a result, the first and second order statistical moments, which characterize the mean and variance of the distributions , have a small value. The values of higher orders statistical moments , which determine the asymmetry and excess of polycrystalline dendritic network BF, are quite large—Table 2.
The magnitude of the BF circular birefringence (globulin crystals and shaped elements of erythrocytes, platelets, leukocytes, etc.) [15,16,57,58,59], is quite large. Moreover, for a drop of blood, a significant concentration of spherulites provides an almost commensurate value for the entire volume of the optical activity parameter with the value of the linear birefringence parameter of the needle dendritic network of albumin crystals. Accordingly, the statistical moments and are given in Table 2.
In digital holographic phase scanning of volumetric depth BF, various implementations of polycrystalline networks with optically anisotropic parameter distributions (directions of optical axes, phase shifts between orthogonal amplitude components) are consistently distinguished. As a result, individual orientation distributions () with a certain random variance of their values are reproduced for each phase plane. In addition, when the conditions of small or single scattering are reached, the range of changes in the values of random phase shifts narrows. Approaching the conditions of an optically thin layer (ratios (1)–(14)), the statistics of the BF phase anisotropy ( and ) changes in the following scenarios—.
Along with the phase-shifting capacity of the supramolecular networks of blood facies, mechanisms of optically anisotropic absorption are realized, the reconstruction and analysis of which is devoted to the next part of the article.
4.4. Jones Matrix Theziography of Amplitude Anisotropy of Polycrystalline Blood Films
Figure 4 illustrates, similar to the data of polarization-interference Jones matrix phase theziography (Figure 2), coordinate (fragments (1), (2), (5), (6), (9), (10), (13), and (14)) and probability (fragments (3), (4), (7), (8), (11), (12), (15), and (16)) distributions of linear (fragments (1), (3), (5), (7), (9), (11), (13), and (15)) and circular (fragments (2), (4), (6), (8), (10), (12), (14), and (16)) dichroism of BF polycrystalline architectonics. Integral theziograms and of amplitude anisotropy were reconstructed using algorithms (7), (8), and (11). To recreate layer-by-layer theziograms of linear and circular dichroism, relations (14), (18), (19), and (20) were used.
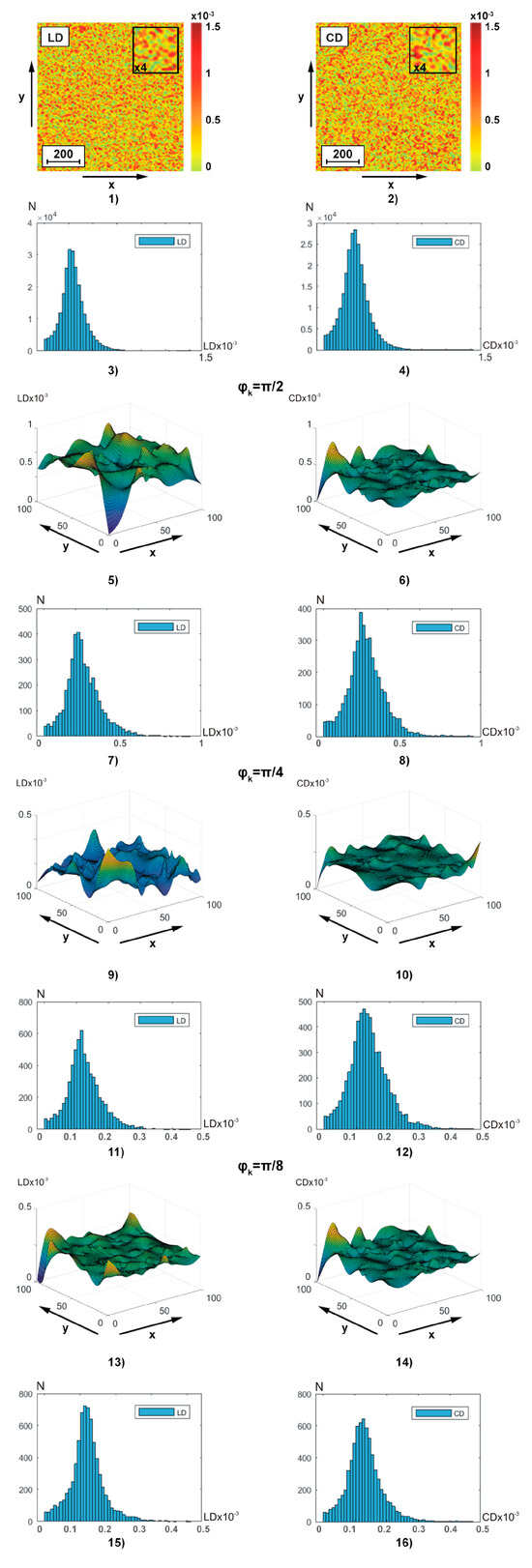
Figure 4.
Two-dimensional distributions and histograms of integral ((1)–(4)) and layer-by-layer () ((5)–(16)) linear ((1), (3), (5), (7), (9), (11), (13), (15)) and circular ((1), (3), (5), (7), (9), (11), (13), (15)) birefringence BF theziograms. Explanation in the text.
From the analysis of the obtained theziograms and of amplitude anisotropy (Figure 4) it is evident that for each coordinate distribution of random values of the magnitude of linear and circular dichroism of the BF polycrystalline architectonics, an individual coordinate (fragments (1), (5), (9), and (13) and fragments (2), (6), (10), and (14)) and probabilistic (fragments (3), (7), (11), and (15) and fragments (4), (8), (12), and (16)) structure is characteristic. A comparison of a series of layered theziograms of amplitude anisotropy (Figure 4, fragments (5), (7), (9), (11), (13), and (15)) and (Figure 4, fragments (6), (8), (10), (12), (14), and (16)) demonstrated a tendency, similar to the phase theziograms and (Figure 4), of decreasing the magnitude of fluctuations of the parameters of optically anisotropic absorption in the phase planes (),respectively) of the components of the object field of complex amplitudes with a low multiplicity of light scattering.
Quantitively phase transformation of the and theziograms is illustrated the 1st—4th orders central statistical moments—Table 3.

Table 3.
1st–4th orders statistical moments of the BF linear and circular dichroism.
Analysis has shown that:
- difference from zero (for all phase facies depths) values of all central statistical moment’s ;
- dependence of the magnitude of statistical parameters from the phase scan depth;
- the most sensitive markers for changes in amplitude anisotropy theziograms are 3rd and 4th orders statistical moments ;
- as the phase scanning parameter value increases (approaching single scattering conditions), the statistical parameters values increase to 85%, and increase by 60–80%.
From a physical point of view, the obtained results can be related to the fact that the value of linear dichroism , as well as linear birefringence, at all phase depths, is determined by the degree of spatial orientation optical axes needle protein crystals (albumin, fibrin, and elastin). Under the conditions of phase approximation to the optically thin layer, the changes in the orientations of the needle crystals optical axes, as well as the magnitude of phase shifts, the following scenario of changes in the first and fourth orders statistical moments magnitude is implemented——Table 3. Along with this, the value of circular dichroism combined “shaped elements—albumin—globulin grids” polycrystalline network (globulin crystals, shaped elements) is not less than the value of linear dichroism . Accordingly, the statistical moments and . Thus, the conducted cycle of fundamental polarization-interference studies BF optical anisotropy polycrystalline structure layer-by-layer maps is provided the basis for the applied Jones matrix theziography implementation.
The most sensitive markers () to changes in the optical anisotropy of the BF supramolecular networks, determined within the framework of statistical analysis of layered Jones matrix theziograms of the blood facies supramolecular networks, were used in applied studies of the diagnostic power of the polarization-interference method in the early detection of papillary thyroid cancer and differentiation of its stages.
5. Diagnostic Capabilities of Jones Matrix Theziography of Polycrystalline Blood Films
This part of the work includes three data arrays of experimental studies of blood facies.
The first part is devoted to a comparative study of the statistical structure of Jones matrix theziograms of linear and circular birefringence and dichroism of blood facies of donors (control group 1, 26 samples) and patients with the first stage of papillary cancer (stage 1—experimental group 2, 26 samples).
The second part is devoted to the study the diagnostic efficiency by BF layer-by-layer Jones matrix theziography for detection early stage of papillary thyroid carcinoma.
The third part contains the results of a comparative analysis of the effectiveness of diagnostics (group 1) and differentiation of stage 1 (group 2) and stage 2 (group 3, 26 samples) thyroid cancer using Jones matrix theziography and Mueller matrix tomography of blood facies.
5.1. Jones Matrix Theziograms of BF Phase and Amplitude Anisotropy
The diagnostic methodology of the developed polarization-interference method includes the following stages:
- polarization-interference mapping (Figure 2) of object fields of the set of samples of blood facies of group 1, group 2 and group 3;
- calculation (ratios (7), (8)) of the integral elements of the Jones matrix and the matrix operator of “single” (phase plane ) scattering;
- reconstruction of integral and layer-by-layer theziograms of the BF phase and amplitude anisotropy;
- statistical analysis (ratios (21)) of theziograms and determination of the most sensitive parameters (markers) and to pathological changes in the BF optically anisotropic architecture;
5.1.1. Phase Anisotropy Theziograms and
Figure 5 and Figure 6 show integral (a,b) (fragments (1) and (2)) and layer-by-layer (fragments (5) and (6)) linear (Figure 4) and circular (Figure 5) birefringence theziograms, as well as histograms of distributions (fragments (3), (4), (7), and (8)) from control group 1 (fragments (1), (3), (5), and (7)) and experimental group 2 (fragments (2), (4), (6), and (8)).
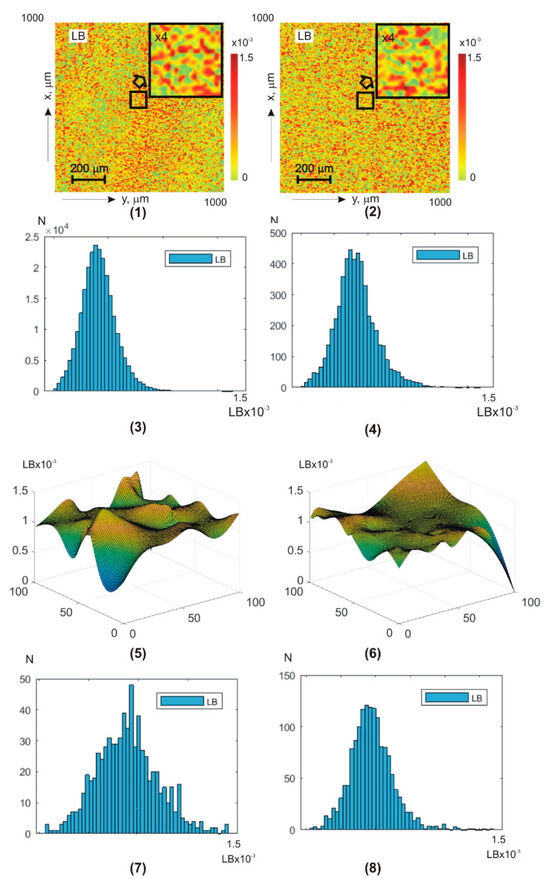
Figure 5.
BF theziograms and histograms of healthy donors (left column) and patients with papillary thyroid carcinoma (right column). Explanation in the text.
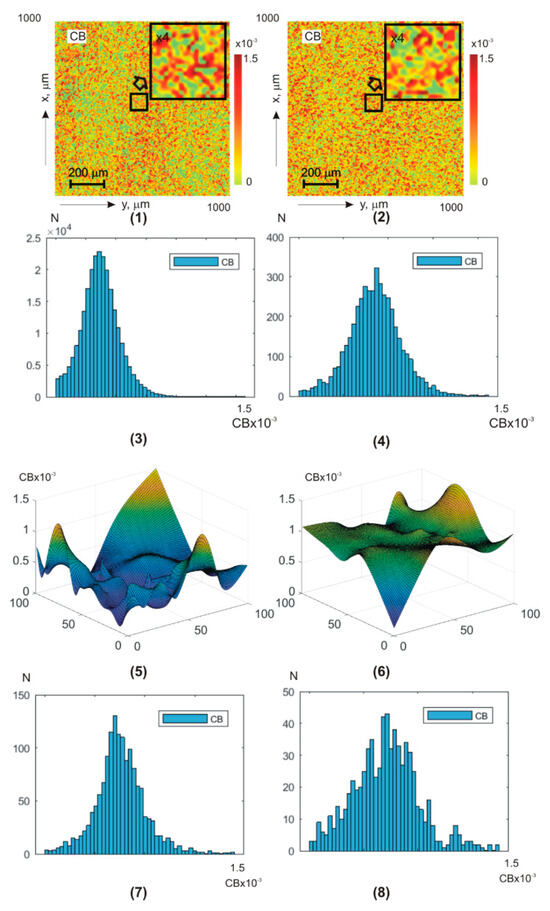
Figure 6.
BF theziograms and histograms of healthy donors (left column) and patients with papillary thyroid carcinoma (right column). Explanation in the text.
Quantitative phase transformation and intergroup differences between the and BF theziograms are illustrated by the statistical analysis results—Table 4.

Table 4.
Statistical parameters of and .
Statistical analysis of the phase anisotropy theziograms and revealed:
- for all phase depths, the central first–fourth-order statistical moments are non-zero- the third and fourth order statistical moments are the most sensitive markers (especially in the phase plane ) to changes in BF birefringence;
- for theziograms , the differences between the values of BF control and experimental groups diagnostic markers are 30–40%;
- for theziograms , the differences between the values of diagnostic markers increase and reach 45–55%.
From a physical point of view, the results obtained can be associated with the following features of BF architectonics polycrystalline networks pathological changes.
First, in previous classical vector parametric studies of optical anisotropy blood films and their plasma was demonstrated that the linear birefringence value is mainly determined by the degree of the albumin, fibrin, and elastin needle crystals’ optical axes spatial orientation [54,55,56].
The orientation changes in the directions of the optical axes in the dendritic grid are very large and almost equidistant—. As a result, the values of the first and second order statistical moments, which characterize distributions’ means and variance, are quite large. The values of higher-order statistical moments , on the contrary, are insignificant.
During the cancer process, blood crystallization increases. Due to this, for patients’ blood droplets, dehydrated films from experimental group 2, the range of changes decreases. As a result, the parameters decrease and, conversely, the third and fourth order statistical moments increase.
Secondly, the value of the globulin crystals and shaped elements (erythrocytes, platelets, leukocytes, and monocytes) of the spherulite optically anisotropic network of the circular birefringence [53,54,55] is commensurate with the linear birefringence values. With cancer inflammation, the globulin and white blood cell molecule concentration increases. This increases the blood droplets’ dehydrated films’ chiral molecular domains’ optical activity in patients with papillary thyroid carcinoma samples.
By this, first–fourth-order statistical moments, which characterize the circular birefringence random values distributions, undergo the following changesand, conversely, .
Third, as the scan phase shift decreases, a more optically thin rat blood-dehydrated film volume is released.
As a result, the albumin, fibrin, and elastin needle crystals’ optical axes directions distribution are transformed into an asymmetric one () with a value certain random dispersion. In addition, the range of changes in random values of phase shifts between laser radiation amplitudes orthogonal components is narrowed. These changes in the phase anisotropy theziograms statistics of dehydrated blood drop films and . Against this background, cancer differences in the optically anisotropic network’s polycrystalline structure of blood samples from experimental group 2 are more clearly revealed.
5.1.2. Amplitude Anisotropy Theziograms and
Figure 7 and Figure 8 show integral (a,b) (fragments (1) and (2)) and layer-by-layer (fragments (5), (6)) (Figure 7) and (Figure 8) theziograms, as well as histograms of (fragments (3), (4), (7), and (8)).
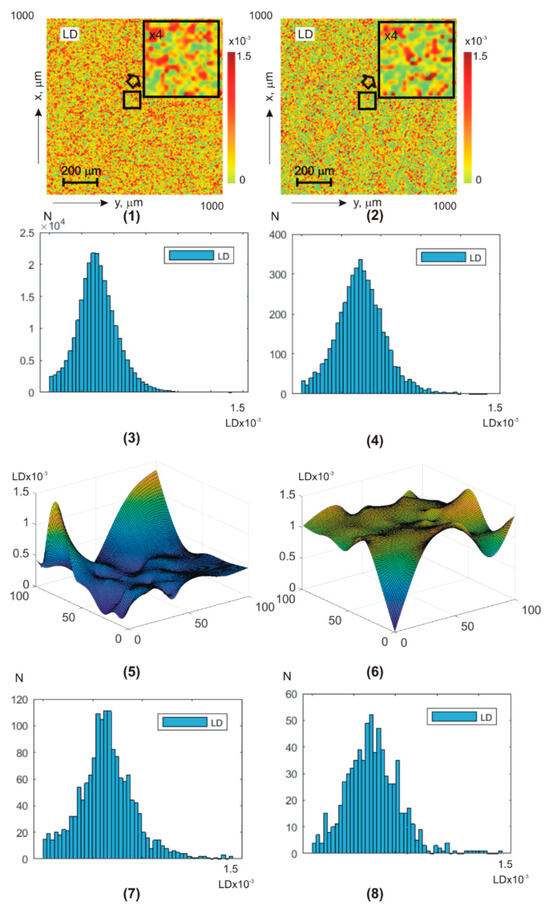
Figure 7.
BF theziograms and histograms of healthy donors (left column) and patients with papillary thyroid carcinoma (right column). Explanation in the text.
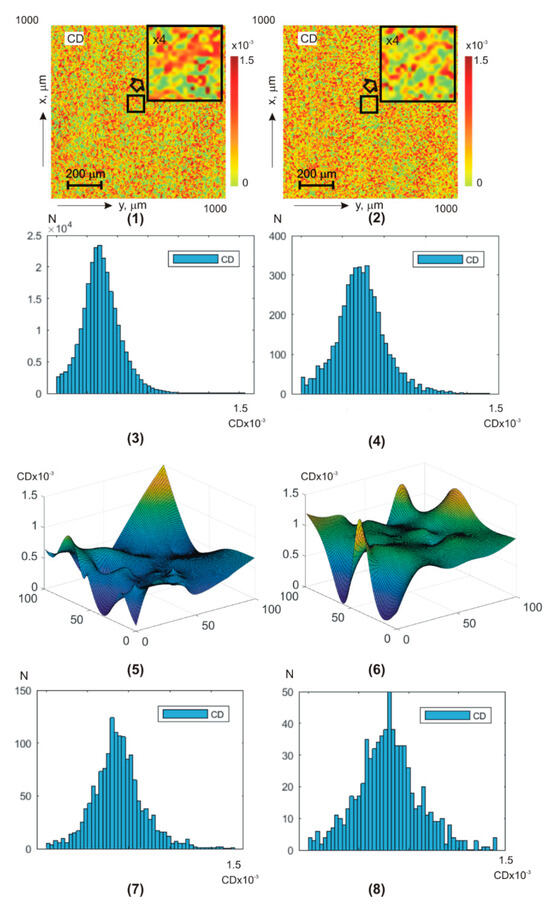
Figure 8.
BF theziograms and histograms of healthy donors (left column) and patients with papillary thyroid carcinoma (right column). Explanation in the text.
Control group 1 (fragments (1), (3), (5), and (7)) and experimental group 2 (fragments (2), (4), (6), and (8)).
Analysis of BF amplitude anisotropy theziograms for all phase depths revealed:
- difference all first–fourth-order statistical moment values from zero dependence of statistical distributions on the value of the phase scanning parameter of BF polycrystalline architectonics;
- the most sensitive diagnostic markers are third- and fourth-order statistical moments ;
- for linear dichroism theziograms, the differences between the diagnostic marker’s values of the control and experimental BF samples groups are 25–30%;
- for circular dichroism theziograms, the differences between the diagnostic marker’s values increase and reach 35–45%.
Quantitative phase transformation and intergroup differences between the and BF theziograms are illustrated by the statistical analysis results—Table 5.

Table 5.
Statistical parameters of and .
From a physical point of view, the results obtained can be attributed to the fact that phase scanning provides the ability to isolate a more optically thin volume of BF. Due to this, the topographic structure of BF theziograms becomes as close as possible to the statistics of the needle crystals (linear dichroism) optical axes directions distribution, as well as the values of phase shifts (circular dichroism). As a result, the maximum possible accuracy of detecting polycrystalline differences between BF rat samples from both groups is achieved.
A slightly lower accuracy level (information analysis of phase anisotropy theziograms—Table 5) can be associated with a lower level of anisotropic absorption compared to laser scattering by BF samples. As a result, the sensitivity of the BF polycrystalline component matrix mapping decreases.
It should be noted that the sensitivity of the developed and experimentally tested method of polarization-interference Jones matrix theziography of blood facies in the diagnosis of early stages of papillary thyroid cancer can be improved by further improving the algorithmic apparatus to eliminate the influence of the depolarized background during the reconstruction of the anisotropy parameters of polycrystalline architecture.
5.2. Information Analysis of the Diagnostic Efficiency of Matrix Polarization-Interference Methods
The information analysis of the experimental results uses a set of operational characteristics from evidence-based medicine [60,61]:
- Sensitivity ()—is the proportion of true positive results () of the diagnostic method among all samples in the experimental group 2 (); —false negative results
- Specificity ()—is the proportion of true negative results () of the method among all samples in the control group 1 (); —false positive results
- Accuracy ()—is the proportion of correct results () of the test among all samples ()If , then is referred to as balanced accuracy.
To assess the levels of diagnostic accuracy and differentiation of changes in the parameters of optical anisotropy of polycrystalline films of blood facies, we used the classification given in [61]—Table 6. This provides the possibility of conducting a comparative analysis of the diagnostic efficiency of the polarization-interference Jones matrix theziography method with the data of 3D Mueller matrix studies of pathological and necrotic changes in the optical anisotropy of biological preparations [34,35].

Table 6.
Threshold balanced accuracy levels.
5.3. Comparative Information Analysis of Jones Matrix Theziography and Mueller Matrix Tomography Data
This section presents the results of a comparative analysis with a group of donors (group 1) of the diagnostic power of Jones matrix theziography and Mueller matrix tomography of blood facies in early diagnostics of stage 1 (the formation develops inside the gland; the organ capsule is not deformed and symptoms do not appear, group 2); detection of stage 2 (proliferation of nodes and deformation of the capsule, groups 3–26 samples) of thyroid cancer and differentiation of cancer stages (group 2 and group 3). The studies were conducted in the most sensitive phase plane , Table 7.

Table 7.
Operational characteristics of the diagnostic power of the Jones matrix theziography and Mueller matrix tomography of blood facies methods.
The following maximum levels of balanced accuracy for papillary thyroid cancer diagnostics have been established.
- Jones matrix theziography (stage 1):
- linear birefringence —good level 88.5% ();
- circular birefringence —very good level 90.4% ();
- linear dichroism —good level 82.7% ();
- circular dichroism —good level 88.5% ().
- Mueller matrix tomography (stage 1)—unsatisfactory accuracy for tomograms of linear and circular birefringence and dichroism.
- Jones matrix theziography (stage 2):
- linear birefringence —very good level 94.2% ();
- circular birefringence —excellent level 96.2% ();
- linear dichroism —very good level 92.3% ();
- circular dichroism —very good level 94.2% ().
- Mueller matrix tomography (stage 2):
- linear birefringence —good level 86.5% ();
- circular birefringence —good level 88.2% ();
- linear and circular dichroism —unsatisfactory level ().
The following maximum levels of balanced accuracy of differentiation of papillary thyroid cancer stages were established.
- Jones matrix theziography (stages 2 and 3):
- linear birefringence —very good level 92.3% ();
- circular birefringence —very good level 94.2% ();
- linear dichroism —very good level 90.4% ();
- circular dichroism —very good level 92.3% ().
- Mueller matrix diffuse tomography (stages 2 and 3):
- linear birefringence —good level 82.7% ();
- circular birefringence —good level 84.6% ();
- linear and circular dichroism —unsatisfactory level ().
6. Prospects for Further Research
In order to expand the functionality and increase the sensitivity of the developed technique of laser polarization-interference theziography of blood facies, the following set of theoretical and experimental studies will be implemented:
- Modernization of the algorithmic description of the processes of formation of object fields of complex amplitudes by using the logarithmic decomposition [62,63,64,65] of the Jones matrix on the basis of differential matrices of the first (single scattering) and second (diffuse component) components. This will ensure the possibility of almost complete elimination of the influence of the depolarized background and will maximally increase the sensitivity, specificity, and accuracy of differential diagnostics cancer stages.
- The developed technique of polarization-interference Jones matrix differential theziography of blood facies will be tested in diagnostics of various benign and malignant pathologies of the thyroid gland—nodular goiter, autoimmune thyroiditis, and papillary cancer of stages 1–4.
- Diagnostically relevant relationships between Jones matrix theziograms and the features of the polycrystalline architectonics of the facies of other types of biological fluids—saliva (laryngeal cancer), bile (cholecystitis, cholelithiasis), urine (albuminuria), and synovial fluid (joint inflammation) will be determined and studied.
- In order to increase the reliability of the data obtained using the polarization-interference Jones matrix theziography method, additional diagnostic markers will be developed within the framework of correlation (statistical moments that characterize the distribution of autocorrelation functions), wavelet (distribution of the amplitudes of the wavelet coefficients of optical anisotropy maps), and fractal (spectra of singularities of the distributions of optical anisotropy parameters) analysis.
7. Conclusions
The main fundamental result of the conducted research is a new polarization-interference multifunctional technique of laser Jones matrix theziography of the polycrystalline structure of supramolecular networks of dehydrated blood films was developed. This method increased the sensitivity and expanded the functional capabilities of Mueller matrix tomography, which provided the possibility of minimally invasive early diagnosis of asymptomatic stage 1 papillary cancer, as well as differentiation of its first and second stages.
An equally important, “instrumental” result is the possibility of a more express (four dimensions) in comparison with Mueller matrix (eight dimensions) direct polarization-interference extraction of Jones matrix images from phase-stationary speckle fields.
As a result, a set of blood facies polycrystalline component phase (birefringence—) and amplitude (dichroism—) anisotropy integral and layered maps () was obtained and physically analyzed.
Regularities and statistical scenarios of phase transformations in the structure of holographically reconstructed theziograms of optical anisotropy of blood facies have been established—.
The most sensitive markers to changes in the layer–by–layer topographic structure of blood facies phase and amplitude anisotropy are established—the third- and fourth-order statistical moments.
The main advantages of the Jones matrix method in comparison with the Mueller matrix diffuse tomography technique are shown, as follows:
- high accuracy of early diagnostics (stage 1: and ) of papillary cancer at its asymptomatic stage;
- excellent detection rate of stage 2 papillary cancer: and ) of cancer diagnostics
- very good accuracy ( and ) of differentiation of papillary thyroid cancer stages.
Author Contributions
Conceptualization, O.U. and Y.U.; methodology, L.B.; software, A.D. and M.G.; validation, O.U., Y.U. and L.B.; formal analysis, I.S.; investigation, O.B.; resources, Y.R. and N.P.; data curation, V.B.; writing—original draft preparation, O.U.; writing—review and editing, Y.U.; visualization, O.S.; supervision, I.M.; project administration, O.U.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Ethics Committee of Bukovinian State Medical University (protocol code 7 from 6 June 2024).
Informed Consent Statement
The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Acknowledgments
Authors acknowledge the support from the National Research Foundation of Ukraine; Project 2023.01/0174.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hunter, R. Foundations of Colloid Science; Oxford University Press: New York, 2004; p. 806. [Google Scholar]
- Chen, X.; Chen, P.G.; Ouazzani, J.; Liu, Q. Numerical simulations of sessile droplet evaporating on heated substrate. Eur. Phys. J. Spec. Top. 2017, 226, 1325–1335. [Google Scholar] [CrossRef]
- Dash, S.; Garimella, S.V. Droplet evaporation on heated hydrophobic and superhydrophobic surfaces. Phys. Rev. E 2014, 89, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Gleason, K.; Putnam, S.A. Microdroplet evaporation with a forced pinned contact line. Langmuir 2014, 30, 10548–10555. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Larson, R.G. Evaporation of a sessile droplet on a substrate. J. Phys. Chem. B 2020, 106, 1334–1344. [Google Scholar] [CrossRef]
- Serra, J. Image Analysis and Mathematical Morphology; Academic Press: New York, NY, USA, 1988; 411p. [Google Scholar]
- Shirvaikar, M.; Trivedi, M. Developing texture-based image clutter measures for object detection. Opt. Eng. 1992, 31, 2628–2639. [Google Scholar] [CrossRef]
- Thiele, U. Patterned deposition at moving contact lines. Adv. Colloid. Interface Sci. 2014, 206, 399–413. [Google Scholar] [CrossRef] [PubMed]
- Sabarth, E.; Williams, H.N. Sensitive Crystallization Process as Demonstration of Formative Forces in the Blood, 2nd ed.; Anthroposophic Press: Spring Valley, NY, USA, 1975. [Google Scholar]
- Kuczlowski, J.; Zaorski, P.; Betlejewski, A. Crystallization test in patients with head and neck neoplasms. Otolaryngol. Pol. 1995, 49 (Suppl. S20), 121–124. [Google Scholar]
- Angelsky, O.V.; Ushenko, A.G.; Ushenko, Y.A.; Pishak, V.P. Statistical and fractal structure of biological tissue Mueller matrix images. In Optical Correlation Techniques and Applications; SPIE Publications: Bellingham, WA, USA, 2007; pp. 213–265. [Google Scholar]
- Ushenko, A.G.; Angelsky, P.O.; Sidor, M.; Marchuk, Y.F.; Andreychuk, D.R. Spatial-frequency selection of complex degree of coherence of laser images of blood plasma in diagnostics and differentiation of pathological states of human organism. Appl. Opt. 2014, 53, B172–B180. [Google Scholar] [CrossRef]
- Garazdyuk, M.S.; Bachinskyi, V.T.; Vanchulyak, O.Y.; Ushenko, A.G.; Dubolazov, O.V.; Gorsky, M.P. Polarization-phase images of liquor polycrystalline films in determining time of death. Appl. Opt. 2016, 55, B67–B71. [Google Scholar] [CrossRef] [PubMed]
- Ushenko, V.A.; Pavlyukovich, N.D.; Trifonyuk, L. Spatial-Frequency Azimuthally stable Cartography of Biological Polycrystalline Networks. Int. J. Opt. 2013, 7, 683174. [Google Scholar] [CrossRef]
- Dubolazov, A.V.; Pashkovskaya, N.V.; Ushenko, Y.A.; Marchuk, Y.F.; Ushenko, V.A.; Novakovskaya, O.Y. Birefringence images of polycrystalline films of human urine in early diagnostics of kidney pathology. Appl. Opt. 2016, 55, B85–B90. [Google Scholar] [CrossRef]
- Ushenko, A.G.; Pashkovskaya, N.V.; Dubolazov, O.V.; Ushenko, Y.; Marchuk, Y.; Ushenko, V. Mueller Matrix Images of Polycrystalline Films of Human Biological Fluids. Rom. Rep. Phys. 2015, 67, 1467–1479. [Google Scholar]
- Wang, L.V.; Wu, H.-I. Biomedical Optics. Biomedical Optics: Principles and Imaging; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; 362p. [Google Scholar]
- Ghosh, N. Tissue polarimetry: Concepts, challenges, applications, and outlook. J. Biomed. Opt. 2011, 16, 110801. [Google Scholar] [CrossRef] [PubMed]
- Jacques, S.L. Polarized light imaging of biological tissues. In Handbook of Biomedical Optics; Boas, D., Pitris, C., Ramanujam, N., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 649–669. [Google Scholar]
- Vitkin, A.; Ghosh, N.; de Martino, A. Tissue Polarimetry. In Photonics: Scientific Foundations, Technology and Applications; Andrews, D.L., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015; pp. 239–321. [Google Scholar]
- de Boer, J.F.; Milner, T.E. Review of polarization sensitive optical coherence tomography and Stokes vector determination. J. Biomed. Opt. 2002, 7, 359–371. [Google Scholar] [CrossRef] [PubMed]
- Spandana, K.U.; Mahato, K.K.; Mazumder, N. Polarization-resolved Stokes-Mueller imaging: A review of technology and applications. Lasers Med. Sci. 2019, 34, 1283–1293. [Google Scholar]
- He, Y.; Li, K.; Li, W.; Qiu, Y.; Li, D.; Wang, C.; Tang, Q.; Li, Z. Polarization coherency matrix tomography. J. Biophotonics 2023, 16, e202300093. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Yuan, Z.; Hu, M.; Liang, Y. Zebrafish brain and skull imaging based on polarization-sensitive optical coherence tomography. J. Biophotonics 2022, 15, e202200112. [Google Scholar] [CrossRef]
- Park, J.E.; Xin, Z.; Kwon, D.Y.; Kim, S.W.; Lee, H.; Jung, M.J.; Tang, S.; Ko, T.Y.; Choi, J.H.; Kim, J.H.; et al. Application of Polarization Sensitive-Optical Coherence Tomography to the Assessment of Phase Retardation in Subpleural Cancer in Rabbits. Tissue Eng. Regen. Med. 2021, 18, 61–69. [Google Scholar] [CrossRef]
- Willemse, J.; Gräfe, M.G.O.; Verbraak, F.D.; de Boer, J.F. In Vivo 3D Determination of Peripapillary Scleral and Retinal Layer Architecture Using Polarization-Sensitive Optical Coherence Tomography. Transl. Vis. Sci. Technol. 2020, 9, 21. [Google Scholar] [CrossRef] [PubMed]
- Baumann, B.; Augustin, M.; Lichtenegger, A.; Harper, D.; Muck, M.; Eugui, P.; Wartak, A.; Pircher, M.; Hitzenberger, C. Polarization-sensitive optical coherence tomography imaging of the anterior mouse eye. J. Biomed. Opt. 2018, 23, 086005. [Google Scholar] [CrossRef] [PubMed]
- Hariri, L.P.; Adams, D.C.; Applegate, M.B.; Miller, A.J.; Roop, B.W.; Villiger, M.; Bouma, B.E.; Suter, M.J. Distinguishing Tumor from Associated Fibrosis to Increase Diagnostic Biopsy Yield with Polarization-Sensitive Optical Coherence Tomography. Clin. Cancer Res. 2019, 25, 5242–5249. [Google Scholar] [CrossRef] [PubMed]
- Tao, K.; Sun, K.; Ding, Z.; Ma, Y.; Kuang, H.; Zhao, H.; Lai, T.; Zhou, Y.; Liu, T. Catheter-Based Polarization Sensitive Optical Coherence Tomography Using Similar Mueller Matrix Method. IEEE Trans. Biomed. Eng. 2020, 67, 60–68. [Google Scholar] [CrossRef]
- Ushenko, O.G.; Grytsyuk, M.; Ushenko, V.O.; Bodnar, G.B.; Vanchulyak, O. Differential 3D Mueller-matrix mapping of optically anisotropic depolarizing biological layers. In Proceedings of the Thirteenth International Conference on Correlation Optics, Chernivtsi, Ukraine, 11–15 September 2017; Volume 10612, pp. 395–402. [Google Scholar]
- Padure, A.; Bakun, O.; Mikirin, I.; Dubolazov, O.; Soltys, I.; Olar, O.; Ushenko, Y.; Ushenko, O.; Palii, I.; Kumargazhanova, S. Differential Mueller-matrix mapping of the polycrystalline component of biological tissues of human organs. Inform. Autom. Pomiary Gospod. Ochr. Sr. 2024, 14, 23–27. [Google Scholar] [CrossRef]
- Ushenko, A.; Dubolazov, A.; Zheng, J.; Bakun, O.; Gorsky, M.; Ushenko, Y. Mueller matrix polarization interferometry of optically anisotropic architectonics of biological tissue object fields: The fundamental and applied aspects. Front. Phys. 2023, 11, 1302254. [Google Scholar] [CrossRef]
- Ushenko, A.; Zheng, J.; Gorsky, M.; Dubolazov, A.; Ushenko, Y.; Soltys, I.; Mikirin, I.; Chen, Z.; Wanchuliak, O.; Gordey, I.; et al. 3D digital holographic polarimetry of diffuse optically anisotropic biological tissue object fields. Front. Phys. 2023, 111288935. [Google Scholar] [CrossRef]
- Ushenko, A.; Zheng, J.; Litvinenko, A.; Gorsky, M.; Wanchuliak, O. A Dubolazov 3D digital polarization-holographic wavelet histology in determining the duration of mechanical damage to the myocardium. J. Biophotonics 2024, 17, e202300372. [Google Scholar]
- Ushenko, A.; Dubolazov, A.; Zheng, J.; Litvinenko, A.; Gorsky, M.; Ushenko, Y.; Soltys, I.; Salega, O.; Chen, Z.; Wanchuliak, O. 3D polarization-interference holographic histology for wavelet-based differentiation of the polycrystalline component of biological tissues with different necrotic states. J. Biomed. Opt. 2024, 29, 052920. [Google Scholar] [CrossRef]
- Ushenko, V.; Sdobnov, A.; Syvokorovskaya, A.; Dubolazov, A.; Vanchulyak, O.; Ushenko, A.; Ushenko, Y.; Gorsky, M.; Sidor, M.; Bykov, A.; et al. 3D Mueller-matrix diffusive tomography of polycrystalline blood plasma films for cancer diagnosis. Photonics 2018, 5, 54. [Google Scholar] [CrossRef]
- Lee, H.R.; Lotz, C.; Groeber-Becker, K.; Dembski, S.; Novikova, T. Digital histology with Mueller polarimetry and FastDBSCAN. Appl. Opt. 2022, 61, 9616–9624. [Google Scholar] [CrossRef]
- Kim, M.; Lee, H.R.; Ossikovski, R.; Malfait-Jobart, A.; Lamarque, D.; Novikova, T. Optical diagnosis of gastric tissue biopsies with Mueller microscopy and statistical analysis. J. Eur. Opt. Soc. Rapid Publ. 2022, 18, 10. [Google Scholar] [CrossRef]
- Lee, H.R.; Li, P.; Yoo, T.S.H.; Lotz, C.; Groeber-Becker, F.K.; Dembski, S.; Garcia-Caurel, E.; Ossikovski, R.; Ma, H.; Novikova, T. Digital histology with Mueller microscopy: How to mitigate an impact of tissue cut thickness fluctuations. J. Biomed. Opt. 2019, 24, 076004. [Google Scholar] [CrossRef]
- Li, P.; Lee, H.R.; Chandel, S.; Lotz, C.; Groeber-Becker, F.K.; Dembski, S.; Ossikovski, R.; Ma, H.; Novikova, T. Analysis of tissue microstructure with Mueller microscopy: Logarithmic decomposition and Monte Carlo modeling. J. Biomed. Opt. 2020, 25, 015002. [Google Scholar] [CrossRef]
- Lee, H.R.; Yoo, T.S.H.; Li, P.; Lotz, C.; Groeber-Becker, F.K.; Dembski, S.; Garcia-Caurel, E.; Ossikovski, R.; Novikova, T. Mueller microscopy of anisotropic scattering media: Theory and experiments. Proc. SPIE 2018, 10677, 1067718. [Google Scholar]
- Ma, H.; He, H.; Ramella-Roman, J.C. Mueller matrix microscopy. In Polarized Light in Biomedical Imaging and Sensing; Ramella-Roman, J.C., Novikova, T., Eds.; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Zabolotna, N.I.; Pavlov, S.V.; Ushenko, A.G.; Karachevtsev, A.O.; Savich, V.O.; Sobko, O.V.; Olar, O.V. System of the phase tomography of optically anisotropic polycrystalline films of biological fluids. Proc. SPIE 2014, 9166, 916616. [Google Scholar]
- Angelsky, O.V.; Polyanskii, P.V.; Mokhun, I.I.; Zenkova, C.Y.; Bogatyryova, H.V.; Felde, C.V.; Bachinskiy, V.T.; Boichuk, T.M.; Ushenko, A.G. Optical measurements: Polarization and coherence of light fields. In Modern Metrology Concerns; INTECH Open Access Publisher: London, UK, 2012. [Google Scholar]
- Eftimie, L.G.; Glogojeanu, R.R.; Tejaswee, A.; Gheorghita, P.; Stanciu, S.G.; Chirila, A.; Stanciu, G.A.; Paul, A.; Hristu, R. Differential diagnosis of thyroid nodule capsules using random forest guided selection of image features. Sci. Rep. 2022, 12, 21636. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.-T.; Ma, B.-Y.; Chen, Y. A narrative review of deep learning in thyroid imaging: Current progress and future prospects. Quant. Imaging Med. Surg. 2024, 14, 2069–2088. [Google Scholar] [CrossRef]
- Tokarz, D.; Cisek, R.; Joseph, A.; Asa, S.L.; Wilson, B.C.; Barzda, V. Characterization of pathological thyroid tissue using polarization-sensitive second harmonic generation microscopy. Lab. Investig. 2020, 100, 1280–1287. [Google Scholar] [CrossRef]
- Cisek, R.; Joseph, A.; Harvey, M.; Tokarz, D. Polarization-Sensitive Second Harmonic Generation Microscopy for Investigations of Diseased Collagenous Tissues. Front. Phys. Sec. Opt. Photonics 2021, 9, 726996. [Google Scholar] [CrossRef]
- Hristu, R.; Eftimie, L.G.; Stanciu, S.G.; Tranca, D.E.; Paun, B.; Sajin, M.; Stanciu, G.A. Quantitative second harmonic generation microscopy for the structural characterization of capsular collagen in thyroid neoplasms. Biomed. Opt. Express. 2018, 9, 3923–3936. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.R. New calculus for the treatment of optical systems. VII. Properties of the N-matrices. J. Opt. Soc. Am. 1948, 38, 671–685. [Google Scholar] [CrossRef]
- Azzam, R.M.A. Propagation of partially depolarized light through anisotropic media with or without depolarization. A differential 4x4 matrix calculus. J. Opt. Soc. Am. 1978, 68, 1756–1767. [Google Scholar] [CrossRef]
- Arteaga, O.; Canillas, A. Analytic inversion of the Mueller-Jones polarization matrices for homogeneous media. Opt. Lett. 2010, 35, 559–561. [Google Scholar] [CrossRef] [PubMed]
- Barakat, R. Exponential versions of the Jones and Mueller–Jones polarization matrices. J. Opt. Soc. Am. A 1996, 13, 158–163. [Google Scholar] [CrossRef]
- Vladimir, Z.; Wang, J.B.; Yan, X.H. Human Blood Plasma Crystal and Molecular Biocolloid Textures—Dismetabolism and Genetic Breaches. Nat. Sci. J. Xiangtan Univ. 2001, 23, 118–127. [Google Scholar]
- Killeen, A.A.; Ossina, N.; McGlennen, R.C.; Minnerath, S.; Borgos, J.; Alexandrov, V.; Sarvazyan, A. Protein self-organization patterns in dried serum reveal changes in B-cell disorders. Mol. Diag. Ther. 2006, 10, 371–380. [Google Scholar] [CrossRef] [PubMed]
- Brutin, D.; Sobac, B.; Loquet, B.; Sampol, J. Pattern formation in drying drops of blood. J. Fluid Mech. 2011, 667, 85–95. [Google Scholar] [CrossRef]
- Marchesini, R.; Bertoni, A.; Andreola, S.; Melloni, E.; Sichirollo, A.E. Extinction and absorption coefficients and scattering phase functions of human tissues in vitro. Appl. Opt. 1989, 28, 2318–2324. [Google Scholar] [CrossRef] [PubMed]
- Edwards, D.K.; Gier, J.T.; Nelson, K.E.; Roddick, R.D. Integrating Sphere for Imperfectly Diffuse Samples. J. Opt. Soc. Am. 1961, 51, 1279–1288. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Properties of Laser Speckle Patterns; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar] [CrossRef]
- Robinson, S.P. Principles of Forensic Medicine; Greenwich Medical Media: London, UK, 1996. [Google Scholar]
- Cassidy, L.D. Basic concepts of statistical analysis for surgical research. J. Surg. Res. 2005, 128, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Ortega-Quijano, N.; Arce-Diego, J.L. Mueller matrix differential decomposition. Opt. Lett. 2011, 36, 1942–1944. [Google Scholar] [CrossRef] [PubMed]
- Ortega-Quijano, N.; Arce-Diego, J.L. Depolarizing differential Mueller matrices. Opt. Lett. 2011, 36, 2429–2431. [Google Scholar] [CrossRef]
- Ossikovski, R.; Devlaminck, V. General criterion for the physical realizability of the differential Mueller matrix. Opt. Lett. 2014, 39, 1216–1219. [Google Scholar] [CrossRef] [PubMed]
- Ossikovski, R.; Arteaga, O. Statistical meaning of the differential Mueller matrix of depolarizing homogeneous media. Opt. Lett. 2014, 39, 4470–4473. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).