A Method to Evaluate Orientation-Dependent Errors in the Center of Contrast Targets Used with Terrestrial Laser Scanners
Abstract
1. Introduction
2. Literature Review
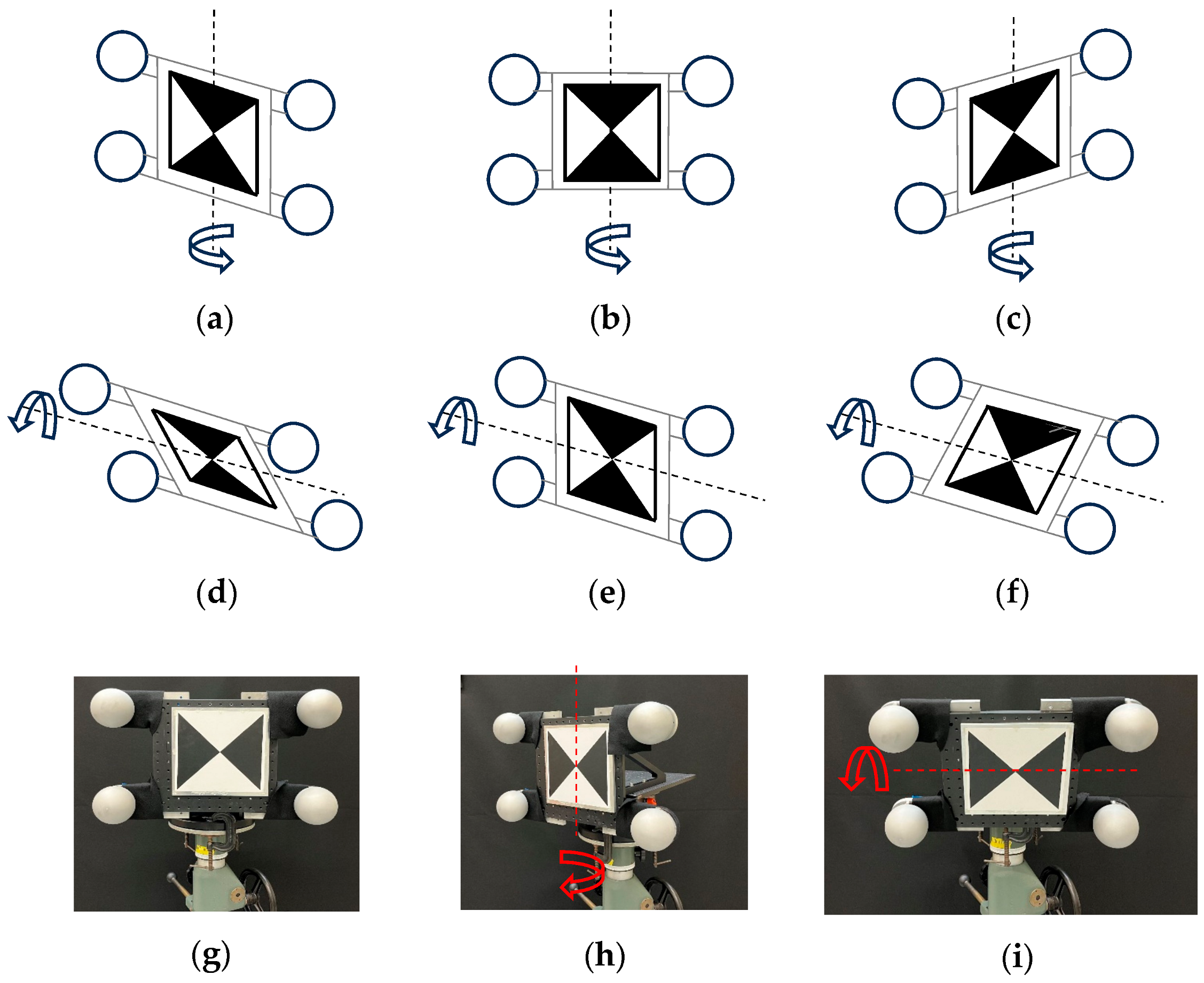
3. Approach
4. Results
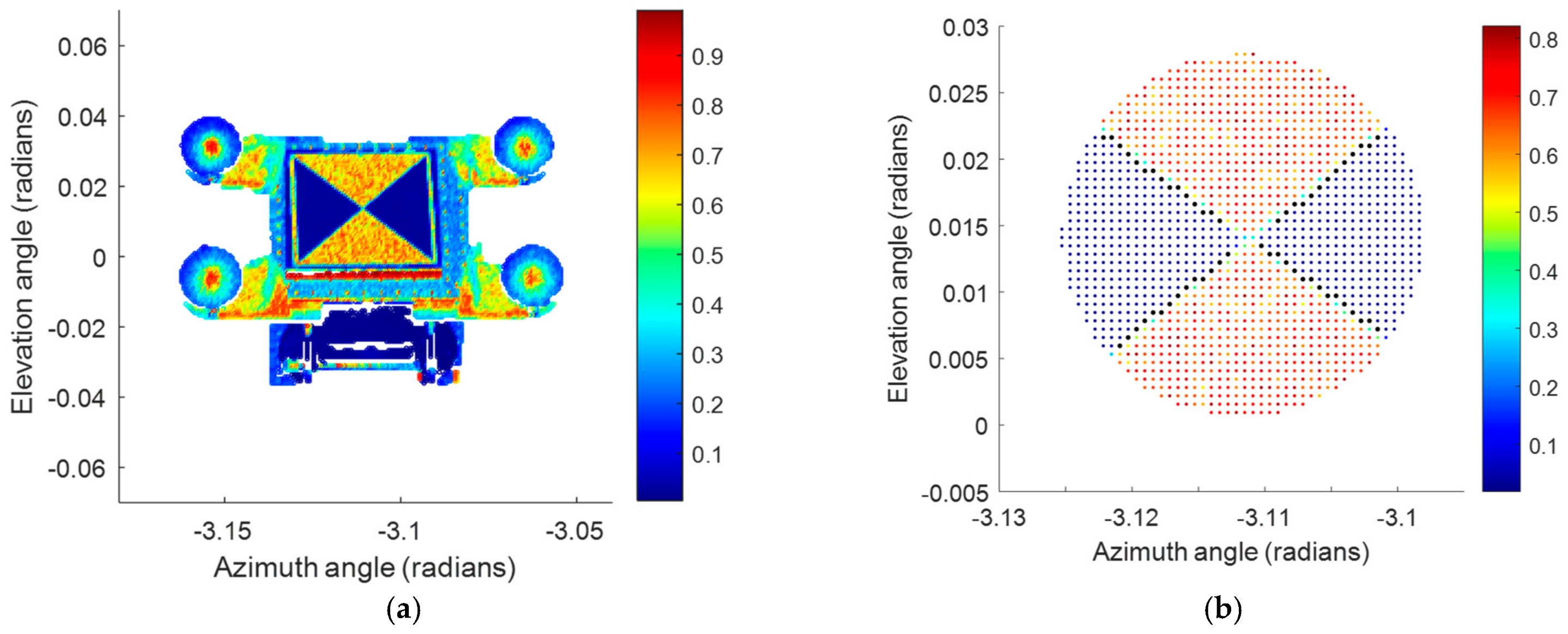
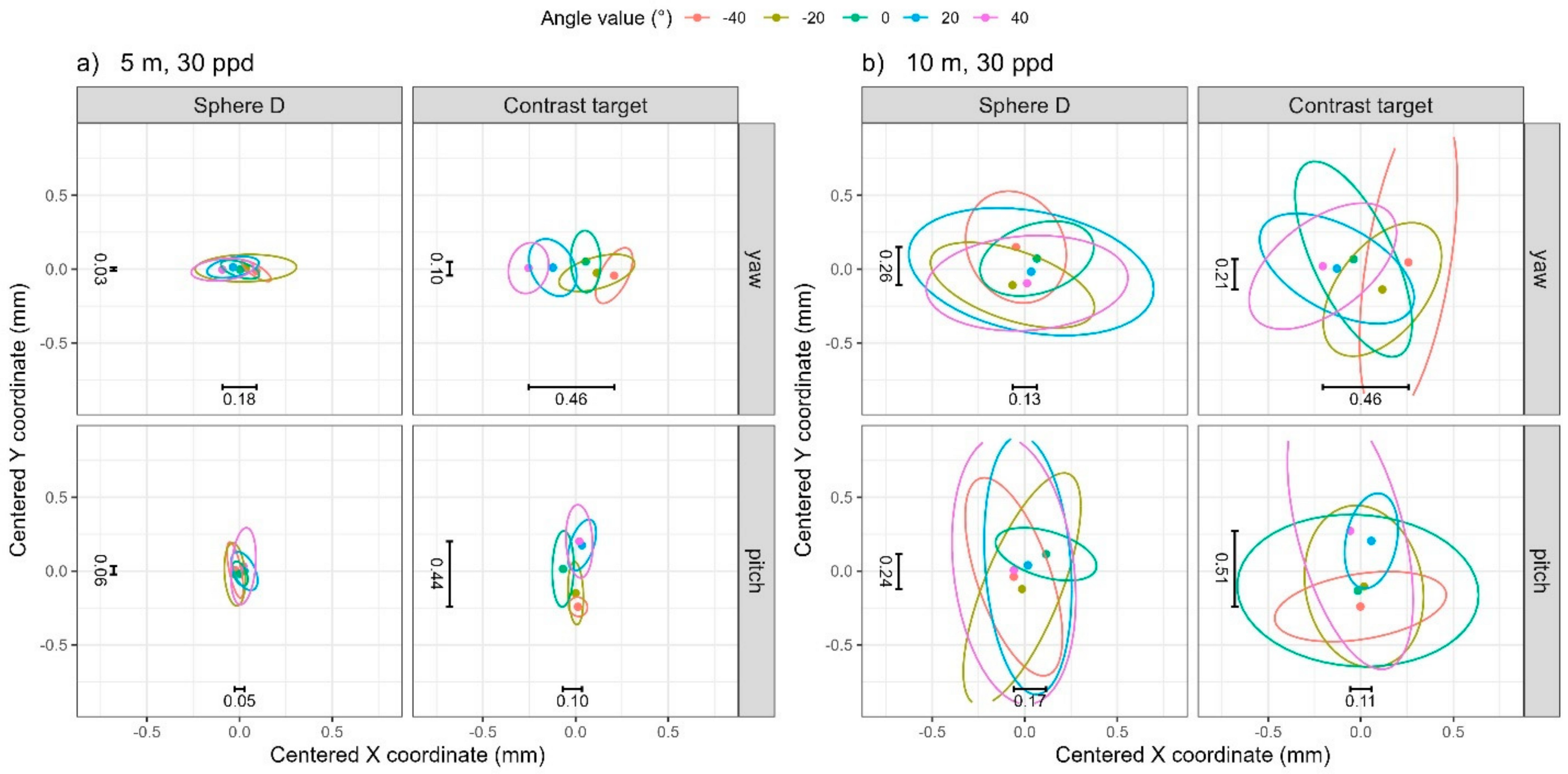
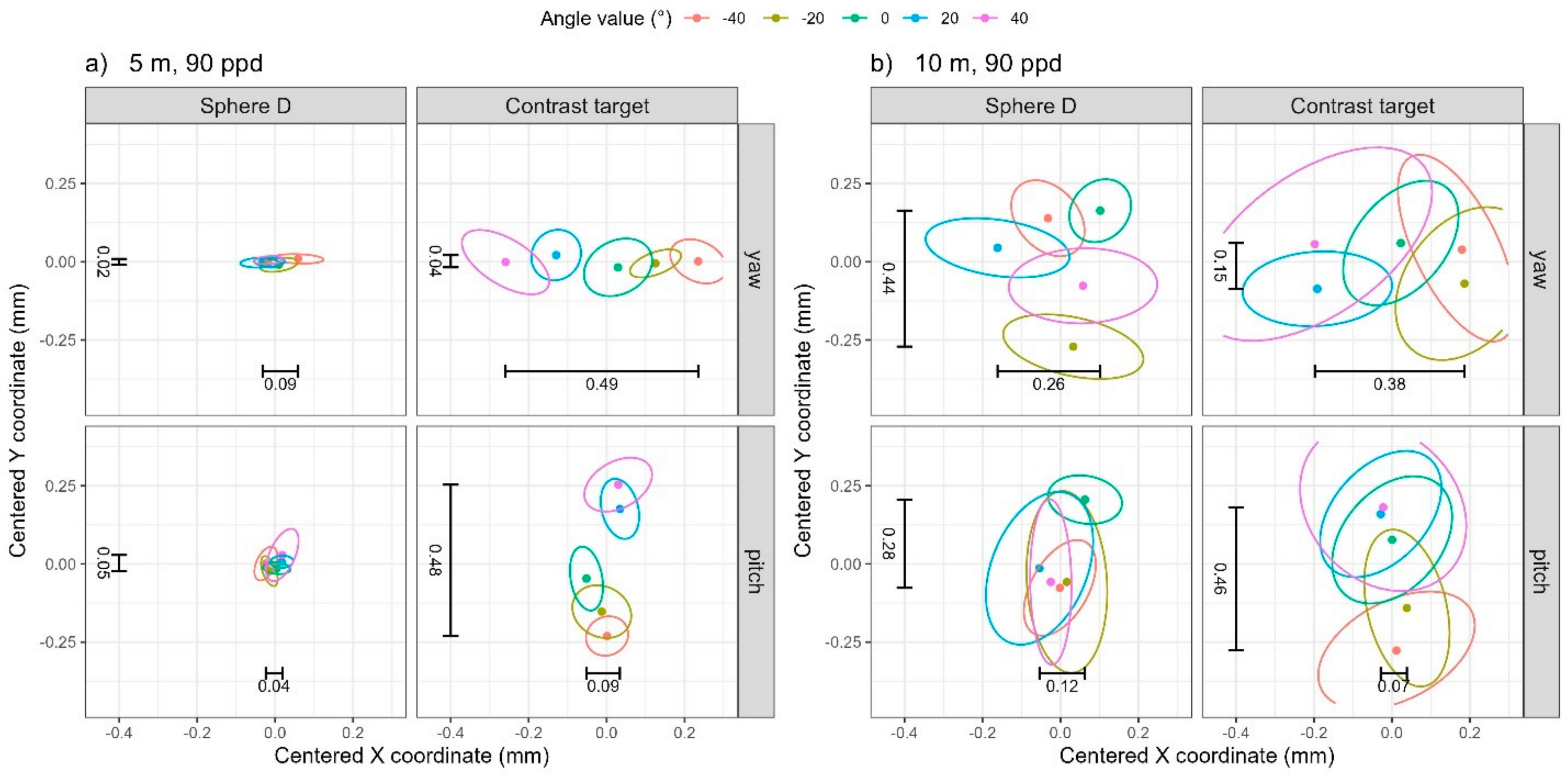
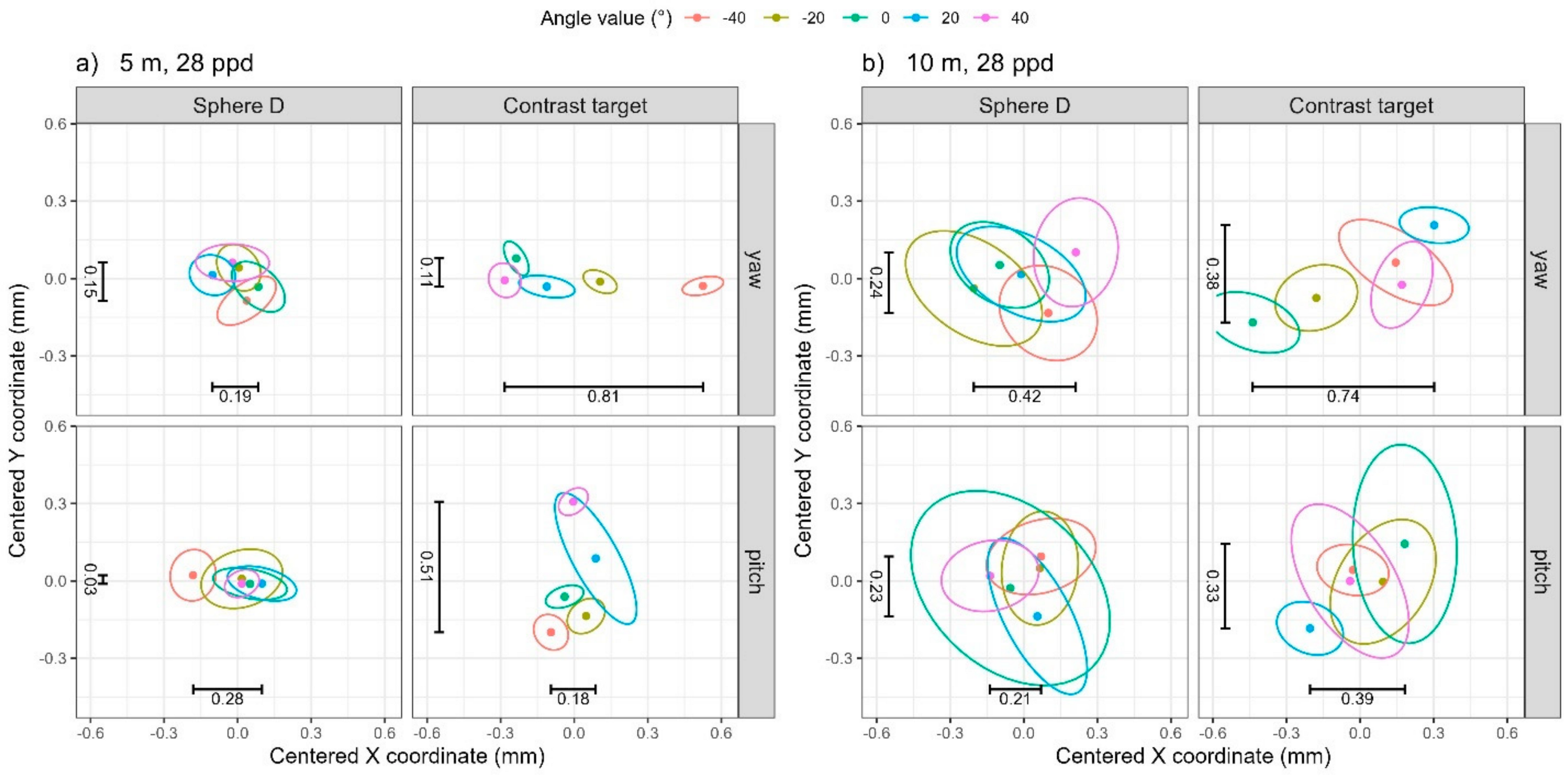
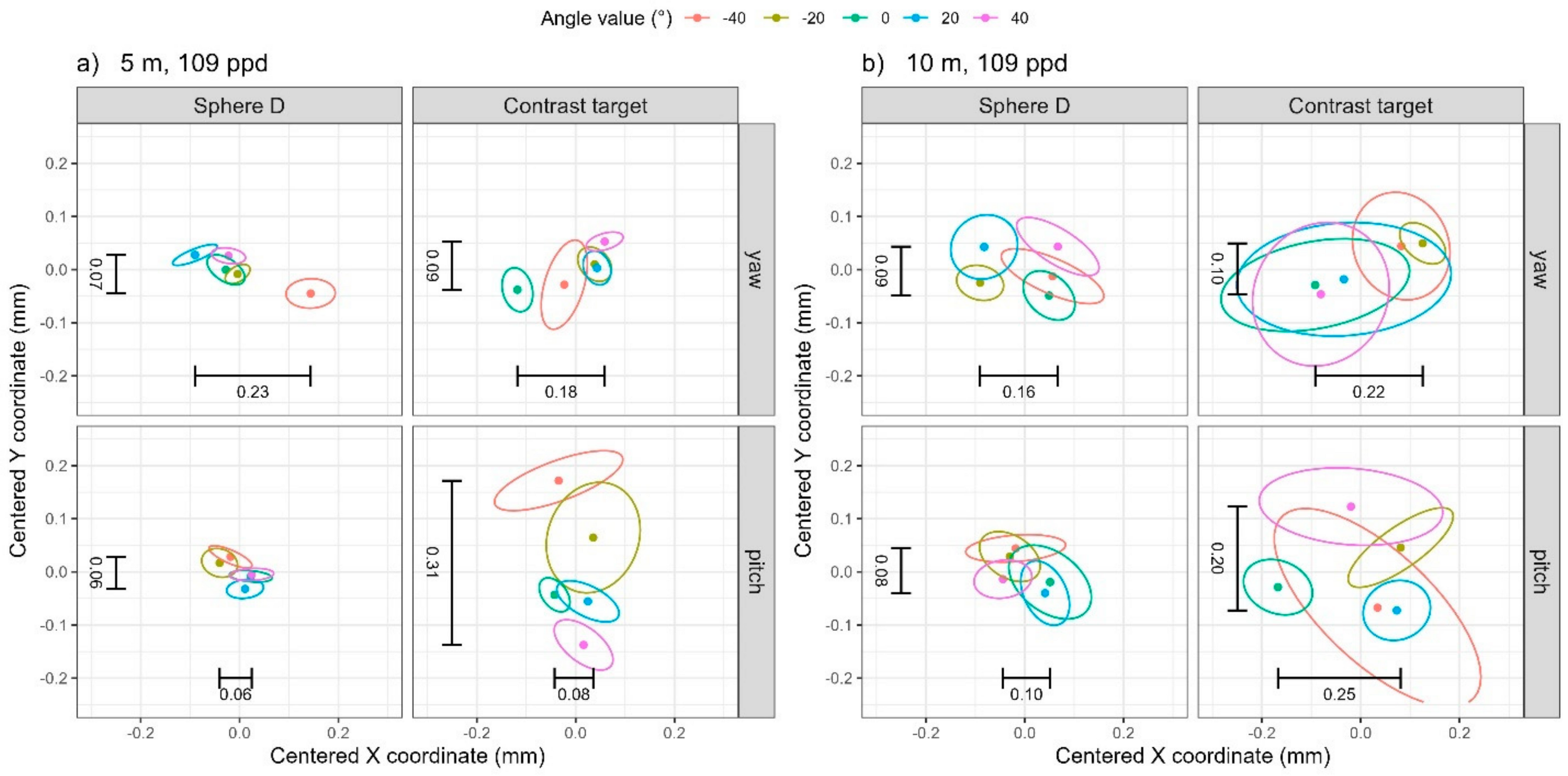
4.1. Visual Summaries of Bivariate Data Through Data Ellipses
4.2. TLS I

| Sphere D | Contrast Target | |||||||
|---|---|---|---|---|---|---|---|---|
| Angle | Distance (m) | Resolution (ppd) | X (mm) | Y (mm) | Z (mm) | X (mm) | Y (mm) | Z (mm) |
| Yaw | 5 | 30 | 0.06 | 0.03 | 0.02 | 0.05 | 0.06 | 0.01 |
| 10 | 30 | 0.16 † | 0.12 | 0.07 | 0.12 | 0.23 | 0.04 | |
| 5 | 90 | 0.02 ‡ | 0.01 | 0.01 | 0.03 | 0.03 | 0.01 | |
| 10 | 90 | 0.05 | 0.04 | 0.03 | 0.07 | 0.08 | 0.02 | |
| Pitch | 5 | 30 | 0.02 | 0.06 | 0.02 | 0.02 | 0.07 | 0.03 |
| 10 | 30 | 0.10 | 0.25 | 0.08 | 0.14 | 0.19 | 0.08 | |
| 5 | 90 | 0.01 | 0.02 | 0.01 | 0.02 | 0.03 | 0.01 | |
| 10 | 90 | 0.03 | 0.08 | 0.03 | 0.06 | 0.08 | 0.03 | |
4.3. TLS II
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Staiger, R. 10 Years of Terrestrial Laser Scanning—Technology, Systems and Applications; GEO-Siberia: Novosibirsk, Russia, 2011. [Google Scholar]
- Shan, J.; Toth, C.K. Topographic Laser Ranging and Scanning: Principles and Processing; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- ASTM E3125–17; Standard Test Method for Evaluating the Point-to-Point Distance Measurement Performance of Spherical Coordinate 3D Imaging Systems in the Medium Range. ASTM International: West Conshohocken, PA, USA, 2017.
- Böhler, W.; Vincent, M.B.; Marbs, A. Investigating laser scanner accuracy. In Proceedings of the XIXth International Symposium, CIPA 2003: New Perspectives to Save Cultural Heritage, Antalya, Turkey, 30 September–4 October 2003. [Google Scholar]
- Schmitz, B.; Kuhlmann, H.; Holst, C. Investigating the resolution capability of terrestrial laser scanners and its impact on the effective number of measurements. ISPRS J. Photogramm. Remote Sens. 2020, 159, 41–52. [Google Scholar] [CrossRef]
- Measurements made in the dimensional metrology laboratory at NIST.
- Website of the Organization for Scientific Area Committees for Forensic Science. Available online: https://www.nist.gov/organization-scientific-area-committees-forensic-science (accessed on 1 December 2024).
- Muralikrishnan, B. Performance evaluation of terrestrial laser scanners—A review. Meas. Sci. Technol. 2021, 32, 072001. [Google Scholar] [CrossRef] [PubMed]
- Abbas, M.A.; Lichti, D.D.; Chong, A.K.; Setan, H.; Majid, Z. An on-site approach for the self-calibration of terrestrial laser scanner. Measurement 2014, 52, 111–123. [Google Scholar] [CrossRef]
- Wang, L.; Muralikrishnan, B.; Rachakonda, P.; Sawyer, D. Determining geometric error model parameters of a terrestrial laser scanner through two-face, length-consistency, and network methods. Meas. Sci. Technol. 2017, 28, 065016. [Google Scholar] [CrossRef] [PubMed]
- Muralikrishnan, B.; Wang, L.; Rachakonda, P.; Sawyer, D. Terrestrial laser scanner geometric error model parameter correlations in the Two-face, Length-consistency, and Network methods of self-calibration. Precis. Eng. 2018, 52, 15–29. [Google Scholar] [CrossRef]
- Medić, T.; Holst, C.; Kuhlmann, K. Towards system calibration of panoramic laser scanners from a single station. Sensors 2017, 17, 1145. [Google Scholar] [CrossRef]
- Shi, S.; Muralikrishnan, B.; Sawyer, D. Terrestial laser scanner calibration and performance evaluation using the network method. Opt. Lasers Eng. 2020, 134, 106298. [Google Scholar] [CrossRef]
- Reshetyuk, Y. A unified approach to self-calibration of terrestrial laser scanners. ISPRS J. Photogramm. Remote Sens. 2010, 65, 445–456. [Google Scholar] [CrossRef]
- García-San-Miguel, D.; Lerma, J.L. Geometric calibration of a terrestrial laser scanner with local additional parameters: An automatic strategy. ISPRS J. Photogramm. Remote Sens. 2013, 79, 122–136. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Ferrucci, M.; Sawyer, D.; Gerner, G.; Lee, V.; Blackburn, C.; Phillips, S.; Petrov, P.; Yakovlev, Y.; Astrelin, A.; et al. Volumetric performance evaluation of a laser scanner based on geometric error model. Precis. Eng. 2015, 40, 139–150. [Google Scholar] [CrossRef]
- Staiger, R. The geometrical quality of terrestrial laser scanner (TLS). In Proceedings of the FIG Working Week 2005 and GSDI-8: From Pharaohs to Geoinformatics, Cairo, Egypt, 16–21 April 2005. [Google Scholar]
- Kersten, T.P.; Mechelke, K.; Lindstaedt, M.; Sternberg, H. Geometric accuracy investigations of the latest terrestrial laser scanning systems. In Proceedings of the FIG Working Week 2008, Integrating Generations, Stockholm, Sweden, 14–19 June 2008. [Google Scholar]
- Wunderlich, T.; Wasmeier, P. Objective Specifications of Terrestrial Laserscanners—A Contribution of the Geodetic Laboratory at the Technische Universität München. Blue Ser. Books Chair Geod. 2013, 21, 1–38. [Google Scholar]
- Walser, B.; Gordon, B. Der laserscanner, eine black-box? In Terrestrisches Laserscanning 2013 (TLS 2013); Schriftenreihe Des DVW; Wissner-Verlag: Augsburg, Germany, 2013; Volume 72, pp. 149–164. [Google Scholar]
- ISO 17123-9; Optics and Optical Instruments—Field Procedures for Testing Geodetic and Surveying Instruments—Part 9: Terrestrial laser scanners. ISO: Geneva, Switzerland, 2018.
- Lee, J.S.; Hong, S.H.; Park, I.S.; Cho, H.S.; Sohn, H.G. Evaluation of geometric error sources for terrestrial laser scanner. J. Korean Soc. Geospat. Inf. Sci. 2016, 24, 79–87. [Google Scholar] [CrossRef]
- Pejić, M.; Ogrizović, V.; Božić, N.; Milovanović, B.; Marošan, S. A simplified procedure of metrological testing of the terrestrial laser scanners. Measurement 2014, 53, 260–269. [Google Scholar] [CrossRef]
- Delčev, S.; Pejić, M.; Gučević, J.; Ogrizović, V. A procedure for accuracy investigation of terrestrial laser scanners. In Proceedings of the 10th IMEKO TC14 Symposium Laser Metrology for Precision Measurement and Inspection in Industry, Braunschweig, Germany, 12–14 September 2011. [Google Scholar]
- Ferrucci, M.; Muralikrishnan, B.; Sawyer, D.; Phillips, S.; Petrov, P.; Yakovlev, Y.; Astrelin, A.; Milligan, S.; Palmateer, J. Evaluation of a laser scanner for large volume coordinate metrology: A comparison of results before and after factory calibration. Meas. Sci. Technol. 2014, 25, 105010. [Google Scholar] [CrossRef]
- Lin, P.; Cheng, X.; Zhou, T.; Liu, C.; Wang, B. A target-based self-calibration method for terrestrial laser scanners and its robust solution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11954–11973. [Google Scholar] [CrossRef]
- Kersten, T.P.; Lindstaedt, M. Geometric accuracy investigations of terrestrial laser scanner systems in the laboratory and in the field. Appl. Geomat. 2022, 14, 421–434. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, S.; Liu, X.; Xu, H.; Wu, Y.; Li, M.; Chen, Y. Registration of laser scanning point clouds: A Review. Sensors 2018, 18, 1641. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppä, J.; et al. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 163, 327–342. [Google Scholar] [CrossRef]
- Akca, D. Full automatic registration of laser scanner point clouds. In Optical 3-D Measurement Techniques VI; Gruen, A., Kahmen, H., Eds.; ETH Zurich: Zurich, Switzerland, 2003; Volume 22–25, pp. 330–337. [Google Scholar]
- Yi, C.; Xing, H.; Wu, Q.; Wei, M.; Wang, B.; Zhou, L. Automatic Detection of Cross-Shaped Targets for Laser Scan Registration. IEEE Access 2018, 6, 8483–8500. [Google Scholar] [CrossRef]
- Becerik-Gerber, B.; Jazizadeh, F.; Kavulya, G.; Calis, G. Assessment of target types and layouts in 3D laser scanning for registration accuracy. Autom. Constr. 2011, 20, 649–658. [Google Scholar] [CrossRef]
- Stenz, U.; Hartmann, J.; Paffenholz, J.-A.; Neumann, I. A framework based on reference data with superordinate accuracy for the quality analysis of terrestrial laser scanning-based multi-sensor-systems. Sensors 2017, 17, 1886. [Google Scholar] [CrossRef]
- Berezowski, V.; Mallett, X.; Moffat, I. Geomatic techniques in forensic science: A review. Sci. Justice 2020, 60, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Raneri, D. Enhancing forensic investigation through the use of modern three-dimensional (3D) imaging technologies for crime scene reconstruction. Aust. J. Forensic Sci. 2018, 50, 697–707. [Google Scholar] [CrossRef]
- NIST Updates. Collaboration with Industry Leads to Improved Forensics Work and Industry Growth. 20 August 2013. Available online: https://www.nist.gov/news-events/news/2013/08/collaboration-industry-leads-improved-forensics-work-and-industry-growth (accessed on 1 December 2024).
- Liscio, E.; Hayden, A.; Moody, J. A comparison of the terrestrial laser scanner & total station for scene documentation. J. Assoc. Crime Scene Reconstr. 2016, 20, 1–8. [Google Scholar]
- Kwan, N.; Liscio, E.; Rogers, T. 3D bloodstain pattern analysis on complex surfaces using the FARO Focus laser scanner. J. Bloodstain Pattern Anal. 2016, 2, 32. [Google Scholar]
- Berezowski, V.; Keller, J.; Liscio, E. 3D documentation of a clandestine grave: A comparison between manual and 3D digital methods. J. Assoc. Crime Scene Reconstr. 2018, 22, 23–37. [Google Scholar]
- Dustin, D.; Liscio, E. Accuracy and repeatability of the laser scanner and total station for crime and accident scene documentation. J. Assoc. Crime Scene Reconstr. 2016, 20, 57–68. [Google Scholar]
- Janßen, J.; Medic, T.; Kuhlmann, H.; Holst, C. Decreasing the uncertainty of the target center estimation at terrestrial laser scanning by choosing the best algorithm and by improving the target design. Remote Sens. 2019, 11, 845. [Google Scholar] [CrossRef]
- Ge, X.; Wunderlich, T. Target identification in terrestrial laser scanning. Surv. Rev. 2014, 47, 129–140. [Google Scholar] [CrossRef]
- Rachakonda, P.; Muralikrishnan, B.; Sawyer, D.; Wang, L. Method to determine the center of a contrast target from terrestrial laser scanner data. In Proceedings of the 32nd Annual Meeting of the Association for Precision Engineering, Charlotte, NC, USA, 29 October–3 November 2017. [Google Scholar]
- Rachakonda, P.; Muralikrishnan, B.; Sawyer, D. Metrological evaluation of contrast target center algorithm for terrestrial laser scanners. Measurement 2019, 134, 15–24. [Google Scholar] [CrossRef]
- Abmayr, T.; Hartl, F.; Hirzinger, G.; Burschka, D.; Frohlich, C. A correlation based target finder for terrestrial laser scanning. J. Appl. Geod. 2008, 2, 131–137. [Google Scholar] [CrossRef]
- Rosa, M. TLS Target Designs Compared in Terms of Center Estimation Accuracy. Diploma Thesis, Technische Universität Wien, Vienna, Austria, 2023. [Google Scholar] [CrossRef]
- Fryskowska, A. An improvement in the identification of the centres of checkerboard targets in point clouds using terrestrial laser scanning. Sensors 2019, 19, 938. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, Z.; Zhang, Q.; Wu, E.; Huang, H. Fast extraction algorithm of planar targets based on point cloud data for monitoring the synchronization of bridge jacking displacements. Struct. Control. Health Monit. 2024, 2024, 9687805. [Google Scholar] [CrossRef]
- Friendly, M.; Monette, G.; Fox, J. Elliptical insights: Understanding statistical methods through elliptical geometry. Stat. Sci. 2013, 28, 1–39. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 1 December 2024).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]



| Sphere D | Contrast Target | |||||||
|---|---|---|---|---|---|---|---|---|
| Angle | Distance (m) | Resolution (ppd) | X (mm) | Y (mm) | Z (mm) | X (mm) | Y (mm) | Z (mm) |
| Yaw | 5 | 30 | 0.18 | 0.03 | 0.02 | 0.46 | 0.10 | 0.07 |
| 10 | 30 | 0.13 | 0.26 | 0.10 | 0.46 | 0.21 | 0.10 | |
| 5 | 90 | 0.09 | 0.02 | 0.00 | 0.49 | 0.04 | 0.12 | |
| 10 | 90 | 0.26 | 0.44 | 0.08 | 0.38 | 0.15 | 0.06 | |
| Pitch | 5 | 30 | 0.05 | 0.06 | 0.04 | 0.10 | 0.44 | 0.18 |
| 10 | 30 | 0.17 | 0.24 | 0.04 | 0.11 | 0.51 | 0.18 | |
| 5 | 90 | 0.04 | 0.05 | 0.04 | 0.09 | 0.48 | 0.15 | |
| 10 | 90 | 0.12 | 0.28 | 0.13 | 0.07 | 0.46 | 0.12 | |
| Sphere D | Contrast Target | |||||||
|---|---|---|---|---|---|---|---|---|
| Angle | Distance (m) | Resolution (ppd) | X (mm) | Y (mm) | Z (mm) | X (mm) | Y (mm) | Z (mm) |
| Yaw | 5 | 28 | 0.04 | 0.03 | 0.03 | 0.03 | 0.02 | 0.02 |
| 10 | 28 | 0.08 † | 0.07 | 0.07 | 0.06 | 0.05 | 0.04 | |
| 5 | 109 | 0.01 ‡ | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | |
| 10 | 109 | 0.03 | 0.02 | 0.02 | 0.05 | 0.03 | 0.03 | |
| Pitch | 5 | 28 | 0.04 | 0.03 | 0.03 | 0.03 | 0.04 | 0.03 |
| 10 | 28 | 0.09 | 0.09 | 0.06 | 0.07 | 0.09 | 0.03 | |
| 5 | 109 | 0.01 | 0.01 | 0.01 | 0.03 | 0.02 | 0.03 | |
| 10 | 109 | 0.03 | 0.02 | 0.02 | 0.05 | 0.03 | 0.04 | |
| Sphere D | Contrast Target | |||||||
|---|---|---|---|---|---|---|---|---|
| Angle | Distance (m) | Resolution (ppm) | X (mm) | Y (mm) | Z (mm) | X (mm) | Y (mm) | Z (mm) |
| Yaw | 5 | 28 | 0.19 | 0.15 | 0.13 | 0.81 | 0.11 | 0.13 |
| 10 | 28 | 0.42 | 0.24 | 0.25 | 0.74 | 0.38 | 0.21 | |
| 5 | 109 | 0.23 | 0.07 | 0.04 | 0.18 | 0.09 | 0.28 | |
| 10 | 109 | 0.16 | 0.09 | 0.13 | 0.22 | 0.10 | 0.19 | |
| Pitch | 5 | 28 | 0.28 | 0.03 | 0.05 | 0.18 | 0.51 | 0.18 |
| 10 | 28 | 0.21 | 0.23 | 0.24 | 0.39 | 0.33 | 0.47 | |
| 5 | 109 | 0.06 | 0.06 | 0.06 | 0.08 | 0.31 | 0.22 | |
| 10 | 109 | 0.10 | 0.08 | 0.07 | 0.25 | 0.20 | 0.18 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muralikrishnan, B.; Lu, X.; Gregg, M.; Shilling, M.; Czapla, B. A Method to Evaluate Orientation-Dependent Errors in the Center of Contrast Targets Used with Terrestrial Laser Scanners. Sensors 2025, 25, 505. https://doi.org/10.3390/s25020505
Muralikrishnan B, Lu X, Gregg M, Shilling M, Czapla B. A Method to Evaluate Orientation-Dependent Errors in the Center of Contrast Targets Used with Terrestrial Laser Scanners. Sensors. 2025; 25(2):505. https://doi.org/10.3390/s25020505
Chicago/Turabian StyleMuralikrishnan, Bala, Xinsu Lu, Mary Gregg, Meghan Shilling, and Braden Czapla. 2025. "A Method to Evaluate Orientation-Dependent Errors in the Center of Contrast Targets Used with Terrestrial Laser Scanners" Sensors 25, no. 2: 505. https://doi.org/10.3390/s25020505
APA StyleMuralikrishnan, B., Lu, X., Gregg, M., Shilling, M., & Czapla, B. (2025). A Method to Evaluate Orientation-Dependent Errors in the Center of Contrast Targets Used with Terrestrial Laser Scanners. Sensors, 25(2), 505. https://doi.org/10.3390/s25020505






